研究静电场中导电液滴的电场效应是电流体动力学(electro-hydro dynamics, EHD)领域的一个关键问题, 过去的几十年里, 关于电场对流体影响的理论研究从未停止. 1884年, 瑞利极限[1]的提出揭开了EHD研究的新篇章, O’konski等[2]最先提出的理想介电模型表明, 极性和非极性液滴在电场中都会发生扁长型变形, 但其他研究者发现, 液滴也会发生扁圆型变形, 在此基础上, Taylor提出了漏介质模型[3], 可以成功地预测液滴的变形模式, 但当液滴的变形较大时, 该模型的预测并不准确.
随着计算机技术的不断发展, 数值模拟成为了研究EHD问题的新方法. Feng等[4]利用有限元法(FEM)观察电场中水滴的变形, 研究了流体粘性对均匀电场中漏电液滴变形的影响规律. Yan等[5]和Hartman等[6, 7]提出了更完整的方法. Tomar等[8]提出了一种耦合水平集(LS)和流体体积(VOF)法的两相EHD模型, 模拟了电场作用下导电液滴的变形. Lac等[9]采用边界积分法, 通过同时求解电场和流场, 得到了均匀电场中中性漏电液滴的变形与稳定性规律. 黄伟峰等[10]利用格子Boltzmann方法研究了均匀电场中液滴的变形和失稳. Lim等[11]基于CFD的有限体积法(FVM), 求解了喷嘴末端附近的液相和周围空气的N–S方程, 并使用前跟踪方法对气液界面进行了监控, 成功地模拟了液体射流和液滴的形成, López-Herrera等[12]使用 VOF法对导电液滴进行了三维模拟, 结果与Tomar等[8]得到的结果接近. Wei等[13]基于VOF方法, 提出电流体流场与电场双向耦合的数值方法, 研究中性漏电液滴和带电液滴在均匀电场和非均匀电场下的变形及运动规律, 成功观察到了液滴的形成过程.
以上对于电流体的研究对象多为高电导率流体, 因为其更容易观察到实验现象而被广泛采用, 例如酒精. 而对于低电导率液体的研究很少, 本文建立了模拟低电导率导电液滴在电场中变形过程的多物理场计算模型. Fluent、Flow3D和 Comsol 等商业代码已被用于模拟EHD问题, 它们已经提供了模拟Navier-Stokes方程的模型, 但缺少灵活性. 而本文采用具有流体体积方法的OpenFOAM软件处理两相EHD问题, 利用OpenFOAM开源的特性, 基于流体流动控制方程和电场控制方程, 通过添加自定义源项的方法, 编译设计了求解两相EHD问题的数值求解器EHDAFoam. 仿真结果中成功地观察到了低电导率液滴在电场中发生电变变形的过程, 揭示了电场作用下导电液滴的电场效应.
1 方法论 1.1 控制方程在考虑等温和不可压缩流体时, 重力场中两相EHD问题的主要控制方程为质量守恒(连续性)方程和动量守恒方程[14]:
| $ \nabla \cdot {\boldsymbol{U}} = 0 $ | (1) |
| $ \frac{{\partial \rho {\boldsymbol{U}}}}{{\partial t}} + \nabla \cdot (\rho {\boldsymbol{UU}}) = - \nabla p + \nabla \cdot ({\tau ^m} + {\tau ^e}) + \rho g $ | (2) |
其中,
| $ {\tau ^e} = \varepsilon {\boldsymbol{EE}} - \frac{1}{2}\varepsilon \left(1 - \frac{\rho }{\varepsilon }{\left(\frac{{\partial \varepsilon }}{{\partial \rho }}\right)_T}\right){E^2}I $ | (3) |
其中,
Chen[15]和Melcher[16]认为Korteweg-Helmholz力密度可以评估
| $ F_e^{K {\textit{-}} H} = {\rho _e}{\boldsymbol{E}} - \frac{1}{2}{E^2}\nabla \varepsilon + \nabla \left[\frac{1}{2}\rho {\left(\frac{{\delta \varepsilon }}{{\delta \rho }}\right)_T}{E^2}\right] $ | (4) |
式(4)右侧第1项表示库仑力, 该力作用于流体中存在的电荷:
| $ {{\boldsymbol{F}}_{{{e1}}}} = {\rho _e}{\boldsymbol{E}} $ | (5) |
其中,
当电荷受到库仑力的加速时, 动量转移到流体中, 促使流体发生变形或运动, 库仑力是EHD力中最强的, 在直流电区占据主导地位[17].
第2项是介电常数梯度力:
| $ {{\boldsymbol{F}}_{{{e2}}}} = - \frac{1}{2}{E^2}\nabla \varepsilon $ | (6) |
该力比库仑力弱得多, 仅在交流频率下占主导地位, 由于常用的EHD雾化流体各向同性且不可压缩, 介电常数没有梯度, 所以此项为零, 然而, 在流体表面边界上, 介电常数具有很大的梯度, 这种不连续性具有与库仑力作用下的表面电荷相同的效果.
第3项是由于电场的不均匀性引起的, 被称为电致伸缩力:
| $ {{\boldsymbol{F}}_{{{e3}}}} = \frac{1}{2}\nabla \left(\rho \frac{{\partial \varepsilon }}{{\partial {\rho _T}}}{E^2}\right) $ | (7) |
电致伸缩力仅在可压缩的流体中才出现, 在不可压缩的牛顿流体中, 例如水, 电致伸缩力为零. 因此, Korteweg-Helmholz力密度可以被简化为:
| $ {{\boldsymbol{F}}_{{e}}} = {\rho _e}{\boldsymbol{E}} - \frac{1}{2}{E^2}\nabla \varepsilon $ | (8) |
在电流体动力学中, 电场是无旋场[16]:
| $ \nabla \times {\boldsymbol{E}} = 0 $ | (9) |
电场强度
| $ {\boldsymbol{E}} = - \nabla \Phi $ | (10) |
其中,
根据高斯定律, 电荷密度可以表示为电位移矢量
| $ \nabla \cdot {\boldsymbol{D}} = {\rho _e} $ | (11) |
在流体中,
| $ {\boldsymbol{D}} = \varepsilon {\boldsymbol{E}} $ | (12) |
所以电荷密度
| $ \varepsilon \nabla \cdot {\boldsymbol{E}} = {\rho _e} $ | (13) |
最后, 利用Melcher[16]、Saville[18]和Levich[19]的方法, 推导出电荷守恒方程如下:
| $ \frac{{\partial {\rho _e}}}{{\partial t}} + \nabla \cdot ({\rho _e}{\boldsymbol{U}}) + \nabla \cdot (\sigma {\boldsymbol{E}}) = 0 $ | (14) |
其中,
对于各向同性的非电介质连续性流体, 漏介质模型在界面处出现切向电应力, 使流体处于运动状态, 直到粘性应力提供平衡, 并且可以忽略电荷随时间的变化量[20]. 因此, 式(14)可以简化为[18]:
| $ \nabla \cdot \left( {\sigma {\boldsymbol{E}}} \right) = 0 $ | (15) |
VOF法[21]是CFD中处理自由表面流的常用方法, 在VOF模型中, 表面张力可以根据连续介质表面力模型(CSF)[22]计算获得:
| $ {\boldsymbol{F}} = \gamma \kappa \nabla \alpha $ | (16) |
其中,
式(17)为牛顿流体中的粘性应力张量项[23]:
| $ \nabla \cdot \tau = \nabla \cdot \left( {\nu \nabla {\boldsymbol{U}}} \right) + \nabla {\boldsymbol{U}}\nabla \nu $ | (17) |
其中,
除此之外, 为使边界条件的定义更加简单, 采用修正压力[24]:
| $ {p_{rgh}} = p - \rho g \cdot h $ | (18) |
其中,
对式(18)进行梯度操作:
| $ \nabla {p_{rgh}} = \nabla p - g \cdot h\nabla \rho - \rho g $ | (19) |
所以, VOF模型中流体流动的动量方程为:
| $ \begin{split} & \frac{{\partial \rho {\boldsymbol{U}}}}{{\partial t}} + \nabla \cdot \left( {\rho {\boldsymbol{UU}}} \right) - \nabla \cdot \left( {\nu \nabla {\boldsymbol{U}}} \right) - \nabla {\boldsymbol{U}} \cdot \nabla \nu \\ & =- \nabla {p_{rgh}} - g \cdot h\nabla \rho + \sigma \kappa \nabla \alpha \end{split} $ | (20) |
在传统的流体体积法中, Hamilton-Jacobi函数与N-S方程同时求解. 连续性方程求解如下:
| $ \frac{{\partial \alpha }}{{\partial t}} + {\boldsymbol{U}} \cdot \nabla \alpha = 0 $ | (21) |
其中,
在VOF模型中, 只有一组方程会被求解, 所以计算域中两种不相溶的流体只有一种被认为是主相(
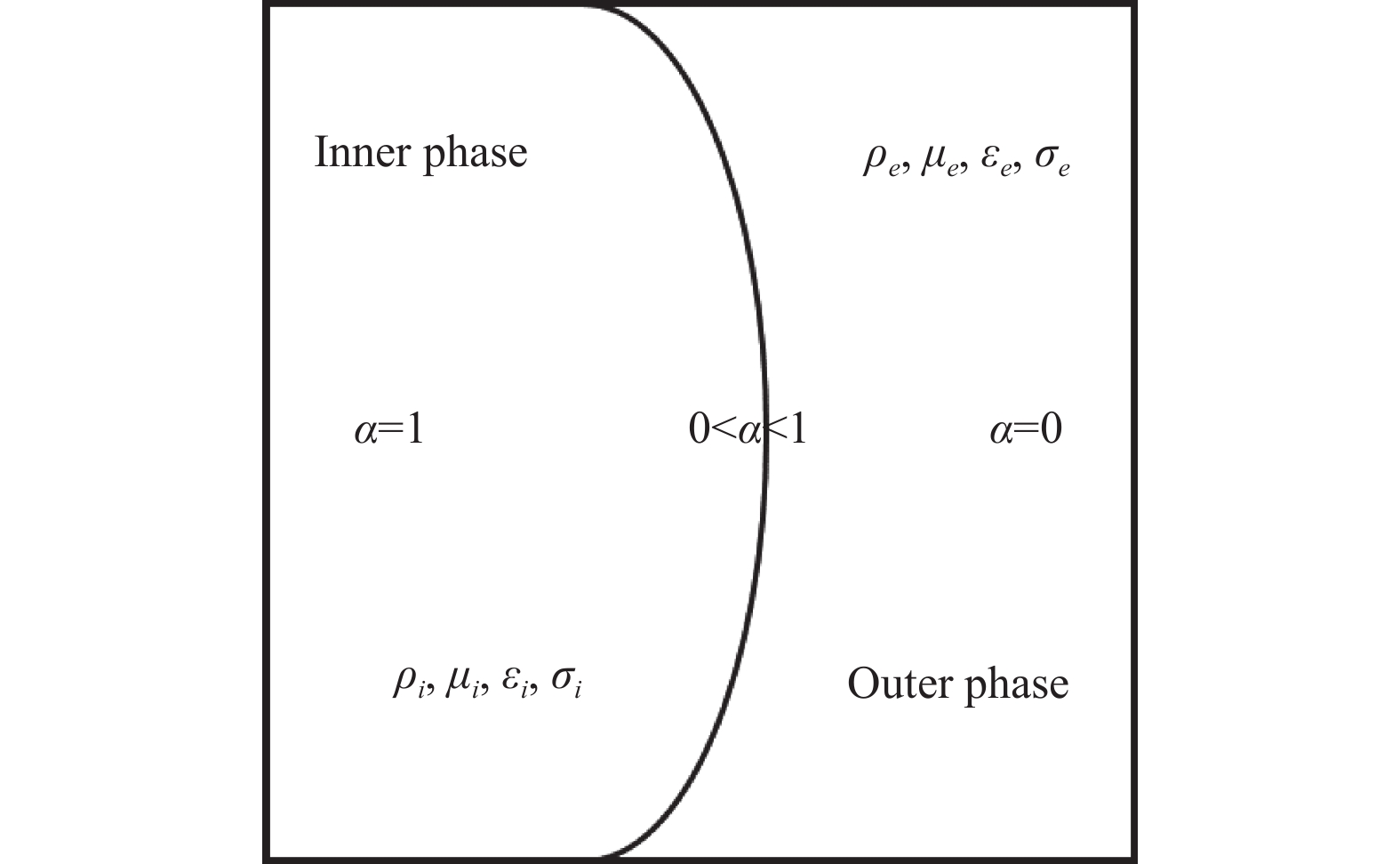
|
图 1 相界面Γ表示 |
在整个计算域内, 流体属性只在流体界面上发生变化, 界面处的物理属性可以通过流体体积分数的加权平均来求得:
| $\left\{ { \begin{array}{l} \rho=\alpha \rho_{i}+(1-\alpha) \rho_{e} \\ \mu=\alpha \mu_{i}+(1-\alpha) \mu_{e} \\ \varepsilon=\alpha \varepsilon_{i}+(1-\alpha) \varepsilon_{e} \\ \sigma=\alpha \sigma_{i}+(1-\alpha) \sigma_{e} \end{array} } \right.$ | (22) |
其中,
本文研究的是均匀电场中导电液滴的EHD效应, 将球形液滴插入到两个平行板之间, 对上下极板施加恒定的电势, 由于电位差的存在, 极板间会形成匀强电场, 液滴将发生电离或极化, 从而在表面产生电场力, 计算模型如图2所示.
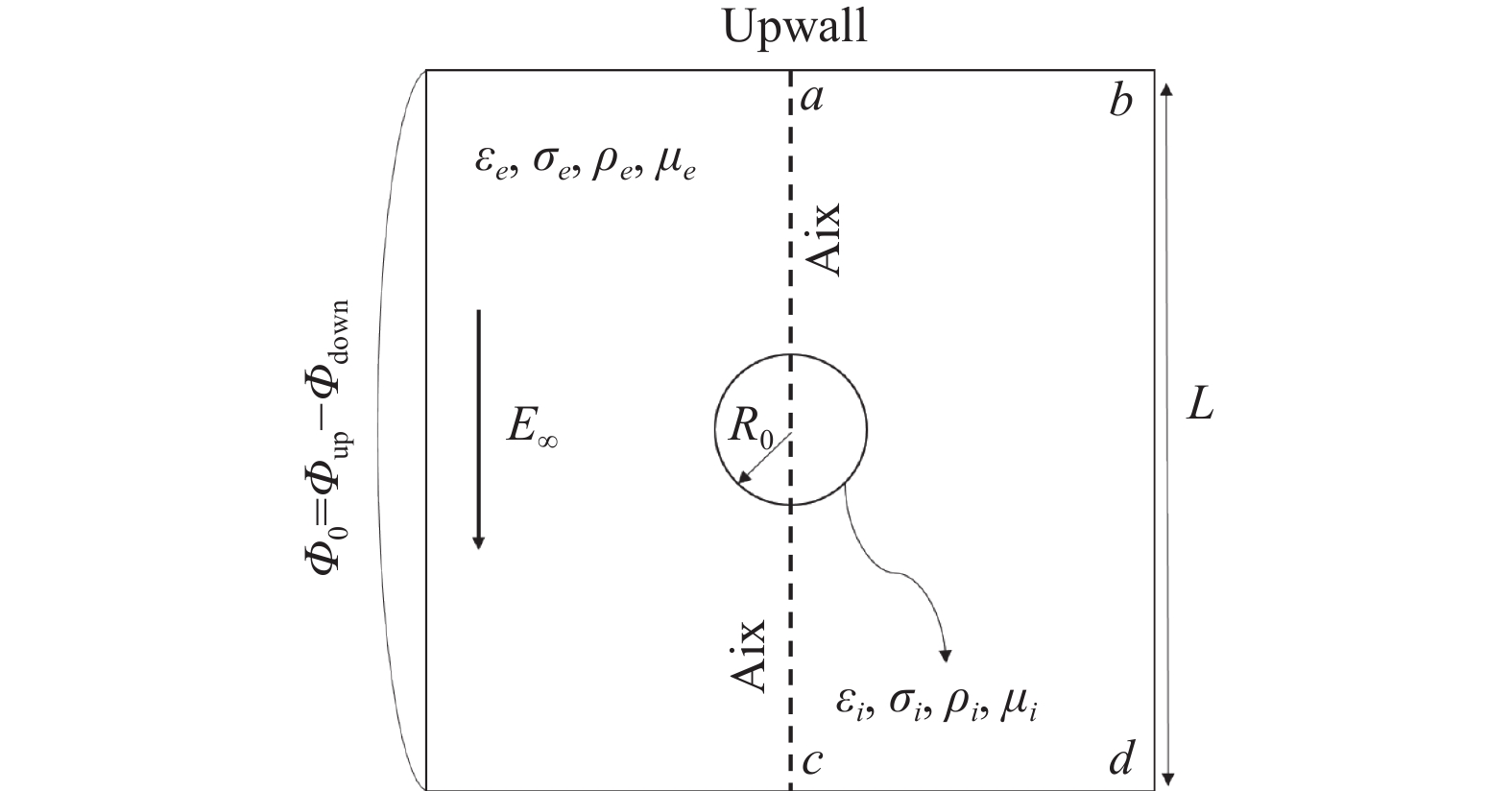
|
图 2 计算模型示意图 |
液滴与周围流体互不相溶且液滴的密度、黏度、介电常数、电导率分别为
整个计算模型采用轴对称模型, 以消除边界对液滴力学行为的影响, 对称轴垂直于极板并通过液滴的中心, 在上下极板分别施加电势, 会产生一个由上到下的外电场
Taylor[3]用变形系数
| $ D = \frac{{a - b}}{{a + b}} $ | (23) |
其中, a为液滴沿电场方向的变形量, b为液滴垂直于电场方向的变形量. 当D > 0时, 液滴发生长型变形, 当 D< 0时, 液滴发生扁圆变形.
除此之外, Taylor[3]还定义了液滴与周围流体的电导率比、介电常数比、粘度比和密度比, 公式如下:
| $ S = \frac{{{\sigma _i}}}{{{\sigma _e}}},\;M = \frac{{{\varepsilon _i}}}{{{\varepsilon _e}}},\;N = \frac{{{\mu _i}}}{{{\mu _e}}},\;R = \frac{{{\rho _i}}}{{{\rho _e}}} $ | (24) |
并给出了液滴变形的解析解, 如式(25)所示:
| $ {D_A} = \frac{9}{{16}}\frac{{C_{aE}}}{{{{\left( {2 + S} \right)}^2}}}f\left( {S, M, N} \right) $ | (25) |
其中, 毛细管数
| $ {C_{aE}} = \frac{{{\varepsilon _0}E_\infty ^2{R_0}}}{\gamma } $ | (26) |
其中,
| $ {E_\infty } = \frac{{{\Phi _0}}}{L} $ | (27) |
其中, L为极板间距.

|
图 3 电场中导电液滴的变形类型 |
| $ f\left( {S, M, N} \right) = 1 + {S^2} - 2M + \frac{3}{5}\left( {S - M} \right)\frac{{2 + 3N}}{{1 + N}} $ | (28) |
由于模拟采用两种粘度相同的流体, 因此N是弱函数, N= 1.
1.3 求解流程整个计算过程在开源CFD软件OpenFOAM[26]下进行, 采用PIMPLE算法求解动量方程, 从而将SIMPLE算法与PISO算法相结合, 只需设定
为保证计算结果的稳定性, 使数值模拟能够捕捉到液滴变形的所有细节, 模拟的时间步长应小于弛豫时间(式(29)). 本次模拟设置最大库朗数为0.1, 并将模拟的时间步长设置为10−6s.
| $ {\tau ^\mu } = \frac{{\rho d_c^2}}{\mu } $ | (29) |
其中, dc可以估计为毛细管的直径或液滴的直径.
1.4 边界条件和网格划分计算域的边界条件设置如图4.
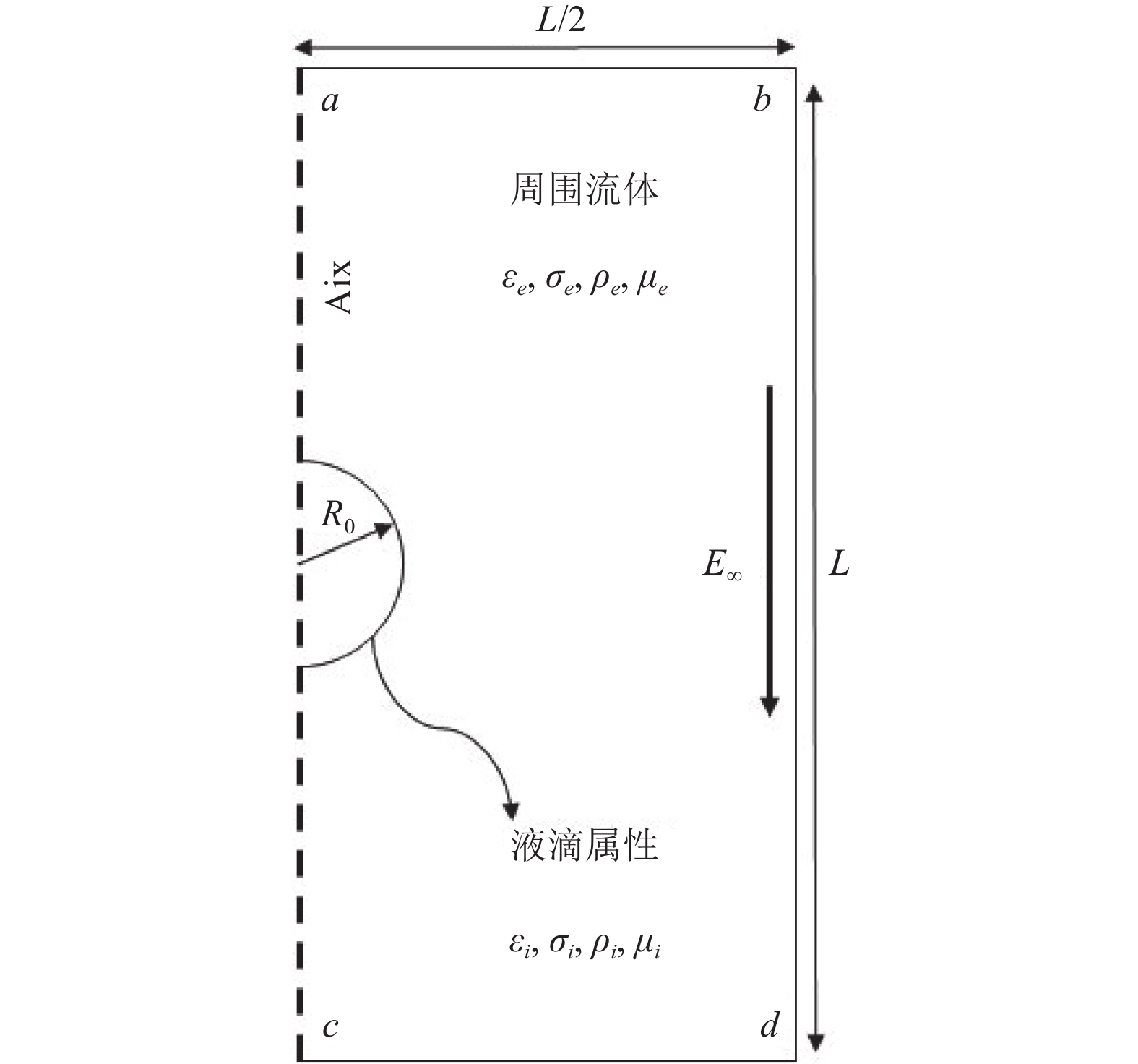
|
图 4 边界条件设置 |
(1)边界a-b. 无滑移边界条件,
(2)边界c-d. 无滑移边界条件,
(3)边界b-d. 大气边界条件.
(4)边界a-c. 轴对称边界条件.
为了设计出最佳的计算域尺寸, 分别测试了
根据测试, 当

|
图 5 不同计算域尺寸对液滴变形的影响 |
确定了最佳的计算域大小, 下一步需要进行网格密度测试. 由于电参数是主要的评估参数, 因此两种流体的密度比被设置为1. 图6显示

|
图 6 |
| 表 1 相对误差统计表 |
以上测试可以明显看出, 当网格变得更细时, 相对误差减小. 因此, 为所有模拟选择192的网格密度.
2 模拟结果与讨论采用硅油-氧化蓖麻油体系进行模拟, 物理参数如表2所示.
| 表 2 液体物理属性表 |
整个流体系统的表面张力为
由图7、图8可以看出, 内外流体物理属性的差异会导致液滴内部的自由电荷发生迁移与再分配, 当

|
图 7 |

|
图 8 |
由式(8)可以看出, 影响
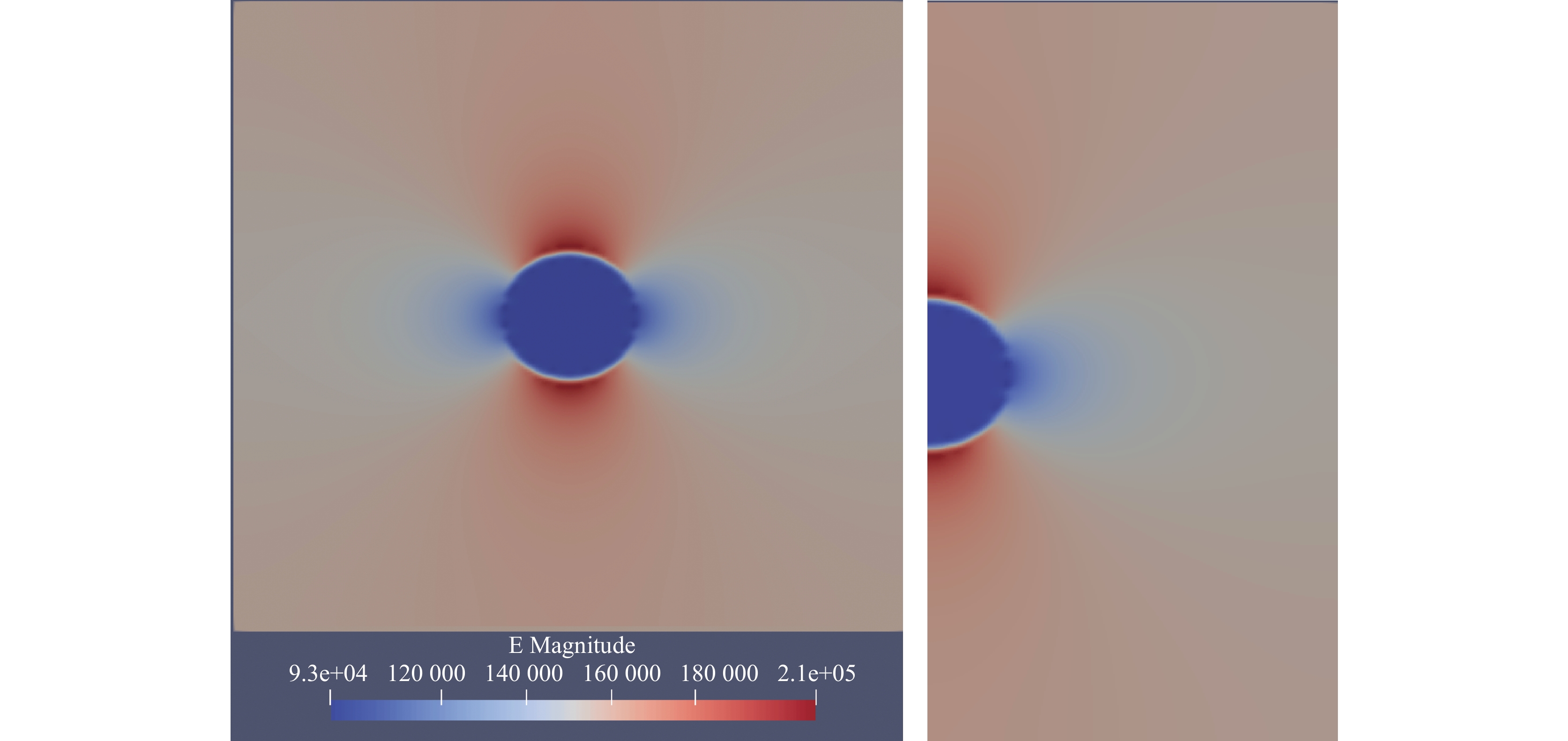
|
图 9 导电液滴周围电场的分布状态 |
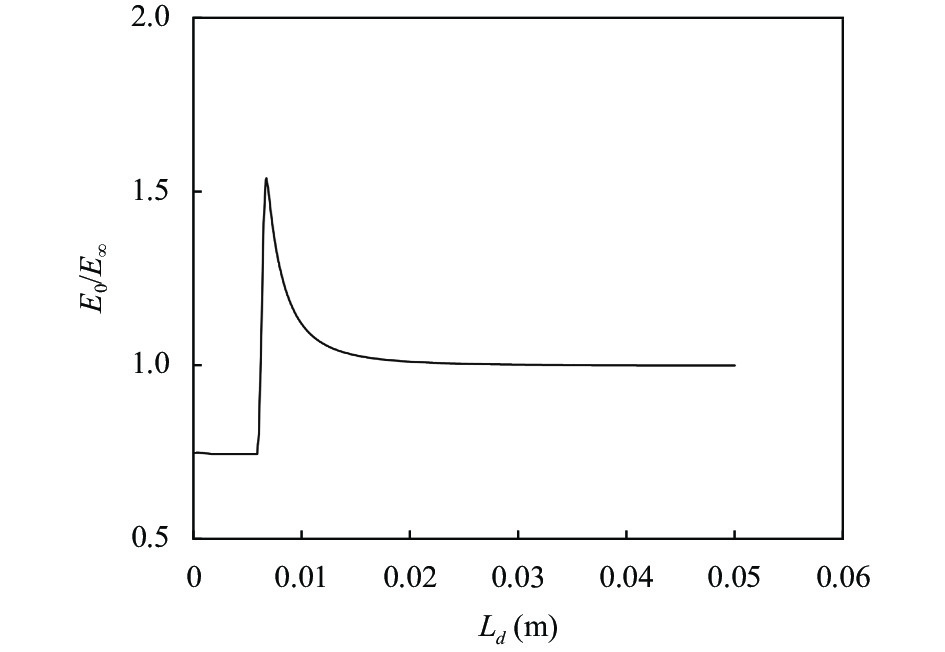
|
图 10 导电液滴内外电场分布曲线 |
通过调整CaE的值从0到2.0, 模拟分析不同外加电压下液滴的变形. 图11给出了不同区间液滴变形的模拟结果与解析值之间的比较. 结果显示, 随着外加电场增加, 液滴变形越来越大, 小变形情况下(CaE<0.12), 模拟结果与理论值基本吻合. 对于大变形, 模拟结果开始偏离理论值, 与Feng等[4]以及Ha等[27]所观察到的一样, Lim等[11]也获得了大变形情况下实验值与理论值不同的结果. 因此, 理论式(25)是基于小变形的假设, 小变形情况下, 与实验结果具有良好的一致性, 当变形增加时, 泰勒所预测的变形系数DA会变得不准确.

|
图 11 变形D与CaE的关系图 |
为了评估液滴变形与电导率比
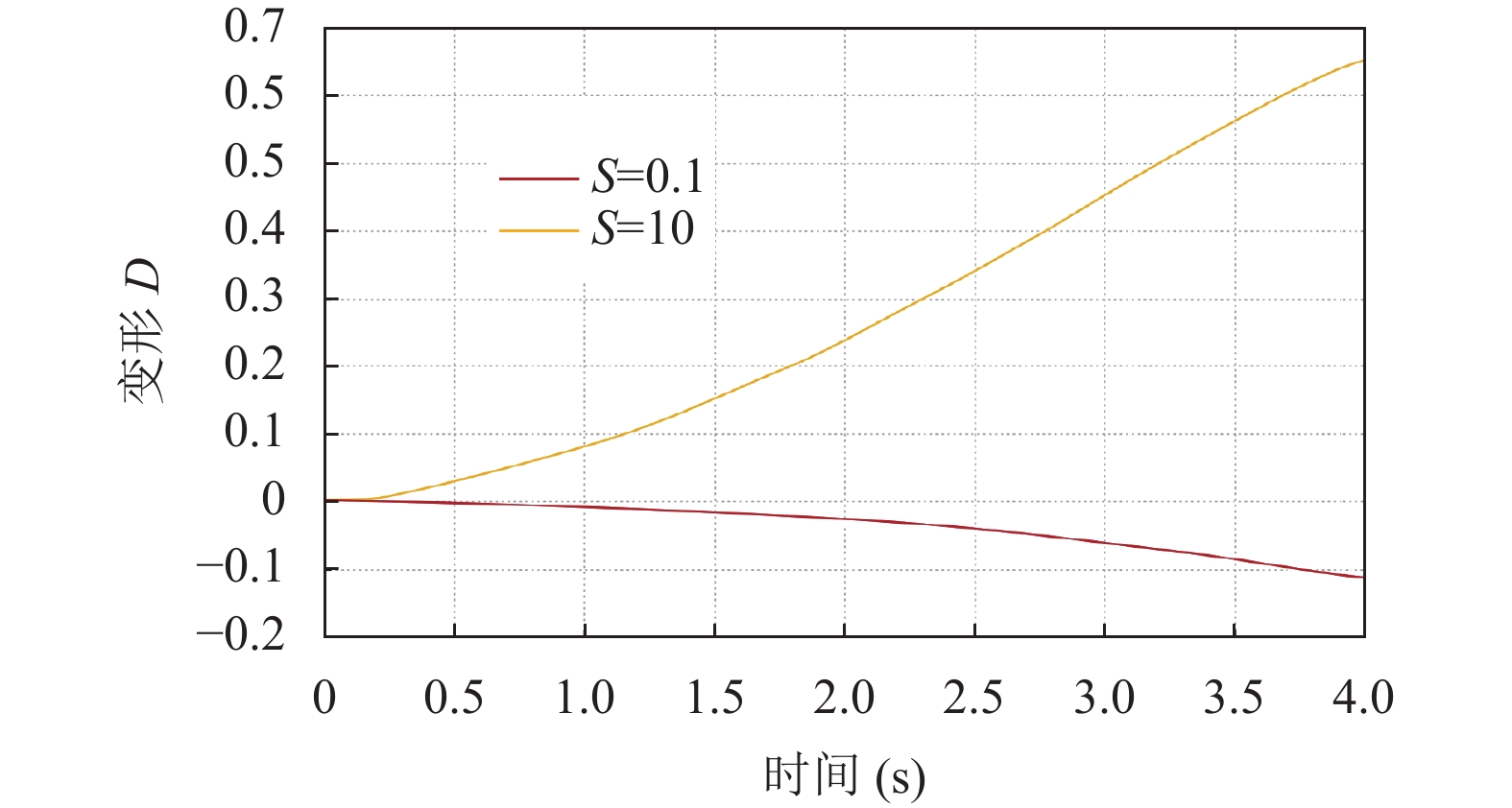
|
图 12 S = 10和S = 0.1时液滴的变形 |
模拟还评估了不同电导率比下液滴的变形, 保持M = 2.0, CaE = 0.1, 如图13所示, 观察到了更明显的变形. 尽管数值结果与解析值相比有较大偏差, 但模拟结果所预测的趋势与解析结果是相同的. 模拟仍然显示出小变形情况下模拟值与解析值的良好一致性.

|
图 13 不同电导率比下液滴的变形 |
此外, 模拟也获得了变形不太明显的结果, 如图14所示. 保持S、CaE和R的值分别为2.5、0.1和1.0. 从2.0到16逐渐增加介电常数比M的值, 可以发现变形量与理论值偏差较小.
在某些情况下, 由于液滴内外的再循环流动而产生的流体动力直接影响液滴的变形. 当S>M时, 电剪切应力引起再循环流, 该再循环流从赤道平面吸入并沿液滴的垂直对称轴排出, 如图15(a)所示. 对于S<M的情况, 产生的流动与 时相反, 再循环流从垂直对称轴吸入, 并沿赤道平面排出, 如图15(b)所示.

|
图 14 不同介电常数比下液滴的变形 |
3 结论
本文基于漏介质模型, 将电场力作为源项添加到流体运动的Navier-Stokes方程中, 并采用VOF方法追踪两相流的界面变化, 设计了求解两相EHDA问题的数值求解器, 模拟分析了导电液滴在电场中的电场效应. 模拟得到了外加电场作用下导电液滴内部自由电荷的迁移与再分配特性, 结果表明, 由于液滴与外部流体物理属性的差异, 自由电荷在液滴表面再分配的形式不同, 导致液滴可能会发生“扁长型”或“扁圆型”变形, 液滴内部会形成稳定的环流, 液滴只会发生变形, 而不会发生宏观运动. 模拟也分析了外加电压对导电液滴变形的影响, 并将数值结果与Taylor的解析解进行了比较, 结果显示, 随着外加电压的增加, 液滴的变形越来越大, 小变形情况下, 模拟值与理论值基本吻合, 当液滴的变形量较大时, 模拟结果开始偏离理论值, 与实验观察到的现象一致, 验证了数值方法的正确性. 此外, 研究还发现, 电导率比值的改变同样可以控制液滴的变形, 并且依旧显出示了小变形条件下模拟结果与理论值的良好一致性, 而介电常数比的改变对于液滴变形的影响则不太明显. 通过对电场作用下导电液滴的电场效应的数值模拟, 不仅完成了电流体动力学基本课题的研究, 而且为其在工业工程等领域的实际应用提供了理论基础.

|
图 15 环流模式图 |
| [1] |
Rayleigh L. On the equilibrium of liquid conducting masses charged with electricity. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1882, 14(87): 184-186. |
| [2] |
O’konski CT, Thacher Jr HC. The distortion of aerosol drop-lets by an electric field. The Journal of Physical Chemistry, 1953, 57(9): 955-958. DOI:10.1021/j150510a024 |
| [3] |
Taylor GI. Studies in electrohydrodynamics. The circulation produced in a drop by an electric field. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1966, 291(1425): 159-166. |
| [4] |
Feng JQ, Scott TC. A computational analysis of electrohydrodynamics of a leaky dielectric drop in an electric field. Journal of Fluid Mechanics, 1996, 311: 289-326. DOI:10.1017/S0022112096002601 |
| [5] |
Yan F, Farouk B, Ko F. Numerical modeling of an electrostatically driven liquid meniscus in the cone-jet mode. Journal of Aerosol Science, 2003, 34(1): 99-116. |
| [6] |
Hartman RPA, Brunner DJ, Camelot DMA, et al. Electrohydrodynamic atomization in the cone-jet mode physical modeling of the liquid cone and jet. Journal of Aerosol Science, 1999, 30(7): 823-849. DOI:10.1016/S0021-8502(99)00033-6 |
| [7] |
Hartman RPA, Brunner DJ, Camelot DMA, et al. Jet break-up in electrohydrodynamic atomization in the cone-jet mode. Journal of Aerosol Science, 2000, 31(1): 65-95. DOI:10.1016/S0021-8502(99)00034-8 |
| [8] |
Tomar G, Gerlach D, Biswas G, et al. Two-phase electrohydrodynamic simulations using a volume-of-fluid approach. Journal of Computational Physics, 2007, 227(2): 1267-1285. DOI:10.1016/j.jcp.2007.09.003 |
| [9] |
Lac E, Homsy GM. Axisymmetric deformation and stability of a viscous drop in a steady electric field. Journal of Fluid Mechanics, 2007, 590: 239-264. DOI:10.1017/S0022112007007999 |
| [10] |
黄伟峰, 李勇, 刘秋生. 格子Boltzmann方法在电流体动力学中的应用: 均匀电场中液滴的变形和失稳. 科学通报, 2007, 52(11): 1232-1236. DOI:10.3321/j.issn:0023-074X.2007.11.002 |
| [11] |
Lim LK, Hua JS, Wang CH, et al. Numerical simulation of cone-jet formation in electrohydrodynamic atomization. Aiche Journal, 2011, 57(1): 57-78. DOI:10.1002/aic.12254 |
| [12] |
López-Herrera JM, Popinet S, Herrada MA. A charge-conservative approach for simulating electrohydrodynamic two-phase flows using volume-of-fluid. Journal of Computational Physics, 2011, 230(5): 1939-1955. DOI:10.1016/j.jcp.2010.11.042 |
| [13] |
Wei W, Zhang YW, Gu ZL. Deformation and mechanical behavior of electrohydrodynamic droplet under external electric field. Chinese Science Bulletin, 2013, 58(3): 197-205. DOI:10.1360/972012-107 |
| [14] |
Ferziger JH, Perić M. Computational Methods for Fluid Dynamics. 3rd ed., Berlin: Springer, 2002.
|
| [15] |
Chen CH. Electrohydrodynamic stability, electrokinetics and electrohydrodynamics in microsystems. Vienna: Springer, 2011. 177–220.
|
| [16] |
Melcher JR. Continuum Electromechanics. Cambridge: MIT Press, 1981.
|
| [17] |
Lastow O. Numerical and experimental study of electrohydrodynamic atomisation of aqueous liquids [Ph.D. thesis]. London: Brunel University, 2007.
|
| [18] |
Saville DA. Electrohydrodynamics: The Taylor-Melcher leaky dielectric model. Annual Review of Fluid Mechanics, 1997, 29: 27-64. DOI:10.1146/annurev.fluid.29.1.27 |
| [19] |
Levich VG. Physicochemical Hydrodynamics. Englewood Cliffs: Prentice-Hall, 1962.
|
| [20] |
Hua JS, Lim LK, Wang CH. Numerical simulation of deformation/motion of a drop suspended in viscous liquids under influence of steady electric fields. Physics of Fluids, 2008, 20(11): 113302. DOI:10.1063/1.3021065 |
| [21] |
Hirt CW, Nichols BD. Volume of fluid (VOF) method for the dynamics of free boundaries. Journal of Computational Physics, 1981, 39(1): 201-225. DOI:10.1016/0021-9991(81)90145-5 |
| [22] |
Brackbill JU, Kothe DB, Zemach C. A continuum method for modeling surface tension. Journal of Computational Physics, 1992, 100(2): 335-354. DOI:10.1016/0021-9991(92)90240-Y |
| [23] |
Pozrikidis C. Introduction to Theoretical and Computational Fluid Dynamics. New York: Oxford University Press, 1997.
|
| [24] |
Deshpande SS, Anumolu L, Trujillo MF. Evaluating the performance of the two-phase flow solver interFoam. Computational Science & Discovery, 2012, 5(1): 014016. |
| [25] |
Taylor GI. Disintegration of water drops in an electric field. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1964, 280(1382): 383-397. |
| [26] |
Weller H. OpenFOAM: The open source CFD toolbox user guide. London: The OpenFOAM Foundation Ltd., 2010.
|
| [27] |
Ha JW, Yang SM. Deformation and breakup of Newtonian and non-Newtonian conducting drops in an electric field. Journal of Fluid Mechanics, 2000, 405: 131-156. DOI:10.1017/S0022112099007223 |
 2022, Vol. 31
2022, Vol. 31


