进化算法(evolutionary algorithms, EAs)^[1-3] 由于其鲁棒性强、收敛速度快、全局搜索能力强等特点, 被广泛应用于求解优化问题. 而在科学研究和工程实践中, 诸如有限元分析(finite element analysis, FEA)^[4]、计算流体动力学^[5]等优化问题, 缺乏目标函数解析式, 且需要十分耗时的计算机仿真分析或是财务昂贵的实验对候选解进行评估, 这类黑箱问题被称为昂贵优化问题. 由于进化算法采用迭代搜索的方式使种群中的个体逐渐逼近最优解或达到最优解, 势必需要对大量候选解进行评估, 但对于昂贵优化问题, 过高的评估次数会带来计算成本灾难. 解决此类问题的常用方法是建立评估候选解的代理模型^[6], 用代理模型的预测替换对候选解的昂贵评估.

最流行的代理模型是回归模型, 例如: Kriging模型^[7], RBF神经网络模型^[8], 此类方法用预测目标函数值的方法来评估候选解, Shi等人^[6]对回归模型在进化算法中的应用做了系统性的论述, 这种绝对适应度模型的不足之处是模型类型的选择需要先验知识, 对候选解评估的准确性依赖模型的输出精度.

Runarsson^[9]指出, 在种群中选择优良个体并不需要精确预测出候选解的目标函数值, 而只需要预测个体排名, 即个体的相对关系. 且相对适应度模型只关注个体间的相对性, 建模更简单. 但根据Tong等人在文献[10]中的研究可知, 现有的相对适应度模型通常没有绝对适应度模型准确与精细, 在进化算法中往往仅作为局部模型进行预筛选. 如在文献[11]中, 基于排序的SVM被用于协方差矩阵自适应进化策略(covariance matrix adaptation evolutionary strategies, CMA-ES)中的预筛选, 通过对预选子代进行预测得到其排名, 选择排名靠前的个体进行真实适应度评估, 并将排名映射到正态分布, 以便依据分布情况选择子代, 以维持种群的多样性. 在文献[12]中, SVM分类器被用于差分进化算法中(classification and regression-assisted differential evolution, CREDA)的预筛选, 仅当子代被分类为优于父代的个体时, 才考虑对其进行真实适应度评估或回归预测, 否则将被直接舍弃.

为了减少预测建模对先验知识的依赖, 避开对绝对适应度回归预测模型的高精度要求, 并使预测模型具有更好的泛化性, 需要建立更加有效的相对适应度模型. 故本文研究候选解优劣性的序评价和预测方法. 余下内容阐述序的定义及特点, 扼要介绍用于序分类预测的支持向量机方法, 详细阐述序样本集的约简算法以及序预测方法与遗传算法的集成, 并对序预测以及在遗传算法中集成的仿真实验进行比较分析.

1 候选解优劣性的序评价方法 1.1 最优化问题

通俗地讲, 最优化问题就是求定义在给定集合上的目标函数的最小值或最大值的问题. 不失一般性, 以最小化问题为例, 一个最优化问题可表述为:

$ \left\{ {\begin{array}{*{20}{l}} {\mathop {\min }\limits_{{\boldsymbol{x}} \in \Omega } f({\boldsymbol{x}})} \\ {{\rm s.t.}{\text{ }}\;{g_i} {({\boldsymbol{x}})} \leqslant 0, i = 1, 2, \cdots, s} \\ {{\text{ }}\begin{array}{*{20}{c}} {}&{{h_j}({\boldsymbol{x}}) = 0, j = 1, \cdots, p} \end{array}} \end{array}} \right. $

(1)

其中, ${\boldsymbol{x}} = ({x_1}, {x_2}, \cdots, {x_n})$ 是 $ n $ 维决策向量, $f({\boldsymbol{x}})$ 为目标函数值, ${g_i}({\boldsymbol{x}})$ 表示第 $ i $ 个不等式约束, ${h_j}({\boldsymbol{x}})$ 表示第 $ j $ 个等式约束, $ \Omega $ 为搜索空间.

1.2 序的定义

由于进化算法采用适者生存的选择策略, 本文定义两个候选解 ${\boldsymbol{u}}$ , ${\boldsymbol{v}}$ 之间的序 $r({\boldsymbol{u}}, {\boldsymbol{v}})$ 来评价他们的相对适应性.

定义. 给定两个候选解 ${\boldsymbol{u}}$ , ${\boldsymbol{v}}$ , 其目标函数值分别为 $f({\boldsymbol{u}})$ , $f({\boldsymbol{v}})$ , 候选解 ${\boldsymbol{u}}$ , ${\boldsymbol{v}}$ 之间的序:

$ r({\boldsymbol{u}}, {\boldsymbol{v}}) = {\text{sign}}(f({\boldsymbol{u}}) - f({\boldsymbol{v}})) $

(2)

其中, sign表示数的正负性. 当 $f({\boldsymbol{u}}) \leqslant f({\boldsymbol{v}})$ 时, $r({\boldsymbol{u}}, {\boldsymbol{v}})= -1$ , 称 ${\boldsymbol{u}}$ 优于 ${\boldsymbol{v}}$ , 记为 ${\boldsymbol{u}} \prec {\boldsymbol{v}}$ . 反之当 $f({\boldsymbol{u}}) > f({\boldsymbol{v}})$ 时, $r({\boldsymbol{u}}, {\boldsymbol{v}}){\text{ = }} 1$ , 称 ${\boldsymbol{u}}$ 劣于 ${\boldsymbol{v}}$ , 记为 ${\boldsymbol{u}} \succ {\boldsymbol{v}}$ .

显然, 序表示了两个候选解目标函数值之间的大小关系, 在进化算法中可用来评价两个候选解的相对适应性.

1.3 序的性质

由序的定义很容易证明序值具有以下性质:

自反性. 若 $\;r({\boldsymbol{u}}, {\boldsymbol{v}}){\text{ = }}1$ , 必有 $\;r({\boldsymbol{v}}, {\boldsymbol{u}})=-1$ . 反之亦然.

传递性. 若 $\;r({\boldsymbol{u}}, {\boldsymbol{v}}){\text{ = }}1$ , $\;r({\boldsymbol{v}}, {\boldsymbol{w}}){\text{ = }}1$ , 必有 $\;r({\boldsymbol{u}}, {\boldsymbol{w}}){\text{ = }}1$ . 反之亦然.

序不变性. 序值的决策并不依赖精确的目标函数差值, 候选解目标函数的差值在一定范围内均可映射成相同的序值.

1.4 序的预测

在优化昂贵问题时, 序的决策可通过预测方法实现, 以减少对候选解昂贵评估的计算成本. 由序的定义可见, 序的决策既可用回归预测方法, 也可用分类预测方法. 相对于回归预测对目标函数值代理模型的精确性要求, 序的分类预测能更自然地利用序不变性性质, 这将有利于提高预测的容错能力和鲁棒性.

给定候选解样本集:

$ S = \{ ({{\boldsymbol{x}}_1}, f({{\boldsymbol{x}}_1})), \cdots, ({{\boldsymbol{x}}_l}, f({{\boldsymbol{x}}_l}))\} $

(3)

可构造最多 $ \;l \times (l - 1) $ 个无重复样本的序样本集. 分类预测的每个序样本可以用三元组表示, 序样本集:

$ R = \left\{ {({{\boldsymbol{x}}_i}, {{\boldsymbol{x}}_j}, r({{\boldsymbol{x}}_i}, {{\boldsymbol{x}}_j}))} \right\} , {\text{ }}i, j = 1, \cdots, l \wedge i \ne j $

(4)

其中, 二元组 $({{\boldsymbol{x}}_i}, {{\boldsymbol{x}}_j})$ 表示序样本的输入, $r({{\boldsymbol{x}}_i}, {{\boldsymbol{x}}_j})$ 表示序样本的输出.

由于序样本集的规模是原始样本集规模的平方数量级, 势必显著增加分类器的训练成本. 序的自反性和传递性性质反映了序样本集中存在信息冗余, 可以对其进行约简.

2 支持向量机分类

支持向量机(SVM)^[13]将原始输入空间的学习问题转换为高维特征空间的学习问题, 已被广泛应用于各种分类问题的求解^[14–17]. 相较于其他分类器的优势在于SVM不会引起局部最小值, 泛化误差不依赖于输入空间的维度. 由于序样本的输入由两个候选解的输入拼接而成, 势必引起输入维数的显著增加, 为了减少输入维数增加引起的泛化误差, 本文选取SVM分类器实现序的分类预测.

设给定以下训练集:

$ \{ {{\boldsymbol{x}}_i}, {y_i}\} _{i = 1}^l, \;\;{{\boldsymbol{x}}_i} \in {R^m}, \;\;{y_i} \in \{ 1, - 1\} $

(5)

其中, ${{\boldsymbol{x}}_i}$ 为 $ m $ 维的输入向量, ${{{y}}_i}$ 为分类标签. $ l $ 为训练集大小, 当数据线性可分时, SVM将找到一个最优超平面来最大化正样本与负样本之间的间隔, 超平面的等式如下:

$ g({\boldsymbol{x}}) = ({{\boldsymbol{w}}^{\text{T}}} \cdot {\boldsymbol{x}}) + b = 0 $

(6)

其中, ${\boldsymbol{x}}$ 是候选解向量, ${\boldsymbol{w}}$ 是超平面的权重向量, $ b $ 是偏差, $ {\text{T}} $ 代表转置. 超平面的位置由参数 ${\boldsymbol{w}}$ 和参数 $ b $ 决定, 寻找最优超平面需要寻找到最优的 ${\boldsymbol{w}}$ 参数. 为了寻找到最优的 ${\boldsymbol{w}}$ 参数, 需要解决下列二次规划问题:

$ \left\{ {\begin{gathered} \min \;\;\frac{1}{2}\parallel {\boldsymbol{w}}{\parallel ^2} \\ {\rm s.t.}\;\;{y_i}({\boldsymbol{w}} \cdot {{\boldsymbol{x}}_i} + b) \geqslant 1, \;\;i = 1, \cdots, n \\ \end{gathered} } \right.$

(7)

而当需要被分类的数据线性不可分时, 需要解决的优化问题变成如下形式:

$\left\{ { \begin{gathered} \min \;\;\frac{1}{2}\parallel {\boldsymbol{w}}{\parallel ^2} + C\sum\limits_{i = 1}^n {{\xi _i}} , \;\;\;\;{\xi _i} \geqslant 0 \\ \;{\rm s.t.}\;\;\;{y_i}({\boldsymbol{w}} \cdot {{\boldsymbol{x}}_i} + b) \geqslant 1 - {\xi _i}, \;\;\;\;i = 1, \cdots, n \\ \;\;\;\;\;\;\;\;{\xi _i} \geqslant 0, \;\;\;\;i = 1, \cdots, n \\ \end{gathered} } \right.$

(8)

其中, $ C $ 是惩罚参数, 用来在最小化训练误差和模型复杂程度之间做折中. $ {\xi _i} $ 是松弛变量, 用来控制SVM对错误分类的容忍程度. 为了方便计算, 通常求解式(8)的拉格朗日对偶形式:

$\left\{ { \begin{gathered} \max \;\;W({\mathbf{\alpha }}) = \sum\limits_{i = 1}^n {{\alpha _i}} - \frac{1}{2}\sum\limits_{i, j = 1}^n {{\alpha _i}{\alpha _j}} {y_i}{y_j}K({{\boldsymbol{x}}_i}, {{\boldsymbol{x}}_j}) \\ \;{\rm s.t.}\;\;\;\sum\limits_{i = 1}^n {{\alpha _i}{y_i}} = 0, \;\;\;\;C \geqslant {\alpha _i} \geqslant 0, \;\;\;\;i = 1, \cdots, n \\ \end{gathered}} \right. $

(9)

其中, $K({{\boldsymbol{x}}_i}, {{\boldsymbol{x}}_j})$ 表示的是核函数, 用来将非线性数据映射到更高维的空间以使其变得线性可分. $ {\alpha _i} $ 是拉格朗日乘子. 通过求解式(9)优化问题, 可得到原始问题(7)的解 ${\boldsymbol{w}}$ , $ b $ . 再将其代入式(6)中, 则可得到用来分类的最优超平面. SVM的分类决策函数如下:

$ f({\boldsymbol{x}}) = {\rm sign}\left(\sum\limits_{i, j = 1}^n {{\alpha _i}} {y_i}K({{\boldsymbol{x}}_i}, {{\boldsymbol{x}}_j}) + b\right) $

(10)

${\rm sign}$ 函数使得模型的输出为固定值{−1, 1}, 即起到了将样本分类的作用.

3 序预测比较实验

为验证序分类预测的有效性, 选取常用的CEC2015昂贵测试函数集(Matlab版本下载地址 https://github.com/P-N-Suganthan/CEC2015)^[18], 分别应用SVM分类器、RBF神经网络与Kriging模型开展序预测对比实验. 其中, SVM直接预测序样本的类标签, 而RBF和Kriging模型预测候选解的目标函数值.

3.1 测试函数

CEC2015测试函数集共包含15个测试函数. 其中, $ f1 $ , $ f2 $ 为单峰函数, $f3-f9$ 为多峰函数, $f10-f12$ 为混合函数, 样本会被随机分成若干子集, 然后对不同的子集使用不同的基函数, 对应于现实世界中不同子集具有不同属性的复杂情况, $f13-f15$ 为组合函数, 由多个基准函数以特定结构组合而成, 往往具有多峰、不可分、非对称的性质, 且局部最优解周围的属性也各不相同. 组合函数融合了多个子函数的性质, 优化难度被极大提高.

由于CEC2015测试函数集目前只提供了10维和30维的实现, 故本文实验仅在10维和30维上进行.

3.2 实验设置

实验平台采用Intel(R) Core(TM) i5-4210M CPU, 8 GB内存, Matlab R2017b软件. 支持向量机工具取自LIBSVM工具箱^[19]中的C-SVM, 参数c设置为1, g设置为0. 1. RBF神经网络模型取自Matlab神经网络工具箱, 参数spread设置为10. Kriging模型取自DACE工具箱, 基函数为高斯函数, 核函数分别使用零阶多项式、一阶多项式、二阶多项式, 统计结果取最优数据.

对于每个测试函数, 分别使用拉丁超立方采样方法^[20]在其定义域内生成100个原始样本, 并通过CEC2015的软件计算其目标函数值. 对于序预测方法, 将100个原始样本两两配对生成大小为9 900的序样本集. 对序样本集进行5折交叉验证, 即将序样本集分为5等份, 每次将其中一等份作为验证集, 其余4等份作为训练集, 这5次预测结果的均值记为预测准确率. 而对于回归预测, 由于不需要对其构造序样本集, 故直接对原始样本集进行5折交叉验证. 实验结果为30次独立运行实验结果的平均值.

需要说明的是: 对于序的分类预测, 其序样本标签直接代表序样本内两个原始样本间的优劣关系. 而对于回归预测, 需通过对预测得到的目标函数值大小进行比较, 从而得到原始样本间的优劣关系.

3.3 实验结果与分析

表1中统计了序的分类预测(C-SVM), 回归预测(Kriging, RBF), 两种预测方式、3种预测模型在15个测试函数上运行30次的实验结果.

由表1可得, 在以上15个昂贵优化测试函数上, 序的分类预测方法总体优于回归预测方法. 在回归预测模型中, Kriging模型的预测准确率在10维测试函数上显著高于RBF神经网络模型, 但当函数维度升至30维时, RBF神经网络在一些测试函数上的预测准确率开始高于Kriging模型. 具体分析两种预测方法的实验结果可得, 在 $ f1 $ , $ f2 $ 两个相对平滑的单峰函数上, 回归预测方法可以更准确地得到样本间的关系. 而在f3–f9这类多峰函数中. 回归预测仅在 $ f6 $ , $ f7 $ 两个函数上表现更优, 而序的分类预测总体表现更好. f10–f12这类混合函数和f13–f15这类组合函数, 由于结构复杂, 性质多样, 优化十分困难. 但序的分类预测方法却对此表现出了极强的鲁棒性, 在其他预测模型的性能随着问题维数升高而显著降低时, 序预测模型依然可以维持其预测能力. 除了在10维的 $ f10 $ 函数上, 回归预测表现略优一点. 总结可得, 对于峰间距较小的多峰函数、子集具有不同属性的混合函数、融合了多个基函数性质的组合函数而言, 序预测有着更好的预测能力, 可在样本数量有限的情况下取得更好的预测结果, 而昂贵优化问题的数据时常需要通过财务昂贵的实验才可得到, 缺乏用于训练的大量数据, 故序预测在处理昂贵优化问题时具有极大的应用潜力.

4 序样本集的约简

传统的SVM分类器并不适于处理大型数据集, 其主要缺点在于大型数据集的高训练时长和高空间复杂性, 训练的时间复杂度和空间复杂度分别为 ${\rm O}({N^3})$ 和 ${\rm O}({N^2})$ ( $ N $ 是训练集的大小). 由于序样本的构造方式为原始样本的两两配对, 使得序样本相比于原始样本有着更高的样本数和样本维度, 这无疑会给SVM分类器的训练带来很高的计算成本, 故需要对序样本集进行约简.

4.1 样本约简方法

本文采用数据清洗的思想, 通过删减序样本集中的冗余样本减少序样本集的大小, 以确定一个有价值的子集送去SVM分类器, 提高SVM分类的训练效率.

文献[21]指出, 在SVM模型训练中, 最后决定分类边界的是少量被称之为支持向量(support vector, SV)的样本, 而样本中的非支持向量并不会显著影响分类器的性能, 故尽可能地减少样本中非支持向量的个数可提高分类模型的训练效率. 本文提出的样本约简方法是通过特定方式构建几个序样本集的子集, 并用SVM分类器对这几个子集进行训练从而得到几个分类超平面, 再分别计算序样本集中样本到这几个超平面的距离. 若某序样本到多数分类超平面的距离都超过预定范围, 则被认为是支持向量的概率很小, 故将其删除.

若仅使用一个子集对最大序样本集进行约简, 则对最大序样本集中非SV的删减效果仅由该子集的分类超平面所决定, 而由于子集样本数量的限制, 使得训练得到的分类超平面精度不高, 这势必会造成一些SV被误删. 故为提高对非SV的识别能力, 需要创建 $ k $ 个子集 $ (k > 1) $ , 同时利用 $ k $ 个分类超平面对最大序样本集中的非SV进行判断. 但子集数过多会增加序样本集约简的时间成本, 为平衡约简的效率与准确性, 这里 $ k $ 值取3.

序样本标签表示的是两个被拼接的原始样本的相对好坏, 但没有表示出两个原始样本相差的程度, 两个原始样本目标函数值差值的绝对值即可体现两个样本的相对程度. 本文在构造子集时, 优先选取那些相对程度较高的原始样本. 将 $ n $ 个原始样本依照目标函数值的大小进行排序, 并将前 $ n/2 $ 个样本分别与后 $ n/2 $ 个样本配对成序样本, 一共 $ n $ 个序样本(其中包括正序和反序). 以此构造最具代表性的序样本.

算法具体细节如算法1.

算法1. 序样本集约简方法

输入: n个原始样本, 参考距离dis_r

输出: 简约序样本集S_r

原始样本集两两配对构成最大序样本集S_max

生成S_max的k个子集S_1,S_2, …, S_k (1≤k≤n/2)

子集S_v的生成(1≤v≤k):

If v=1

　For i=1 to n/2

　　将x(i), x(i+n/2)构成一对自反样本加入S_1

　Endfor

Else

　Fori=1 to n/2–v+1

　　将x(i), x(i+n/2–1)构造成一对自反样本加入S_v

　Endfor

　For i=n/2–v+2 to n/2

　　将x(i), x(n)构造成一对自反样本加入S_v

　Endfor

Endif

用SVM对k个子集进行训练, 得到k条决策边界

计算S_max中每个样本到k条决策边界的距离dis_1, …, dis_k

对S_max中的每个样本有:

j=1;

For i=1 to k

　Ifdis_i>dis_r

　　j=j+1;

　Endif

End

If j≥k/2

　在S_max中删除该样本

End

经过删减后的S_max即为S_r

算法1中, 正序样本和负序样本的参考距离分别记为 $ di{s_p} $ 、 $ di{s_n} $ , 计算方式如下:

$\left\{ { \begin{gathered} di{s_p} = di{s_p}_{\max } \times \lambda {\mathbf{, }}\;\;\lambda \in (0, 1) \\ di{s_n} = di{s_n}_{\max }\; \times \lambda {\mathbf{, }}\;\;\lambda \in (0, 1) \\ \end{gathered} } \right.$

(11)

$ di{s_p}_{\max } $ 、 $ di{s_n}_{\max } $ 分别为正序样本集与负序样本集中离分类超平面最远的距离. 当正/负序样本距离分类超平面的距离大于等于正/负参考距离时, 则认为该序样本离分类边界太远, 是SV的可能性较低, 可以被删减掉. $ \lambda $ 参数决定了对最大序样本集删减的程度, $ \lambda $ 值越小, 对最大序样本集的删减程度越高, $ \lambda $ 值越大, 对最大序样本集的删减程度越低. 当 $ \lambda $ 过小时, 序样本集在约简之后依然含有大量冗余样本; 而当 $ \lambda $ 过大时, 又会造成对SV的误删, 使得训练出来的序预测模型性能不佳, 故需要为模型选取合适的 $ \lambda $ 参数.

4.2 样本约简对比实验

使用此样本约简方法对CEC2015昂贵测试函数集中的6个测试函数分别在10d和30d上进行5折交叉验证的实验. 对于10d, 30d的测试函数, $ \lambda $ 值分别取0.4, 0.3. 其余实验设置同第3节的对比实验并与其在预测准确率和cputime上进行比较, 结果如表2, 表3所示.

从表2, 表3可看出, 对序样本集进行样本约简后很大程度减少了实验运行的cputime, 且几乎不影响序预测的准确率. 且对于 $ f3 $ 、 $ f4 $ 、 $ f5 $ 这类多峰函数而言, 序样本约简方法在10d问题上表现更佳. 而对于 $ f11 $ 、 $ f12 $ 、 $ f14 $ 这类更加复杂的混合函数和组合函数, 该样本约简方法在30d问题上表现最加优异.

5 序预测与遗传算法的集成 5.1 序预测辅助遗传算法

为体现序预测在解决昂贵优化问题上的应用潜力, 将序预测与遗传算法相结合用于求解昂贵优化问题. 模型管理方式采用基于个体的模型管理^[22].

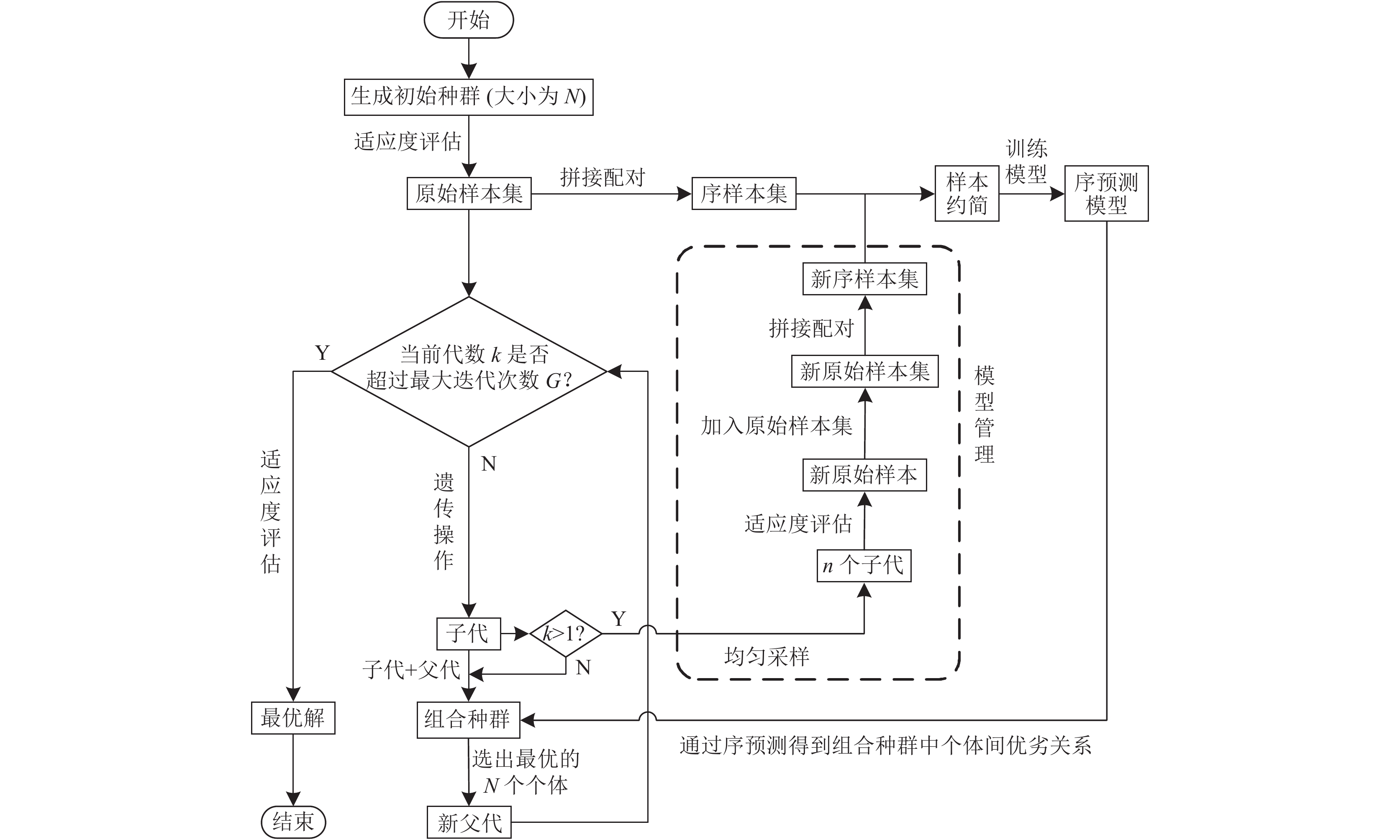
序预测辅助遗传算法的具体流程如图1所示. 首先生成大小为N的初始种群, 并对其进行真实适应度评估以生成原始样本集. 在此基础上, 通过对原始样本进行两两拼接配对以生成序样本集, 其后使用序样本约简方法对序样本集进行约简, 并通过约简后的序样本集训练序预测模型. 随后对初始种群进行迭代循环操作, 对当前种群进行遗传操作以生成其子代, 将父代与子代合并为组合种群, 并用序预测模型对其进行预测, 以得到组合种群中每个个体与其他个体之间的优劣关系, 依据此关系对组合种群进行优劣性排序, 选取排名靠前的 $ N $ 个个体进入下一代. 从第2代开始, 每次生成子代后, 对其进行均匀采样, 抽取 $n\;(n < N)$ 个个体进行真实适应度评估, 将评估后的个体加入原始样本集并以此生成新的序样本集, 通过对新序样本集的训练以调整序预测模型, 图1中虚线框内的内容即为模型管理过程. 重复以上内容, 直到满足预先定义的最大迭代次数. 迭代停止时, 对种群中排名第一的个体进行真实适应度评估并输出.

一般情况下, 基于个体的模型管理方法往往会选取那些被认为较优的解进行重评估, 以提高模型对于优秀解的预测能力. 但对于序预测方法而言, 其模型的预测能力主要取决于模型中含有的序样本集空间分布信息, 而序样本的空间信息表示的是两个原始候选解之间的相对性, 若只对优秀解进行重评估, 则无法构造表示优解与劣解之间关系的序样本, 故为了尽可能地利用序样本集空间信息, 通过均匀采样的方式来选取重评估的个体. 原始样本集来自于对搜索空间的均匀采样, 故其所构成的序样本集包含较多的序样本空间全局信息. 而对于来自子代的重评估个体加入原始样本集后生成的新序样本集, 其中不仅包括一部分关于子代的序样本集空间局部信息, 还包括一部分表示父代与子代关系的序样本空间局部信息, 故调整后的模型对组合种群有着更好的预测能力.

遗传算法的选择操作一般仅限于子代和其对应的父代之间, 当一个子代个体优于产生他的父代个体时, 会被选中进入下一代, 若该子代个体不及父代个体优秀, 则将选择其父代个体进入下一代. 但当父代个体为劣解时, 其产生的子代很可能也是劣解, 选择他们之中的任何一个都无法达到优化种群的效果. 故为了尽可能保证进入下一代的解为优解, 对组合种群整体进行选优, 以排除那些父子都不优秀的情况, 加快算法的收敛.

5.2 仿真实验

为检验序预测辅助遗传算法的性能, 将序预测辅助遗传算法与依靠真实评估的遗传算法在一些基准函数上做对比实验. 将代理模型用于解决昂贵优化问题的核心是为了减少耗时耗材的真实评估次数, 故本文设定几个不同的真实评估次数, 以观察序预测辅助遗传算法在不同评估资源条件下所展现出的性能. 实验测试函数选自CEC2015中的6个测试函数, 分别为两个多峰函数 $ f{\text{4}} $ 、 $ f{\text{8}} $ ; 两个混合函数 $ f11 $ 、 $ f12 $ ; 以及两个组合函数 $ f13 $ 、 $ f15 $ . 测试函数的维度选择10维. 遗传算子选择多项式变异和模拟二进制交叉. 遗传算法的具体参数如表4所示.

对于两种进化算法, 记录下50次迭代中所搜寻到的最优解. 分别记录下30次实验中这些最优解的均值与标准差, 以评价序预测辅助遗传算法在昂贵优化问题上的具体应用效果. 实验结果如表5、表6所示.

分析表5和表6的实验数据可得, 在以上不同测试函数上, 序预测辅助遗传算法均体现出了不同程度的寻优能力. 其中, 对于函数 $ f{\text{11}} $ , 序预测遗传算法仅使用1 000次真实适应度评估便搜索到了与遗传算法相近的最优解. 而在 $ f{\text{8}} $ 、 $ f{\text{13}} $ 、 $ f{\text{15}} $ 三个测试函数上, 序预测辅助遗传算法也通过使用2500次适应度评估达到了与遗传算法相同的效果. 对于 $ f{\text{4}} $ 与 $ f{\text{12}} $ 两个测试函数, 序预测辅助遗传算法虽然也搜索到了优秀的解, 但其结果与遗传算法相比还有一定的差距. 两种算法在函数 $ f{\text{4}} $ 上的标准差都比较大, 可见函数 $ f{\text{4}} $ 的优化难度较高. 昂贵优化问题的真实评估往往耗时耗财, 而序预测可仅使用部分评估资源达到与全部使用真实评估相近的结果, 可见序预测辅助的进化算法对求解昂贵优化问题有着巨大的应用潜力.

6 结论与展望

本文对候选解优劣性的序预测方法展开了研究, 通过序的分类预测方法判断候选解之间的优劣性, 相比于传统的回归预测方法, 不仅建模更简单, 而且泛化性更强. 针对序样本集规模过大的问题设计了序样本约简方法, 有效降低了预测模型的训练时长. 将序预测模型与遗传算法相结合, 有效降低了求解昂贵优化问题时的真实评估次数.

用于求解多目标昂贵优化问题的代理辅助进化算法其本质是分别对多个目标函数进行回归, 再根据预测出的目标函数值判断个体间的Pareto支配关系, 故序预测在多目标昂贵优化问题上也有着一定的应用前景. 接下来的研究工作是利用序预测中的不确定信息对不确定度较大的样本进行处理, 从而改善样本分布, 提高模型性能. 此外, 更加适合于序预测的模型管理方式也是一个有价值的研究方向.