2. 中国人民解放军32069部队, 北京 100091;
3. 中国人民解放军32269部队, 兰州 730030
2. 32069 Unit of PLA, Beijing 100091, China;
3. 32269 Unit of PLA, Lanzhou 730030, China
随着机器学习的不断发展, 机器学习在各个领域中得到了广泛的应用, 如医药[1], 生物学[2, 3]以及天文学[4]等. 但是, 大部分机器学习模型, 特别是神经网络模型, 为缺少透明性的黑盒模型, 即模型预测的过程无法被人们所理解[5]. 伴随着机器学习的深入研究和广泛应用, 人们对黑盒模型的可信度提出要求, 对于黑盒模型的可解释研究也随之发展起来.
近年来, 可解释方法研究工作得到了不断推进, 对黑盒模型进行解释的技术手段逐渐丰富起来, 比如类激活图[6], 梯度变化[7, 8]等可视化的方法. 但是其中一些方法是定性分析而非定量分析, 解释结果看似能够对模型做出解释, 实际上与模型预测不一定相关[9]. 为使解释结果可信度更高, 研究人员将博弈论中公平分配的Shapley值引入到黑盒模型可解释的研究工作中[10, 11], 用Shapley值表示每个输入特征对模型预测结果的贡献程度. 虽然在理论上基于Shapley值的解释方法有诸多良好的性质[12], 但最大的问题在于其过高的计算时间复杂度, 为指数级 , 并不适用于高维输入的黑盒模型, 因此需要一种准确快速的近似算法去计算Shapley值.
针对XGBoost、随机森林、梯度增强树等树结构模型, Lundberg等人[13]提出了基于TreeSHAP算法解释树结构模型的方法, TreeSHAP算法能够在多项式时间复杂度内计算出特征的Shapley值. 本文在TreeSHAP算法的基础上提出一种名为KDSHAP的可解释方法, 该方法引入KD树重新整理待解释数据集及其模型预测结果, 继承了TreeSHAP算法能够在多项式时间内计算Shapley值的优点, 同时能够解释除树结构模型之外的黑盒模型.
本文的主要工作包括: 通过插入虚节点改造KD树, 对待解释模型的预测数据进行了重新整理, 使得利用TreeSHAP算法快速计算Shapley值成为可能; 基于KD树及TreeSHAP算法提出了KDSHAP方法, 该方法在继承了TreeSHAP算法多项式时间复杂度的同时, 保证了Shapley值解释的准确度, 也避免了高维输入模型中Shapley值计算的限制; 通过KDSHAP方法与其它近似算法的对比实验, 显示出KDSHAP方法在准确性方面的优势; 另外, 也用实验证实了本文提出方法对高维输入模型的适用性.
1 基础知识近些年的可解释方法的研究中, 归因解释方法得到了研究人员的广泛关注, 归因解释方法探究样本特征对样本预测结果的贡献程度, 其中Shapley值是解释黑盒模型一种重要的归因方法.
1.1 归因方法归因方法(attribution methods)是一种基于特征的解释方法[14-16], 通过给样本中每个特征附上一个权值的方式解释黑盒模型. 假设黑盒模型
Lundberg等人[10]认为归因方法应具有以下属性:
(1)局部准确性(local accuracy)要求下列等式成立:
| $ \sum\limits_{i = 1}^d {{\phi _i}} = M({\boldsymbol{x}}) - {\phi _0} $ | (1) |
其中,
(2)缺失性(missingness) 要求若样本
(3)一致性(consistency) 要求对于两个不同的黑盒模型
Lundberg等人[10]认为联盟博弈中的Shapley值能够满足上述的是3种属性, 并提出了SHAP (Shapley value attribution explanation)的概念, 即基于Shapley值的归因方法.
1.2 基于Shapley值的特征贡献程度计算Shapley值是联盟博弈中用于解决可信公平分配问题的最优解, 由Shapley于1953年提出[17], 其计算过程如下所示:
| $ \begin{split} {\phi _i}(M, \mathcal{X}) =& {\sum _{\mathcal{S} \subseteq \mathcal{X}\backslash \{ {X_i}\} }}\frac{{|\mathcal{S}|!(|\mathcal{X}| - |\mathcal{S}| - 1)!}}{{|\mathcal{X}|!}} \\ &\times[\mu (\mathcal{S} \cup \{ {X_i}\} ) - \mu (\mathcal{S})] \end{split} $ | (2) |
式(2)的计算结果是特征
根据黑盒模型
| $ \begin{array}{*{20}{l}} {\mu (\mathcal{S})}{ = \mathbb{E}[M({\boldsymbol{x}})|\mathcal{S}]} {}{ \approx {\mathbb{E}_{{\mathcal{S}^C}}}[M({\boldsymbol{x}})]} \end{array} $ | (3) |
其中,
对于实际问题, 具体做法(如图1所示, 图中不同颜色代表不同的值)如下: 存在黑盒模型

|
图 1 RealSHAP算法计算联盟值 |
2 KDSHAP
RealSHAP算法解释黑盒模型就必须考虑样本集
KDSHAP方法伪代码如算法1所示.
算法1. KDSHAP
输入: 待解释样本
输出: Shapley值向量
1. Procedure
2. 初始化:
3.
4.
5.
6.
7. return
本文提出来一种可解释方法KDSHAP, 该方法能够快速计算Shapley值来解释黑盒模型. KDSHAP方法所需的参数有待解释数据集
TreeSHAP算法[13, 18]利用树结构模型的特点, 能够在多项式时间内计算出样本
为使TreeSHAP算法适用于所有的黑盒模型, 本文采用两步走的思路: 首先, 引入KD树将黑盒模型的输入/输出数据整理成树状结构; 然后利用TreeSHAP算法计算目标样本特征的Shapley值.
KD树作为一种数据结构, 避免了决策树复杂的特征选择过程, 能够在短时间内快速地重新组织待解释数据集. KD树是在K维欧几里得空间组织点的数据结构, 其中所有的非叶子节点都可看作是一个超平面, 将当前空间划分成两个半空间, 左子树上的点在超平面左边, 超平面的右边的点在右子树上, 该特点与决策树相似. 相对于决策树, KD树在选择中间节点的特征时没有复杂的计算, 能够更快速地得到数据集的树状结构. 假设存在数据集
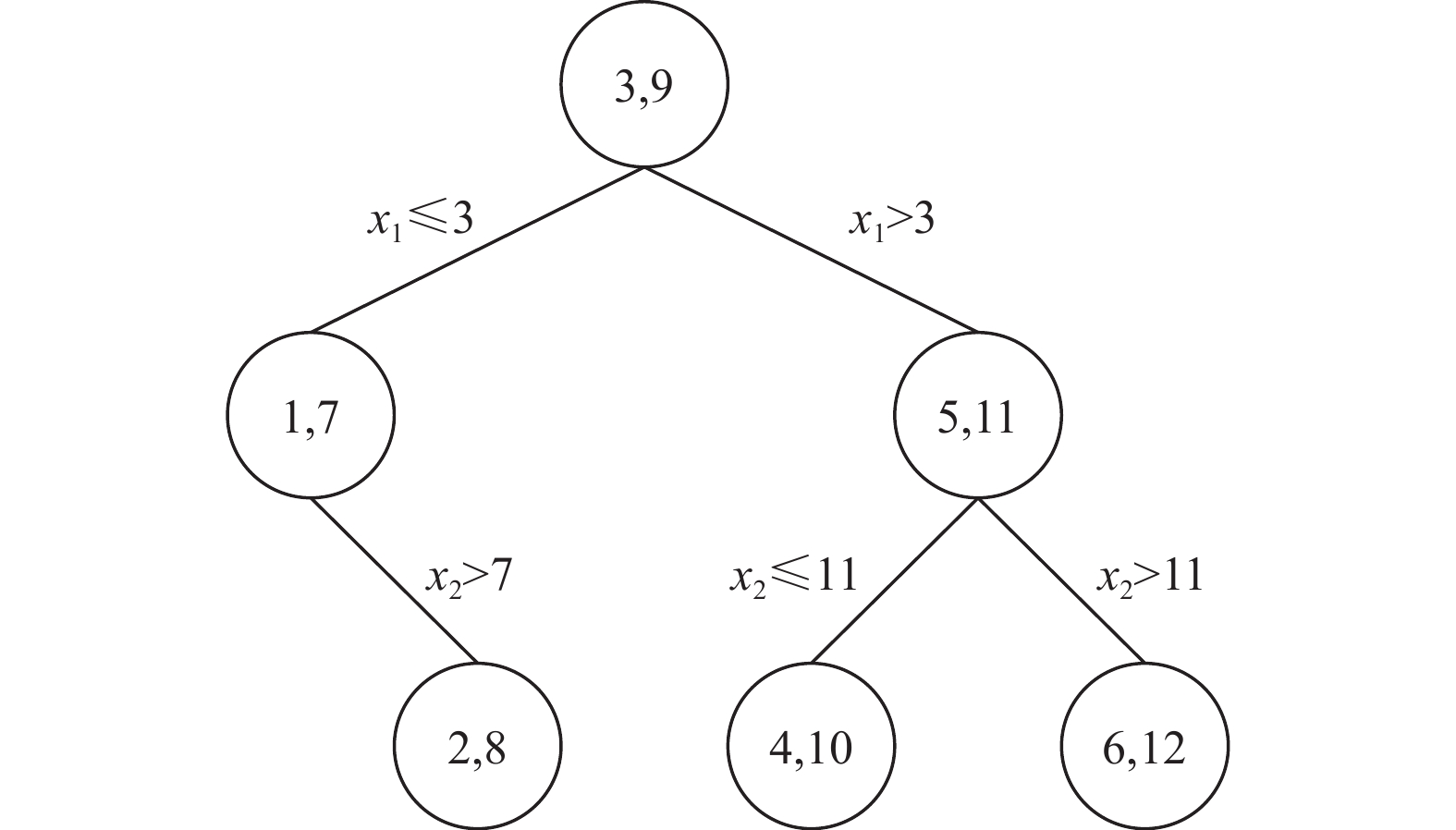
|
图 2 KD树构造示例 |
虽然KD树能够重新组织数据集成树状结构, 但是直接构造出的KD树不能满足TreeSHAP算法的适用条件. 因为树结构模型中的关于样本预测结果的信息仅存在于叶子节点上, 而KD树中的所有节点都保存有样本预测结果. 为更好地利用TreeSHAP算法, 需要对原始KD树结构进行改造.
相较于TreeSHAP算法所需的树结构, KD树存在的主要问题是树中所有的节点都包含样本预测结果信息. 为解决适用性问题, 本文通过在KD树中插入虚节点的方式改造KD树, 生成过程如算法 2.
算法2.CreateKDTree
输入: 待解释数据集
输出: KD树
1. Procedure CreateKDTree(
2.
3. if
4.
// 如果
5. else
6.
7. if
8.
9.
10.
11.
12. return
改造后的KD树由两种不同的节点构成, 分别是虚节点和样本节点. 虚节点充当KD树的中间节点(算法 2中第10, 11行), 其作用是选择左右分支以及保存流经该节点上的样本数量等信息. 样本节点也是叶子节点(算法 2中第4行), 树中的每一个叶子节点都对应数据集中的一个样本, 叶子节点中保存了样本数据以及模型对该样本的预测结果. 经过上述算法改造, 图2中的KD树结构改变为图3所示, 满足了TreeSHAP算法的适用要求.
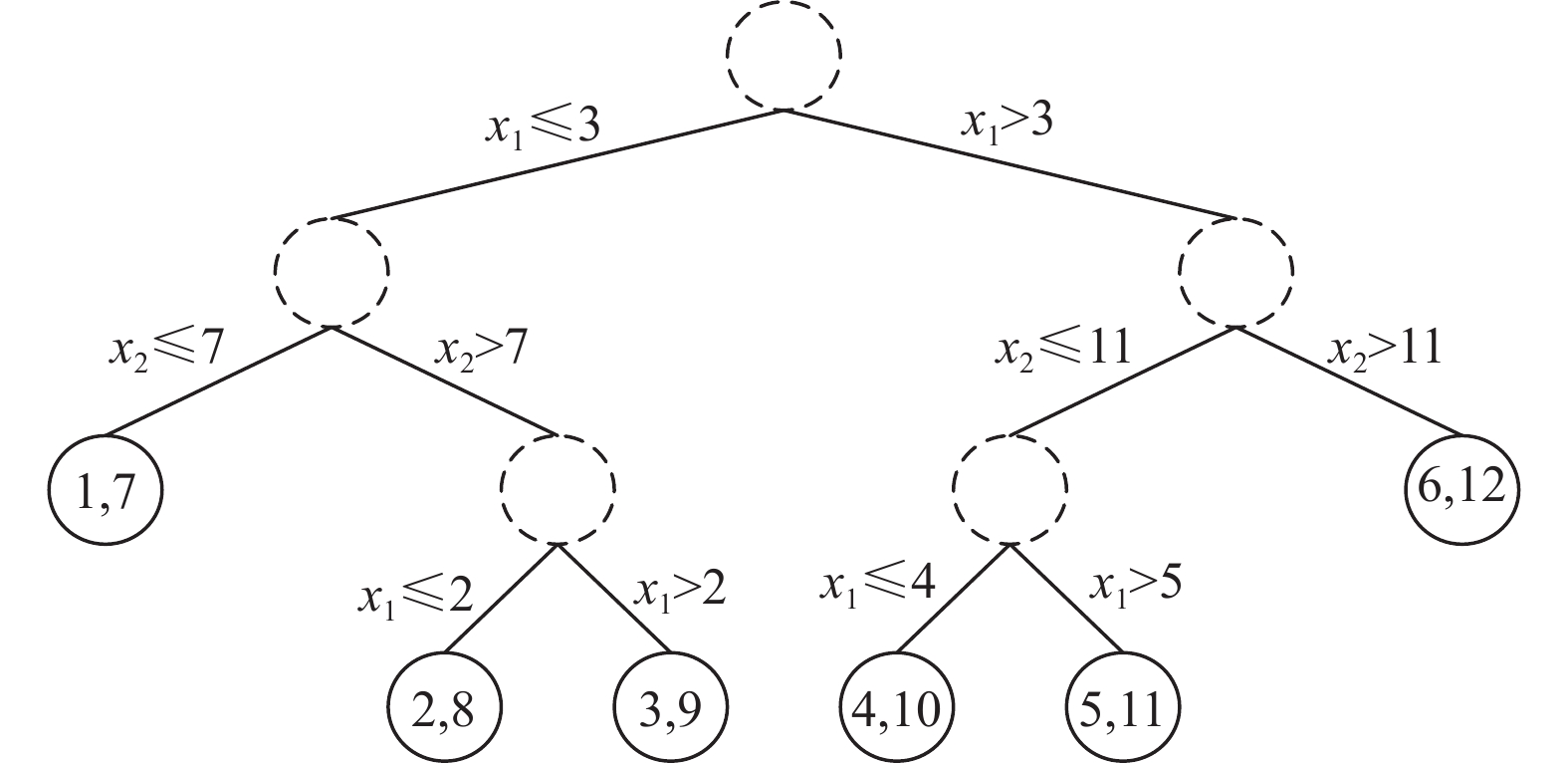
|
图 3 经改造后的KD树 |
3 实验分析
本文设计了3个实验来探究KDSHAP的可行性以及准确性. 实验1, 比较KDSHAP方法的解释结果与其它Shapley值近似算法的准确性; 实验2, 研究不同样本数量构成的KD树对解释结果准确性的影响; 实验3, 使用KDSHAP方法解释高维输入模型, 证明KDSHAP方法在高维数据上的可行性. 需要说明的是, 实验1与实验2都是使用RealSHAP算法的解释结果作为基准.
3.1 实验1. KDSHAP的准确性实验1使用的数据集共有10 000条数据, 单个样本由3个特征组成, 每个特征的数据类型都是浮点型. 构造KD树时使用了整个数据集, 即10 000条数据, 为了说明KDSHAP的准确性, 对照组使用填充缺失特征的近似算法[19]. 对于缺失特征
| 表 1 实验1结果对比 |
RealSHAP算法的解释结果在实验中充当基准值. 假设近似算法的解释结果为
平均绝对值损失函数用来衡量近似算法与RealSHAP算法解释结果的平均
| $ L_1^{\rm mean}{\text{ = }}\frac{1}{{nH}}\sum\limits_{k = 1}^H {\sum\limits_{i = 0}^{n - 1} | } {\phi _{k, i}} - {\hat \phi _{k, i}}{\text{|}} $ | (4) |
均方误差指标是近似算法解释结果偏离RealSHAP算法解释结果差值的平方和的均值, 其计算过程如下所示:
| $ {\textit{MSE}} = \frac{1}{{nH}}\sum\limits_{k = 1}^H {\sum\limits_{i = 0}^{n - 1} {{{({\phi _{k, i}} - {{\hat \phi }_{k, i}})}^2}} } $ | (5) |
斯皮尔曼秩相关系数又称等级相关系数, 主要用来描述存在等级变量的两个变量间关联的程度, 其计算结果的绝对值越靠近1, 说明这两组数据的相关性越强, 绝对值越接近0, 等级相关性越弱. 本实验使用平均斯皮尔曼秩相关系数衡量近似算法与RealSHAP算法结果的相关程度, 首先计算出对单条样本使用的斯皮尔曼秩相关系数(
| $ {r_s} = 1 - \frac{{6 \times \displaystyle\sum\limits_{i = 0}^{n - 1} {{{({\phi _i} - {{\hat \phi }_i})}^2}} }}{{n \times ({n^2} - 1)}} $ | (6) |
| $ r_s^{\rm mean} = \frac{1}{H}\sum\limits_{k = 1}^H {r_s^{(k)}} $ | (7) |
实验结果表明, KDSHAP在3个指标上全部是最优的, 说明本文提出的方法与RealSHAP算法的解释结果最为接近. 此外, 还可以发现, 不同的填充样本对解释结果也有较大的影响.
3.2 实验2. 不同样本数量对KDSHAP准确性的影响通过对KD树生成过程分析可知, 如果样本数量越多, KD树的深度越深, 那么就可能存在同一特征在不同深度位置分裂多次的情况. 设计本次实验的目的是探究不同的样本数量对KDSHAP方法解释结果的影响.
本实验使用的数据集与实验1为同一数据集, 为达到实验目的, 从整个数据集中进行10次采样, 从1 000个样本容量开始, 每次增加1 000个样本. 根据不同容量的采样结果构建KD树, 计算不同样本容量下的解释结果与RealSHAP算法解释结果的均方误差(MSE), 实验结果如图4所示.
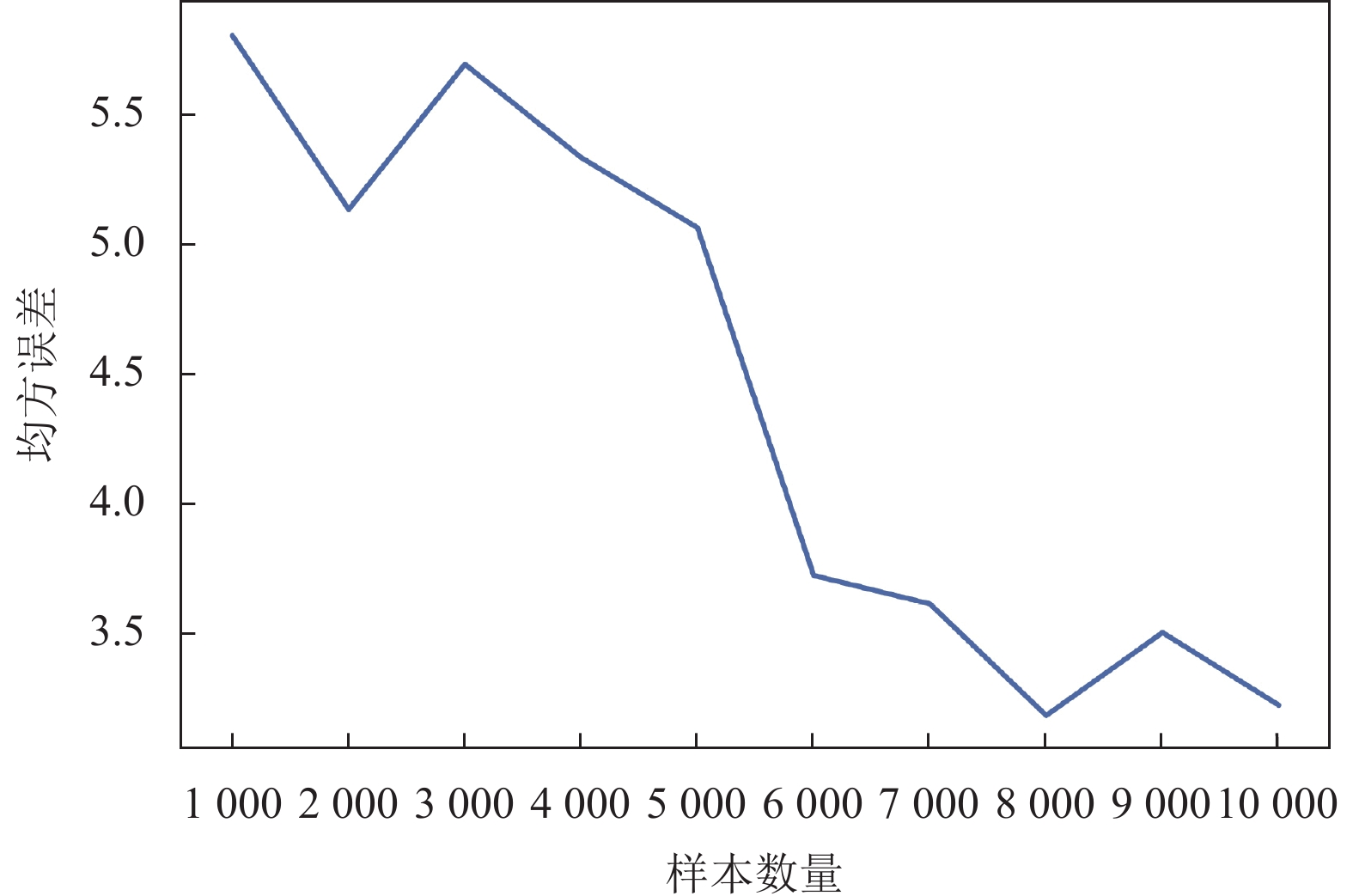
|
图 4 均方误差随样本数量的变化情况 |
通过对比不同样本容量下均方误差的变化情况发现, 随着样本容量的增加, 均方误差值总体上呈现减小趋势. 这说明参与构建KD树的样本容量越大, KDSHAP的解释结果误差越小越准确.
3.3 实验3. KDSHAP对大规模数据集的适用性该实验使用的数据集共有8 000条数据, 每条数据有20维特征, 每个维度上的数据符合正态分布, 模型
表2中, 共有权重
而RealSHAP算法要考虑
通过实验对比发现, 本文提出的KDSHAP方法对黑盒模型的解释结果更接近真实Shapley值, 而且在计算时间复杂度上相较于RealSHAP 算法, KDSHAP方法的计算代价更容易接受, 更适用于高维输入的黑盒模型. 现阶段本文只是在一些简单的表格数据及模型上做了一些尝试性工作, 在未来可以应用在处理计算机视觉和自然语言处理等任务的模型上. 此外, KDSHAP还可以在KD树特征选择上做一些改进工作, 使得KD树能更准确表达出待解释数据集中样本分布信息, 达到更精准的效果.
| 表 2 KDSHAP对样本x的解释结果 |
| [1] |
Wainberg M, Merico D, Delong A, et al. Deep learning in biomedicine. Nature Biotechnology, 2018, 36(9): 829-838. DOI:10.1038/nbt.4233 |
| [2] |
Xiong HY, Alipanahi B, Lee LJ, et al. The human splicing code reveals new insights into the genetic determinants of disease. Science, 2015, 347(6218): 1254806. DOI:10.1126/science.1254806 |
| [3] |
Zhang S, Hu HL, Jiang T, et al. TITER: Predicting translation initiation sites by deep learning. Bioinformatics, 2017, 33(14): i234-i242. DOI:10.1093/bioinformatics/btx247 |
| [4] |
Parks D, Prochaska JX, Dong S, et al. Deep learning of quasar spectra to discover and characterize damped Lyα systems. Monthly Notices of the Royal Astronomical Society, 2018, 476(1): 1151-1168. DOI:10.1093/mnras/sty196 |
| [5] |
Rudin C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nature Machine Intelligence, 2019, 1(5): 206-215. DOI:10.1038/s42256-019-0048-x |
| [6] |
Zhou BL, Khosla A, Lapedriza A, et al. Learning deep features for discriminative localization. Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas: IEEE, 2016. 2921–2929.
|
| [7] |
Shrikumar A, Greenside P, Kundaje A. Learning important features through propagating activation differences. Proceedings of the 34th International Conference on Machine Learning. Sydney: PMLR, 2017. 3145–3153.
|
| [8] |
Sundararajan M, Taly A, Yan QQ. Gradients of counterfactuals. arXiv: 1611.02639, 2016.
|
| [9] |
Jacovi A, Goldberg Y. Towards faithfully interpretable NLP systems: How should we define and evaluate faithfulness? Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics. Association for Computational Linguistics, 2020, 4198-4205. |
| [10] |
Lundberg SM, Lee SI. A unified approach to interpreting model predictions. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 4768–4777.
|
| [11] |
Štrumbelj E, Kononenko I. Explaining prediction models and individual predictions with feature contributions. Knowledge and Information Systems, 2014, 41(3): 647-665. DOI:10.1007/s10115-013-0679-x |
| [12] |
Shapley LS. A value for n-person games. Contributions to the Theory of Games (AM-28), Volume II. In: Kuhn HE, Tucker AW, eds. Princeton: Princeton University Press, 2016. 307–318.
|
| [13] |
Lundberg SM, Erion GG, Lee SI. Consistent individualized feature attribution for tree ensembles. arXiv: 1802.03888, 2018.
|
| [14] |
Chen JB, Jordan M. LS-tree: Model interpretation when the data are linguistic. Proceedings of the 34th AAAI Conference on Artificial Intelligence. New York: AAAI, 2020. 3454–3461.
|
| [15] |
Arras L, Montavon G, Müller KR, et al. Explaining recurrent neural network predictions in sentiment analysis. Proceedings of the 8th Workshop on Computational Approaches to Subjectivity, Sentiment and Social Media Analysis. Copenhagen: Association for Computational Linguistics, 2017. 159–168.
|
| [16] |
Bach S, Binder A, Montavon G, et al. On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation. PLoS One, 2015, 10(7): e0130140. DOI:10.1371/journal.pone.0130140 |
| [17] |
Shapley LS. A value for n-person games. Contributions to the Theory of Games, 1953: 307–317.
|
| [18] |
Lundberg SM, Erion G, Chen H, et al. From local explanations to global understanding with explainable AI for trees. Nature Machine Intelligence, 2020, 2(1): 56-67. DOI:10.1038/s42256-019-0138-9 |
| [19] |
Chen H, Lundberg S, Lee SI. Understanding Shapley value explanation algorithms for trees. https://hughchen.github.io/its_blog/index.html. (2021-12-22).
|
 2022, Vol. 31
2022, Vol. 31


