根据节点的某种重要性对节点排序是目前研究热点之一[1]. 基于复杂网络理论, 在进行节点重要性研究时常用的统计指标有度中心性、特征向量中心性、k-核分解、接近中心性、介数中心性、PageRank算法等[2]. 这些中心性度量方法从不同的角度衡量节点重要性, 在不同的场景下应根据研究目的选择恰当的中心性方法评估节点的重要性. 对于交通运输网络, 由于此类网络中枢纽节点和链路具有鲜明的空间属性, 节点的位置差异使得其在网络中扮演着独特的角色. 如何找到网络中具有位置优势的关键节点, 对整个运输任务的空间战略部署具有重大经济决策价值[3].
戈佳威等[4]选取不同节点中心性指标与传播动力学视角下的SIS模型得到的集装箱海运网络节点传播能力排序进行比较, 指出节点间最短路径距离是衡量港口节点重要性的重要因素. 冯慧芳等[5]采用基于DWNodeRank的有向加权网络节点重要性排序算法, 识别城市交通路网的关键节点. Zhou等[6]使用了一种考虑节点连接权重的效率指标的方法识别关键机场和评估航空运输网络的鲁棒性.
综上, 节点间最短路径距离因其从全局上很好地衡量了节点的位置优势, 成为交通运输网络场景下识别关键节点的重要拓扑指标. 接近中心性基于这一指标评价节点的重要程度, 具体表现为该度量越大, 节点可以以平均更短的距离到达其他所有节点. 它可以通过从相应节点执行广度优先遍历(BFT)来精确计算. 对于一个含有n个节点、m条边的网络, 每个节点的计算时间复杂度是O(m), 则网络所有节点的计算时间复杂度为O(nm). 随着网络规模的增大, 该精确计算方法将非常耗时, 因此不适用于大规模复杂网络. 由于真实的交通网络往往是大规模、动态的, 如何在保持较高的近似准确性的同时降低计算复杂性成为一个关键问题.
刘微等[7]从图论的角度将图构造成一棵树来搜索目标顶点, 提出了基于树分解搜索算法的最短路径近似算法. Grando等[8]从网络特征学习的角度, 认为假设以包含节点局部特征的指标作为模型的输入, 通过构建机器学习算法模型可以近似得到某一全局指标的排序. 目前最新的研究进展采用基于机器学习和神经网络模型近似估计中心性度量, 这种方法已经被证明在大型真实网络上能够取得较好的效果[9]. 然而, 机器学习算法的缺点是需要大量的训练时间, 用于真实网络的模型首先需要在大量的不同结构特征的小规模网络上训练[10]. 此外, Grando等 [11]建立的回归模型, 使用均方误差(MSE)作为损失函数. 但在实际应用中, 我们更应该关注节点重要性的相对顺序, 而不是中心性度量的绝对误差.
基于此, 本研究提出了一种基于排序学习算法快速逼近节点接近中心性排序的方法. 为了验证模型的排序效果, 本文将所提出的模型与基准模型进行了对比分析, 以一个真实航空运输网络为案例, 验证该方法的有效性.
1 网络节点重要性指标分析 1.1 接近中心性定义本文从公开网络数据库
| 表 1 USAir97网络结构参数 |
根据复杂网络理论, 节点的接近中心性表示一个节点到网络其他所有节点的接近程度. 设G(V, E)为无向无权的全联通网络, 其中V表示节点集合, E为边的集合, 令n = |V|, m = |E|, 分别表示网络的节点个数和边的条数. 节点i的接近中心性C(i)定义为节点i到其余所有节点最短路径距离之和的倒数, 即:
| C(i)=n−1∑j≠idij | (1) |
其中, dij表示节点i和节点j之间的最短路径距离. 由于一个非全联通网络的节点之间不存在最短路径, 本文只考虑实验网络的最大联通子图. 根据节点的接近中心性的重要程度, 渲染得到的USAir97航空网络如图1所示.

|
图 1 依据节点接近中心性渲染的USAir97网络 |
1.2 相关性分析
在描述节点在网络中的重要程度的指标中, 指标的计算复杂度与涵盖的节点邻接矩阵信息呈正相关. 根据指标所包含的节点邻接矩阵信息可以分为局部中心性、半局部中心性和全局中心性. 局部中心性如节点度值不包含相邻节点的信息, 半局部中心性如特征向量中心性包含一阶邻接节点的信息, 而全局中心性如k-核分解包含了节点在网络中的位置、接近中心性包含了节点间的距离, 从全局网络结构刻画了节点重要性. 由于接近中心性的精确计算非常耗时, 为得到尽可能精确的接近中心性指标排序, 选取节点度值、特征向量中心性、k-核这3个低复杂度指标, 分析与接近中心性的相关关系.
(1) 度中心性
节点的度是指与该节点直接相连的节点个数. 值越大对应节点直接连接的节点越多, 对应节点的重要度越高. 从理论上讲, 度中心性与接近中心性呈正相关. 如果一个节点平均只需更短距离就能被其他节点到达, 那么这个节点一定是高度连通的.
(2) 特征向量中心性
特征向量中心性是一种半局部特征指标, 取值受节点的周围环境(相邻节点的数量和质量)影响, 其本质是节点的中心性是相邻节点中心性的总和. 因此, 节点可以通过连接许多其他重要节点来增强其重要性.
(3) k-核
节点的k-核表示其在全局网络结构中的位置, 可以通过对网络进行k-核分解得到. 采用k-核迭代分解的方法对网络进行分解, 中心壳层节点的核数大于外围壳层节点的核数. 最后, 节点的k-核取值等于对应的壳层. 显然, 一个节点的k-核值越大, 说明该节点位于网络的中心, 可能与网络中的其他节点平均距离更近.
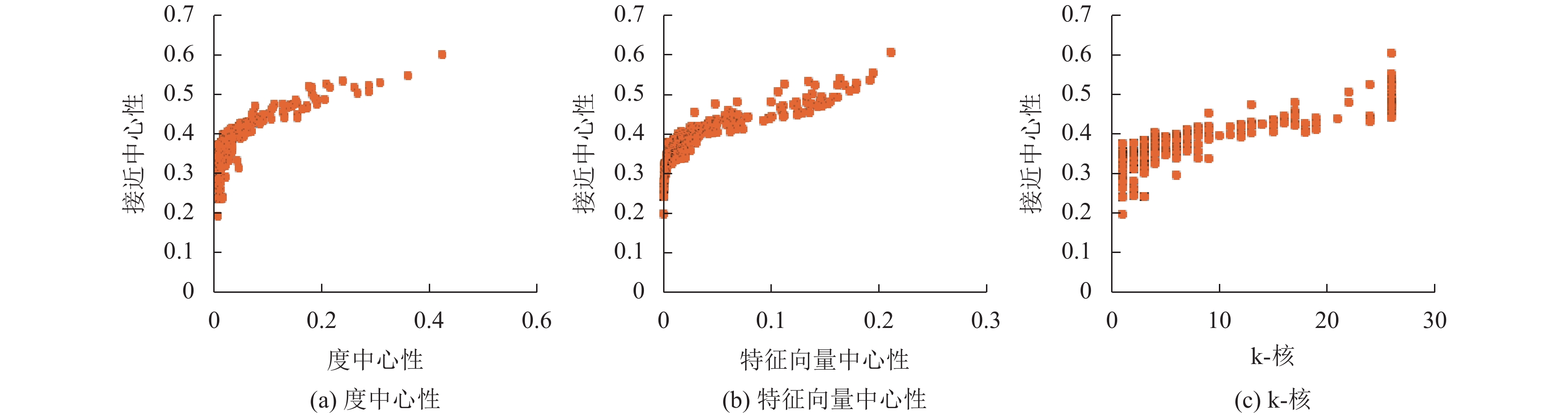
如图2所示, 总体上不同节点的接近中心性和度中心性、特征向量中心性和k-核呈正相关. 因此, 本文选择这3个指标作为节点接近中心性排序模型的输入特征.
|
图 2 USAir97网络低复杂度中心性与接近中心性的相关性 |
2 节点接近中心性近似排序模型
根据节点的接近中心性对节点排序以快速识别关键节点, 本文将该任务转化为一个排序问题.
RankNet算法是Burges等[12]提出的一种基于Pairwise的排序学习算法, 即每次考虑一对样本. 基本思想是将排序问题转化为二元分类问题, 考虑两个样本的相对顺序. RankNet算法基于神经网络模型从概率的角度解决二元分类问题. 每对训练样本都与一个概率相关联. 概率值为1、0和0.5表示一个样本的排序在另一个样本之前、之后或不确定. 因此, 对神经网络模型进行训练, 找到一个模型可以将样本对映射到一个接近它们目标概率的概率, 对样本对的顺序进行预测. RankNet采用交叉熵损失函数, 利用梯度下降法训练神经网络模型.
基于上述算法, 本文提出节点接近中心性重要度排序模型, 用度值、特征向量中心性及k-核来作为输入特征, 学习节点接近中心性排序. 与目前研究提出的基于机器学习或者神经网络的节点中心性近似方法区别在于: 本文用被研究网络的随机采样节点作为训练集; 利用交叉熵损失函数迭代优化神经网络的参数. 具体实现步骤如下.
Step 1. 从给定的网络中随机选取α比例数量的采样节点作为训练集V'. 通过重复实验模拟, 取α在[0.1, 0.2]范围内.
Step 2. 假设训练集V' 有n个节点, 计算每个节点的度中心性, 特征向量中心性, k-核3个指标. Xij表示第i个节点的第j个指标, i = 1, 2, 3, …, n, j = 1, 2, 3. 则训练样本节点的特征矩阵为:
| X=[X11X21⋮Xn1X12X22⋮Xn2X13X23⋮Xn3] |
为提升模型精度, 将X矩阵进行z-score标准化处理.
Step 3. 前向传播函数. 建立多层感知器(multilayer perceptron, MLP)神经网络, 该神经网络有3个隐藏层, 每个隐藏层有20个神经元, 最后选择一个线性输出层. 输入特征为标准化以后的X矩阵, 则模型预测输出的接近中心性排名分数向量Y为:
| Y=ReLU(ReLU(ReLU(XW1)W2)W3)W4 | (2) |
Step 4. 迭代优化. 基于Pairwise的交叉熵损失函数, 利用梯度下降的原理更新神经网络的权重W.
给定一个节点对(u, v), 假设接近中心性度量的真值分别为cu和cv, 本文构建的模型输出的预测排名得分分别为yu和yv. 模型需要训练前向传播函数可以将样本对映射到一个接近它们目标概率的概率, 对样本对的顺序进行预测. 记cuv ≡ cv – cv, yuv ≡ yv – yv. 选择一个可导的函数进行概率的映射, 这里选择Sigmoid 函数. 目标概率
| ¯Pu,v=Sigmoid(cuv)=11+e−cuv | (3) |
排名概率为:
| Pu,v=Sigmoid(yuv)=11+e−yuv | (4) |
使用以下交叉熵损失函数:
| Cu,v=−¯Pu,vlgPu,v−(1−¯Pu,v)lg(1−Pu,v) | (5) |
因此, 总的损失定义为:
| LTOTAL=∑u,v∈V′Cu,v | (6) |
设n和m为网络的节点数和连边数, 各节点中心性指标的计算时间复杂度如表2所示.
| 表 2 节点中心性指标计算时间复杂度 |
算法主要的时间复杂度来自两个方面: 预计算时间和训练时间.
1) 预计算时间: 在数据预处理步骤中, 需要计算给定网络中所有节点的3个低复杂度指标(度中心性、特征向量中心性和k-核)和训练集节点的接近中心性指标. 由表3可知, 3个低复杂度指标的计算时间远小于接近中心性, 因此可忽略. 当随机采样αn个节点作为训练集时, 计算接近中心性的时间复杂度为O(αnm), 其中α在[0.1, 0.2]范围内, 大大降低了时间成本.
| 表 3 超参数配置 |
2) 训练时间: 由式(6)可知, 理论上训练过程的时间与训练迭代的次数成正比, 迭代次数和神经网络的超参数有关. 本文采用了批量训练的方式, 每一个batch按1.5:1的比例随机形成节点对. 源节点从当前训练的batch中选择, 目标节点从之前的所有迭代中选择. 例如, 假设一个batch的大小有N个训练样本, 本文的实验随机抽取1.5N个源节点和1.5N个目标节点形成1.5N个随机节点对计算损失. 表3给出了本文基于实验优化后的超参数值. 实际实验的训练时间小于1 min.
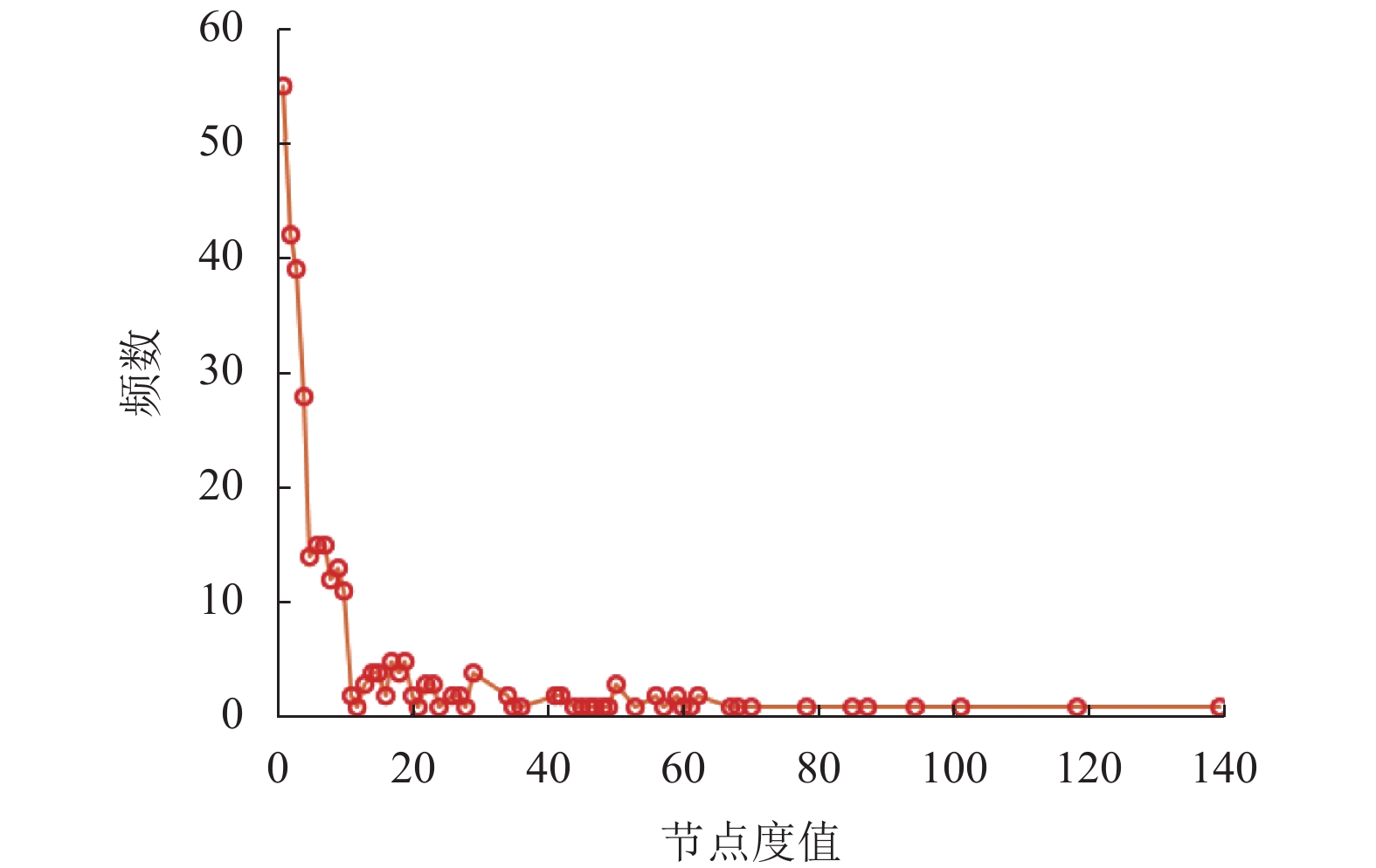
3.2 数据集为了有效评估本文所提方法的性能, 本文在人工生成的网络模型上进行了补充实验. 根据现实世界真实网络表现出的结构特点, 本文选择了3种常见网络模型: ER随机图模型, BA无标度网络[13], 聚类系数可变无标度网络HK模型[14]. ER随机图模型是早期研究较多的一类复杂网络模型之一, 模型的基本思想是以概率p连接n个节点中的每一对节点. 而Barabási等[13]发现现实世界真实网络的度分布服从幂律分布, 存在枢纽节点(拥有大量连接的节点), 由此提出了区别于随机网络模型的两个要素生长和偏好连接, 建立BA无标度模型. HK模型也是一种无标度模型, 实现了近似平均聚类使网络增长. 图3是USAir97航空网络的度分布图, 可以发现, 少数节点度非常高, 而大多数节点度相对较低, 服从幂律分布. 因此, 这也验证了USAir97航空网络也属于BA无标度模型.
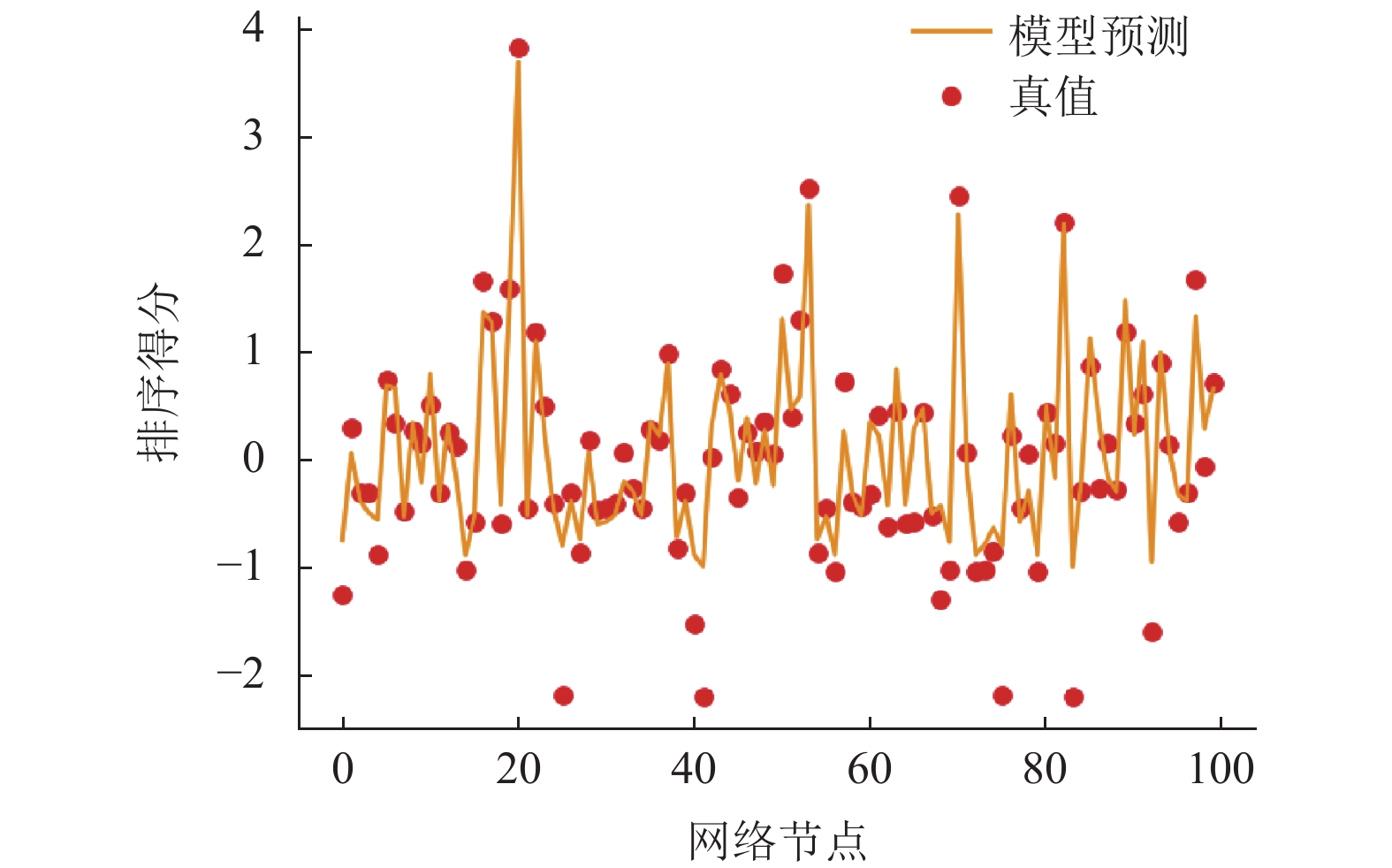
3.3 实验结果及分析本文首先在USAir97网络上验证所提方法的有效性. 如第3.1节所述, 如果选择网络中大量的节点来训练模型, 该方法在计算代价上没有优势. 随机选取60个节点作为训练集, 占节点总数的18%. 从剩余节点中随机抽取100个样本节点进行测试. 如图4所示, 从预测排序的拟合线可以看出, 模型可以估计大部分节点的相对排序. 将预测排名和实际排名的前10个节点进行比较, 即20、53、70、82、19、89、16、97、50、17和20、53、70、82、50、97、16、19、52、17. 前4位节点是完全相同的, 其余节点基本相同, 只有少数节点交换了它们的顺序. 说明排序模型在头部节点的预测效果上要比尾部节点的表现更好. 进一步分析, 由图2和图3可知, 接近中心性高的节点具有更大的度, 根据幂律分布, 头部节点的训练输入特征更显著, 因此模型的预测准确度更高.
|
图 3 USAir97网络度分布图 |
|
图 4 USAir97网络节点排序得分预测 |
为了进一步比较模型的精度, 本文将文献[11]提出的回归模型, 采用相同的MLP神经网络结构作为基准, 与本文的方法进行比较. 采用Top-K%准确率进行描述, 并使用Kendall 相关系数作为评价指标. Top-K%准确率通过模型输出与实际真值的Top-K%节点重叠率来评价排序质量, 定义为:
| Top-K%=|{returnedTop-K%nodes}∩{true Top-K%nodes}|[|V|×K%] | (7) |
其中, |V|为测试节点数,
Kendall 相关系数是用来衡量两个有序变量之间的一致性. 设节点接近中心性的真值排序为X, 模型输出得到的节点排序为Y, 由此得到有序对应的元素, (x1, y1), (x2, y2),···, (xn, yn), 对于任意的 i 和 j , 如果xi > xj (或 xi < xj ), 且 yi > yj (或 yi < yj ), 那么称这一对元素为同序对, 反之则称其为异序对. 定义为:
| K(x,y)=2(P−Q)n×(n−1) | (8) |
其中, P为同序对的数目, Q为异序对的数目, n为样本总数. 由式(8)可知: 取值为1表示两个排序完全相同; 相关系数越大, 两个排序越接近, 反映模型预测更符合真实的节点接近中心性排序, 从而证明该模型的预测准确度较其他模型更高.
对于3种人工网络模型, 生成含有1 000个节点的大规模网络. 对于BA模型和HK模型, 每个节点具有相同的k-核. 因此, 相应的算法输入特征只使用度中心性和特征向量中心性. 表4为本文提出的模型和基准模型在3种人工网络模型上的效果评价对比. 所有的实验结果均是在5个随机测试集上进行实验并取平均值得到的. 可以发现, 在Top-10%节点准确率方面两种模型取得了相当的准确性. 而在Top-1%节点准确率方面本文的方法与基准模型相比表现更好. 当选择100个节点作为测试样本, Top-1%的准确率是指接近中心性最高的节点. 意味着本文的模型可以更准确地找到给定节点集的最中心节点. 从Kendall相关系数分析可知, 本文方法在这3种网络模型上的性能都优于基准模型. 尤其是对于聚类系数可变无标度网络HK模型, 本文方法的预测准确度较基准模型大幅度提升. 横向对比3种网络模型, 可以发现, 属于无标度网络的BA模型、HK模型较ER随机图的预测效果更好. 真实世界网络大多是符合幂律分布的无标度网络, 说明根据节点的局部特征重要度指标, 近似全局特征的重要度排序这种方法是适用于真实网络的有效方法.
4 结论与展望本文提出了一种不需要计算所有节点的接近中心性就能快速逼近节点接近中心性排序的方法. 与以往的研究使用大量的小规模合成网络训练模型, 然后将其应用到大规模网络不同, 本文的实验表明网络本身的拓扑结构特征允许使用少量的节点作为训练样本来建立预测模型. 在此前提下, 将预测节点的重要性转化为排序学习问题, 采用基于RankNet的算法进行排序. 实验结果表明, 该方法对接近中心性高的节点排序和无标度网络模型具有较好的准确率. 依据现实网络大多是符合幂律分布的无标度网络, 说明根据节点的局部特征重要度指标, 近似全局特征的重要度排序这种方法是适用于真实网络的有效方法, 对交通、航空等复杂网络中具有区位优势的节点进行智能识别具有重要意义.
| 表 4 不同网络上基准模型与排序学习模型的结果对比 |
| [1] |
安沈昊, 于荣欢. 复杂网络理论研究综述. 计算机系统应用, 2020, 29(9): 26-31. DOI:10.15888/j.cnki.csa.007617 |
| [2] |
Lü LY, Chen DB, Ren XL, et al. Vital nodes identification in complex networks. Physics Reports, 2016, 650: 1-63. DOI:10.1016/j.physrep.2016.06.007 |
| [3] |
Wang JE, Mo HH, Wang FH, et al. Exploring the network structure and nodal centrality of China’s air transport net-work: A complex network approach. Journal of Transport Geography, 2011, 19(4): 712-721. DOI:10.1016/j.jtrangeo.2010.08.012 |
| [4] |
戈佳威, 袁克镖, 殷明, 等. 传播动力学视角下集装箱海运网络关键港口节点识别. 交通运输系统工程与信息, 2021, 21(4): 256-262. DOI:10.16097/j.cnki.1009-6744.2021.04.031 |
| [5] |
冯慧芳, 柏凤山, 徐有基. 基于轨迹大数据的城市交通感知和路网关键节点识别. 交通运输系统工程与信息, 2018, 18(3): 42-47, 54. DOI:10.16097/j.cnki.1009-6744.2018.03.007 |
| [6] |
Zhou YM, Wang JW, Huang GQ. Efficiency and robustness of weighted air transport networks. Transportation Research Part E: Logistics and Transportation Review, 2019, 122: 14-26. DOI:10.1016/j.tre.2018.11.008 |
| [7] |
刘微, 肖华勇. 复杂网络中近似最短路径问题. 计算机系统应用, 2016, 25(5): 107-112. |
| [8] |
Grando F, Lamb LC. Estimating complex networks centrality via neural networks and machine learning. Proceedings of 2015 International Joint Conference on Neural Networks. Killarney: IEEE, 2015. 1–8.
|
| [9] |
Maurya SK, Liu X, Murata T. Fast approximations of betweenness centrality with graph neural networks. Proceedings of the 28th ACM International Conference on Information and Knowledge Management. Beijing: ACM, 2019. 2149–2152.
|
| [10] |
Mendonça MRF, Barreto AMS, Ziviani A. Approximating network centrality measures using node embedding and machine learning. IEEE Transactions on Network Science and Engineering, 2021, 8(1): 220-230. DOI:10.1109/TNSE.2020.3035352 |
| [11] |
Grando F, Granville LZ, Lamb LC. Machine learning in network centrality measures: Tutorial and outlook. ACM Computing Surveys, 2019, 51(5): 102. |
| [12] |
Burges C, Shaked T, Renshaw E, et al. Learning to rank using gradient descent. Proceedings of the 22nd International Conference on Machine Learning. Bonn: ACM, 2005. 89–96.
|
| [13] |
Barabási AL, Albert R. Emergence of scaling in random networks. Science, 1999, 286(5439): 509-512. DOI:10.1126/science.286.5439.509 |
| [14] |
Holme P, Kim BJ. Growing scale-free networks with tunable clustering. Physical Review E, 2002, 65(2): 026107. DOI:10.1103/PhysRevE.65.026107 |
 2022, Vol. 31
2022, Vol. 31



