2. 中国科学院 沈阳计算技术研究所, 沈阳 110168;
3. 辽宁省生态环境监测中心, 沈阳 110161
2. Shenyang Institute of Computing Technology, Chinese Academy of Sciences, Shenyang 110168, China;
3. Liaoning Ecological Environment Monitoring Center, Shenyang 110161, China
河流突发水污染事件会对河流下游区域的生态系统造成破坏, 并且随污染排放时间增加, 污染扩散面积逐渐扩大, 对人民群众以及生态环境的影响逐渐加大, 因此河流突发水污染事件的第一要素是确定污染源位置[1]. 本文主要通过研究污染物在河流中的扩散规律, 并通过监测站所观测到的污染物浓度变化对污染物排放的位置、时间、质量进行溯源[2], 从而还原污染物排放的变化过程, 研究的难点在于污染源溯源求解过程中的求解不唯一、污染源溯源相关的水文参数测量阶段存在误差, 污染物回溯模型参数设置存在误差, 并且污染物的传播过程不能通过实验来重复[3].
水污染溯源的方法最初来自于空气污染的溯源, 最开始被应用于地下水污染的研究[4], Alapati等[5]通过最小二乘法结合一维地下水扩散模型研究了的地下水污染源参数, 国内的白玉堃等[6]通过卡尔曼滤波方法溯源地下水的污染源个数和位置, 张双圣等[7]采用贝叶斯公式结合二维水质的对流模型研究了地下水的污染源瞬时排放模式. 在河流污染中也采用了和学者研究地下水污染中类似的方法[8], 国内外学者在对河流污染的污染源排放相关参数的求解做了大量的工作, 大致可以把研究分为3大类, 分别为数学分析法、模拟优化法、概率分析法, 其中, 前2个称为确定性方法, 最后1个称为不确定性方法.
在数学分析法的研究上, 辛小康等[9]通过遗传算法和数学分析方法相结合, 通过一维水质模型研究了单点源和多点源的瞬时污染源参数识别问题; 饶清华等[10]通过有限元法研究了闽江下游不同地点的污染物浓度情况. 在模拟优化法上, 刘洁等[11]通过遗传算法在一维对流扩散方程求解目标函数; 吴一亚等[12]通过微分进化算法求解宽浅河道瞬时污染排放迁移问题. 确定性方法通过污染物浓度数据反推污染源参数, 但是当数据出现一点偏差时通过确定性方法求解结果偏差较大.
在概率分析法的研究上, 陈海洋等[13]通过贝叶斯推理和二维水体扩散规律构建模型, 并通过马尔科夫链蒙特卡罗法求解污染源相关参数; 程伟平等[2]通过逆向概率密度法求解了一维水质的污染源参数识别问题; 王家彪等[14]通过结合正向位置概率密度和逆向位置概率密度之间的耦合关系建立求解模型, 并通过微分进化算法求解模型, 能够实现求解参数之间的解耦, 降低时间复杂度, 并且结合了确定性和不确定性分析方法, 一定程度上降低了参数误差造成的影响. 概率分析方法在一定程度上能够避免参数误差造成的误差较大, 但是受观测误差影响比较大, 具有一定的随机性.
上述研究中, 污染物浓度监测数据使用所有监测站点不同时刻的数据, 不同监测站间数据没有做区分, 但实际河流中, 污染物浓度也存在水流和污染物混合不均匀导致监测浓度不准确现象, 监测站的数据可以分为不准确、相对准确两种数据类型. 基于大部分监测站点的数据都是相对准确的事实, 本文提出一种基于多萤火虫种群的求解方法, 通过在算法初期隔离不同监测站间的数据来避免不准确数据使相对准确数据失真, 在算法后期通过不同种群间相互作用通过多数效应来淘汰不准确数据类型的种群, 从而避免某个监测站数据不准确对求解造成的系统误差.
本文采用耦合概率密度方法对所需求解的参数进行建模[14], 并考虑到观测误差和一维水质模型需要污染物混合均匀条件, 代入实时的水文特征, 采用改进的萤火虫算法(firefly algorithm, FA)算法, 引入多种群机制将多个污染物监测站数据同时代入求解, 改进后的算法具有更强的全局搜索能力和跳出局部极值能力, 对建模后的目标函数进行求解, 寻找污染源排放相关的排放位置、排放时间、排放强度.
1 水动力模型构建河流水污染问题主要是通过已知的水文参数、监测站监测数据信息对污染物的溯源需要根据具体河道的水文特征进行水动力学模型构建, 利用污染物在水流中的正向质量概率密度和逆向质量概率密度之间的耦合概率密度关系, 使污染物排放强度与排放位置和排放时间之间解耦.
1.1 污染源扩散关系对于污染物的排放问题, 污染物进入河流后的扩散规律满足质量守恒定律[15], 可表示为:
| $ \begin{split} & \frac{{\partial m}}{{\partial t}} + {u_x}\frac{{\partial m}}{{\partial x}} + {u_y}\frac{{\partial m}}{{\partial y}} + {u_{\textit{z}}}\frac{{\partial m}}{{\partial {\textit{z}}}} = \\ &\qquad {D_x}\frac{{{\partial ^2}m}}{{\partial {x^2}}} + {D_y}\frac{{{\partial ^2}m}}{{\partial {y^2}}} + {D_{\textit{z}}}\frac{{{\partial ^2}m}}{{\partial {{\textit{z}}^2}}} - {k} m \end{split} $ | (1) |
其中, m为河道内点(x, y, z) 在t时刻污染物的浓度, 单位mg/L; t 为污染物排放后的时间, 单位s;
对于内陆河流, 污染物扩散主要受河流两岸和河流底部的约束, 因此污染物在水流中会产生边界反射, 水中对流、扩散、吸附等现象. 考虑到河流宽度和河流深度远小于河流长度, 在非洪讯期, 水流速度基本不变, 污染物在被投放到河流内后, 能在投放点断面附近迅速扩散, 扩散后断面附近污染物浓度基本相同. 因此可以把污染源在内河扩散问题简化为一维水体扩散模型, 排入河流后的污染物浓度随时间和位置的变化情况可忽略y, z方向上的变化[16], 将式(1)简化为:
| $ \frac{{\partial m}}{{\partial t}} + {u_x}\frac{{\partial m}}{{\partial x}} = {D_x}\frac{{{\partial ^2}m}}{{\partial {x^2}}} - {k} m $ | (2) |
若污染物为瞬时排放模式, 则可对式(2)进行傅里叶变换[17], 可以得到
| $ \begin{split} m(x, t)=&\frac{{M}}{\sqrt{4 \pi D_{x}\left(t-{t}_{0}\right)}} \\ &\exp \left(-\frac{\left(x-{x}_{0}-u\left(t-{t}_{0}\right)\right)^{2}}{4 D_{x}\left(t-{t}_{0}\right)}-{k}\left(t-{t}_{0}\right)\right) \end{split} $ | (3) |
其中, m(x, t) 表示污染物在河道x位置时间为
由式(3)可知, 对于河流突发水污染事件溯源问题, 需要确定污染物排放处强度M, 污染物排放位置
本文利用正向位置浓度概率密度(从污染源排放断面判断污染源出现在下游的浓度分布情况)和逆向位置浓度概率密度(从监测断面判断污染源在不同断面处的可能性大小)的关系[14], 将求解污染源的浓度分布问题转化为求解污染源的逆向位置浓度概率问题, 从而将
设
| $ {m_1}({x_s}, {{x} _{{\rm{ob}}}}, t) = m({x_s}, {{x} _{{\rm{ob}}}}, t)/{M} $ | (4) |
| $ {m_2}({x_s}, {{x} _{{\rm{ob}}}}, {t_s}) = m({x_s}, {{x} _{{\rm{ob}}}}, t)/{M} $ | (5) |
其中,
由式(4)、式(5)可知, 正向位置浓度概率密度和逆向位置浓度概率密度两者在计算中具有高度耦合性, 在同一位置, 计算方向不同, 计算结果概率密度相同[18]. 因此可以得出:
| $ {m_1}({x_s}, {{x} _{{\rm{ob}}}}, t) = {m_2}({x_s}, {{x} _{{\rm{ob}}}}, {t_s}) $ | (6) |
由于
| $ \begin{split} & m_{2}\left(x_{s}, {x}_{\mathrm{ob}}, t_{s}\right)=\frac{1}{\sqrt{4 \pi D_{x}\left({t}_{\mathrm{ob}}-t_{s}\right)}} \\ &\qquad\exp\left(-\frac{\left({x}_{\mathrm{ob}}-x_{s}-u\left({t}_{\mathrm{ob}}-t_{s}\right)\right)^{2}}{4 D_{x}\left({t}_{\mathrm{ob}}-t_{s}\right)}-k\left({t}_{\mathrm{ob}}-t_{s}\right)\right) \end{split} $ | (7) |
由式(7)可知, 污染源的逆向位置浓度概率与污染物排放强度无关, 可以通过求解
由式(4)可知,
| $ {R} = \frac{{\displaystyle\sum\limits_{i = 1}^n {\left( {{m^i} - \overline m} \right)} \left( {m_2^i - {{\overline m}_2}} \right)}}{{\sqrt {\displaystyle\sum\limits_{i = 1}^n {{{\left( {{m^i} - \overline m} \right)}^2}} } \sqrt {\displaystyle\sum\limits_{i = 1}^n {{{\left( {m_2^i - {{\overline m}_2}} \right)}^2}} } }} $ | (8) |
其中, n为观测断面浓度数据和对应的逆向位置浓度概率密度数据的个数,
设
| $ \min (1 - {R} ) $ | (9) |
目标函数的约束条件是通过已有的监测站断面数据确定的排放位置的范围和排放时间的范围:
| $ {{x} _{{\rm{ob}}}} \lt x' \lt {{x} _{\max }}; \; {{t} _{{\rm{ob}}}} \lt t' \lt {{t} _{\max }} $ | (10) |
通过求解式(9), 寻找其最小值即可得到最近接近
通过位置时间模型求得的
| $ {M} = \frac{1}{n}\sum\limits_{i = 1}^n {\frac{{{m^i}}}{{m_2^i}}} $ | (11) |
可以通过式(11)估算污染物排放处的强度M的大小范围作为约束范围.
为了进一步确定M的大小, 可以通过正向位置浓度概率密度构建目标函数:
| $ \min \left[ {\sum\limits_{i = 1}^n {{{\left( {{M} m_2^i - {m^i}} \right)}^2}} } \right] $ | (12) |
目标函数中M的约束范围由式(11)确定的范围确定:
| $ {{M} _{{\rm{min}}}} \leqslant {M} \leqslant {{M} _{{\rm{max}}}} $ | (13) |
通过求解式(12), 寻找其最小值即可得到最接近真实值的污染物排放处的强度M.
3 溯源优化模型求解在第2节将污染物溯源需要求解的污染物排放位置
在原始的萤火虫算法中, 控制随机扰动的步长
对应到本问题, 在求解目标函数式(7)时, 污染物排放位置x的范围相对于污染物排放时间范围较大, 因此需要提供一个缩放系数k, 来调整不同维度的步长相对值, 可表示为:
| $ {\alpha _0} = {{k} _i}{\alpha _0} $ | (14) |
其中,
由于污染物溯源问题在初期搜索范围较大需要更大的步长来加快搜索速度和全局搜索能力, 在后期需要较小的步长来提升搜索精度, 因此针对本问题参考文献[21]提出一种自适应步长改进策略, 可表示为:
| $ {\alpha _{t + 1}} = \left(1 - \frac{{{t}}}{{{{T} _{\max }}}}\right) \cdot {\alpha _t} $ | (15) |
其中, t (t=1, …, n)表示当前的迭代次数,
原始的萤火虫算法在移动位置时没有考虑在该维度的搜索范围, 对应到污染物溯源问题上,
| $ {x_i} = \left\{ {\begin{array}{*{20}{c}} {{{x} _{{\rm{min}}}}, \;{x_i} \lt {{x} _{{{\rm min}}}}} \\ {{{x} _{{\rm{max}}}}, \; {x_i} \gt {{x} _{{\rm{max}}}}} \end{array}} \right. $ | (16) |
其中,
原始的萤火虫算法中, 萤火虫亮度较高的个体只会对其附近的亮度相对较低的个体有吸引力, 但是对距离较远的萤火虫个体没有吸引力, 因此原始算法容易陷入局部极值过早收敛导致求解误差较大. 针对上述问题本文参考文献[22]提出的多萤火虫种群的优化策略改进算法, 具体内容见第3.3节算法流程中步骤3–11.
3.3 算法流程对于污染物溯源问题, 早期的学者采用耦合概率密度分析方法建模求解时, 没有区分不同监测站的污染物浓度数据, 某个监测站的监测值可能因为污染物和河流混合不均匀或者某个设备本身存在系统误差, 从而导致通过该监测站数据求解误差较大.
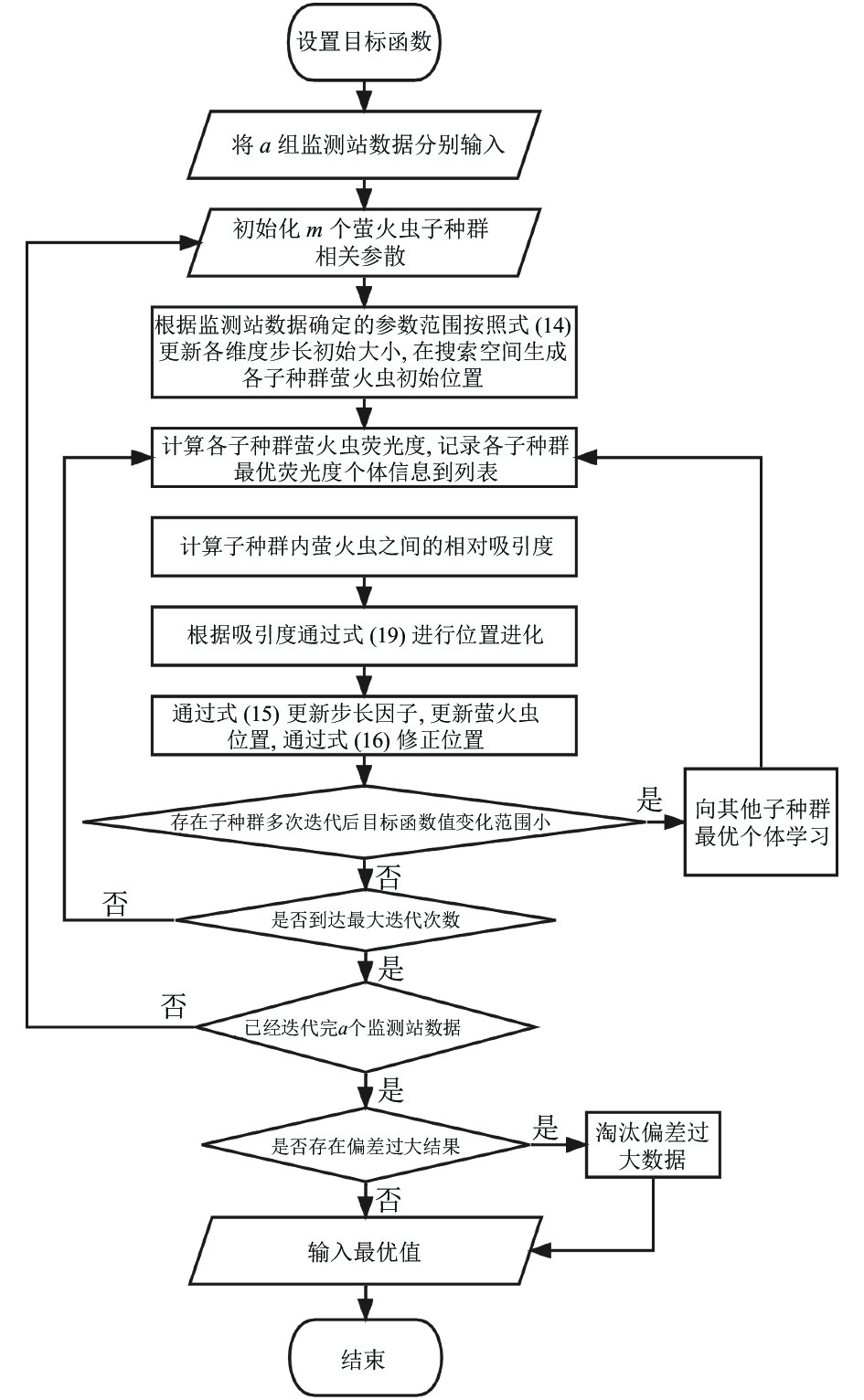
针对本问题提出如下改进: 首先监测站间数据相互独立, 使用单个监测站数据依次使用多种群萤火虫算法求解, 最后分析各个监测站的求解结果, 采用标准差分析法, 若通过某一个监测站求解的结果相对于其他使用其他监测站数据求解结果偏差较大, 证明该监测站数据为不准确数据, 淘汰该结果[23]. 整体算法结构如图1所示, 具体算法流程如下.
|
图 1 改进的FA算法流程图 |
步骤1. 确定溯源优化模型求解需要求解的内容, 式(9)、式(12).
步骤2. 设总共有a个监测站的监测数据, 每个监测站的污染物浓度系列为
步骤3. 假设所有子种群的萤火虫数目之和为m, 子种群数目为n, 分别为子种群初始化不同的光强吸收系数
步骤4. 根据监测站数据和河道信息通过式(16)确定需要求解的参数
步骤5. 根据参数
步骤6. 根据步骤4结果设定不同维度的搜索空间范围, 根据该范围在不同维度随机生成萤火虫的初始位置:
| $ {X_{ij}} = ({x_{ij1}}, {x_{ij2}}, \cdots , {x_{ijd}}) $ | (17) |
其中,
步骤7. 将生成的
步骤8. 计算子种群内萤火虫之间的相对吸引度:
| $ \beta = {\beta _0}{{\rm{e}}^{ - \gamma {r^2}_{ii'}}} $ | (18) |
其中,
各子种群中萤火虫个体开始位置进化, 根据式(19)更新空间位置:
| $ \begin{gathered} {X_{ij}}\left( {t + 1} \right) = {X_{ij}}\left( t \right) + \beta \left( {{X_{i'j}}\left( t \right) - {X_{ij}}\left( t \right)} \right) + \alpha \left( {{{rand}} - 1/2} \right) \end{gathered} $ | (19) |
其中,
根据式(16)修改
步骤9. 查询List列表数据, 若存在某个子种群
步骤10. 如果步骤9结果存在则向其学习, 如果不存在则通过遗传算法中的变异操作来调整该种群最优萤火虫个体的位置, 从而增加该子种群的种群多样性, 如式(20)、式(21)所示:
| $ \eta = 1 - \frac{t}{{{{T} _{{\rm{max}}}}}} $ | (20) |
| $ {X_{ij}} = {X_{ij}} + \eta \times {X_{ij}} \times N(0, 1) $ | (21) |
其中,
步骤11. 判断是否达到最大迭代次数, 若达到转步骤12, 没有达到转步骤7继续迭代过程.
步骤12. 收集步骤2中的a个监测站分别迭代后获取的a组污染物位置x, 污染物排放时间t污染物排放浓度M的数据[24]. 由式(2)可知, 在一维模型情况下, 给定x时, t也唯一确定, 并且M是由确定的
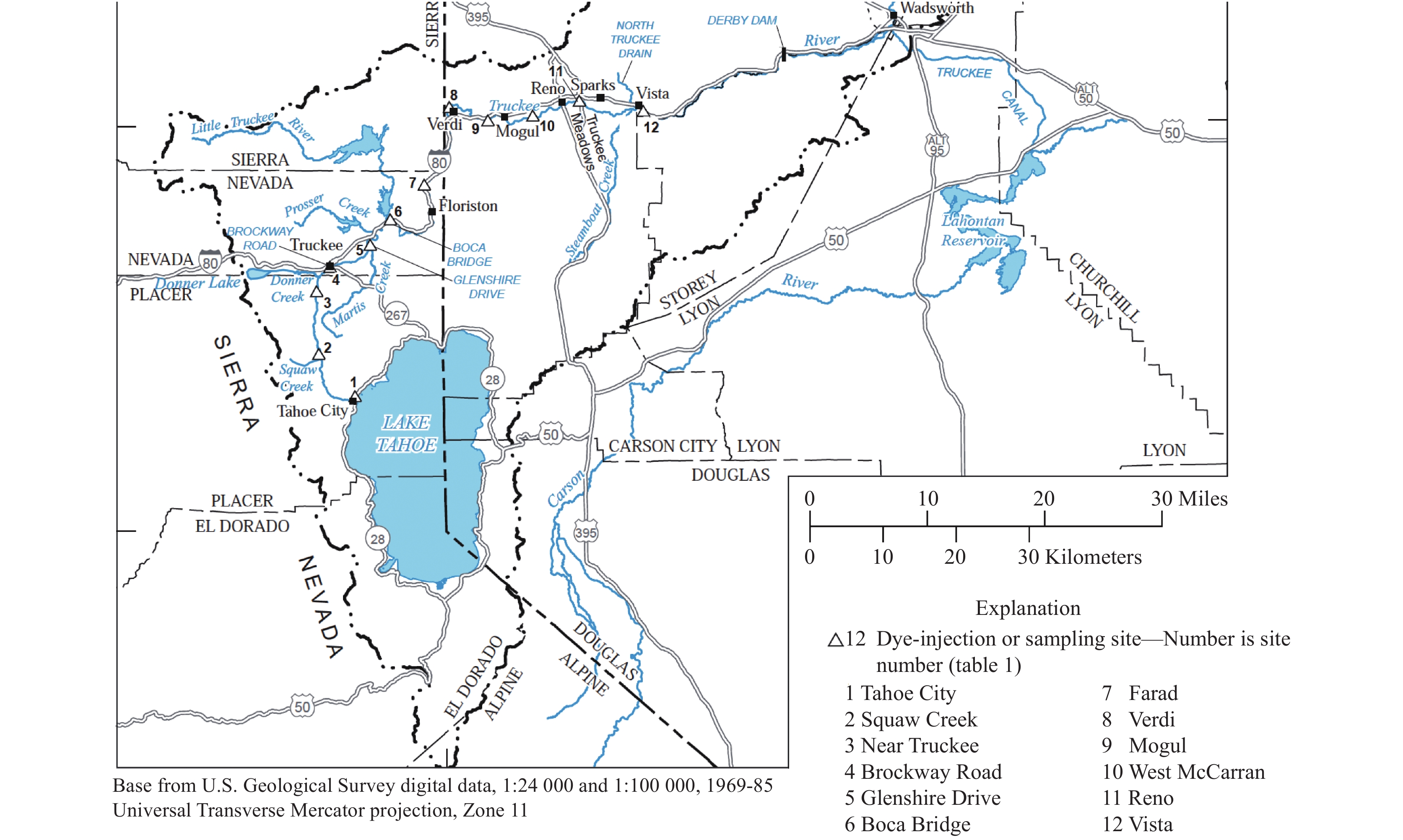
为了验证提出的改进FA算法的可行性, 本文采用文献[25]美国地质勘探局公布的2006年在特拉基河做的染料示踪实验数据. 为了研究混合不均匀情况下监测值对溯源结果的影响[24], 采用文献中低流量(4.05–18.04
|
图 2 特拉基河监测站点图 |
4.1 溯源参数优化调整
本文使用特拉基河监测断面的数据, 采用改进的FA的算法对污染物的排放相关的
表2中FA算法为单种群算法, 只需要输入一组参数; 而本文采用的改进FA算法在案例分析中子种群数量设置为3, 3个子种群各代入一组参数, 由于每组参数中
| 表 1 示踪剂投放监测断面分布情况 |
| 表 2 算法参数表 |
针对河流的水文参数, 由文献[22]可大致估计, 污染物的降解系数k为
将修正后的水文参数应用到实验集监测断面2–监测断面6号数据中, 分别采用改进的FA算法和FA算法对目标函数式(9)、式(12)进行求解, 从而对污染源参数排放位置
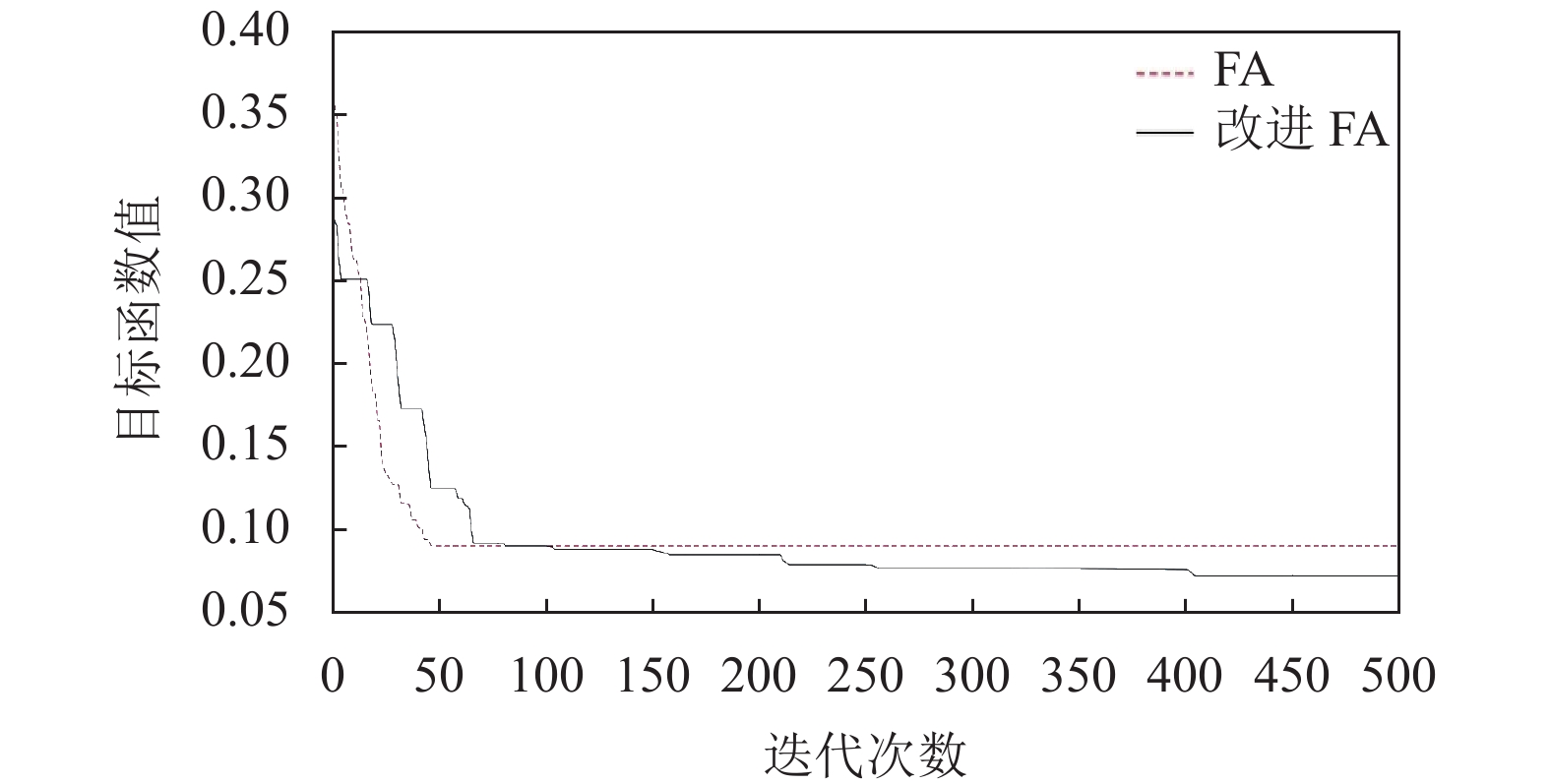
|
图 3 目标函数1迭代过程图 |
通过图3、图4和表3可知, FA算法在迭代到50代左右时, 开始快速收敛, 但与真实值相比求解结果偏差较大, 问题为陷入局部极值, 种群多样性较低, 没办法跳出局部极值. 改进的FA算法在300代左右开始收敛, 并且图像呈现阶梯下降趋势, 虽然迭代速度相对于FA慢, 但求解精度高, 具有以下优点: 由于引入了自适应步长策略, 使算法前期全局搜索能力较强, 后期局部搜索精度更高所以具有更好的种群多样性, 全局搜索能力更强; 引入了多种群互相学习策略, 当某个种群陷入局部极值时会向其他种群学习或者自身进行高斯扰动, 所以具有更好的跳出局部极值能力.
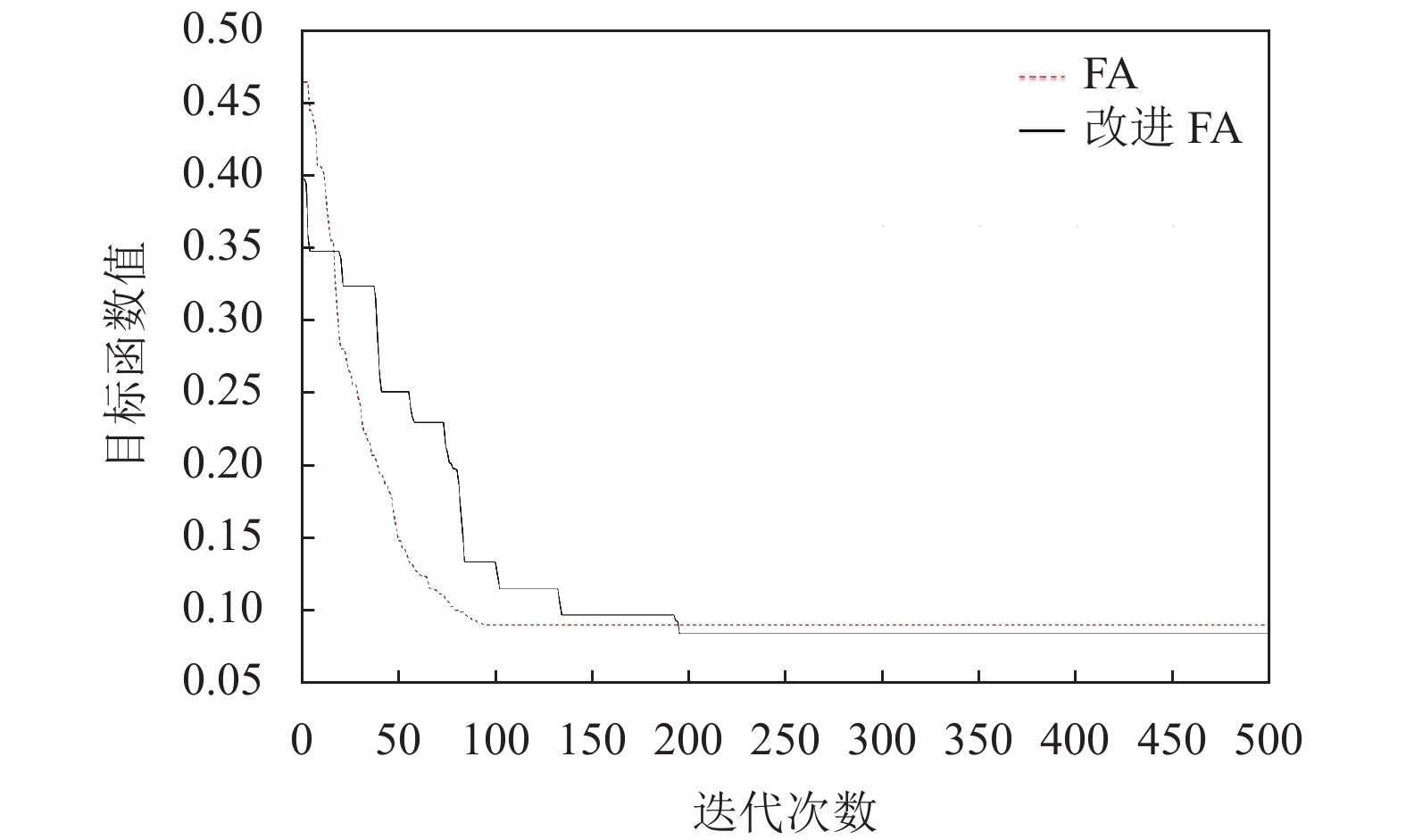
|
图 4 目标函数2迭代过程图 |
| 表 3 多断面溯源结果 |
由表3可知, 断面2计算值明显偏大, 根据本文第3.2节算法步骤, 对断面2–5溯源得到的污染源位置
| 表 4 多断面溯源位置标准差 |
通过上述溯源结果分析, 改进的FA算法溯源结果污染源位置范围[−156.36, 165.24] m、污染源排放时间范围[22:17, 22:35]、污染源排放强度范围[801.45, 895.36] g相对于污染源真实值排放位置0 m、排放时间22:30、排放强度820 g偏差不大. 本文方法在实际的河流污染物溯源分析中具有相对的准确性, 并且在通过标注差排除异常监测断面溯源结果后, 不同断面溯源结果相对真实值偏差范围在可接受范围内.
5 结论与展望本研究采用耦合概率密度法和一维水质扩散模型进行建模, 通过改进的FA算法对模型进行求解, 为了检验算法可靠性采用特拉基河的示踪剂实验真实场景数据. 在实验求解过程中通过多次试算的形式对改进FA算法的最大迭代次数、子种群个数等参数进行合理选取, 在确定河流水文参数时, 结合资料给定的水文参数(水流速度、降解系数、扩散系数)和通过算法分析对河流长度方向扩散系数进行修正, 进一步提高在对河流突发水污染事件溯源的可靠性. 最后通过多监测断面分别进行溯源求解, 采用标准差分析法, 排除了因为污染物混合不均匀导致的监测数据偏差. 通过特拉基河染料示踪实验表明, 该方法在单污染源识别问题上, 其精度高于原始的FA算法, 具有一定的可靠性.
| [1] |
张芳, 王炜亮, 成杰民. 流域突发性水污染事故应急体系构思. 环境科技, 2010, 23(1): 57-60. DOI:10.3969/j.issn.1674-4829.2010.01.016 |
| [2] |
程伟平, 廖锡健. 基于逆向概率密度函数的一维污染源排放重构. 水动力学研究与进展A辑, 2011, 26(4): 460-469. DOI:10.3969/j.issn1000-4874.2011.04.010 |
| [3] |
刘晓东, 姚琪, 薛红琴, 等. 环境水力学反问题研究进展. 水科学进展, 2009, 20(6): 885-893. |
| [4] |
Sidauruk P, Cheng AHD, Ouazar D. Ground water contaminant source and transport parameter identification by correlation coefficient optimization. Groundwater, 1998, 36(2): 208-214. DOI:10.1111/j.1745-6584.1998.tb01085.x |
| [5] |
Alapati S, Kabala ZJ. Recovering the release history of a groundwater contaminant using a non-linear least-squares method. Hydrological Processes, 2000, 14(6): 1003-1016. |
| [6] |
白玉堃, 卢文喜, 李久辉. 卡尔曼滤波方法在地下水污染源反演中的应用. 中国环境科学, 2019, 39(8): 3450-3456. DOI:10.3969/j.issn.1000-6923.2019.08.039 |
| [7] |
张双圣, 强静, 刘汉湖, 等. 基于贝叶斯公式的地下水污染源识别. 中国环境科学, 2019, 39(4): 1568-1578. DOI:10.3969/j.issn.1000-6923.2019.04.027 |
| [8] |
刘晓东, 王珏. 地表水污染源识别方法研究进展. 水科学进展, 2020, 31(2): 302-311. |
| [9] |
辛小康, 韩小波, 李建, 等. 基于遗传算法的水污染事故污染源识别模型. 水电能源科学, 2014, 32(7): 52-55, 136. |
| [10] |
饶清华, 曾雨, 张江山, 等. 闽江下游突发性水污染事故时空模拟. 环境科学学报, 2011, 31(3): 554-559. |
| [11] |
刘洁, 陈昊辉, 张丰帆, 等. 基于改进遗传算法的河流水质模型多参数识别. 东北农业大学学报, 2020, 51(1): 73-82. DOI:10.3969/j.issn.1005-9369.2020.01.009 |
| [12] |
吴一亚, 金文龙, 吴云波, 等. 宽浅河道瞬时源源项反问题及反演精度主要影响因子分析. 水资源保护, 2015, 31(5): 58-61. DOI:10.3880/j.issn.1004-6933.2015.05.011 |
| [13] |
陈海洋, 滕彦国, 王金生, 等. 基于Bayesian-MCMC方法的水体污染识别反问题. 湖南大学学报(自然科学版), 2012, 39(6): 74-78. |
| [14] |
王家彪, 雷晓辉, 廖卫红, 等. 基于耦合概率密度方法的河渠突发水污染溯源. 水利学报, 2015, 46(11): 1280-1289. |
| [15] |
韩龙喜, 陈丽娜. 可降解的地表水污染物随机游走改进模式. 水科学进展, 2009, 20(5): 689-694. DOI:10.3321/j.issn:1001-6791.2009.05.014 |
| [16] |
杨海东, 肖宜, 王卓民, 等. 突发性水污染事件溯源方法. 水科学进展, 2014, 25(1): 122-129. |
| [17] |
范玉科, 侯为根, 徐浩. 河道污染的一维对流-扩散方程源项识别反问题. 安徽工业大学学报(自然科学版), 2014, 31(3): 323-327. |
| [18] |
王忠慧, 贡力, 康春涛, 等. 基于BAS算法的河渠突发水污染溯源. 水资源保护, 2020, 36(5): 87-92. DOI:10.3880/j.issn.1004-6933.2020.05.013 |
| [19] |
Neupauer RM, Wilson JL. Adjoint method for obtaining backward-in-time location and travel time probabilities of a conservative groundwater contaminant. Water Resources Research, 1999, 35(11): 3389-3398. DOI:10.1029/1999WR900190 |
| [20] |
Cheng WP, Jia YF. Identification of contaminant point source in surface waters based on backward location probability density function method. Advances in Water Resources, 2010, 33(4): 397-410. DOI:10.1016/j.advwatres.2010.01.004 |
| [21] |
符强, 童楠, 钟才明, 等. 基于改进型进化机制的萤火虫优化算法. 计算机科学, 2014, 41(3): 228-231, 248. DOI:10.3969/j.issn.1002-137X.2014.03.049 |
| [22] |
符强, 童楠, 赵一鸣. 一种基于多种群学习机制的萤火虫优化算法. 计算机应用研究, 2013, 30(12): 3600-3602, 3617. DOI:10.3969/j.issn.1001-3695.2013.12.021 |
| [23] |
陈小雪, 尉永清, 任敏, 等. 基于萤火虫优化的加权K-means算法. 计算机应用研究, 2018, 35(2): 466-470. DOI:10.3969/j.issn.1001-3695.2018.02.031 |
| [24] |
陶宇夏, 蒋晶, 魏永长, 等. 基于差分进化算法的河流突发性污染事故溯源. 工业工程与管理, 2021, 26(2): 9-14. |
| [25] |
Crompton EJ. Traveltime for the Truckee River between Tahoe City, California, and Vista, Nevada, 2006 and 2007. U.S. Geological Survey, 2008.
|
 2022, Vol. 31
2022, Vol. 31


