随着医疗科技不断的发展和进步, 超声图像诊断是一项重要的医学图像诊断手段, 由于超声成像的图像质量较差, 需要采用相对应的方法来对超声图像进行增强^[1], 当前, 超声成像技术在临床医学诊断方面应用的越来越广泛, 超声成像技术作为一种非侵入性, 对人体无害的病理检测技术^[2], 一直受到国内外相关科学研究人员的关注. 超声诊断通过超声仪向人体发射超声波, 并通过不断的扫描来对不同的人体组织进行探测, 当探头接收到由人体组织和器官反射回来的超声信号后, 再通过放大信号以及一系列信息的处理, 最终形成人体组织器官的超声实时成像, 三维成像可以提供直观的立体图像信息, 在心肌损伤定位, 胸腹部肿瘤的检测等方面有着重要的作用^[3]. 由于超声探头的材质例如超声陶瓷换能器制造的局限性以及为了降低成本和提高帧速率, 而采用的低通道扫描方案, 往往会使原始的超声成像包含束状条纹伪影, 这些伪影往往会掩盖人体的组织信息, 从而引起医生错误的诊断. 常规的伪影抑制方法都是在空间域来进行的, 对于周期性伪影难以实现最佳的去除效果. 目前, 随着医学超声图像处理技术不断地成熟, 具体的研究方向包括降噪, 分割, 压缩等图像处理技术, 还包括超声图像采集技术^[2]. 本研究提出了一种基于图像的频率域的伪影抑制算法, 根据大量的实验结果进行定性的分析及定量的MSE和SNR来验证该算法的准确性, 其结果对超声成像的周期性伪影有着显著的抑制效果, 进而帮助医生得到更清晰的超声成像, 以提高医生的诊断效率和效果.

1 超声图像通用伪影抑制介绍

在传统的超声图像处理领域, 图像噪声抑制是数字图像处理中的重要环节和步骤, 去噪效果的好坏直接影响后续图像处理的相关工作. 通常, 抑制伪影的算法分为两大类, 第一类是基于空间域滤波的图像噪声抑制算法, 第二类是基于频率域滤波的图像噪声抑制算法, 本研究将列出一些常用的空间域滤波去噪算法以及接下来将使用的频率域伪影抑制算法的设计思想, 并通过对比空间域伪影抑制算法和频率域伪影抑制算法的优缺点及采用空间域滤波算法的局限性, 详细阐述本研究使用基于频率域的超声实时成像的周期性伪影抑制算法的原因.

1.1 空间域伪影抑制

图像空间域伪影抑制常常使用的是平滑处理, 平滑主要利用卷积运算对图像邻域的像素灰度进行平均化, 从而减少图像中的噪点^[4]. 图像的平滑处理分为线性平滑和非线性平滑, 线性平滑包括均值滤波和高斯滤波, 非线性平滑包括中值滤波和双边滤波. 目前随着空间域滤波技术不断地发展, 越来越多的改进滤波技术不断的应用于图像平滑之中, 接下来介绍并分析目前改进的典型滤波算法.

以迭代均值滤波算法^[5]为例, 它改进了传统的均值滤波算法, 它利用邻域内已经估算的重构灰度级参与当前像素灰度级的运算, 提高了图像重构的质量和效率. 虽然迭代均值滤波算法能够有效地抑制噪声, 但是也会破坏图像的细节部分, 因此对于具有强边界信息的图像, 此算法会破坏图像的边缘信息, 这就导致图像整体变得模糊.

文献[6]提出了一种自适应各项异性高斯滤波算法, 该算法首先计算图像中各个像素位置的梯度值以及梯度方向, 根据梯度值的大小来决定采用的滤波类型, 采用各项异性高斯滤波, 通过该点的梯度方向角得到各项异性高斯算子的长轴方向, 此算法在边缘信息的维护方面强于传统的高斯滤波算法. 此算法的局限性在于只能够对高斯噪声进行平滑, 对于在空间域上周期性分布的噪声, 该算法就失去了作用效果.

文献[7]提出了一种可以保留图像细节信息的中值滤波改进算法, 通过检查待处理像素点是否存在于角点以及线段中, 并根据结果来决定是否进行保留或者采用中值滤波算法进行处理, 该算法可以保留图像中的细节信息同时可以避免图像的模糊. 该算法的局限性在于当噪声像素个数大于窗口内像素个数的一半时, 会导致排序后的中间值仍为噪声, 因此去噪效果非常差.

文献[8]提出了一种改进的双边滤波和阈值函数的图像增强算法, 该算法对带有噪声的图像进行小波分解, 从而获取图像的低频和高频系数, 采用改进的双边滤波的Retinex算法对图像的低频系数进行处理, 采用阈值函数对高频系数进行处理, 最后进行小波反变换重构来实现图像中噪声的消除以及图像细节部分的增强. 但对于周期性伪影, 由于其在小波域上均存在于高频分量以及低频分量中, 因此难以实现对其进行分离从而达到抑制的目的.

1.2 频率域伪影抑制

上面主要介绍了4种基于空间域伪影抑制的滤波算法, 但它们在对特定分布的伪影在进行抑制的同时往往会具有局限性, 例如周期性伪影, 在空间域上采用平滑操作, 虽然会在一定程度上降低伪影的灰度级, 但是通过平滑后的图像会变得模糊, 图像伪影附近的有效信息会产生丢失, 为了解决这一问题, 在CT领域, 常常需要获取纹理在频率域上的相位分布和幅值分布, 来达到伪影抑制的目的^[9]. 对于带有周期性伪影的超声图像需要通过变换域处理的方式来对其进行抑制, 变换域处理主要指的是图像的频率域变换及小波变换, 通常情况下, 频率域具有和空间域的互补性, 例如周期性伪影的抑制在空间域处理往往需要对图像进行分割以及融合, 而这些伪影在频率域就显得具有一定规律, 这些特定在频率域表现得更为直观, 它可以解释空间域滤波的一些属性, 因此只需要找出周期性伪影在频率域上的分布并对其进行衰减^[10]就可以达到去除的目的, 本课题将对于带有周期性伪影的超声图像来进行基于频率域上^[11]算法研究.

2 正弦波模拟伪影抑制

这一节主要使用正弦波来模拟周期性伪影, 并通过正弦波的叠加实验来判断周期性伪影在频域的表现特征.

2.1 二维傅立叶变换

本研究对周期性伪影的抑制在超声图像的频率域来进行处理主要是通过图像的二维傅立叶变换来完成的, 它是由20世纪60年代的Cooley和Tukey提出的一种算法^[12], 能够明显提高运算效率. 二维快速傅立叶变换(FFT)是图像处理领域中常用的分析和计算工具, 常常应用于频谱分析, 频域滤波和卷积计算等相关图像分析当中^[13]. 二维傅立叶变换可以看出两个一维傅立叶变换的结合, 一维傅立叶变换的作用是将一个一维信号分解成若干个复指数波, 即有:

$ F(u) = \int_{ - \infty }^\infty {f(x){{\rm e}^{ - j2\pi ux}}} dx $

(1)

再根据欧拉方程:

$ {{\rm e}^{jwx}} = \cos (wx) + j\sin (wx) $

(2)

对于一个正弦波, 想要确定它就要定义3个参数, 分别是频率w, 幅值A, 相位φ, 因此在频率域中, 一维坐标代表频率, 每个坐标对应的函数值为F(u)的一个复数, 它的幅度值|F(u)|. 一维傅立叶变换是一种基变换, 在空间域中, 基是一族脉冲信号δ(x–n), 在频率域中, 基是 ${\rm e}^{-j2\pi u}$ , 这组基是正交基. 一维信号可以看成一个序列, 傅立叶变换能将其分解成若干个简单函数之和. 对于图像来说, 可以将它看成一个二维信号, 一个二维信号可以分解为若干个复平面波之和. 对于一个长度为M, 宽度为N的图像f(x, y), 其二维离散傅立叶变换由式(3)决定:

$ F(u, v) = \frac{1}{{MN}}\sum {\sum {f(x, y){{\rm e}^{ - j2\pi (\frac{{ux}}{M} + \frac{{vy}}{N})}}} } $

(3)

类似于一维中的情景, 要完成表达式的计算, 需要对u, v进行计算, 其中对应的二维傅立叶反变换表达式有:

$ f(x, y) = \sum {\sum {F(u, v){{\rm e}^{j2\pi (\frac{{ux}}{M} + \frac{{vy}}{N})}}} } $

(4)

通过式(4), 可以计算出每一个平面波在图像中的成分. 二维傅立叶变换实质是将图像与每个不同频率的不同方向的复平面波做內积运算, 也就是求在基向量 ${\rm e}^{-j2\pi \left(ux+vy\right)}$ 上投影的过程. 根据式(4)可以得到傅立叶变换的一些特性: 平移性, 旋转不变性, 卷积性^[14]. 根据式(4)可以推断出在频域中原点平移到(u₀, v₀)时, 其空间域要乘以一个正的指数项 ${\rm e}^{j2\pi \left(u_{0}x/M+v_{0}y/N\right)}$ , 空间域中原图像原点移动到(x₀, y₀)时, 其频率域F(u, v)要乘以一个负的指数项 ${\rm e}^{-j2\pi \left(u_{0}x/M+v_{0}y/N\right)}$ , 在进行图像的傅立叶变换时, 往往需要将F(u, v)原点平移到频域中心, u₀ =M/2, v₀ = N/2, 代入公式中得到将图像的频域原点平移到中心就需要在f(x, y)上乘以(−1)^(x+y)即可实现, 体现出二维FFT变换结果均具有中心共轭对称性^[14]. 二维傅立叶变换的旋转不变性指的是如果f(x, y)旋转了一个角度, 那么f(x, y)旋转后的图像的傅立叶变换也会旋转相同的角度, 用极坐标代替平面直角坐标系即有:

$ \left\{ {\begin{split} &x = r\cos \theta u = w\cos \varphi \\ &y = r\sin \theta v = w\sin \varphi \end{split} } \right.$

(5)

替换法则有 $ f\left(x, y\right)\to f\left(r, \theta \right)\to F(w, \phi ) $ , 如果f(x, y)被旋转同一角度, 那么有 $f\left(r, \theta +\theta_0\right)\to F(w, w+\theta_0)$ ^[14]得出结论一幅图像的空间域上的旋转角度和频率域上的旋转角度是一致的. 同时二维傅立叶变换还有卷积特性, 即空间域上的卷积运算等于频率域上的乘积运算, 该性质的好处在于将需要进行复杂的卷积运算转化为乘积运算, 极大地提高了计算效率, 这也是本研究采用频率域抑制伪影的原因.

2.2 正弦波的模拟实验

根据上述的结论, 为了更好地达到频率域上周期性伪影抑制的效果, 本研究模拟了两个正弦波的叠加后然后通过二维傅立叶变换后的频谱图, 再通过上述的特性来抑制特定频率的正弦波. 设计的步骤如实验1.

实验1. 正弦波模拟伪影实验

1) 编程分别实现一幅256×256, 频率为1/18的水平正弦波和垂直正弦波;

2) 将水平正弦波和垂直正弦波进行叠加, 得到混合正弦波;

3) 分别对水平, 垂直正弦波进行二维傅立叶变换, 观察各自得到的频率域谱.

4) 将混合正弦波做二维傅立叶变换, 观察得到的频谱, 并比较之前获取的傅立叶频谱;

5) 找出频谱上水平方向的亮点并置为0, 这些亮点根据傅立叶变换的特性可以判断出属于垂直正弦波;

6) 对频谱进行逆傅立叶变换到空间域, 观察到最终结果.

上述设计步骤通过竖直正弦波模拟周期性伪影并进行傅立叶变换和逆傅立叶变换, 来验证在频率域抑制周期性伪影的效果, 如图1、图2. 上述两个正弦波分别代表频率为1/18的垂直于水平正弦波, 按照步骤进行叠加得到混合正弦波, 这里采用OpenCV提供的add接口来实现正弦波的叠加, 如图3. 分别对垂直和水平正弦波及混合正弦波进行二维傅立叶变换, 得到垂直和水平正弦波频谱, 如图4、图5. 通过以上观察发现, 当竖直正弦波旋转90度到水平位置后, 其频域也会旋转90度, 这验证了空间域和频域变换之间对应旋转不变性的特征, 图6是混合正弦波的频谱. 下一步通过将混合正弦波水平中线上的数值置为0, 再通过逆向傅立叶变换观察复原后的正弦波, 如图7、图8.

通过观察, 发现通过抑制水平中心线上的脉冲可以达到去除垂直正弦波的效果, 说明在频域上对周期性信号的抑制有着显著的效果, 下一步将通过这种方法抑制超声视频序列中周期性伪影, 来达到理想的结果.

3 超声实时成像中周期性伪影抑制实验

本研究将对超声实时成像进行分帧处理, 对每一帧的超声图像进行2D-FFT到其频率域上, 并通过设计算法达到抑制周期性伪影抑制的效果, 再对所有的超声图像进行合帧处理, 完成超声视频的伪影抑制.

3.1 超声实时成像的帧率及OpenCV分帧合帧

超声实时就是一系列捕获的超声图像以给定的频率显示, 通过在一序列的特定帧处停止可获得单个视频帧, 也就是图像, 对于超声实时成像中带有的周期性伪影, 本研究采用的方法为使用OpenCV这一计算机视觉开源库^[15]来对成像进行离线分帧处理, OpenCV提供了视频帧的读取, 显示函数以及获得视频帧率的函数^[16], 帧率代表以帧为单位的图像连续出现在显示器上的频率以及单位时间内通过图像的数量, 对超声实时成像中的伪影进行处理首先需要对单个成像帧中的图像进行采样, 采样完成后对单个图像进行伪影抑制, 才能达到理想的效果.

OpenCV分帧的主要步骤为首先使用OpenCV提供的接口VideoCapture来打开一个视频, 获取视频的相关信息, 输出视频的高度和宽度以及帧率, 视频的每一帧宽度和高度都是一致的, 根据上述信息来获取单个超声图像. 合帧的主要步骤为创建VideoWriter对象, 用来读取图像并输出到指定文件中, 包括设置参数例如帧数以及图像尺寸大小, 从而获取到处理后的超声成像. 图9是使用单个帧内的部分超声图像作为样本.

图9是人体某组织通过超声探头扫描的通道数据的视频通过分帧后的图像呈现, 可以发现这些图像普遍具有周期性的扫描线, 这些是由超声探头采用的低通道扫描导致的, 同时, 这些伪影会遮挡该人体组织中的有用信息, 会对医生的诊断造成干扰. 本研究将采取在频率域对这些周期性扫描线进行抑制, 这样也会提高伪影抑制的效率.

3.2 伪影脉冲检测算法及结果的定量分析

在大部分图像中, 邻近像素高度相关, 距离较远的像素相关性较弱, 在频域上也存在相关特性^[17], 根据之前做的正弦波模拟伪影实验, 可以发现具有周期性的正弦波在频率域上的方向和空间域的方向垂直, 对于竖直周期性伪影, 其在频率域上的方向是在水平方向上, 通常表现为具有对称性的峰值^[18], 为了更加准确的定位周期性伪影在频率域上的位置, 需要设计一个算法模型, 该算法模型能准确地找出伪影在频率域上的坐标. 可以采用滑动窗口扫描结合合适的阈值大小这一算法模型用来选取疑似伪影脉冲频率域上的点并进行幅值降低处理.

该算法模型的实现过程如算法1.

算法1. 滑动窗口阈值扫描算法模型

1) 定义一个扫描路径, 被扫描点到频域中心的距离由大到小来进行搜索;

2) 定义一个大小为3×3的滑动窗口, 依次从左往右, 从上往下开始滑动;

3) 找出滑动窗口内中心点的幅值大于当前点的上下左右各点幅度值的所有点.

4) 定义一个阈值T, 阈值大小由超声图像的动态范围决定, 例如动态范围为60 db, 阈值可以设置为图像动态范围的k倍(0≤k < 1), k由超声图像伪影抑制结果评估模型决定, 对系数-预期结果做采样, 找出最佳阈值系数大致范围, 然后设置截止半径R, 截止半径由图像频域幅度峰值到左右两侧下一个峰值的距离确定, 用来保证频域中心点的数据不被破坏, R的范围由采样决定. 如果该点所在的滑动窗口内的动态范围大于T, 那么将该点保存至集合中.

5) 将满足步骤4的点存入集合P, P中的点就是疑似周期性伪影在频谱上的坐标点, 分别是P1, P2, P3,…,Pn, 并且r(P1) > r(P2)>r(P3) >…> r(Pn), r(P)为P集合中各个点到频谱中心点的距离.

6) 对P中的点进行降低幅值处理, 压低后的幅值大小为小于等于通过阈值计算后的大小.

通过该算法模型, 可以找出频域上疑似周期性伪影的点集, 然后就可以通过对找到的点集进行幅值降低的处理, 再通过逆向傅立叶变换得到抑制周期性伪影的超声图像. 然后根据客观准则来定量的计算超声图像的伪影抑制效果, 定义两个集合, 分别用来标记伪影区域A和非伪影区域B, 假设O为无伪影超声图像, G为原始含伪影图像, 其大小为M×N, G_n为伪影抑制后的图像, 需要统计G中伪影区域A及非伪影区域B和G_n中原伪影区域A_n及非伪影区域B_n然后通过计算区域之间偏离程度的方法来分析图像的伪影抑制质量, 通常采用的方法是均方误差估计算法, 它通过计算输入输出图像的均方值MSE (mean square error)来判定^[19]. 对于该图像中的任意一点(x, y), 它的误差值表达式有:

$ e(x, y) = O(x, y) - {G_n}(x, y) $

(6)

均方误差可以表示为:

$ {\textit{MSE}} = \frac{1}{{MN}}{\sum {\sum {(O(x, y) - {G_n}(x, y))} } ^2} $

(7)

均方误差值越小, 其伪影抑制效果越好. 同时也可以采用信噪比SNR (signal-to-noise ratio)^[19]作为另一种对伪影进行抑制所产生效果的评价准则, 同时也是使用最广泛的客观测量法之一, 即有:

$ {\textit{SNR}} = 10\log \left(\dfrac{{{{255}^2}}}{{\dfrac{1}{{MN}}\displaystyle\sum {\displaystyle\sum {{{(O(x, y) - {G_n}(x, y))}^2}} } }}\right) $

(8)

根据式(8), 对于伪影区域A, 假设其区域大小为S₁, 则非伪影区域B大小为S₂, 则其均方误差为:

$ {\textit{MSE}}(A) = \frac{1}{{{S_1}}}{\sum {\sum {(A(x, y) - {A_n}(x, y))} } ^2} $

(9)

$ {\textit{MSE}}(B) = \frac{1}{{{S_2}}}{\sum {\sum {(B(x, y) - {B_n}(x, y))} } ^2} $

(10)

其信噪比为:

$ {\textit{SNR}}(A) = 10\log \left(\frac{{{{255}^2}}}{{{\textit{MSE}}(A)}}\right) $

(11)

$ {\textit{SNR}}(B) = 10\log \left(\frac{{{{255}^2}}}{{{\textit{MSE}}(B)}}\right) $

(12)

对于伪影区域, 其处理前后的均方误差应尽可能大, 对于非伪影区, 其均方误差应尽可能小. 接下来, 分别通过以上两种评估模型MSE和SNR可以来验证这个算法模型的准确性.

3.3 算法模型的验证和实现

根据上述算法模型, 该算法实现的功能在于输入一幅带有周期性伪影的(M×N)超声图像, 通过2D-FFT后变换到频率域, 采用第3.2节中设计的算法, 再使用2D-IFFT反变换到空间域, 得出去除周期性伪影的超声图像, 经过本研究提供的算法模型测试, 通过处理后的超声图像伪影得到去除, 算法作用效果明显. 整体周期性伪影抑制模型如图10.

根据算法实现功能模块来对该算法模型进行验证. 使用OpenCV编程实现该算法模型思想, 首先在一幅超声图像中(大小为M×N), 分别对其伪影区域A和非伪影区域B进行标记, 作为后续定量分析的参考, 如图11、图12.

在图12中左侧方框为伪影区, 右侧方框为非伪影区. 获得该频谱后, 再由算法模型确定包含这些点的坐标, 为了验证这些点坐标的准确性, 本研究需要获取到位于水平中心线上所有点的幅值曲线函数, 即当x = M/2时, 来判断该点的大致范围是否坐落于该曲线上, 如图13.

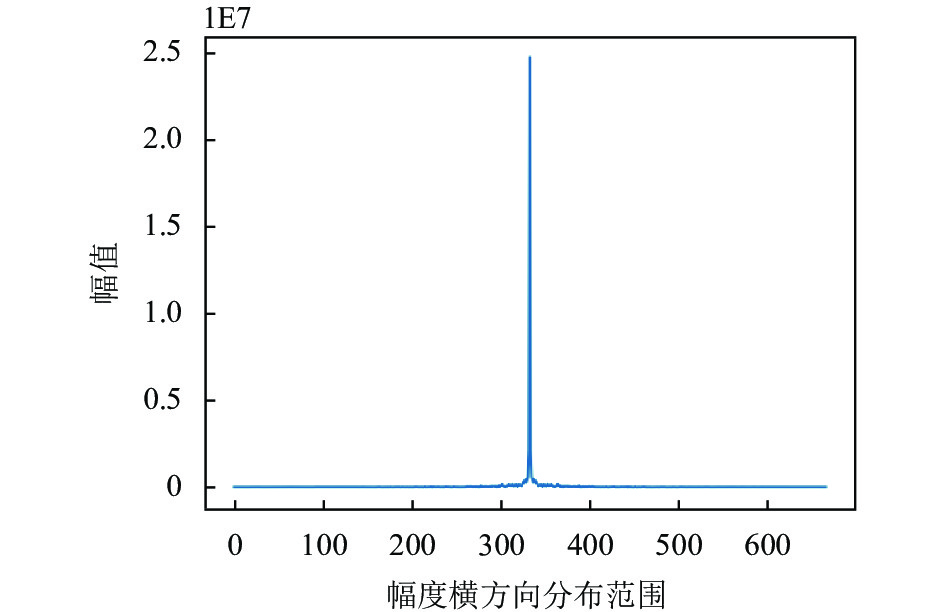
通过获取到的幅值曲线函数, 可以发现, 位于中心点的幅值最高, 其左右两侧也有部分峰值, 可以确定该峰值是周期性伪影在频域上的表现形式, 将获取的点集的坐标来和峰值进行对比, 能够确定通过该算法模型获取频域上疑似的伪影坐标是正确的, 这些点存入集合P中, d为集合P中距离频域中心的最短距离, 同时需要保留频谱中心点上的有用信息, 避免由于该算法误判导致图像的非伪影区纹理细节被破坏, 假设频域某点坐标为(x₀, y₀)则其到中心点(M/2, N/2)的欧氏距离为:

$ R = \sqrt {{{\left({x_0} - \frac{M}{2}\right)}^2} + {{\left({y_0} - \frac{N}{2}\right)}^2}},\; 0\leqslant R < d $

(13)

对于一幅超声图像, 其频率域中心点范围代表的是图像的低频信号, 其四周范围代表的是图像的高频信息, 根据R的范围, 来对R进行采样, 分别计算原始超声图像和逆傅立叶变换之后的伪影区和非伪影区的MSE和SNR值来计算出最优截止半径, 并观察它们之间的相关性, 伪影抑制效果以及图像中有用信息是否完整. 确定R值后, 下一步就是对P中的点根据图像的动态范围进行幅度值上的降低. 动态范围是一个用于定义在一定的范围内能够捕捉图像细节的术语, 通常用一幅图像的最低值到最高溢出值之间的范围来描述, 动态范围越大, 就能尽可能地保留图像高光区和阴影区的信息. 所以通过改变集合P中点的幅度值来达到符合预期的动态范围. 假设一幅图像G, 它的频率域幅值的最大值为max(G), 最小值为min(G), 它的全局动态范围计算公式为:

$ D = 10\log \left(\frac{{\max (G)}}{{\min (G)}}\right) $

(14)

计算出动态范围, 根据给定的阈值系数K(0≤K<1), 根据P集合确定滑动窗口内所有点的幅度值, 重新计算其中心点动态范围, 用来确定相应的动态范围大小为:

$ T = DK,\; 0 < K \leqslant 1 $

(15)

再根据式(14)得出新的幅度值为:

$ A = {10^{\frac{T}{{10}}}}\min (G) $

(16)

将P集合中的点幅度值设置成符合当前滑动窗口内的数值A, 通过修改幅度值来实现了周期性伪影的抑制效果, 可以通过逆向傅立叶变换观察算法的使用效果. 为了确定阈值系数K的大小, 需要对其范围进行采样, 在本次实验验证中, 采样周期为0.1, 并从视频中获取1张超声图像, 依次对不同采样点区域A(伪影区域)区域B(非伪影区域)的MSE和SNR作为伪影抑制标准, 找出最佳阈值系数. 确定阈值系数后, 使用上面的单帧部分超声图像来进行验证伪影抑制算法模型的准确性. 通过该算法的程序并选取4个在阈值系数为0的情况下不同截止半径以及3个在截止半径为d时不同阈值系数的采样点并进行对比从而确定最佳截止半径及阈值系数, 如图14–图20. 左侧为原始超声图像, 中间为通过该算法改进后的频率域图像, 右侧为通过频率域图像进行逆傅立叶变换后的图像.

通过上述人体组织的伪影抑制仿真实验, 发现阈值系数K以及截止半径R对超声图像的伪影区域A及非伪影区域B的MSE和SNR具有相关性, 所以在该算法中, 需要选取合适的截止半径R以及阈值系数K来实现超声图像的伪影抑制效果.

在超声实时成像领域, 对于超声图像处理效果上的判断通过定性分析以及定量分析两者结合来完成的, 本研究在表1以及表2中对于伪影的抑制效果和有效信息的完整程度分别给出了3个评价标准. 伪影抑制效果评价分为3个等级, 分别是很差, 一般, 良好. 非伪影区域有效信息完整程度评价分为3个等级, 分别是无效, 一般, 良好. 定性的评价标准往往由超声医师的经验来决定. 本研究在前文中提到了将超声图像分为伪影区域以及非伪影区域, 这是在超声医师的帮助下完成的. 本文同时也给出了定量的分析, 对于超声医师勾勒出的伪影区域以及非伪影区域, 本文分别计算了在采用该算法之后两个区域内的MSE数值和SNR数值, 通过对这些数据进行分析结合超声医师的经验完成超声图像质量上的评估.

截止半径R对该算法在超声图像上的作用起着重要的作用, 当截止半径过小时, 频域中心的数据会被破坏, 不仅不能够对超声图像进行伪影抑制, 而且还会破坏图像中有效的医学信息, 结合超声医师对超声图像判断的经验, 有效信息的完整程度的评价等级为无效. 当随着截止半径不断扩大, 部分频域中心数据得以保留, 但仍有部分数据被破坏, 此时即使能够抑制部分伪影, 有效的医学信息仍然会被部分破坏, 因此结合超声医师的经验, 有效信息完整程度的评价等级为一般. 随着截止半径不断地扩大, 会有部分伪影在频域上的脉冲信号点被囊括在截止半径之外, 因此部分伪影无法得到抑制, 此时伪影抑制的评价等级逐渐从一般到很差.

阈值系数K对于伪影抑制的效果同样具有非常重要的作用, 当阈值系数过大时, 疑似伪影的脉冲点的幅度值没有超过阈值, 因此得以保留, 此时伪影抑制的评价等级为很差. 随着阈值系数的降低, 结合医师的判断, 伪影抑制效果逐渐从一般转变为良好.

表1为不同截止频率在超声图像伪影抑制前后区域A(伪影区)和区域B(非伪影区)的均方误差, 信噪比结果以及伪影抑制效果和有效信息的完整程度的对比, 表2为不同阈值系数在超声图像伪影抑制前后区域A (伪影区)和区域B (非伪影区)的均方误差和信噪比结果以及伪影抑制效果和有效信息的完整程度的对比(伪影抑制效果评估标准)

通过表1的结果可以判断出在R < 3时, 频域中心有用信息被抑制, 导致通过IFFT后的图像部分有用信息及伪影的损失, 以在区域 A及区域B的MSE值偏大, 当R >10时, 由于部分频域上伪影亮点在截止半径之内没有进行任何压低处理, 导致通过IFFT后仍然会有部分周期性伪影存在(如 图17), 在此截止半径下图像区域A及区域B的MSE值会非常小. 当R位于3和6之间时, 由于部分周期性伪影分布在该区域内, 对该区域内的亮点幅值进行适当压低, 可以达到去除周期性伪影的效果.

取R=4, 来对P集合中[0, M/2–R]和[M/2+R, M]范围内的亮点通过阈值系数K来进行幅值压低处理获取表2的数据.

由于当阈值系数K不断增大, 集合P中满足当前阈值的亮点逐渐减少, 当K等于0.8时, 所有亮点都不满足超过阈值的条件, 因此没有对集合P中的任何亮点进行压低, 所以处理前后的区域A及区域B的MSE值近似于0, 证明K值与伪影抑制的效果呈负相关, 即K越大伪影抑制效果越差.

根据采样结果, 在当前超声图像中能够确定最优的截止半径R和阈值系数K后通过该算法进一步实现的部分连续超声图像伪影抑制效果, 如图21、图22.

实验结果表明, 对于原始超声低通道扫描图像包含的周期性伪影, 该算法基本能在保留图像有用信息的基础上将其去除, 并且该算法效果明显, 实验结果证明了该算法模型的正确性.

4 结论及下一步研究

医学超声实时成像的研究是一项比较新型的研究方向, 近几年的发展非常迅速, 从早期的A型, M型, B型超声诊断技术到目前的超声多普勒成像技术, 三维成像技术的发展历程来看, 超声成像技术的发展在于提高图像质量, 已经取得较大的突破^[20], 并且广泛应用于医生的辅助诊断等领域, 在超声实时成像领域也有着广泛的研究空间, 伴随着现代医学的进步以及发展, 医学超声诊断仪的重要性不言而喻. 超声实时成像的质量确面临的巨大的挑战, 由于超声声波固有的特点和技术缺陷, 超声实时成像上往往都带有斑点, 周期性等类型的伪影, 这些伪影往往会严重影响到医生的诊断效果, 所以如何抑制这些类型的伪影成为了一个新的课题.

本研究对于超声实时成像的周期性伪影抑制提出了一种新的算法, 用来解决目前遇到的难题, 通过正弦波的模拟实验以及人体组织的算法仿真实验, 该算法能够较好地解决人体组织上周期性伪影影响医生诊断的难题, 视频中的周期性伪影得到了明显的抑制, 能够提高医生诊断的准确度. 伪影的来源是由超声探头制造上的局限性以及采用低通道扫描而产生的, 可以发现该伪影垂直于人体的组织器官, 因此有别于超声波束作用于不同纹理的器官组织的表面产生回波导致的伪影. 本研究当中的伪影, 与器官组织的纹理无关, 对于任何人体组织器官, 在超声领域内采用该类型探头以及扫描方式均会产生该类型的伪影, 因此针对不同的器官组织不会有任何区别.

尽管如此, 在本研究中, 还有一些地方需要改进, 例如对于截止频率的判定以及阈值系数的选取由于采样周期较大, 只能确定一个大致的范围, 并不能准确的定位出具体数值, 在极端情况下可能会出现“误判”, 将非伪影区域当成伪影给抑制掉, 需要通过下一步研究来对算法模型进行改进.

当前, 超声图像的修复技术尚未成熟, 图像修复不是一个单一学科的问题, 它涉及很多相关领域的研究^[21], 随着科学技术的不断发展, 医学超声领域将会不断地进行深耕, 新的医学超声技术也将会出现, 这一行业会随着技术的不断成熟和完善不断蓬勃发展, 在保证人体健康的过程中发挥越来越大的作用.