1 引言

近年来, 随着人工智能技术的快速发展和广泛应用, 数据隐私保护也得到了密切关注. 欧盟出台了首个关于数据隐私保护的法案《通用数据保护条例》(General Data Protection Regulation, GDPR)^[1], 明确了对数据隐私保护的若干规定. 中国自2017年起实施的《中华人民共和国网络安全法》和《中华人民共和国民法总则》中也对用户隐私数据的使用做出了明确的规定. 在机器学习中, 模型的好坏很大程度上依托于建模的数据. 但由于相关法律法规的限制, 数据孤岛问题变得十分普遍, 导致企业很难获取训练数据. 为此, 谷歌在2016年提出了联邦学习的概念. 联邦学习是一种基于分布式机器学习的框架, 在这种框架中, 多个客户端在中央服务器的协调下共同训练模型, 并保证训练数据可以保留在本地, 不需要像传统的机器学习方法一样将数据上传至中央服务器^[2], 从而保护了用户隐私.

构建一个高性能的联邦模型通常需要多轮通信, 同时规模庞大的神经网络模型, 往往包含数百万个参数^[3], 这导致了巨大的通信开销. 此外, 相较于传统的分布式机器学习, 联邦学习还面临如下问题:

1)客户端数据非独立同分布: 在传统分布式机器学习中的训练数据随机均匀地分布在客户端上^[4], 即遵循独立同分布(independent and identically distributed, IID). 这在联邦学习中通常是不成立的, 由于用户的喜好不同, 客户端的数据通常是非独立同分布(non-IID)的. 即客户端拥有的局部数据集不能代表整体数据的分布, 不同客户端之间的数据分布也不同.

2)数据不平衡: 不同的客户端可能拥有不同的数据量.

3)客户端数量庞大且不可靠: 参与训练的客户端为大量的移动设备, 通常大部分客户端经常离线或者处于不可靠的连接上, 因此无法确保客户端参与每一轮的训练.

本文主要研究联邦学习中的通信效率问题, 利用梯度稀疏化的思想减少客户端与服务器之间通信的参数量, 并在服务器聚合时使用投影的方式缓解非独立同分布数据带来的影响. 经过在MNIST和CIFAR10数据集上的实验证明, 本文提出的算法能够在联邦学习的约束条件下高效训练模型.

2 相关工作

一般来说, 减少联邦学习中的通信开销有两种策略, 一种是减少训练过程中的通信轮次, 另一种是减少每轮传递的通信量. 减少通信轮次的经典方案是联邦学习中最常用的FedAvg算法^[2], 即令客户端在本地执行多轮本地更新, 服务器再进行全局聚合, 来减少通信轮数. FedAvg在每次通信中, 客户端需要上传或下载整个模型, 由于联邦客户端通常运行在缓慢且不可靠的网络连接上, 这一要求使得使用FedAvg训练大型模型变得困难. 在实际应用中, FedAvg算法可以较好地处理非凸问题, 但该算法不能很好处理联邦学习中数据non-IID的情况, 在此应用场景很可能导致模型不收敛^[5]. 因此针对non-IID场景, Briggs等^[6]在FedAvg的基础上引入层次聚类技术, 根据局部更新与全局模型的相似度对客户端进行聚类和分离, 以减少总通信轮数. 此外Karimireddy等^[7]通过估计服务器与客户端更新方向的差异来修正客户端本地更新的方向, 有效地克服了non-IID问题, 能在较少的通信轮次达到收敛.

另一类方法的核心思想在于减少传输的数据量, 主要通过量化、稀疏化等一系列方法对模型参数或者梯度进行压缩. 量化通过将元素低精度表示或者映射到预定义的一组码字来减少梯度张量中每个元素的位数, 例如Dettmers^[8]将梯度的32位浮点数量化至8位, SignSGD^[9-11]则只保留梯度的符号来更新模型, 将负梯度量化为–1, 其余量化为1, 实现了32倍的压缩. 稀疏化方法通过只上传部分重要的梯度来进行全局模型的更新, 如何选择这些梯度成为该方法的关键. Strom^[12]提出使用梯度的大小来衡量其重要性, 通过预先设立阈值, 当梯度大于该阈值时对其进行上传. 然而在实际情况中, 由于不同的网络结构参数分布差异较大, 导致我们无法选择合适的阈值. 因此目前稀疏化方法通常使用Aji等^[13]提出的固定稀疏率, 每次传递一定比例的最大梯度或每次传递前k个最大梯度的Topk方法^[14]. 上述工作有效地解决了分布式机器学习中的通信开销问题, 针对联邦学习的训练环境, Rothchild等^[15]使用了一种特殊的数据结构计数草图(count sketch)对客户端梯度进行压缩. Chen等^[16]将神经网络的不同层分为浅层和深层, 并认为深层参数更新频率低于浅层参数, 因此提出了异步更新策略, 有效减少了每轮传递的参数量. Haddadpour等^[17]在FedAvg的基础上对每轮传递的参数进行压缩, 并针对non-IID场景采用梯度跟踪技术对客户端梯度方向进行修正, 在收敛速度和准确率上都取得了较好的效果.

Sattler等^[18]也针对联邦学习的训练环境提出了稀疏三元压缩(sparse ternary compression, STC), 该方法在Topk梯度稀疏化的基础上进行了量化进一步减少了通信量, 并利用错误反馈机制实现了客户端与服务器之间的双向压缩, 在联邦学习场景中表现出了良好的效果. 该方法考虑了联邦学习中客户端non-IID数据的场景, 通过利用稀疏的特性以及减少本地训练次数与服务器端频繁通信去减轻non-IID数据带来的问题, 但该方法对non-IID数据的优化能力有限. 因此本文将在稀疏三元压缩算法的基础上, 关注non-IID下的联邦场景, 提升联邦学习的通信效率.

3 算法设计 3.1 稀疏三元压缩

常规的Topk稀疏方法以全精度传递稀疏元素, Sattler等^[19]证明了当稀疏化与非零元素的量化相结合时, 可以获得更高的压缩增益. 如算法1所示, 当获得Topk稀疏元素 ${T^{\rm masked}}$ 后, 会将其量化为稀疏元素的平均值, 因此最后只需要传递一个包含值 $\left\{ { - \mu , 0, \mu } \right\}$ 的三元张量. 如果将每一层的梯度看做一个矩阵, 那么使用Topk和稀疏三元压缩后得到的结果如图1所示, 原始梯度是一个稠密矩阵, 颜色深浅代表值的大小, 通过Topk方法会得到一个保留较大值的稀疏矩阵, 值较小的则置为0, 而稀疏三元压缩则在Topk的基础上做了量化, 进一步提升了压缩率.

算法1. STC^[18]: 稀疏三元压缩算法

输入: 张量 $\scriptstyle T \in {\mathbb{R}^n}$ , 稀疏率p

1. $\scriptstyle k \leftarrow {\text{max}}\left( {np, 1} \right)$

2. $\scriptstyle v \leftarrow {\text{to}}{{\text{p}}_k}\left( {\left| T \right|} \right)$

3. $\scriptstyle mask \leftarrow \left( {\left| T \right| \geqslant v} \right) \in {\left\{ {0, 1} \right\}^n}$

4. $\scriptstyle {T^{\rm masked}} \leftarrow mask \odot T$

5. $\scriptstyle \mu \leftarrow \frac{1}{k}\mathop \sum \nolimits_{i = 1}^n |T_i^{\rm masked}|$

6. 输出 $\scriptstyle  {T}^{*}\leftarrow \mu \times {\rm sign}\left({T}^{\rm masked}\right)$

Sattler等^[18]在联邦学习中使用稀疏三元压缩对客户端和服务器之间通信的梯度进行双向压缩, 并结合错误反馈机制^[20]在客户端和服务器保留压缩前后的误差累加至下一轮训练过程.

$ \hat g_i^t = STC\left\{ {g_i^t + erro{r^{t - 1}}} \right\} $

(1)

$ erro{r}^{t} = {g}_{i}^{t}- {\widehat{g}}_{i}^{t} $

(2)

其中, $g_i^t$ 为第 $i$ 个客户端第 $t$ 轮训练得到的原始梯度, $\hat g_i^t$ 为压缩后的梯度, $erro{r^t}$ 为压缩前后的误差. 该方法取得了与非压缩算法相似的收敛速度并大大减少了每一轮的通信量, 因此本文也将使用稀疏三元压缩方法进行梯度压缩.

3.2 Non-IID数据的处理

目前在联邦学习中, 我们通常采用平均各个客户端梯度的方法计算全局模型. 当不同客户端数据满足IID条件时, 各客户端梯度更新方向相近, 且聚合后梯度与基于传统的集中式学习获得的梯度相似性较高. 故此方法能获得全局目标函数的最优解. 若客户端数据non-IID且数据量差异较大, 各客户端梯度差异性较大, 存在相互干扰的情况, 导致全局模型收敛速率降低. 同时, 简单平均各方梯度易使数据量多的客户端占主导作用, 使得全局模型无法较好地处理数据量较少的客户端, 最终导致全局模型整体性能低下.

Wang等^[21]提出使用梯度投影处理non-IID数据的问题, 服务器端在进行梯度平均之前, 通过修改梯度方向减轻non-IID数据带来的影响. 该方法首先对客户端之间的梯度冲突做出定义, 当客户端 $i$ 的梯度 ${g_i}$ 和客户端 $j$ 的梯度 ${g_j}$ 满足 $  {g}_{i}\cdot {g}_{j} < 0 $ 时, 则称为客户端 $i$ 和客户端 $j$ 之间存在梯度冲突. 当客户端之间存在梯度冲突时, 梯度方向差异性较大, 这时可以通过将一个客户端的梯度投影到另一个有冲突的客户端梯度平面上, 使用原梯度减去投影来缩小客户端之间的梯度差异, 如式(3)所示:

$ {g_i} = {g_i} - \frac{{\left( {{g_i} \cdot {g_j}} \right){g_j}}}{{{\text{||}}{g_j}{\text{|}}{{\text{|}}^2}}} $

(3)

此外, 该方法定义了内部冲突和外部冲突, 分别对其进行投影处理. 将参与训练的客户端之间的梯度冲突定义为内部冲突, 将客户端梯度按照训练损失从小到大排序得到 $ P{O_t} = \left\{ {g_1^t, g_2^t, \cdots, g_m^t} \right\} $ , 并引入参数 $\alpha $ 来控制每轮参与投影的客户端数目. 从 $P{O_t}$ 中选择损失较小的客户端 $S_t^\alpha $ 迭代的判断与其他客户端之间的梯度冲突, 并进行投影修改梯度方向以缓解内部冲突. 对于未选择的损失较大的客户端则保持原有的梯度, 此后进行梯度平均得到聚合后的梯度 ${g^t}$ , 如算法2所示.

在实际联邦场景中, 客户端non-IID程度较大, 在每轮聚合中, 若对所有客户端统一采用投影方案, 则导致训练损失大的客户端的梯度方向不断靠近损失小的客户端. 这将导致聚合模型无法学习到所有客户端的信息. 但通过调整参数 $\alpha $ , 自适应地让部分训练损失较大的客户端直接参与最终的聚合阶段, 有效地缓解了上述问题.

算法2. MitigateInternalConflict^[21]: 缓解内部冲突算法

输入: 客户端梯度投影顺序 $\scriptstyle P{O}_{t}  $ , 参数 $\scriptstyle \alpha $

1. 　服务器从 $\scriptstyle P{O_t}$ 选择损失较小的客户集合 $\scriptstyle S_t^{1{{ - }}\alpha }$ 参与投影, 保留 $\scriptstyle \alpha $ 比例损失较大的客户端梯度

2. 　 for each client $\scriptstyle k \in S_t^{1{{ - }}\alpha }$ in parallel do

3.　　 $\scriptstyle g_k^{pc} \leftarrow g_k^t $

４.　　 for each $\scriptstyle {g}_{i}^{t}\in P{O}_{t}  $ , $\scriptstyle i = 1, \cdots, m$ do

5. 　　　 if $\scriptstyle g_k^{PC} \cdot g_i^t < 0$ and $\scriptstyle k \ne i$ then

6.　　　　　 投影修正客户端梯度: $\scriptstyle g_k^{PC} \leftarrow g_k^{PC} - \frac{{\left( {g_i^t} \right) \cdot g_k^{PC}}}{{{\text{||}}g_i^t{\text{|}}{{\text{|}}^2}}}g_i^t$

7. 　　　 end if

8. 　　 end for

9. 　 end for

10. 计算聚合梯度: $\scriptstyle {g^t} \leftarrow \frac{1}{m}\mathop \sum \nolimits_{k = 1}^m g_k^{PC}$

11. 返回聚合梯度 $\scriptstyle {g^t}$

由于联邦学习中客户端的部分参与和不可靠连接, 在第 $t$ 轮未被选中参与训练的客户端可能会遭受被全局模型遗忘的风险, 因此可以在服务端保留其最近一次参与训练的梯度 $GH = \left\{ {g_1^{{t_1}}, g_2^{{t_2}}, \cdots, g_K^{{t_K}}} \right\}$ , 根据它们的近邻历史梯度来估计真实梯度以避免客户端被遗忘, 如算法3第6步所示. 第 $t$ 轮未被选中客户端的估计梯度 ${g_{\rm con}}$ 与参与更新的客户端平均后的梯度 ${g^t}$ 之间的冲突称为外部冲突, 通过将 ${g^t}$ 迭代的投影到不同轮次的估计梯度 ${g_{\rm con}}$ 的法平面以缓解外部冲突, 通过参数 $\tau $ 控制投影的轮次. 具体步骤如算法3所示.

算法3. MitigateExternalConflict^[21]: 缓解外部冲突算法

输入:聚合梯度 $\scriptstyle {g^t}$ , 所有客户端近邻历史梯度 $\scriptstyle GH$ , 参数 $\scriptstyle \tau $

1. 　 for round $\scriptstyle t - i,\; i = \tau ,\; \tau - 1, \cdots,\; 1$ do

2. 　　初始化估计梯度: $\scriptstyle {g_{\rm con}} \leftarrow 0$

3.　　 for each client $\scriptstyle k = 1, 2, \cdots, K$ do

4. 　　　 if $ \scriptstyle  {t}_{k}=t-i $ then

5. 　　　　 if $\scriptstyle {g^t} \cdot g_k^{{t_k}} < 0$ then

6. 　　　　　计算未被选中客户端的估计梯度: $\scriptstyle {g_{\rm con}} \leftarrow {g_{\rm con}} + g_k^{{t_k}}$

7. 　　　　 end if

8. 　　　 end if

9. 　　 end for

10.　　 if $\scriptstyle {g^t} \cdot {g_{\rm con}} < 0$ then

11. 　　　对聚合梯度投影修正: $\scriptstyle {g^t} \leftarrow {g^t} - \frac{{{g^t} \cdot {g_{\rm con}}}}{{{\text{||}}{g_{\rm con}}{\text{|}}{{\text{|}}^2}}}{g_{\rm con}}$

12.　 end if

13. end for

14. 返回聚合梯度 $\scriptstyle {g^t}$

3.3 基于投影聚合的稀疏三元压缩算法

鉴于投影能够有效地处理联邦学习中的non-IID数据问题, 因此本文将在稀疏三元压缩的基础上, 在服务器端使用投影聚合的方式, 进一步提高模型的正确率与收敛速度, 具体步骤如算法4所示.

在算法4中使用网络模型更新量表示客户端梯度 $g_i^t \leftarrow w_i^{t - 1} - w_i^t$ , 因此在算法的第5–6行客户端接收到聚合梯度 $\bar g$ 后首先计算本轮的初始网络训练模型 $w_i^t$ . 在第7行根据随机梯度下降方法训练新的模型, 并计算本轮的客户端梯度 $g_i^t$ . 此后在第8–9行使用结合错误反馈机制的STC算法压缩梯度, 在客户端本地保留压缩前后的梯度差异在下一轮压缩时重新引入, 减小由于压缩导致的梯度信息丢失. 之后客户端将压缩后的梯度与训练损失发送给服务器.

服务器端接收到客户端梯度与训练损失后, 首先在算法第14行更新每个客户端最近一次参与训练的梯度 $GH = \left\{ {\hat g_1^{{t_1}}, \hat g_2^{{t_2}}, \cdots, \hat g_K^{{t_K}}} \right\}$ 以便在缓解外部冲突时使用, 其中 $K$ 是所有客户端个数, $ {t_K} $ 是客户端最近一次参与训练的轮次. 之后在第15行根据训练损失的大小对本轮参与训练的客户端梯度进行排序得到 $P{O_t} = \left\{ {\hat g_1^t, \hat g_2^t, \cdots, \hat g_m^t} \right\}$ , 其中 $m$ 是本轮参与训练的客户端个数. 然后依次根据算法2中的缓解内部冲突算法和算法3中的缓解外部冲突算法得到聚合梯度 ${g^t}$ . 算法2和算法3的主要作用是对聚合梯度 ${g^t}$ 的方向进行修正以缓解non-IID问题, 因此在第20行中, 保留修正后的聚合梯度 ${g^t}$ 的方向与原始聚合梯度的大小得到最终的聚合梯度. 最后使用与客户端相同的STC压缩算法压缩聚合梯度并发送至客户端.

算法4. 基于投影聚合的稀疏三元压缩算法

输入: 初始化模型 $\scriptstyle w$

1.　 for $\scriptstyle t = 1,\; \cdots ,\; T$ do

2. 　　服务器从K个客户端随机选取m个客户端参与训练

3.　　 for $\scriptstyle i = 1,\; \cdots,\; m$ in paralleldo

4. 　　　客户端 $\scriptstyle {C_i}$ :

5. 　　　　从服务器端下载聚合梯度 $\scriptstyle \bar g$

6. 　　　　 $ \scriptstyle {w}_{i}^{t}\leftarrow {w}_{i}^{t-1}- \overline{g} $

7. 　　　　 $\scriptstyle {g}_{i}^{t}\leftarrow  SGD\left({w}_{i}^{t}, Dat{a}_{i}\right)-{w}_{i}^{t} $

8. 　　　　 $\scriptstyle {\widehat{g}}_{i}^{t}\leftarrow  STC\left({g}_{i}^{t}+erro{r}^{t-1}, p\right) $

9. 　　　　 $\scriptstyle  erro{r}^{t}= {g}_{i}^{t}- {\hat{g}}_{i}^{t}$

10. 　　　　上传客户端梯度 $\scriptstyle \hat g_i^t$ 和训练损失 $\scriptstyle  {l}_{i}^{t} $ 至服务器

11.　　 end for

12. 　　　服务器器端:

13. 　　　　接收参与训练的客户端梯度 $\scriptstyle \hat g_i^t$ 和训练损失 $\scriptstyle  {l}_{i}^{t} $

14. 　　　　更新所有客户端近邻历史梯度信息: $\scriptstyle GH = \left\{ {\hat g_1^{{t_1}},\; \hat g_2^{{t_2}},\; \cdots,\; \hat g_K^{{t_K}}} \right\}$

15. 　　　　根据客户端训练损失对梯度排序: $\scriptstyle P{O_t} = \left\{ {\hat g_1^t,\; \hat g_2^t,\; \cdots,\; \hat g_m^t} \right\}$

16. 　　　　缓解内部冲突: $\scriptstyle {g^t} \leftarrow {{MitigateInternalConflict}}\left( {P{O_t},\; {\alpha }} \right)$

17.　　　　 if $\scriptstyle t \geqslant \tau $ then

18. 　　　　　缓解外部冲突: $\scriptstyle {g^t} \leftarrow {{MitigateExternalConflict(}}{g^t}, GH, \tau {\text{)}}$

19.　　　　 end if

20. 　　　　 $\scriptstyle {g}^{t} = {g}^{t}/\text{||}{g}^{t}\text{||}*\text{||}\frac{1}{m}{{ \sum }}_{i}^{m}{\hat{g}}_{i}^{t}\text{||}$

21.　　　　 $\scriptstyle \overline{g} = STC\left({g}^{t}+error, p\right) $

22. 　　　　 $\scriptstyle error = {g}^{t}-\overline{g}  $

23.　　　　 发送聚合梯度 $\scriptstyle \overline g$ 至客户端

24.　 end for

算法4中的步骤可简化为图2, 在客户端, 首先接收聚合梯度 $\overline g$ , 然后根据模型和客户端数据进行本地训练得到客户端梯度 $g_i^t$ , 本地训练完成后使用STC算法压缩梯度上传至服务器, 并计算压缩误差存储在本地, 在下一轮被选中训练时进行梯度修正.

服务端接收到所有参与训练的客户端发送的梯度后判断客户端梯度之间是否存在梯度冲突, 并依次通过缓解内部冲突和外部冲突的算法对梯度方向进行修正. 最终聚合投影后的梯度生成全局梯度 $ {g^t} $ , 采用STC算法压缩全局梯度 $ {g^t} $ 得到 $\overline g$ 发送至客户端. 该算法实现了客户端与服务器之间的双向压缩, 并且在服务器端进行投影缓解数据异构的问题.

4 实验分析 4.1 实验设置

本文的实验使用了MNIST和CIFAR10数据集. MNIST数据集包含60 000张训练图片, 10 000张测试图片, 每张图片是2 828的灰度手写数字图像, 实验使用带有3个卷积层的CNN模型对MNIST进行训练. CIFAR10数据集包含50 000张训练图片, 10 000张测试图片, 每张图片是3 232的RGB图像, 使用文献[18]中简化的VGG11网络进行训练. 客户端数据集划分参照文献[2], 首先按照数据集的类别进行排序, 然后将数据集划分为200个分片, 每个客户端随机选择两个不会替换的分片来模拟客户端数据非独立同分布的场景. 实验中部分参数设置如表1所示.

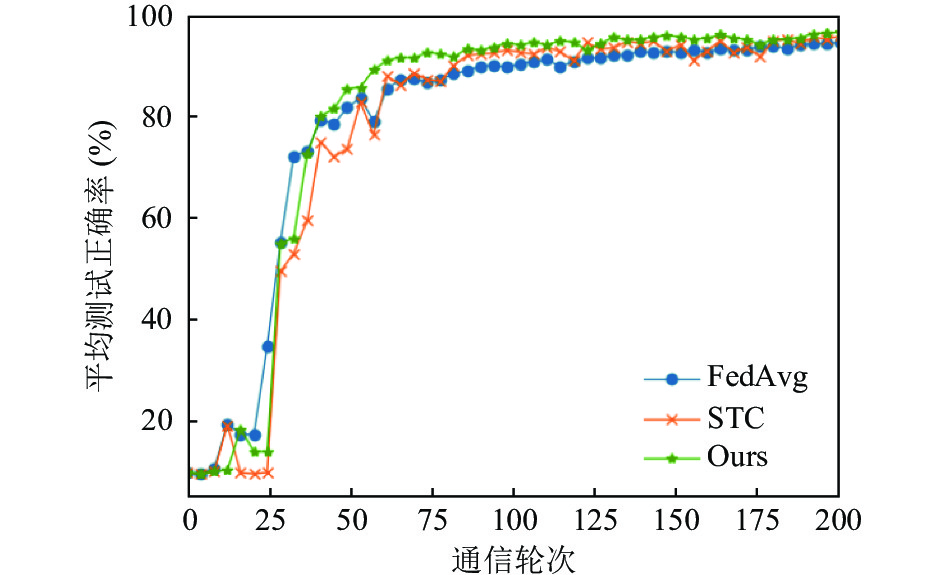
4.2 实验结果

我们将本文提出的算法与FedAvg以及稀疏三元压缩算法进行了对比, 图3和图4是在MNIST数据集上的结果, 图3是全局模型在所有客户端上的平均测试准确率, 图4为测试准确率的方差, 其中稀疏三元压缩以及本文提出的算法在实验中设置了0.1的稀疏率, 也就是每轮传递10%的参数进行训练, 根据图1的实验结果可以看到本文提出的算法相较于其他算法收敛速度和收敛精度都略有提升, 特别是相较于STC算法, 在相同压缩率的条件下本文提出的算法大约在第75轮收敛, 而STC算法在训练过程非常震荡, 并且在大约100轮才收敛.

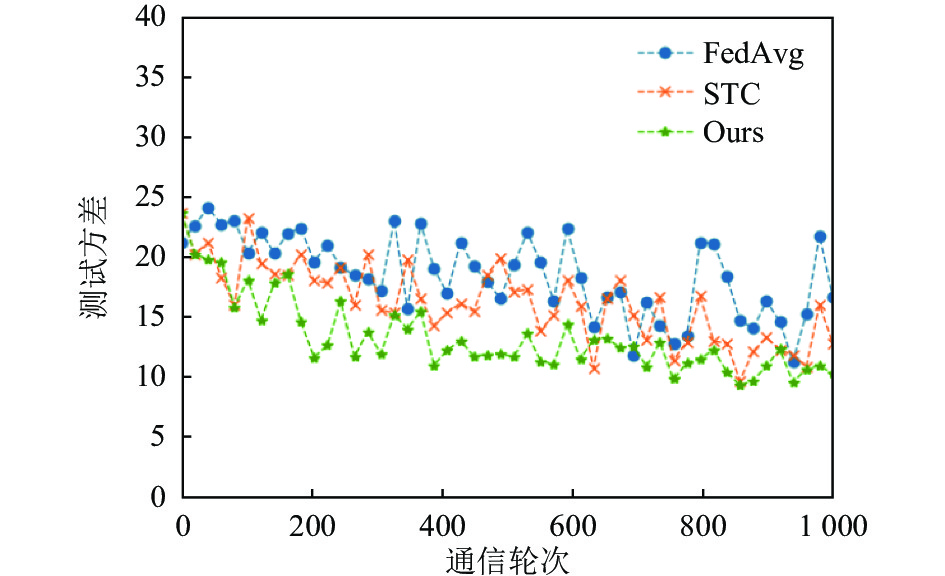
图5和图6是在CIFAR10数据集上的测试准确率和测试方差, 稀疏率同样为0.1, 与MNIST数据集相比, 在CIFAR10数据集上的训练过程更加震荡, 但是本文提出的算法相较其他算法收敛速度和收敛精度都有大幅度提升, 并且训练过程中的震荡幅度远远小于FedAvg和STC算法, 这说明本文的算法是非常有效的.

表2中记录了客户端与服务器之间每轮通信的参数大小, 通信轮次是达到固定正确率(MNIST 95% CIFAR10 50% )大约所用的通信轮数, 以FedAvg作为基线算法, 本文提出的算法在上传和下载时都进行了压缩, 在MNIST数据集上相较于FedAvg每轮的通信量减少了45倍, 并且本文的算法在第100轮时就达到了指定的正确率, 相较于FedAvg和STC分别减少了97和57个通信轮次, 在CIFAR10数据集上每轮的通信量更是减少了47倍, 通信轮次相较于FedAvg和STC减少了295轮和300轮.

5 结论

本文提出了基于投影聚合的稀疏三元压缩算法, 提升联邦学习的通信效率. 该算法在客户端和服务端采用稀疏三元压缩减少客户端在每一轮训练过程中上传和下载的通信量, 同时在服务器端利用梯度投影的方式缓解了由于客户端数据异构以及部分参与导致的梯度冲突问题. 通过在MNIST和CIFAR10数据集上的实验验证, 本文提出的算法在通信量、收敛速度和正确率3个方面都要由于传统的FedAvg算法和稀疏三元压缩算法. 由于梯度压缩会略微改变原始梯度的方向, 在未来我们将针对不同的压缩方法对投影聚合的方式做进一步的研究, 进一步提高算法的有效性.