2. 长沙理工大学 计算机与通信工程学院, 长沙 410114
2. School of Computer and Communication Engineering, Changsha University of Science & Technology, Changsha 410114, China
人的大脑是复杂而高效的. 多年来, 人们一直试图模拟大脑的功能和运行机制来执行复杂的信号处理功能. 人工神经网络是从大脑神经系统中衍生出来的一种模型, 被广泛应用于模式识别领域. 脑电图(EEG)是研究大脑活动最常用的信号之一, 不同场景下脑电信号的识别, 则被用于诊断各种脑相关的疾病, 如癫痫[1-3]、抑郁症[4]、阿兹海默症[5]等, 同时在认知[6-8]、记忆和情绪[9-11]等相关脑活动的研究方面也显示出巨大的潜力. 因此, 借助人工神经网络来对脑电信号进行识别, 对脑疾病的诊断, 大脑相关活动的功能和机制的研究具有重要的意义.
在众多人工神经网络模型中, 传统的人工神经网络模型依靠研究者手动提取原始数据的特征, 来引导模型识别准确率的提高; 以深度学习为代表的人工神经网络模型将传统模型中的原始数据特征提取和分类两步融为一步, 在训练数据足够的情况下能获得更好的识别效果.
但是, 研究一种有效的脑电信号特征提取方法本身比较费时费力, 且对于一些中小型脑电数据集而言, 可能存在特征提取方法有效, 却由于训练样本数量不够导致的识别效果不够理想的情况. 因此, 探求一种新的人工神经网络模型对脑电信号进行识别, 具有重要的研究前景和价值.
针对脑电信号的识别问题, 本文研究了一种重要性可能被忽略的海马神经回路模型—KIV模型. KIV模型是K系列模型的最高级别模型. K系列模型包括K0、KI、KII、KIII、KIV模型, 从低到高层次逐步实现了从细胞水平到大脑半球的模拟. 其中, 基于嗅觉神经系统的解剖结构, KIII模型模拟了嗅觉神经系统, 包括其主要结构, 如球周细胞(periglomerular cell, PG)、嗅球(olfactory bulb, OB)、前嗅核(anterior olfactory nucleus, AON)和梨状皮质(prepyriform cell, PC), 能够模拟嗅觉信息的传递过程. KIII模型表现出良好的模式识别能力, 只需少量迭代次数就可记忆不同的模式. 目前的研究已经将KIII模型应用于图像识别[12, 13], 语音识别[14], 文本分类[15], 脑电识别[16]等方面, 并获得了良好的识别结果. KIV模型包含3个KIII模型和一个KII模型, 分别模拟了大脑中的感觉皮层(sensory cortices)、海马(hippocampus)、中线前脑(midline forebrain)和杏仁核(amygdala) , 描述了行动、规划和空间定位功能的选择. 在模拟的火星环境中[17, 18], 作为机器人的控制系统, 3个KIII模型分别接收感觉信息(包括视觉、听觉、触觉等)、方位信息和内部感受信息, 使得KIV模型能够模拟大脑在导航时的记忆功能, 对环境信息的输入做出迅速、准确的学习和反应.
基于KIII模型的功能和特性, 本文扩展了KIV模型在脑电识别领域的应用. 癫痫脑电和情感脑电信号的识别一直是脑电识别领域的研究热点, 分别对癫痫发作的诊断治疗和与情绪相关的大脑活动的研究具有重要意义. 本文介绍了KIV模型的结构和原理, 分析了KIV模型的动力学行为, 并针对癫痫脑电和情感脑电的识别问题, 使用KIV模型进行探索和研究.
1 KIV模型及分析 1.1 KIV模型KIV模型由Kozma等人提出[19], 模拟了感觉皮层-海马的神经回路, 描述了大脑的非线性动力学, 以非周期时空振荡形式对感觉信息进行编码, 能够模拟原始脊椎动物前脑在简单意向行为中的作用. KIV模型的构建具有较强的生理学基础. 从模型搭建依据来看, 构建模型所需的参数是通过分析从感觉皮层和大脑边缘结构的多个电极同时记录的脑电图得到的[20]; 从结构上来讲, KIV模型模拟了原始脊椎动物前脑中的关键结构, 包括感觉皮层、海马、中线前脑和杏仁核.
K系列模型基于神经团理论而建立, 神经团理论[21]是指相似的神经元组成的细胞团具有相似的功能和一致的特性. K0模型模拟了兴奋性和抑制性的细胞团的活动, 是K系列模型最基本的组成单元. 通过耦合多个兴奋性或抑制性细胞团的K0模型, 可以形成
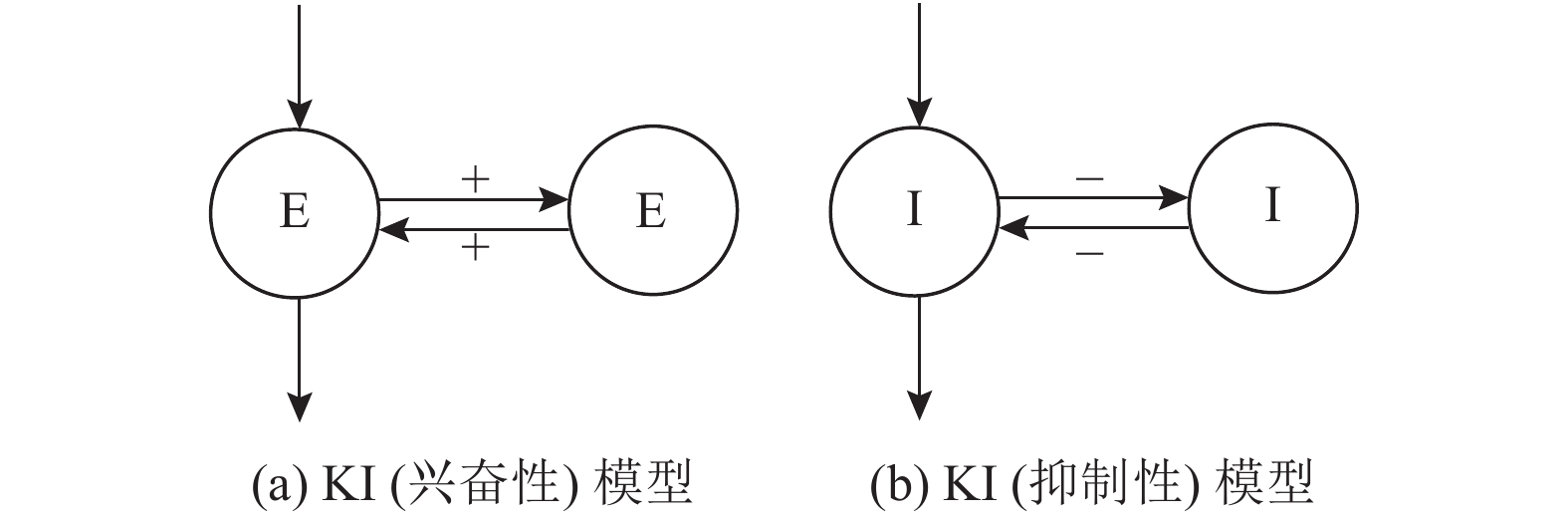
|
图 1 KI模型拓扑结构图 |

|
图 2 KII模型拓扑结构图 |

|
图 3 K系列模型层次结构关系 |
由神经团理论和生理学基础, K系列模型所有细胞团的脉冲状态变化可以用式(1)–式(3)来描述:
| $ \begin{split} & \frac{1}{{a \cdot b}}[x_i^{''}(t) + (a + b) \cdot x_i^{'}(t) + a \cdot b \cdot {x_i}(t)] = \\ & \sum\limits_{j \ne i}^N {{W_{ij}} \cdot Q({X_j}(t), {q_j}) + {I_i}(t)} , \; (i = 1, \cdot \cdot \cdot , N)\;\;\; \end{split} $ | (1) |
| $ Q({X_i}(t), q) = \left\{ \begin{gathered} q(1 - {{\rm{e}}^{ - (\exp (x(t) - 1))/q}}), \;x(t) \geqslant {x_0} \\ - 1,\;x(t) < {x_0} \\ \end{gathered} \right.\;\; $ | (2) |
| $ {x_0} = \ln (1 - q\ln (1 + 1/q))\;\;\;\; $ | (3) |
其中, a和b是基于生理实验确定的反映输入快慢的速率常数,
本文研究的是模拟了大脑边缘系统的KIV模型, 不包括中线前脑, 其组成结构如图4所示. 完整的KIV模型结构详见文献[19]. 边缘系统的KIV模型由2个KIII模型和1个KII模型组成, 分别模拟感觉皮层、海马区和杏仁核. 其中, 感觉皮层包括球周细胞(periglomerular, PG)、嗅球层(olfactory bulb, OB)、前嗅核(anterior olfactory nucleus, AON)、梨状皮质(prepyriform cortex, PC), 海马区包括齿状回(dentate gyrus, DG)和海马切片(hippocampal sections, CA1–CA3). DG、PG为KI模型, CA1、CA2、CA3、OB、AON、PC、AMY为KII模型.

|
图 4 KIV模型结构图 |
根据KIV模型的结构, 本文给出了KIV模型的拓扑结构图, 如图5所示. 图中各细胞层中的E1、E2代表兴奋性神经元, I1、I2代表抑制性神经元, D1–D7表示延迟反馈连接. 根据图5和文献[23]的参数, 本文在Matlab上对KIV模型进行建模实现.
1.2 KIV模型动力学特性分析KIV模型中每个神经团细胞的动力学方程通过Runge-Kutta方法求解, 在迭代过程中产生了各个神经元节点的状态变量数值解以及一阶微分值(t=0时刻所有神经元状态变量及其一阶微分值均为0). 因此, 可通过仿真输入的方法对KIV模型的动力学特性进行分析.
1.2.1 无外加刺激时典型神经元节点的响应无论何时, KIV模型中PG层和AON层都分别接收外周噪声和中间噪声, 即图5中的peripheral noise和central noise, 该噪声用均值为0的高斯分布来模拟. 噪声的引入不但不会破坏KIV模型的稳定性, 反而会使模型随时保持一种激活的状态, 消除模型对初值和参数的敏感性, 从而提高模型的鲁棒性. 这也是KIV模型和一般的人工神经网络模型不同之处之一.
首先, 研究在没有外加输入刺激、只有内部噪声的情况下, KIV模型中典型神经元节点的动力学行为. 设置总时长为1200 s, 分别选取每一层中的兴奋性输入神经元E1和OB层的抑制性神经元I1, 其响应图如图6所示. 图中, 横轴表示仿真输入的时间, 单位为s; 纵轴表示神经元节点对输入刺激的响应幅值, 单位为mV.
从图6可以看到, 在没有外加刺激、只有外周噪声和中间噪声的情况下, 整个KIV模型处于一种低水平的静息状态.

|
图 5 KIV模型拓扑结构 |
1.2.2 有外加刺激时典型神经元节点的响应
接下来, 研究有外加刺激时, KIV模型PG层和OB层中输入和输出节点的响应. 在300 s时, 给予KIV模型幅值为1 mV的输入刺激, 并在900 s时撤去刺激, 刺激持续时间为600 s, 其响应如图7所示.
可以看到, 在加入刺激后, PG1节点在300–900 s之间出现了阶跃响应, 900 s后PG层对外周噪声更加敏感, 主要表现为PG1节点在900 s后的幅值比300 s前的幅值要大. 而OB层的E1节点和I1节点在300–900 s之间也产生一定的阶跃现象, 并表现出等幅振荡, 且撤去刺激后OB层的输入输出节点仍然表现出高活跃状态.

|
图 6 无外加刺激时KIV模型中典型神经元的响应 |

|
图 7 有外加刺激时KIV模型中典型神经元的响应 |
1.2.3 无/有外加刺激时的相图
KIV模型中一共有30种节点, 要描述整个系统在空间中的轨迹显然是不可能的, 因此只能通过系统中部分节点状态变量之间形成的轨迹, 即系统的相图, 来间接地对整个系统的空间轨迹进行分析. 本节从细胞层的角度对KIV模型的动力学行为进行分析, 通过选取OB层、AON层、CA3层和AMY层中的输入和输出节点, 刺激时间及强度同第1.2.2节, 分别研究这4对节点在无/有外加刺激时的响应, 其相图分别如图8、图9所示, 其中, 横纵坐标分别表示该层E1、I1节点在不同时刻的响应幅值.
从图8和图9可以看到, CA3层和AMY层一直处于收敛状态, 加入刺激前, OB层和AON层处于一个复杂的非收敛状态, 但大多数时间内处于有界区域; 加入刺激后, OB层和AON层轨迹迅速收敛, 且在OB层的E1-I1节点相图中出现了稳定的极限环. 整个KIV模型从局部稳定进入了全局稳定的状态.
1.2.4 输入不同强度刺激时的M1-G1相图从第1.2.3节可以得知, 当外加恒定输入时, KIV模型会对外加刺激形成稳定的极限环. 接下来, 本文研究当输入不同强度刺激时E1-I1节点相图的变化. 同样设置在300 s时, 给KIV模型输入持续时间为600 s的刺激, 刺激幅值分别为1 mV、2 mV、3 mV、4 mV. 不同强度刺激下的E1-I1节点相图依次如图10所示, 其中, 红色部分表示300–900 s之间E1-I1节点的轨迹.
从图10中可以看到, 对于不同强度的输入刺激, E1-I1相图中形成的系统轨迹是不同的, 即不同的刺激能使KIV模型形成不同的稳定极限环.
对应到实际的应用情景(如脑电识别)中, 当KIV模型接收了脑电信号, 系统的时空模式会迅速转换到对应的局部吸引子(即极限环)中. 对于不同模式的脑电信号, KIV模型可以通过系统表现出的极限环对其不同的时空模式进行区分, 并通过KIV模型的学习算法, 调整输入层对应节点间的连接权值对目标模式进行记忆和识别. 即KIV模型具有一定的脑电识别潜力, 后续的研究可将KIV模型应用于脑电信号识别.

|
图 8 无外加刺激时KIV模型的相图 |
2 基于KIV模型的脑电识别 2.1 癫痫脑电识别
癫痫是一种由脑部神经元阵发性异常放电引起的慢性神经系统疾病, 也是全球最常见的神经系统疾病之一. 癫痫的发作人群不分年龄和性别, 发作时可导致短暂的大脑功能失调, 如意识丧失, 运动、知觉、情绪或精神功能的混乱等. 癫痫反复发作会对患者的精神与认知功能造成持续性的负面影响, 严重时甚至危及生命.
临床上对癫痫发作的监测通常是通过检测癫痫发作期间或发作前不久所特有的棘波或尖波[24]等实时脑电波形, 来分析并诊断患者是否发作. 目前, 基于EEG的癫痫发作自动检测技术获得了越来越多的研究者的关注.
癫痫发作自动检测[25]是指在连续脑电监测过程中, 当患者癫痫发作时, 系统以尽可能短的延迟识别发作的开始, 并描述持续时间, 它包括4个步骤: 信号采集、信号预处理、特征提取、分类模型学习与评估, 其核心是对癫痫波的检测与识别. 基于KIV模型的动力学特性, 本节使用KIV模型对癫痫脑电信号进行识别研究.

|
图 9 有外加刺激时KIV模型的相图 |

|
图 10 不同强度刺激下的M1-G1相图 |
2.1.1 数据集介绍
本节所用的数据集是公开的Bonn脑电数据集. 它采集的是5个受试者在不同状态下的原始脑电信号, 这5个子数据集分别被命名为I、II、III、IV、V, 数据集的详细描述见表1. 每一个子数据集中包含100导联信号, 每一导联信号包含4097个数据点. 信号的采样频率是173.61 Hz, 每一导联信号的采样持续时间为23.6 s.
脑电信号属于时变信号, 复杂的特征提取过程不是必须的. 因此, 本文在识别脑电信号时, 对原始脑电信号不做特征提取, 只进行维度上的切分预处理. 本节中, 首先对这5个子数据集进行分割处理, 主要包含两部分: (1)将通道数对半分割, 分别分为1段、2段、4段, 对应的子样本分别有100通道、50通道、25通道; (2)将每一通道上的数据点分别分为30段、40段、50段、60段, 相应的每一段的数据点即序列长度分别为136、102、81、68. 因此, 每个子数据集分割后的样本有12种规模, 相应的产生了12组实验.
| 表 1 BONN数据集描述 |
2.1.2 实验过程
KIV模型学习和识别脑电信号的过程见图11, 详细如下.

|
图 11 实验过程流程图 |
(1)训练: 将处理后的数据输入到多通道KIV模型中, 通过提取每一通道中OB层脑电信号的方差, 来计算训练集中当前样本的聚类中心, 在此过程中不断更新OB层输入神经元间的连接权重和模型的Hebbian学习参数. 得到训练集所有样本的聚类中心后, 通过分别取平均值得到每一类脑电数据的聚类中心, 并固定输入层神经元间的连接权重和Hebbian学习参数.
(2)测试: 输入测试集进行测试. 同样提取OB层中每一通道脑电信号的方差, 以计算当前测试样本的聚类中心, 并利用欧式距离与每一类脑电信号的聚类中心进行对比, 根据最小值得到当前样本的识别结果. 测试集中所有样本的识别结果得出后, 根据测试集中正确识别样本个数与样本总个数得出最终的识别准确率.
2.1.3 实验结果及分析在实验中, 不同的训练集和测试集的比例可能会对识别结果造成一定的影响. 因此, 本节设计了3组实验, 其训练集的比例分别为60%、70%和80%, 然后按照第3.1.2节的实验流程进行实验, 得到的实验结果如图12–图14所示.
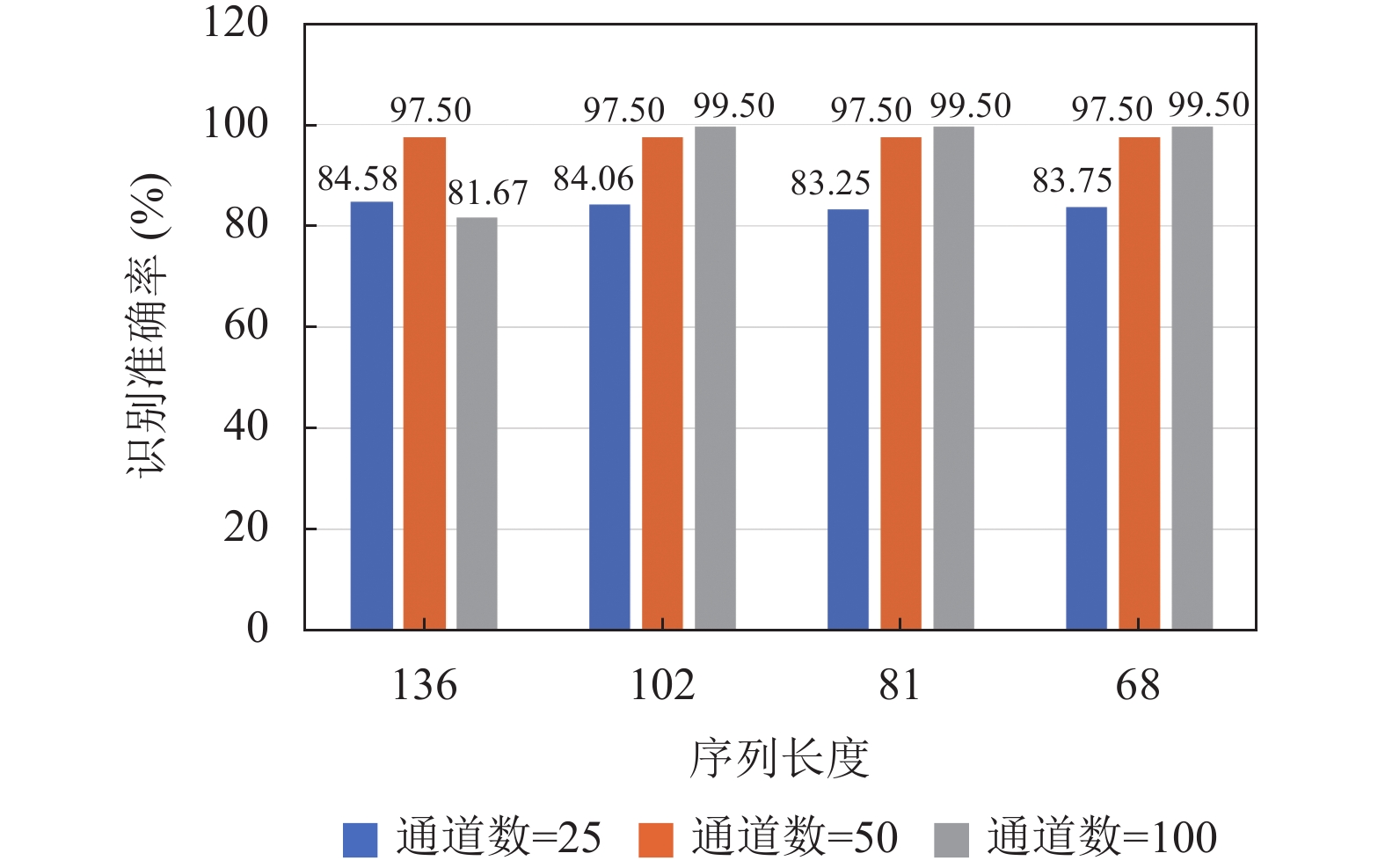
|
图 12 训练集比例为60%时的识别结果 |
图12–图14分别表明, 当通道数为25时, 不管将同一通道上的数据点分为多少段, 不同序列长度样本的识别准确率均能达到81%以上. 而随着样本通道数的增加, 输入KIV模型的脑电信号趋于完整, 模型的识别准确率越高. 当通道数为50时, 识别准确率最为稳定, 为98%左右; 当通道数为100时, 随着样本数的增加, 识别准确率最高可达99.50%.
比较图12–图14, 对于相同通道数和序列长度的子样本, 当训练集比例分别为60%、70%、80%时, KIV模型的识别准确率有一定的提升. 本节的实验结果表明, KIV模型具有较强的对不同模式的学习与分类能力, 即只需学习60%的数据, 且只需学习一次, 就能准确地识别癫痫脑电信号.
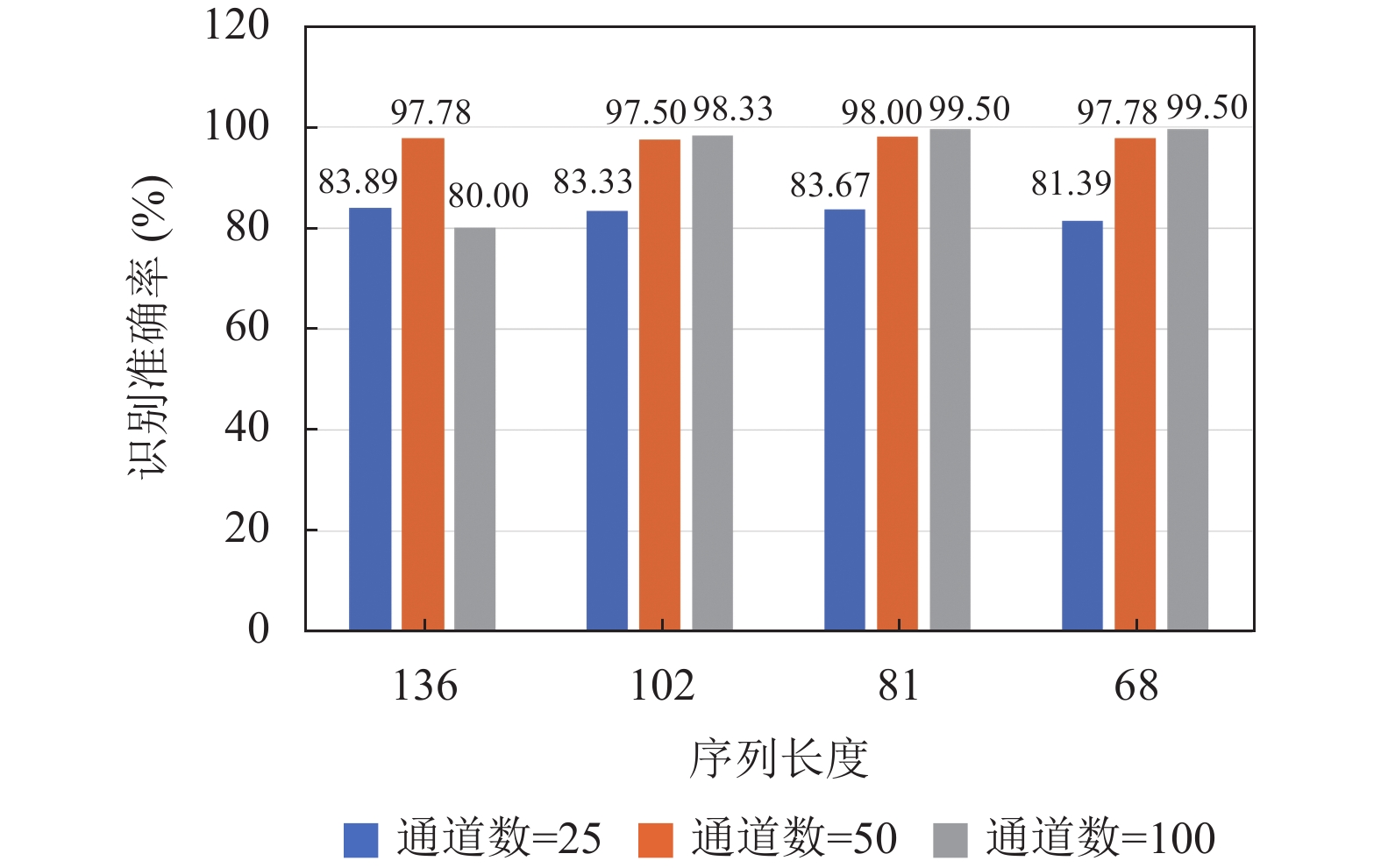
|
图 13 训练集比例为70%时的识别结果 |

|
图 14 训练集比例为80%时的识别结果 |
将本节的实验结果与已有的模型识别结果进行对比, 见表2. 可以看到, 与已有模型需复杂特征提取过程的实验结果相比, KIV模型在BONN数据集的五分类任务上的识别准确率最高, 为99.50%, 即, KIV模型在BONN数据集上的识别能力优于现有方法.
2.2 情感脑电识别情感是人类日常生活中的基础, 在认知、交流、决策中扮演着重要的角色, 情感的实时评估和调节可以改善人们的生活. 近年来, 情感识别已成为认知科学、计算机科学、心理学等诸多领域的研究热点. 情感识别方法[26]大致上可以分为两类, 一种是基于非生理信号, 例如面部表情、身体姿势和语音信号等, 另一种是基于生理信号, 如脑电图、肌电图(EMG)和心电图(ECG)等. 与非生理信号相比, 生理信号不受外界环境和主观意志的影响, 对情感状态的估计具有可重复性和客观性. 其中, 脑电信号, 由于是从大脑皮层直接采集的, 有利于反映人的情感状态, 成为了研究大脑面对刺激时产生情绪反应的首选载体.
| 表 2 多种模型在BONN上的识别准确率对比 |
情感分为很多类, 研究者认为, 情感是有维度的, 目前广泛应用的二维模型是效价度(valence)和激活度(arousal)组成的激活度-效价空间[30], 如图15所示, 水平轴表示效价维, 评价情感的积极和消极程度, 数值越大情感越积极; 垂直轴表示激活维度, 描述情感的激烈程度, 数值越大情感越激烈.
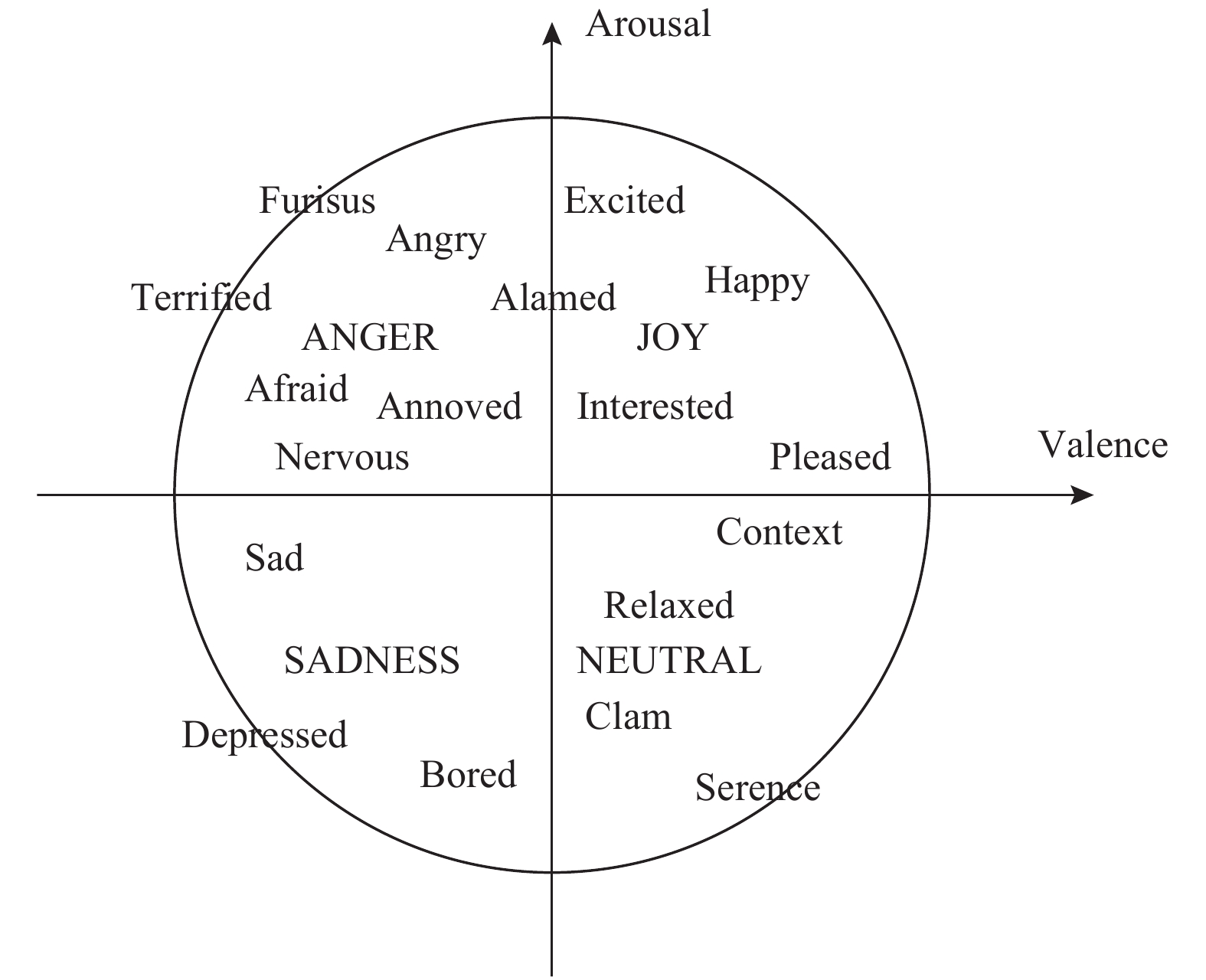
|
图 15 激活度-效价情感空间 |
然而, 不同于癫痫脑电识别中癫痫波的检测, 情感评价本身具有一定的主观性, 因而准确识别一段脑电信号中蕴含的情感具有更大的挑战性.
2.2.1 数据集介绍本节使用的数据集为公开的GAMEEMO数据集[31], 它采集的是受试者在视听刺激下的原始脑电信号, 包含4种情感: funny、horror、boring、calm, 分别在激活度-效价空间的不同象限. GAMEEMO脑电信号的采样通道数为14, 每一通道上有38252个数据点. 根据数据集的情感评价结果, 本文选取了不产生重复情感的子数据集.
同对BONN数据集的处理方法, 本节对GAMEEMO数据集中每一通道上的数据点进行切分预处理, 将38252个数据点分别切分为100段、150段、200段、250段, 相应的每一段信号的序列长度分别为380、255、190、153, 由此产生了4组实验.
2.2.2 实验结果及分析根据KIV模型的识别原理及过程, 本节得到的实验结果如表3所示. KIV模型在GAMEEMO数据集上的平均识别准确率为88.80%. 其中, 对于序列长度为380的子样本, 训练集的比例为70%时, 识别效果最好, 为90.83%. 其混淆矩阵如图16所示, KIV模型对4种情绪的识别准确率分别为86.67%、100%、96.67%、80.00%, 其中horror最高, calm最低, 这是由于horror情绪较为激烈易于识别, 而calm时脑电波形较为平缓, 相对难以识别.
| 表 3 KIV在GAMEEMO不同训练集比例上的识别结果 (%) |

|
图 16 第2组实验结果混淆矩阵 |
将本节的实验结果与已有模型的识别结果进行对比, 见表4. 可以看到, 本文采用GAMEEMO数据集全部14个通道的脑电信号, 对比同样的14通道脑电信号分类任务, KIV模型的识别准确率相比文献[31]和文献[32]分别高19%和14%左右; 对比四分类任务, KIV模型也表现出不错的识别性能, 识别准确率最高为90.83%. 整体而言, 本节设置的情感脑电信号识别任务难度最高, 但是相比于经典的分类器KNN、SVM、Bi-LSTM等, KIV模型仍表现出优于已有方法的识别性能.
| 表 4 多种模型在GAMEEMO上的识别准确率对比 |
3 结论与展望
本文分析了KIV模型的动力学特性, 发现KIV模型能在输入刺激后, 从局部收敛状态迅速进入全局收敛状态, 并表现出对刺激的高度敏感性. 根据相图中KIV模型针对不同输入模式形成了不同的稳定极限环, 本文拓展了KIV模型在脑电识别分类方面的应用, 在癫痫脑电识别和情感脑电识别中分别获得了99.50%和90.83%的识别准确率. 与现有模型提取脑电特征之后的识别结果进行对比, 本文的实验结果为脑电识别提供了新的思路和方法.
KIV模型是一种优秀的大脑半球仿生模型, 对比一般的深度学习模型, 具有较好的脑电信号识别能力. 未来的工作可将KIV模型应用于模式识别的更多方面, 这对探索和研究KIV模型的模式识别能力具有重要的意义.
| [1] |
Wang SQ, Wang SD, Zhang S, et al. Time-ResNeXt for epilepsy recognition based on EEG signals in wireless networks. EURASIP Journal on Wireless Communications and Networking, 2020, 2020(1): 195. DOI:10.1186/s13638-020-01810-5 |
| [2] |
Tao YW, Jiang YZ, Xia KJ, et al. Classification of EEG signals in epilepsy using a novel integrated TSK fuzzy system. Journal of Intelligent & Fuzzy Systems, 2021, 40(3): 4851-4866. DOI:10.3233/JIFS-201673 |
| [3] |
Li YR, Qian PJ, Wang SH, et al. Novel multi-view Takagi-Sugeno-Kang fuzzy system for epilepsy EEG detection. Journal of Ambient Intelligence and Humanized Computing, 2021.
|
| [4] |
Cai HS, Qu ZD, Li Z, et al. Feature-level fusion approaches based on multimodal EEG data for depression recognition. Information Fusion, 2020, 59: 127-138. DOI:10.1016/j.inffus.2020.01.008 |
| [5] |
Ieracitano C, Mammone N, Hussain A, et al. A novel multi-modal machine learning based approach for automatic classification of EEG recordings in dementia. Neural Networks, 2020, 123: 176-190. DOI:10.1016/j.neunet.2019.12.006 |
| [6] |
She QS, Hu B, Luo ZZ, et al. A hierarchical semi-supervised extreme learning machine method for EEG recognition. Medical & Biological Engineering & Computing, 2019, 57(1): 147-157. DOI:10.1007/s11517-018-1875-3 |
| [7] |
Liu MJ, Zhou MM, Zhang T, et al. Semi-supervised learning quantization algorithm with deep features for motor imagery EEG Recognition in smart healthcare application. Applied Soft Computing, 2020, 89: 106071. DOI:10.1016/j.asoc.2020.106071 |
| [8] |
Liu L. Recognition and analysis of motor imagery EEG signal based on improved BP neural network. IEEE Access, 2019, 7: 47794-47803. DOI:10.1109/ACCESS.2019.2910191 |
| [9] |
Zhuang N, Zeng Y, Tong L, et al. Emotion recognition from EEG signals using multidimensional information in EMD domain. BioMed Research International, 2017, 2017: 8317357. DOI:10.1155/2017/8317357 |
| [10] |
Song TF, Zheng WM, Song P, et al. EEG emotion recognition using dynamical graph convolutional neural networks. IEEE Transactions on Affective Computing, 2020, 11(3): 532-541. DOI:10.1109/TAFFC.2018.2817622 |
| [11] |
Li X, Song DW, Zhang P, et al. Exploring EEG features in cross-subject emotion recognition. Frontiers in Neuroscience, 2018, 12: 162. DOI:10.3389/fnins.2018.00162 |
| [12] |
Carlos LFM, Rosa JLG. Face recognition through a chaotic neural network model. Proceedings of the 13th International Joint Conference on Neural Networks (IJCNN). Beijing: IEEE, 2014. 859–863.
|
| [13] |
Obayashi M, Koga S, Feng LB, et al. Handwriting character classification using Freeman’s olfactory KIII model. Artificial Life and Robotics, 2012, 17(2): 227-232. DOI:10.1007/s10015-012-0047-z |
| [14] |
Obayashi M, Suda R, Kuremoto T, et al. A class identification method using Freeman’s olfactory KIII model. Journal of Image and Graphics, 2016, 4(2): 130-135. DOI:10.18178/joig.4.2.130-135 |
| [15] |
Zhang J, Li G, Freeman WJ. Application of novel chaotic neural networks to text classification based on PCA. Proceedings of the 6th Pacific-Rim Symposium on Image and Video Technology. Hsinchu: Springer, 2006. 1041–1048.
|
| [16] |
Zhang J, Tian TT, Wang SC, et al. Research on an olfactory neural system model and its applications based on deep learning. Neural Computing and Applications, 2020, 32(10): 5713-5724. DOI:10.1007/s00521-019-04498-x |
| [17] |
Voicu H, Kozma R, Wong D, et al. Spatial navigation model based on chaotic attractor networks. Connection Science, 2004, 16(1): 1-19. DOI:10.1080/09540090410001664641 |
| [18] |
Kozma R, Hunstberger T, Aghazarian H, et al. Implementing intentional robotics principles using SSR2K platform. Proceedings of the 20th IEEE/RSJ International Conference on Intelligent Robots and Systems. San Diego: IEEE, 2007. 2262–2267.
|
| [19] |
Kozma R, Freeman WJ. Basic principles of the KIV model and its application to the navigation problem. Journal of Integrative Neuroscience, 2003, 2(1): 125-145. DOI:10.1142/S0219635203000159 |
| [20] |
Freeman III WJ, Burke BC, Holmes MD. Application of Hilbert transform to scalp EEG containing EMG. Human Brain Mapping, 2003, 19(4): 248-272. DOI:10.1002/hbm.10120 |
| [21] |
张锦, 赵二群, 王如龙, 等. 基于神经团的视网膜神经系统建模研究. 系统仿真学报, 2013, 25(9): 1996-2000. DOI:10.16182/j.cnki.joss.2013.09.027 |
| [22] |
Kozma R. Intentional systems: Review of neurodynamics, modeling, and robotics implementation. Physics of Life Reviews, 2008, 5(1): 1-21. DOI:10.1016/j.plrev.2007.10.002 |
| [23] |
Myers MH, Kozma R. Mesoscopic neuron population modeling of normal/epileptic brain dynamics. Cognitive Neurodynamics, 2018, 12(2): 211-223. DOI:10.1007/s11571-017-9468-7 |
| [24] |
Xue J, Gu XQ, Ni TG. Auto-weighted multi-view discriminative metric learning method with fisher discriminative and global structure constraints for epilepsy EEG signal classification. Frontiers in Neuroscience, 2020, 14(9): 586149. DOI:10.3389/fnins.2020.586149 |
| [25] |
彭睿旻, 江军, 匡光涛, 等. 基于EEG的癫痫自动检测: 综述与展望. 自动化学报, 2022, 48(2): 335-350. DOI:10.16383/j.aas.c200745 |
| [26] |
Alarcão SM, Fonseca MJ. Emotions recognition using EEG signals: A survey. IEEE Transactions on Affective Computing, 2019, 10(3): 374-393. DOI:10.1109/TAFFC.2017.2714671 |
| [27] |
Choubey H, Pandey A. A combination of statistical parameters for the detection of epilepsy and EEG classification using ANN and KNN classifier. Signal, Image and Video Processing, 2021, 15(3): 475-483. DOI:10.1007/s11760-020-01767-4 |
| [28] |
Mandhouj B, Cherni MA, Sayadi M. An automated classification of EEG signals based on spectrogram and CNN for epilepsy diagnosis. Analog Integrated Circuits and Signal Processing, 2021, 108(1): 101-110. DOI:10.1007/s10470-021-01805-2 |
| [29] |
Tuncer T, Dogan S, Naik GR, et al. Epilepsy attacks recognition based on 1D octal pattern, wavelet transform and EEG signals. Multimedia Tools and Applications, 2021, 80(16): 25197-25218. DOI:10.1007/s11042-021-10882-4 |
| [30] |
陈婧, 李海峰, 马琳, 等. 多粒度特征融合的维度语音情感识别方法. 信号处理, 2017, 33(3): 374-382. DOI:10.16798/j.issn.1003-0530.2017.03.018 |
| [31] |
Alakus TB, Gonen M, Turkoglu I. Database for an emotion recognition system based on EEG signals and various computer games—GAMEEMO. Biomedical Signal Processing and Control, 2020, 60: 101951. DOI:10.1016/j.bspc.2020.101951 |
| [32] |
Alakus TB, Turkoglu I. Emotion recognition with deep learning using GAMEEMO data set. Electronics Letters, 2020, 56(25): 1364-1367. DOI:10.1049/el.2020.2460 |
| [33] |
Tuncer T, Dogan S, Subasi A. A new fractal pattern feature generation function based emotion recognition method using EEG. Chaos, Solitons & Fractals, 2021, 144: 110671. DOI:10.1016/j.chaos.2021.110671 |
| [34] |
Dogan A, Akay M, Barua PD, et al. PrimePatNet87: Prime pattern and tunable q-factor wavelet transform techniques for automated accurate EEG emotion recognition. Computers in Biology and Medicine, 2021, 138: 104867. DOI:10.1016/j.compbiomed.2021.104867 |
 2022, Vol. 31
2022, Vol. 31


