残差密集块的卷积神经网络图像去噪

引用本文

李小艳, 宋亚林, 乐飞. 残差密集块的卷积神经网络图像去噪. 计算机系统应用, 2022, 31(10): 166-174.http://www.c-s-a.org.cn/1003-3254/8742.html

Li XY, Song YL, Yue F. Image Denoising Based on Convolutional Neural Networks with Residual Dense Block. Computer Systems and Applications, 2022, 31(10): 166-174(in Chinese).http://www.c-s-a.org.cn/1003-3254/8742.html

残差密集块的卷积神经网络图像去噪

李小艳, 宋亚林, 乐飞

河南大学软件学院, 开封 475004

收稿日期：2022-01-13; 修改日期：2022-02-17; 采用时间：2022-03-03; csa 在线出版时间：2022-07-07

基金项目：河南省科技研发项目(212102210078); 河南省重大科技专项(201300210400); 河南省重点研发与推广专项(科技攻关)(202102210380)

通讯作者：宋亚林, E-mail: syl@vip.henu.edu.cn.

摘要：针对加性高斯白噪声的图像信噪比低, 图像细节丢失问题, 结合现有卷积神经网络算法, 提出了一种基于残差密集块的卷积神经网络图像去噪模型. 该模型通过引入多级残差网络和密集连接, 并对整体网络使用Leaky ReLU激活函数, 去除不同等级强度噪声的同时, 更好保留图像的有效信息, 有效避免特征丢失. 本文提出算法和深度卷积神经网络残差学习(DnCNN)模型对比, 本文提出的模型在Set12和BSD68测试集上峰值信噪比平均提升了约0.12 dB, 结构相似性平均提升了约0.008 6, 通过观察实验效果, 表明该模型能够充分提取图像特征, 保留图像细节, 同时降低网络计算的复杂度.

关键词: 图像去噪卷积神经网络 (CNN) 残差学习残差密集块 Leaky ReLU激活函数

Image Denoising Based on Convolutional Neural Networks with Residual Dense Block

LI Xiao-Yan, SONG Ya-Lin, YUE Fei

School of Software, Henan University, Kaifeng 475004, China

Abstract: Considering the low signal-to-noise ratio (SNR) and image detail loss caused by additive white Gaussian noise (AWGN), an image denoising model based on the convolutional neural network (CNN) with residual dense blocks is proposed on the basis of the existing CNN algorithms. By introducing a multi-stage residual network and dense connections and using the Leaky ReLU activation function on the whole network, the model can better retain the effective information of images and effectively avoid feature loss while removing the noise of different levels of intensity. Compared with the residual learning model of the denoising CNN (DnCNN), the proposed model has an improved peak SNR by about 0.12 dB on the Set12 and Bsd68 test sets and improved structural similarity by about 0.008 6 on average. The test results reveal that the proposed model can fully extract image features, retain image details, and reduce the computational complexity of the network.

Key words: image denoising convolutional neural network (CNN) residual learning dense block of residual Leaky ReLU activation function

图像在采集、存储、记录和传输过程中常常会受到众多不良因素的干扰影响, 从而导致图像在一定程度上会退化失真, 质量下降, 导致获取的图像中有噪声的存在, 从而影响图像的质量. 图像去噪是在保持原始图像细节信息完整的同时, 去除图像中的无用噪声信息, 以便于后续对图像进行应用^{[1, 2]}. 图像去噪是计算机视觉研究中的一个经典问题, 同时也是图像领域中一个具有挑战性的研究课题^[3-5].

传统的图像去噪方法主要是高斯滤波降噪^{[6, 7]}, 这种方法属于局部平滑滤波, 这种去噪方法针对图像的非平滑部分, 不能进行有效的处理. 非局部均值降噪^[8]方法可以解决图像的非平滑这一问题, 该方法利用了图像中存在的冗余信息进行去噪处理, 能够较好地去除图像中存在的高斯噪声, 该方法的最大缺陷就是计算复杂度太高, 程序非常耗时, 导致该算法不够实用. 小波阈值降噪^{[9, 10]}主要是利用滤除高频信号这一原理, 小波阈值降噪如果选择的阈值过大, 会导致图像中的高频信息被无区别的抑制, 从而导致图像边缘信息, 纹理细节丢失. 如果阈值过小, 就不能对高频噪声进行有效的去除. Dabov等人在2007年提出了一种基于融合变换算法的块匹配和三维滤波降噪方法^[11], 简称为BM3D (block matching and 3D filtering), 该方法采用不同的去噪策略, 通过与相邻图像块进行匹配搜索, 在三维空间进行滤波, 得到块评估值, 最后通过加权求和将各个块复原得到最终去噪效果. BM3D降噪方法虽然去噪效果显著, 但时间复杂度比较高. 采用传统图像去噪算法的复杂度较低, 实时性比较强, 处理速度快, 但在去噪过程中边缘细节信息和纹理信息很容易丢失.

随着深度学习特别是卷积神经网络(CNN)^{[12, 13]}在计算机领域的逐渐发展, CNN被众多研究学者应用在图像去噪问题上并取得了较好的研究成果. Holt^[14]在研究神经网络去噪的过程中, 其选用的研究方法是多层感知机(multi layer perceptron, MLP). 在他看来多层感知机网络具有强大的拟合能力和非线性能力, 通过学习带噪声的图像和无噪声图像来实现图像之间的映射关系, MLP模型对各种类型的噪声影响不大, 通过对含有此类噪声的图像进行分类, 可以获得良好的效果. 这种模型的缺点是由于不能很好地处理各种等级噪声, 因此用不同等级噪声图像进行训练, 则很难获得较好的去噪效果. Mao等人^[15]提出了一种深卷积编解码网络应用于图像去噪, 该网络具有对称结构的编码(encoding)和解码(decoding), 每一层编码卷积和解码卷积之间都有跳跃连接, 可以获得更好的泛化能力. 但是由于网络变深会导致图像细节的丢失. Zhang等人^[16]提出用较深层的CNN网络实现图像去噪, 称为DnCNN, 该网络模型通过利用残差学习^[17]和归一化^[18]的共同作用, 提高去噪性能, 该算法使用端到端的神经网络模型来进行降噪, 同时该算法具有较好的盲去高斯噪声的能力. 但是, 由于所建立的神经网络模型是由单一大小的卷积核卷积运算完成, 因此, 图像的特征信息提取很少. Zhang等人^[19]采用扩张卷积来学习残差图像并提出了IRCNN模型, 该模型基于半二次方分裂(HQS)算法, 利用卷积神经网络学习快速有效的去噪器, 以此来处理不同的图像修复问题, 但是该模型收敛速度慢, 计算成本大, 比较耗时. Zhang等人将估计的噪声水平和图像下采样后的多张子图像作为输入, 提出了快速灵活的图像去噪网络FFDNet^[20], 该模型能够在较大程度上改善降噪性能, 同时能较好地处理真实场景下的图像去噪问题. 该方法只有在噪声水平较大时, 才能保持更好的视觉效果, 当噪声较小时, 去噪后的视觉效果不佳. Creswell等人^[21]介绍了GAN用于图像合成、图像超分辨率和图像分类. Wang等人提出了一种基于GAN和CNN相结合的图像去噪网络^[22], 该网络采用GAN进行降噪处理, 采用CNN实现对图像细节的恢复. 该方法存在网络训练不稳定, 收敛速度慢, 模型不可控等问题. 席志红等人^[23]提出了一种深层残差神经网络用于图像的超分辨率重建, 通过实验验证该网络可以更好地还原图像中的细节信息, 消除伪影. 但该方法特征表达能力不足, 难以去除密集的噪声. 陈人和等人^[24]采用对抗损失和重建损失的加权和, 该网络虽然能够去除噪声并且针对图像的细节信息得到保留, 然而该算法可能会导致图像的边缘模糊. 秦毅等人^[25]针对不同类型的图像, 通过采用一个边缘感知损失函数去除图像噪声, 同时恢复图像的边缘细节. 该算法的浅层像素级信息利用率低, 纹理细节容易丢失. 朱斯琪等人^[26]提出一种循环一致性生成对抗网络, 实现了从低剂量CT图像到标准剂量CT图像的端到端映射, 同时将密集型残差学习网络模型引入到该网络生成器中, 利用残差网络的特征复用性来恢复图像细节, 但是该方法在去除噪声后仍然会有伪影存在, 且该方法目前只适用于腹部CT图像.

上述图像去噪算法尽管在网络结构设计, 目标损失函数以及数据集的选择上存在差异, 但是这些算法都能够取得显著的成果. 上述这些算法在进行网络训练时, 图像特征不能被充分学习, 导致图像细节丢失, 降低去噪效果. 因此为进一步改善图像去噪质量, 本文在去除噪声的过程中, 保存图像的边缘特征信息的基础上, 提出一种密集连接残差块的卷积神经网络去噪算法. 该网络模型由卷积层, Leaky ReLU层, 批量归一化, 密集残差块组成, 其中密集残差块通过多级残差网络和密集连接, 用优化的残差映射代替原始的卷积层, 相邻的卷积层之间通过短连接, 以提高残差网络的学习能力. 该网络结构以含噪声的图像作为输入, 去噪后的图片作为输出, 构成了由噪声图像到去噪后图像的非线性映射. 本文算法在去除噪声的同时, 能够保留更多的图像细节信息和图像边缘特征, 去噪后的图像视觉效果更好, 且具有更高的峰值信噪比值和结构相似性值.

1 相关技术原理 1.1 基于卷积神经网络的图像去噪算法

Zhang等人^[16]设计出一种经典的基于残差学习的卷积神经网络去噪模型称为DnCNN, 相比于MLP和BM3D等传统的图像去噪算法, 去噪性能有明显的提高.

DnCNN网络共有17层, 其中第1层由64个大小为 $ 3 \times 3 \times 1 $ 的滤波器被用来生成64个特征映射, 然后经过ReLU激活函数. 第2至第16层由64个大小为 $ 3 \times 3 \times 1 $ 的滤波器, 而后经过BN和ReLU激活函数; 网络的最后一层采用1个大小为 $ 3 \times 3 \times 64 $ 的滤波器对网络模型进行重构. DnCNN网络的训练通过式(1)进行学习:

$ x = y - F(x) $

(1)

其中, $x$ 为去除噪声后的图像, $y$ 为噪声图像, $F(x)$ 为网络预测的噪声. 对于DnCNN图像去噪, 实际上 $F(x)$ 不可能包含全部的噪声信息, 因此 $x$ 会丢失掉部分的细节信息, 因此DnCNN的去噪效果仍有待提高.

1.2 残差学习

为了提高卷积神经网络的精确度, 通常情况下都是通过简单的堆叠网络增加网络的深度, 与此同时网络的加深致使网络梯度发生爆炸或者衰减到很小, 误差值乘上权重后向后传播, 使得权重越来越小, 神经网络的训练精度先上升然后达到饱和, 因此提出残差学习用来解决网络性能退化的问题. He等人^[17]提出了残差学习的方法, 其框架结构如图1所示.

$ H(x) = F(x) + x \Rightarrow F(x) = H(x) - x $

(2)

$x$ 为残差模块的输入, $F(x) + x$ 是残差模块的输出. 只要 $F(x) = 0$ 就构成了一个恒等映射 $H(x) = x$ , 残差为 $F(x)$ , 残差学习结构通过前向神经网络和shortcut连接的方式实现, shortcut连接执行了一个恒等映射, 这种方式不会产生额外的参数, 同时也不会增加网络的计算复杂度. 采用残差学习策略使得深度卷积神经网络容易被训练并且能更好地提升精确度.

1.3 Leaky ReLU函数

带泄露修正线性单元函数(Leaky ReLU)^[27]是基于ReLU激活函数的改进, 带泄露修正线性单元函数在保留ReLU函数的优点的同时, 还可以做到修正数据分布. 激活函数如图2所示, 通过在ReLU函数的负半区间引入一个泄露值, 解决部分神经元因为失活不能参与参数的更新.

图 1 残差结构

图 2 Leaky ReLU激活函数

在反向传播过程中, 经过激活函数负区间的神经元在参与网络训练过程时, 由于泄露值的存在, 神经元对应的权重和偏置参数也得到了更新, 计算得到的梯度不会恒为0, 网络的拟合能力得到提高. 由于图像在噪声环境下的有效特征信息相对来说较为有限, 因此在网络训练中对于图像中的特性信息需要充分挖掘. Leaky ReLU函数替换掉原始网络中的ReLU激活函数, 该激活函数可以实现网络梯度更快的更新, 同时拥有比原始网络更好的图像去噪效果.

2 结合残差密集块的卷积神经网络去噪算法 2.1 密集连接残差块(RRDB)结构

卷积神经网络的输入都是上一层的输出, 不同卷积层所提取到的特征各不相同, 所以通过单一层的卷积不能尽可能多地获取到图像的特征信息, 仅依靠残差块的叠加同样会限制网络的性能, 所以为了优化残差网络的性能, Huang等人^[28]提出了一种新的密集连接残差模块, 用于缓解梯度消失问题, 加强特征传播与特征复用, 极大地减少了参数量. 本文提出了一个密集连接残差(RRDB)的卷积神经网络结构. RRDB模块如图3所示.

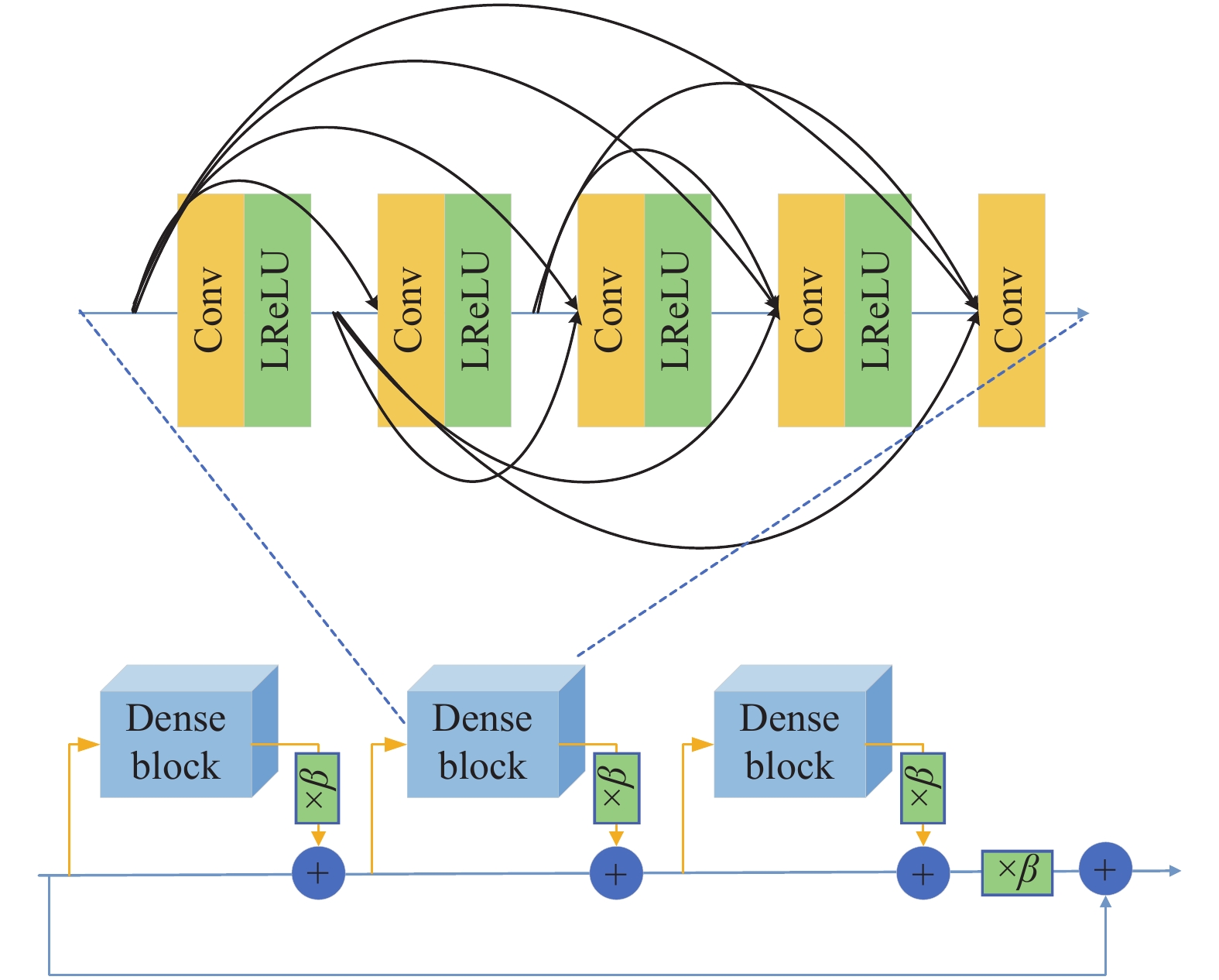
图 3 RRDB残差块

RRDB模块包括3个dense block块, 每一个dense block里面又包含4组卷积层与Leaky ReLU激活函数, 卷积核的大小为 $3 \times 3$ , 每组由32个卷积核组成, 每组都通过密集连接, 最后通过一个 $3 \times 3$ 的卷积层. 每一个dense block的输出进行残差缩放^{[29, 30]}, 乘以一个0到1之间的数, 以用于防止网络模型的不稳定.

通过多级残差网络和密集连接, 用优化的残差映射代替原始的卷积层, 相邻的卷积层之间通过短连接, 以提高残差网络的学习能力. RRDB模块中的卷积与卷积之间以跳跃连接的方式, 让模块中每一层卷积层的特征可以做到被充分利. RRDB模块提高了网络的整体训练的速度, 加深了网络的深度, 通过每一层特征的融合, 输出的特征图可以更好地包含原图像的特征信息.

2.2 网络模型结构

图像去噪是通过对含噪图像进行处理, 通过非线性映射到噪声图像, 从而得到去噪后图像的过程.

为了对网络进行特征提取, 同时为了降低网络训练的复杂度, 通过结合密集连接残差块, 设计了一种基于密集连接残差的卷积神经网络模型(DRCNN). 图4展示了本文算法网络整体架构示意图, 该模型结构分为3个部分: 特征提取模块, 密集连接残差模块(RRDB)和重建模块.

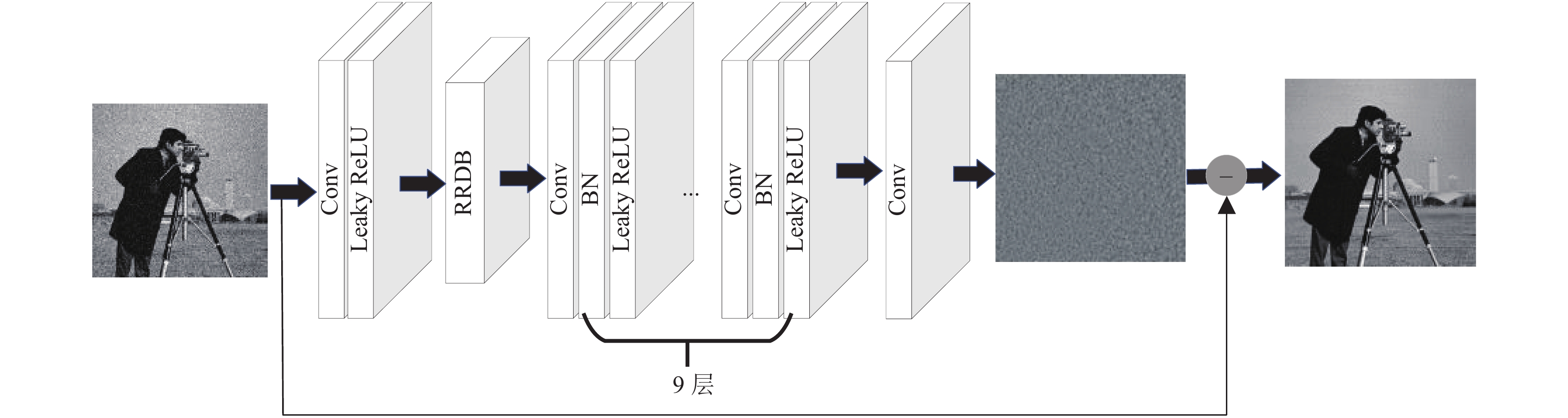
图 4 网络模型结构

本文提出的去噪网络, 共有12层, 网络架构由3部分组成: 卷积层(Conv), 激活函数(ReLU), 批规范化操作处理(BN), 具体如下:

网络模型第1层: Conv + Leaky ReLU, 由64个卷积核大小为 $3 \times 3 \times c$ 的滤波器用来生成64个特征映射, 并使用Leaky ReLU激活函数对特征实现非线性变换形成非线性特征映射, 步长为 $1 \times 1$ , $c$ 表示图像的通道数, 该网络模型使用灰度图像, 故 $ c = 1 $ .

网络模型第2层: dense block + dense block + dense block, 结构如图3所示, 每一个dense block里面又包含4组卷积层与Leaky ReLU激活函数, 卷积层由32个卷积核大小为 $3 \times 3$ 的滤波器用来生成32个特征映射, 每组都通过密集连接, 最后通过64个卷积核大小为 $3 \times 3$ 的卷积层生成64个特征映射.

网络模型第3–11层: Conv + BN + Leaky ReLU, 由64个卷积核大小为 $3 \times 3 \times c$ 的滤波器用来生成64个特征映射, 并使用Leaky ReLU激活函数对特征实现非线性变换形成非线性特征映射, 步长为 $1 \times 1$ , $c$ 表示图像的通道数, 该网络模型使用灰度图像, 故 $c = 1$ .

网络模型第12层: Conv, 采用 $c$ 个大小为 $ 3\times 3\times 64 $ 的滤波器进行网络重构, 步长为 $1 \times 1$ , 通过式(1)的残差学习策略进行训练, 最终输出去噪后的图片.

在网络结构中, 采用0填充的方法保持每层卷积特征图的大小保持不变, 用来防止产生边界伪影.

2.3 损失函数

通过从预测的噪声图片中恢复无噪声图片, 训练数据是带有噪声的图像 $y = x + v$ , 去噪模块采用残差学习获取到残差映射 $R(y) \approx v$ , 然后得到 $x = y - R(y)$ . 本文所设置网络训练的目标损失函数为:

$ L(\theta ) = \frac{1}{{2N}}\sum\nolimits_{i = 1}^N {||R({y_i};\theta ) - ({y_i} - {x_i})||_F^2} $

(3)

其中, $N$ 为训练样本数, ${x_i}$ 代表原始图像, ${y_i}$ 表示带噪声的图片. 实际噪声为 $({y_i} - {x_i})$ (噪声图像值减去无噪声图像值), $\theta $ 为当前网络的训练参数数值, 估计的噪声残差 $R({y_i};\theta )$ 与图片中实际噪声的平方误差是损失函数的期望值. 为了计算函数 $L(\theta )$ 的最小值, 本文采用Adam优化器进行迭代和参数更新. 定义如下:

$ {m_t} = {\beta _1}{m_{t - 1}} + (1 - {\beta _1}){g_t} $

(4)

$ {v_t} = {\beta _2}{v_{t - 1}} + (1 - {\beta _2}){g_t}^2 $

(5)

$ {\hat m _t} = \frac{{{m_t}}}{{1 - {\beta _1}^t}}, {\hat v _t} = \frac{{{v_t}}}{{1 - \beta _2^t}} $

(6)

$ {\theta _{t + 1}} = {\theta _t} - \frac{\eta }{{\sqrt {\mathop {{v_t}}\limits^ \wedge } + \xi }}\mathop {{m_t}}\limits^ \wedge $

(7)

其中, ${m_t}$ 表示一阶动量项, ${v_t}$ 表示二阶动量项, $ \;\beta _1^{} $ 值为0.9, $\; \beta _2^{} $ 值为0.999, ${\hat m _t}$ , ${\hat v _t}$ 为偏移修正值, ${\theta _t}$ 表示迭代t次模型的参数, 利用式(7)的参数更新过程, 能够通过训练得到网络模型.

3 实验分析 3.1 数据集

本文使用来自伯克利分割数据集(BSD)的400幅大小为 $ 180\times 180 $ 的灰度图像来训练高斯合成去噪模型. 深度学习模型在训练上往往需要大量的训练图像, 但是训练集的图片数量一般都有限, 所以为了防止出现过拟合的情况, 需要对样本图像进行数据增强. 本文所设计的算法中, 首先对每一张图像进行1、0.9、0.8、0.7倍的缩放, 然后采用 $40 \times 40$ 的裁剪框, 滑动步长设置为10, 随后将每一个子图像块都进行随机旋转, 原图像进行水平、垂直、顺时针翻转90°、180°、270°进行数据增广操作, 将400张图像裁剪成238 336个子图像块, 充足的训练图像块有助于促进特征的鲁棒性并提高训练去噪模型的效率. 通过上述数据增强操作后的不含噪声的原始图像, 随后将高斯白噪声添加到原始图像中生成含噪图像. 为了测试不同噪声强度对网络性能的影响, 将 $\sigma = 5,\;$ $\sigma = 10$ , $\sigma = 25,\;$ $\sigma = 50$ 的高斯白噪声分别添加到原始图像中用以生成不同的训练集. 测试数据集采用BSD68和Set12组成, Set12数据集如图5所示, 包含5张人像, 3张动物以及房子轮船飞机场景. BSD68数据集包含建筑, 人物, 动物, 植物, 飞机等场景, 共68张图片. 两个测试集均为灰度图像.

图 5 数据集Set12示例图片

3.2 评价指标

为了评估去噪后的图像质量, 通常从峰值信噪比(PSNR)和结构相似性(SSIM)两方面进行定量的评估分析, 其中PSNR是一种基于对应像素点之间误差的指标, PSNR和SSIM的值越大, 就代表失真越少, 图像去噪效果更好. 计算公式如下:

(1)峰值信噪比(PSNR)

$ {\textit{PSNR}} = 10{\log _{10}}\left(\frac{{{{({2^n} - 1)}^2}}}{\textit{MSE}}\right) $

(8)

n为每像素的比特数, 一般取8, 即像素灰阶数为256, 单位为dB.

(2)均方误差(MSE)

$ {\textit{MSE}} = \frac{1}{{M \times N}}\sum\nolimits_{i = 1}^M {\sum\nolimits_{j = 1}^N {{{(\hat f (i, j) - f(i, j))^2}}} } $

(9)

MSE表示当前图像 $\hat f (i, j)$ 和参考图像 $f(i, j)$ 的均方误差; 其中M, N为图像的高度和宽度.

(3)结构相似性(SSIM)

结构相似性分别从样本图像的亮度( ${{{\rm luminance},\; l}}$ )、对比度( ${{{\rm contrast},\; c}}$ )和结构( ${{{\rm structure},\; s}}$ )这3个方面来度量图像的质量. 其中亮度l、对比度c和结构s的计算公式如下:

$ l(x, y) = \frac{{2{u_x}{u_y} + {c_1}}}{{u_x^2 + u_y^2 + {c_1}}} $

(10)

$ c(x, y) = \frac{{2{\sigma _x}{\sigma _y} + {c_2}}}{{\sigma _x^2 + \sigma _y^2 + {c_2}}} $

(11)

$ s(x, y) = \frac{{{\sigma _{xy}} + {c_3}}}{{{\sigma _x}{\sigma _y} + {c_3}}} $

(12)

其中, ${c_3} = {c_2}/2$ , ${u_x}$ 代表图像x的像素的均值, ${u_y}$ 代表图像y的像素的均值, $\sigma _x^2$ 代表图像x的像素的方差, $\sigma _y^2$ 代表图像y的像素的方差, ${\sigma _{xy}}$ 代表图像x和图像y的协方差, SSIM的计算公式为:

$ \begin{split} {\textit{SSIM}}(x, y) &= [l(x, y) \times c(x, y) \times s(x, y)] \\ & = \frac{{(2{u_x}{u_y} + {c_1})(2{\sigma _{xy}} + {c_2})}}{{(u_x^2 + u_y^2 + {c_1})(\sigma _x^2 + \sigma _y^2 + {c_2})}} \end{split} $

(13)

3.3 实验环境

为了验证本文所提出的网络结构的去噪性能, 将本文所提出的算法与BM3D, DnCNN, FFDNet, IRCNN几种常见的卷积神经网络去噪模型进行了实验对比, 为了验证图像在不同等级噪声下网络去噪性能的影响, 分别对训练集添加噪声等级为5, 10, 15, 25, 50的高斯噪声.

为了对本文所设计的算法进行验证, 实验的硬件配置为GPU为Tesla P4, 内存为8 GB, 软件配置为CUDA 10.1, Python 3.7, 神经网络的搭建采用深度学习框架PyTorch 0.4. 采用Adam优化器进行训练, 学习率设置为 $1 \times {10^{ - 3}}$ , 训练轮数为50. 为了提高网络训练效率, 对网络的输入数据采用批量输入, batchsize为128.

3.4 实验分析

为了考察不同的dense block模块对网络去噪模型的影响, 将分别对含有1, 2, 3个Conv+Leaky ReLU层的dense block模块进行图像去噪性能比较, 实验结果如表1、表2所示. 表1表示在噪声等级为25时, 不同数量的dense block在测试集Set12上的PSNR和SSIM值. 表2表示在噪声等级为25时, 不同数量的dense block在测试集BSD68上的PSNR和SSIM值.

表 1 不同dense block (DB)模块在Set12数据集上的PSNR/SSIM值

表 2 不同dense block (DB)模块在BSD68数据集上的PSNR/SSIM值

从表1和表2中可以看出, 将3个dense block模块进行串联拼接, 可以融合更多的图像特征信息, 在网络输出时可以对输入图像进行更细节的恢复, 平均峰值信噪比和结构相似性均具有较好的效果. 此实验说明dense block模块的特征融合对图像去噪是有效的.

对Set12和BSD68两种数据集分别添加不同等级 $\sigma = 5,\; \sigma = 10,\; \sigma = 15, \;\sigma = 25, \;\sigma = 50$ 的高斯噪声, 由于图像自身结构的差异性, 不同的图像在不同的去噪算法上的结果存在差异, 导致PSNR和SSIM的值不相同. 表3显示在不同噪声等级下, Set12数据集的每一张图片的去噪结果的PSNR值, 本文提出的算法在 $\sigma = 5, \sigma = 10,\; \sigma = 15,\; \sigma = 25,\; \sigma = 50$ 时, 图像去噪效果优于其他去噪算法, 在高噪声 $\sigma = 50$ 场景下, 本文的图像去噪效果一般, PSNR提升较小. 表4显示在不同噪声等级下, Set12数据集在不同图像去噪算法下的平均SSIM值, 本文提出算法的图像去噪上取得了良好的效果. 从表3和表4可以看出, 本文所提出的算法在5种噪声等级下的PSNR与经典的BM3D图像去噪算法相比平均超出了2.7 dB, SSIM平均超出了0.2776. 与深度神经网络图像去噪方法中的DnCNN方法比较, 在噪声等级为5, 10, 15, 25, 50时, 本文提出的去噪算法平均PSNR分别提高了0.09 dB, 0.11 dB, 0.1dB, 0.12 dB, 0.18 dB, 平均SSIM分别提高了0.0003, 0.0007, 0.0006, 0.0021, 0.0049. 表5展示了在5种不同噪声等级下, 本文算法在数据集BSD68下,PSNR取得最好的平均值, 表6使用了SSIM作为评价指标, 在不同噪声等级下, 不同算法在数据集BSD68下的平均SSIM值, 表明本文算法在不同强度的噪声环境下, 去噪性能整体效果最优.

表 3 不同算法在Set12数据集上的PSNR值(dB)

$\sigma $	Method	a	b	c	d	e	f	g	h	i	j	k	l	Average
5	BM3D	38.17	39.82	38.03	37.30	38.09	37.40	37.86	38.75	38.16	37.27	37.77	37.49	38.01
	DnCNN	38.62	39.54	38.35	38.17	39.22	37.81	38.14	38.90	38.14	37.20	38.17	37.66	38.32
	IRCNN	38.65	39.60	38.25	38.10	39.11	37.80	38.18	38.74	38.03	36.93	38.14	37.60	38.26
	FFDNet	38.29	39.50	37.87	37.91	38.76	37.55	37.91	38.78	37.83	37.04	38.01	37.52	38.08
	Ours	38.69	39.69	38.43	38.24	39.34	37.89	38.20	38.97	38.20	37.34	38.23	37.73	38.41
10	BM3D	34.07	36.58	34.57	33.09	34.11	33.22	33.47	35.92	34.78	33.88	33.98	33.97	34.30
	DnCNN	34.60	36.34	35.05	34.23	35.30	33.83	33.97	36.04	34.45	34.02	34.37	34.20	34.70
	IRCNN	34.66	36.41	35.13	34.12	35.21	33.87	34.03	36.07	34.43	34.08	34.33	34.24	34.71
	FFDNet	34.44	36.53	34.79	34.12	35.07	33.68	33.88	36.13	34.42	33.99	34.33	34.25	34.64
	Ours	34.72	36.49	35.14	34.35	35.46	33.88	34.03	36.16	34.61	34.13	34.45	34.31	34.81
15	BM3D	31.91	34.93	32.69	31.14	31.85	31.07	31.37	34.26	33.10	32.13	31.92	32.10	32.37
	DnCNN	32.59	34.99	33.24	32.13	33.25	31.67	31.88	34.58	32.61	32.42	32.43	32.43	32.85
	IRCNN	32.53	34.88	33.21	31.96	32.98	31.66	31.88	34.50	32.41	32.36	32.36	32.37	32.76
	FFDNet	32.37	35.05	33.02	31.95	32.92	31.55	31.79	34.60	32.48	32.36	32.37	32.43	32.74
	Ours	32.70	35.12	33.37	32.21	33.35	31.75	31.94	34.66	32.77	32.50	32.48	32.53	32.95
25	BM3D	29.45	32.85	30.16	28.56	29.25	28.42	28.93	32.07	30.71	29.90	29.61	29.71	29.97
	DnCNN	30.21	33.10	30.82	29.36	30.41	29.07	29.44	32.41	30.01	30.20	30.08	30.08	30.43
	IRCNN	30.12	33.02	30.81	29.21	30.20	29.05	29.47	32.40	29.93	30.17	30.02	30.05	30.37
	FFDNet	30.05	33.26	30.72	29.28	30.29	29.01	29.42	32.57	29.98	30.23	30.07	30.15	30.42
	Ours	30.34	33.27	30.94	29.46	30.54	29.13	29.50	32.55	30.21	30.30	30.14	30.21	30.55
50	BM3D	26.13	29.69	26.68	25.04	25.82	25.10	25.90	29.05	27.22	26.78	26.81	26.46	26.72
	DnCNN	27.26	29.96	27.35	25.64	26.83	25.83	26.42	29.34	26.15	27.19	27.19	26.86	27.17
	IRCNN	27.16	29.90	27.33	25.48	26.66	25.78	26.48	29.36	26.17	27.17	27.14	26.86	27.12
	FFDNet	27.24	30.36	27.41	25.68	26.92	25.79	26.57	29.63	26.41	27.30	27.26	27.04	27.30
	Ours	27.41	30.26	27.51	25.81	26.96	25.91	26.58	29.56	26.53	27.33	27.26	27.06	27.35

表 3 不同算法在Set12数据集上的PSNR值(dB)

表 4 不同算法在Set12数据集上的SSIM值

表 5 不同算法在BSD68数据集上的PSNR值(dB)

图6选取了Set12数据集中的5幅图像, 在5种不同噪声等级下, 通过不同的算法对含噪声图像进行去噪, 每一张去噪后的图片给出了局部放大效果, 图片中的白框区域为放大区域, 图片右下角为局部细节放大图, 由图可见, 本文提出的方法在去噪时很好地保留了图像的纹理细节, 有效地较少边界伪影和边缘细节损失.

表 6 不同算法在BSD68数据集上的SSIM值

4 结论与展望

本文针对图像去噪存在不能充分提取图像特征导致图像细节丢失且收敛时间过长的问题, 提出了一种基于残差密集块的卷积神经网络图像去噪方法, 该模型通过引入密集连接残差块并添加Leaky ReLU激活函数操作进一步提高网络性能, 能够有效去除不同等级强度的噪声, 同时利用PSNR和SSIM值进行网络性能评估. 与经典图像去噪算法相比较, 实验结果显示, 本文提出算法的PSNR和SSIM均有明显的提升, 本文算法提高了图像去噪的性能, 提升图像的纹理细节信息, 随着残差结构的加入, 网络训练的过程也随之加快, 与此同时减少了边界伪影, 但本文所提出的算法针对高噪声环境下的图像进行去噪时, 依然存在图像细节丢失问题, 针对该问题, 后续将针对该网络模型作进一步的研究. 此外, 结合真实场景, 例如医学成像、遥感图像产生的真实噪声问题, 需要继续研究.

图 6 不同算法不同噪声等级下数据集Set12的部分去噪图片

参考文献

[1]	魏江, 刘潇, 梅少辉. 基于卷积神经网络的遥感图像去噪算法. 微电子学与计算机, 2019, 36(8): 59-62, 67.
[2]	张文秀, 朱振才, 张永合, 等. 基于残差块和注意力机制的细胞图像分割方法. 光学学报, 2020, 40(17): 1710001.
[3]	李传朋, 秦品乐, 张晋京. 基于深度卷积神经网络的图像去噪研究. 计算机工程, 2017, 43(3): 253-260. DOI:10.3969/j.issn.1000-3428.2017.03.042
[4]	尹海涛, 邓皓. 基于混合注意力的对偶残差去噪网络. 激光与光电子学进展, 2021, 58(14): 1410002.
[5]	尹佳琪, 王世勇, 李范鸣. 基于改进主成分分析的分焦平面偏振图像去噪算法. 光学学报, 2021, 41(7): 64–73.
[6]	Buades A, Coll B, Morel JM. A review of image denoising algorithms, with a new one. Multiscale Modeling & Simulation, 2005, 4(2): 490-530.
[7]	Guan XP, Zhao LX, Tang YG. Mixed filter for image denoising. Journal of Image and Graphics, 2005, 10(3): 332-337.
[8]	Mairal J, Bach F, Ponce J, et al. Non-local sparse models for image restoration. Proceedings of the 2009 IEEE 12th International Conference on Computer Vision. Kyoto: IEEE, 2009. 2272–2279.
[9]	Xu YS, Weaver JB, Healy DM, et al. Wavelet transform domain filters: A spatially selective noise filtration technique. IEEE Transactions on Image Processing, 1994, 3(6): 747-758. DOI:10.1109/83.336245
[10]	Donoho DL, Johnstone IM. Ideal spatial adaptation by wavelet shrinkage. Biometrika, 1994, 81(3): 425-455. DOI:10.1093/biomet/81.3.425
[11]	Dabov K, Foi A, Katkovnik V, et al. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Transactions on Image Processing, 2007, 16(8): 2080-2095. DOI:10.1109/TIP.2007.901238
[12]	Jain V, Seung HS. Natural image denoising with convolutional networks. Proceedings of the 21st International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2008. 769–776.
[13]	林景栋, 吴欣怡, 柴毅, 等. 卷积神经网络结构优化综述. 自动化学报, 2020, 46(1): 24-37.
[14]	Holt MJJ. Comparison of generalization in multi-layer perceptrons with the log-likelihood and least-squares cost functions. Proceedings of the 11th IAPR International Conference on Pattern Recognition. Vol. II. Conference B: Pattern Recognition Methodology and Systems. The Hague: IEEE, 1992. 17–20.
[15]	Mao XJ, Shen CH, Yang YB. Image restoration using very deep convolutional encoder-decoder networks with symmetric skip connections. Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona: Curran Associates Inc., 2016. 2810–2818.
[16]	Zhang K, Zuo WM, Chen YJ, et al. Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising. IEEE Transactions on Image Processing, 2017, 26(7): 3142-3155. DOI:10.1109/TIP.2017.2662206
[17]	He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 770–778.
[18]	Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. Proceedings of the 32nd International Conference on Machine Learning. Lille: PMLR, 2015. 448–456.
[19]	Zhang K, Zuo WM, Gu SH, et al. Learning deep CNN denoiser prior for image restoration. Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 2808–2817.
[20]	Zhang K, Zuo WM, Zhang L. FFDNet: Toward a fast and flexible solution for CNN-based image denoising. IEEE Transactions on Image Processing, 2018, 27(9): 4608-4622. DOI:10.1109/TIP.2018.2839891
[21]	Creswell A, White T, Dumoulin V, et al. Generative adversarial networks: An overview. IEEE Signal Processing Magazine, 2018, 35(1): 53-65. DOI:10.1109/MSP.2017.2765202
[22]	Wang Z, Li JW, Song G. DTDN: Dual-task de-raining network. Proceedings of the 27th ACM International Conference on Multimedia. Nice: ACM, 2019. 1833–1841.
[23]	席志红, 侯彩燕, 袁昆鹏, 等. 基于深层残差网络的加速图像超分辨率重建. 光学学报, 2019, 39(2): 0210003.
[24]	陈人和, 赖振意, 钱育蓉. 改进的生成对抗网络图像去噪算法. 计算机工程与应用, 2021, 57(5): 168-172. DOI:10.3778/j.issn.1002-8331.2003-0336
[25]	秦毅, 赵二刚. 基于轻量深度残差网络的图像多类型噪声去除算法. 计算机应用与软件, 2021, 38(9): 250-255. DOI:10.3969/j.issn.1000-386x.2021.09.039
[26]	朱斯琪, 王珏, 蔡玉芳. 基于改进型循环一致性生成对抗网络的低剂量CT去噪算法. 光学学报, 2020, 40(22): 2210002.
[27]	Zhang XH, Zou YX, Shi W. Dilated convolution neural network with LeakyReLU for environmental sound classification. Proceedings of the 2017 22nd International Conference on Digital Signal Processing. London: IEEE, 2017. 1–5.
[28]	Huang G, Liu Z, van der Maaten L, et al. Densely connected convolutional networks. Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 2261–2269.
[29]	Lim B, Son S, Kim H, et al. Enhanced deep residual networks for single image super-resolution. Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops. Honolulu: IEEE, 2017. 1132–1140.
[30]	Szegedy C, Ioffe S, Vanhoucke V, et al. Inception-v4, inception-ResNet and the impact of residual connections on learning. Proceedings of the 31st AAAI Conference on Artificial Intelligence. San Francisco: AAAI, 2017. 4278–4284.