2. 安徽省高性能计算重点实验室, 合肥 230026
2. Key Laboratory of High Performance Computing of Anhui Province, Hefei 230026, China
第二代测序技术(NGS)[1]的出现使生物学家能够以较低的成本快速确定DNA分子的核苷酸排列. 如今, NGS平台每天均会产生海量的长度为75至300个碱基对(bp)的测序片段(reads, 也称之为读段)需要进行序列比对分析, 这是下游生物学应用的基础步骤. 序列比对分析结果可以解释人类种群之间的基因多样性, 对研究物种进化过程和引发遗传病的基因变异有着深远意义[2].
一般地, 序列比对算法可以分为找最佳比对算法(best-mapper)和找全比对算法(all-mapper)两类, 前者用于找到每条读段在参考基因组上匹配概率最高的一个或几个位置, 而后者则用于找到满足误差的全部匹配位置. 这两类算法应用场景不同, 如全转录组测序分析以及DNA和蛋白质之间的作用关系分析, 利用找最佳比对算法找出读段的一个或几个最佳匹配位置已能达到要求. 而对于结构变异探测以及拷贝数变异(CNV)分析这类需要找出所有基因组重复区域信息的应用, 找全比对算法是必不可少的. 由于找全比对算法需要枚举所有可能的匹配位置, 故而其计算成本更高, 更迫切需要研究高性能的算法. 目前主流的找全比对算法存在验证阶段时间开销过大的问题, 提高验证阶段的时间效率, 成为了测序序列找全比对算法中的重要优化环节.
主流的测序序列找全比对算法普遍采用种子扩展(seed-and-extend)方法, 该方法分为过滤和验证两个阶段. 在过滤阶段, 首先从读段中选取多个长度固定的碱基序列片段作为种子(seeds), 然后在参考基因组索引中检索种子的出现位置并过滤出合适的候选位置; 在验证阶段, 需要利用动态规划算法验证候选位置是否是读段匹配参考基因组的实际位置. 该方法过滤阶段使用的参考基因组索引主要包括哈希索引和FM索引[3]两类. 哈希索引的优势是种子定位速度快, 而问题是空间开销大, 像人类基因组的哈希索引超过11 GB, 并且种子越长其空间开销会指数级地增长. FM索引优势是空间开销要小得多, 人类基因组的索引仅需要大约3 GB, 其缺陷是定位操作时间相对前者要大得多, 并且种子越长时间开销越大. 受这些因素的限制, 现有找全比对算法通常选取较短的种子来处理读段, 一般为11至14 bp. 由于短种子在参考基因组上的出现频率高, 导致过滤和验证的位置数量过多, 而验证阶段时间开销占比更大, 是提升比对算法时间性能的关键.
为此, 本文提出了一种基于长种子的二代测序序列找全比对算法. 该算法中的参考基因组索引是结合普通哈希索引与布隆过滤器(Bloom filter, BF)[4]构建的面向长种子的哈希索引. 该索引方法通过模运算缩减哈希空间, 避免了哈希索引在长种子情况下空间开销过大, 并应用布隆过滤器识别同一存储位置上的不同种子. 对于31亿碱基位点的人类基因组, 本文的索引方法可以在约8 GB空间上索引长度达30 bp的种子, 我们的找全比对算法相比于已有最好的找全比对算法时间减少26%.
1 相关研究 1.1 基因组索引技术(1) 经典索引方法
参考基因组索引是大部分序列比对算法中的基本数据结构, 索引的空间开销和检索效率都是影响序列比对算法性能的重要因素. 依据索引结构不同, 可将基因组索引分为后缀数组、FM索引和哈希索引3类.
后缀数组的思路是对给定文本串S的所有后缀按照字典序进行排序, 并将所有后缀在S中的起始位置存在数组SA中. 对于一个待检索的模式串P, 所有以P为前缀的文本串在S上的位置就存储在后缀数组的一个连续区间之中. 虽然后缀数组支持定位非固定长度的种子, 但是其空间开销相比于哈希索引没有优势并且检索速度要慢得多. 因此, 目前只有少数序列比对算法采用后缀数组来索引参考基因组, 这类算法包括Vmatch[5]和Segemehl[6]等.
Ferragina和Manzini将后缀数组与BWT变换(Burrows-Wheeler transform)结合, 提出了FM索引[3]. 该索引方法对后缀数组中的特定位置进行采样, 并利用BWT变换来求解非采样位置. FM索引的定位速度相比于后缀数组进一步下降, 但通过仅存储采样位置使所需存储空间大大减少, 是目前空间消耗最小的参考基因组索引. 由于FM索引定位种子速度较慢, 目前常用于找最佳的序列比对算法, 如BWA[7]、SOAP2[8]、Bowtie2[9]等BLAST[10]算法首次提出用哈希表构建基因组索引. 哈希索引保存了参考基因组上每条q-gram(长度为q的连续子序列)的位置信息, 将q-gram作为哈希表的key, 并把此q-gram在基因组上出现的位置保存为value. 由于哈希索引仅需一次哈希函数运算即可定位种子, 非常适合需要频繁定位种子的找全比对问题, 因此大部分找全比对算法都采用哈希索引方法来构建参考基因组索引, 包括mrFAST[11]、Hobbes2[12]、FEM[13]、BitMapper[14]等. 哈希索引结构如图1所示.

|
图 1 哈希索引结构 |
(2) 索引技术新发展
基因组索引技术的改进是提升序列比对算法性能的重要一环. 目前针对FM索引的改进主要集中在种子定位速度方面. Chacón等人提出了n-step FM索引[15], 该索引方法利用二维的BWT结构使得FM索引中的向后搜索算法(backward search algorithm)能一次向后搜索n个字符, 较大程度地提升了定位速度. Fernandes等人将采样后的最长公共前缀数组应用到FM索引方法中[16], 提升了定位速度并节省了空间. Cheng等人提出了FMtree种子定位算法[17], 将FM索引定位操作的搜索空间组织成多叉树, 使多个采样位置能被同时计算出, 极大地提升了定位速度.
对于哈希索引, 其种子定位操作的时间复杂度已经是常数级. 因此, 改进策略主要集中于减少空间消耗. 稀疏化的哈希索引[13,18]是降低哈希索引空间开销的有效方法. 文献[18]中按照特定规则采样出部分q-gram, 并将它们的位置保存在哈希表中, 后续再计算出未采样q-gram的位置. 该方法以较小的时间复杂度代价大大降低了哈希索引的空间消耗. 文献[13]同样是基于采样q-gram的思路, 与前者不同的是, 该方法在选取种子时采用分组选种策略尽量选择已被采样的q-gram作为种子, 避免了计算未采样q-gram的位置的时间消耗.
1.2 主流的过滤阶段方法早期的找全比对算法, 如BLAST算法, 采用连续种子方法, 将读段的每一个q-gram当作种子在索引中检索, 之后扩展并合并这些种子的位置. 这种方法需要定位大量种子, 时间开销大, 尤其对于大型基因组, 其种子出现频率较高, 导致需要验证的候选位置过多, 极大增加了后续验证阶段的计算量. 另外, 连续种子方法也无法正确匹配包含插入删除错误的读段.
MAQ[19]和SOAP[20]等方法采用了填充种子方法(spaced seed), 其利用多个填充种子模板来覆盖一条读段. 每个模板由特定长度的0和1组成, 忽略掉0对应的碱基字符. 这类方法一般会设计多个0位位置不同的种子模板, 可以保证当读段有少量置换错误时至少有一个模板可以命中. 填充种子方法时间开销比连续种子方法小, 但同样无法正确匹配包含插入删除错误的读段.
目前性能最好的几种找全比对算法普遍采用基于鸽巢原理的过滤方法. 这类方法不仅降低了过滤阶段的时间开销, 还能正确匹配包含插入删除错误的读段. mrFAST是采用这类方法的经典算法之一, 其假定每条读段最多允许e个误配, 并在读段上不重叠地划分出e+2个种子, 由鸽巢原理可知, 至少存在2个种子不包含误配. 这表示对于一个读段与参考基因组匹配的位置, 该位置至少是两个或两个以上的种子的出现位置. mrFAST将只出现一次的种子位置过滤掉, 从而减少候选位置数量. Hobbes2的过滤阶段方法目前效果最好, 其在mrFAST的基础上采用动态规划算法选取种子出现频次和最小的组合, 进一步减少了候选位置数量.
2 问题定义及相关数据结构 2.1 找全序列比对问题定义测序序列找全比对问题本质上是求解海量短字符串在长文本串中的全部匹配位置. 从数学的角度上可以定义为四元组
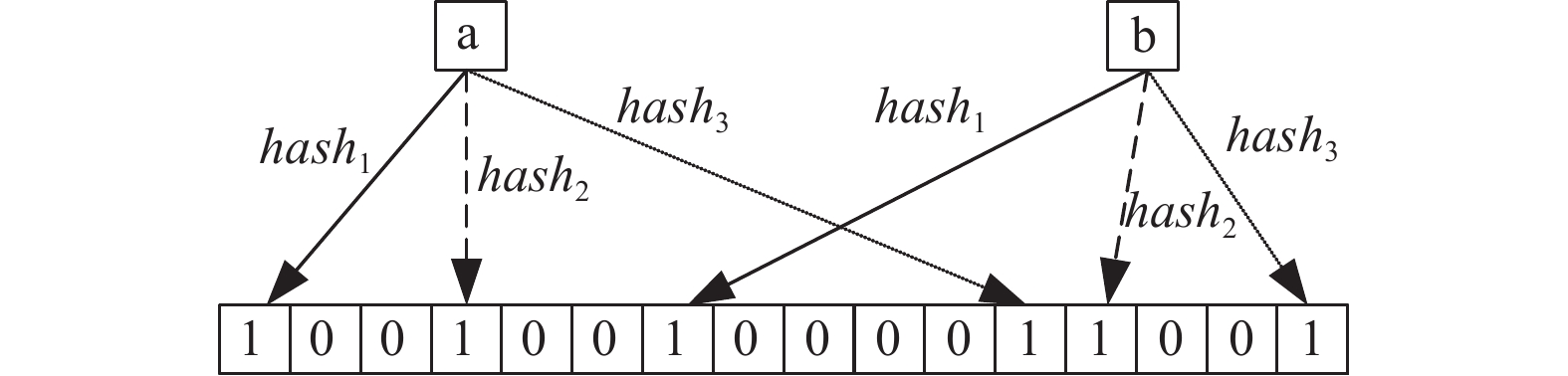
布隆过滤器能够查询一个数据是否包含于此过滤器对应的数据集合, 它由k个哈希函数和1个二进制位向量组成, 位向量的初始值全为0. 插入新数据时, k个哈希函数会将该数据映射到位向量上的k个不同位置, 并将相应位置的值置1. 查询时, 用相同的k个哈希函数进行映射, 检查映射的位置上的值是否全为1即可确定集合中是否包含该元素. 布隆过滤器的结构如图2所示.
|
图 2 布隆过滤器结构 |
布隆过滤器是一种时间和空间效率都比较高的数据结构, 其时间复杂度仅与哈希函数个数有关, 空间复杂度为 , 其中m是位向量的长度. 当两个数据元素的k个哈希函数映射的位置均相同时, 布隆过滤器会产生假阳性结果, 将原本不存在于集合中的数据报告为存在. 为降低假阳性率, 在实际使用中需权衡k、m和数据集合大小n之间的关系, 一般先考虑好m的大小, 然后即可求得假阳性概率最小时的哈希函数个数k, 根据已有研究工作[21], 其计算式可表示为:
| k=|(m/n)ln2| | (1) |
假阳性概率p与k、m、n相关, 根据文献[21], 其计算式如式(2):
| p=(1−(1−(1/m))kn)k≈(1−e−(kn/m))k | (2) |
本文首先利用Jellyfish软件[22]统计种子的长度与出现频率的关系, 进而确定合适的种子长度. 随后设计并实现了面向长种子的哈希索引, 该索引结构的优势在于支持长种子的同时定位速度快, 能够得到较少的候选位置. 然后固定间隔选取q-gram作为种子, 并在长种子哈希索引中定位. 最后利用目前效率最高的位并行算法来验证候选位置. 该算法流程可分为4个步骤: (1)构建索引; (2)选取种子; (3)定位及过滤; (3)验证候选位置.
3.1 构建索引在构建长种子索引之前, 首先需要确定种子的长度. 由Jellyfish软件得到的统计结果可知, 对于包含31亿个字符的人类基因组hg19, 30 bp长度的种子中出现频率在10次以内的占比达90%, 如图3所示.

|
图 3 种子出现频率与其长度变化关系曲线 |
由图3可知, 种子长度达到30 bp时, 出现频率小于10的种子占比趋于稳定. 另一方面, 二代测序平台产生的读段长度较短, 过长的种子容易包含测序错误. 因此, 本文将种子长度设定为30 bp.
长种子哈希索引主要包括一张哈希表以及多个布隆过滤器. 其中, 每个布隆过滤器对应参考基因组的一个区域. 采用这种结构的根本目的是缩减哈希索引存储长种子的空间开销. 以种子长度取30 bp为例, 普通哈希索引中需要存储430个不同key的信息. 而在实现索引结构时每个key对应一个4 B大小的指针, 仅指针信息的空间开销就达到430×4 B=222 TB. 这样的存储代价过大, 显然无法投入实际应用. 为此, 本文通过模运算将哈希空间限制为固定值M, 极大减小了长种子情况下哈希索引的空间开销, 以M取225为例(实际实现时, 为减少哈希碰撞, M应取质数), 存储全部指针信息仅需225×4 B=128 MB. 索引构建过程如图4所示, 首先用长度为30的滑动窗口在参考基因组上逐位选取q-gram. 将每个q-gram转换成64位无符号整型数值后, 再模M转换为对应的key值, 然后将q-gram在基因组上的位置记录在哈希表中该key对应的表项中.

|
图 4 索引构建过程 |
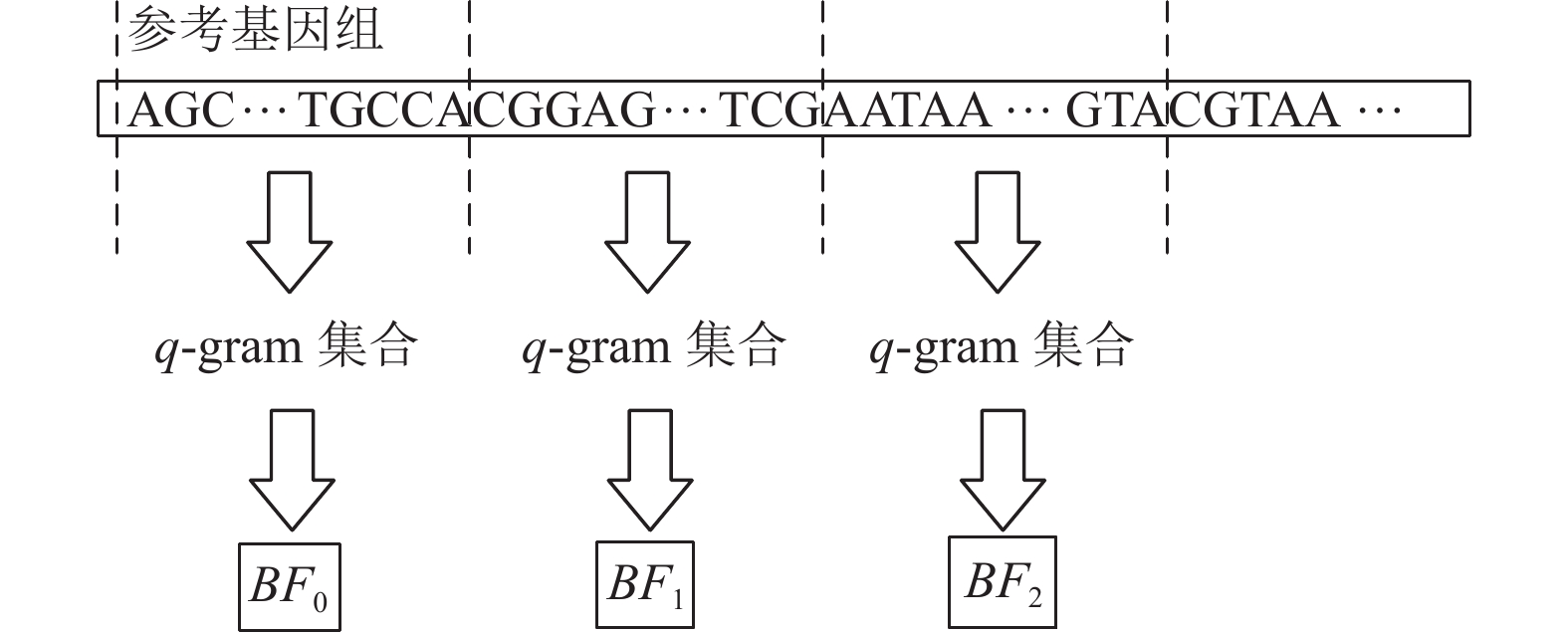
利用模运算限制哈希空间大小的做法会引起新的问题: 若两个不同的q-gram模M后的key值相同, 则它们在基因组上的位置会记录在哈希表中同一个key对应的value中, 导致定位种子时产生大量错误的候选位置. 本文利用布隆过滤器来筛选掉错误候选位置, 首先将整个参考基因组均匀划分为多个不重叠区域, 为每个区域建立一个对应的布隆过滤器, 具体过程如图5所示.
|
图 5 索引构建过程 |
每个布隆过滤器存储的元素为其对应的基因组区域内所有q-gram. 其作用是验证某个q-gram是否属于该布隆过滤器对应的基因组区域. 对于某个待定位种子, 检索哈希表得到其位置集合后, 需利用布隆过滤器验证每个位置所在的基因组区域是否包含该种子. 这样可判断此位置是否为待定位种子的实际出现位置, 从而筛选掉错误的候选位置.
3.2 选取种子由于二代测序产生的读段长度短, 基于鸽巢原理的种子选取方法不再适用于基于长种子的算法. 本文采用滑动窗口方法: 设定步长l-step, 并用长度30的滑动窗口在读段上每次右移l-step位选取种子, 具体过程如图6所示.

|
图 6 种子的生成 |
采用滑动窗口方法是为了尽可能选出不包含测序错误的种子, 能有效避免定位得到的位置集合中不包含读段与基因组实际匹配位置的情况. 参数l-step会影响比对结果, 过大会使部分读段无法匹配到参考基因组上或漏掉部分匹配位置; 过小会提升比对精度, 但需要定位的种子数量会成倍增多, 导致定位过程的时间开销增大. 本文经过多次实验比较后发现, 将l-step设定为10时, 我们的比对算法能达到与现有找全比对算法同等的精度.
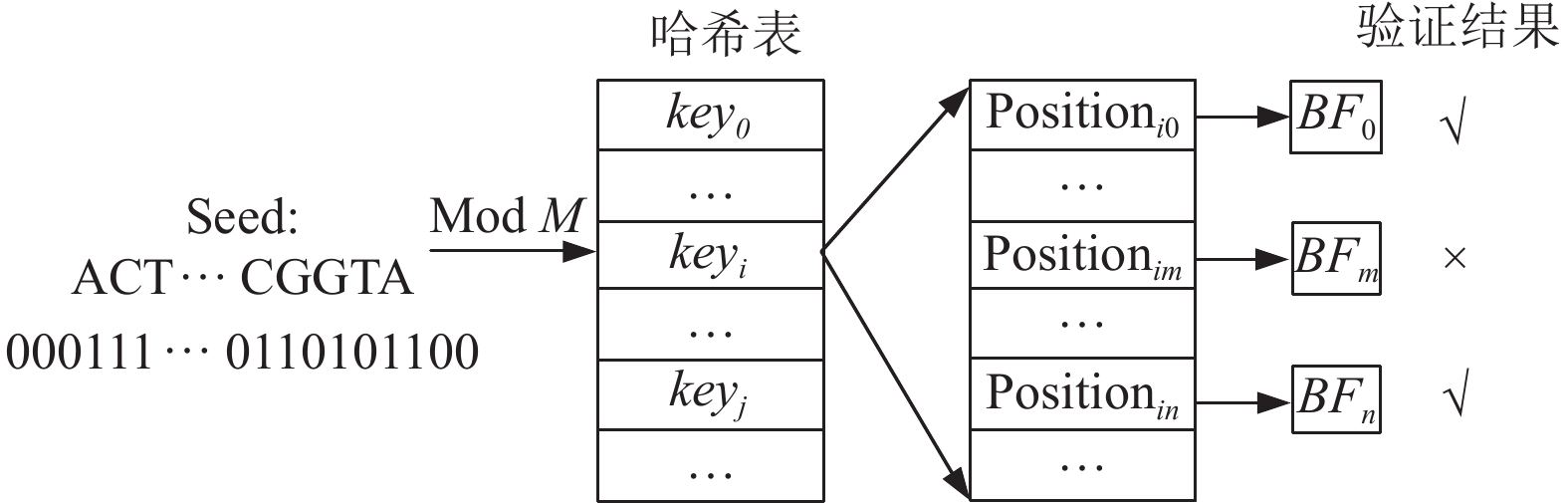
3.3 定位及过滤将选取的种子转换为key, 在哈希表中检索. 对于检索出的每个位置, 利用该位置所在基因组区域的布隆过滤器验证此位置是否为对应种子实际的出现位置, 验证通过则保留下来作为候选位置. 种子定位及过滤过程如图7所示.
3.4 验证候选位置候选位置是读段与参考基因组最有可能匹配上的位置, 但其中仍包含部分非实际匹配的位置, 需要在验证阶段将这些错误位置筛选掉. 本文采用“带状”Myers算法[23]的一种高效版本[14]来校验每个候选位置, 此版本的算法通过位并行提高了计算速度, 并利用CPU上的128位寄存器和SSE指令集来加速验证过程, 实现了同一时间验证多个候选位置的操作, 极大降低了验证阶段的时间开销.
|
图 7 种子定位及过滤 |
4 实验分析
本文所有实验均在同一机器的相同配置环境下运行. 实验平台为: Intel Xeon Gold 5120 CPU (14核心28线程, 2.20 GHz), 503 GB DDR4 RAM, Ubuntu 18.04 64位操作系统.
实验所用数据均下载自NCBI数据库. 其中参考基因组为千人基因组项目中的Genome Reference Consortium GRCh37参考序列, 版本号为 hg19. 测序数据集说明如下:
(1) R1: 千人基因组项目中第NA17871号测序序列SRR007347, 包含30万条长度100 bp的读段.
(2) R2: 千人基因组项目中第NA11840号测序序列ERR012100, 包含10万条长度100 bp的读段.
4.1 候选位置数量对比实验为验证本文所采用的长种子方法能得到更少量的候选位置, 选择mrFAST和Hobbes2来进行读段平均候选位置数量的对比实验, 所用数据集为R1. 其中Hobbes2的过滤方法是目前效果最好的方法. 实验结果如表1所示.
| 表 1 各算法的读段平均候选位置数量结果 |
由表1可知, 本文算法得到的读段平均候选位置数比mrFAST少约87%, 比Hobbes2少约69%. 采用长种子定位的方法在候选位置数量上有明显的优势.
4.2 算法性能对比实验在找全比对算法的整体流程中, 验证阶段的时间占比最大. 以目前速度最快的BitMapper为例, 其验证阶段的时间占比在70%以上. 因此, 相比于定位长种子的额外时间消耗, 本文方法在验证阶段带来的时间性能提升更为显著. 为验证此观点, 选择目前速度最快的几种找全比对算法与本文算法做对比, 实验结果如表2所示.
| 表 2 各算法性能测试结果 |
本文利用匹配上的读段比例和召回率来衡量找全比对算法的精度, 其中, 匹配上的读段比例表示成功匹配到参考基因组上的读段占比; 召回率表示读段的正确匹配位置被算法报告出来的比例. 由表2可知, 对于匹配上的读段比例, mrFAST的结果最好, 其他4个算法相差不大. 对于召回率, FEM和BitMapper的结果较好, 本文算法则略优于Hobbes2和mrFAST. 在内存开销上, mrFAST表现最好, FEM次之, 本文算法优于Hobbes2和BitMapper. 在时间性能方面, 本文算法比目前速度最快的BitMapper快了约26%.
5 结论与展望本文提出一种二代测序序列找全比对算法, 在算法中采用哈希索引与布隆过滤器结合的方法实现了长种子的定位. 利用长种子的低频特性可得到更少量的候选位置, 从而提升算法的运行速度. 实验结果表明, 本文算法相比于其他主流的找全比对算法, 候选位置数量更少, 在维持相同水平精度的同时速度更快. 由于定位长种子带来的额外时间开销, 我们的算法在过滤阶段比其他算法需要更长的运行时间, 如何优化布隆过滤器筛选位置的策略从而提高长种子的定位速度将是下一步的工作重点.
| [1] |
Mardis ER. The impact of next-generation sequencing technology on genetics. Trends in Genetics, 2008, 24(3): 133-141. DOI:10.1016/j.tig.2007.12.007 |
| [2] |
Trost B, Walker S, Wang ZZ, et al. A comprehensive workflow for read depth-based identification of copy-number variation from whole-genome sequence data. The American Journal of Human Genetics, 2018, 102(1): 142-155. DOI:10.1016/j.ajhg.2017.12.007 |
| [3] |
Ferragina P, Manzini G. Opportunistic data structures with applications. Proceedings of the 41st Annual Symposium on Foundations of Computer Science. Redondo Beach: IEEE, 2000. 390–398.
|
| [4] |
Bloom BH. Space/time trade-offs in hash coding with allowable errors. Communications of the ACM, 1970, 13(7): 422-426. DOI:10.1145/362686.362692 |
| [5] |
Abouelhoda MI, Kurtz S, Ohlebusch E. Replacing suffix trees with enhanced suffix arrays. Journal of Discrete Algorithms, 2004, 2(1): 53-86. DOI:10.1016/S1570-8667(03)00065-0 |
| [6] |
Hoffmann S, Otto C, Kurtz S, et al. Fast mapping of short sequences with mismatches, insertions and deletions using index structures. PLoS Computational Biology, 2009, 5(9): e1000502. DOI:10.1371/journal.pcbi.1000502 |
| [7] |
Li H, Durbin R. Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics, 2009, 25(14): 1754-1760. DOI:10.1093/bioinformatics/btp324 |
| [8] |
Li RQ, Yu C, Li YR, et al. SOAP2: An improved ultrafast tool for short read alignment. Bioinformatics, 2009, 25(15): 1966-1967. DOI:10.1093/bioinformatics/btp336 |
| [9] |
Langmead B, Trapnell C, Pop M, et al. Ultrafast and memory-efficient alignment of short DNA sequences to the human genome. Genome Biology, 2009, 10(3): R25. DOI:10.1186/gb-2009-10-3-r25 |
| [10] |
Altschul SF, Gish W, Miller W, et al. Basic local alignment search tool. Journal of Molecular Biology, 1990, 215(3): 403-410. DOI:10.1016/S0022-2836(05)80360-2 |
| [11] |
Xin HY, Lee D, Hormozdiari F, et al. Accelerating read mapping with FastHASH. BMC Genomics, 2013, 14(1): S13. DOI:10.1186/1471-2164-14-S1-S13 |
| [12] |
Kim J, Li C, Xie XH. Improving read mapping using additional prefix grams. BMC Bioinformatics, 2014, 15(1): 42. DOI:10.1186/1471-2105-15-42 |
| [13] |
Zhang HW, Chan YD, Fan KC, et al. Fast and efficient short read mapping based on a succinct hash index. BMC Bioinformatics, 2018, 19(1): 92. DOI:10.1186/s12859-018-2094-5 |
| [14] |
Cheng HY, Jiang HP, Yang JY, et al. BitMapper: An efficient all-mapper based on bit-vector computing. BMC Bioinformatics, 2015, 16(1): 192. DOI:10.1186/s12859-015-0626-9 |
| [15] |
Chacón A, Moure JC, Espinosa A, et al. n-step FM-index for faster pattern matching
. Procedia Computer Science, 2013, 18: 70-79. DOI:10.1016/j.procs.2013.05.170 |
| [16] |
Fernandes F, Freitas AT. slaMEM: Efficient retrieval of maximal exact matches using a sampled LCP array. Bioinformatics, 2014, 30(4): 464-471. DOI:10.1093/bioinformatics/btt706 |
| [17] |
Cheng HY, Wu M, Xu Y. FMtree: A fast locating algorithm of FM-indexes for genomic data. Bioinformatics, 2018, 34(3): 416-424. DOI:10.1093/bioinformatics/btx596 |
| [18] |
Cheng HY, Zhang Y, Xu Y. BitMapper2: A GPU-accelerated all-mapper based on the sparse q-gram index
. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2019, 16(3): 886-897. DOI:10.1109/TCBB.2018.2822687 |
| [19] |
Li H, Ruan J, Durbin R. Mapping short DNA sequencing reads and calling variants using mapping quality scores. Genome Research, 2008, 18(11): 1851-1858. DOI:10.1101/gr.078212.108 |
| [20] |
Li RQ, Li YR, Kristiansen K, et al. SOAP: Short oligonucleotide alignment program. Bioinformatics, 2008, 24(5): 713-714. DOI:10.1093/bioinformatics/btn025 |
| [21] |
Guo D, Wu J, Chen H, et al. Theory and network applications of dynamic bloom filters. Proceedings of the 25th IEEE International Conference on Computer Communications. Barcelona: IEEE, 2007. 1–12.
|
| [22] |
Marçais G, Kingsford C. A fast, lock-free approach for efficient parallel counting of occurrences of k-mers
. Bioinformatics, 2011, 27(6): 764-770. DOI:10.1093/bioinformatics/btr011 |
| [23] |
Myers G. A fast bit-vector algorithm for approximate string matching based on dynamic programming. Journal of the ACM, 1999, 46(3): 395-415. DOI:10.1145/316542.316550 |
 2022, Vol. 31
2022, Vol. 31



