2. 华电国际十里泉电厂, 枣庄 277100
2. Huadian International Shiliquan Power Plant, Zaozhuang 277100, China
当前全球能源发展面临资源紧缺、利用效率低等深层次矛盾与问题, 能源转型迫在眉睫[1]. 根据国际可再生能源署(international renewable energy agency, IRENA)数据统计, 截至2020年底, 中国光伏与风电装机容量分别为254 GW和282 GW, 占世界领导地位[2]. 随着新能源装机量增加, 能源消纳问题日益凸显, 每年我国因“三弃”问题带来的损失达百亿元, 近几年能源消纳问题虽有所缓解, 但截止到2019年, 新能源弃光电量仍然高达26.1亿千瓦时[3]. 因此精确的负荷预测对于优化能源调度、解决“三弃”问题具有重要意义.
负荷预测不仅在综合能源管理与能源调度中占据主导地位, 对于电价制定和电网的稳定运行也尤为重要[4]. 早在20世纪80年代便有专家学者针对负荷预测进行了研究, 诸如回归分析法[5]、时间序列法[6, 7]等传统负荷预测算法, 但此类模型的预测能力仅针对线性模型表现较好, 而用户用电负荷具有典型的非线性特征. 尤其近几年随着智能化设备的广泛普及, 用电量大幅度提升, 捕获到的诸如天气、经济、人口数量、地理位置等电力负荷影响因素越来越多, 负荷预测的难度也随之增大[8]. 为综合考虑多个影响因素, ANN[9]、SVM[10]、集成学习[11, 12]等智能化算法开始被广泛应用于负荷预测, 例如Chahkoutahi等人[13]分别采用基于自适应网络的模糊推理系统、多层感知器神经网络和季节性自回归综合滑动平均法对电力负荷进行预测, 预测精确度有所提高. 与传统预测算法相比, 智能化预测算法适用范围更广和精确度也相对较高.
1 电力负荷预测 1.1 电力负荷负荷是指供电地区或电网在某一瞬间所承担的用电功率, 根据用户结构的不同, 可将电力负荷划分为工业负荷、商用负荷、城市民用负荷、农村负荷以及其他负荷等. 其中城市民用负荷主要指城市居民家用电器的用电负荷, 与居民日常生活息息相关, 是目前的主要研究领域.
负荷预测[14]是指充分考虑各种自然因素、社会影响、系统运行等条件, 利用各种数学方法或智能化模型预测用户未来一定时间内的负荷数值. 根据研究目的与预测时长的不同, 可将负荷预测分为超短期负荷预测、短期负荷预测、中期负荷预测以及长期负荷预测[15]. 精确的短期负荷预测对于制定发电计划、安排机组启停与检修以及电价制定具有重要意义.
1.2 负荷预测影响因素电力是维持用户日常生活的基础能源, 容易受到如天气、建筑的物理特性、用户行为、人口密度等多种因素的影响. 本文将用户用电负荷影响因素划分为地区天气因素、经济因素、建筑结构以及人口密度等4大类别.
(1)天气因素主要包括室内外气温、空气湿度、太阳照射角以及风速等; 天气是影响用户负荷的主要因素之一, 尤其表现在夏季气温升高时, 空调制冷等大功率电器用电量大幅度提升.
(2)经济因素是指居民家庭收入、城区能源配比与价格、区域生活水平及教育水平等; 家庭经济水平对居民用户用电行为以及设备所有权起决定性作用, 从而对用户用电负荷产生影响.
(3)建筑结构包括建筑材料、绿化规划、住户位置等要素; 其中建筑高度与建筑位置等因素通过影响太阳辐射度、通风效果进而影响用户用电负荷, 建筑材料则会影响房间的制冷制热问题. 另外室内设备条件也会对用户用电负荷产生较大影响.
(4)人文特点是指某地区的居民密集度、生活风俗以及居民特点, 地域风俗习惯、居民职业特点以及家庭人口年龄构成对用户用电习惯与负荷高低都会产生一定的影响.
2 典型负荷预测算法目前负荷预测可分为传统预测和基于深度学习的智能化预测模型, 本文简要介绍了回归分析、ANN、SVM、CNN以及RNN等预测方法, 总结概括各预测方法的优缺点与适用范围, 以期为未来负荷预测提供参考.
2.1 回归分析法回归分析法指在分析因变量与自变量的基础上, 建立回归方程来预测因变量未来的变化趋势. 该模型构建简单, 预测速度较快. 但随着科技的快速发展, 可收集到的用电负荷影响因素数据与日俱增, 回归分析模型往往会忽略负荷变化的内在规律性以降低预测精度. 目前回归分析逐渐开始作为基础模型用于处理负荷预测问题, 例如文献[16]在基础回归模型的基础上, 引入虚拟变量用于描述时间的周期变化规律, 同时考虑即时温度、滞后温度以及24小时平均温度实现用户负荷预测.
2.2 时间序列法时间序列算法最初由美国学者Box等人[17]提出, 该方法根据时间序列历史数据, 建立数学模型描述时间与负荷值之间的关系. Boroojeni等人[18]通过模拟不同季节周期(每天、每周、每季度和每年)的离线数据, 借助自回归(auto regressive model, AR)和移动平均(moving average model, MA)模型, 分别对季节性和非季节性负荷周期进行建模, 有效降低了预测误差. 时间序列分析算法只考虑时间变量, 需求数据量少, 预测速度快. 但该模型理论复杂, 对原始数据平稳性要求较高, 并且未考虑其他不确定性影响因素, 最终的预测精确度存在较大误差.
除回归分析与时间序列法外, 统计负荷预测模型还包括灰色模型法(grey model, GM)[19]、相似日法[20]、负荷求导法等. 灰色模型对不确定性因素处理较好, 仅适用于长期负荷预测; 相似日法在一定程度上解决负荷预测中的“积温效应”问题, 但过于依赖历史数据; 负荷求导对超短期负荷预测表现出较好的性能, 但计算复杂度较高.
2.3 人工神经网络BPNN因其强大的非线性映射能力和柔性的网络结构使之成为应用最广泛的人工神经网络之一[21]. 但目前没有统一标准来定义神经元个数与网络层数, 同时BPNN还存在学习收敛速度慢以及局部最优解的问题. 许多专家学者针对这些问题进行改进. 文献[22]利用蝙蝠算法优化模型参数选择, 从负荷曲线形状以及距离相似性两个维度设计灰色关联模型以选取负荷相似日, 与单一BPNN等模型相比, RMSE降低了1.06%.
用户因地理位置、地域经济等情况不同导致用电负荷量产生较大差异, 主成分分析以及Pearson相关系数等常用方法具有一定的主观性. 针对该问题, 文献[23]利用最小二乘法、最小方差以及遗传算法等模型计算各因素权重, 利用加权方式得出影响因素的重要性排名, 结合径向基函数模型进行预测. 文献[24]构建新型随机嵌入式分布框架, 利用核密度估计法拟合多个神经网络预测结果形成概率密度函数, 结合期望估计法计算得到最终预测值, 适用于数据较少的情况, 并且BPNN结构与隐含层节点个数仍需通过反复试验确定. 文献[25]利用鲁棒性较强的CIM度量方式作为ANN的损失函数以减少噪声和异常值的影响.
2.4 支持向量机SVM[26]最早主要用于数据分类, 由于其良好的非线性数据处理能力, 也可被用于处理负荷预测问题. 与BPNN相比, SVM收敛速度快, 不存在网络层数与局部最优解的问题, 但针对复杂结构数据, 计算难度高, 模型较难实现. Chu等人[27, 28]利用决策树和加权平均法划分季节属性, 利用时间序列与SVM支持向量机针对不同变量进行预测, 呈现较好的预测效果. 文献[29]采用最小二乘支持向量机进行负荷预测, 并结合改进并行粒子群优化算法(improved particle swarm optimization, IPPSO)优化参数选择, 有效提高了数据处理效率与算法预测准确率. Wu等人[30]提出了一种面向预测成本的线性非对称损失函数, 对预测过高或过低实施不同惩罚措施, 同时充分优化LSSVM的不敏感参数, 大大降低了负荷预测的经济成本. 文献[31, 32]分别将经验小波变换、变分模式分解与LSSVM模型相结合, 在数据预处理阶段将数据分解, 合并所有子序列的预测结果, 以获得更满意的预测结果.
模式搜索算法(pattern search, PS)在局部搜索方面呈现较好的效果, 而萤火虫群优化(glowworm swarm optimization, GSO)算法则具有全局搜索能力, 文献[33]结合这两个算法的优点, 提出一种综合算法GSOPS, 并利用多层次粒度提高SVM的训练效率, 模型训练效率高, 但模型复杂, 构建有难度. 文献[34]在基础负荷预测的基础上引入实时电价, 利用加权灰色关联投影算法预测节假日负荷, PSO算法优化SVM模型参数用于预测基本负荷, 该模型更具有现实意义.
各种传统负荷预测模型受到历史数据影响较大, 并且考虑因素不全面, 导致预测准确度较低. 随着大数据的发展, 深度学习预测模型应运而生. 深度学习模型由于其强大的泛化能力和无监督学习等特征, 被广泛应用于图像识别、自然语言处理等领域[35]. 本文以CNN、LSTM、深度置信网络(deep belief network, DBN)以及集成学习与组合模型等多种预测算法为例, 简要介绍深度学习模型在短期负荷预测中的应用.
2.5 卷积神经网络CNN依赖卷积层从负荷数据中提取特征, 利用全连接层实现回归预测与分类. 最初CNN主要被用于图像处理, 但若将数据像图像一样以二维或三维表示时, 也可使用CNN进行处理数据预测. 如表1所示, 文献[36]结合CNN和K-means聚类的最佳特征, 开发了一种混合预测方法, 使用从电网获得的大数据集, 利用K-means算法将其聚类成子集, 获得的子集用于训练CNN, 最终将子集预测结果集成得到最终负荷预测结果. Sadaei等人[37]将多变量时间序列数据转换成多通道图像输入至CNN模型, 同时使用模糊空间、频谱等逻辑模型来表示时间序列的一维结构, 有效控制CNN的过拟合问题. 文献[38]以历史负荷为输入特征, 同时考虑数据时间序列分布, 降低负荷数据噪声误差和增强时间序列特性, 采用多时空尺度CNN (multi-temporal-spatial-scale temporal convolutional network, MTCN)处理负荷数据; 该方法可同时学习负荷数据的非线性特征和时间序列特征. Imani等人[39]将CNN应用到住宅负荷预测中, 利用非线性关系抽取方法(nonlinear relationship extraction, NRE)将历史负荷的附近两周前中后3天的同时刻负荷与温度数据抽取集成为一个负荷-温度立方体, 利用CNN二维卷积算子从邻域中提取负荷值之间的局部特征, 同时使用负荷温度立方体学习隐藏的非线性负荷温度特征来训练CNN模型; 结合高斯核SVR来最小化预测误差, 预测结果表明该方法具有优越的性能.
| 表 1 CNN模型在短期负荷预测中的应用 |
2.6 循环神经网络
RNN在负荷预测方面也做出了巨大贡献. 文献[42]针对家庭用电负荷预测中的波动性和不确定性问题, 将住宅消费者的负荷概况作为池化深度递归神经网络(pooling-based deep recurrent neural network, PDRNN)的输入, 直接对不确定性信息进行处理学习, 有效解决模型过拟合问题. RNN一般被用于离线学习, 每次训练都存在无法从新数据中及时学习新知识, 针对此问题, Fekri等人[43]利用RNN捕捉时间相关性, 并根据新数据更新RNN的权重, 自动调整RNN超参数以适应数据变化. 文献[44]则将RNN与一维CNN网络相结合, 提出了用于短期电力负荷预测的递归检验神经网络模型(recurrent inspection CNN, RICNN), 利用RNN学习电力负荷时间序列数据中存在的长期和短期时间相关性, CNN则处理负荷时间序列的谷峰特征, 与MLP模型相比, 有效提高了MAPE.
RNN通过共享所有时间步的参数来学习过去时刻的模式表示, 但随着时间的推移, 序列的增长使过去时刻的模式记忆逐渐消失, LSTM利用门控记忆单元可以将数据信息保持更长的时间, 并做出更好的预测. 文献[45]充分考虑能耗数据的周期性, 利用自相关性分析影响因素特征, 构建LSTM网络对序列数据进行建模和预测, 与ARMA、BPNN等传统模型相比, RMSE大幅度降低. 文献[46]则将LSTM应用到非住宅用户负荷预测上, 利用K-means分类挖掘用户能耗行为模式, 应用Spearman相关系数研究非住宅消费者在多个时间序列下的时间相关性, 最终设计提出一种基于多序列LSTM递归神经网络的非住宅负荷预测框架. 而针对住宅用户, 文献[47,48]利用负荷序列分解和基于互信息的多源输入数据重构双层特征方式处理住宅用户负荷数据, 引入自注意力机制(self-attention mechanism, SAM)为时间序列特征分配权重, 最终采用LSTM和SAM相结合的混合模型进行预测, 弥补了单一LSTM的不足. 针对个人用户负荷预测, 文献[49]则利用LSTM结合多分位数原理实现概率预测. Han等人[50]将时间序列划分为53组, 每层设计7个输入节点和1个输出节点; 将371个的日用电负荷数据点输入至具有53个神经元的全连接层, 全连接层的输出作为LSTM循环层的输入, 有效减少输入负荷序列的长度, 缓解了梯度消失问题. 面对高维海量特征数据, 文献[51]构建影响因素特征矩阵, 利用密度聚类将用户聚为2类, 利用3层BiLSTM对某地区未来一周的负荷进行预测.
除LSTM外, 门控循环单元(gate recurrent unit, GRU)也由于其超群的记忆学习能力而受到各专家学者的青睐. Du等人[52]建立具有时空相关性的历史负荷矩阵(historical load matrix, HLM), 利用3层CNN提取负荷数据特征, GRU则负责将序列映射到最终预测值. 用电负荷的影响因素不断叠加导致负荷序列非平稳性逐渐增强, 为提高负荷序列的稳定性, Gao等人[53]利用EMD将分离出负荷序列的不平稳因素, 采用Pearson分析序列相关性, 将相关性较高的序列输入GRU中进行预测; 而文献[54]则利用差分分解与误差补偿平滑负荷序列后利用GRU进行预测; 这两种方法均有效提高了模型精度. Eskandari等人[55]利用二维卷积层提取电力负荷矩阵的隐藏特征, 有效避免了卷积层中参数爆炸的问题, 其中卷积核大小由电力负载的自相关系数确定; 针对预测, 该模型充分利用LSTM和GRU网络的优点, LSTM单元用于前向传播, GRU单元用于反向传播, 以获得更高的预测精度. 表2展示了RNN模型在短期负荷预测中的应用.
| 表 2 RNN模型在短期负荷预测中的应用 |
2.7 其他深度学习模型
除CNN、LSTM、GRU等常用模型外, 还有部分其他深度学习模型也被应用于短期负荷预测中. 例如Dedinec等人[56]将多层受限玻尔兹曼机组成的深度信念网络(deep belief networks, DBN)用于负荷预测, 在逐层无监督训练后使用有监督反向传播训练方法微调模型参数, 同时引入电价变量, 有效提高了预测精度.
为降低由于复杂的网络结构和受限于确定性点预测而导致的计算成本问题, Dong等人[57]利用K近邻算法寻找与未来值相似的历史电力负荷时间序列特征, 采用DBN进行预测, 而文献[58]则利用纵横交叉算法(crisscross optimization, CSO)优化DBN, 利用互信息算法筛选影响因素, 这两种模型均表现出较好的性能.
Alipour等人[59]利用自动编码器与级联神经网络构建DNN模型进行负荷预测. 文献[60]同时考虑历史负荷与温度、阳光等气象数据, 利用梯度增强回归树(gradient boosting regression tree, GBRT)进行概率净负荷预测. 文献[61]研究光伏渗透率、季节性和负荷需求增加对净负荷预测间隔的影响, 采用分位数回归和动态高斯模型进行日负荷区间概率预测. 文献[62]采用相空间重构和BNN相结合进行短期净负荷预测.
深度学习模型可以更深层次的挖掘负荷数据集特征, 提高预测精确度, 但模型框架、参数选择仍然是亟待解决的难题.
2.8 集成学习与组合模型一直以来, 高稳定性和准确度都是模型训练所追求的目标, 但单一的模型训练结果往往不如人意. 为此各大专家学者将多个弱学习器组合成一个强学习器以期获得更好的效果[63], 即集成学习. Hu等人[64]提出了一种基于综合加权矢量角和基于移位的密度估计的多模态进化算法, 设计了包括预测性能评估、模型属性分析、结构和融合策略优化以及最优模型偏好选择的智能决策支持方案, 以改进基于随机向量函数链网络的集成学习模型.
目前应用比较广泛的是Bagging、AdaBoost、XGBoost、GBDT等集成学习模型. Bagging采用并行方式, 训练速度快, 但有放回抽样导致部分数据集取不到, 且每个学习器权重一致, 未考虑其重要性. AdaBoost采用串行方式运行, 可根据模型训练结果调整权重, 模型训练精度更高, 但弱学习器个数不好设定且训练比较耗时. 针对此问题, 文献[65]将决策树作为弱学习器构建随机森林(random forest, RF)模型进行负荷预测, 分别利用粗糙集、灰色投影技术、果蝇优化算法对模型进行优化, 均取得了较好的效果.
XGBoost算法采用二阶导, 提高了计算效率并有效减小过拟合问题, 但每次迭代运行都需遍历整个数据集, 不适合处理较大数据集, 对内存也有较高的要求. 为解决此问题, 文献[66]利用集成学习的stacking技术将XGBoost与轻量级梯度提升树(light gradient boosting machine, LGBM)、多层感知机MLP三个模型组合用于负荷预测, 表现出较好的性能优势. 孙超等人[67]构建筛选特征集的数据处理层以及优化参数选择的负荷预测层的双层XGBoost模型结构, 该模型将第1层筛选得到的特征集与负荷作为第2层的输入, 有效避免特征数据相互依赖的问题.
除以上集成学习模型外, 部分专家还将SVM、神经网络、集成学习等算法集成进行组合预测(如表3所示). Malekizadeh等人[68]将电力系统划分为若干小区域, 利用模糊神经网络(fuzzy neural network, FNN)、SVM等多个算法分别预测单个区域的用电负荷, 采用局部线性模型树(locally linear model tree, LOLIMOT)方式将小区域的预测结果组合, 结合模糊推理灵活设置网络拓扑结构, 更加有效的提取负荷分布趋势. 文献[69]将CNN与RF结合使用, 有效减小了MAPE. 针对数据特征少导致的预测低精度问题, Tian等人[70]利用CNN提取用户用电负荷局部趋势, 结合LSTM模型进行预测. 陈振宇等人[71, 72]则利用误差倒数法(MAPE-reciprocal weight, MAPE-RW)选取模型组合最佳权重, 将XGBoost与LSTM模型预测的时序数据进行加权组合, 有效降低了单一模型的预测误差. Zhang等人[73]利用CNN提取数据特征, Seq2Seq对用户用能负荷进行预测, 同时引入注意机制和多任务学习方法来提高负荷预测的准确性. Nie等人[74]将数据预处理、多目标优化、模型预测以及模型评估组合成一个新型负荷预测系统, 利用EMD将负荷数据分解, 结合RBF、ELM与GRNN三种预测模型进行预测, 将结果加权形成最终预测值.
| 表 3 组合模型在短期负荷预测中的应用 |
研究发现, 基于深度学习的预测算法已成功解决了大多数负荷预测分析问题, 组合模型在性能与准确性方面表现都要优于单一模型, 挖掘深度学习模型的更多组合方式是未来的研究热点.
3 实验分析为进一步分析各预测模型的优缺点, 本文利用2个国外负荷数据与2个国内负荷数据进行实验对比, 选取较为典型的SVM[27, 28]、LSTM[49]、Bagging[65]、XGBoost[67]等模型进行实验, 国外数据集包括2016年国外建筑能耗数据(energydata)[75]以及2019年比利时负荷数据集(Elia_data)[76]; 国内数据集包括2016年电工数学建模竞赛负荷预测数据集(math_load)与2014年上海市真实用电数据集(2014_上海). 4种电力负荷数据属性如表4所示.
| 表 4 实验测试数据集 |
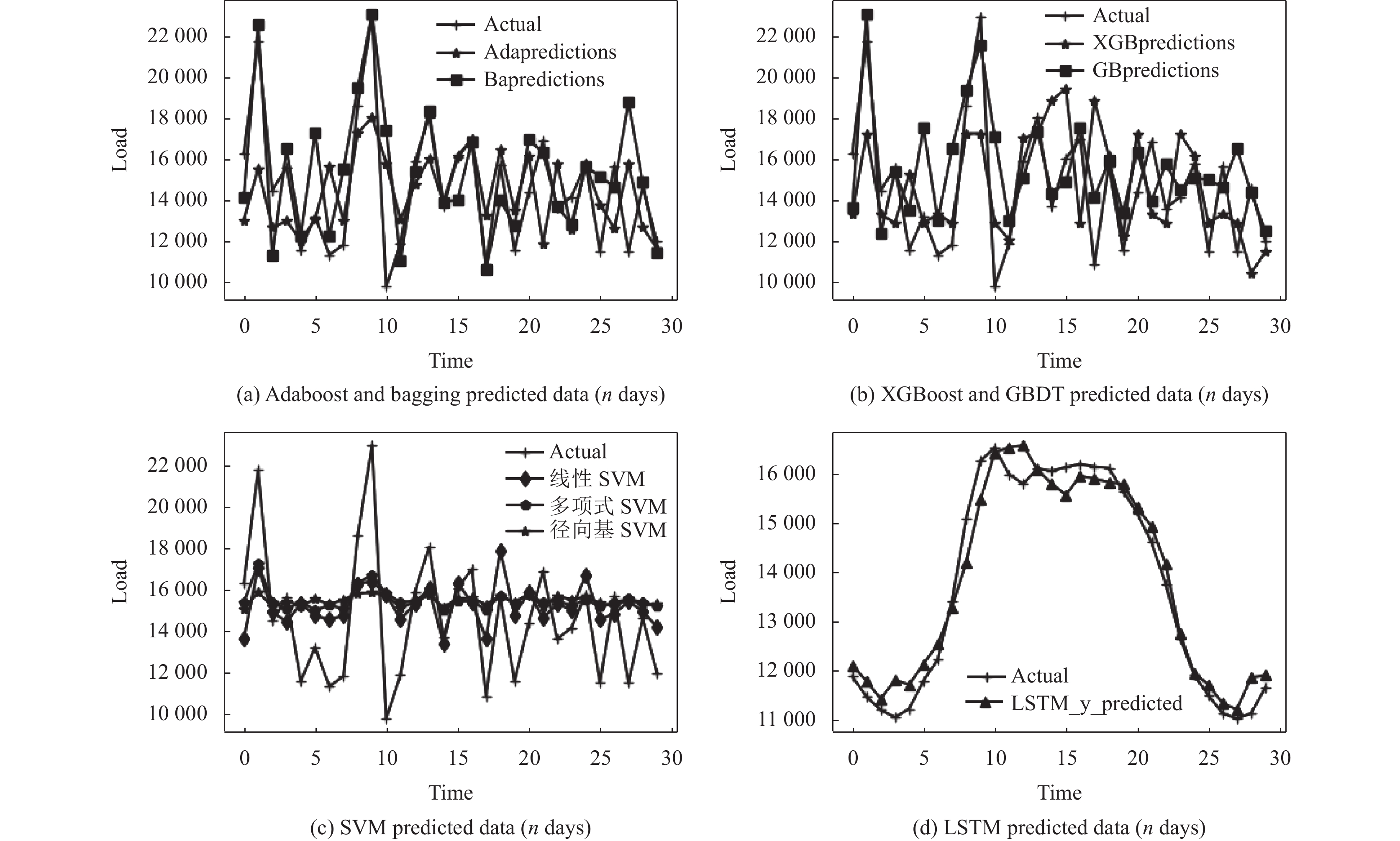
为精确对比各模型优缺点, 统一划分数据集, 选取前80%为训练数据集, 后20%为测试数据集, 本实验基于Python 3.8进行. 6种常用的负荷预测模型预测值与用户用电真实值的对比图1所示.
|
图 1 各模型预测值与真实值对比图 |
图1由4个子图组成, 图1(a)–图1(d)分别代表AdaBoost与Bagging模型、XGBoost与GBDT模型、选取3种核函数的SVM模型以及LSTM模型. 由图可知, Bagging、GBDT以及LSTM等负荷预测模型的数值拟合度较高, 而Adaboost与XGBoost的拟合度有待提高. 由于SVM处理数据的局限性, 使得该模型的拟合度表现较差.
6种常用模型的运行结果的MAPE与运行时间(运行10次取均值)如表5和表6所示. 由实验结果可知, Bagging模型泛化能力较好, 适用于各种大小的数据集, 并且预测效果也较为可观. 与Bagging模型相比, AdaBoost运行时间较长, 精确度也有待提高. 针对小数据集, 各个集成学习表现都较为稳定. 但针对高维稀疏数据, 例如energydata数据集, GBDT的预测效果有待提高.
综合看来, Bagging模型与AdaBoost模型具有很高的泛化能力, 适合处理各种数据集. XGBoost预测效果较好, 但其对内存需求大, 不适合处理大规模数据集. 而GBDT训练速度快, 但对高维稀疏数据集的处理存在一定的局限. LSTM模型预测效果较好, 但模型参数的选择对预测结果影响较大.
| 表 5 部分预测模型的MAPE比较 (%) |
| 表 6 部分模型的运行时间比较(ms) |
4 结论与展望
随着信息时代的高速发展, 负荷预测已经成为电力系统领域不可或缺的重要部分[1]. 本文简单介绍了有关负荷预测的传统预测方法与基于深度学习的智能预测算法, 可发现传统负荷预测算法速度快、模型简单, 对于非线性数据处理存在一定局限[16,19,20]. 基于深度学习的智能化预测算法因其泛化能力强、自学习能力高等优点被各大专家青睐, 但也存在模型复杂、过拟合、局部最优解等问题[35]. 模型组合策略、权重参数设置问题则成为集成学习模型发展的阻碍.
在实际应用中, 短期电力负荷预测在以下方面仍有待发展:
(1)随着智能化设备的发展, 可获取的负荷数据影响因素越来越多, 但由于服务提供商出于安全考虑, 对实时和历史数据保密, 高质量的标记数据仍然缺乏, 利用传感器获取的数据存在重复、错误标记以及数据流的暂时丢失等问题, 因此高效可靠的数据预处理在负荷预测中变得尤为重要[14].
(2)传统模型与智能化模型各有优点, 如何利用各个模型的优点, 扬长避短, 提高模型的准确率仍是目前的研究热点[55,59,60].
(3)目前电力负荷预测涉及训练数据的准确性和完整性、深度学习模型及其性能限制等多个不确定度的量化问题. 不确定性的量化问题对于提高深度学习模型的可靠性与准确性具有重要意义.
(4)无人机、电动汽车、可再生能源的发展都使电力系统变得庞大而复杂, 挖掘更深层次的影响因素、考虑更接近实际情况的用电负荷是未来努力方向.
| [1] |
曾鸣, 张硕. “十四五”电力规划的综合能源发展探析. 中国电力企业管理, 2020(13): 26-28. DOI:10.3969/j.issn.1007-3361.2020.13.006 |
| [2] |
International Renewable Energy Agency. Renewable energy statistics 2020. https://www.irena.org/publications/2020/Jul/Renewable-energy-statistics-2020. (2020-07-01) [2021-11-11].
|
| [3] |
国家能源局. 2019上半年光伏发电建设运行情况. http://www.nea.gov.cn/2019-08/23/c_138330885.htm. (2019-08-23) [2021-11-11].
|
| [4] |
康重庆, 夏清, 刘梅. 电力系统负荷预测. 第2版, 北京: 中国电力出版社, 2017.
|
| [5] |
Li YT, Su Y, Shu LJ. An ARMAX model for forecasting the power output of a grid connected photovoltaic system. Renewable Energy, 2014, 66: 78-89. DOI:10.1016/j.renene.2013.11.067 |
| [6] |
Bikcora C, Verheijen L, Weiland S. Density forecasting of daily electricity demand with ARMA-GARCH, CAViaR, and CARE econometric models. Sustainable Energy, Grids and Networks, 2018, 13: 148-156. DOI:10.1016/j.segan.2018.01.001 |
| [7] |
Wu F, Cattani C, Song WQ, et al. Fractional ARIMA with an improved cuckoo search optimization for the efficient Short-term power load forecasting. Alexandria Engineering Journal, 2020, 59(5): 3111-3118. DOI:10.1016/j.aej.2020.06.049 |
| [8] |
Khashei M, Chahkoutahi F. A comprehensive low-risk and cost parallel hybrid method for electricity load forecasting. Computers & Industrial Engineering, 2021, 155: 107182. |
| [9] |
Aly HHH. A proposed intelligent short-term load forecasting hybrid models of ANN, WNN and KF based on clustering techniques for smart grid. Electric Power Systems Research, 2020, 182: 106191. DOI:10.1016/j.jpgr.2019.106191 |
| [10] |
王奔, 冷北雪, 张喜海, 等. 支持向量机在短期负荷预测中的应用概况. 电力系统及其自动化学报, 2011, 23(4): 115-121. DOI:10.3969/j.issn.1003-8930.2011.04.022 |
| [11] |
Khwaja AS, Anpalagan A, Naeem M, et al. Joint bagged-boosted artificial neural networks: Using ensemble machine learning to improve short-term electricity load forecasting. Electric Power Systems Research, 2020, 179: 106080. DOI:10.1016/j.jpgr.2019.106080 |
| [12] |
Moon J, Jung S, Rew J, et al. Combination of short-term load forecasting models based on a stacking ensemble approach. Energy and Buildings, 2020, 216: 109921. DOI:10.1016/j.enbuild.2020.109921 |
| [13] |
Chahkoutahi F, Khashei M. A seasonal direct optimal hybrid model of computational intelligence and soft computing techniques for electricity load forecasting. Energy, 2017, 140: 988-1004. DOI:10.1016/j.energy.2017.09.009 |
| [14] |
夏博, 杨超, 李冲. 电力系统短期负荷预测方法研究综述. 电力大数据, 2018, 21(7): 22-28. |
| [15] |
Alkhayat G, Mehmood R. A review and taxonomy of wind and solar energy forecasting methods based on deep learning. Energy and AI, 2021, 4: 100060. DOI:10.1016/j.egyai.2021.100060 |
| [16] |
王宝财. 基于温度近因效应的多元线性回归电力负荷预测. 水电能源科学, 2018, 36(10): 201-205. |
| [17] |
Box GEP, Jenkins GM. Time Series Analysis: Forecasting and Control. San Francisco: Holden-Day, 1976. 238–242.
|
| [18] |
Boroojeni KG, Amini MH, Bahrami S, et al. A novel multi-time-scale modeling for electric power demand forecasting: From short-term to medium-term horizon. Electric Power Systems Research, 2017, 142: 58-73. DOI:10.1016/j.jpgr.2016.08.031 |
| [19] |
Wang JZ, Du P, Lu HY, et al. An improved grey model optimized by multi-objective ant lion optimization algorithm for annual electricity consumption forecasting. Applied Soft Computing, 2018, 72: 321-337. DOI:10.1016/j.asoc.2018.07.022 |
| [20] |
李啸骢, 李春涛, 从兰美, 等. 基于动态权值相似日选取算法的短期负荷预测. 电力系统保护与控制, 2017, 45(6): 1-8. DOI:10.7667/PSPC160412 |
| [21] |
Dietrich B, Walther J, Weigold M, et al. Machine learning based very short term load forecasting of machine tools. Applied Energy, 2020, 276: 115440. DOI:10.1016/j.apenergy.2020.115440 |
| [22] |
吴云, 雷建文, 鲍丽山, 等. 基于改进灰色关联分析与蝙蝠优化神经网络的短期负荷预测. 电力系统自动化, 2018, 42(20): 67-72. DOI:10.7500/AEPS20180125004 |
| [23] |
邹京希, 曹敏, 董立军, 等. 基于总体测辨和人工神经网络的负荷建模及预测方法. 电力系统及其自动化学报, 2018, 30(8): 108-112. DOI:10.3969/j.issn.1003-8930.2018.08.018 |
| [24] |
李国庆, 刘钊, 金国彬, 等. 基于随机分布式嵌入框架及BP神经网络的超短期电力负荷预测. 电网技术, 2020, 44(2): 437-444. |
| [25] |
蔡秋娜, 潮铸, 苏炳洪, 等. 基于一种新型鲁棒损失的神经网络短期负荷预测方法. 电网技术, 2020, 44(11): 4132-4139. |
| [26] |
王霞, 董永权, 于巧, 等. 结构化支持向量机研究综述. 计算机工程与应用, 2020, 56(17): 24-32. |
| [27] |
Chu YY, Xu P, Li MX, et al. Short-term metropolitan-scale electric load forecasting based on load decomposition and ensemble algorithms. Energy and Buildings, 2020, 225: 110343. DOI:10.1016/j.enbuild.2020.110343 |
| [28] |
Ghelardoni L, Ghio A, Anguita D. Energy load forecasting using empirical mode decomposition and support vector regression. IEEE Transactions on Smart Grid, 2013, 4(1): 549-556. DOI:10.1109/TSG.2012.2235089 |
| [29] |
王保义, 王冬阳, 张少敏. 基于Spark和IPPSO_LSSVM的短期分布式电力负荷预测算法. 电力自动化设备, 2016, 36(1): 117-122. |
| [30] |
Wu JR, Wang YG, Tian YC, et al. Support vector regression with asymmetric loss for optimal electric load forecasting. Energy, 2021, 223: 119969. DOI:10.1016/j.energy.2021.119969 |
| [31] |
Zhang ZC, Hong WC. Application of variational mode decomposition and chaotic grey wolf optimizer with support vector regression for forecasting electric loads. Knowledge-Based Systems, 2021, 228: 107297. DOI:10.1016/j.knosys.2021.107297 |
| [32] |
张金金, 张倩, 马金辉, 等. 基于EWT和LSSVM模型的短期电力负荷预测. 制造业自动化, 2021, 43(1): 38-42. DOI:10.3969/j.issn.1009-0134.2021.01.010 |
| [33] |
唐承娥, 韦军. 改进的支持向量回归机在电力负荷预测中的应用. 计算机科学, 2020, 47(S1): 58-65. |
| [34] |
Dai YM, Zhao P. A hybrid load forecasting model based on support vector machine with intelligent methods for feature selection and parameter optimization. Applied Energy, 2020, 279: 115332. DOI:10.1016/j.apenergy.2020.115332 |
| [35] |
朱俊丞, 杨之乐, 郭媛君, 等. 深度学习在电力负荷预测中的应用综述. 郑州大学学报(工学版), 2019, 40(5): 12-21. |
| [36] |
Dong XS, Qian LJ, Huang L. Short-term load forecasting in smart grid: A combined CNN and K-means clustering approach. Proceedings of 2017 IEEE International Conference on Big Data and Smart Computing. Jeju: IEEE, 2017. 119–125.
|
| [37] |
Sadaei HJ, de Lima e Silva PC, Guimarães FG, et al. Short-term load forecasting by using a combined method of convolutional neural networks and fuzzy time series. Energy, 2019, 175: 365-377. DOI:10.1016/j.energy.2019.03.081 |
| [38] |
Yin LF, Xie JX. Multi-temporal-spatial-scale temporal convolution network for short-term load forecasting of power systems. Applied Energy, 2021, 283: 116328. DOI:10.1016/j.apenergy.2020.116328 |
| [39] |
Imani M. Electrical load-temperature CNN for residential load forecasting. Energy, 2021, 227: 120480. DOI:10.1016/j.energy.2021.120480 |
| [40] |
Makonin S, Ellert B, Bajić IV, et al. Electricity, water, and natural gas consumption of a residential house in Canada from 2012 to 2014. Scientific Data, 2016, 3: 160037. DOI:10.1038/sdata.2016.37 |
| [41] |
Smart* Data Set for Sustainability. UMass Smart* dataset-2017 release. http://traces.cs.umass.edu/index.php/Smart/Smart. (2021-11-28).
|
| [42] |
Smart Grids. New smart grids study findings reported from university of bath (deep learning for household load forecasting—A novel pooling deep RNN). Journal of Technology & Science, 2018.
|
| [43] |
Fekri MN, Patel H, Grolinger K, et al. Deep learning for load forecasting with smart meter data: Online adaptive recurrent neural network. Applied Energy, 2021, 282: 116177. DOI:10.1016/j.apenergy.2020.116177 |
| [44] |
Kim J, Moon J, Hwang E, et al. Recurrent inception convolution neural network for multi short-term load forecasting. Energy and Buildings, 2019, 194: 328-341. DOI:10.1016/j.enbuild.2019.04.034 |
| [45] |
Wang JQ, Du Y, Wang J. LSTM based long-term energy consumption prediction with periodicity. Energy, 2020, 197: 117197. DOI:10.1016/j.energy.2020.117197 |
| [46] |
Networks. New networks findings from North China Electric Power University discussed (short-term non-residential load forecasting based on multiple sequences LSTM recurrent neural network). Computers Networks & Communications, 2019.
|
| [47] |
Zang HX, Xu RQ, Cheng LL, et al. Residential load forecasting based on LSTM fusing self-attention mechanism with pooling. Energy, 2021, 229: 120682. DOI:10.1016/j.energy.2021.120682 |
| [48] |
Smart Grids. Investigators from University of New South Wales release new data on smart grids (short-term residential load forecasting based on LSTM recurrent neural network). Computers Networks & Communications, 2019.
|
| [49] |
Wang Y, Gan DH, Sun MY, et al. Probabilistic individual load forecasting using pinball loss guided LSTM. Applied Energy, 2019, 235: 10-20. DOI:10.1016/j.apenergy.2018.10.078 |
| [50] |
Han LY, Peng YX, Li YH, et al. Enhanced deep networks for short-term and medium-term load forecasting. IEEE Access, 2018, 7: 4045-4055. |
| [51] |
杨龙, 吴红斌, 丁明, 等. 新能源电网中考虑特征选择的Bi-LSTM网络短期负荷预测. 电力系统自动化, 2021, 45(3): 166-173. |
| [52] |
Du LF, Zhang LH, Wang X. Spatiotemporal feature learning based hour-ahead load forecasting for energy internet. Electronics, 2020, 9(1): 196. DOI:10.3390/electronics9010196 |
| [53] |
Gao X, Li XB, Zhao B, et al. Short-term electricity load forecasting model based on EMD-GRU with feature selection. Energies, 2019, 12(6): 1140. DOI:10.3390/en12061140 |
| [54] |
王增平, 赵兵, 贾欣, 等. 基于差分分解和误差补偿的短期电力负荷预测方法. 电网技术, 2021, 45(7): 2560-2568. |
| [55] |
Eskandari H, Imani M, Moghaddam MP. Convolutional and recurrent neural network based model for short-term load forecasting. Electric Power Systems Research, 2021, 195: 107173. DOI:10.1016/j.jpgr.2021.107173 |
| [56] |
Dedinec A, Filiposka S, Dedinec A, et al. Deep belief network based electricity load forecasting: An analysis of Macedonian case. Energy, 2016, 115: 1688-1700. DOI:10.1016/j.energy.2016.07.090 |
| [57] |
Dong YX, Ma XJ, Fu TL. Electrical load forecasting: A deep learning approach based on K-nearest neighbors. Applied Soft Computing, 2021, 99: 106900. DOI:10.1016/j.asoc.2020.106900 |
| [58] |
吴伟杰, 吴杰康, 雷振, 等. 基于CSO优化深度信念网络的园区能源需求预测方法. 电网技术, 2021, 45(10): 3859-3868. |
| [59] |
Alipour M, Aghaei J, Norouzi M, et al. A novel electrical net-load forecasting model based on deep neural networks and wavelet transform integration. Energy, 2020, 205: 118106. DOI:10.1016/j.energy.2020.118106 |
| [60] |
Wang Y, Zhang N, Chen QX, et al. Data-driven probabilistic net load forecasting with high penetration of behind-the-meter PV. IEEE Transactions on Power Systems, 2018, 33(3): 3255-3264. DOI:10.1109/TPWRS.2017.2762599 |
| [61] |
van der Meer DW, Munkhammar J, Widén J. Probabilistic forecasting of solar power, electricity consumption and net load: Investigating the effect of seasons, aggregation and penetration on prediction intervals. Solar Energy, 2018, 171: 397-413. DOI:10.1016/j.solener.2018.06.103 |
| [62] |
Mei F, Wu QL, Shi T, et al. An ultrashort-term net load forecasting model based on phase space Reconstruction and deep neural network. Applied Sciences, 2019, 9(7): 1487. DOI:10.3390/app9071487 |
| [63] |
史佳琪, 张建华. 基于多模型融合Stacking集成学习方式的负荷预测方法. 中国电机工程学报, 2019, 39(14): 4032-4041. |
| [64] |
Hu Y, Qu BY, Wang J, et al. Short-term load forecasting using multimodal evolutionary algorithm and random vector functional link network based ensemble learning. Applied Energy, 2021, 285: 116415. DOI:10.1016/j.apenergy.2020.116415 |
| [65] |
吴潇雨, 和敬涵, 张沛, 等. 基于灰色投影改进随机森林算法的电力系统短期负荷预测. 电力系统自动化, 2015, 39(12): 50-55. DOI:10.7500/AEPS20140916005 |
| [66] |
Massaoudi M, Refaat SS, Chihi I, et al. A novel stacked generalization ensemble-based hybrid LGBM-XGB-MLP model for short-term load forecasting. Energy, 2021, 214: 118874. DOI:10.1016/j.energy.2020.118874 |
| [67] |
孙超, 吕奇, 朱思曈, 等. 基于双层XGBoost算法考虑多特征影响的超短期电力负荷预测. 高电压技术, 2021, 47(8): 2885-2895. |
| [68] |
Malekizadeh M, Karami H, Karimi M, et al. Short-term load forecast using ensemble neuro-fuzzy model. Energy, 2020, 196: 117127. DOI:10.1016/j.energy.2020.117127 |
| [69] |
肖玉东. 基于随机森林与卷积神经网络的电力负荷预测研究. 计算技术与自动化, 2020, 39(3): 13-16. |
| [70] |
Tian CJ, Ma J, Zhang CH, et al. A deep neural network model for short-term load forecast based on long short-term memory network and convolutional neural network. Energies, 2018, 11(12): 3493. DOI:10.3390/en11123493 |
| [71] |
陈振宇, 刘金波, 李晨, 等. 基于LSTM与XGBoost组合模型的超短期电力负荷预测. 电网技术, 2020, 44(2): 614-620. |
| [72] |
庄家懿, 杨国华, 郑豪丰, 等. 基于多模型融合的CNN-LSTM-XGBoost短期电力负荷预测方法. 中国电力, 2021, 54(5): 46-55. |
| [73] |
Zhang G, Bai XQ, Wang YX. Short-time multi-energy load forecasting method based on CNN-Seq2Seq model with attention mechanism. Machine Learning with Applications, 2021, 5: 100064. DOI:10.1016/j.mlwa.2021.100064 |
| [74] |
Nie Y, Jiang P, Zhang HP. A novel hybrid model based on combined preprocessing method and advanced optimization algorithm for power load forecasting. Applied Soft Computing, 2020, 97: 106809. DOI:10.1016/j.asoc.2020.106809 |
| [75] |
Candanedo LM, Feldheim V, Deramaix D. Data driven prediction models of energy use of appliances in a low-energy house. Energy and Buildings, 2017, 140: 81-97. DOI:10.1016/j.enbuild.2017.01.083 |
| [76] |
Elia. Load and load forecast. https://www.elia.be/en/grid-data/load-and-load-forecasts. (2021-11-28).
|
 2022, Vol. 31
2022, Vol. 31



