2. 南京航空航天大学 高安全系统的软件开发与验证技术工业和信息化部重点实验室, 南京 211106;
3. 南京大学 软件新技术与产业化协同创新中心, 南京 210093
2. Key Laboratory of Safety-critical Software, Ministry of Industry and Information Technology, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China;
3. Collaborative Innovation Center of Novel Software Technology and Industrialization, Nanjing University, Nanjing 210093, China
近年来, 互联网应用的逐步普及, 带来便利的同时, 大量数据信息通过个人用户、企业单位、研究机构等源源不断地产生. 对产生的数据进行数据分析, 挖掘事物潜在的关联, 再反馈给互联网应用商, 可以为大众提供更好的服务. 然而, 这些数据中不乏个人隐私数据, 诸如医疗信息、金融信息、轨迹数据等, 直接向外界发布原始数据存在着巨大的隐私泄露风险. 因此, 对外发布数据时, 需要采取一些隐私保护措施来保障数据安全.
K-匿名[1]及其相关扩展L-Diversity[2]、T-closeness[3]是隐私保护的重要方法, 其主要思想是将待发布数据划分为多个等价类, 等价类内的k个实体无法相互区分, 通过限制数据发布实现数据隐私保护. 然而, 一旦攻击者具有相当的背景知识, K-匿名就无法提供很好的隐私保护效果, 而且无法就其隐私保护程度进行定量分析. 差分隐私[4-9]作为一种严格可证的新兴隐私保护模型, 其前提是假设数据攻击者具有的背景知识最大化. 通过向输出中添加随机扰动, 尽可能减小单个记录对输出的影响, 保证攻击者无法通过观察不同的输出结果重构真实的数据信息, 实现了单个记录是否参与数据集的不可区分性.
从已有的研究可以看出, 差分隐私在低维数据发布方面做了诸多努力, 但在实际场景中, 更为常见的却是多属性数据集, 即高维数据集. 如果将以往的低维数据发布算法直接应用于多属性数据发布, 存在查询敏感度大、隐私预算消耗过快等问题, 导致数据发布效用低.
针对高维数据发布场景, 常见方法有: 1) 根据树结构划分高维数据集, 通过平衡分区的近似误差和数据的扰动误差来提高数据发布精度; 2) 通过构建数据集的概率图模型计算属性间的条件分布, 通过噪声条件分布近似原始数据集的联合分布, 以此生成新的合成数据集, 避免直接对原始数据扰动产生巨大的扰动误差; 3) 利用数据降维技术, 将高维数据转化成近似的低维数据, 对转化后的低维数据添加噪声扰动, 减少扰动噪声量.
在利用树结构发布高维数据集的研究中, 文献[10]借助细粒度单元划分和kd-树划分两种分区策略, 实现了差分隐私多维直方图发布. 文献[11]利用kd-树和quad-tree设计混合数据结构实现多维数据划分, 从而减少了注入的噪声量. 文献[12]提出了差分隐私泛化数据发布算法DiffGen, 通过构建决策树的过程完成数据的差分隐私保护. 基于概率图模型的研究也有所成果, 文献[13]提出数据发布方案PrivBayes, 该方案通过构建原始数据集的贝叶斯网络模型, 分析原始数据属性之间的依赖关系, 学习提取近似噪声条件分布, 采样生成新的合成数据集. 文献[14]提出联合树算法Jtree, 根据样本数据属性之间的关联构建依赖关系图, 结合联合树的推理基础, 从边缘关系图中学习一组噪声边缘表, 以此近似原始数据集的联合分布. 通过数据降维来近似高维数据发布的研究中, 文献[15, 16] 利用主成分分析技术识别高维数据的近似低维, 实现了高维数据向低维的转化, 并基于低维数据实现差分隐私保护. 文献[17]提出了差分隐私数据发布算法DPPro, 该算法利用随机投影技术, 完成高维数据在低维上的映射, 保证了高维数据发布效用. 文献[18]提出PriView方法, 通过构建一组含噪声扰动的低维View视图, 提取
然而, 前文提到的各种方法对不同属性的隐私保护处理大多隐含地假设同构性, 即不考虑属性数据敏感性的异构, 不同属性的随机干扰程度均相同. 由于不同属性携带的信息量不同, 从而对攻击者推理目标对象隐私信息的贡献不同, 即隐私泄露风险与属性敏感性呈正相关. 例如, 性别属性只有两个属性值, 与年龄属性相比, 携带的信息量更少, 对目标对象的刻画程度较浅, 对攻击者推理敏感信息的贡献较少, 需要的隐私保护强度相对较低, 相应的属性敏感性也就较低. 不考虑属性信息量差异带来的敏感性异构, 会导致没有充分保护高敏感属性数据, 或者过度丢失低敏感属性数据的信息.
文献[19]提出了一种加权贝叶斯网络数据发布方法, 虽然该方法是根据属性的多样性分配权重, 但其目标是借助属性权重构建更好的贝叶斯网络. 文献[20, 21]均在基于贝叶斯网络的数据发布算法中引入属性聚类, 以属性关联强弱分割属性集, 在减少隐私预算分割次数的基础上提高算法计算效率. 然而, 两者在隐私预算的分配上依然采取等分措施, 没有兼顾属性敏感性差异.
针对已有方法的不足之处, 本文提出了一种基于属性分割的差分隐私异构多属性数据发布算法HMPrivBayes (heterogeneous multi-attribute private data publishing via Bayesian networks), 主要贡献包括以下3个方面:
1) 根据属性之间的关联程度, 引入最大信息系数量化属性之间的相关关系, 设计满足差分隐私的谱聚类算法分割属性集, 能在一定程度上缩减贝叶斯网络结构空间, 提高算法计算效率.
2) 针对构建贝叶斯网络随机选取首个属性可能降低数据发布质量的问题, 以属性信息熵为权重选择属性, 尽可能提高数据发布质量, 保留数据实用价值.
3) 考虑到属性携带的信息量的不同, 基于贝叶斯网络提取属性条件分布时, 以属性归一化风险熵为权重分配隐私预算, 实现异构多属性保护.
2 基础知识 2.1 差分隐私差分隐私(differential privacy, DP)保护模型保证在数据集中对一条记录进行增、删、改操作后, 查询返回的扰动输出没有明显差异, 以至于攻击者不能推断出目标记录是否在发布的数据集中, 即数据集中单个记录对输出的影响有限, 从而实现保护个体隐私.
定义1.
| Pr(M(D1)∈S)Pr(M(D2)∈S)⩽exp(ε) | (1) |
则称算法
任何满足定义1的噪音机制都可以视为差分隐私机制, 差分隐私中常见噪音机制有Laplace机制[22]和指数机制[23], 其噪声扰动大小与随机函数的敏感度以及隐私预算参数密切相关.
定义2. 全局敏感度[5]. 设查询函数
| Δf=maxD1,D2||f(D1)−f(D2)|| | (2) |
其中,
定义3. Laplace机制[22]. 对任意数据集
| M(D)=f(D)+Lap(Δf/ε) | (3) |
则算法
定义4. 指数机制[23]. 对任意数据集
| M(D,u)={r|Pr[r∈O]∝exp(εu(D,r)2Δu)} | (4) |
则算法
对于一组满足差分隐私的随机独立算法, 差分隐私的串行组合性质和并行组合性质[24]可以用于证明整体算法满足差分隐私保护.
性质1. 串行组合[24]. 给定数据集
串行组合表明, 当一系列差分隐私机制应用于同一数据集时, 隐私预算和噪声数量呈线性累积.
性质2. 并行组合[24]. 给定数据集
并行组合表明, 当一系列差分隐私机制应用于数据集的不同子集时, 隐私保护的程度取决于
谱聚类(spectral clustering, SC)[25]是利用图论中的图分割完成数据聚类的算法. 它的主要思想是先将数据集映射成一张带权无向图, 基于两点之间的距离计算顶点相似度, 通过最优划分准则分割图中结点, 最大化子图内部的相似度, 实现数据聚类. 标准的谱聚类算法实现流程如算法1所示.
算法1. 谱聚类算法
输入: 数据集
输出: 簇划分
1. 计算n×n的相似矩阵S:
2. 根据相似矩阵S构建邻接矩阵W:
3. 计算n×n的度矩阵B:
4. 计算并标准化拉普拉斯矩阵
5. 计算L最小的k1个特征值以及各自对应的特征向量
6. 将特征向量组成矩阵并按行进行标准化, 最终组成n×k1维的特征矩阵U;
7. 将U中的每一行作为一个k1维的样本, 按照输入的聚类方式进行聚类, 聚类维数为k;
8. 返回簇划分
在本文中, 谱聚类主要用于属性聚类, 即根据属性之间的关联程度分割属性集. 本文选用最大信息系数(maximal information coefficient, MIC)[26]度量属性之间关联程度. 在此之前, 互信息是常用的属性关联度量手段, 然而, 互信息需要考虑连续属性的离散化, 而且不同数据集上的互信息计算结果无法相互比较. MIC利用网格划分属性值域, 结合属性互信息, 可以更准确地识别出大数据集中属性间的线性或非线性关系, 以及非函数依赖关系.
定义5. 最大信息系数[26]. 给定属性
| MIC\left( {X, Y} \right) = \mathop {\max }\limits_{a \times b < B} \frac{{I\left( {X, Y} \right)}}{{{{\log }_2}\min \left( {a, b} \right)}} | (5) |
其中,
| I\left( {X, Y} \right) = \sum\nolimits_{i = 1}^n {\sum\nolimits_{j = 1}^m {Pr ( {{x_i}, {y_j}} )} } \log \frac{{Pr ( {{x_i}, {y_j}} )}}{{Pr ( {{x_i}} )Pr ( {{y_j}} )}} | (6) |
其中,
贝叶斯网络(Bayesian network)是常用的概率图模型之一, 用来表示一组随机变量(属性)之间的依赖关系. 形式上, 贝叶斯网络
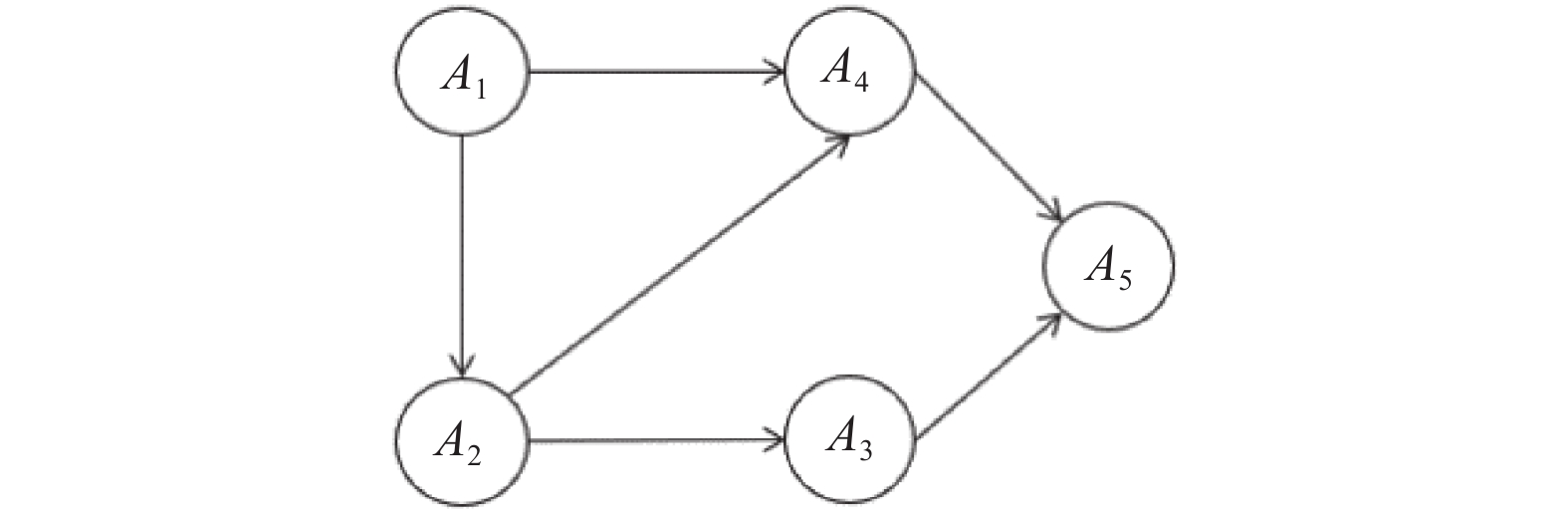
|
图 1 含5个节点的贝叶斯网络示例 |
3 基于属性分割的差分隐私异构多属性数据发布 3.1 HMPrivBayes算法概述
HMPrivBayes算法的整体流程如图2所示, 包括4个阶段: 属性聚类划分、构建差分隐私贝叶斯网络、生成属性加噪条件分布、生成待发布数据集. 为了方便描述, 本文假设所有属性均是二进制属性. 对于非二进制属性, 利用文献[13]提出的等宽法将非二进制属性转化成一组二进制属性. 由于等宽法的转化过程只依赖非二进制属性的值域, 且属性的值域是公开信息, 不涉及隐私数据. 因此, 属性转化过程不存在隐私泄露问题.
HMPrivBayes算法的实现过程如算法2所示.
算法2. HMPrivBayes算法
输入: 数据集
输出: 数据集D满足差分隐私的合成数据集D′
1. 初始化D′=
2. 分配隐私预算ε1+ε2+ε3=ε;
3. 执行算法3, 返回聚类结果
4. 依据C划分原始数据集
5. for i=1 to k do
执行算法4, 求贝叶斯网络Ni;
基于
执行算法5, 求带噪条件分布
end for
6. 返回
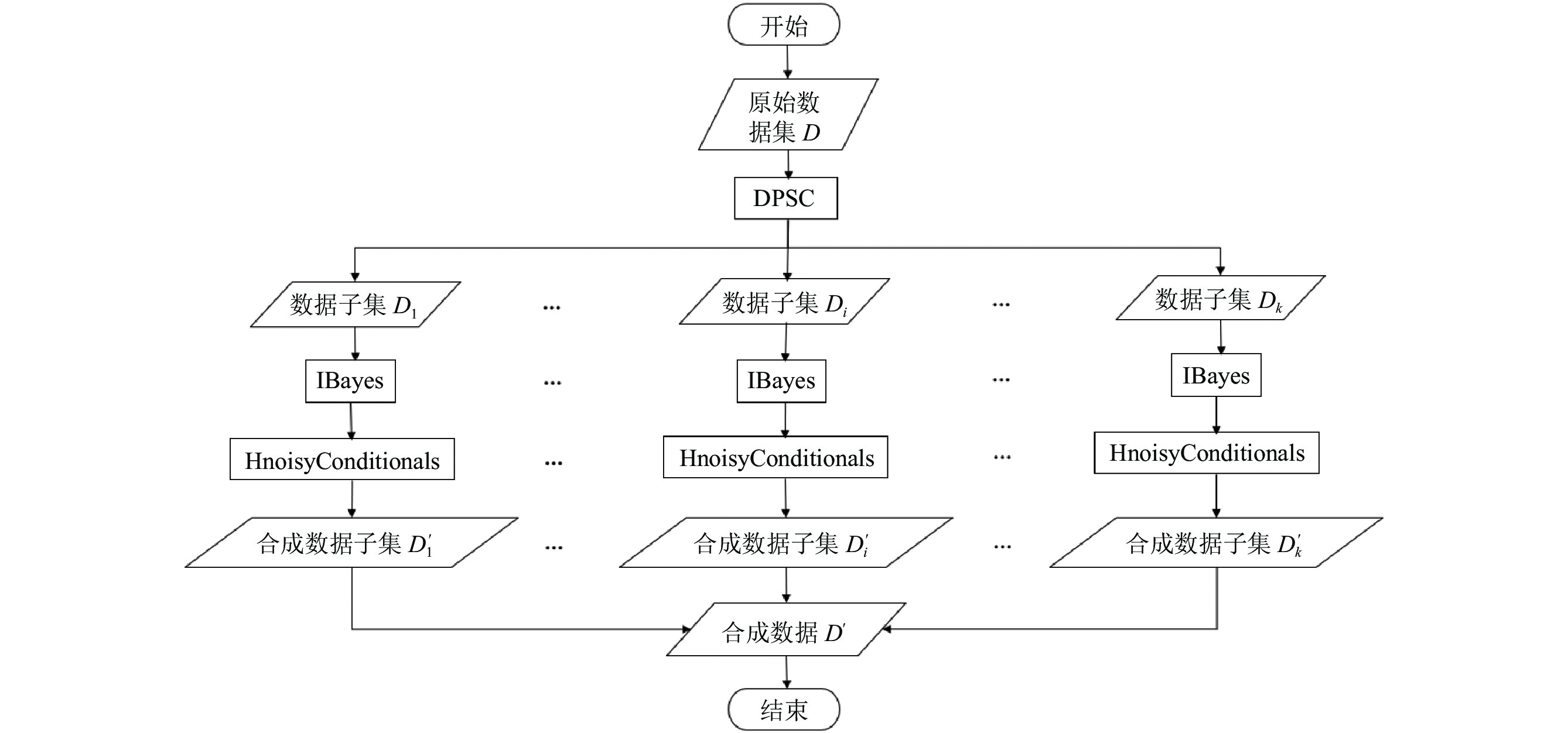
|
图 2 HMPrivBayes算法流程图 |
3.2 差分隐私谱聚类算法
谱聚类算法是根据数据点之间相似性程度进行数据集聚类, 对于关联程度不高的属性对, 其相似值相应较小, 从而分割至不同的子集. 本文采用最大信息系数作为属性之间关联程度衡量指标, MIC不仅能高效检测大数据集中不同类型属性之间关联关系, 而且不需要进行归一化处理. 选用K-means++聚类算法实现特征矩阵
算法3. DPSC算法
输入: 数据集
输出: 属性集
1. 计算
2. 执行算法1的步骤2–步骤6;
3. 使用K-means++算法对新样本点
4. 返回属性聚类结果
由于在计算属性关联程度时涉及到了原始数据集
首先计算属性间的最大信息系数的全局敏感度
从算法3可以看出, Laplace机制是通过多次扰动加噪过程实现的, 每次加噪都需要消耗部分隐私预算
在基于贝叶斯网络构建数据发布模型的现有研究中, 大多以文献[13]中的PrivBayes为参照进一步改进贝叶斯网络的构建设计发布算法[19-21]. 由于PrivBayes在构建贝叶斯网络时, 随机选取首个属性加入父节点集合, 这样构建的贝叶斯网络不一定能真实反映原始数据集. 与此同时, 通过枚举的方式选取互信息最大的
算法4. IBayes算法
输入: 数据子集
输出: 数据子集
1. 初始化
2. 使用指数机制从
3. for
初始化
for
令
If
将
将
end for
使用指数机制从
end for
4. 返回
信息熵是对信息不确定性的度量, 与信息的不确定性呈正相关. 信息熵越大, 携带的信息量越多, 能更多地反映出数据的多样性, 增加数据的实用价值, 反之亦然. 因此, 引入信息熵作为选取首个属性的依据是合理的.
对于数据集
| H({X_j}) = - \sum\nolimits_{j = 1}^n {{p_j}\log } {p_j} | (7) |
根据式(7)可知, 当取不同值的概率相等时信息熵最大, 即
通过图3的实例可以说明属性信息熵的最大差异.
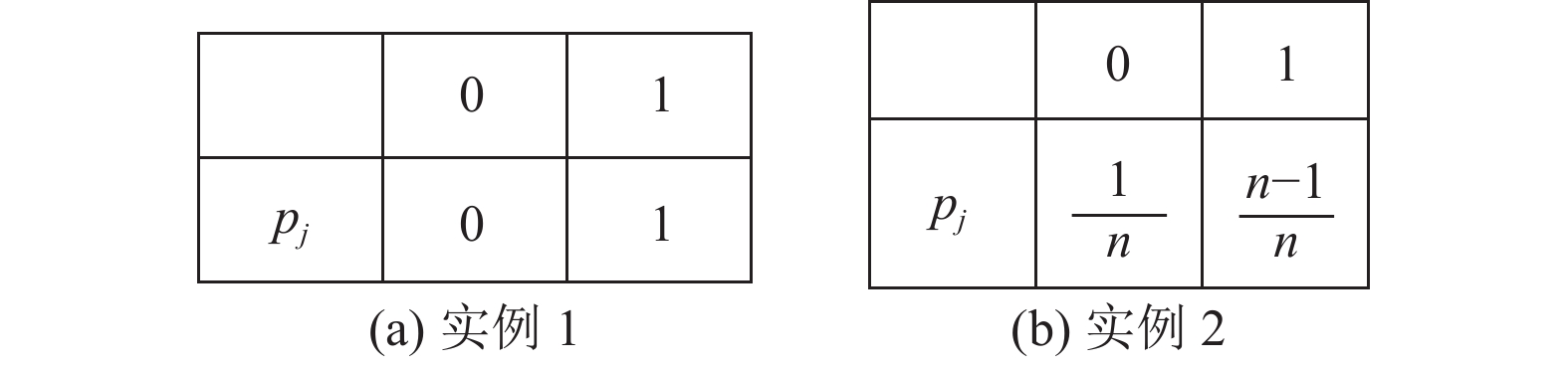
|
图 3 信息熵差异实例 |
根据图3(a)取值概率分布计算
| \Delta H = \frac{1}{n} \cdot \log n + \frac{{n - 1}}{n} \cdot \log \frac{n}{{n - 1}} | (8) |
PrivBayes通过枚举选择互信息最大的属性对时, 候选
| {S_i}\left( {{X_s}, {X_c}} \right) = \left\{ \begin{array}{l} 1, {\text{ }}{\rm{else}} \\ 0, {\text{ }}\left\{ \begin{gathered} S\left( {{X_s}, {X_c}} \right) \leqslant \eta \times \max S\left( {{X_s}} \right){\text{ }} \\ S\left( {{X_c}, {X_s}} \right) \leqslant \eta \times \max S\left( {{X_c}} \right) \\ \end{gathered} \right.{\text{or}} \end{array} \right. | (9) |
IBayes算法使用指数机制选取加入
| P\left( {{X_t}, {\prod _t}} \right) = \dfrac{{\exp \left( {\dfrac{{{\varepsilon _2}u\left( {{X_t}, {\prod _t}} \right)}}{{2\left| {{C_i}} \right|\Delta u}}} \right)}}{{\displaystyle\sum\limits_{\left( {{X_t}, {\prod _t}} \right) \in \Omega } {\exp \left( {\dfrac{{{\varepsilon _2}u\left( {{X_j}, {\prod _j}} \right)}}{{2\left| {{C_i}} \right|\Delta u}}} \right)} }} | (10) |
IBayes算法最终输出一个贝叶斯网络
通过贝叶斯网络计算属性的联合分布, 生成合成数据集, 可以近似原始数据集. 尽管贝叶斯网络的构建过程满足差分隐私保护, 但仍存在隐私泄露的可能. 因此, 需要对计算出来的属性联合分布添加噪声扰动, 以进一步保护隐私数据. 之前的研究均通过均分隐私预算实现联合分布噪声扰动, 这种方式没有考虑到属性敏感性差异. 属性携带的信息量越多, 帮助攻击者推出目标信息的贡献越大, 也就意味着它对外发布的敏感性越高. 基于此, 本文提出差分隐私异构条件分布计算算法HnoisyConditionals, 具体实现过程如算法5所示.
算法5. HnoisyConditionals算法
输入: 数据集
输出: 根据
1. 初始化
2. for
构建
加入拉普拉斯噪声
设
从
end for
3. for
从
end for
4. 返回
根据式(7), 归一化风险熵计算公式如下:
| O{E_j} = - \frac{1}{{\log n}}\sum\nolimits_{i = 1}^n {{p_i}\log } {p_i} | (11) |
在算法5中, 向联合分布注入噪声不再采取均分策略, 而是以归一化风险熵为权重分配隐私预算. 由文献[13]可知, 联合分布全局敏感度为
| Lap\left( {\frac{2}{{n{\varepsilon _3}}} \times \frac{{\displaystyle\sum\nolimits_{j = l' + 1}^{\left| {{C_i}} \right|} {\exp \left( { - O{E_j}} \right)} }}{{\exp \left( { - O{E_j}} \right)}}} \right) | (12) |
其中, 属性归一化风险熵
定理1. HMPrivBayes算法满足
证明: 在HMPrivBayes的整个执行过程中, 其中有3步涉及原始数据集的访问, 分别是属性分割、构建差分隐私贝叶斯网络和提取属性噪声条件分布, 下面分别讨论这3步的隐私保护强度.
对于属性分割, 需要重复访问数据集
在贝叶斯网络构建阶段, 需要借助指数机制
从贝叶斯网络
综上, HMPrivBayes算法满足
本次实验使用Python编程语言来实现所有的方法, 其中贝叶斯网络模型部分的实现参考了Zhang等人[13]论文的实验相关代码. 实验的硬件环境为AMD Ryzen7 4800H (2.90 GHz), 操作系统为Windows 10 (64位), 内存为16 GB.
实验采用两个公开可用的数据集Adult[27]和Big5[28]. 其中, Adult为美国人口普查数据集, 包含45222条个体信息记录, 每条记录包含15个属性. Big5是包含19719条人口普查记录的信息集合, 每条记录包含57个属性. 利用等宽法完成属性转化后, 二进制属性的数量分别为52和175. 两个数据集的详细信息如表1所示.
| 表 1 数据集属性信息描述 |
对于这两个数据集, 隐私预算分配策略为
本文通过
| Dis{t_{{\rm{AVD}}}}\left( {P, Q} \right) = \frac{1}{2}\sum\nolimits_{\omega \in \mho } {\left| {P\left( \omega \right) - Q\left( \omega \right)} \right|} | (13) |
其中,
实验通过度量SVM分类的准确性, 分析生成的噪声数据集的有效性. 本组实验在噪声数据集上同时训练2个分类器, 通过分析合成数据集的其他属性预测目标属性的分类结果. 对于Adult数据集, 选取salary作为分类实例, 预测个体每年收入是否超过50k. 对于Big5数据集, 选取age作为分类实例, 预测个体年龄是否在50岁以下. 每个分类任务, 将合成数据集按照8:2分为训练数据集和测试数据集, 重复运行50次, 并记录实验结果的平均值.
4.3 实验结果本文将通过3个不同的实验来分析HMPrivBayes算法的可用性和高效性. 为了更好地评估HMPrivBayes方案的性能, 本节采用的对比算法包括: PrivSCBN、PrivBayes、Jtree、NoPrivacy. 其中, PrivSCBN算法[20]、PrivBayes算法[13]均是基于贝叶斯网络的数据发布算法, Jtree[14]是基于联合树的数据发布算法, NoPrivacy是HMPrivBayes不添加噪声扰动的数据发布情况.
第1个实验是为了验证HMPrivBayes算法的安全性, 比较在不同记录数量下, 敏感属性隐私泄露的可能性. 在Adult数据集原有的45222条记录的基础上, 随机产生54778条记录, 生成包含100000条记录的数据集, 并将salary作为敏感属性. 由于隐私预算
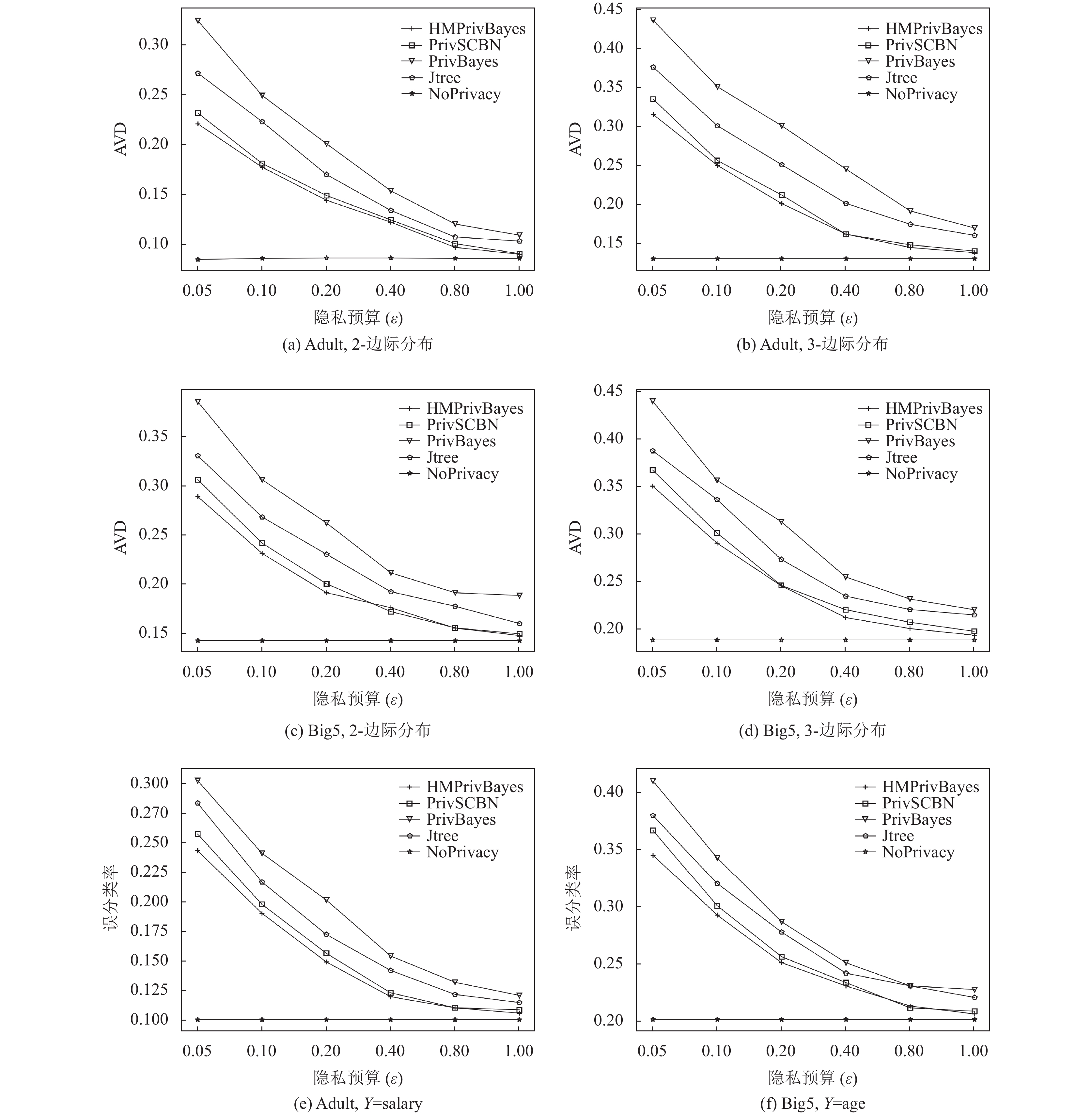
第2个实验是对HMPrivBayes算法数据性能的分析, 图5(a)–图5(d)分别对比了在不同
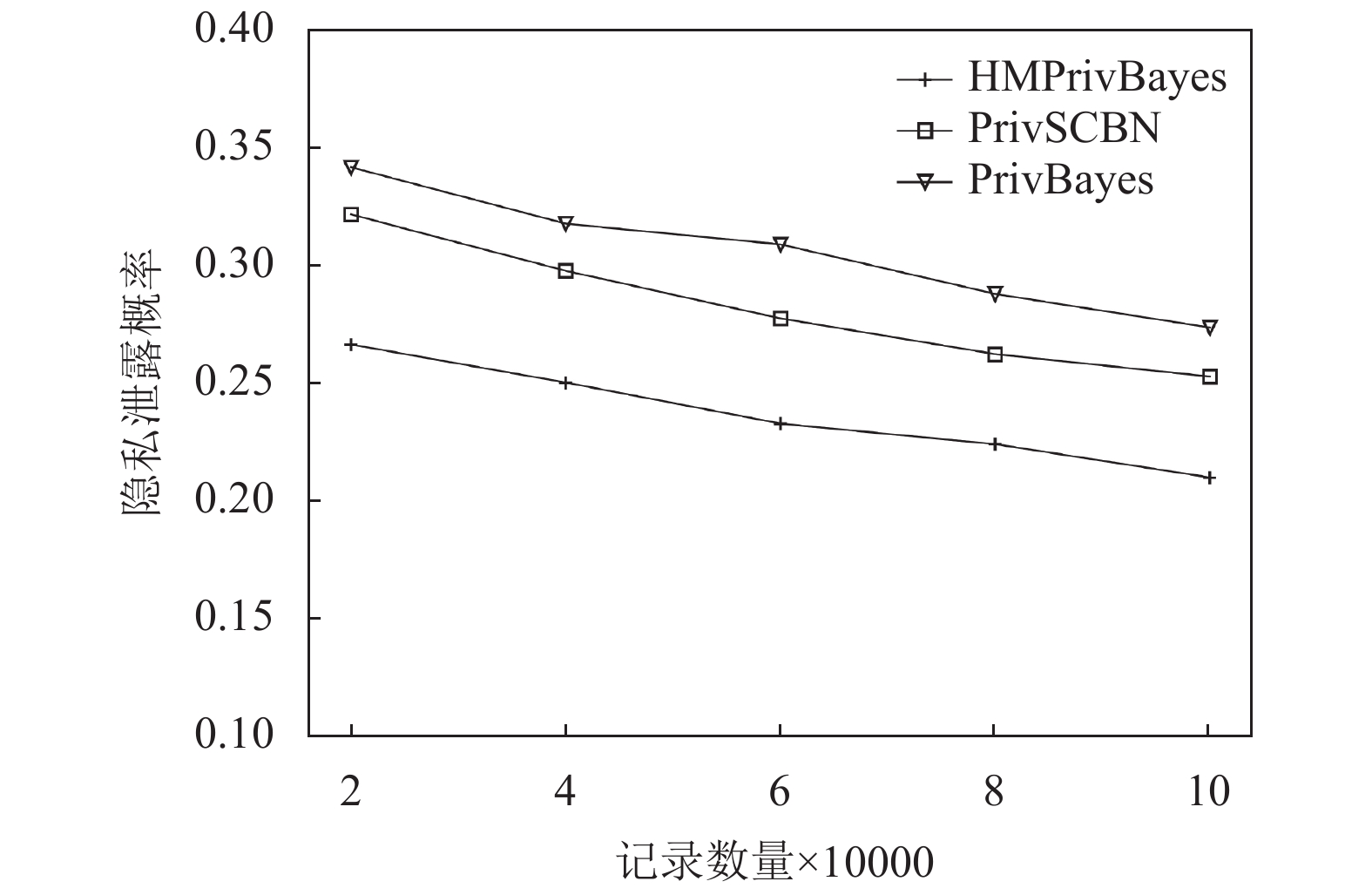
|
图 4 数据安全性分析 |
可以看出, 对于NoPrivacy, 边际分布之间的AVD和分类器的误分类率均与隐私预算
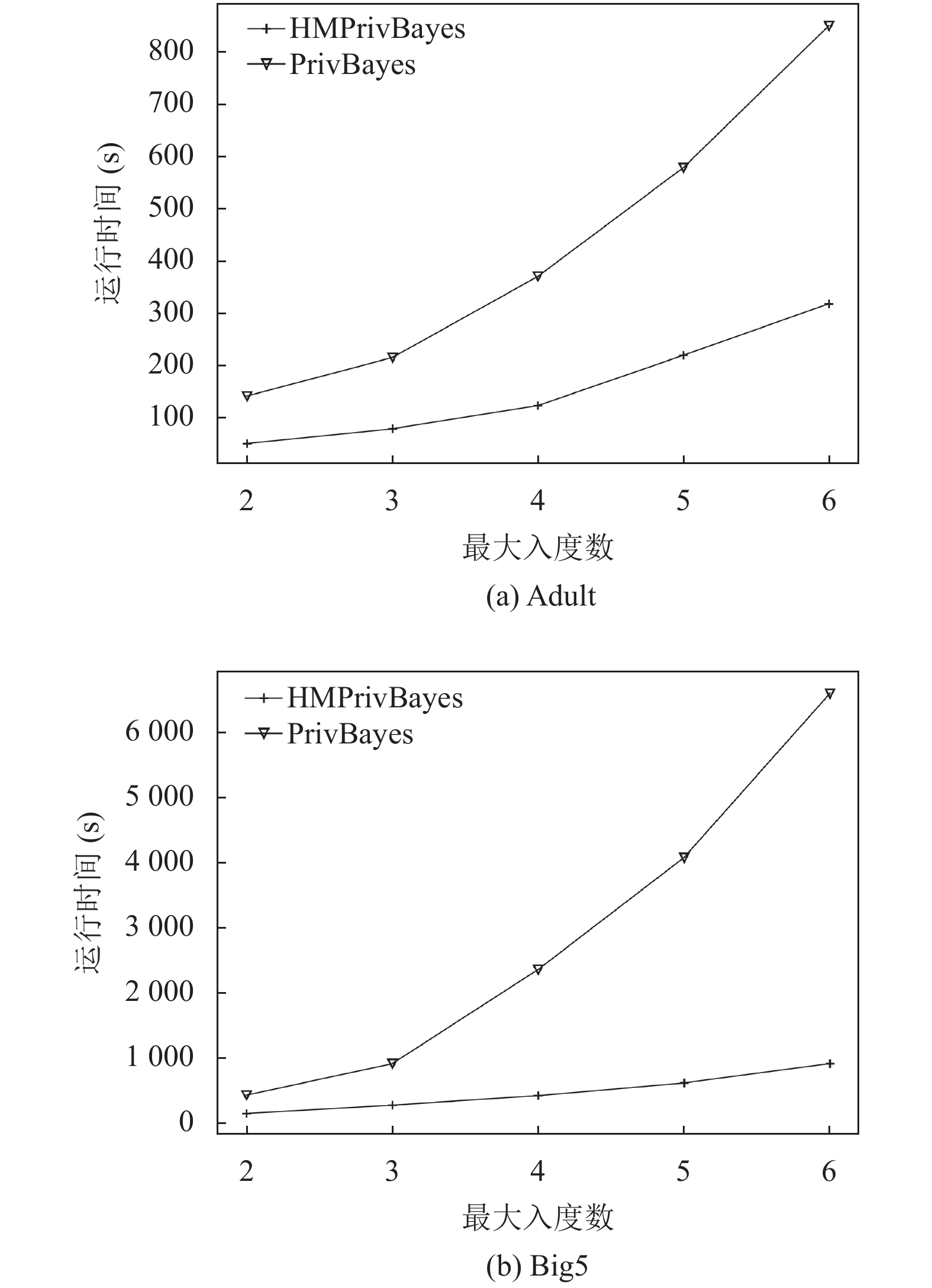
第3个实验是对HMPrivBayes算法计算效率的分析, 比较在贝叶斯网络不同最大入度数
|
图 5 算法HMPrivBayes、PrivSCBN、PrivBayes、Jtree在不同隐私预算下的性能分析 |
5 结束语
针对差分隐私异构多属性数据发布问题, 本文提出了一种基于属性分割的异构多属性数据差分隐私发布方法HMPrivBayes. 与已有多属性数据发布算法不同的是, HMPrivBayes基于属性敏感性差异给予属性数据相对应的隐私保护强度, 避免了多属性数据隐私保护不均匀的问题, 进而提高数据可用性. 与此同时, 该方法通过引入属性分割、改进贝叶斯构建过程等都实现了算法整体计算效率的提升. 在不破坏属性关联的前提下, 以属性归一化风险熵为权重分配隐私预算, 实现异构多属性数据发布. 理论证明, HMPrivBayes满足
|
图 6 算法运行时间分析 |
| [1] |
Sweeney L. K-Anonymity: A model for protecting privacy. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2002, 10(5): 557-570. DOI:10.1142/S0218488502001648 |
| [2] |
Vel Kumar P M, Karthikeyan M. L diversity on K-anonymity with external database for improving privacy preserving data publishing. International Journal of Computer Applications, 2012, 54(14): 7-13. DOI:10.5120/8632-2341 |
| [3] |
Li NH, Li TC, Venkatasubramanian S. t-Closeness: Privacy beyond k-anonymity and l-diversity. 2007 IEEE 23rd International Conference on Data Engineering. Istanbul: IEEE, 2007. 106–115.
|
| [4] |
Dwork C. Differential privacy. 33rd International Colloquium on Automata, Languages and Programming. Venice: Springer, 2006. 1–12.
|
| [5] |
Dwork C, McSherry F, Nissim K, et al. Calibrating noise to sensitivity in private data analysis. 3rd Theory of Cryptography Conference on Theory of Cryptography Conference. New York: Springer, 2006. 265–284.
|
| [6] |
McSherry F, Talwar K. Mechanism design via differential privacy. Proceedings of the 48th Annual IEEE Symposium on Foundations of Computer Science. Providence: IEEE, 2007. 94–103.
|
| [7] |
熊平, 朱天清, 王晓峰. 差分隐私保护及其应用. 计算机学报, 2014, 37(1): 101-122. |
| [8] |
张啸剑, 孟小峰. 面向数据发布和分析的差分隐私保护. 计算机学报, 2014, 37(4): 927-949. |
| [9] |
Zhu TQ, Li G, Zhou WL, et al. Differentially private data publishing and analysis: A survey. IEEE Transactions on Knowledge and Data Engineering, 2017, 29(8): 1619-1638. DOI:10.1109/TKDE.2017.2697856 |
| [10] |
Xiao YH, Xiong L, Yuan C. Differentially private data release through multidimensional partitioning. 7th VLDB Workshop on Secure Data Management. Singapore: Springer, 2010. 150–168.
|
| [11] |
Cormode G, Procopiuc C, Srivastava D, et al. Differentially private spatial decompositions. 2012 IEEE 28th International Conference on Data Engineering. Arlington: IEEE, 2012. 20–31.
|
| [12] |
Mohammed N, Chen R, Fung BCM, et al. Differentially private data release for data mining. Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Diego: ACM, 2011. 493–501.
|
| [13] |
Zhang J, Cormode G, Procopiuc CM, et al. PrivBayes: Private data release via Bayesian networks. ACM Transactions on Database Systems, 2017, 42(4): 25. |
| [14] |
Chen R, Xiao Q, Zhang Y, et al. Differentially private high-dimensional data publication via sampling-based inference. Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Sydney: ACM, 2015. 129–138.
|
| [15] |
Chaudhuri K, Sarwate AD, Sinha K. A near-optimal algorithm for differentially-private principal components. The Journal of Machine Learning Research, 2013, 14(1): 2905-2943. |
| [16] |
Wang S, Chang JM. Differentially private principal component analysis over horizontally partitioned data. 2018 IEEE Conference on Dependable and Secure Computing (DSC). Kaohsiung: IEEE, 2018. 1–8.
|
| [17] |
Xu CG, Ren J, Zhang YX, et al. DPPro: Differentially private high-dimensional data release via random projection. IEEE Transactions on Information Forensics and Security, 2017, 12(12): 3081-3093. DOI:10.1109/TIFS.2017.2737966 |
| [18] |
Qardaji WH, Yang WN, Li NH. PriView: Practical differentially private release of marginal contingency tables. Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data. Snowbird: ACM, 2014. 1435–1446.
|
| [19] |
王良, 王伟平, 孟丹. 基于加权贝叶斯网络的隐私数据发布方法. 计算机研究与发展, 2016, 53(10): 2342-2352. |
| [20] |
洪金鑫, 吴英杰, 蔡剑平, 等. 基于属性分割的高维二值数据差分隐私发布. 计算机研究与发展, 2022, 59(1): 182-196. DOI:10.7544/issn1000-1239.20200701 |
| [21] |
陈恒恒, 倪志伟, 朱旭辉, 等. 基于聚类分析的差分隐私高维数据发布方法. 计算机应用, 2021, 41(9): 2578-2585. DOI:10.11772/j.issn.1001-9081.2020111786 |
| [22] |
Dwork C, Lei J. Differential privacy and robust statistics. Proceedings of the 41st Annual ACM Symposium on Theory of Computing. Bethesda: Association for Computing Machinery, 2009. 371–380.
|
| [23] |
Dwork C, Naor M, Reingold O, et al. On the complexity of differentially private data release: Efficient algorithms and hardness results. Proceedings of the 41st Annual ACM Symposium on Theory of Computing. Bethesda: Association for Computing Machinery, 2009. 381–390.
|
| [24] |
McSherry FD. Privacy integrated queries: An extensible platform for privacy-preserving data analysis. Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data. Providence: Association for Computing Machinery, 2009. 19–30.
|
| [25] |
Ng AY, Jordan MI, Weiss Y. On spectral clustering: Analysis and an algorithm. Proceedings of the 14th International Conference on Neural Information Processing Systems: Natural and Synthetic (NIPS’01). Vancouver: NIPS, 2001. 849–856.
|
| [26] |
Reshef DN, Reshef YA, Finucane HK, et al. Detecting novel associations in large data sets. Science, 2011, 334(6062): 1518-1524. DOI:10.1126/science.1205438 |
| [27] |
Adult Data Set. https://archive.ics.uci.edu/ml/datasets/adult. [2021-12-15].
|
| [28] |
Open-source Psychometrics Project. http://personality-testing.info/_rawdata/. [2021-12-15].
|
| [29] |
Barak B, Chaudhuri K, Dwork C, et al. Privacy, accuracy, and consistency too: A holistic solution to contingency table release. Proceedings of the 26th ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems. Beijing: ACM, 2007. 273–282.
|
| [30] |
周志华. 机器学习. 北京: 清华大学出版社, 2016.
|
| [31] |
Tsybakov AB. Introduction to Nonparametric Estimation. New York: Springer, 2009.
|
 2022, Vol. 31
2022, Vol. 31



