近年来, 关于多元统计过程的监控策略可谓百花齐放, 早期由于主成分分析方法(principal components analysis, PCA)拥有良好的降维能力被普遍应用, 但由于PCA不适用于非线性系统, Schölkopf等人^[1]提出了核主元分析法(kernel principal components analysis, KPCA), KPCA通过非线性映射函数将原始输入空间映射到高维特征空间, 然后再利用特征空间中映射数据点的内积就可解决非线性问题. 吴天昊等人^[2]将KPCA引入核电厂设备在线监控领域中, 使监测手段提供更为早期的预报警. 吕宁等人^[3]提出一种改进的多向核主元分析故障诊断模型, 使得非线性主元能够在高维特征空间中被快速提取. 吴洪艳等人^[4]提出了基于小波的KPCA故障监测方法, 降低了KPCA计算的复杂性, 缩短了计算时间. 霍特林的T²统计量和Q统计量(也称平方预测误差, squared prediction error, SPE)是PCA与KPCA在过程监控中常用的两个统计量指标. T²统计量用于监控模型空间的变化, 而Q统计量用于监控剩余空间的变化. 然而, T²和Q统计量仅适用于高斯分布过程的监控. 借鉴文献[5–8]提出的算法, 本文采用核密度估计(kernel density estimation, KDE)方法推导核主元分析的控制限; 然后, 比较了基于高斯分布统计量控制限的KPCA和KPCA-KDE在田纳西伊斯曼(TE)过程中的故障检测性能. 结果表明, 基于KPCA-KDE的监测方法比基于高斯假设的KPCA具有更好的性能.

1 基于KPCA-KDE的过程监控 1.1 KPCA算法

给定m个训练样本 $X_{k} \in {\mathfrak{R}}^{n}, k=1, 2, \cdots, m$ , 由非线性映射 $X_{k} \in {\mathfrak{R}}^{n} \rightarrow \varphi\left(X_{k} \in {\mathfrak{R}}^{F}\right).$ 可以映射到高维特征空间. 特征空间中的协方差矩阵为:

$ {C_F} = \frac{1}{m}\sum\limits_{j = 1}^m { \left\langle \varphi ({X_j}), \varphi ({X_j}) \right\rangle } $

(1)

在 $\varphi\left(X_{j}\right)$ 中, $ j = 1, \cdots, m $ 假设均值和单位方差为零. 为了对角化协方差矩阵, 在特征空间中求解特征值问题:

$ \lambda a = {C_F}a $

(2)

其中, λ是 $ {C}_{F} $ 的特征值, 满足 $\lambda \geqslant 0, \; a \in {R^F}$ 是对应的特征向量( $ a \ne 0 $ ). 特征向量可表示为映射数据点的线性组合如下:

$ a = \sum\limits_{i = 1}^m {{\alpha _i}\phi ({X_i})} $

(3)

用 $ \varphi \left(X\right) $ 两边同时左乘式(2):

$ \lambda \left\langle \phi ({X_k}), a \right\rangle \; = \; \left\langle \phi ({X_k}), {C_F}a \right\rangle $

(4)

将式(1)、式(3)代入式(4), 得:

$ \begin{split} \lambda \sum\limits_{i = 1}^m & {{\alpha _i} \left\langle \phi ({X_k}), \phi ({X_i}) \right\rangle \; = }\\ & \frac{1}{m}\sum\limits_{i = 1}^m {{\alpha _i} \left\langle \phi ({X_k})\sum\limits_{j = 1}^m \phi ({X_j}) \right\rangle \left\langle \phi ({X_j}), \phi ({X_i}) \right\rangle } \end{split} $

(5)

不直接对式(1)中 $ {C}_{F} $ 的进行特征值分解并找到特征值和主成分, 而采用核技巧, 定义一个 $ m \times m $ 的核矩阵, 如式(6):

$ {\left[ K \right]_{ij}} = {K_{ij}} = \left\langle {\phi ({X_i}), \phi ({X_j})} \right\rangle = k({X_i}, {X_j}) $

(6)

对于所有 $ i, j = 1, \cdots, m $ 引入核函数的形式 $ k(x, y) = (\varphi (x), \varphi (y)) $ 在式(5)使内积的计算 $\left\langle \varphi ({x_i}), \varphi ({x_i}) \right\rangle$ 在特征空间中作为输入数据的函数. 在特征空间中不需要进行非线性映射和计算内积. 对于核矩阵, 将式(5)重写为:

$ \lambda \sum\limits_{i = 1}^m {{\alpha _i}{K_{ki}}} = \frac{1}{m}\sum\limits_{i = 1}^m {{\alpha _i}} \sum\limits_{j = 1}^m {{K_{kj}}{K_{ji}}} $

(7)

注意, $ k = 1, \cdots, m $ , 因此, 式(7)可以表示为:

$ \lambda mK\alpha = {K^2}\alpha $

(8)

式(8)等价于特征值问题:

$ m\lambda \alpha = K\alpha $

(9)

更进一步, 核矩阵可以表示为式(10):

$ {K_{ctr}} = K - UK - KU + UKU $

(10)

其中, U是一个 $ m \times m $ 矩阵, 其中每个元素都等于 $ 1/m $ . $ {K_{ctr}} $ 的特征值分解相当于 $ {\Re ^F} $ 中的PCA. 本质上相当于解决式(9)中的特征值问题, 它产生特征向量为 $ {\alpha _1}, {\alpha _2}, \cdots, {\alpha _m} $ , 相应的特征值为 $ {\lambda _1} \geqslant {\lambda _2} \geqslant \cdots \geqslant {\lambda _m} $ .

由于核矩阵 $ {K_{ctr}} $ 是对称的, 故导出的主元是标准正交的, 即:

$ \left\langle {{\alpha _i}, {\alpha _j}} \right\rangle = {\delta _{i, j}} \; (i, j = 1, 2, \cdots, m) $

(11)

然后, 将 $\varphi\left(X_{j}\right)$ 投影到由特征向量张成的PC空间上, 就可提取出主元训练观测值 $ {X_j}, j = 1, \cdots, m $ 的非线性映射的得分向量.

$ {Z_{K, j}} = \left\langle {{\alpha _k}, ({K_{ctr}})} \right\rangle = \sum\limits_{i = 1}^m {{\alpha _{k, i}}\left\langle {\phi ({X_i}), \phi ({X_j})} \right\rangle } $

(12)

应用内核技巧, 这可以表示为:

$ {Z_{K, j}} = \sum\limits_{i = 1}^m {{\alpha _{K, i}}{{\left[ {{K_{ctr}}} \right]}_{i, j}}} $

(13)

1.2 故障检测指标

特征空间中第j个样本的霍特林的 $ {T^2} $ , 其KPCA故障检测表达式为:

$ T_j^2 = \left[ {{Z_{1, j}}, \cdots, {Z_{q, j}}} \right]{\Omega ^{ - 1}}{\left[ {{Z_{1, j}}, \cdots, {Z_{q, j}}} \right]^{\rm{T}}} $

(14)

其中, ${Z_{i, j}}, i = 1, \cdots, q$ 表示第j个样本的主元得分, $ q $ 为保留主元的数量, $ {\Omega ^{ - 1}} $ 表示保留主元对应的特征值矩阵的逆. 从 $ {T^2} $ 的分布可估计其控制极限. 如果所有采样都是高斯分布的, 那么F分布的控制限对应于一个显著性水平 $ \alpha $ , $ {T^2} $ , 可以表示为:

$ T_\alpha ^2 \sim \frac{{q(m - 1)}}{{m - q}}{F_{q, m - q, \alpha }} $

(15)

其中, $ {F_{q, m - q, \alpha }} $ 为显著性水平 $ \alpha $ 对应的自由度为条件下的F分布临界值. Choi等人^[9]还提出了对 $ Q $ 统计量的简化计算. 对于第j个样本:

$ {Q_j} = {\left\| {\phi ({X_j}) - \mathop {{\phi _q}}\limits^ \wedge ({X_j})} \right\|^2} = \sum\limits_{i = 1}^m {Z_{i, j}^2} - \sum\limits_{i = 1}^q {Z_{i, j}^2} $

(16)

如果所有分数都是正态分布, $ Q $ 统计量在 $100(1-\alpha )\mathrm{{\text{%}}}$ 置信水平的控制极限可以推导如下:

$ {Q_\alpha } = {\theta _1}{\left[ {\frac{{{C_a}{h_0}\sqrt {2{\theta _2}} }}{{{\theta _1}}} + 1 + \frac{{{\theta _2}{h_0}({h_0} - 1)}}{{\theta _1^2}}} \right]^{1/{h_0}}} $

(17)

其中, $ {\theta _1} = \displaystyle\sum\nolimits_{j = q + 1}^n {\lambda _j^i} $ , $ {h_0} = 1 - 2{\theta _1}{\theta _3}/3\theta _2^2 $ , $ {\lambda _i} $ 为特征值, $ {C}_{\alpha } $ 为 $100(1-\alpha ) \mathrm{{\text{%}}}$ 正态百分位数.

1.3 核密度估计

KDE是从一组随机样本中使用合适的平滑概率密度函数对数据集进行拟合的过程. 它被广泛应用于概率密度函数(probability density functions, PDFS)的估计, 特别是单变量的随机数据^[10-13]. 尽管这些统计特征的过程是多变量的, 因为两者都是单变量的, 所以KDE可应用于 $ {T^2} $ 和 $ Q $ 统计. 给定一个随机变量 $ y $ , 从其m个样本中获得它的概率密度函数 $ g(y), \; {y}_{j}, \; j=1, \cdots, m $ 如下:

$ g(y) = \frac{1}{{mh}}\sum\limits_{j = 1}^m {k\left(\frac{{y - {y_j}}}{h}\right)} $

(18)

其中, k为核函数, h为带宽或平滑参数. 基于Cheng等人^[14]提出的选择带宽的最佳方法, 本文在连续范围内对密度函数积分得到概率. 因此, 假设PDF在指定的显著水平上, y小于c的概率为:

$ p(y < c) = \int\limits_{ - \infty }^c {g(y)dy} = \alpha $

(19)

因此, 监测统计量( $ {T^2} $ 和 $ Q $ )的控制限可由各自的概率密度函数估算值计算:

$ \int\limits_{ - \infty }^{{T^2}} {g({T^2})d{T^2}} = \alpha $

(20)

$ \int\limits_{ - \infty }^{{Q_\alpha }} {g(Q)dQ} = \alpha $

(21)

1.4 在线监测

对于一个以均值为中心的观测样本, 使用训练例子计算相应的核向量 $ {X_j}, j = 1, \cdots, m $ 如下:

$ {\left[ {{K_{tt}}} \right]_j} = k({X_j}, {X_{tt}}) $

(22)

然后将测试核向量标准化, 如式(23)所示:

$ {K_{ctt}} = {K_{tt}} - K{u_1} - U{k_{tt}} + UK{u_1} $

(23)

${u_1} = 1/m{\left[ {1, \cdots , 1} \right]^{\rm{T}}} \in {\Re ^m}$ . 计算相应的得分向量(核主元) $ {Z_{tt}} $ :

$ {Z_{tt, k}} = \left\langle {{\alpha _k}, ({K_{ctt}})} \right\rangle = \sum\limits_{i = 1}^m {{\alpha _{k, i}}\left\langle {\phi ({X_i}), \phi ({X_{tt}})} \right\rangle } $

(24)

也可写成:

$ {Z_{tt, k}} = \sum\limits_{i = 1}^m {{\alpha _{k, i}}{{\left[ {{K_{ctt}}} \right]}_i}} $

(25)

用向量形式表示为:

$ {Z_{tt}} = A{K_{ctt}} $

(26)

其中, $ A = \left[ {{\alpha _1}, \cdots, {\alpha _m}} \right] $ .

2 KPCA-KDE故障监测算法过程 2.1 离线监控模型的建立

TR1. 获取正常运行条件下的数据(NOC), 使用数据集中代表不同变量的列的均值和标准差对数据进行规范化;

TR2. 决定内核函数的类型并确定内核参数;

TR3. 构造NOC数据的核矩阵并将其中心化;

TR4. 获得特征值及其对应的特征向量, 并将其按降序排列;

TR5. 使用式(11)对特征向量进行正交化;

TR6. 使用式(13)得到非线性得分向量;

TR7. 根据核化NOC数据, 利用式(14)和式(16)计算监控性能指标( $ {T^2} $ 和 $ Q $ );

TR8. 用式(20)、式(21)确定 $ {T^2} $ 和 $ Q $ 的控制限值.

2.2 在线监控模型的建立

TT1. 获取测试样本 $ {X_{tt}} $ 并使用离线步骤1中的均值和标准差进行规范化;

TT2. 用式(22)获得样本的核向量;

TT3. 据式(23)对核向量进行中心化;

TT4. 据式(25)求出测试样本的主元值;

TT5. 将测试样本的 $ {T^2} $ 和 $ Q $ 与模型建立阶段得到的各自控制极限进行比较;

TT6. 如果 $ {T^2} $ 和 $ Q $ 都小于它们的监控统计数据, 则过程处于控制之中. 如果 $ {T^2} $ 或 $ Q $ 超过控制限度, 则过程失控, 进行故障识别, 识别故障的来源. 基于核主元分析与核密度估计的非线性过程故障监测与识别流程图见图1.

2.3 故障变量识别

在检测到故障之后, 重要的是要识别与故障关联最紧密的变量, 以便于确定故障发生的原因.

贡献图是一种常用的故障识别方法, 它显示了各变量对故障区域的高统计指标值的贡献. 然而, 由于转换后的过程变量与原始过程变量之间存在非线性关系, 基于非线性PCA的故障识别不像线性主成分分析那样简单.

在本文中, 使用Petzold等人^[15]提出的敏感性分析原理识别故障变量. 该方法基于Deng等人^[16]研究的方法, 计算因参数变化而引起系统输出变化的变化率. 给定一个测试数据向量 $ {X_i} \in {\Re ^n} $ , 第i个变量对监测指标的贡献定义为:

$ T_{i, {\rm{con}}}^2 = {x_i}{\alpha _i}, \; {Q_{i, {\rm{con}}}} = {x_i}{b_i} $

(27)

其中, $ {a_i} = \partial {T^2}/\partial {x_i} $ , $ {b_i} = \partial Q/\partial {x_i} $ .

在使用多元统计方法的故障识别中, 一种获得变量贡献的有效方法, 即通过对定义 $ {T^2} $ 和 $ Q $ 的函数在参考故障瞬间进行阶跃微分得到偏导数的方法来识别故障^[17].

3 应用程序 3.1 田纳西伊斯曼过程

TE过程是基于真实工业过程的模拟^[18], 具有较强的非线性和动态特性, Chiang等人^[19]把它用作评价和比较过程监控的基准过程. 该过程由分离器、压缩机、反应器、汽提器和冷凝器5个关键部件和编码为A到H的8个部件组成, 共采样960个, 变量53个, 其中连续变量22个, 3个成分分析器采样的成分测量值19个, TE过程中的操纵变量为12个. 采样每隔3分钟进行一次, 而每个故障在采样数160处引入. McAvoy等人^[20]阐述了干扰和基线操作的信息工艺条件.

由于 $ {T^2} $ 和 $ Q $ 数据具有互补性, 因此联合使用它们进行故障检测. 由于可检测到的过程变化并不总是同时发生在模型空间和剩余空间中, 故当任一监控统计数据检测到故障时, 即检测到故障.

3.2 计算监控性能指标

由于从化学过程获得的测量通常是有噪声的, 统计量可能会随机地超过其控制限. 这相当于在没有实际发生故障的情况下统计量可能超过控制限, 即虚假警报. 换句话说, 一个统计量可能会超过它的控制限一次, 但是如果没有出现故障, 在随后的监控中, 统计量可能不会总是保持在它的控制限之上. 相反, 如果在连续的测量中统计量保持在其控制限以上, 则可能发生故障. van Sprang等人^[21]使用故障检测规则解决了假警报的问题. 检测规则也为比较不同的监测方法提供了统一的依据. 在本文中, 当一个统计量在至少两个连续监控中超过其控制限时, 即认为发生了故障. 所有实验在使用基于此准则的数据进行测试时, 都记录了一个零的误报率的数据来用于评估不同技术的监视性能. 性能监控基于3个指标: 故障检出率(fault detection rate, FDR)、误报率(false alarm rate, FAR)和检测延迟(detection delay, DD). 故障检出率是正确识别的故障样本的百分比:

$ {\textit{FDR}} = \frac{{{n_{fc}}}}{{{n_{tf}}}} \times 100 {\text{%}} $

(28)

其中, $ {n_{fc}} $ 为正确识别的故障样本数, $ {n_{tf}} $ 为故障样本总数. FAR是指在工厂正常运行期间, 正常样本中被确定为故障(或异常)的百分比:

$ {\textit{FAR}} = \frac{{{n_{nf}}}}{{{n_{tf}}}} \times 100 {\text{%}} $

(29)

其中, $ {n_{nf}} $ 表示被识别为故障的正常样本的数量, $ {n_{tf}} $ 为正常样本的总数量. 检测延迟为检测到引入故障之前经过的时间.

3.3 应用结果

使用TE流程的故障11显示了基于KPCA的故障检测. 故障11是反应堆冷却水入口温度的随机变化, 图2显示了故障的监控图. 实线代表监测指标, 红线和绿线分别代表基于高斯分布和基于KDE的99%置信水平的控制限值. 在 $ {T^2} $ 控制图中, 基于KDE的控制限值都低于基于高斯分布的控制限值. 即与基于高斯分布的控制限相比, 监测指标超出基于KDE的控制限的程度更大. 意味着使用基于KDE的KPCA技术的控制限比使用基于高斯分布的控制限具有更高的监控性能.

图3显示了故障14在 $ \omega = 40 $ 时KPCA和KPCA-KDE的监视图表. 该故障表现为反应堆冷却水阀卡死, 大多数统计过程监测方法都能很容易地检测出该故障. 在 $ \omega = 40 $ 时, KPCA和KPCA-KDE结果一样, 在 $ \omega = 10 $ 时, KPCA记录的误报率为8.13%, 而KPCA-KDE的仍为零. 此外, 当保留25个主元个数时, KPCA记录的误报率也同样高. 相反, KPCA-KDE方法仍然没有记录任何假警报. 通过研究KPCA和KPCA-KDE所有20个故障的检出率, 结果表明, 与相应的基于高斯分布的方法进行比较, KDE具有较高的故障检出率; 此外, 基于KDE的检测延迟等于或低于其他方法. 这意味着基于KDE控制限的方法比基于高斯分布的同类方法更早地检测出故障. 因此, 相对于使用基于高斯假设的控制限, 将基于KDE的控制限方法与基于KPCA的故障检测方法相结合, 可提供更好的监控效果.

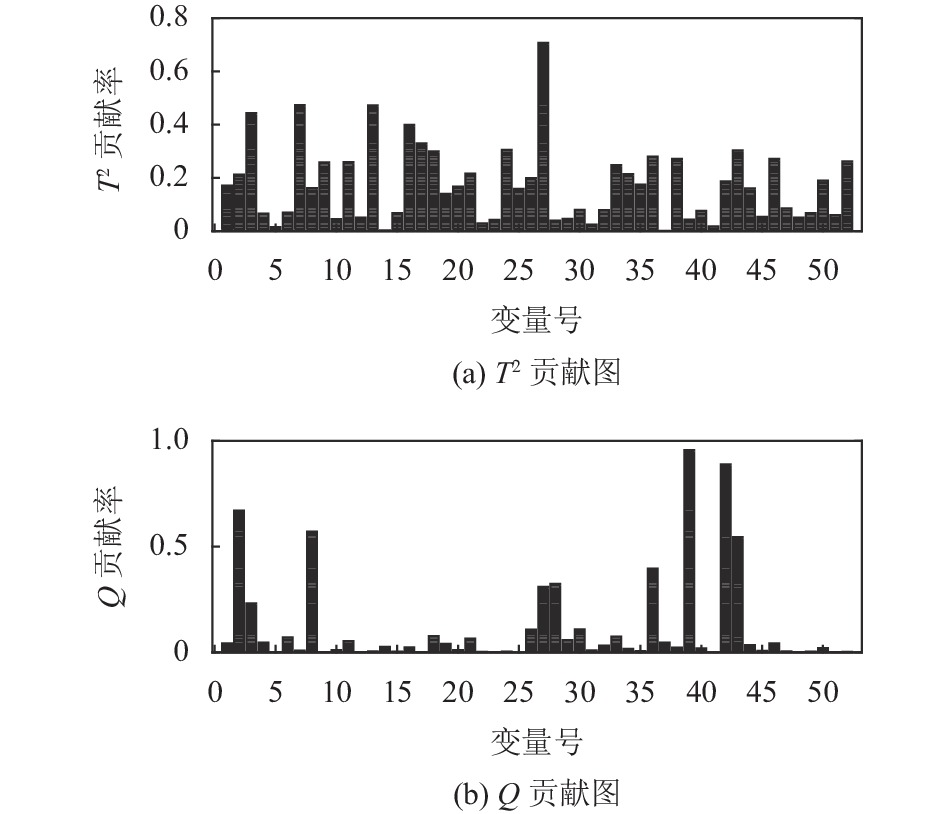
以故障11为例, 显示了基于KPCA-KDE的故障识别. 故障11的出现引起反应堆冷却水流量的变化, 从而导致反应堆温度波动. 在图4中所示的样本300处, 基于 $ {T^2} $ 和 $ Q $ 的贡献图均正确识别了两个故障变量. 变量9是反应堆温度, 变量32对应于反应堆冷却水流速. 尽管控制回路有可能在经过较长时间后补偿反应堆温度的变化, 但是通过贡献图可以正确识别出在引入故障后早期受影响的两个变量的波动.

为了测试KPCA-KDE技术的性能, 通过改变两个参数进行故障检测: 带宽和保留的主元数量. 表1显示, 当保留25个主元时, KPCA记录的FAR值也同样高. 相反, KPCA-KDE方法仍然没有记录任何假报警. 因此, 除了提供更高的FDR和更早的检测外, KPCA-KDE比基于高斯假设的KPCA方法监控性能更好, 当故障及早发现时, 操作人员将有更多的时间找出故障的根本原因, 以便采取补救措施. 其次, 虽然有方法可获得开发过程监控模型的最优设计参数, 但不能保证最优值一直使用. 造成这种情况的原因可能是人员缺乏经验, 以及对流程本身缺乏了解. 因此, 监控方法性能越好, 就更利于过程监控.

4 结论与展望

本文研究了基于KPCA-KDE技术的非线性过程故障检测与识别. 在这种方法中, 用于构建控制图的控制限是直接从监测指标的概率密度函数得到的, 而不是基于高斯分布的控制限. 将该方法应用于田纳西伊斯曼过程, 并与基于高斯假设的核主成分分析方法进行了性能比较. 结果表明, 基于KPCA-KDE比基于高斯分布的KPCA检测到的故障更多、更早. 研究还表明, 基于KDE的控制限比基于高斯假设的控制限更符合监测统计量的实际分布, 因此具有更好的监控性能. 接下来的研究工作是设计更优化的方法, 既在复杂的环境中更能迅速准确的检测出故障, 此外, 将KPCA-KDE结合自适应算法也是一个有价值的研究方向.