2. 东北大学 医学影像智能计算教育部重点实验室, 沈阳 110169
2. Key Laboratory of Intelligent Computing in Medical Image, Ministry of Education, Northeastern University, Shenyang 110169, China
海洋表面温度是全球海洋的一个重要物理量, 常作为研究水团性质、鉴别洋流的基本指标. 研究海表面温度时空分布及其变化规律, 从而进行海表面温度预测是海洋环境信息预报的基础[1]. 海水温度通常作为数值天气预报和海洋预报模型的边界条件. 这些模型越来越多地用于实际应用中, 包括: 海上作业、海洋航运业务、海上安全应急响应、波浪和冲浪的研究、渔业支持和旅游等. 近年来, CTD和XTB测温数据、卫星高度计数据、Argo温盐剖面数据越来越丰富, 基于神经网络的预测方法、三维变分技术等的出现促进了海洋预报的快速发展. 特别是随着海洋观测技术的快速发展, 海洋数据规模呈现了爆炸性增长, 这对海表温的预测带来了新的机遇和挑战. 在这种情况下, 如何充分利用这些海洋大数据和先进的人工智能技术, 实现对海表温度的高效精确预测就成为一个非常重要的课题, 也是当前海洋研究领域的研究热点之一. 预测海表温度方法可大致分为两大类[2, 3], 分别为基于数值的方法和基于数据驱动的方式. 基于数值的方法是建立在物理、化学、生物参数以及相互作用的复杂关系基础上, 利用微分方程对海表温度进行定义和描述. 该方法复杂度高, 不同海域需要不同的数值预测模型, 预测时效较差. 数据驱动的方法是以数据为中心来解决海表温度预测问题, 是通过机器学习技术来学习海表温度变化规律, 从而去预测未来温度的变化情况. 数据驱动方法有马尔可夫模型[4]、支持向量机(SVM)[5]、神经网络[6]等, 这些方法大多缺少对长时序时间依赖特征的提取, 其预测精度有限.
近年来, 随着深度学习的不断发展, 研究人员将深度学习技术运用到了海表面温度的预测中. Zhang等人[7]采用LSTM模型实现了海表面温度的预测, 并取得了较好的预测结果, 但该模型没有考虑海表面温度之间的空间相关性, 因而不适合局部海表温的预测. 2019年ConvLSTM模型被应用到了海表面温度预测中[8], 该模型通过CNN网络提取温度之间空间特征, 通过LSTM网络提取时间特征, 有效利用了时空特征, 取得了较好的预测结果. 但对于长时序预测, 该模型复杂度较高, 还存在梯度消失问题. 张弛等人[9]使用向量回归模型对海洋次表层温度异常进行了预测, 对于浅水域有较好的精度, 但当海洋深度增加时, 其预测精度逐渐降低. 吴琦[10]在ConvLSTM模型的基础上添加了ConvGRU, 对海洋表面温度遥感预测, 但是不能很好地预测长期海洋表面温度. 韩震等人[11]使用基于遥感数据的多层ConvLSTM进行海表温度预测计算, 但是对于小区域, 误差较大, 不能很好地对局部短时间进行预测.
因此, 本文将视频预测时序学习网络PredRNN++[12]引入到了海表温的预测中, 提出了一种基于XGBoost[13]结合PredRNN++ (XGBoost-PredRNN++) 的海表温预测方法. 该方法首先将海表温数据处理成灰度图片, 然后利用机器学习模型XGBoost来提取相应的时间特征, 并采用CNN模型将时间特征融合到海表温数据中, 并提取融合后海表温数据之间的空间依赖关系. 在此基础上, 利用PredRNN++网络将时空依赖关系融合在数据序列中. 避免了梯度消失问题.通过实验验证, 本文相较于传统方法中表现最好的结果, 在MSE评价标准下数值减少了0.107 5. 在SSIM评价标准下, 由误差值0.044降到了0.038 7, 减少了12.15%的误差.
2 基于XGBoost-PredRNN++的海表温预测针对区域海表温预测, 本文提出了一种XGBoost结合PredRNN++的海表温预测方法(XGBoost-PredRNN++), 主要由3部分构成, 分别为数据预处理、时间特征抽取与融合、时空特征抽取与预测, 方法总体框架如图1所示.
数据预处理首先对原始SST数据进行标准化处理, 并采用Gamma校正算法将其处理成一系列灰度图片. 时间特征抽取与融合主要利用XGBoost模型提取预处理阶段形成的灰度图片数据的时间特征, 并利用CNN网络将其融入到原始海表温度数据中, 并提取数据之间的空间依赖特征, 形成新的SST时序序列. 时空特征抽取与预测就是用前一阶段形成的SST时序数据训练PredRNN++预测模型, 提取SST时序数据之间的时间和空间依赖特征, 从而实现对区域海表温度的预测, 后续将分别进行详细介绍.
2.1 数据预处理数据预处理主要完成对原始区域海表温时序数据的预处理, 主要包括数据的标准化和Gamma矫正处理.
(1)数据标准化. 对于原始海表温时序数据, 本文采用最大最小标准化方法将所有数据标准化到[0, 1]范围内, 其计算过程如式(1)所示.
| x∗=x−xminxmax−xmin | (1) |
其中,
(2) Gamma矫正处理. 某一区域同一时刻海表面温度可以看作是一幅图片, 通过Gamma矫正处理将其变换为灰度图片, 一方面降低图片数据的维度, 从而加快后续处理速度, 另一方面通过Gamma矫正增强图像的细节, 从而更好支持后续PredRNN++模型来提取时空特征.
经过数据预处理后, 一组海表温时序数据就变成一组由灰度图片组成的海表温时序数据, 再通过滑动窗口对数据划分, 从而形成相应的训练和测试数据, 供下一阶段使用.
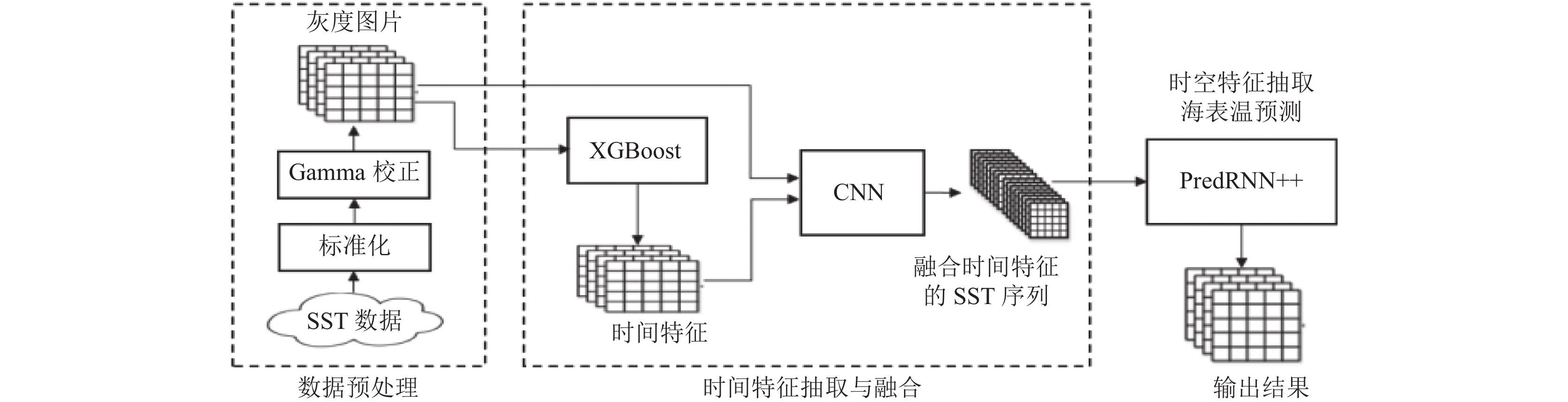
|
图 1 XGBoost-PredRNN++海表温预测方法总体框架 |
2.2 时间特征抽取与融合
区域海表温度预测是利用过去一段时间某个区域的历史海表温度数据来预测该区域未来一段时间的海表温度, 是一种自回归的问题. SST原始数据经过数据预处理后, 形成灰度图片形式的海表温时序数据, 本文考虑到海表温数据所受的季节周期性影响, 筛选出与海表温度最相关的4个时间特征, 然后采用XGBoost模型将其融合为一个统一的长周期时间特征, 然后再与海表温数据一起作为CNN模型的输入, 来提取海表温数据之间的时空依赖特征, 并将其融合成为新的具有时间特征的海表温特征图时序数据, 由于增加了周期性时间特征, 并提取了数据之间的空间特征, 因而能够提高预测的准确度[14].
假设某海洋区域有k个观测点来观测该区域的海表面温度变化情况, 若观测次数为n, 则可以用二维向量X来表示. 向量元素
| {Z=Conv2D(X,ˆX)Y=ReLU(Z) | (2) |
本文将海洋表面温度看作视频中的一帧, 并将每一帧的温度制作成为灰度图片, 连续的多张灰度图片就构成了某个海域海洋表面温度的变化视图. 在此基础上, 利用CNN网络进行空间特征的初步提取与融合, 并将最新的PredRNN++网络引入到海表温时序预测中, 充分利用PredRNN++网络所具有的更强空间依赖特征捕获能力和自适应长短期特征提取能力, 从而实现高精度海表温的预测. PredRNN++模型由独特的Casual LSTM (时空记忆单元的级联操作)结构和GHU(梯度高速公路单元)构成, 具有对时空序列预测问题的强大预测能力, 同时也解决了PredRNN[15]网络梯度消失问题, 在视频预测领域有着很好的表现. Casual LSTM是3层级联结构, 第1层与LSTM结构类似, 其结构如图2所示.
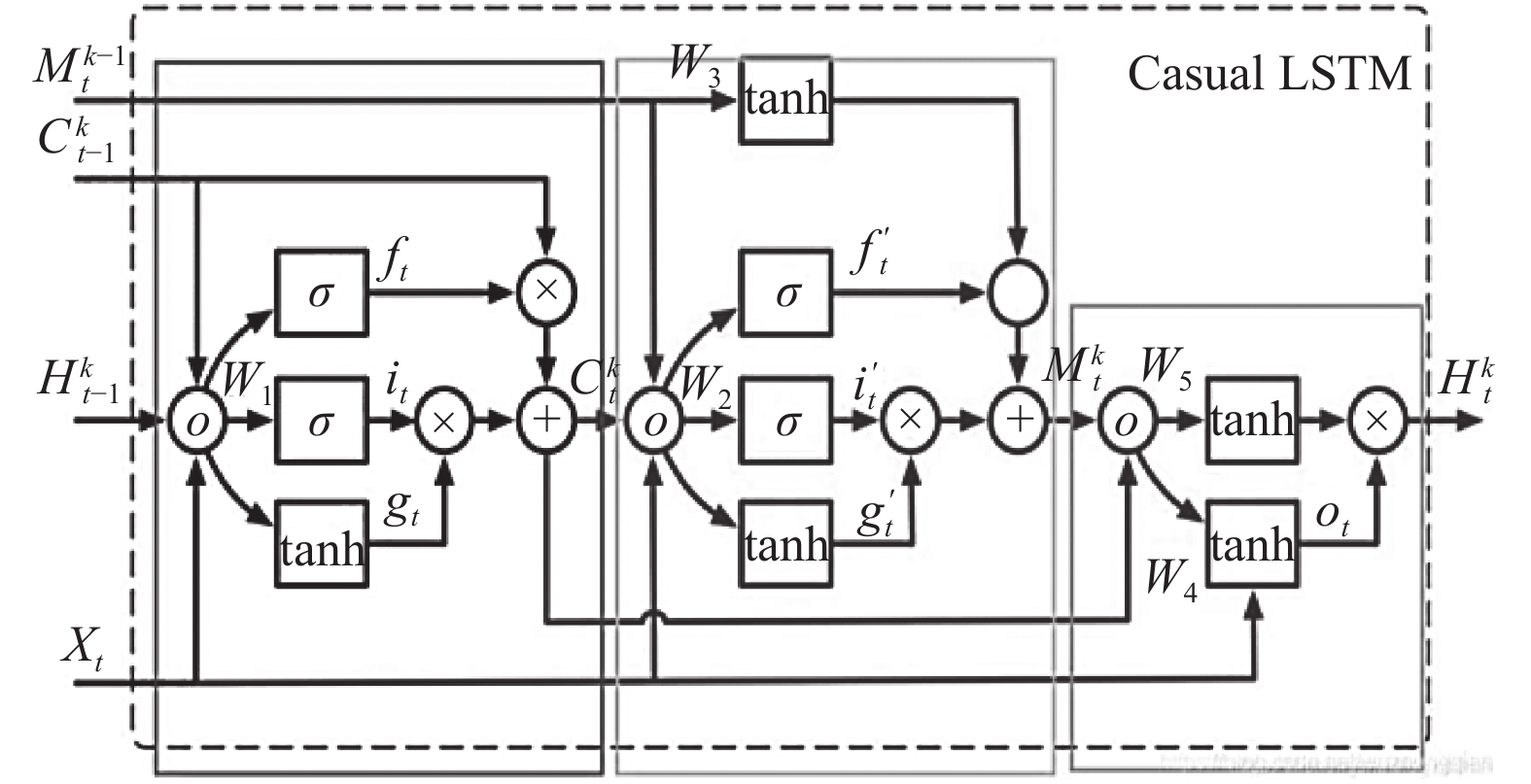
|
图 2 Casual LSTM结构 |
图2中,
| [gtitft]=[tanhσσ]∗W1∗[Xt,Xkt−1,Ckt−1] | (3) |
| Ckt=ft⊙Ckt−1+it⊙gt | (4) |
| [g′ti′tf′t]=[tanhσσ]∗W2∗[Xt,Ckt,Mk−1t] | (5) |
| Mkt=f′t⊙tanh(W3∗Mk−1t)+i′t⊙g′t | (6) |
| ot=tanh(W4∗[Xt,Ckt,Mkt]) | (7) |
| Hkt=ot⊙tanh(W5∗[Ckt,Mkt]) | (8) |
PredRNN++网络采用一种新的时空递归结构梯度高速公路单元(gradient highway unit, GHU)来直接传递时间中的重要特征, 从而在进行反向传播时能够更好地保留长期梯度, 解决梯度消失的问题. GHU的方程式可以表示如下:
| Pt=tanh(Wpx∗Xt+Wpz∗Zt−1) | (9) |
| St=σ(Wsx∗Xt+Wsz∗Zt−1) | (10) |
| Zt=St⊙Pt+(1−St)⊙Zt−1) | (11) |
其中, W为滤波器, S为选择门, P为激活函数, Z为GHU单元的输出矩阵. 本模型中, W取值维度为5×5, S的维度为8×64×16×16, P的维度为8×64×16×16. Z的输出维度为8×64×16×16.
本文采用的PredRNN++网络结构如图3所示, 主要由3层Casual LSTM结构堆叠而成, 步长t为10. 在1–2层Casual LSTM之间加入了GHU单元, 从而使得梯度在第1层与第2层之间高速传播, 缩短传播距离, 有效避免梯度消失. 后续实验也证明, GHU单元在1–2层之间的预测精度优于在2–3层之间. 具体PredRNN++网络计算机公式如下:
| H1t,C1t,M1t=Casual LSTM1(Xt,H1t−1,C1t−1,MLt−1) | (12) |
| Zt=GHU(H1t,Zt−1) | (13) |
| H2t,C2t,M2t=Casual LSTM2(Zt,H2t−1,C2t−1,M1t−1) | (14) |
| H3t,C3t,M3t=Casual LSTM3(H2t,H3t−1,C3t−1,M2t−1) | (15) |
X是输入数据, 维度为8×16×16×16, Hi是第i张图片输入到PredRNN++的混合结果, 维度大小为8×64×16×16, C是Casual LSTM共同决定门, 维度为8×64×16×16.
3 性能评估为了验证本文提出的方法的有效性, 本文设计实验对所提出的方法和模型的性能进行了测试, 下面就实验数据、实验环境及实验结果进行详细说明.
3.1 实验数据本文所采用的实验数据来自于美国联合台风预警中心 (Joint Typhoon Warning Center, JTWC), 其数据网址为
本文实验所采用的软硬件环境配置如表1所示.

|
图 3 PredRNN++网络结构 |
| 表 1 实验环境配置 |
3.3 评估指标
本文采用均方误差(MSE)和结构相似性(SSIM)评估指标来评估所提出方法的性能. 假设预测值
| MSE=1nΣni=1(ˆyi−yi)2 | (16) |
MSE的范围为
结构相似性SSIM是一种衡量图片相似度的常用指标, 假设
| SSIM(x,y)=(2μxμy+c1)(2σxy+c2)(μ2x+μ2y+c1)(σ2x+σ2y+c2) | (17) |
其中,
在实验中, 各个模型采用默认设置, 具体参数设置如下: XGBoost模型最大深度为4, 学习率为0. 05, 迭代次数为100, 叶子节点最小样本数为2, 损失函数为均方误差, L2 则化项lambda为1. CNN模型的卷积核为3
本文分别使用前面所述的西北太平洋的7 304条海表温时序数据来进行测试, 前5 844条数据作为训练集, 后1 460条数据作为测试集, 对本文提出的XGBoost-PredRNN++区域海表温预测方法进行了测试, 并和现有的PredRNN模型和ConvLSTM模型进行了比较, 下面将从3个方面给出具体实验结果.
(1) GHU位置影响分析
PredRNN++模型中, GHU单元可以放在第1层和第2层之间, 也可以放在第2层与第3层之间. 本文采用前述的海表温数据, 进行了实验研究, 实验结果如表2所示. 从中可以看出, 将GHU单元放在第1层与第2层之间的预测精度要优于放在第2层和第3层之间, 这和前述的分析一致, 同时也说明数据的原始特征对于预测结果十分重要, 因此后续实验中, 本文将GHU单元放在了第1层和第2层之间.
(2)时间特征影响分析
本文采用XGBoost模型和CNN模型进行海表面温度时间特征提取与融合处理, 为了验证其有效性, 本文进行了消融实验研究, 设计实现了无时间特征提取与融合的方法(PredRNN++), 并和本文提出的融合时间特征的XGBoost-PredRNN++方法进行了对比分析, 结果如图4和图5所示.
| 表 2 GHU单元位置对比 |

|
图 4 MSE随训练次数的变化情况 |
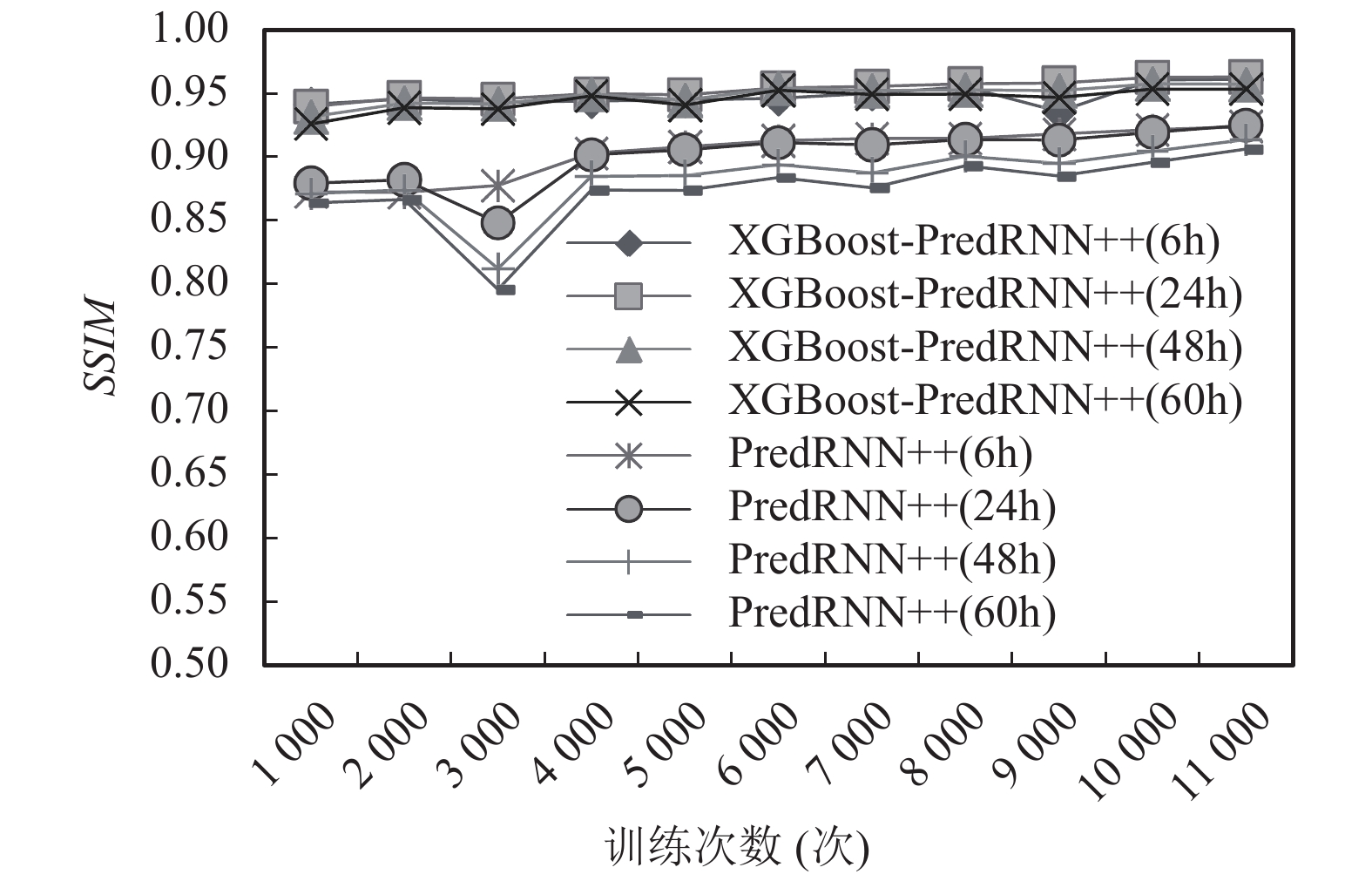
|
图 5 SSIM随训练次数的变化情况 |
图4是两种预测方法在预测步长分别为6小时、24小时、48小时和60小时时, 其预测均方误差MSE随训练次数的变化情况. 从图中可以看出, 随着训练次数的增加, 两种预测方法的MSE总体呈现下降趋势. 在每一种预测步长下, PredRNN++方法的MSE值波动较大, 其MSE值远远高于XGBoost-PredRNN++方法, 这说明XGBoost-PredRNN++方法具有很好的预测精度, 这是由于该方法考虑了数据的时间特征及其空间依赖关系, 因而取得较好预测结果. 同时可以看出随着预测步长的增加, 两种方法的预测误差也在增大, 这和理论预期相一致.
图5为两种方法在4种预测步长下的SSIM值随训练次数的变化情况. 同样可以看出, 随着训练次数的增加, 两种预测模型的SSIM值都在增大, XGBoost-PredRNN++模型的SSIM值明显大于PredRNN++模型. 同一种模型预测步长越短, 其SSIM越大. 以上说明XGBoost-PredRNN++模型具有较低的预测误差和较高的SSIM值, 明显优于原有PredRNN++模型. 这说明时间特征对于海表温的预测精度具有较大的影响, 同时也说明本文提出的融合时间特征方法XGBoost-PredRNN++是有效的.
(3)预测精度比较分析
为了验证XGBoost-PredRNN++方法的有效性, 本文进行实验研究, 并和当前主流的PredRNN预测模型和ConvLSTM预测模型进行了对比实验分析. 实验使用前述的训练和测试数据, 3种方法的输入维度均为10×64×64, 即使用过去连续60小时(每6小时采样一次, 共10个时刻)的海表温数据预测未来6小时, 24小时, 48小时和60小时的海表温度, 并分别观察MSE和SSIM两个指标的变化情况, 下面分别进行详细说明.
1) 3种方法的预测误差MSE比较. 图6是3种模型在不同预测步长下的预测误差对比. 从图6中可以看出, 3种预测方法6小时MSE值最小, 24小时MSE次之, 48小时MSE较大, 60小时MSE最大, 这和理论预测一致. 在每一种预测步长下, 3种模型的MSE总体随着训练次数增加而下降, 但是PredRNN和ConvLSTM模型的预测误差不稳定, 在下降过程中波动较大, 其MSE值下降到一定程度后开始慢慢增加, 说明这两种模型对于较少的训练数据存在过拟合情况. 而本文提出的XGBoost-PredRNN++方法预测误差随训练次数增加而稳定减少, 其MSE值明显要小于前两种模型, 即预测精度是最好的, 这主要是由于本文模型采用XGBoost提取时间周期性特征, 并采用CNN提取空间特征并进行了融合, 增加了信息含量和深度, 并采用了最新PredRNN++模型避免梯度消失和过拟合问题, 因而具有更强预测能力, 实验结果也有力的证明这一点.
2)结构相似性指标SSIM对比分析. 图7是3种方法在不同预测步长下的SSIM比较. 从图中可以看出, 在不同预测步长的实验中, 3种方法的SSIM值总体随着训练次数的增加而增大. PredRNN和ConvLSTM模型的SSIM值增加到一定程度后有所降低, 这是由于训练次数过多导致模型过拟合引起的. 在4种不同预测步长的测试中, SSIM值从大到小分别为6小时SSIM值、24小时SSIM值、48小时SSIM和60小时SSIM值, 这和理论预测相一致. 在3种预测模型中, 本文提出的XGBoost-RredRNN++方法的SSIM值随训练次数增加而稳定增加, 其SSIM值明显要高于前两种模型, 这说明本文提出的模型具有很高的预测精度, 明显优于PredRNN和ConvLSTM模型, 主要原因是本文采用了XGBoost和CNN网络融合了周期性时间特征, 并用最新的PredRNN++模型, 因而达到了较好的预测效果. 从SSIM指标的比较可以看出, 本文提出的XGBoost-PredRNN++海表温预测方法, 具有较好的预测能力. 从上述MSE和SSIM两个指标的比较可以看出, 本文提出的XGBoost-PredRNN++方法具有很高的预测精度, 在训练的初始阶段就能达到不错的效果, 明显优于现有的ConvLSTM和PredRNN预测方法.
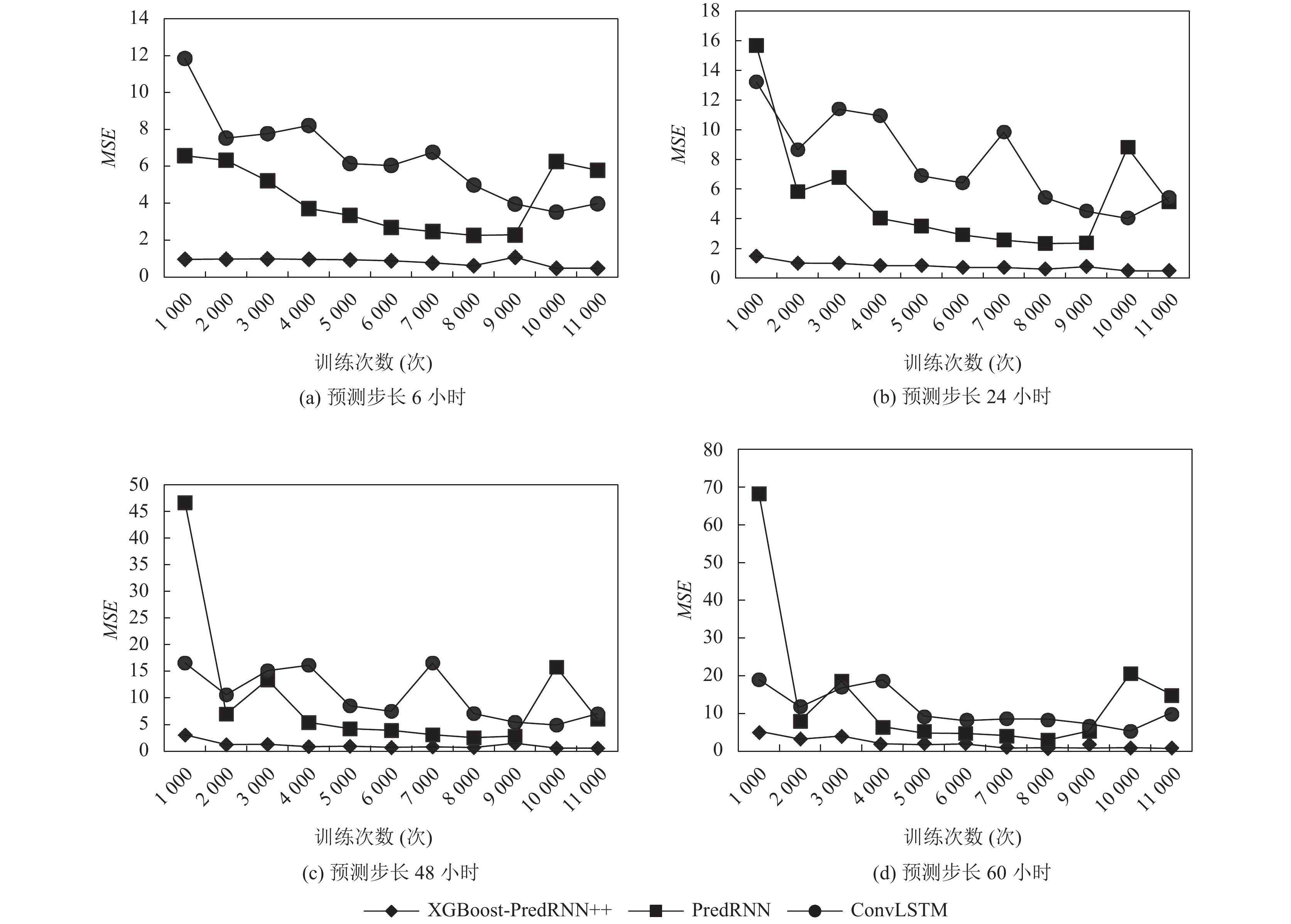
|
图 6 不同预测步长下3种预测方法误差比较 |
为了进一步分析模型的预测效果, 本文也测试了融合时间特征后的SST数据在ConvLSTM和PredRNN模型上的预测结果. 在预测步长分别为6小时、24小时、48小时和60小时时, 从实验结果能够看出, 采用XGBoost提取时间特征后, 几种模型的预测大明显提高, 本文提出的XGBoost-PredRNN++方法仍然是这几种方法中精度最高的, 明显优于其他方法. 由于篇幅有限, 这里仅给出预测步长为6小时时, 几种模型的实验结果, 见表3.
4 结论海表面温度是进行海洋环境信息预测预报的重要因子, 对于海上捕捞、水产养殖、海洋气象、航海等具有重要影响, 因此准确预测海表面温度对于海洋产业和相关科学研究具有非常重要的意义. 本文结合先进的深度学习技术, 提出了一种基于XGBoost结合PredRNN++的区域海表温预测方法. 该方法首先将某个区域的海表面温度处理成灰度图片, 然后利用XGBoost模型提取季节周期性特征, 并采用CNN模型进行特征融合, 在此基础上采用最新的PredRNN++时序数据预测网络, 实现了区域海表温度的预测. 一系列真实数据上的实验结果表明, 本文提出的基于XGBoost-PredRNN++的海表温预测方法, 明显优于现有的ConvLSTM和PredRNN模型, 取得了较好的预测精度. 后续将扩大模型的应用范围, 进一步优化模型的结构, 进一步提升模型的预测精度和效率.

|
图 7 不同预测时长3种模型的SSIM对比 |
| 表 3 几种模型实验结果 |
| [1] |
李嘉康, 赵颖, 廖洪林, 等. 基于改进EMD算法和BP神经网络的SST预测研究. 气候与环境研究, 2017, 22(5): 587-600. DOI:10.3878/j.issn.1006-9585.2017.16180 |
| [2] |
Xiao CJ, Chen NC, Hu CL, et al. A spatiotemporal deep learning model for sea surface temperature field prediction using time-series satellite data. Environmental Modelling & Software, 2019, 120: 104502. |
| [3] |
Patil K, Deo MC, Ravichandran M. Prediction of sea surface temperature by combining numerical and neural techniques. Journal of Atmospheric and Oceanic Technology, 2016, 33(8): 1715-1726. DOI:10.1175/JTECH-D-15-0213.1 |
| [4] |
Xue Y, Leetmaa A. Forecasts of tropical Pacific SST and sea level using a Markov model. Geophysical Research Letters, 2000, 27(17): 2701-2704. DOI:10.1029/1999GL011107 |
| [5] |
Lins ID, Das Chagas Moura M, Silva MA, et al. Sea surface temperature prediction via support vector machines combined with particle swarm optimization. Proceedings of the 10th International Probabilistic Safety Assessment & Management Conference. Shanghai: PSAM, 2010. 956–966.
|
| [6] |
周志华, 陈世福. 神经网络集成. 计算机学报, 2002, 25(1): 1-8. DOI:10.3321/j.issn:0254-4164.2002.01.001 |
| [7] |
Zhang Q, Wang H, Dong JY, et al. Prediction of sea surface temperature using long short-term memory. IEEE Geoscience and Remote Sensing Letters, 2017, 14(10): 1745-1749. DOI:10.1109/LGRS.2017.2733548 |
| [8] |
Mu B, Li J, Yuan SJ, et al. Prediction of North Atlantic oscillation index associated with the sea level pressure using DWT-LSTM and DWT-ConvLSTM networks. Mathematical Problems in Engineering, 2020, 2020: 2413041. |
| [9] |
张驰, 孙佳龙, 秦江涛, 等. 基于支持向量回归的海洋次表层温度异常预测. 江苏海洋大学学报(自然科学版), 2020, 29(2): 50-57. |
| [10] |
吴琦. 基于深度学习的海洋表面温度预测方法研究[硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2020
|
| [11] |
韩震, 张雪薇, 周玮辰. 一种基于遥感数据的多层ConvLSTM海表面温度预测计算方法: 中国, 202011235234.6, 2021-03-23.
|
| [12] |
Wang YB, Gao ZF, Long MS, et al. PredRNN++: Towards a resolution of the deep-in-time dilemma in spatiotemporal predictive learning. Proceedings of the 35th International Conference on Machine Learning. Stockholm: ICML, 2018. 5123–5132.
|
| [13] |
Chen TQ, Guestrin C. XGBoost: A scalable tree boosting system. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco: ACM, 2016. 785–794.
|
| [14] |
Qiao BY, Wu ZQ, Tang Z, et al. Sea surface temperature prediction approach based on 3D CNN and LSTM with attention mechanism. 2021 23rd International Conference on Advanced Communication Technology (ICACT). PyeongChang: IEEE, 2021. 342–347.
|
| [15] |
Wang YB, Long MS, Wang JM, et al. PredRNN: Recurrent neural networks for predictive learning using spatiotemporal LSTMs. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: NIPS, 2017. 879–888.
|
 2022, Vol. 31
2022, Vol. 31



