1 引言

随着我国物流行业的发展, 以及劳动力成本的不断上升, 自动化仓储物流近年来不断发展, 自动化运输设备的需求不断提升. 自动叉车是一种自动驾驶车辆, 可以完成对货物的自动搬运, 能有效降低人力成本, 被广泛应用于自动化物流中. 在仓储物流中, 因为货物的外观存在大小、形状、颜色等明显的差异, 所以直接对货物定位非常困难. 而托盘用于承载和搬运货物, 且具有通用的规格和形状. 因此自动叉车一般通过托盘定位来叉取和搬运货物.

托盘定位方法主要分为以下3类: 第1类是基于激光雷达传感器的检测方法. 赵俊宏等人^[1]根据2D激光雷达扫描结果分析托盘的距离和姿态. 虽然基于激光雷达的方法对光照有比较好的鲁棒性, 但是激光雷达成本高昂、不利于大规模普及. 第2类是传统图像处理的方法. Cui等人^[2]使用传统图像处理的方法直接分析图像本身特征, 如角点、边缘和颜色等特征来检测托盘. Seelinger等人^[3]提出了一种利用标签来定位托盘的方法, 但存在标签安装和维护的成本, 而且在使用过程中容易损坏. 武文汉^[4]使用tof相机和纸标签分别完成了对远距离托盘和近距离托盘的检测定位, 但是算法速度较慢, 实时性不高, 因此难以应用于工业场景. 此类方法易受到光照等环境因素影响, 鲁棒性较差. 第3类是基于深度学习的托盘检测方法. Mohamed等人^[5]使用了Faster R-CNN^[6]来训练模型, 实现了对托盘的定位. 李天健等人^[7]使用改进的SSD算法^[8]实现了仓储环境中托盘的定位. 叶伟^[9]首先使用YOLOv4算法^[10] 对托盘进行目标检测, 再使用GrabCut分割方法^[11]提高精度. 此类方法准确率高, 抗干扰能力强, 而且成本远低于激光雷达, 适合部署于实际工业场景中.

在实际物流场景中, 自动叉车为完成自动叉卸货任务, 需要将叉铲对准托盘中心点, 将叉铲方向与托盘水平方向保持一致, 以保证安全无碰撞地叉取托盘. 因此托盘定位任务可分为2部分: (1)托盘中心点定位; (2)托盘水平方向估计. 目前基于目标检测的托盘定位算法, 一般使用矩形框进行定位, 只能检测托盘区域位置, 使用目标框中心点对托盘中心点定位精度不高, 且无法有效估计托盘水平方向, 难以应用于自动叉车系统中. 基于此问题, 本文提出了一种基于改进CenterNet^[12]的托盘定位方法. 在目标检测的基础上, 通过托盘关键点检测, 在精准定位托盘中心点的同时, 完成对托盘水平方向的估计.

本文的贡献如下: (1)本文使用迁移学习的方法, 将人体姿态估计引入托盘定位任务, 完成了托盘关键点定位. (2)针对托盘定位任务, 本文对CenterNet网络做出2点改进: 1)改进关键点分组方法, 提出基于托盘关键点位置的区域约束方法; 2)提出关键点回归评价指标与自适应补偿, 提高关键点检测精度. (3)在关键点定位的基础上, 提出基于几何约束的托盘中心点计算方法, 以及托盘水平方向估计方法. (4)使用RGB摄像头拍摄并标注了托盘数据集.

2 相关工作

Mohamed等人^[5]、李天健等人^[7]与叶伟^[9]所使用的目标检测算法, 都需要人工设计特定长宽比的锚框, 以训练出更好的检测器. 但是人工设计的锚框难以兼顾所有长宽比的目标, 针对此问题, Law等人提出了 CornerNet^[13], 通过检测目标的左上角和右下角关键点来检测目标, 不需要人工设计锚框. ExtremeNet^[14]通过检测目标的顶部、底部、最左侧、最右侧和中心点这5点信息来完成目标检测. 以上两种无锚框目标检测算法在关键点检测之后, 都需要进行复杂且耗时的后处理步骤, 这大大降低了算法的实时性. 而Zhou等人^[12]提出的CenterNet较好解决了这个问题. CenterNet将目标检测简化成为对目标中心点的检测. 使用3×3最大池化选取目标中心点, 从而避免了NMS等后处理步骤.

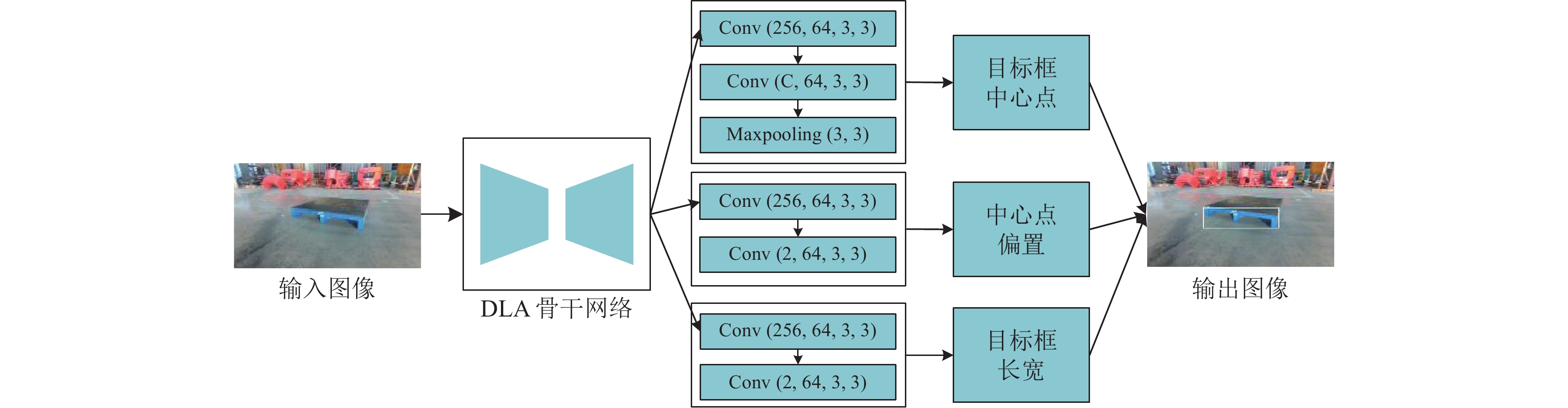
2.1 CenterNet目标检测算法

CenterNet可选取3种不同的骨干网络, 分别为Hourglass^[15]、ResNet^[16]、DLA^[17], 都是编码-解码结构. 其中Hourglass在3种骨干网络中精度最高但预测速度较慢, 而使用DLA可以得到较好的精度以及较快的速度, 因此选择DLA作为算法的骨干网络. 如图1所示, CenterNet网络的头部可分为3个互相独立的部分, 分别完成目标框中心点、中心点偏置和目标框宽高的检测. CenterNet使用二维高斯核函数将输入图像映射成为热力图作为训练目标. 二维高斯核函数的公式为:

$ {Y_{xyc}}{\text{ = }}\exp \left( { - \frac{{{{(x - {{\tilde p}_x})}^2} + {{(y - {{\tilde p}_y})}^2}}}{{2{\sigma _p}^2}}} \right) $

(1)

其中, ${Y_{xyc}}$ 是归一化后的热力图, $(x, y)$ 为热力图中点的坐标, $({\tilde p_x}, {\tilde p_y})$ 为目标中心点4倍下采样后的坐标(向下取整), ${\sigma _p}$ 是自适应标准差^[13]. CenterNet目标检测任务中损失函数为 ${L_{\det }}$ :

$ {L_{\det }} = {L_k} + {\lambda _{\rm size}}{L_{\rm size}} + {\lambda _{\rm off}}{L_{\rm off}} $

(2)

$ {L_{\det }} $ 由3部分组成, 分别为置信度损失 $ {L_k} $ 、下采样损失 ${L_{\rm off}}$ 和目标框宽高损失 ${L_{\rm size}}$ , 超参数 ${\lambda _{\rm size}}$ 为0.1, ${\lambda _{\rm off}}$ 为1. $ {L_k} $ 用来训练目标中心点位置. 由于正样本远少于负样本数量, 为了使模型在训练时更加关注于难检测的样本, $ {L_k} $ 使用focal loss^[18]. 因为输出的热力特征图为原图大小的0.25倍, 所以中心点位置预测存在离散化误差, ${L_{\rm off}}$ 用来训练下采样偏置的大小.

$ {L_K} = \frac{{ - 1}}{N}\sum\limits_{xyc} {\left\{ {\begin{array}{*{20}{l}} {{{(1 - {{\hat Y}_{xyc}})}^\alpha }\log ({{\hat Y}_{xyc}})},&{{\text{if}}{\kern 1pt} {\kern 1pt} {Y_{xyc}} = 1} \\ {\begin{array}{*{20}{l}} {{{(1 - {Y_{xyc}})}^\beta }{{({{\hat Y}_{xyc}})}^\alpha }} \\ {\log (1 - {{\hat Y}_{xyc}})}, \end{array}}&{{\text{otherwise}}} \end{array}} \right.} $

(3)

其中, $ {Y_{xyc}} = 1 $ 表示正样本, $ {\hat Y_{xyc}} $ 是目标检测的预测值. $N$ 是图像中正样本的数量. 超参数 $\alpha $ 和 $\;\beta $ 分别为2和4.

$ {L_{\rm off}} = \frac{1}{N}\sum\limits_p {\left| {{{\hat O}_{\tilde p}} - \left(\frac{p}{R} - \tilde p\right)} \right|} $

(4)

其中, $ {\hat O_{\tilde p}} $ 为预测的中心点偏置大小, $p$ 为中心点真实值坐标, $R$ 为下采样倍数, 中心点坐标 $p$ 下采样 $R$ 倍后向下取整得到 $\tilde p$ .

$ {L_{\rm size}} = \frac{1}{N}\sum\limits_{k = 1}^N {\left| {{{\hat S}_{pk}} - {s_k}} \right|} $

(5)

其中, ${s_k} = ({w^k}, {h^k})$ 为目标 $k$ 的宽高, ${{{\hat S_{pk}}}}$ 为宽高估计值.

2.2 CenterNet人体姿态估计

CenterNet具有良好可扩展性, 可以将CenterNet应用到人体姿势估计任务中. 人体姿势估计的任务要求估计出图像中每个人体实例的人体关键点位置. 首先直接回归每个关键点与中心点之间的偏移量, 得到关键点的初步定位, 使用L1损失函数 ${L_{\rm reg}}$ 进行训练. 然后为了细化关键点定位, 类似目标检测, 通过热力特征图以及中心点偏置来进行关键点检测, 并以初步定位位置为依据进行分组. 关键点检测使用目标检测任务中的置信度损失 ${L_K}$ 和偏移损失 ${L_{\rm off}}$ 进行训练.

$ {L_{\rm reg}} = \frac{1}{N}\sum\limits_{k = 1}^N {\frac{1}{{\displaystyle\sum\limits_{i = 1}^E {{M_{ki}}} }}\displaystyle\sum\limits_{j = 1}^E {\left| {{{\hat J}_{kj}} - {J_{kj}}} \right| \times {M_{kj}}} } $

(6)

其中, $E$ 为关键点个数, $M$ 为关键点掩码, 对于图像中被遮挡等不可见的关键点 ${M_{ki}} = 0$ , 可见关键点 ${M_{ki}} = 1$ . ${\hat J_{kj}} = ({x_{kj}}, {y_{kj}})$ 为第 $k$ 个目标的第 $j$ 个关键点坐标的偏移量. 关键点检测失函数为 ${L_{\rm key}} = {L_k} + {L_{\rm off}} + {L_{\rm reg}}$ , 得到总损失函数 $Loss$ :

$ Loss = {L_{\det }} + {L_{\rm key}} $

(7)

在多人姿态检测场景中, 通过关键点检测得到的结果无法确定属于哪个人体实例. CenterNet使用初步定位结果作为分组依据, 使用3项规则进行匹配: (1)所匹配的热力特征图关键点置信度得分大于0.1; (2)匹配欧氏距离最近的初步定位位置; (3)仅匹配目标框内的关键点.

3 算法 3.1 算法框架

如图2所示, 不同类型托盘外观存在一定差异, 主要可分为两柱形托盘和三柱形托盘. 为适应不同类型托盘, 选取托盘正面外轮廓的4个角点作为关键点. 从左上角点开始顺时针将关键点分别编号为1, 2, 3, 4. 托盘定位算法可分为托盘检测、托盘关键点检测以及托盘中心点计算与水平方向估计的后处理部分. 算法框架如图3所示, 其具体流程如算法1所示. 算法1中的所有步骤均在图3中标出, 其中本文提出的工作用星号标记, 在原算法基础上改进的工作用菱形标记.

算法1. 托盘定位算法

1) 将输入图片通过仿射变换转为512×512固定大小输入;

2) 通过骨干网络生成128×128高分辨率热力特征图;

3) 基于热力特征图进行托盘检测获得托盘目标框;

4) 直接回归得到托盘关键点初步定位位置;

5) 使用自适应补偿对初步定位位置进行调整;

6) 使用热力特征图进行关键点检测;

7) 以托盘目标框和关键点初步定位位置为分组依据, 对步骤6)的结果进行关键点分组;

8) 基于托盘关键点定位结果, 计算托盘中心点, 估计托盘的水平方向.

3.2 基于关键点位置的区域约束

CenterNet网络为了对关键点进行分组, 只对目标框内的关键点进行匹配.由于托盘关键点分布于托盘边缘, 托盘检测轻微的精度误差就可能导致目标框无法包含关键点位置, 严重影响关键点分组结果, 针对此问题, 本文根据托盘关键点分布特点, 如图4所示, 分别为左右两边的关键点设置了两组约束区域.

$\left\{ { \begin{gathered} {P_{\rm right}} = \left\{ {\begin{array}{*{20}{l}} {\left| {x - {x_m} - 0.5w} \right| < 0.15w} \\ {\left| {y - {y_m}} \right| < 0.6h} \end{array}} \right. \\ {P_{\rm left}} = \left\{ {\begin{array}{*{20}{l}} {\left| {x - {x_m} + 0.5w} \right| < 0.15w} \\ {\left| {y - {y_m}} \right| < 0.6h} \end{array}} \right. \\ \end{gathered}} \right. $

(8)

其中, ${P_{\rm left}}$ 和 ${P_{\rm right}}$ 分别为托盘左右两边关键点的约束区域, $({x_m}, {y_m})$ 为托盘目标框中心点, $(w, h)$ 为托盘目标框宽高, $(x, y)$ 为图像中点的坐标.

3.3 关键点回归自适应补偿

关键点回归结果作为关键点定位的初步结果, 是关键点检测的分组依据. 较差的关键点回归结果, 会直接影响关键点定位的最终精度. 因为关键点分布于托盘外边缘, 所以关键点的最小外接矩形与托盘的目标框相近. 托盘目标框中心点与第 $i$ 个关键点的欧式距离为 $D_i^{\rm reg}$ , 目标框中心点与目标框角点欧式距离 ${D_{\det }}$ . ${D_{\det }}$ 反映了目标的大小情况, 对 $D_i^{\rm reg}$ 有一定参考意义. 在 $D_i^{\rm reg}$ 与 ${D_{\det }}$ 数值差距较大时, 认为托盘关键点回归效果较差. 根据二者大小关系得到关键点回归评价指标 $\;\rho _i^{\rm reg}$ .

$ \rho _i^{\rm reg} = 1 - \min \left(1, \left| {1 - \frac{{D_i^{\rm reg}}}{{{D_{\det }}}}} \right|\right) $

(9)

其中, $\;\rho _i^{\rm reg}$ 为第 $i$ 个关键点回归评价, $\;\rho _i^{\rm reg}$ 越高代表回归效果越好, 根据 $\;\rho _i^{\rm reg}$ 使用对应的目标框角点坐标对关键点回归结果进行补偿.

$ P_i^{\rm reg} = \rho _i^{\rm reg}P_i^{\rm reg} + (1 - \rho _i^{\rm reg})P_i^{\rm rect} $

(10)

其中, $P_i^{\rm reg} = ({x_i}, {y_i})$ 为第 $i$ 个托盘关键点回归的坐标. 将目标框角点从左上角按顺时针编号为1, 2, 3, 4, $P_i^{\rm rect} = (x_i^{\rm rect}, y_i^{\rm rect})$ 为第 $i$ 个托盘目标框角点坐标. 当 $D_i^{\rm reg}$ 与 ${D_{\det }}$ 接近时, $\;\rho _i^{\rm reg}$ 接近于1, 关键点回归效果好, 补偿比重小; 当 $D_i^{\rm reg}$ 与 ${D_{\det }}$ 差距较大时, $\;\rho _i^{\rm reg}$ 接近于0, 关键点回归效果差, 补偿比重大.

3.4 基于几何约束的托盘中心点计算方法

自动叉车相机与托盘空间关系如图5所示, 坐标系 ${\textit{z}}$ 轴指向相机正前方, $y$ 轴垂直向下. 因为托盘承载货物一般水平放置于地面, 所以设定托盘放置平面与自动叉车相机坐标系 $x{\textit{z}}$ 平面平行. ${P_i}$ 为托盘关键点 $(i = 1, 2, 3, 4)$ , ${P_i}$ 在自动叉车相机坐标系中的坐标为 $({X_i}, {Y_i}, {Z_i})$ . ${P_c}$ 为托盘中心点, 在自动叉车相机坐标系中的坐标为 $({X_c}, {Y_c}, {Z_c})$ . ${p_i}$ 为托盘关键点在归一化平面中的坐标 $({x_i}, {y_i})$ , ${p_c}$ 为托盘中心点在归一化平面的坐标 $({x_c}, {y_c})$ . 基于针孔相机模型, 本文提出基于几何约束的托盘中心点计算方法, 通过托盘关键点计算托盘中心点.

$ \left( {\begin{array}{*{20}{c}} {{x_i}} \\ {{y_i}} \\ 1 \end{array}} \right) = \frac{1}{{{Z_i}}}\left( {\begin{array}{*{20}{c}} {{f_x}}&0&{{c_x}} \\ 0&{{f_y}}&{{c_y}} \\ 0&0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{X_i}} \\ {{Y_i}} \\ {{Z_i}} \end{array}} \right) \triangleq \frac{1}{{{Z_i}}}K{P_i} $

(11)

其中, $K$ 为相机内参矩阵. 因为托盘放置平面与自动叉车相机坐标系 $x{\textit{z}}$ 平面平行, 在自动叉车相机坐标系中 ${Z_1} = {Z_4}$ , ${Z_2} = {Z_3}$ , 根据式(11)可得:

$ \mu = \frac{{{Z_1}}}{{{Z_2}}} = \frac{{{y_2} - {y_3}}}{{{y_1} - {y_4}}} $

(12)

托盘中心点 ${P_c}$ 与托盘关键点的空间关系为:

$ {X_c} = 0.5({X_1} + {X_2}) = 0.5({X_3} + {X_4}) $

(13)

$ {Y_c} = 0.5({Y_1} + {Y_4}) = 0.5({Y_2} + {Y_3}) $

(14)

$ {Z_c} = 0.5({Z_1} + {Z_2}) = 0.5({Z_3} + {Z_4}) $

(15)

将式(12)–式(15)带入式(11)得到托盘中心点坐标 $({x_c}, {y_c})$ :

$ \left( {\begin{array}{*{20}{c}} {{x_c}} \\ {{y_c}} \end{array}} \right) = \frac{1}{{2(\mu + 1)}}\left( {\begin{array}{*{20}{c}} {2{x_1}}&{2{x_2}} \\ {{y_1} + {y_4}}&{{y_2} + {y_3}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} 1 \\ \mu \end{array}} \right) $

(16)

3.5 托盘水平方向估计

为了估计托盘水平方向, 本文在自动叉车相机坐标系中分析了托盘关键点坐标与水平方向的关系. 如图5, 定义托盘水平方向的角度 $\theta $ 为托盘正面所在平面 ${P_1}{P_2}{P_3}$ 与坐标系 $x$ 轴正方向所成夹角, 设定 ${Z_1} < {Z_2}$ 时 $\theta $ 为正, 反之为负. 通过托盘关键点 ${p_1}$ 和 ${p_2}$ 的 $y$ 坐标之差 $\Delta y = {y_1} - {y_2}$ 来估计托盘水平方向. 关键点 ${P_1}$ 和 ${P_2}$ 在空间中的关系如式(17), 其中 $W$ 为关键点 ${P_1}$ 和 ${P_2}$ 的空间距离, 也即托盘正面长度.

$ \left( {\begin{array}{*{20}{c}} {{X_2}} \\ {{Y_2}} \\ {{Z_2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{X_1}} \\ {{Y_1}} \\ {{Z_1}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {W\cos \theta } \\ 0 \\ {W\sin \theta } \end{array}} \right) $

(17)

将式(17)带入式(11), 得到:

$ \Delta y = \frac{{{f_y}{Y_1}W}}{{{Z_1}}}\left( {\frac{{\sin \theta }}{{{Z_1} + W\sin \theta }}} \right) $

(18)

在 ${Z_1}$ 不变的前提下, $\Delta y$ 对 $\theta $ 求导:

$ \Delta y' = \frac{{{f_y}{Y_1}W\cos \theta }}{{{{({Z_1} + W\sin \theta )}^2}}} $

(19)

由式(18)和式(19)可知, 当 $\theta $ 为0时, ${p_1}$ 和 ${p_2}$ 的y坐标之差 $\Delta y$ 为0; 当 $\theta $ 大于0时, $\Delta y$ 大于0; 当 $\theta $ 小于0时, $\Delta y$ 小于0. 同一距离下 $\Delta y$ 在 $\theta \in \left[ { - 0.5\pi , 0.5\pi } \right]$ 的区间内单调递增, 因此通过 $\Delta y$ 可以有效估计托盘水平方向. 考虑到关键点检测误差, 设 $\Delta y \in \left[ { - 10, 10} \right]$ 时, 托盘水平方向正对; $\Delta y < - 10$ 时, 托盘水平方向左偏; $\Delta y > 10$ 时, 托盘水平方向右偏.

4 实验分析 4.1 数据集

本文采用的数据集为笔者自己采集制作的数据集. 笔者使用 $1920 \times 1080$ 分辨率的RGB摄像头拍摄了一个数据集. 如图6所示, 摄像头安装在自动叉车系统前方的叉齿架上. 叉齿架可上升下降, 在不同高度拍摄托盘照片. 整个数据集拍摄了合力叉车公司2种类型的托盘, 在多个场景中采集了时长60分钟的视频. 从中选取1 251帧图片, 使用coco-annotator工具标注. 将其中80%图片作为训练集, 10%用作验证集, 10%用作测试集.

4.2 实验过程

实验所用的机器配置如表1所示. 实验有两个评价指标. 第1个是关键点定位精度指标 ${{A}}{{{P}}^{{\text{kp}}}}$ , 用以衡量关键点定位的精度, ${{A}}{{{P}}^{{\text{kp}}}}$ 越高代表托盘关键点定位越精确. 第2个指标是笔者提出的托盘中心点定位指标平均定位精度 ${{ALP}}$ (average location precision), 通过托盘定位中心点与托盘实际中心点的欧式距离 ${D_c}$ 和托盘真实框面积 ${A_{\rm bbox}}$ 得到.

$ ALP = 1 - \frac{1}{N}\sum\limits_{i = 1}^N {\frac{{{D_c}}}{{\sqrt[2]{{{A_{\rm bbox}}}}}}} $

(20)

在 ${{ALP}}$ 中只考虑检测目标框和真实框 ${\text{IOU}}$ 大于0.5的样本, 式(20)中 $N$ 为样本数量. ${{ALP}}$ 越高代表对托盘中心点定位越准确. 因为数据集规模较小, 模型在训练时随机对输入图像进行反转, 同时叠加一个服从正态分布的随机白噪声, 用以提高模型的鲁棒性. 学习率设为0.000 25, 训练的epoch设为120, 为了防止过拟合, 笔者在验证集Loss不再下降时停止训练.

4.3 实验结果

为了验证本文对CenterNet算法提出改进方法的有效性, 笔者使用关键点定位精度指标 ${{A}}{{{P}}^{{\text{kp}}}}$ , 做了模型自身的纵向对比实验. 将关键点位置约束设为改进1, 关键点回归自适应补偿设为改进2, 实验结果如表2所示, 两项改进均显著提高了 ${{A}}{{{P}}^{{\text{kp}}}}$ , 证明了本文方法的有效性.

为了验证本文方法定位托盘中心点的有效性, 笔者使用评价指标 ${{ALP}}$ , 与其他目标检测算法进行了横向对比实验. 对于其他目标检测算法, 笔者使用托盘目标框中心点作为托盘中心点的定位结果. 实验结果如表3所示. 可以看到, 本文方法对比其他目标检测算法, 中心点定位精度均有显著提高.

为验证本文方法估计托盘水平方向的有效性, 笔者分别选取托盘左偏、右偏与正对3种具有代表性的情况进行实际测试. 结果如图7所示, 图7(a)中, 关键点 ${p_1}$ 和 ${p_2}$ 的 $y$ 坐标之差 $\Delta y = - 75$ , 托盘水平方向左偏; 图7(b)中, $\Delta y = 1$ , 托盘水平方向正对; 图7(c)中, $\Delta y = 59$ , 托盘水平方向右偏. 通过 $\Delta y$ 可有效对托盘水平方向进行估计.

5 结论与展望

本文提出了一种基于关键点检测的托盘定位方法. 首先将CenterNet人体姿态估计引入到托盘定位任务中, 完成对托盘外边缘4个关键点的检测. 然后改进关键点分组约束, 并提出关键点回归自适应补偿, 显著提高了托盘关键点定位精度. 在关键点检测的基础上, 提出了托盘中心点计算与托盘水平方向估计方法, 提高了托盘中心点的定位精度, 解决了目前目标检测算法无法有效估计托盘水平方向的问题. 与其他托盘检测方法相比, 本文提出的方法表现优异, 下一步计划将本文方法应用于自动叉车系统中.