随着网络技术和微电子技术的发展, 智能电网应运而生, 它作为下一代电网技术受到世界各国的广泛关注. 在我国智能电网已经成为国家重大发展战略之一, 2019年, 国家电网提出要求全面加快智能电网建设的战略部署, 随后国有电力企业投入大量的人力、物力和财力开展相关研究和试点工作^[1]. 智能电网将传统电网与信息技术相融合, 支持双向通信, 能够对发电、输电和用电的实时状况进行采集和分析, 通过信息流和能量流的双向控制实现能源优化, 并且减少碳排放量, 与新时代的环保理念相呼应^[2].

智能电网周期性的收集智能电表的数据并在远程云服务器上进行处理和分析. 然而, 智能电网规模的不断扩大, 实时数据量的急剧增加, 使得有限的带宽资源无法满足远程云服务器实时数据处理对传输低延时的要求. 2012年, “雾计算”的概念由思科公司率先提出, 相比于单一的云计算架构, 雾计算在延迟、聚合、位置感知和地理分布提供了额外的能力. 基于该计算模式, 智能电表数据上传到云服务器之前, 先在雾节点进行数据聚合处理, 从而节约了带宽资源, 满足实时数据处理的需求.

然而, 雾辅助智能电网的架构仍然存在用户隐私泄露的风险. 在整个数据收集过程中, 智能电表周期的上报用户电量数据(如10–15 min上报一次^[3]), 大量细粒度的电量数据使得恶意的攻击者可以推断出用户的行为活动、生活习惯、经济状况以及其他一些隐私信息. 例如, 结合电器电力消耗情况在时间维度上的关联性, 可表征用电设备的使用情况, 而此类隐私信息将被第三方用于提供准确的商业营销, 以及被恶意人员用于判断用户是否居家从而实现入室盗窃. 而雾辅助智能电网的架构因为引入了第三方公司提供的雾节点, 如Cisco, 反而使得隐私泄露的风险增大^[4].

为了保护用户的隐私, 一些学者提出了轻量级的数据聚合方案^[5–7]. 此类方案将一组和为零的随机整数作为盲因子分配给智能电表和聚合器, 智能电表利用盲因子对电量数据进行加密, 聚合器消除盲因子得到聚合密文, 最后控制中心解密获得聚合结果. 在这个过程中, 控制中心无法得到任一智能电表的具体数据, 在一定的程度上保护了用户的隐私. 但如果其中一个智能电表故障, 或者网络连接中断, 数据提交失败, 将使得整个密文聚合过程中的盲因子无法消除, 导致控制中心无法获得正确聚合结果, 因而方案不具备容错功能.

一些学者提出其他类别的数据聚合方案, 并尝试解决容错问题, 但由于内在的运行机制, 给系统带来额外的计算开销或者通信开销. 文献[8]中, Xue等人提出了一种无可信权威中心的数据聚合方案, 该方案对隐私数据进行同态加密, 并通过Shamir秘密共享方案实现了容错功能. 但方案容错机制中用户组重新协商密钥的过程将占用额外的计算和通信资源. Wang等人^[9]提出一种支持容错的多子集数据聚合方案, 该方案同样存在效率较低的问题. 当某些智能电表无法正常工作时, 聚合器将发布事件和故障智能电表的标识, 随后相关区域内的智能电表必须重新协商更新盲因子, 再加密数据后上报, 这些给系统带来了额外的开销. Lyu等人^[10]提出了一种雾计算架构下的差分隐私数据聚合方案, 该方案使用OTP (one-time-pad)加密算法和高斯机制来最小化数据隐私泄露. 但该方案每次执行加密操作之前需要生成新的密钥; 并且当设备出现故障需要容错处理时, 需要雾节点和可信任中心进行交互, 这些都给系统带来额外的负担. 另外, 这类满足差分隐私的数据聚合方案^{[10, 11]}, 往往只能得到数据聚合结果的近似值, 方案设计者需要在数据隐私性和可用性之间取得一个平衡.

此外, 整个数据收集应用系统部署在大范围复杂的环境下, 容易受到各种外部攻击. Pan等人^[12]利用中国剩余定理实现了多维数据聚合, 但该方案无法抵御篡改和伪造等攻击, 不能保证数据的完整性. Li等人^[13]基于Paillier同态加密算法提出了一种多子集的隐私保护数据聚合方案, 但该方案无法确认数据源的合法性和确保数据的完整性, 给系统带来了安全隐患.

针对现有方案存在的不足, 本文提出了一种新的高效隐私保护数据聚合方案. 本文工作包含以下3点: (1)将BGN同态加密算法和Shamir秘密共享方案进行巧妙地结合, 构建了扩展的BGN同态加密算法, 确保了用户数据的隐私性. (2)实现了两种容错措施, 当智能电表端电量数据无法到达服务端时, 或者服务端云服务器出现故障时, 系统还能继续运作. (3)基于椭圆曲线离散对数困难问题构造了高效的签名认证方法, 实现了数据完整性和数据源合法性的有效验证. 此外, 采用标量乘法运算代替较为耗时的双线性配对运算, 极大提高了方案计算效率. 理论分析和性能实验证明了本文方案的安全性和有效性.

1 预备知识

在本节中, 简要回顾相关的背景知识, 包括BGN加密算法、Shamir秘密共享方案和椭圆曲线离散对数困难问题.

1.1 BGN加密算法

BGN加密算法^[14]是Boneh、Goh和Nissim于2005年提出的一种同态加密算法, 该算法支持无限次加法运算但最多只支持一次乘法运算, 它由以下3个子算法构成:

密钥生成: 给定安全参数 $\tau \in {Z^ + }$ , 运行算法 $\varsigma (\tau )$ 得到元组 $ (p, q, G) $ , 其中, $p$ 和 $q$ 是2个不同的大素数, $G$ 是 $N = pq$ 阶的乘法循环群. 随机选取 $G$ 的2个生成元 $g$ 和 $x$ , 并计算 $\chi = {x^q}$ . 最后公布公钥 $ PK = (N, G, g, \chi ) $ , 保存私钥 ${\textit{SK}} = p$ .

明文加密: 给定消息 $ m \in \left[ {0, M} \right] $ , $M < q$ , 选取随机数 $r \in \left[ {0, N - 1} \right]$ , 计算密文 $C = {g^m}{\chi ^r}$ .

密文解密: 使用私钥 ${\textit{SK}} = p$ 解密密文 $C$ , 计算 ${C^p} = {({g^m}{\chi ^r})^p} = {g^{mp}}{({x^{pq}})^r} = {({g^p})^m}$ , 令 $ {g_1} = {g^p} $ , 则 $ {C^p} = {g_1}^m $ , 随后使用Pollard’s Lambda算法^[15]求解离散对数得到明文 $m$ .

1.2 Shamir秘密共享方案

Shamir秘密共享方案^[16]存在管理者和 $k$ 个参与者, 秘密 $\theta $ 被管理者划分为 $k$ 个碎片, 只有当秘密的碎片数达到给定的阈值 $d + 1$ 才能恢复出秘密 $\theta $ . 方案由以下两部分组成.

秘密分发: 管理者通过以下多项式对秘密进行分发:

$ f(x) = \theta + {a_1}x + {a_2}{x^2} + \cdots + {a_{(k - 1)}}{x^d}\bmod \sigma $

(1)

其中, $\sigma $ 是一个大素数, 秘密 $\theta $ 为 $ f(x) $ 的常数项, 即 $\theta = f(0)$ . 管理者为每个参与者选择一个公开值 $ {x_i} $ , 并计算子份额 $ {y_i} = f({x_i}) $ , 随后将份额 $({x_i}, {y_i})$ 发送给相应的参与者.

秘密重构: 任意不少于 $d + 1$ 个参与者通过拉格朗日插值法可重构出秘密 $\theta $ , 如下所示:

$ {l_j}(x) = \prod\limits_{i = 1, i \ne j}^{d + 1} {\frac{{x - {x_i}}}{{{x_j} - {x_i}}}} $

(2)

$ \theta = \sum\limits_{j = 1}^{d + 1} {({y_i}{l_j}(x))} = \sum\limits_{j = 1}^{d + 1} {\left({y_i}\prod\limits_{i = 1, i \ne j}^{d + 1} {\frac{{x - {x_i}}}{{{x_j} - {x_i}}}} \right)} $

(3)

1.3 困难问题

椭圆曲线离散对数问题(elliptic curve discrete logarithm problem, ECDLP): ${G_1}$ 为定义在椭圆曲线 $E$ 上的 $\omega $ 阶循环群, 存在 $ B = \alpha P $ , 其中 $P, B \in {G_1}$ , $\alpha \in Z_\omega ^*$ , 在已知 $ B $ 和 $ P $ 的情况下求出整数 $ \alpha $ 使其满足 $ B = \alpha P $ 属于ECDLP.

椭圆曲线离散对数问题假设(elliptic curve discrete logarithm assumption, ECDLA): 不存在算法能够在多项式时间内以不可忽略的优势 $\varepsilon $ 解决椭圆曲线离散对数问题.

2 模型与目标 2.1 系统模型

智能电网下典型的系统模型如图1所示, 其中包含4种实体对象, 即智能电表、雾节点、云服务器和可信任机构.

智能电表(SM): 周期性地收集用户用电数据, 并将加密数据提交给雾节点.

雾节点(FN): 负责对SM的数据进行合法性认证(包括数据源认证和数据完整性认证), 并对加密数据进行聚合计算.

云服务器(CS): 由一组服务器 $C{S_j}$ 组成, 其中 $j = 1, 2, \cdots, k$ , $k \geqslant 3$ , 在这组服务器中选举计算资源最大的服务器作为主服务器, 让其负责FN和SM的注册以及对FN数据的认证, 并对聚合的密文进行解密.

可信任机构(TA): 是可信任的第三方实体对象, 负责生成系统所需参数并分配给相应实体对象.

2.2 安全模型

安全模型包含以下两点假设:

1) SM被认为是完全可信的, 而FN和CS则设定为“诚实且好奇”的角色, 即FN和CS能正确的执行协议, 但他们仍尝试各种方法推断用户的隐私数据.

2)恶意的攻击者可能对CS进行攻击并使其瘫痪. 由于CS是强大的实体, 攻击者破坏CS需要付出极大的代价, 因此假设攻击者只能破坏或妥协一定数量的CS, 即不超过 $d = \left\lceil {k/2} \right\rceil - 1$ , 但系统仍然有 $(k - d)$ 个 $C{S_j}$ 用来恢复聚合数据, 其中, $\; k - d \geqslant d + 1$ .

2.3 设计目标

根据安全模型中的假设, 同时考虑到系统内各实体之间传输的信道是不安全的, 恶意的攻击者可能发起数据修改、数据伪造以及重放攻击等. 方案应实现以下设计目标:

1)隐私性: 应确保授权的实体能获得聚合数据, 但不能获得单一用户的具体数据, 同时又要防止没有授权的外部实体窃取用户的隐私数据.

2)容错性: 部分智能电表可能会出现故障或因为网络波动等原因导致数据无法正常上传, 部分服务器也可能受到恶意攻击而停止工作. 所提聚合方案应具备容错功能以保证聚合方案能够有条不紊地进行.

3)完整性: 攻击者可能窃取数据进行修改, 并利用错误的数据进行犯罪, 消息接收方应能检测接收的数据是否被篡改.

4)认证性: 攻击者可能伪装成合法实体发送错误信息, 消息接收方应能认证发送方是否为合法实体.

3 具体方案

所提方案包含6个阶段: 初始化阶段、注册阶段、数据收集阶段、数据聚合阶段、数据解密阶段和容错处理阶段.

3.1 初始化阶段

TA通过执行以下步骤生成系统所需参数.

步骤1. 给定安全的参数 $\tau \in {Z^ + }$ , TA运行算法 $\varsigma (\tau )$ 得到元组 $(p, q, G)$ , 其中 $p$ 和 $q$ 是2个不同的素数, $G$ 是 $N = pq$ 阶的乘法循环群. TA选取 $G$ 的3个随机生成元 $\eta $ 、 $g$ 和 $u$ , 并计算 $\chi = {u^q}$ .

步骤2. 设 ${F_\rho }$ 是一个有限域, $\rho $ 是素数, TA定义椭圆曲线E: ${y^2} = {x^3} + ax + b \; {\rm{mod}} \; \rho$ , 其中 $a, b \in {F_\rho }$ . TA从E上选取一个阶为 $\omega $ 的加法循环群 ${G_1}$ , $P$ 为 ${G_1}$ 的生成元, TA选取随机数 $\;\beta \in Z_\omega ^*$ 并计算公钥 ${P_{\rm{pub}}} = \beta P$ .

步骤3. TA选取随机数 $\lambda \in Z_\omega ^*$ , 计算 ${P_{cs}} = \lambda P$ . TA将 $(\lambda , {P_{cs}})$ 作为所有 $CS$ 共同的私钥和公钥, 并通过安全信道发送给所有 $CS$ .

步骤4. TA选取3个安全的哈希函数 $ {H_1}, {H_2}, {H_3}: $ $ {\{ 0, 1\} ^*} \to Z_\omega ^* $ .

步骤5. TA使用伪随机数生成器生成 $n + 1$ 个伪随机数 $ {\pi _0}, {\pi _1}, \cdots, {\pi _n} \in Z_\omega ^* $ , 伪随机数满足下式关系:

$ {\pi _0} + \sum\limits_{i = 1}^n {{\pi _i}} = 0 $

(4)

TA将 ${\pi _i}$ 和 ${\pi _0}$ 分别作为 ${{\textit{SM}}_i}$ 和CS的密钥并通过安全通道发送给 ${{\textit{SM}}_i}$ 和 $CS$ , 随后TA计算 ${Q_i} = {\eta ^{{\pi _i}}}$ 并发送给 $CS$ .

步骤6. TA利用 ${\pi _0}$ 生成哈希值 ${h_1} = {H_1}({\pi _0})$ 并计算 $p \cdot {h_1}$ , 随后将其作为密钥嵌入随机生成的 $d$ 次多项式函数:

$ F(x) = p{h_1} + {a_1}x + {a_2}{x^2}+\cdots + {a_d}{x^d}\bmod \sigma $

(5)

其中, ${a_i} \in {Z_n}$ , $\sigma $ 是一个素数. TA将 $F({x_j})$ 和 ${l_j}(0)$ 作为 $C{S_j}$ 的私钥并通过安全通道发送给 $C{S_j}$ , 其中 $ {l_j}(0) = \displaystyle\prod\nolimits_{i = 1, i \ne j}^{d + 1} {\dfrac{{{x_i}}}{{{x_i} - {x_j}}}} $ .

步骤7. TA公布系统参数 $(\omega , \eta , g, {h_1}, N, G, {G_1}, P, $ ${P_{\rm{pub}}}, \chi , {H_i}:i = 1, 2, 3)$ .

3.2 注册阶段

为了成为系统的合法实体, ${{\textit{SM}}_i}$ 和 $F{N_i}$ 分别向 $CS$ 进行注册. 详细的步骤如下:

(1) ${{\textit{SM}}_i}$ 注册

步骤1. ${{\textit{SM}}_i}$ 的身份标识为 $i{d_i}$ , ${{\textit{SM}}_i}$ 随机选择私钥 ${v_i} \in Z_\omega ^*$ 和 ${r_i} \in Z_\omega ^*$ , 计算公钥 ${R_i} = {r_i}P$ , 并计算签名:

$ \left\{ \begin{gathered} {V_i} = {v_i}P \\ {h_{2, i}} = {H_2}(i{d_i}||{V_i}||{R_i}||{P_{{\rm{pub}}}}) \\ {s_i} = {v_i} + {r_i}{h_{2, i}} \\ \end{gathered} \right. $

(6)

${{\textit{SM}}_i}$ 获取当前的时间戳 ${t_{\rm{req}}}$ , 随后将 $(i{d_i}, {V_i}, {R_i}, {s_i}, {t_{\rm{req}}})$ 通过安全通道发送给 $CS$ .

步骤2. $CS$ 在收到注册请求消息 $(i{d_i}, {V_i}, {R_i}, {s_i}, $ ${t_{\rm{req}}})$ 后, 如果检查时间戳为最新, 则验证式(7)是否成立:

$ {s_i}P = {V_i} + {R_i}{h_{2, i}} $

(7)

如果式(7)成立, $CS$ 将参数 ${P_{cs}}$ 发送给 ${{\textit{SM}}_i}$ , 以此证明其为合法实体.

(2) $F{N_i}$ 注册

步骤1. $F{N_i}$ 的身份标识为 $i{d_{FN}}$ , $F{N_i}$ 随机选择私钥 ${v_{FN}} \in Z_\omega ^*$ 和 ${r_{FN}} \in Z_\omega ^*$ , 计算公钥 ${R_{FN}} = {r_{FN}}P$ , 并计算签名:

$ \left\{ \begin{gathered} {V_{FN}} = {v_{FN}}P \\ {h_{2, i}} = {H_2}(i{d_{FN}}||{V_{FN}}||{R_{FN}}||{P_{\rm{pub}}}) \\ {s_{FN}} = {v_{FN}} + {r_{FN}}{h_{2, i}} \\ \end{gathered} \right. $

(8)

$F{N_i}$ 获取当前的时间戳 ${t_{\rm{req}}}$ , 并将 $ (i{d_{FN}}, {V_{FN}}, {R_{FN}}, $ ${s_{FN}}, {t_{{\rm{req}}}})$ 通过安全通道发送给 $CS$ .

步骤2. $CS$ 在收到注册请求消息 $ (i{d_{FN}}, {V_{FN}}, {R_{FN}}, $ ${s_{FN}}, {t_{\rm{req}}})$ 后, 如果检查时间戳为最新, 则验证式(9)是否成立:

$ {s_{FN}}P = {V_{FN}} + {R_{_{FN}}}{h_{2, i}} $

(9)

如果式(9)成立, $CS$ 将参数 ${P_{cs}}$ 发送给 $F{N_i}$ , 以此证明其为合法实体.

3.3 数据收集阶段

${{\textit{SM}}_i}$ 周期性地(如每隔15 min)收集用电数据 ${m_i} \in Z_N^*$ , 随后对数据 ${m_i}$ 进行加密, 并生成相应的签名, ${{\textit{SM}}_i}$ 执行如下步骤.

步骤1. ${{\textit{SM}}_i}$ 收集实时的用电数据, 随后选择一个随机数 ${d_i} \in Z_N^*$ 并结合 ${\pi _i}$ 对数据进行加密:

$ {c_i} = {g^{\tfrac{{{m_i}}}{{{h_1}}}}}{\chi ^{\tfrac{{{d_i}}}{{{h_1}}}}}{\eta ^{N{\pi _i}}} $

(10)

步骤2. ${{\textit{SM}}_i}$ 选取随机数 ${w_i} \in Z_\omega ^*$ 并计算签名:

$ \left\{ \begin{gathered} {W_i} = {w_i}P \\ {h_{3, i}} = {H_3}(i{d_i}||{P_{cs}}||{V_i}||{W_i}||{c_i}||{t_i}) \\ {e_i} = {s_i} + {w_i}{h_{3, i}} \\ \end{gathered} \right. $

(11)

其中, ${t_i}$ 为当前的时间戳.

步骤3. ${{\textit{SM}}_i}$ 将 $(i{d_i}, {V_i}, {R_i}, {W_i}, {c_i}, {e_i}, {t_i})$ 发送给 $F{N_i}$ .

3.4 数据聚合阶段

在收到 $n$ 个 ${{\textit{SM}}_i}$ 发送的消息 $(i{d_i}, {V_i}, {R_i}, {W_i}, {c_i}, {e_i}, $ ${t_i})$ 后, $F{N_i}$ 开始执行以下步骤.

步骤1. $F{N_i}$ 先检查 ${t_i}$ 是否有效, 如果无效, 输出拒绝. 否则, 验证式(12)是否相等:

$ {e_i}P = {V_i} + {h_{2, i}}{R_i} + {h_{3, i}}{W_i} $

(12)

为了提高验证速度, 将在 $F{N_i}$ 上运用小指数测试技术^[17]对消息进行批量验证. $F{N_i}$ 随机选择一系列的小数 ${o_1}, {o_2}, \cdots, {o_n} \in [1, {2^n}]$ , 并验证式(13)是否成立:

$ \left(\sum\limits_{i = 1}^n {{o_i}{e_i}} \right)P = \sum\limits_{i = 1}^n {({o_i}{V_i})} + \sum\limits_{i = 1}^n {({o_i}{h_{2, i}}{R_i})} + \sum\limits_{i = 1}^n {({o_i}{h_{3, i}}{W_i})} $

(13)

步骤2. 如果式(13)成立, $F{N_i}$ 将对密文进行聚合:

$ {C_\gamma } = \prod\limits_{i = 1}^n {{c_i}} = {g^{\sum\nolimits_{i = 1}^n {\tfrac{{{m_i}}}{{{h_1}}}} }}{\chi ^{\sum\nolimits_{i = 1}^n {\tfrac{{{d_i}}}{{{h_1}}}} }}{\eta ^{N\sum\nolimits_{i = 1}^n {{\pi _i}} }} $

(14)

步骤3. $F{N_i}$ 选取随机数 ${w_{FN}} \in Z_\omega ^*$ 并计算签名:

$ \left\{ \begin{gathered} {W_{FN}} = {w_{FN}}P \\ {h_{3, i}} = {H_3}(i{d_{FN}}||{P_{cs}}||{V_{FN}}||{W_{FN}}||{C_\gamma }||{t_i}) \\ {e_{FN}} = {s_{FN}} + {w_{FN}}{h_{3, i}} \\ \end{gathered} \right. $

(15)

步骤4. $F{N_i}$ 将 $ (i{d_{FN}}, {V_{FN}}, {R_{FN}}, {W_{FN}}, {C_\gamma }, {e_{FN}}, {t_i}) $ 发送给 $CS$ .

3.5 数据解密阶段

在收到 $F{N_i}$ 发送的消息 $ (i{d_{FN}}, {V_{FN}}, {R_{FN}}, {W_{FN}}, {C_\gamma }, $ $ {e_{FN}}, {t_i}) $ 后, CS将执行以下步骤.

步骤1. CS先检查 ${t_i}$ 是否有效, 如果无效, 则输出拒绝. 否则, 验证式(16)是否成立:

$ {e_{FN}}P = {V_{FN}} + {h_{2, i}}{R_{FN}} + {h_{3, i}}{W_{FN}} $

(16)

步骤2. 如果式(16)成立, 主服务器使用密钥 ${\pi _0}$ 进行解密操作:

$ \begin{split} C &= {C_\gamma }{\eta ^{N{\pi _0}}} = {g^{\sum\nolimits_{i = 1}^n {\tfrac{{{m_i}}}{{{h_1}}}} }}{\chi ^{\sum\nolimits_{i = 1}^n {\tfrac{{{d_i}}}{{{h_1}}}} }}{\eta ^{N\sum\nolimits_{i = 1}^n {{\pi _i}} }}{\eta ^{N{\pi _0}}} \\ & = {g^{\sum\nolimits_{i = 1}^n {\tfrac{{{m_i}}}{{{h_1}}}} }}{\chi ^{\sum\nolimits_{i = 1}^n {\tfrac{{{d_i}}}{{{h_1}}}} }}{\eta ^{N({\pi _0} + \sum\nolimits_{i = 1}^n {{\pi _i}} )}} \xrightarrow{{ {\pi _0} + \sum\nolimits_{i = 1}^n {{\pi _i}} = 0}} \\ & = {g^{\sum\nolimits_{i = 1}^n {\tfrac{{{m_i}}}{{{h_1}}}} }}{\chi ^{\sum\nolimits_{i = 1}^n {\tfrac{{{d_i}}}{{{h_1}}}} }} \\ \end{split} $

(17)

步骤3. 各个服务器 $C{S_j}$ 利用 $\{ {l_j}(0), F({x_j})\} $ 计算 $ {\phi _j} = {l_j}(0)F({x_j}) $ , 其中:

$ \left\{ \begin{gathered} {l_j}(0) = \prod\limits_{i = 1, i \ne j}^{d + 1} {\frac{{{x_i}}}{{{x_i} - {x_j}}}} \\ F({x_j}) = p{h_1} + {a_1}{x_j} + {a_2}x_j^2 + \cdots + {a_d}x_j^d \\ \end{gathered} \right. $

(18)

随后主服务器负责收集所有的 $ {\phi _j} $ 进行密钥重构, 得到密钥 $p{h_1}$ (只有主服务器被妥协或自然宕机, 才进行新一轮的主服务器选举以及密钥的重构):

$ p{h_1} = \sum\limits_{j = 1}^{d + 1} {({\phi _j}) = \sum\limits_{j = 1}^{d + 1} {[{l_j}(0)F({x_j})]} } $

(19)

步骤4. 主服务器通过使用密钥 $p{h_1}$ 进行解密:

$\begin{split} V & =C^{p h_{1}} =\left(g^{\sum_{i=1}^{n} \frac{m_{i}}{h_{1}}} \chi^{\sum_{i=1}^{n} \frac{d_{i}}{h_{1}}}\right)^{p h_{1}}\\ &=\left(g^{p}\right)^{\sum_{i=1}^{n} m_{i}}\left(\chi^{p}\right)^{\sum_{i=1}^{n} d_{i}} {\xrightarrow{\chi^{p}=\left(u^{q}\right)^{p}=u^{p q}=1, g^{p}={\hat{g}}}}\\ &={\hat{g}}^{\sum_{i=1}^{n} m_{i}} \end{split}$

(20)

步骤5. 主服务器使用Pollard’s Lambda方法^[15]求解式(20)获得数据聚合值:

$ M = \sum\limits_{i = 1}^n {{m_i}} $

(21)

3.6 容错处理阶段

服务器端容错: 系统部署了 $k$ 台服务器进行协同工作. 正如安全模型的假设, 在最坏情况下攻击者也只能破坏或妥协 $d$ 个服务器并获得它们的私钥 $\{ {l_j}(0), F({x_j})\} $ , 但本着Shamir秘密共享方案“全有或全无”的属性, 至少需要 $d + 1$ 个份额才能重构密钥 $p{h_1}$ 进行解密, 系统仍有 $k - d \; ( \geqslant d + 1)$ 个服务器能正常进行解密, 保证聚合方案能够有条不紊地进行.

智能电表端容错: 当部分SM数据无法正常发送, FN仍然能进行数据聚合, CS也能将密文进行解密. 假设用户总数为 $U$ , 未能正常上传数据的用户为 $\hat U$ , $\hat U \subset U$ . 具体步骤如下.

步骤1. FN聚合的密文为:

$ \begin{split} {{\bar C_\gamma }} &= \sum\nolimits _{{U_i} \in U/\hat U } {{c_i}} \\ &= {g^{\sum\nolimits_{{U_i} \in U/\hat U } {\tfrac{{{m_i}}}{{{h_1}}}} }}{\chi ^{\sum\nolimits_{{U_i} \in U/\hat U } {\tfrac{{{d_i}}}{{{h_1}}}} }}{\eta ^{N\sum\nolimits_{{U_i} \in U/\hat U } {{\pi _i}} }} \end{split} $

(22)

步骤2. FN将 ${\bar C _\gamma }$ 和 $\hat U$ 发送给CS, 随后CS计算 $\hat C$ :

$ \hat C = \prod\limits_{{U_i} \in \hat U } {{Q_i}} = {\eta ^{N\sum\nolimits_{{U_i} \in \hat U } {{\pi _i}} }} $

(23)

步骤3. CS计算聚合密文 $C$ :

$ \begin{split} C & =\bar{C}_{\gamma} \hat{C} =g^{\sum_{U_{i} \in U / {\hat{U}}} {\frac{m_{i}}{h_{1}}}} \chi^{\sum_{U_{i} \in U / {\hat{U}}} \frac{d_{i}}{h_{1}}} \eta^{N \sum_{U_{i} \in U / {\hat{U}}} \pi_{i}} \eta^{N \sum_{U_{i} \in {\hat{U}}} {\pi}_{i}} \\ &=g^{\sum_{U_{i} \in U / {\hat{U}}} \frac{m_{i}}{h_{1}}} \chi^{\sum_{U_{i} \in U / {\hat{U}}} \frac{d_{i}}{h_{1}}} \eta^{N \sum_{U_{i} \in U} \pi_{i}} \end{split} $

(24)

步骤4. 同数据解密阶段, CS可获得数据聚合值:

$ M = \sum\limits_{{U_i} \in U/\hat U } {{m_i}} $

(25)

4 安全性分析

结合文献[18, 19]中的加密模型, 本节将证明在随机预言机模型下本方案具有不可伪造性, 并在此基础上对本方案是否实现所提的设计目标进行分析.

4.1 安全属性说明

安全属性(不可伪造性)通过挑战者 $\mathcal{C}$ 和攻击者 $\mathcal{A}$ 之间的博弈来定义. 挑战者 $\mathcal{C}$ 和攻击者 $\mathcal{A}$ 在进行博弈的过程中, 攻击者 $\mathcal{A}$ 向挑战者 $\mathcal{C}$ 发起以下查询:

$hash$ 查询: 在 $\mathcal{C}$ 中存在列表 $ {L_{Hi}} $ , 其中 $i = 1, 2, 3$ , 后文将会详细说明. 在 $\mathcal{A}$ 的查询下, $\mathcal{C}$ 返回随机值给 $\mathcal{A}$ .

$CreateS{M_i}$ 查询: $\mathcal{A}$ 输入 $i{d_i}$ , $\mathcal{C}$ 生成相对应 ${{\textit{SM}}_i}$ 的公钥、私钥和伪随机数并发送给 $\mathcal{A}$ .

$ExtractS{M_i}$ 查询: $\mathcal{A}$ 输入 $i{d_i}$ , $\mathcal{C}$ 生成相对应 ${{\textit{SM}}_i}$ 的私钥并发送给 $\mathcal{A}$ .

$Signcrytion$ 查询: $\mathcal{A}$ 输入 ${{\textit{SM}}_i}$ 的明文 ${m_i}$ , $\mathcal{C}$ 生成相对应 ${{\textit{SM}}_i}$ 的密文 ${c_i}$ 并发送给 $\mathcal{A}$ .

$Designcrytion$ 查询: $\mathcal{C}$ 对密文 ${c_i}$ 进行解密, 随后将明文 ${m_i}$ 发送给 $\mathcal{A}$ .

上述查询是自适应的, 即每次查询都可以根据上一次的询问结果进行调整.

博弈. 自适应选择消息攻击下具有不可伪造性(existentially unforgeable under the adaptive chosen message attack, EUF-CMA)由以下博弈定义:

设置: $\mathcal{C}$ 生成系统所需参数并发送给 $\mathcal{A}$ , $\mathcal{A}$ 选择一个挑战者的身份 $i{d'_i}$ 并发送给 $\mathcal{C}$ .

查询: $\mathcal{A}$ 可以进行 $hash$ 查询, ${{\textit{CreateSM}}_i}$ 查询, ${{\textit{ExtractSM}}_i}$ 查询, $Signcrytion$ 查询和 $Designcrytion$ 查询, 但不能使用挑战者的身份 $i{d'_i}$ 进行 ${{\textit{ExtractSM}}_i}$ 查询和 $Designcrytion$ 查询.

伪造: $\mathcal{A}$ 用挑战者的身份 $i{d'_i}$ 输出一个有效的密文 ${c_i}$ .

攻击者 $\mathcal{A}$ 想赢得博弈, 需满足以下条件:

1) $\mathcal{A}$ 从未使用挑战者的身份 $i{d'_i}$ 进行 ${{\textit{ExtractSM}}_i}$ 查询.

2)输出的密文 ${c_i}$ 是有效的.

定义1. 不可伪造性: 若不存在攻击者 $\mathcal{A}$ 能够在多项式时间内以不可忽略的优势 $\varepsilon $ 赢得上述博弈, 则所提方案在自适应选择消息攻击下具有不可伪造性.

4.2 安全属性证明

定理1. 基于椭圆曲线离散对数问题, 所提方案能够抵抗自适应选择消息伪造攻击.

证明: 假设攻击者 $\mathcal{A}$ 能够在多项式时间内以不可忽略的优势 $\varepsilon $ 赢下上述博弈, 则证明在自适应选择消息伪造攻击下, 存在挑战者 $\mathcal{C}$ 可以解决椭圆曲线离散对数问题(ECDLP).

设置: 假定提供一个椭圆曲线离散对数问题(ECDLP)的实例 $ (P, B = \alpha P) $ . $\mathcal{C}$ 选择一个挑战者的身份 $i{d'_i}$ , 随机选择 $\beta \in Z_\omega ^*$ 计算 ${P_{\rm{pub}}} = \beta P$ , 随后将生成的系统参数 $(\omega , \eta , g, {h_1}, N, G, {G_1}, P, {P_{\rm{pub}}}, \chi , \alpha , {H_i}:i = 1, 2, 3)$ 和身份 $i{d'_i}$ 一起发送给 $\mathcal{A}$ .

查询: 在博弈中, 为了及时回应 $\mathcal{A}$ , $\mathcal{C}$ 进行以下查询:

${H_1}$ 查询: 列表 ${L_{H1}}$ 由元组 $({\pi _0}, {h_1})$ 构成, $\mathcal{C}$ 首先检查 $({\pi _0}, {h_1})$ 是否存在于 ${L_{H1}}$ 中. 如果存在, $\mathcal{C}$ 将 ${L_{H1}}$ 中的数据 ${h_1} = {H_1}({\pi _0})$ 返回给 $\mathcal{A}$ . 否则, $\mathcal{C}$ 将随机选取 ${h_1} \in Z_\omega ^*$ 存入列表 ${L_{H1}}$ , 并返回 ${h_1}$ 给 $\mathcal{A}$ .

${H_2}$ 查询: 列表 ${L_{H2}}$ 由元组 $(i{d_i}, {V_i}, {R_i}, {P_{{\rm{pub}}}}, {h_{2, i}})$ 构成, 当 $\mathcal{A}$ 查询 $(i{d_i}, {V_i}, {R_i}, {P_{{\rm{pub}}}})$ 时, $\mathcal{C}$ 首先检查 $(i{d_i}, {V_i}, {R_i}, $ ${P_{{\rm{pub}}}}, {h_{2, i}})$ 是否存在于 ${L_{H2}}$ 中. 如果存在, $\mathcal{C}$ 将 ${L_{H2}}$ 中的数据 ${h_{2, i}} = {H_2}(i{d_i}||{V_i}||{R_i}||{P_{\rm{pub}}})$ 返回给 $\mathcal{A}$ . 否则, $\mathcal{C}$ 将随机选取 ${h_{2, i}} \in Z_\omega ^*$ 存入列表 ${L_{H2}}$ , 并返回 ${h_{2, i}}$ 给 $\mathcal{A}$ .

${H_3}$ 查询: 列表 ${L_{H3}}$ 由元组 $(i{d_i}, {P_{cs}}, {V_i}, {W_i}, {c_i}, {t_i}, {h_{3, i}})$ 构成, 当 $\mathcal{A}$ 查询 $(i{d_i}, {P_{cs}}, {V_i}, {W_i}, {c_i}, {t_i})$ 时, $\mathcal{C}$ 首先检查 $(i{d_i}, {P_{cs}}, {V_i}, {W_i}, {c_i}, {t_i})$ 是否存在于 ${L_{H3}}$ 中. 如果存在, $\mathcal{C}$ 将 ${L_{H3}}$ 中的数据 ${h_{3, i}} = {H_3}(i{d_i}||{P_{cs}}||{V_i}||{W_i}||{c_i}||{t_i})$ 返回给 $\mathcal{A}$ . 否则, $\mathcal{C}$ 将随机选取 ${h_{3, i}} \in Z_\omega ^*$ 存入列表 ${L_{H3}}$ , 并返回 ${h_{3, i}}$ 给 $\mathcal{A}$ .

${{\textit{CreateSM}}_i}$ 查询: 列表 ${L_{{\textit{SM}}i}}$ 由元组 $(i{d_i}, {v_i}, {V_i}, {r_i}, {R_i},$ ${s_i}, {\pi _i})$ 构成, 当 $\mathcal{A}$ 查询 ${{\textit{SM}}_i}$ 的 $i{d_i}$ 时, $\mathcal{C}$ 首先检查 $(i{d_i}, {v_i}, {V_i}, {r_i}, {R_i}, {s_i}, {\pi _i})$ 是否存在于 ${L_{{\textit{SM}}i}}$ 中. 如果存在, $\mathcal{C}$ 将 ${L_{SMi}}$ 中的数据 $({V_i}, {R_i})$ 返回给 $\mathcal{A}$ . 否则, $\mathcal{C}$ 将执行以下过程:

1)如果 $i{d'_i} \ne i{d_i}$ , $\mathcal{C}$ 随机选取 ${v_i}, {r_i}, {h_{2, i}}, {\pi _i} \in Z_\omega ^*$ , 计算 ${V_i} = {v_i}P$ , ${R_i} = {r_i}P$ 和 ${s_i} = {v_i} + {r_i}{h_{2, i}}$ , 随后分别将 $(i{d_i}, {V_i}, {R_i}, {h_{2, i}})$ 和 $(i{d_i}, {v_i}, {V_i}, {r_i}, {R_i}, {s_i}, {\pi _i})$ 存入列表 ${L_{H2}}$ 和 ${L_{{\textit{SM}}i}}$ , 最后 $\mathcal{C}$ 将 $({V_i}, {R_i})$ 返回给 $\mathcal{A}$ .

2) 否则 $(i{d'_i} = i{d_i})$ , $\mathcal{C}$ 随机选取 ${s_i}, {h_{2, i}}, {\pi _i} \in Z_\omega ^*$ , 计算 ${V_i} = {v_i}P$ , ${R_i} = \alpha P$ 和 ${s_i}P = {V_i} + {R_i}{h_{2, 1}}$ , 随后分别将 $(i{d_i}, {V_i}, {R_i}, {h_{2, i}})$ 和 $(i{d_i}, {v_i}, {V_i}, { \bot _i}, {R_i}, {s_i}, {\pi _i})$ 存入列表 ${L_{H2}}$ 和 ${L_{{\textit{SM}}i}}$ . 最后C将 $({V_i}, {R_i})$ 返回给 $\mathcal{A}$ .

${{\textit{ExtractSM}}_i}$ 查询: 当 $\mathcal{A}$ 查询 ${{\textit{SM}}_i}$ 的 $i{d_i}$ 时, $\mathcal{C}$ 首先检查 $i{d_i}$ 和 $i{d'_i}$ 是否相等. 如果是, 游戏结束. 否则, $\mathcal{C}$ 将检查在列表 ${L_{SMi}}$ 中的 $(i{d_i}, {v_i}, {V_i}, {r_i}, {R_i}, {s_i}, {\pi _i})$ , 并将 $({r_i}, {s_i}, {\pi _i})$ 返回给 $\mathcal{A}$ .

$Signcrytion$ 查询: 当 $\mathcal{A}$ 输入数据 ${m_i}$ 时, $\mathcal{C}$ 首先检查 $i{d'_i}$ 和 $i{d_i}$ 是否相等. 如果相等, $\mathcal{C}$ 随机选择 ${e_i}, {h_{2, i}}, {h_{3, i}} \in Z_\omega ^*$ , 计算 $ {c_i} = {g^{\tfrac{{{m_i}}}{{{h_1}}}}}{\chi ^{\tfrac{{{d_i}}}{{{h_1}}}}}{\eta ^{N{\pi _i}}} $ , $ {W_i} = {w_i}P $ 和 $ {V_i} = {e_i}P - ({h_{2, i}}{R_i} + {h_{3, i}}{W_i}) $ , 随后 $\mathcal{C}$ 分别将 $(i{d_i}, {V_i}, {R_i}, $ ${P_{{\rm{pub}}}}, {h_{2, i}})$ 和 $(i{d_i}, {P_{cs}}, {V_i}, {W_i}, {c_i}, {t_i}, {h_{3, i}})$ 存入列表 ${L_{H2}}$ 和列表 ${L_{H3}}$ . 最后 $\mathcal{C}$ 将密文 $({V_i}, {W_i}, {c_i}, {e_i}, {t_i})$ 返回给 $\mathcal{A}$ . 否则, $\mathcal{C}$ 根据本方案的既定流程生成密文 $({V_i}, {W_i}, {c_i}, {e_i}, {t_i})$ 并返回给 $\mathcal{A}$ .

$Designcrytion$ 查询: 当 $\mathcal{A}$ 输入密文 ${c_i}$ 时, $\mathcal{C}$ 首先检查 $i{d_i}$ 和 $i{d'_i}$ 是否相等. 如果相等, 游戏结束. 否则, $\mathcal{C}$ 按照本方案既定流程对密文进行解密.

伪造: $\mathcal{A}$ 以 ${{\textit{SM}}_i}$ 的 $i{d_i}$ 伪造并输出密文 $({V_i}, {W_i}, {c_i}, {e_i}, {t_i})$ , 其中:

$ {e_i}P = {V_i} + {h_{2, i}}{R_i} + {h_{3, i}}{W_i} $

(26)

$\mathcal{C}$ 首先检查 $i{d_i}$ 和 $i{d'_i}$ 是否相等. 如果相等, 游戏结束. 否则, 基于交叉引理^[20], $\mathcal{C}$ 在选择不同的哈希函数 ${H_2}$ 下可以输出有效密文 $({V_i}, {W_i}, {c_i}, {e'_i}, {t_i})$ , 可得:

$ {e_i}^\prime P = {V_i} + {h'_{2, i}}{R_i} + {h_{3, i}}{W_i} $

(27)

根据式(26)和式(27)可得:

$ \begin{split} ({e_i} - {{e'}_i})P &= {e_i}P - e'P \\ & = {V_i} + {h_{2, i}}{R_i} + {h_{3, i}}{W_i} - ({V_i} + {{h'}_{2, i}}{R_i} + {h_{3, i}}{W_i}) \\ & = ({h_{2, i}} - {{h'}_{2, i}}){R_i} \\ & = ({h_{2, i}} - {{h'}_{2, i}})\alpha P \end{split} $

(28)

最后, $\mathcal{C}$ 输出 $\alpha = {({h_{2, i}} - {h'_{2, i}})^{ - 1}}({e_i} - {e'_i})$ 作为椭圆曲线离散对数问题(ECDLP)解决方案.

优势分析: 为了评估挑战者 $\mathcal{C}$ 解决椭圆曲线离散对数问题(ECDLP)的优势, 进行了以下3个操作:

${O_1}$ : 在进行 ${{\textit{ExtractSM}}_i}$ 和 $Designcrytion$ 查询过程中, $\mathcal{C}$ 不会停止上诉博弈.

$O{}_2$ : 进行上述查询时 $i{d_i}$ 和 $i{d'_i}$ 相等.

$O{}_3$ : $\mathcal{A}$ 伪造出合法密文.

根据以上操作, 可得出优势分别为 $Pr[{O_1}] = (1 - 1/{q_{H2}})^{{q_e} + {q_d}}$ 、 $ Pr[{O_2}|{O_1}] = 1/{q_{H2}} $ 和 $ Pr[{O_3}| $ $ {O_1} \wedge {O_2}] = \varepsilon $ , 其中 $ {q_{H2}} $ 、 $ {q_e} $ 和 $ {q_d} $ 分别表示 ${H_2}$ 查询次数、 ${{\textit{ExtractSM}}_i}$ 查询次数和 $Designcrytion$ 查询次数. 因此, $\mathcal{C}$ 解决椭圆曲线离散对数问题(ECDLP)的优势为 $ Pr[{O_1} \wedge {O_2} \wedge {O_3}] = Pr[{O_3}|{O_1} \wedge {O_2}]Pr[{O_2}|{O_1}]Pr[{O_1}] =\varepsilon \cdot 1/{q_{H2}} \cdot (1 - 1/{q_{H2}})^{{q_e} + {q_d}} $ . 因为优势 $\varepsilon _{}^{}$ 是不可忽略的, 所以优势 $ Pr[{O_1} \wedge {O_2} \wedge {O_3}] $ 也是不可忽略的, 但这与椭圆曲线离散对数困难问题相矛盾. 因此假设不成立, 证得所提方案具备不可伪造性.

4.3 设计目标分析

本节将证明方案实现了第2.3节所提出的设计目标, 即隐私性、完整性、认证性和容错性.

隐私性: 在数据收集阶段, 数据 ${m_i}$ 通过式(10)加密成规范且有效的BGN密文. BGN加密算法被证明在子群决策假设下是语义安全的^[14], 即使密文被攻击者窃听或拦截, 也无法在多项式时间内破解密文; 在加密时选取的伪随机数 ${\pi _i}$ 是由TA随机生成的, 攻击者无法获取全部的伪随机数用以消除密文 $ {c_i} = {g^{\tfrac{{{m_i}}}{{{h_1}}}}}{\chi ^{\tfrac{{{d_i}}}{{{h_1}}}}}{\eta ^{N{\pi _i}}} $ 中的 $ {\eta ^{N{\pi _i}}} $ ; 并且根据安全模型的假设, 恶意的攻击者最多只能妥协 $d$ 个服务器, 所以攻击者无法重构秘密 $p{h_1}$ 进行解密. 因此, 密文中的数据是语义安全的. 另外, 本方案利用密文的同态性在雾节点对密文进行聚合操作, 避免了“诚实且好奇”的雾节点从中获取单一用户的隐私数据, 而CS也只能从聚合数据中解析出总聚合数据, 仍无法获得单一用户的隐私数据. 因此, 所提方案具有隐私保护功能.

完整性: 在方案的数据生成和数据聚合阶段, ${{\textit{SM}}_i}$ 和FN分别生成数字签名 $({W_i}, {e_i})$ 和 $({W_{FN}}, {e_{FN}})$ , FN和CS会对收到的签名进行验证. 由定理1可知, 任何的攻击者都不能伪造出有效的数字签名, 一旦数字签名中的数据被篡改, 篡改数据将会被及时检测. 因此, 所提方案能够确保数据的完整性.

认证性: 在方案的注册阶段, SM和FN的注册信息由CS进行验证, 随后CS会将参数 ${P_{cs}}$ 发送给注册成功的实体以此证明该实体是合法的. 另外, 由定理1可知, 任何的攻击者都不能伪造出有效的密文, 并且在报告的消息 $(i{d_i}, {V_i}, {R_i}, {W_i}, {c_i}, {e_i}, {t_i})$ 和 $ (i{d_{FN}}{V_{FN}}, $ $ {R_{FN}}, {W_{FN}}, {C_\gamma }, {e_{FN}}, {t_i}) $ 中, SM和FN的身份标识被包含在其中, SM和FN可以通过验证式(13)和式(16)是否相等以此证明发送方是否为合法实体. 因此, 所提方案具有认证性.

容错性: 详见第3.6节.

5 性能分析

本文实验运行在Intel Core i7-5500U CPU @2.40 GHz, 8 GB RAM以及64位Windows 10操作系统的笔记本电脑上. 实验采用基于配对的密码学库JPBC^[21]. 设置参数 $ |p| = |q| = 512 $ bits, $|N| = 1024$ bits. 选定的椭圆曲线E中的两个素数 $\;\rho $ 和 $\omega $ 都为160 bits. 为了更好评估本文方案的性能(包括计算开销和通信开销), 实验将本文方案与文献[22-24]进行比较. 为了减少实验误差, 实验取1000次测试结果的平均值. 除非特别说明, 本文方案中的雾节点等同于其他方案的聚合器.

5.1 计算开销

各方案中的主要操作的基准执行时间如表1所示, 实验忽略如哈希运算、ECC点加运算和整数乘法等计算. 为了方便比较, 假设存在 $l$ 个雾节点FN, 每个雾节点FN下有 $n$ 个智能电表SM. 表2列出各阶段的主要操作.

图2展示了4个方案在数据收集阶段SM计算开销的对比情况. 在文献[22]中, SM进行加密和签名需要4次指数运算和2次群上乘法运算. 在文献[23]中, SM进行加密和签名需要4次群上指数运算和2次群上乘法运算. 在文献[24]中, SM进行加密和签名需要3次群上指数运算, 1次群上乘法运算, 1次群上点乘运算和2次双线性配对运算. 在本文方案中, SM进行加密和签名需要3次群上指数运算, 2次群上乘法运算和1次ECC标量乘法运算. 由图2可知, 本文方案在此阶段需要的计算开销最小.

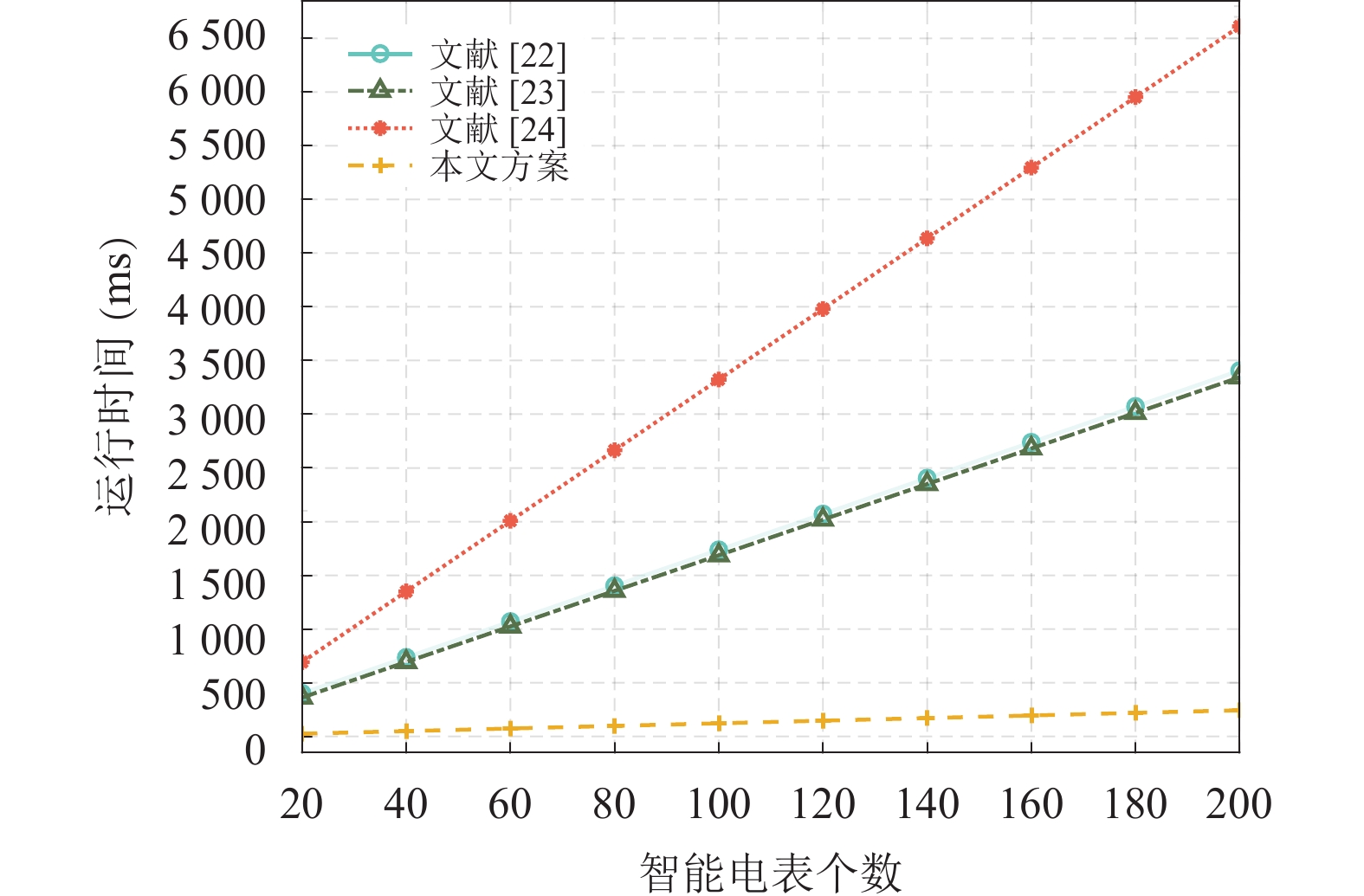
图3展示了4个方案在数据聚合阶段FN计算开销的对比情况, 假设每个FN下有200个SM. 在文献[22]中, FN进行验证需要3次群上指数运算、 $3n - 2$ 次群上乘法运算和 $n + 2$ 次双线性配对运算. FN聚合密文和生成签名需要执行 $2n - 1$ 次乘法运算和2次指数运算. 在文献[23]中, FN进行认证需要 $n + 1$ 次双线性配对运算和 $2(n - 1)$ 次群上乘法运算, FN聚合密文需要1次群上指数运算和 $n$ 次群上乘法运算, FN生成签名需要1次指数运算. 在文献[24]中, FN需要先认证来自终端的询问信息, 需执行 $2n$ 次双线性配对运算, FN进行认证需要2次双线性配对运算, FN聚合密文需要 $2(n - 1)$ 次群上乘法运算, FN生成签名需要1次群上的点乘运算. 在本文方案中, FN进行认证和签名需要 $3n + 2$ 次ECC上标量乘法运算, FN聚合密文需要 $n - 1$ 次群上乘法运算. 由图3可知, 本文方案相比较其他3种方案具有较好的计算性能. 其主要原因是本文方案使用椭圆曲线中标量乘法运算代替较为耗时的双线性配对运算.

图4展示了4个方案在数据解密阶段CS计算开销的对比情况, 假设CS下有20个FN. 在文献[22]中, CS进行验证需要3次双线性配对运算, 恢复密文数据需要2次群上乘法运算和1次双线性配对运算. 在文献[23]中, CS进行批验证需要 $(l + 1)$ 次双线性配对运算和 $2(l - 1)$ 次群上乘法运算, 聚合密文需要 $(l - 1)$ 次群上乘法运算, 恢复密文数据需要1次群上指数运算. 在文献[24]中, CS进行验证需要2次双线性配对运算, 恢复密文数据需要1次群上指数运算和1次群上乘法运算. 在本文方案中, CS进行验证需要3次ECC上标量乘法运算, 恢复密文数据需要2次群上指数运算和1次群上乘法运算. 由图4可知, 由于避免使用双线性配对运算, 本文方案在此阶段的计算开销均小于其他方案.

5.2 通信开销

本小节将分析SM和FN之间以及FN和CS之间的通信开销. $G, {G_1}, Z_\omega ^*, {Z_N}, {Z_{{N^2}}}$ 中元素的长度分别为1024 bits, 160 bits, 160 bits, 1024 bits和2048 bits. 假设单向哈希函数长度是160 bits, 时间戳和身份的长度分别是64 bits和32 bits.

首先, 分析SM和FN之间的通信开销. 在文献[22]中, SM发送信息 $ \{ C{T_i}, {V_i}, {T_i}\} $ 给FN, 其中 $C{T_i} = $ $\{ {c_{1i}}, {c_{2i}}\} $ , $({c_{1i}}, {c_{2i}}) \in G$ , ${V_i} \in G$ 和 ${T_i}$ 是时间戳, 此阶段通信开销为 $ |C{T_i}| + |{T_i}| + |{V_i}| = 3136 $ bits. 在文献[23]中, SM发送信息 $\{ I{D_{T{D_{ij}}}}, {t_{ij}}, {C_{ij}}, {\sigma _{ij}}\} $ 到FN, 其中 $({C_{ij}}, {\sigma _{ij}}) \in G$ , $I{D_{T{D_{ij}}}}$ 和 ${t_{ij}}$ 分别是身份和时间戳. 因此, 此阶段通信开销为 $|{C_{ij}}| + |{\sigma _{ij}}| + |I{D_{T{D_{ij}}}}| + |{t_{ij}}| = 2144$ bits. 在文献[24]中, SM和FN需要先交互来完成认证, 假设授权消息 $A{u_{td}}$ 为32 bits, SM向FN发送 $ \{ P{S_{td}}, A{u_{td}}, Si{g_{pcs - td}}\} $ , 其中 $ Si{g_{pcs - td}} \in G $ 和 $P{S_{td}}$ 是身份. 该过程 $|Si{g_{pcs - td}}| + |A{u_{td}}| + |P{S_{td}}| = 1088$ bits. FN向SM发送 $ \{ I{D_{fn}}, A{u_{fn}}, $ $ Si{g_{pcs - fn}}\} $ 完成认证, 该过程 $|Si{g_{pcs - fn}}| + |A{u_{fn}}| + |I{D_{fn}}| = 1088$ bits. 再者, SM发送信息 $\{ {c_i}, P{S_{td}}, {T_i}, {\sigma _i}\} $ 到FN, 其中 ${c_i} = \{ {c_{i1}}, {c_{i2}}\} $ , $({c_{i1}}, {c_{i2}}, {\sigma _i}) \in G$ 和 ${T_i}$ 是时间戳. 该过程通信开销为 $|{c_i}| + |{\sigma _i}| + |{T_i}| + |P{S_{td}}| = 3168$ bits. 因此, 此阶段通信开销为 $1088 + 1088 + 3168 = 5344$ bits. 在本文方案中, SM发送信息 $\{ i{d_i}, {V_i}, {R_i}, {W_i}, {c_i}, {e_i}, {t_i}\} $ 到FN, 其中 ${c_i} \in G$ , $({V_i}, {R_i}, {W_i}) \in {G_1}$ , ${e_i} \in Z_\omega ^*$ , $i{d_i}$ 和 ${t_i}$ 分别是身份和时间戳. 因此, 此阶段通信开销计算为 $|{c_i}| + $ $|{e_i}| + |{t_i}| + |i{d_i}| + |{V_i}| + |{R_i}| + |{W_i}| = 1760$ bits.

其次, 分析FN和CS之间的通信开销. 在文献[22]中, FN发送信息 $\{ CT, \sigma , {T_c}\} $ 到CS, 其中 $CT = \{ {C_1}, $ ${C_2}\} $ , $({C_1}, {C_2}) \in G$ , $\sigma = \{ U, V\} $ , $(U, V)$ $ \in G$ 和 ${T_c}$ 是时间戳. 因此, 此阶段通信开销为 $|CT| + |\sigma | + |{T_c}| = $ $4160$ bits. 在文献[23]中, FN发送信息 $\{ I{D_{E{S_i}}}, {C_i}, {\sigma _i}, $ ${t_i}\} $ 到CS, 其中 $({C_i}, {\sigma _i}) \in G$ , $I{D_{E{S_i}}}$ 和 ${t_i}$ 分别是身份和时间戳. 因此, 此阶段通信开销为 $|{\sigma _i}| + |{t_i}| + |{C_i}| + $ $|I{D_{E{S_i}}}| = 2144$ bits. 在文献[24]中, FN发送信息 $\{ c, P{S_{td}}, I{D_{fn}}, T, {\sigma _{fn}}\} $ 到CS, 其中 $c = \{ {c_1}, {c_2}\} $ , $({c_1}, {c_2}, $ ${\sigma _{fn}}) \in G$ , $P{S_{td}}$ 和 $I{D_{fn}}$ 是身份, $T$ 是时间戳. 因此, 此阶段通信开销计算为 $|c| + |{\sigma _{fn}}| + |T| + $ $|P{S_{td}}| + |I{D_{fn}}| = 3200$ bits. 在本文方案中, FN发送信息 $ (i{d_{FN}}{V_{FN}}, {R_{FN}}, {W_{FN}}, {C_\gamma }, {e_{FN}}, {t_i}) $ 到CS, 其中 ${C_\gamma } \in G$ , $({V_{FN}}, {R_{FN}}, {W_{FN}}) \in {G_1}$ , ${e_{FN}} \in Z_\omega ^*$ , $i{d_{FN}}$ 和 ${t_i}$ 分别是身份和时间戳. 因此, 此阶段通信开销计算为 $ |{C_\gamma }| + |{V_{FN}}| + |{R_{FN}}| + |{W_{FN}}| + |{e_{FN}}| + |{t_i}| + |i{d_{FN}}| = $ $ 1760 $ bits.

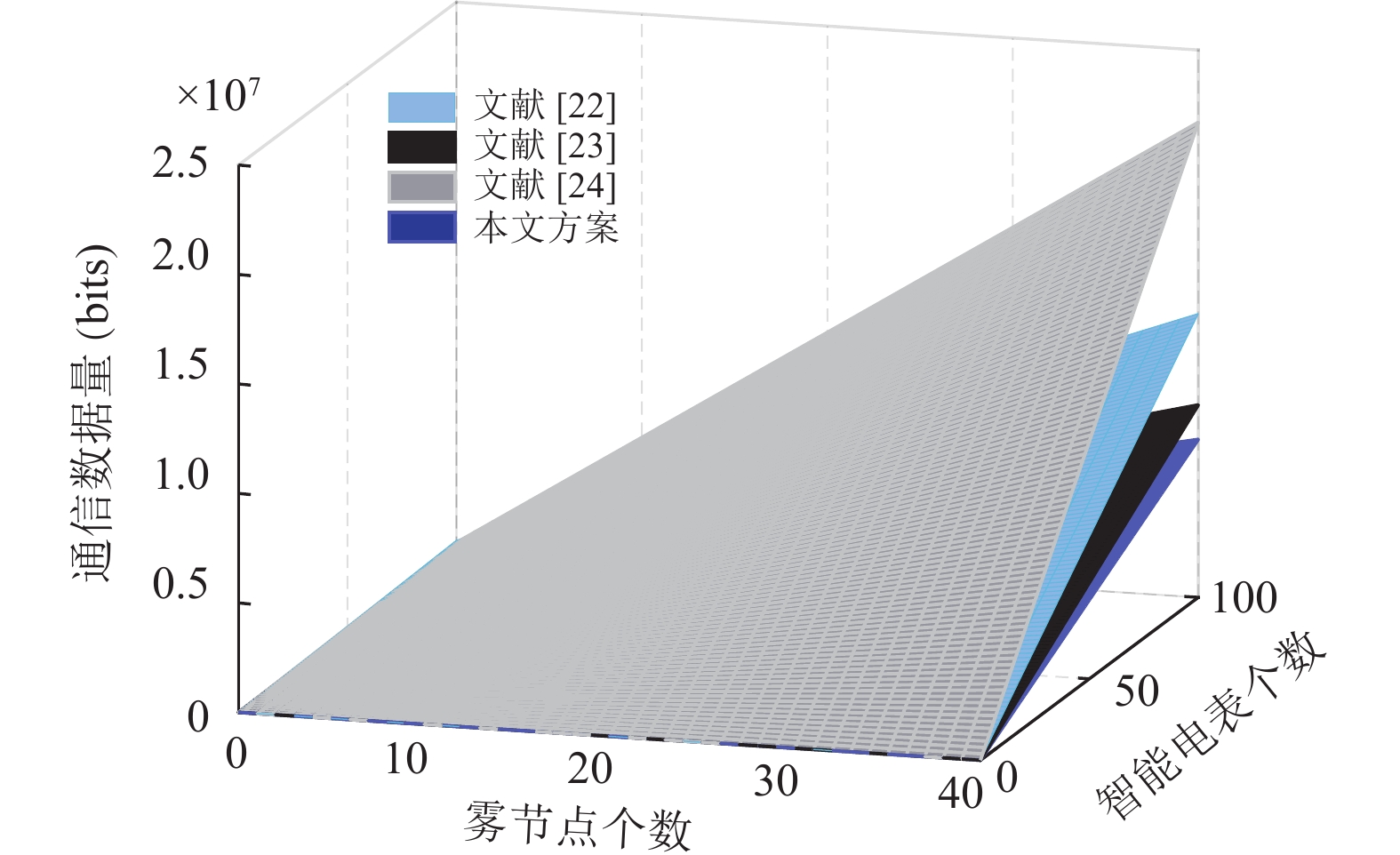
图5展示了4个方案一次会话的总通信开销对比情况. 设置FN数量逐步递增到40个, 每个FN下的SM数量逐步递增到100个. 图5可以直观反映出本文方案具有较优的通信开销性能. 原因是本文方案采用椭圆曲线加密算法进行签名, 在同等安全水平下, 其签名数据占用空间小, 有效地减少通信成本.

6 结论

本文提出了一种基于雾计算的高效隐私保护数据聚合方案, 该方案巧妙地结合了BGN同态加密算法和Shamir秘密共享方案确保了数据的隐私性, 利用椭圆曲线离散对数问题构造高效的签名认证算法保证数据的完整性, 并且该方案实现了两种容错措施. 安全性分析证明了该方案满足智能电网的安全要求. 性能分析表明了该方案具有较低的计算和通信开销.