近代工业革命后, 能源成为了人类社会生活中赖以生存生活的重要构成部分. 石油资源被称为“工业的血液”^[1], 不仅是一种不可再生的资源, 更是国家生存和发展不可或缺的战略资源, 是当今世界各国的经济命脉. 石油的形成过程极其复杂缓慢, 不可再生的石油资源就变得十分关键. 伴随着经济社会的快速发展, 带动着自然资源的消耗也逐年增大, 对石油、天然气等自然资源的使用急剧增长^[2]. 全球从陆地到海洋, 从浅层到中层、再到深层的勘探来满足日常的生活需求. 经过长达多年来的石油勘探, 我国在浅层和中层的石油储量已经基本勘探清楚, 剩下不多井正在开采. 然而, 这已远远无法满足社会需要^[3]. 同时, 由于实际钻井过程施工情况复杂, 工况变化多样, 获取的录井参数环境呈现出明显的非平稳性, 并且采用人为的方式获取录井参数成本昂贵, 影响因素极多难以考虑完全, 钻井效率受到严重的影响. 因此, 如何提高钻井效率、提升钻井速度是当今国内外研究的热点课题^[4].

在钻井工程中, 钻头钻破岩石加深钻孔的速度称为机械钻速. 机械钻速是反映钻井效率的一个关键指标, 受到钻头尺寸、钻井参数、岩石岩性等诸多因素的影响和制约^[5], 它与开采成本、开采时间有着直接关联^[4]. 钻速预测对于钻井参数的确定和钻井成本的优化是必要的. 钻井机械钻速的准确预测, 能够有效地估算钻井周期, 从而根据预测结果优化配置资源, 可以减少钻井开采成本、增大石油产量, 这对于企业降低钻井施工成本、减少钻井风险, 对于国家能够解决能源紧缺问题等有着重大意义.

随着大数据技术的飞速发展以及数据规模的急速增长, 采用机器学习的方法对数据进行挖掘并应用到钻井过程当中, 与基于物理模型的方法相比, 机械钻速的预测精度有着显著的提高. 传统的机器学习方法通常建立于数据独立同分布这一假设之上^[6], 然而在实际钻井过程中, 不同的油田信息具有明显不同的模式, 现有的机器学习方法使用已钻井数据预测新油田时, 预测精度显著下降, 如何高效地进行机械钻速预测并将其应用于后续各种油田处理在石油领域中面临着长期的挑战. 优秀的网络模型皆是基于大量标注数据集(如COCO、ImageNet)训练得到, 然而实际应用中高质量且具有标签的大型井下数据集资源匮乏, 难以支撑优秀网络模型, 可能产生严重的过拟合问题. 迁移学习不受训练数据集与目标数据之间关系的约束, 能够根据不同任务之间的相似性, 实现源域的已有知识迁移, 可有效解决过拟合问题. 目前, 迁移学习方法已经在钻井工程中的岩性识别、钻头选择、异常工况检测等多种场景得到了广泛的应用^[7]. 针对钻井过程中机械钻速预测这一回归问题, 本文以真实历史钻井数据钻头尺寸、钻压等字段为特征, 以机械钻速为标签, 采用将迁移学习与物理模型相结合的方法, 提出一种基于集成迁移学习的机械钻速预测模型. 实践中, 采用真实钻井数据, 尝试了包括linear regression (线性回归)^[8]、传统的AdaBoost回归、只有目标域数据进行训练和几种先进的基于特征与基于实例的迁移学习方法^[9]等建模方法, 采用多种回归评价指标衡量模型的性能, 证明了本文提出的方法进行跨领域机械钻速预测的有效性, 钻速预测精度也得到显著提高.

1 相关工作

在钻井过程中, 提速提效是永恒不变的追求目标. 机械钻速(ROP)的准确预测可显著缩短钻井作业时间, 节约钻井成本. 机械钻速受到多种因素的影响和制约, 有可控因素和不可控因素^[10]. 可控因素是指通过一定的设备和技术手段可进行人为调节的因素, 如地面机泵设备、钻头尺寸、钻井液性质、钻压、转速. 不可控因素是指客观存在的因素, 如所钻的地层岩性、储层埋藏深度以及地层压力等. 针对机械钻速预测, 其研究进展大体可以分为3个阶段: 用现场数据直接统计出钻速方程, 考虑所钻地层性质和钻头结构的钻速方程, 用计算机仿真方法来预测机械钻速.

1.1 传统方法

国内外学者都提出了各自与地层特性和钻头结构性质相关的钻速方程. 1974年, Bourgoyne等^[11]将机械钻速视为钻头压力、转速等8个参数的函数, 但该方法存在局限性, 只适用于牙轮钻头情况. 2008年, Rastegar等^[12]在前人的基础上提出改进的ROP预测模型, 同时考虑了钻头水力参数、钻头的磨损情况和岩石强度等因素的影响. 传统的物理建模方法给机械钻速预测带来了可见的影响, 但方法大多根据专业知识经验, 建模方法高度依赖于岩石岩性, 模型泛化性能不佳. 且由于校准需要进行不断变化, 从而限制了其函数的形式. 随着大数据和机器学习的迅速发展, 很多学者开始将机器学习方法应用到机械钻速预测方面. 2004年, Rommetveit等^[13]提出了一种新型的钻井自动化模拟系统, 通过对比实测数据和预测数据得到钻井过程中的实时诊断结果, 但是该系统还处在功能设想阶段, 目前尚未实现全部功能, 且考虑的ROP影响因素较少; 2008年, Bahari等^[14]基于文献[11]提出的模型井结合遗传算法计算了机械钻速预测模型参数, 但该研究只对ROP进行了计算预测, 并没有作进一步的优化分析. 在数据量较充足、数据质量较高的条件下, 采用多元回归^[15]等机器学习方法构建的预测模型的预测准确度较高, 能够在当前设备和资源条件下准确找寻影响机械钻速的若干个核心因素.

传统的机器学习方法大多借助监督学习的推动, 依赖于已有数据, 即需要足够多的标注好的训练样本进行学习, 在数据样本稀少的场景下, 性能会显著下降. 对新领域执行机器学习常遇到标注稀缺问题, 获取大量标注数据成本较高且耗时, 严重制约了经典监督学习方法的效果. 同时, 伴随着多领域、多媒体大数据的不断涌现, 如何研究自动方法对其进行跨领域分类和组织变得愈加重要^[16]. 在机器学习的领域中, 已经开发了许多用于迁移学习的方法, 通过将在源数据上的预训练模型迁移到感兴趣的目标数据上, 迁移学习思想被证明是更具有普遍有用的. 迁移学习放宽了经典监督学习中关于训练数据和测试数据服从独立同分布这一基本假设, 将相似但具有不同分布的源域和目标域数据映射到同一个特征空间, 尽可能地保留映射后数据的属性同时缩小数据的维度, 最小化两个领域的概率分布差异. 当源域和目标域数据来自不同的分布时, 通常采用领域分布自适应(domain adaptive, DA)算法^[17]来弥补分布差异.

1.2 深度学习

近年来, 深度学习方法在计算机视觉中取得了令人瞩目的成功. 刘胜娃等^[18]结合人工神经网络技术领域知识, 提出一种基于人工神经网络的定向井机械钻速预测模型, 该模型在数据量充足的情况下, 预测准确性较高. 文献[19]通过建立渤中区域深层机械钻速预测神经网络模型, 能够在当前特定区域条件下准确找寻影响机械钻速的若干个核心因素. 目前使用的深度网络模型假设训练数据和测试数据为相同的分布, 然而在实际钻井过程中, 训练数据和测试数据的分布往往并不相同, 高质量且具有标签的大型井下数据集资源匮乏, 难以支撑优秀的深度网络模型, 这导致训练得到的模型鲁棒性能较差. 迁移学习不受源域数据与目标数据之间关系的约束^[9], 对于缺乏标记数据的目标任务, 有很强的动机来构建有效的学习者, 利用来自相关源域的丰富标记数据, 将已训练好的模型参数迁移到新模型进行训练. 研究表明, 先前对象的认识与新对象的相似性和联系, 有助于新对象的学习. 在特定数据集或任务上训练的CNN模型可以针对不同领域的新任务进行微调.

随着深度学习在各个领域的广泛应用, 大量的深度迁移学习^[20]方法被提出. 深度迁移学习(deep transfer learning, DTL)通过将深度学习与迁移学习相结合, 将辅助领域训练的深度模型重用于目标领域, 能够有效地降低模型的训练时间, 使现有数据得到更充分的利用, 提高深度网络在实际应用中的泛化能力. 对比传统的非深度迁移学习方法, 深度迁移学习方法在不同的学习任务上得到一定的提升. 神经网络体系结构基于丰富标记的源域数据和标注缺失的目标域数据进行训练, 根据目标任务进行结构调整, 经过目标数据的再次训练, 形成最终的目标网络, 能够有效地促进特征的出现. 若此目标网络优于未经迁移的网络, 则该迁移为正迁移, 反之则为负迁移^[7].

2 基于集成迁移学习的机械钻速预测方法 2.1 问题定义

在迁移学习当中, 包含两个基本的概念, 分别是领域(domain)和任务(task). 领域 $ D $ 是进行知识学习的主体, 主要有数据以及生成这些数据的概率分布P所组成^[21]. 在迁移学习中对应两个基本的领域, 分别是源领域(source domain, $ {D_s} $ )和目标领域(target domain, $ {D_T} $ ). 源领域是指有知识、有丰富数据标注的领域, 属于迁移对象. 目标领域就是需要最终赋予知识的对象, 一般来说, 目标领域当中大部分都是未标注数据. 任务T指的是学习的目标, 由标签和标签对应的函数组成. 迁移学习旨在从一个或多个源领域中提取知识, 并将知识应用于目标任务当中.

给定一个有标签的源域数据 $ {D_s} = \{ {x_i}, {y_i}\} _{i = 1}^n $ 和一个无标签的目标域 ${D_T} = \{ {x_j}\} _{j = 1}^m$ . 两个领域的数据概率分布 ${{P}}({x_s})$ 和 ${{P}}({x_{{t}}})$ 不同, 即 ${{P}}({x_s}) \ne {{P}}({x_t})$ . 迁移学习的目标就是要借助源域 ${{{D}}_{{S}}}$ 的先验知识来学习目标领域 ${{{D}}_{{T}}}$ 的知识(标签)^[22].

假定源域和目标域的特征空间和样本空间分别相同, 即 ${{{X}}_{{S}}} = {{{X}}_{{T}}}$ 且 ${{{Y}}_{{S}}} = {{{Y}}_{{T}}}$ , 但两个领域的特征分布不同, 即存在条件概率分布不同 ${{{Q}}_{{S}}}({y_s}|{x_s}) \ne {{{Q}}_T}({y_t}|{x_t})$ 或者边缘分布不同 ${{{P}}_{{S}}}({x_s}) \ne {{{P}}_T}({x_t})$ . 领域自适应就是源域和目标域不一样, 具体来说, 两个领域的数据概率分布不同, 但是两个领域共享相同的特征和类别, 其维度是一致的^[17]. 此刻, 迁移学习的目标就是利用有标记的数据来学习一个分类器 $f$ 来预测目标领域 $ {x_t} $ .

2.2 钻前机械钻速预测模型简介

集成学习是通过将许多弱分类器进行集成提升为强学习器的过程^[23]. 一般来说, 用得比较多的是同质学习器, 即同质集成中的个体学习器属于同种类型. 同质学习器根据基学习器之间是否存在依赖关系分为Boosting系列算法^[24]和随机森林系列算法. AdaBoost作为提升算法(Boosting)的一种, 根据基学习器的学习误差率来更新训练样本的权重值, 增加学习误差率高的训练样本权重, 再基于调整样本权重后的训练集训练基学习器, 不断调整基学习器的权重, 将这些弱学习器进行线性组合形成一个强学习器, 进而达到提升整体准确率的效果. 算法的性能通过“少数服从多数”这一方法进行投票决出结果. 随着集成中基学习器数目的不断增加, 集成的错误率将指数级下降, 最终将趋于0.

基于Boosting的迁移学习算法, 也称为TrAdaBoost算法, 是由Dai等^[25]提出的一种典型迁移学习算法. TrAdaBoost算法假设源领域和目标域数据具有完全相同的特征与标签空间, 但两者的数据分布不同. 将源域数据与部分目标域数据整合得到训练实例, 由于源域与目标域之间的分布差异, 源域数据样本可能会对目标任务的学习有利, 有可能没有, 甚至有可能有害. TrAdaBoost算法通过对训练实例赋予权重, 增加被错误分类的目标实例的相对权重^[26]. 当源实例被错误分类时, 降低其权重值, 具体来说, 就是给数据乘上一个0到1的值. 在下一次分类, 被错误分类的样本对分类模型的影响就会比上一次迭代小一些. 通过这种方式, TrAdaBoost旨在识别和利用与目标数据最相似的源实例, 而忽略那些不相似的实例. TrAdaBoost算法模型具体描述如图1.

2.3 带物理模型约束的集成机械钻速回归模型

将钻井数据看作连续的, 在统计学上称为回归问题. 结合TrAdaBoost的原理与传统的回归算法产生了新的回归算法TrAdaBoostR2^[27]. 作为一种基于样本实例的迁移学习方法, TrAdaBoostR2对每个训练实例进行加权, 确保迁移的源域知识与目标任务相关. 然而, 当源域样本数远大于目标域时, 目标实例的总权重可能需要多次迭代才能接近源实例的总权重, 此时目标数据的权重可能会严重偏斜, 那些异常值或与源数据最不相似的目标实例可能会代表大部分权重^[28]. 其次, 即使是那些代表目标概念的源实例, 它们的权重最终也趋于零.

基于Bingham (1965)提出的基本ROP模型^[29], 已知转速( $ ROP $ )、钻头压力( $ RPM $ )和钻头直径( ${D_b}$ )等参数, 可以通过式(1)计算得到机械钻速的预测值. 其中, $\alpha $ 和 $\gamma $ 为岩性模型的经验参数:

$ ROP{\text{ = }}\alpha RPM{\left(\frac{{WOB}}{{{D_b}}}\right)^\gamma } $

(1)

物理模型虽然源自钻井物理原理, 但是涉及经验参数和拟合函数的约束, 这常常会导致较差的结果. 为了克服上述缺点, 选择基于样本实例迁移方法TrAdaBoost.R2作为基础, 提出一种带物理模型约束的集成迁移学习方法, 分两个阶段对样本实例进行调整. 算法在第一阶段, 源实例的权重逐渐向下调整, 直到达到某一个值(该值采用交叉验证确定得到); 在第二阶段, 首先对所有源实例的权重冻结, 而目标实例的权重在AdaBoost.R2中被正常更新, 只有在第2阶段生成的假设被存储并用于确定结果模型的输出.

假定存在 $n$ 个源域训练数据 $ {D_{{S_1}}}, \cdots, {D_{{S_n}}} $ , $m$ 个用于训练的目标域数据 $ {D_{{T_1}}}, \cdots, {D_{{T_m}}} $ , 迁移学习的目的就是充分利用有标记的源域数据来提高目标分类器 $ {f_T} $ 的学习效率. 首先, 定义第h次迭代训练实例的权重向量 $ {w^h} = (w_{{S_1}}^h, \cdots, w_{{S_n}}^h, w_T^h) $ , 其中, ${w_S}$ 表示源域数据样本实例的权重, ${w_T} = (w_T^1, \cdots, w_T^m)$ 表示目标域数据用来训练的 $m$ 个样本权重向量. 初始化权重为:

$ w_{_i}^1 = \frac{1}{{n + m}}, 1 \leqslant i \leqslant n + m $

(2)

清空候选基学习器并对现有的权重进行规范化, 选择基学习器 $ {f_t} $ 对训练集 ${D_{\rm train}} = {D_S} \cup {D_{T - \rm train}}$ 进行训练. 为了保证模型不会因为目标实例划分成训练集和测试集而造成误差, 采用十折交叉验证. 将目标领域数据集随机划分10份, 随机选择其中一份作为测试集, 剩下的9份与源实例进行整合作为训练集进行实验, 依次进行10组实验. 同时, 采用Bingham提出的基本ROP模型对算法进行物理约束, 采用式(3)计算基学习器 $ {f_t} $ 在 ${D_{T - \rm test}}$ 上的误差值, 选取平均绝对误差最小的用于后续模型.

$ {{\text{(}}{e}_t^i)^k} = \displaystyle\sum\limits_{j = 1}^m {\frac{{w_t^j[|{{(f_t^i)}^k} - y_t^j|{\text{ + |(}}y_t^p{{\text{)}}^j}{{ - }}y_t^j{\text{|]}}}}{{\displaystyle\sum\nolimits_{i = 1}^m {w_t^i} }}} $

(3)

其中, $ {{\text{(}}y_t^p)^j} $ 表示采用物理模型(即式(1))计算得到的ROP值, $ y_t^j $ 表示目标域数据的真实标签值, $ {(f_t^i)^k} $ 表示第i个基分类器进行k折交叉验证预测得到的ROP值. 根据误差估计来更新训练样本实例的权重值, 误差越大, 其权重设置越小. 对其进行 ${{S}}$ 次迭代, 并对权重进行更新, $ {Z_t} $ 是一个归一化的常量, 使得最终目标实例的权重为 $\dfrac{m}{{n + m}} + \dfrac{t}{{(S - 1)}}(1 - \dfrac{m}{{n + m}})$ .

$ w_i^{t + 1} = \left\{ \begin{gathered} w_i^t\beta _t^{e_i^t}/{Z_t}, 1 \leqslant i \leqslant n \\ w_i^t/{Z_t}, n + 1 \leqslant i \leqslant n + m \\ \end{gathered} \right. $

(4)

对源实例的权重更新采用加权多数算法(即WMA^[27])机制, 第2阶段首先对所有源实例的权重冻结, 采用Bootstrap对观测信息进行多次重复抽样, 建立起充足的样本, 采用基学习器对取样的样本进行预测, 并计算损失函数, 采用TrAdaBoostR2来更新目标实例的权重向量, 最后对权重进行规范化处理, 生成的模型被存储并用于确定结果模型的输出.

本文选用决策树回归(decision tree regressor)算法^[30]作为基学习器进行集成迁移回归, 对模型参数进行调整, 不断更新模型权重. 在模型优化问题中, 通过计算真实值与预测值的平均绝对误差(mean absolute error, MAE)作为模型性能的一个衡量指标. 平均绝对误差作为回归损失函数中常用的误差计算, 通过计算预测值与真实值之间差值绝对值和的均值, 可以有效地避免误差相互抵消, 因而可以较准确地反应实际预测误差的大小. 其中, ${y_{\rm pred}}$ 表示模型最终的预测值, $ {y_i} $ 表示相应的实际值.

$ MAE = \frac{{\displaystyle\sum\limits_{i = 1}^n {|{y_i} - {y_{\rm pred}}|} }}{n} $

(5)

本文提出了一种带物理模型约束的集成迁移回归模型来对钻前机械钻速进行预测, 算法具体描述如算法1.

算法1. 基于集成迁移回归的机械钻速预测算法

输入: $\scriptstyle {D_s} $ : 源域数据集; $\scriptstyle {D_T} $ : 目标域数据集

输出: $\scriptstyle err$ : 平均绝对误差MAE值

1． 初始化源域数据集 $\scriptstyle {D_s} = [{n_s} \times {m_s}] $ , 目标域数据集 $ \scriptstyle {D_T} = [{n_T} \times {m_T}] $ ;

2． 确定基学习器 $\scriptstyle {f_T} $ 为决策树回归算法;

3． $\scriptstyle feature = D[:, 1:m - 1] $ ; $\scriptstyle label = D[:, - 1] $

4． 采用One-Hot和Z-score标准化对数据集进行预处理;

5． 将目标域划分为训练集和测试集: $\scriptstyle {D_{\rm train}}$ 和 $\scriptstyle {D_{\rm test}}$ ;

6． 确定最大估计次数 $\scriptstyle {n_{\rm estimator}}$ , 步骤数 $\scriptstyle {{S}}$ , $\scriptstyle {{K}} = 10$ ;

7． 初始化权重为 $ \scriptstyle W_i^1 = 1/(n + m) $ ;

8． for $\scriptstyle i = 1 \to {{S}}$ do

9． 　 $\scriptstyle D \leftarrow ({D_{\rm train}} + {D_s})$

10． 　清空候选基学习器, 对现有权重进行规范化;

11．　 采用TrAdaBoostR2进行训练得到模型 $\scriptstyle {\rm model}$ ;

12．　 for $\scriptstyle j = 1 \to {{K}}$ do

13． 　　 $\scriptstyle D_{\rm train}^j = ({D_S} + {D_{{{T}} - \rm train}})$

14．　　 //对用于训练的目标实例进行权重更新

15．　　 采用TrAdaBoostR2对 $\scriptstyle D_{\rm train}^j$ 进行训练并计算 $\scriptstyle {D_{{{T - \rm test}}}}$ 的预测值;

16． 　　采用式(3)计算误差估计;

17． 　　采用式(4)更新权重 $\scriptstyle {W_i}^{(j + 1)}$ ;

18．　　 确保目标实例总权重不随交叉分割而改变;

19．　 end for

20．　 采用Bootstrap对 $\scriptstyle X$ 进行多次重复采样;

21．　 使用基学习器更新目标实例的权重向量;

22．　 返回样本权重 $\scriptstyle {W_i}$ ;

23． end for

24． 得到最优的样本权重 $\scriptstyle {W^*}$ ;

25． 计算目标域数据的预测值 $\scriptstyle {y_{\rm pred}} = {\text{model}}({f_T}, {W^*})$ ;

26． 采用式(5)计算预测值与真实值的误差值 $\scriptstyle err$ ;

27． 返回 $\scriptstyle err$ .

3 实验分析 3.1 实验设置

本论文采用的数据集共包括156次测量, 这些测量是从特定区块的26口S井和3口WD井收集得到的历史钻井数据. 实验数据具体描述如表1, 每个样本数据包含斜深(depth)、钻压(wob)、大钩载荷(hook_load)、泵压(spp)、转盘转速(bit_rpm)、泵排量(flow_rate)、扭矩(torque)、地层类型(formation)、钻头类型(bit_type)、钻头尺寸(bit_size)、岩性类型(lith)等51个特征参数和1个机械钻速(ROP)样本标签. 通过对数据进行预处理操作, 有效保留数据样本在各个维度上的信息分布. 同一口井有多次测量, 其测量结果是连续的, 为了保证井口数据的完整性和独立性, 将同一钻井数据作为一个整体, 目标域共有3口井数据, 分别是WD1、WD2和WD3, 采用交叉验证进行模型预测, 通过随机选择目标域数据将其与源域数据整合作为训练集, 剩下的钻井数据作为测试集样本.

本文使用51个特征参数作为机械钻速预测模型的输入, 由于数据集中的字符类型特征无法被机器模型学习, 因此在建模时需要将其转化成易于机器利用的数值型特征. 独热编码(one-hot)用N位状态寄存器来对N个状态进行编码, 从而将类别变量转换为数值变量, 由于one-hot编码后的特征值只有0或1, 因此采用该方法不会影响原类别特征在模型中的权重比例. 采用独热编码进行数据类型转换会将数据维度扩大, 为了进一步排除数据集维度扩大对实验的影响, 再对其采用主成分分析^[31]对数据维度进行降维. 同时, 利用原始数据的均值和标准差对其进行标准化, 使处理后的数据符合标准正态分布. 数据的标准化处理能够有效地提升模型精度, 加快训练网络的收敛性. Z-Score标准化对样本数据在不同特征维度进行伸缩变换, 使得不同度量之间的特征具有可比性, 并且不会改变原始数据的分布, 通过将不同量级的数据转化为统一量级的Z-Score分值进行比较, 能够在特征提取时有效保留样本各维度上的信息分布. Z-Score标准化的数学表达如下, 其中 $ \;\mu $ , $ \sigma $ 表示原始数据的均值和标准差.

$ x=\frac{x-\mu}{\sigma} $

(6)

采用决策树回归模型作为该模型的弱学习器, 同时对模型参数进行调整, 得到具体参数设置如表2, 其中, n_estimators 表示的是迭代次数, 也就是本次实验中采用弱学习器的个数; learning_rate 表示学习率; steps表示的是步骤数; folds表示的是交叉验证的折叠次数; max_depth表示的是每一个学习器的最大深度, 用于限制回归树的节点数目.

3.2 结果分析

对预处理后的数据进行模型训练与验证. 根据领域特点, 采用交叉验证对模型进行训练与预测, 通过对目标域WD数据中随机选择一份作为测试集, 剩下两口井与源域数据整合用于模型训练, 使用线性回归、物理模型作为基线方法, 同时, 为了验证该模型的有效性并保证实验的严谨性, 采用传统的AdaBoostR2 (即没有采用迁移学习)模型与基于集成迁移学习的机械钻速预测方法进行实验对比. 通过对模型参数的不断调节, 得到WD1、WD2和WD3作为测试集下基于集成迁移学习的机械钻速方法的MAE值分别为1.476 04、0.826 26和0.857 51. 本文模型算法的性能在表3以数字方式进行描述, 在图2中以图形方式展示.

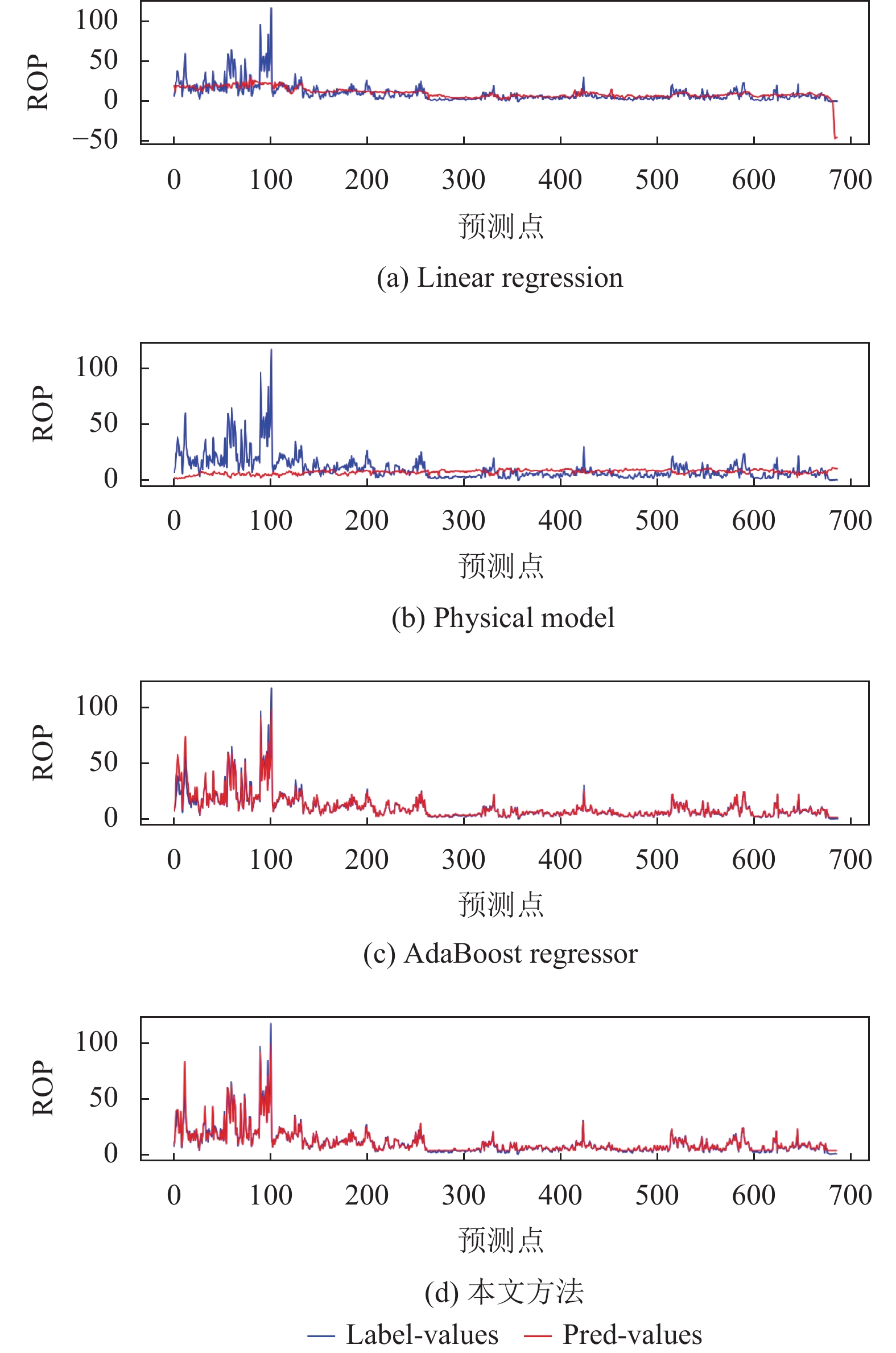
以WD3作为测试集为例, 得到该实验设置下线性回归、物理模型、AdaBoostR2和本文提出算法预测值与真实ROP值的对比图. 很明显, 从图2中可以看到, 基于集成迁移学习的机械钻速模型大大降低了模型的误差值. 与传统的AdaBoostR2方法相比, 基于集成迁移学习的机械钻速预测方法在对峰值进行预测时更接近真实值. 具体来说, 本文方法在3种实验设置下的性能分别提升0.87736、−0.07711和0.040 2. 同时, 该模型下的MSE值也得到了提升, 较传统的AdaBoostR2模型MSE值降低了3.003 6.

3.3 对比实验

对实验数据进行同类型操作处理, 设计并进行对比实验. 本文选择了6种先进的机器学习方法用于验证本模型方法的有效性. 领域自适应(DA)方法通过在一个领域上学习的知识迁移到另一个领域上, 自适应方法分为基于特征的自适应、基于实例的自适应和基于参数的自适应方法. 本文分别选用3种基于实例的方法(KMM^[32]、KLIEP^[33]、TrAdaBoostR2^[27])和3种基于特征迁移的方法(DANN^[34]、DeepCORAL^[35]、MDD^[36])用于进行实验对比. 同时, 添加直接采用目标域数据进行训练(即TgtOnly)作为基线方法.

在实验设置上, 为了保证井口数据的完整性和独立性, 以井为单位选取部分目标域数据与源域数据合并一起进行训练, 剩下的目标域作为测试集, 这样达到交叉验证的效果. 将本文提出的基于集成迁移学习的机械钻速预测方法与其他方法进行性能对比, 得到实验结果如表4. 采用TgtOnly分别对WD1、WD2、WD3进行机械钻速预测, 计算预测值与真实值的最大均值误差MAE值分别为9.341 4、3.739 9和6.632 3. 领域自适应方法通过将一个领域上学习的知识迁移到另一个领域上, 其性能远远好于TgtOnly. 同时, 采用传统的TrAdaBoostR2进行对比验证, 得到本文提出的模型效果明显改善. 实验表明, 本文提出的基于集成迁移学习的机械钻速预测模型拟合效果最佳, 算法的性能远远好于其他几种先进的领域自适应方法, 具有较好的鲁棒性能. 在以WD2作为测试集中, MAE值减小到0.8263, 相较于这里面最优的方法KMM误差减小了1.387 2, 性能提升了1.68倍.

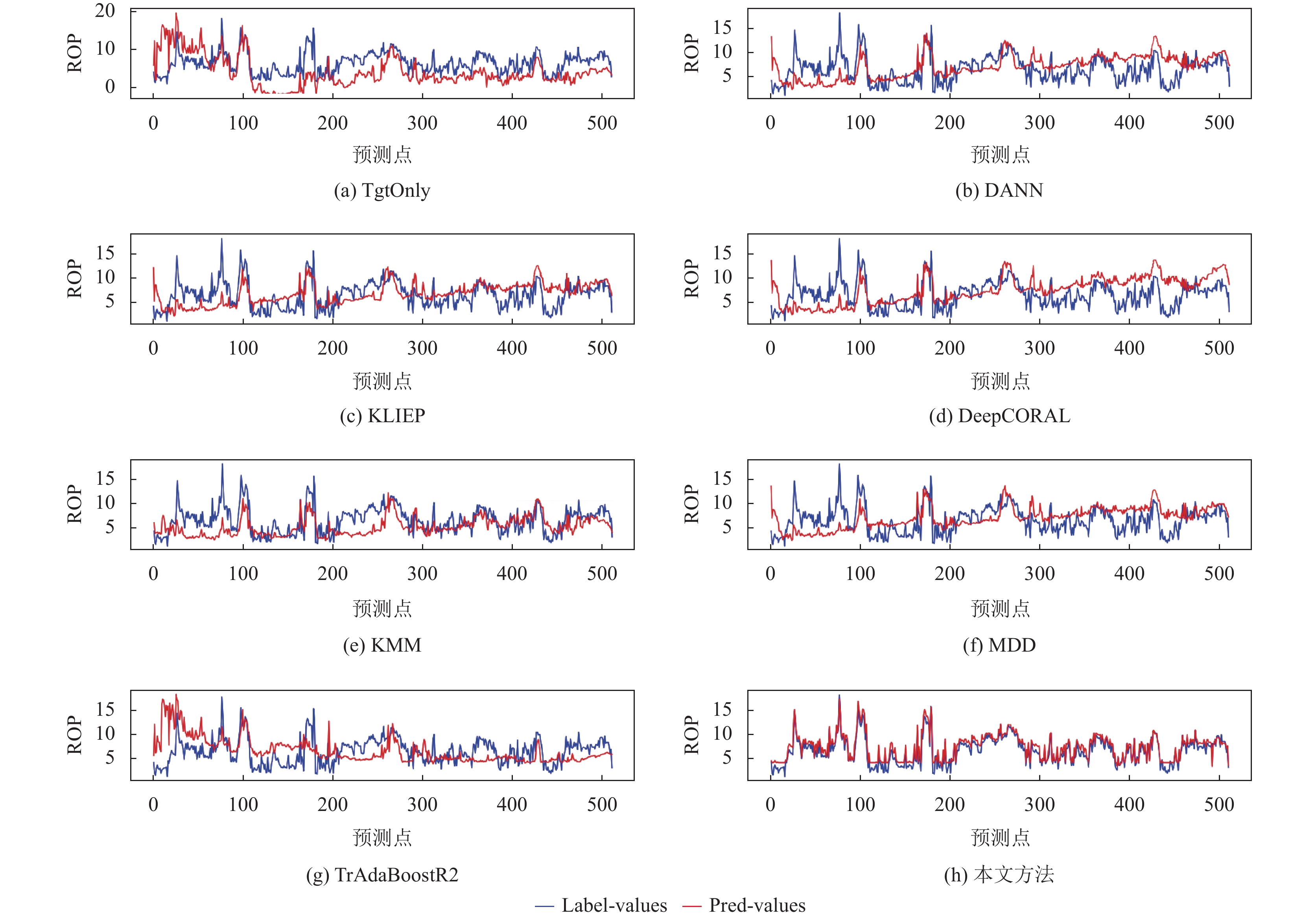
在以WD2为测试集中, 得到本文方法与其他几种主流机械钻速预测方法在目标域数据预测的机械钻速值与真实ROP的对比图(图3), 从图中可以清晰地看到, 本文算法预测得到的机械钻速值与真实标签值具有良好的一致性, 误差值远远小于其他几种主流的机械钻速预测方法, 能够为模型提供相对稳定的效果.

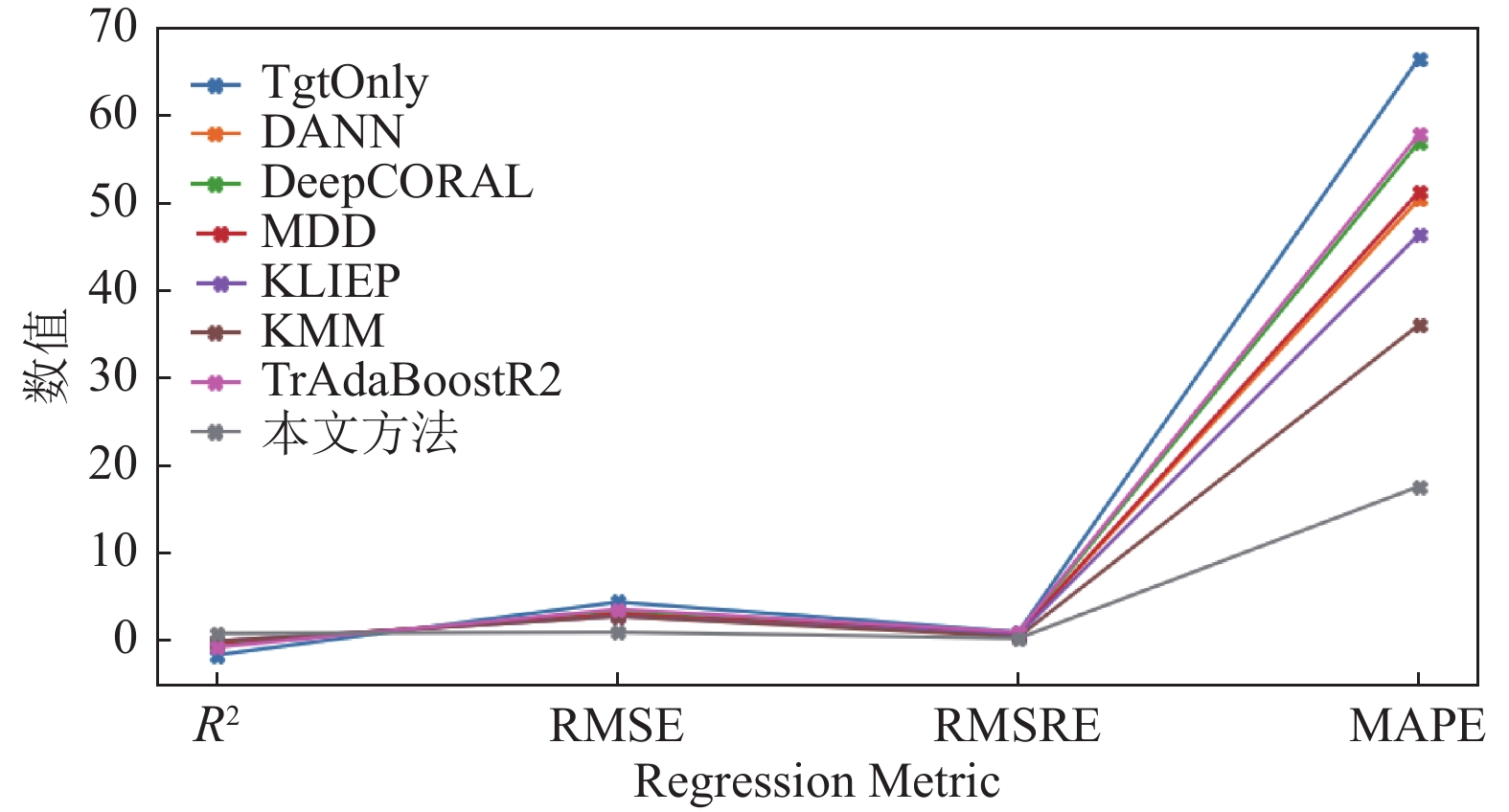
为了更直观进行实验对比, 分别计算本文方法与其他几种机械钻速预测方法的决定系数(R²)、均方根误差(RMSE)、均方根相对误差(RMSRE)和平均绝对百分比误差(MAPE), 多种回归评价指标的对比结果如图4所示. 图4的结果表明, 本文方法的R²值为0.8686, RMSE值为0.9997, RMSRE值为0.2911, MAPE值为17.67%, 在多种评价指标中性能最优. 同时图4也显示结合迁移学习的机械钻速预测方法相较于不使用迁移学习的方法(TgtOnly)性能有明显的提升.

4 结论与展望

本文提出了一种结合物理模型和迁移学习的钻前机械钻速预测方法, 能够在目标油田数据样本缺失或标注的数据样本较少的情形下更准确地预测机械钻速. 本文方法结合机械钻速物理模型, 通过迁移学习识别并利用与目标数据相似的源实例, 确保迁移的知识与目标任务相关. 实验表明, 本文方法机械钻速预测值与实际值之间具有良好的一致性, 与几种主流机械钻速预测方法相比, 在多种回归评价指标中性能最优. 钻前机械钻速的准确预测能给施工现场提供高效有力指导依据, 为进一步有效地提高钻井效率提供可靠的保障.