伴随着我国生态建设力度的加大, 空气质量问题成为生态问题的重要组成部分, 空气质量的好坏有关国家建设“绿水青山”的使命, 有关社会环境治理问题, 有关人民身体健康问题. 我国每年因为大气污染造成呼吸道疾病感染而死亡的人数高达数百万, 空气中雾霾、浮尘等颗粒严重影响了空气质量, 因此能够很好地预测空气质量问题成为人们亟需解决的一大课题. 顺应大数据时代的到来, 很多研究人员已经做了一些针对空气质量预测的相关工作^{[1, 2]}.

早些年间, 人们对于空气质量的预测多基于生活中的主观经验, 这显然缺乏一定的科学性. 后来, 人们也基于数学方法来进行建模, 从而对空气质量问题完成了很好的预估^[3]. 例如, 杨宁等人运用时间序列分析方法, 借助SPSS软件对北京市未来2周的空气污染物变化情况进行了预测, 通过Q检验和拟合统计量R²验证了ARIMA模型预测效果较好, 具有一定的推广价值^[4].

随着机器学习技术的逐渐成熟, 越来越多的研究者采用神经网络建模的方法很好地完成了空气质量的预测工作. 很多国内和国外的研究中, 人们较多使用传统的神经网络方法来建立预测模型. 例如, Samia等人使用非线性的人工神经网络ANN和移动平均模型ARIMA的组合模型完成了对斯法克斯南郊等地区的气象和颗粒数据的实验, 证明了该模型的有效性^[5]. Chauhan等人使用卷积神经网络CNN模型对印度不同城市的空气质量数据集进行了实验, 分析了空气污染物对城市的影响, 验证了模型的准确性和适用性^[6]. Jiang等人提出了一种基于样本自组织聚类的BP神经网络, 利用自组织竞争神经网络的聚类特征对空气质量进行了预测, 模型预测精度得到了提升^[7]. 范彩云等人以北京市空气质量为例, 采用小波降噪和LSTM神经网络的方法, 结合区域关联性等对AQI指数进行了预测, 与ARIMA模型等进行对比, 证明了降噪后带空间因素的LSTM神经网络具有更好的预测结果^[8]. 徐万镛等人选取兰州市PM₁₀等主要污染物浓度数据并进行标准化处理, 搭建4层的LSTM神经网络对未来12小时的AQI指数进行预测, 和传统的3层模型进行对比说明了该LSTM模型具有较好的预测效果^[9]. Menares等人基于LSTM和深度前馈神经网络DFFNN对智利圣地亚哥市监测站气象数据进行了预测, 最终证明了深度学习的LSTM模型的表现一直优于目前使用的确定性模型^[10].

以上方法中, 无论是基于传统的神经网络模型还是数学模型, 其模型的参数都是依据个人经验而定的, 所以预测结果往往存在预测精度低, 训练周期长, 不够可靠的问题. 基于这些问题, 本文引入鲸鱼优化算法, 使用WOA算法对BiLSTM网络的训练参数神经元个数m和学习率l进行寻优, 从而可以达到提升模型的拟合效果、训练过程和预测结果的目的.

1 数据质量提升及算法流程图 1.1 数据来源及可视化

本文数据源自于UCI (University of California Irvine)数据库中陕西省空气质量数据集, 选取2019年7月到2020年12月共13 000条气象数据, 主要包含date、CO、NO₂、O₃、PM₁₀、AQI等8个属性.

对2020年的AQI数据按照一年12个月的变化, 进行可视化统计如图1所示. 可以发现, 在1月AQI最高(167.68), 说明此时空气质量最差; 在8月AQI最低(45.33), 说明此时空气质量最优.

1.2 数据质量提升

首先, 在O₃、CO、NO等特征中, 均存在不同数目的缺失值. 通过计算每一列的平均值来对此列中存在的缺失值“NA”进行了填充, 确保序列数据在进入网络进行训练之前不存在缺失.

其次, 在原始数据集中, 各特征存在较大差异的数据量纲, 容易导致模型精度降低, 模型训练时间长, 因此在将特征输入到网络之前, 还需对特征因子进行归一化操作^[11]. 归一化操作的原理如下:

$ \begin{array}{c}{x}^{*}=\dfrac{x-{x}_{\min}}{{x}_{\max}-{x}_{\min}}\end{array} $

(1)

其中, ${{x}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ 即所在列的最大数据, ${{x}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ 是所在列的最小数据, x是待标准化前的数值, ${{x}}^{{*}}$ 是x标准化后的数值.

特征归一化操作使得数据范围均介于[−1, 1]之间, 样本数据的均值接近于0, 数据既保留了本身的正负属性, 而且可以提高神经网络的学习速度.

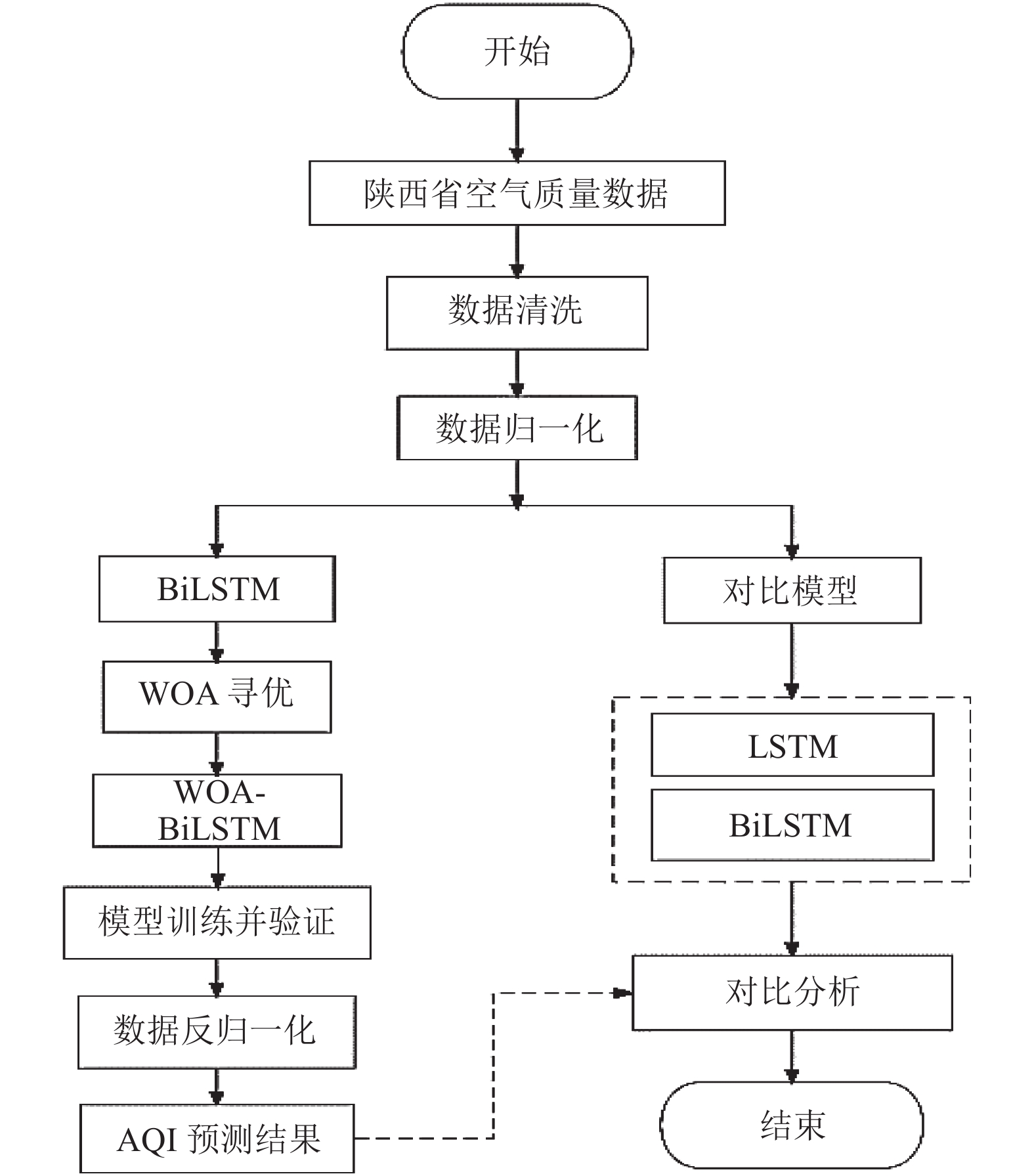
1.3 算法流程图

本文首先对陕西省的空气质量数据进行清洗, 并对数据进行归一化操作, 然后先根据经验函数设定随机参数后将特征输入到BiLSTM网络中进行训练, 再根据WOA算法对网络模型的神经元个数和学习率进行寻优^[12], 输出最优网络超参数, 再根据最优参数, 将特征输入到建立好的WOA-BiLSTM模型中, 然后将测试集输入到该模型中进行验证, 进行数据反归一化得到数据预测结果, 最终还将该模型和BiLSTM以及LSTM进行了对比分析, 证明本文提出的WOA-BiLSTM模型具有更好的预测结果. 本文的算法流程图如图2所示.

2 空气质量预测原理 2.1 BiLSTM网络

LSTM作为一种特殊的RNN网络, 以其可以学习到长时间依赖信息的能力, 而被广泛应用于时间序列预测领域^[13]. LSTM神经网络分别由输入门 ${{i}}_{{t}}$ 、输出门 ${{o}}_{{t}}$ 、遗忘门 ${{f}}_{{t}}$ 三种存储门部件构成.

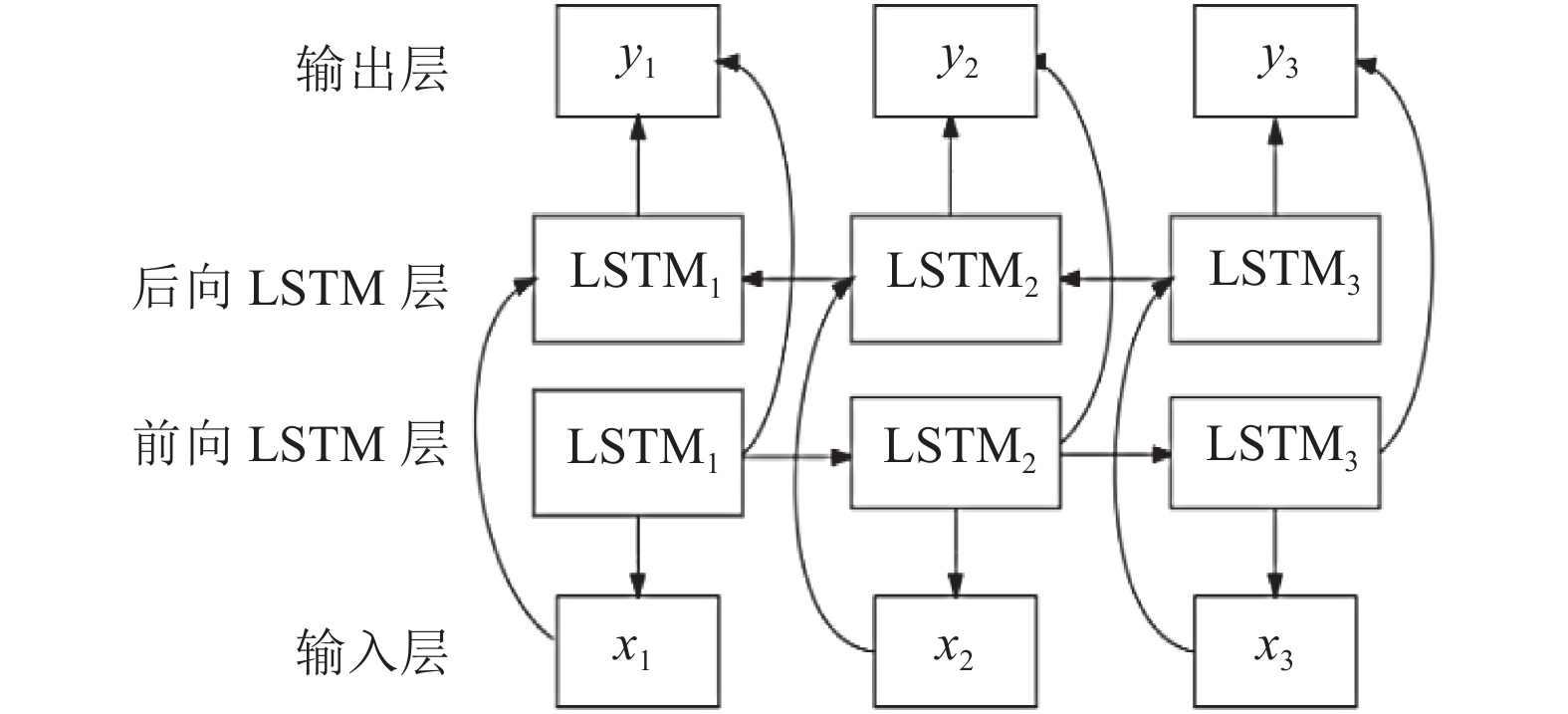
本文引入双向的长短期记忆网络BiLSTM, BiLSTM网络基于前向和后向的双向传播原则, 同时提取过去和未来的隐藏层信息, 使得空气质量信息提取更加充分. BiLSTM网络结构如图3所示.

将图3中的前向LSTM层计算向量记为 $\overleftarrow{{h}}$ , 后向LSTM层计算向量记为 $\overrightarrow{{h}}$ , 可得输出y的最终计算结果为:

$ \begin{array}{c}{h}_{t}=\alpha \overleftarrow{h}+\beta \overrightarrow{h}\end{array} $

(2)

$ \begin{array}{c}y=\sigma \left({h}_{t}\right)\end{array} $

(3)

其中, $ \mathrm{\alpha }\mathrm{、}\mathrm{\beta } $ 为常数, $ \mathrm{\alpha } $ 和 $\; \mathrm{\beta } $ 之和为1.

2.2 WOA算法

本文使用鲸鱼优化算法WOA对BiLSTM的训练参数隐藏神经元个数和学习率进行寻优. WOA的原理就是模拟座头鲸围捕猎物的行为, 实现全局搜索的过程^[14], 主要包含了包围、攻击和搜索3大过程.

(1)包围. 开始鲸鱼会先选择一个局部最优的捕食方向, 设定一个当前最优的猎物位置进行包围. 计算公式如下:

$ \begin{array}{c}\overrightarrow{D}=\left|\overrightarrow{C}{\overrightarrow{X}}^{*} \left(t\right)-\overrightarrow{X}\left(t\right)\right|\end{array} $

(4)

$ \begin{array}{c}\overrightarrow{X}\left(t+1\right)={\overrightarrow{X}}^{*} \left(t\right)-\overrightarrow{A}\overrightarrow{D}\end{array} $

(5)

其中, $ {X}^{*} $ 代表猎物位置的向量, X代表鲸鱼位置的向量, t为迭代轮数, A和C为系数向量. 计算时, 会对A和C向量进行调试, 用来寻找X在最优解周围的位置. A、C的计算公式如下:

$ \begin{array}{c}\overrightarrow{A}=2\overrightarrow{a}\overrightarrow{{r}_{1}}-\overrightarrow{a}\end{array} $

(6)

$ \begin{array}{c}\overrightarrow{C}=2\overrightarrow{{r}_{2}}\end{array} $

(7)

其中, a从2到0线性变化; r是取自于[0, 1]中的随机向量.

(2)攻击. 一般鲸鱼在进行攻击的时候, 主要有两个机制, 分别是收缩包围猎物机制和螺旋更新位置机制.

收缩包围机制: 新的个体位置可以定义在目前的鲸鱼个体和最佳鲸鱼个体间的任何一个位置^[15], 参见式(5).

螺旋更新位置机制: 首先计算出鲸鱼和猎物之间的距离 ${D}^{{'}}$ , 构建方程:

$ \begin{array}{c}X\left(t+1\right)={D}^{{'}}{\rm e}^{bl}\mathrm{cos}\left(2\pi l\right)+{X}^{*}\left(t\right)\end{array} $

(8)

$ \begin{array}{c}{D}^{{'}}=\left|{X}^{*}\left(t\right)-X\left(t\right)\right|\end{array} $

(9)

其中, b为常数, l取[−1, 1]之间的随机数.

本文设定0.5为阈值, 通过判断产生的概率值p来决定鲸鱼在攻击时采取何种机制. 若概率p＜0.5且|A|＜1, 则采取收缩包围的机制; 若概率p＞0.5且|A|＜1时, 则采取螺旋式机制来更新位置.

(3)搜索. 若|A|＞1, 则随机搜索并选取鲸鱼来进行位置的更新, 而非基于已有的最优的鲸鱼个体. 如果算法的迭代轮次已经达到最大, 则算法终止.

2.3 WOA-BiLSTM预测模型

选择最优的隐藏层神经元个数m和学习率l值对于神经网络预测来说, 是至关重要的, 而依据经验选取参数的做法会降低BiLSTM模型预测精度. 因此, 本文通过WOA算法对BiLSTM循环网络的参数m和l做以优化.

将鲸鱼个体作为各个优化策略, 将鲸鱼位置的维数对应BiLSTM模型待优化参数的个数, 在鲸鱼不断更新自身位置的过程中获得BiLSTM循环网络的最优参数组合.

WOA-BiLSTM组合模型如图4所示. WOA算法将计算得到的初始化种群参数传递给已经建立的BiLSTM模型, 输入训练集到BiLSTM模型进行训练, 再对测试集进行预测, 得到真实值和预测值之间的误差, 同时WOA算法种群不断更新, 将更新得到的参数传递给模型进行再训练, 直到WOA算法输出最优的网络超参数, 再将得到的全局最优解传递给BiLSTM模型, 模型根据最优解组合对数据进行训练, 之后再进行测试, 最终输出得到模型的最佳预测结果.

使用WOA算法来对BiLSTM网络模型进行优化, 首先需要给定两个参数的搜索区间, 然后经过第2.2节描述的鲸鱼优化算法在给定的区间范围内进行随机搜索, 使得预测模型的损失函数Loss不断收敛, 得到最高的预测精度, 从而得到最优的网络参数, 将最优网络参数代入BiLSTM模型进行预测. WOA算法用于BiLSTM模型来实现空气质量预测的算法流程图如图5所示.

将WOA用于BiLSTM模型进行预测, 其算法流程按照如下几步进行:

步骤1. 首先对空气质量数据进行清洗和归一化等处理后, 将数据输入到BiLSTM模型;

步骤2. 对BiLSTM模型参数学习率l和神经元个数m进行初始化;

步骤3. 对鲸鱼优化算法种群进行初始化. 将变量组合(m, l)输入到WOA算法中, 作为待优化参数, 种群不断更新;

步骤4. 将初始化完成的参数值作为历史最优参数输入到BiLSTM模型进行训练;

步骤5. 将传统BiLSTM模型进行训练后得到的损失函数值作为系统要求的终止条件, 并同时计算得到基于鲸鱼优化算法的预测模型的损失值;

步骤6. 如果基于鲸鱼优化算法的预测模型损失值比传统的BiLSTM模型的损失值小, 则满足判定条件, 输出最优学习率l和神经元个数m; 相反, 如果基于鲸鱼优化算法的预测模型损失值大于或者等于传统的BiLSTM模型, 则需要进一步更新参数并再次训练模型.

3 基于WOA-BiLSTM模型的空气质量预测分析 3.1 WOA适应度分析

考虑到全局优化算法有多个, 本文对WOA等多个优化算法的适应度值进行了分析, 如图6所示, 可以看出, 当迭代次数达到65代左右时, WOA算法出现最佳适应度值, GSA (gravitational search algorithm)引力搜索算法在第100代时出现最佳适应度值, 而PSO(particle swarm optimization)粒子群优化算法和BOA (Bayesian optimization algorithm)贝叶斯优化算法则是在第200代左右时出现最佳适应度值. WOA算法最佳适应度值为0.000 193 2. 由此可以说明, WOA算法比其他优化算法具有更快的收敛速度和更高的收敛精度.

3.2 WOA-BiLSTM模型参数选择及优化结果

过往研究可以发现, LSTM网络参数中, 隐藏层神经元个数m和学习率l对模型的训练结果影响最大. 一般神经网络中的隐藏层神经元个数都是由经验公式, 见式(10), 而得到一个大致的取值范围, 然后在这个取值范围中, 进行屡次的实验来设定该参数的取值, 并且还要对模型性能进行横向的对比, 最终选取一个最优的参数.

$ \begin{array}{c}m=\sqrt{\alpha +\beta }+n\end{array} $

(10)

其中, $ \mathrm{\alpha } $ 和 $\; \mathrm{\beta } $ 分别为输出层和输入层的节点数, n取介于[0, 10]之间的常数.

学习率l对于BiLSTM网络来说, 关乎网络训练时损失曲线的振幅以及模型收敛的快慢. 学习率如果设置的较小, Loss曲线就会振幅变小, 学习速度也变得缓慢; 而学习率如果设置的过大, Loss曲线就会振幅变大, 下降速度变快. 所以需要选择合适的学习率参数, 实现模型训练“稳中求进”的原则^[16].

WOA-BiLSTM模型具有双向的循环神经网络, 模型具有输入层, 输出层和一个隐藏层结构, 选取Adam优化器来更新模型参数. 本文中隐藏层神经元个数m的值范围为[10, 50], 学习率l的取值范围为[0.001, 0.01], WOA算法对鲸鱼种群进行初始化后, 将参数传递给BiLSTM模型, 初始的隐层神经元个数m为30, 学习率l为0.001. 为避免过拟合问题, 迭代次数设为200, 时间步长设为5. 基于WOA算法的不断更新迭代, 最后将最优的网络超参数进行输出, 最终获得最优参数组合如表1所示.

3.3 WOA-BiLSTM模型预测结果分析

根据模型在训练过程中, 随着迭代轮次的递增, 训练集上损失值不断下降的过程, 得到模型训练的Loss曲线图, 如图7所示. 可以看出, 在前100次迭代时, 损失曲线大幅下降, 而当迭代轮次到达140左右时, Loss已经近乎为0.

将提升后的数据输入本文模型, 训练集取4 000条样本, 测试集取400条样本, 训练WOA-BiLSTM模型如图8所示. 可以看出在训练集和测试集上, AQI的预测值和真实值非常贴近, 曲线波动走向近乎一致, 说明预测误差小, 模型精确度高, 可以实现对AQI的高精度预测.

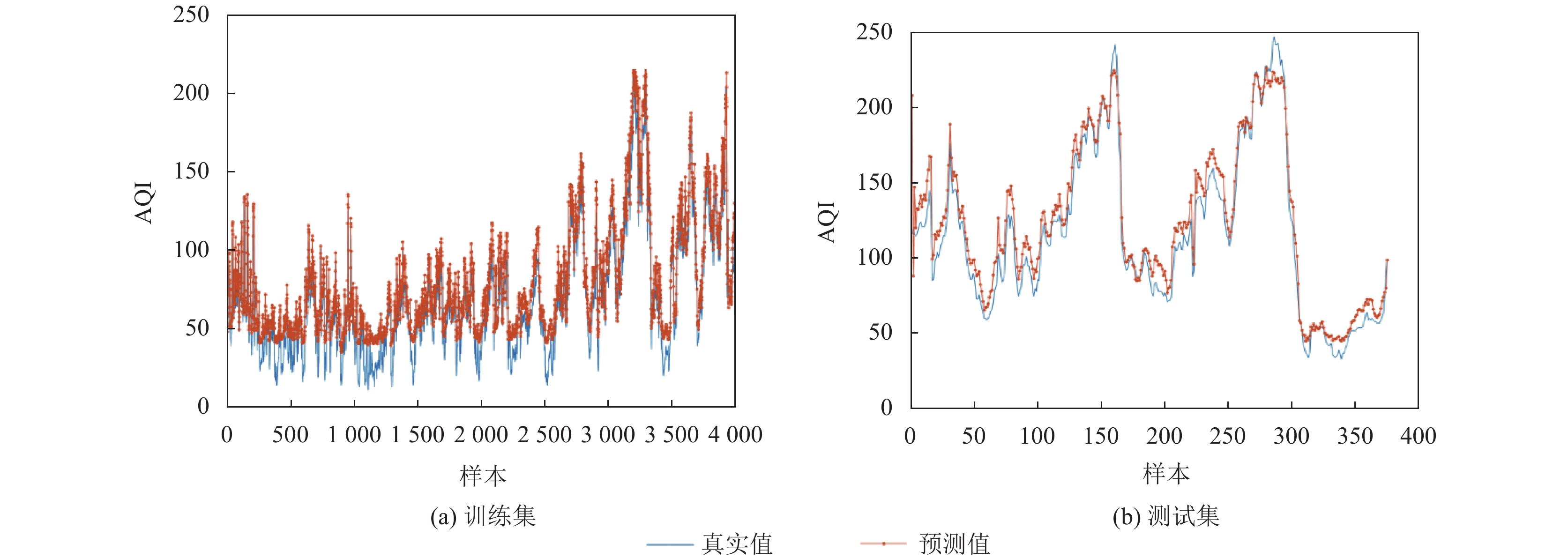
为验证WOA-BiLSTM模型对比其他现有预测模型间所具有的优势, 采用BiLSTM和LSTM模型进行对比试验, 隐藏层中的激活函数均使用tanh函数, 并采用十折交叉验证法对模型进行训练. 图9和图10分别为BiLSTM和LSTM对AQI进行预测的结果, 可以看出, 两个模型的训练精度均低于WOA-BiLSTM模型. 尤其从测试集可以发现, 真实值和预测值在很多峰值处无法达到高度拟合状态.

为了量化表示不同模型的预测值与真实值之间的误差大小, 本文采用绝对均值误差(MAE)、均方根误差(RMSE)以及线性相关系数(R²)作为评价指标^[17]. 评价指标的计算见式(19)–式(21).

$ \begin{array}{c}{\textit{MAE}}=\dfrac{1}{n}\displaystyle\sum _{i=1}^{n}\left|\right({y}_{i}-\tilde{{y}_{i}})|\end{array} $

(11)

$ \begin{array}{c}{\textit{RMSE}}=\sqrt{\dfrac{1}{n}\displaystyle\sum _{i=1}^{n}{\left({y}_{i}-\tilde{{y}_{i}}\right)}^{2}}\end{array} $

(12)

$ \begin{array}{c}{R}^{2}=1-\dfrac{\displaystyle\sum _{i}^{n}{\left({y}_{i}-\tilde{{y}_{i}}\right)}^{2}}{\displaystyle\sum _{i}^{n}{\left({y}_{i}-\bar{{y}_{i}}\right)}^{2}}\end{array} $

(13)

其中, n指测量值的总个数, ${{y}}_{{i}}$ 指AQI预测的实测值, $\tilde{{{y}}_{{i}}}$ 指AQI预测的预测值, $\bar{{{y}}_{{i}}}$ 指 ${{y}}_{{i}}$ 的平均值.

本文分别将WOA-BiLSTM、BiLSTM、LSTM模型在测试集上的预测评价指标进行了记录, 如表2所示.

为了更形象化的对比验证本文模型的合理性, 对模型的评价指标进行可视化展示, 如图11所示.

可以看出, 本文提出的WOA-BiLSTM模型MAE、RMSE值为最低, 分别为6.543 3和7.334 6. 其中MAE值较BiLSTM模型和LSTM模型分别降低了1.876 5和3.913 6. RMSE较BiLSTM模型和LSTM模型分别降低了3.186 9和5.325 1; 同时, 本文模型的R²值亦为最高, 较BiLSTM模型和LSTM模型分别提高了0.26%和1.98%. 这也说明了基于WOA算法的BiLSTM模型对于空气质量具有更好的预测效果, 其中WOA算法帮助BiLSTM模型寻找最优网络参数, 双向的长短期记忆网络帮助模型能够从前向和后向一并提取充足的数据特征, 达到更为精准的AQI预测效果.

4 结论

针对一般的长短期记忆网络在预测过程中, 网络参数需要依据经验而得, 训练周期长, 模型精度不够高的问题, 本文提出的WOA-BiLSTM模型, 以陕西省空气质量数据作为数据集, 验证了本文模型的有效性.

(1)本文WOA-BiLSTM模型中提出的WOA算法作为一种启发式的参数寻优算法, 可以高效的得到网络的最佳训练参数, 能够有效避免模型训练时调参所带来的对预测精度的影响, 而且采用了双向的长短期记忆网络, 能够使得模型在提取数据信息时, 尽可能地关注单向长短期记忆网络所忽略的信息, 从而能够保证空气质量预测结果的优越性.

(2)本文还将WOA-BiLSTM模型和BiLSTM以及LSTM模型进行了预测效果的对比, 发现了本文提出模型的MAE、RMSE、R²值均是最佳的. 这也说明了本文提出的模型能够更为准确的预测空气质量问题, 能够为我省气象局开展空气质量预测工作提供理论支撑和实践依据.