风险控制是衡量金融行业是否健康可持续发展的重要因素, 一直也是金融公司重点研究的内容. 当前金融信贷业务量随着消费升级不断高涨, 但是违约风险也在日趋凸显, 如某些小型贷款机构不得不依赖自己在银行的担保金勉强维持. 据公开数据研究, 中国上市的商业银行不良贷款余额逐年增长, 并在2020年达到了历史最高. 四大国有行合计坏账万亿元, 居商业银行首位, 占上市银行不良贷款总额约6成. 截至2020年末, 中国工商银行不良贷款余额排名第一, 其次为中国建设银行、中国农业银行和中国银行, 不良贷款余额均高于2 000亿元^[1]. 这些结果充分反映了银行由于没有控制好风险导致了巨额不良资产的问题, 因此金融公司在开展贷款业务时应将风险控制放在首要位置.

为了更好地控制业务风险使自身获利, 金融机构不断挖掘存量用户特征信息, 以此区分好用户和坏用户. 早在20世纪90年代开始, 金融公司为了获利, 把各类统计分析算法应用在业务中, 通过模型拟合的方法提前判断出用户风险^[2-5]. 但对于数据样本较少的新业务, 单纯用这类数据容易导致模型结果过拟合. 本文试图结合相似金融业务数据做为模型训练样本, 运用目前金融行业运用较多的算法: 随机森林、LightGBM、XGBoost、DNN和迁移学习, 分别预测新业务出的结果并与真实结果进行比较, 旨在为小样本业务在模型建立过程中样本不足的问题提供一种有效的解决方法.

1 信贷业务在模型上的发展情况

得益于Nasdap系统, 1971年美国的互联网金融进入正式运营, 1995年美国成立了一家网络银行, 从此互联网金融进入了发展期. 20世纪90年代开始, 发达国家在互联网金融领域快速发展, 互联网金融服务逐渐多元化、综合化, 行业之间竞争非常激烈. 各公司为了提升利润, 降低风险逾期率迫在眉睫, 各种统计分析算法应用在金融风控中, 大数据量化风控成为主流思想, 如在信贷引入决策树模型、逻辑回归模型、判别分析以及BP神经网络模型^[2-5] . 由于逻辑回归模型可解释性较强, 在金融领域备受青睐, 然而逻辑回归算法要求数据满足严格的假设, 因此在实践中很难应用^[6]. 相比于逻辑回归模型, 随机森林、LightGBM和XGBoost等树模型采用集成模型的思想, 拟合效果更好. DNN深度学习模型则可在稀疏空间做分类, 通过增加节点数或激活函数的次数来增加线性或者非线性转换能力和次数, 且尽可能的优化损失函数去学习规则, 但其解释性相对较差.

为了满足信贷模型预测效果更好的要求, 可从模型算法、数据输入和变量挖掘3个方面来进行优化. 模型方面可以优化模型算法或是利用组合模型进行预测, 如使用不同核函数建立支持向量机模型、基于XGBoost机器学习算法建模、使用加权投票法建立组合模型、基于梯度提升决策树模型、建立SVM-Logistic组合模型、建立随机森林等与逻辑回归融合模型^[7-12]; 变量方面可扩大量化维度, 如蒋翠清等^[13]将借款用途和社交情况等信息进行量化, 分析了不同软信息对贷款违约的影响作用; 数据方面可进行抽样等操作, 如祝钧桃等^[14]针对小样本数据从数据增强、度量学习、外部记忆、参数优化4个方面解决小样本问题, 为往后的研究提供了有价值的参考.

2 预测模型方法和数据来源

该实战案例分析使用iOS系统 10.14版本, 软件为Jupyter notebook; 具体硬件配置: 内存8 GB、处理器为2.3 GHz Intel Core i5; 实验中使用的工具为Python 3.7 Sklearn、TensorFlow、Kears等.

2.1 基础数据来源

数据源来自某银行信贷业务, 分为历史金融贷款数据和现业务数据, 历史信贷数据时间范围为2014年1月–2017年12月, 按天记录, 共30万条数据. 当前金融业务数据共1.5万条, 时间范围为2017年1月–2017年12月. 由于需要大规模开展业务, 需要结合历史信贷数据评估业务风险, 如通过用户的历史逾期情况、资产负债比例、工作年限等维度, 用于预测个人信誉问题.

该实验数据离散变量主要包括有工作年限、工作行业和房产情况. 连续变量数据情况如表1所示.

2.2 预测模型方法

(1)随机森林算法

随机森林(random forest, RF)模型是2001年由Breiman^[15]提出的基于分类树的算法.它通过对大量分类树的汇总提高了模型的预测精度, 是取代神经网络等传统机器学习方法的新的模型, 在医学、气象、金融、水利等领域被广泛使用.

在算法上, 随机森林是采用bootstrap sample方法, 有放回的抽样方式进行数据选择, 然后从所有属性中随机选择m个属性. 采用树模型训练模型但没有剪枝过程, 每棵树都尽最大程度成长. 重复k次, 建立k个模型, k个模型形成决策森林, 每棵树都是一个弱分类器, 最终的预测结果采用投票的方式整合k个弱分类器结果完成预测. 从整体来看, 单棵树存在过拟合、准确度不高、不稳定的现象, 多棵树共同决策可提升模型稳定性和精度. 算法步骤如下:

输入为样本集 $D = \{ ({x_1}, {y_1}), ({x_2}, {y_2}), \cdots,({x_m}, {y_m})\}$ 迭代100次, 输出最终的强分类器 $f(x), t = 1, 2, 3, \cdots, 100$ ; 对训练集进行100次随机采样, 共使用有放回采集24.8万次, 得到包含24.8万个样本的采样集合 ${D_t}$ ; 用采样集 ${D_t}$ 训练第t个弱学习器 ${G_t}(x)$ , 选择一个最优的特征值作为左右决策的划分点; 分类算法, 则100个弱学习器进行投票; 回归算法, 则100个弱学习器通过算法平均的方法, 最终拟合出模型结果. 本文采用分类算法完成投票.

随机森林算法参数配置: 100个弱学习器, 有放回抽样bootstrap=true, criterion=“gini”.

(2)XGBoost算法

XGBoost是基于GBDT算法的提升, GBDT算法仅支持CART基分类器, XGBoost支持CART基分类器的基础上同时支持线性分类器. 在精度提升方面, XGBoost使用二阶泰勒展开式 $f(x) = f({x_0}) + f'({x_0})(x - {x_0}) + \dfrac{{f''({x_0})}}{{2!}}\times {(x - {x_0})^2}$ , 比GBDT更好的逼近损失函数(loss function). 为了防止过拟合, XGBoost算法一方面代价函数里加入了正则项来控制模型复杂度, 另一方面借鉴了随机森林的做法, 支持列抽样. 具体算法如算法1.

算法1. XGBoost算法

输入: I, instance set of current node; d, feature dimension

$\scriptstyle gain \leftarrow 0$

$\scriptstyle G \leftarrow \sum\nolimits_{i \in I} {{g_i}} , \; H \leftarrow \sum\nolimits_{i \in I} {{h_i}}$

For k=1 to m do

　For j in sorted(I, by $\scriptstyle {x_{jk}}$ ) do

　 $\scriptstyle {G_L} \leftarrow 0, \; {H_L} \leftarrow 0$

　　 $\scriptstyle {G_L} \leftarrow {G_L} + {g_i}, \; {H_L} \leftarrow$ $\scriptstyle {H_L} + {h_j} $

　　 $\scriptstyle {G_R} \leftarrow G - {G_L}, \; {H_R} \leftarrow H - {H_L}$

　　 $\scriptstyle score \leftarrow \max \left(score, \frac{{G_L^2}}{{{H_L} + \lambda }} + \frac{{G_R^2}}{{{H_R} + \lambda }} - \frac{{{G^2}}}{{H + \lambda }}\right)$

　end

end

输出: Split with max score

XGBoost算法参数配置: 采用二元分类逻辑回归的方法, 训练100次, 最大树深度为3, 学习率为0.01, 正则化权重L1和L2为1.

(3) LightGBM算法

LightGBM在XGBoost的基础上做了改进, 主要引入了Histogram 算法, 内存消耗低并且可快速寻找树的分裂节点. LightGBM结合单边梯度采样(gradient-based one-side sampling)和互斥特征合并(exclusive feature bundling), 在减少维度和下采样上面进行优化使Histogram 算法效果更好. 在树的生长上, LightGBM抛弃了Level-wise策略采用leaf-wise, 为防止过拟合, 使用最大树深限制, 如算法2所示.

算法2. LightGBM算法

输入: I: training data, d: iterations; a: sampling ratio of large gradient data; b: sampling ratio of small gradient data;loss: loss function, L:weak learner

$\scriptstyle models \leftarrow \{ \} , fact \leftarrow \frac{{1 - a}}{b}$

$\scriptstyle topN \leftarrow a \times len(I), randN \leftarrow a \times len(I)$

For $\scriptstyle i = 1$ to do

　　 $\begin{gathered} \scriptstyle preds \leftarrow \bmod els.predict(I) \\ \scriptstyle g \leftarrow loss(I, preds), w \leftarrow \{ 1, 1, \cdots\} \\ \scriptstyle sorted \leftarrow GetSortedIndices(abs(g)) \\ \scriptstyle topSet \leftarrow sorted[1:topN] \\ \scriptstyle rankSet \leftarrow RanddomPick(sorted[topN:len(I)], randN) \\ \scriptstyle usedSet \leftarrow topSet + rankSet \\ \end{gathered}$

　　 $\scriptstyle w[rankSet] \times = fact{\text{ Assign weight to the small gradient data}}.$

　　 $\begin{gathered}\scriptstyle newModels \leftarrow L(I[usedSet], - g[usedSet], w[usedSet]) \\\scriptstyle Models.append(newModel) \\ \end{gathered}$

大量的金融信贷场景研究案例表明, LightGBM在预测结果上表现的效果优于XGBoost、Logistic、SVM和随机森林等模型效果, 准确性较高的同时具有较好的鲁棒性^{[16, 17]}.

LightGBM算法训练参数设置: 采用GBDT提升算法类型, 弱学习器数量为100, 最大树深度为3, 学习率为0.01, 正则化权重L1和L2为1.

(4) TrAdaBoost迁移学习算法

迁移学习将某个领域或任务上学习到的知识或模式应用到不同但相关的领域或问题中, 适用于源数据较少的场景或者零数据冷启动场景. 迁移学习分为归纳式迁移、直推式迁移、无监督迁移3种. 依据迁移知识的形式可将迁移学习分为基于实例的迁移学习、基于特征的迁移学习、基于模型的迁移学习、基于关系的迁移学习.

在21世纪初, Ben-David Schuller^[18]提出了学习与任务之间具有相互联系的观点, 为迁移学习提供了理论基础. 利用迁移学习思想在医学上取得了显著成就, 如基于X射线和CT图像预训练的CNN 模型进行 COVID-19检测任务; 把基于自然图像预训练得到的不同ResNet模型迁移到乳腺癌诊断任务; 使用与目标数据相似的脑血管图像在 AlexNet 上进行预训练, 再利用 SVM 分类器进行微调训练^[19-21]. 在文本挖掘上也常常采用迁移学习方法, 如采用迁移学习方法实现交叉语言文本分类; 利用完善的英文标签处理中文标签缺失问题, 解决了交叉语言迁移分类问题^{[22, 23]}. 迁移学习方法在P2P信贷实验上表明迁移学习模型的平均AUC比逻辑回归模型高0.088 0, 比支持向量机模型高0.035 5^[24].

TrAdaBoost 迁移学习算法^[25]利用对 AdaBoost算法加以改来达到迁移学习的效果, 主要通过boosting的作用建立自动调整权重的机制, 加重正确的辅助数据权重, 减少不重要的辅助训练数据权重. 主要方法如下:

输入: 两个数据集 $\scriptstyle {T_a}$ 和 $\scriptstyle {T_b}$ , 合并的训练数据集 $\scriptstyle T = {T_a}\bigcup {{T_b}} $ , 基本分类算法Learner和迭代次数N.

初始化:

1. 初始权重向量 $\scriptstyle {w^1} = {(w_1^1, \cdots, w_{n + m}^1)^a}$ , 其中,

$\scriptstyle w_i^1 = \left\{ \begin{gathered} \scriptstyle \frac{1}{n},\; i = 1, \cdots, n \\ \scriptstyle \frac{1}{m},\; i = n + 1, \cdots, n + m \\ \end{gathered} \right. $

2. 设置 $\scriptstyle \;\beta = 1/(1 + \sqrt {2\ln n/N} )$

For t=1, …, N

设置 $\scriptstyle{P^t}$ 满足 $\scriptstyle {P^t} = {w^t}/\sum\nolimits_{i = 1}^{m + n} {w_i^t}$ , 调用Learner, 根据合并后的训练数据T以及T上的权重分布 $\scriptstyle {P}^{t} $ 和未标注数据S, 得到一个S的分类器 $\scriptstyle {h_t}:X \mapsto Y$ . 计算 $\scriptstyle {h_t}$ 在 $\scriptstyle {T_b}$ 上的容错率: $\scriptstyle {\delta _t} = \sum\limits_{i = n + 1}^{n + m} {\frac{{w_i^t\left| {{h_t}({x_i}) - c({x_i})} \right|}}{{\sum\nolimits_{i = 1}^{n + m} {w_i^t} }}} $

设置 $\scriptstyle \;{\beta _t} = {\delta _t}/(1 - {\delta _t})^b$

设置新的权重向量:

$\scriptstyle w_i^{t + 1} = \left\{ \begin{gathered} \scriptstyle w_i^t{\beta ^{\left| {{h_t}({x_i}) - c({x_i})} \right|}},\; i = 1, \cdots,n \\ \scriptstyle w_i^t\beta _t^{ - \left| {{h_t}({x_i}) - c({x_i})} \right|},\; i = n + 1, \cdots,n + m \\ \end{gathered} \right. $

输出最终分类器:

$\scriptstyle {h_f}(x) = \left\{ \begin{gathered} \scriptstyle 1,\; \sum\nolimits_{t = \left[ {N/2} \right]}^N {\ln\left(\frac{1}{{{\beta _t}}}\right){h_t}(x) \geqslant 1/2\sum\nolimits_{t = [N/2]}^N {\ln\left(\frac{1}{{{\beta _t}}}\right)} } \\ \scriptstyle 0,\; {\rm other} \\ \end{gathered} \right. $

TrAdaBoost迁移学习算法训练参数设置: 基本分类算法采用XGBoost模型算法, 并用二元分类逻辑回归训练, 迭代次数为100, 最大树深度为3, 学习率为0.01, 正则化权重L1和L2为1, TrAdaBoost权重修改次数为8次, 即训练整体训练次数为8次.

(5) DNN算法

DNN (deep neural network)神经网络模型又叫全连接神经网络是基本的深度学习框架, 最早由 Hinton等人^[26]于2006年提出, 可基于对数据进行表征学习, 同时能够学习出高阶非线性特征, 具有特征交叉能力. 神经网络总体可分为3个模块: 输入层、隐藏层和输出层. 目前应用场景较为广泛, 如图像识别、声音识别、广告推荐、风险预测和智能投顾等场景^{[27, 28]}. 本文DNN模型结构如图1所示.

具体逻辑如下:

对客户的数据进行预处理, 包括数据清洗和数据变换. 通过3层隐藏层后输出预测结果. 每一层可以有一个或多个神经元, 文中模型隐层神经元选用8个, 输出层只有1个神经元. 激活函数包括tanh、ELU (exponential linear units)、Sigmoid、ReLU和maxout等, 本文选择ReLU函数. ReLU函数能克服梯度消失的问题, 使得神经网训练速度更快. 输出层设置了1个神经元, 使用Sigmoid作为激活函数, 输出在0和1之间.

$\sigma(x)=1 /\left(1+{\rm e}^{-x}\right)$

由于本文针对金融信贷逾期, 可抽象为好坏预测的二分类问题, 故采用binary cross_entropy作为损失函数.

${loss}=-\sum_{i=1}^{n} \widehat{y}_{i} \log \left(y_{i}\right)+\left(1-\widehat{y}_{i}\right) \log \left(1-\widehat{y}_{i}\right)$

其中, ${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} _i}$ 表示预测结果, ${y_i}$ 表示真实值, 当 ${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} _i} = {y_i}$ 时, loss=0, 表示没有损失.

DNN算法训练参数设置: SGD学习率为0.1, SWA采用周期性学习, 学习长度c为20, 学习率 $ {\alpha }_{1} $ 为0.001. 在训练过程中, 模型初始化参数之后使用SGD进行梯度下降, 迭代20个epoch后, 将模型的参数进行加权平均后得到组合权重的集成模型.

2.3 模型评价指标

TP与TN表示都分对的情况, TP是样本为正, 预测结果为正; 样本为负, 预测结果为负; FP表示样本为负, 预测结果为正; FN表示样本为正, 预测结果为负. AUC (area under curve)为ROC曲线下与坐标轴围成的面积, AUC越接近1.0, 检测方法真实性越高; 当AUC=0.5时, 则真实性最低, 则无应用价值.

ROC曲线的横坐标表示伪正类率, 表示预测为正但实际为负的样本占所有负例样本的比例; 伪正类率即为FPR(false positive rate).

$ FPR = \frac{{FP}}{{(FP + TN)}} $

ROC曲线的纵坐标为真正类率, 表示预测为正且实际为正的样本占所有正例样本的比例. 真正类率即为TPR(true positive rate).

$ TPR = \frac{{TP}}{{(TP + FN)}} $

精准率(accuracy)表示正确预测为正和正确预测为负的结果数量占所有预测结果数量的比例.

$ accuracy = \frac{{(TP + TN)}}{{(TP + FP + TN + FN)}} $

召回率(recall)表示正确预测为负的数量占全部负样本数量的比例.

$ recall = \frac{{TP}}{{(TP + FN)}} $

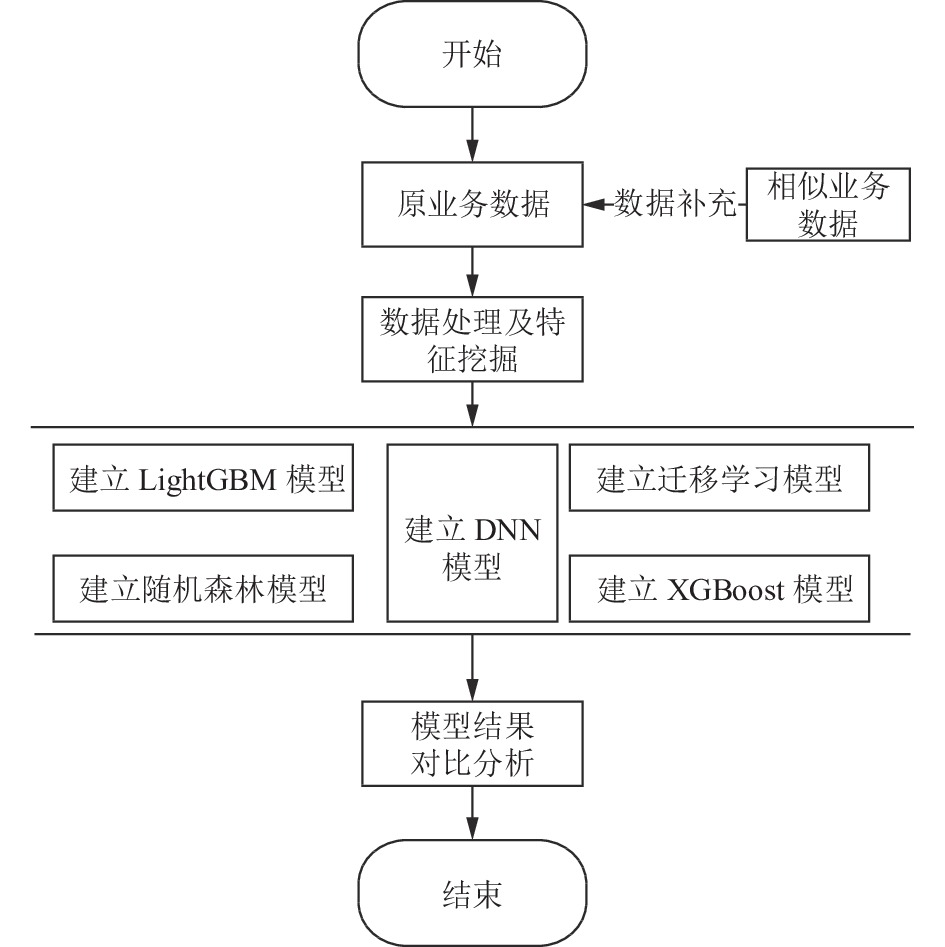
图2为本文流程图.

3 模型预测结果对比分析

考虑到需要预测的金融业务数据共1.5万条, 则其中1万条数据用于模型训练, 5 000条数据用于模型预测. 目标业务数据样本较少, 结合历史相似信贷模型的30万条数据, 模型训练样本共31万, 跨时间预测数据共5 000条. 坏样本选择逻辑为自放贷后12个月的表现期中, 逾期90天及以上的用户. 建模数据好坏样本分布情况如表2所示.

随机森林算法、XGBoost算法、LightGBM算法和DNN算法在数据训练时采用80%训练, 20%预测的方法, 为防止模型过拟合, 树模型深度最大为3. TrAdaBoost算法中训练集为30万历史信贷数据, 预测集目标信贷业务1万条数据. 最终模型评价测试数据均为小业务数据, 共5 000条. 建模数据测试训练测试数据分布如表3所示.

随机森林、XGBoost、LightGBM、DNN和TrAdaBoost算法预测数据ROC曲线结果如图3所示, 5种模型AUC结果分别为84、81、83、84和86. 其中TrAdaBoost算法效果最好, AUC的预测结果为86, 比随机森林和DNN的AUC高2个点, 比XGBoost的结果高5个点.

表4说明了各种算法预测结果的准确率及召回率, 从模型的准确率和召回率来看, TrAdaBoost算法准确率能达到88%, 召回率73%, 均比其他模型效果好; 其次是DNN, 准确率为86%, 召回率为70%; 随机森林算法, 准确率为84%, 召回率为68%; 相比于随机森林算法, XGBoost算法和LightGBM算法对预测数据的召回率更好, 分别是70%、71%, 其中LightGBM算法的准确率比XGBoost算法高1个百分点.

图4的TrAdaBoost算法模型结果分布表明, 模型效果较显著. 把坏账户进行分数的转换后, 按照等量划分的方法把结果分为8份, 每份约1 250条数据, 黑色的曲线表示坏账率, 可以看出坏账率有下降的趋势, 尤其是前两个区间的坏账率尤其高, 在业务中可以按照这个阈值作为cut节点来为业务作辅助决策. 从入模变量的重要性来看, 重要性变量集中在金融属性较强的变量上, 比如借款人提前还款次数和近3个月内提前还款金额, 从这两个变量从一定程度上可以说明借款人的财务状况.

4 结论

本研究的主要目的是在银行新开金融产品数据集很小的情况下, 开发一个能对用户是否逾期作出预测的有效模型. 对于金融机构想预判用户是否有逾期风险, 但由于资源的限制, 阻碍了他们获得有效用户数据的管理者来说具有非凡的意义. 把小样本融于其他类似的金融数据集中, 提高模型的预测能力, 对新金融业务具有很强的数据参考价值. 本文研究结果表明, 小样本业务结合相似业务构建模型的思路是可行的. 随机森林、XGBoost、LightGBM、DNN和TrAdaBoost五种算法在测试集上AUC结果都高于80, 精准度也都高于80%, 召回率平均能达到70%以上, 其中TrAdaBoost算法AUC结果为86, 精准率为88%的情况下召回可达73%, 效果最好. 总体而言, TrAdaBoost算法相较于其他对比方法鲁棒性较好, 在预测集上的结果表现最佳. 但是, 本研究在数据的选择上仍有一些缺陷, 例如, 在入模变量的数据选择上只用了银行内部的数据, 未引入三方数据而导致用户画像不全, 使得预测集的准确率和召回率还有提升空间, 后面可进一步补充民间借贷等相关数据.