2. 江苏省电力试验研究院有限公司, 南京 211103
2. Jiangsu Electric Power Test and Research Institute Co. Ltd., Nanjing 211103, China
随着全球石油资源储量逐渐减少, 碳排放过量与空气污染等环境问题日益严重, 发展清洁有效、环境友好的能源技术对解决能源与环境问题具有重要意义[1, 2]. 以光伏、风力发电为主的分布式电源(distributed generation, DG)接入传统配电网能有效缓解环境问题, 并且提高系统运行的可靠性[3, 4]. 然而DG并网会对配电网造成影响, 其中对整个系统的继电保护影响最为明显[5, 6], DG接入配电网使传统配电网的单一电源辐射网络转变为双端或多端供电网络[7, 8]. 因此, 针对含分布式电源的配电网继电保护研究尤为关键.
关于分布式电源并网的相关研究对进行配电网故障定位与切除工作, 保证系统安全运行尤为重要[9-12]. 文献[13, 14]总结了国内外对直流配电网保护、交直流混合配电网继电保护以及换流器保护等技术以及环境效益方面取得的最新进展与成果. 文献[15]提出将距离保护作为过电流保护的替代方法来进行故障检测. 文献[16]提出了基于本地信息量的自适应电流保护方案, 为DG并网后的继电保护算法研究提供了一定理论依据. 在故障定位方面的研究, 现有的方法主要有阻抗法、行波法、信号注入法、矩阵算法、遗传算法及神经网络算法等[17, 18]. 文献[19]提出了基于分布式智能馈线自动化系统的故障定位方案, 能够准确地对故障进行定位与隔离, 分析方法值得借鉴, 但该系统方案对设备间的通信要求较高. 文献[20]提出了一种自适应矩阵算法, 具有良好的容错性. 文献[21]提出一种基于子网络划分的配电网故障区段定位算法, 无论是单一故障还是多重故障均可准确定位, 但是对算法精确度要求较高. 文献[22]提出了一种环网故障定位的矩阵算法, 但必须要对不同电源假定不同的功率正方向才能确保判别故障区域. 文献[23]对矩阵算法进行了改进, 但是需要对上传的故障信息进行修正.
针对上述不足, 本文选取含DG接入的配电网作为研究对象, 分析DG分别以不同位置接入配电网对电流保护产生的影响, 通过PSCAD仿真验证理论分析的准确性, 针对含DG的配电网发生短路故障动作值难以整定的问题, 提出一种基于智能电子设备(intelligent electronic device, IED)上传故障信息的矩阵算法, 并通过算例验证了该算法的准确性. 该算法无须对元素进行修正与规格化处理, 且适用于单一故障与多重故障, 可实现故障区域的精准定位, 为含DG的配电网稳定可靠运行提供保障.
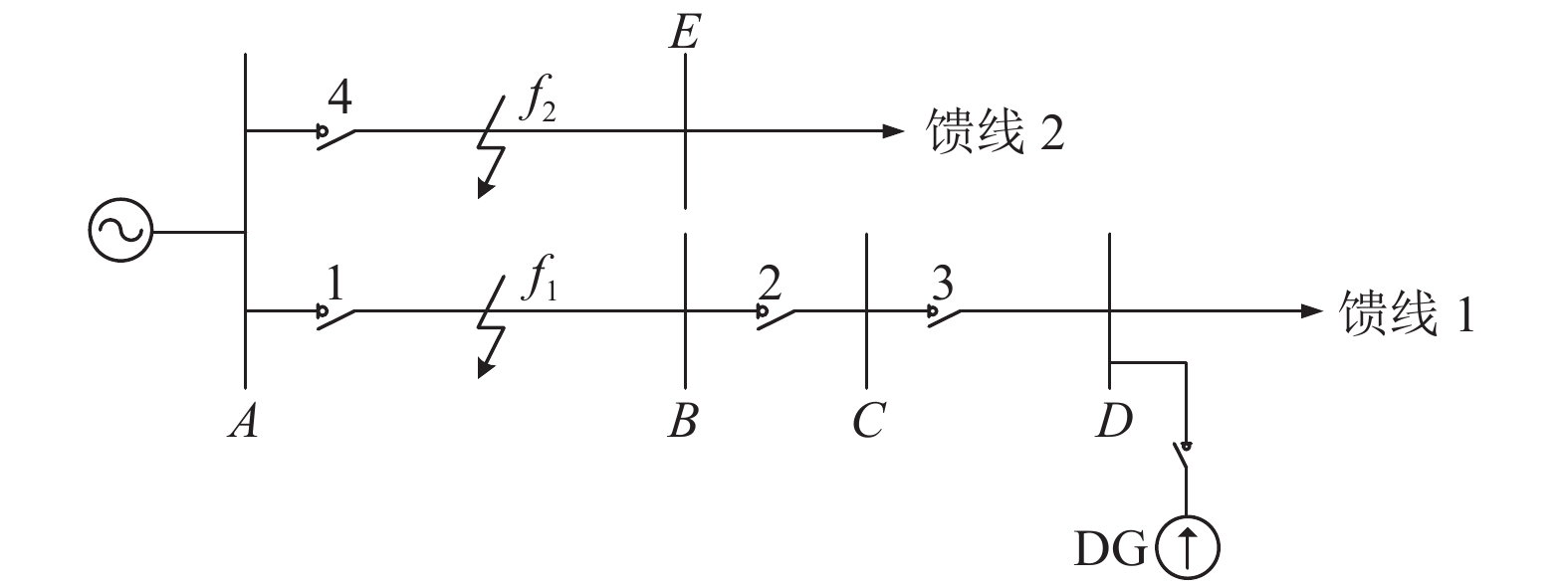
1 DG对配电网电流保护的影响机理本节以双馈线配电网为例, 研究当线路不同区段发生故障时, DG分别接入配电网馈线末端母线、非末端母线与首段母线, 对电流保护的影响. 如图1、图2所示. 由于DG采用电流型PQ控制方式接入配电网, 故在进行故障分析时可将DG简化为电压控制的电流源.
|
图 1 DG接在馈线末端母线D示意图 |
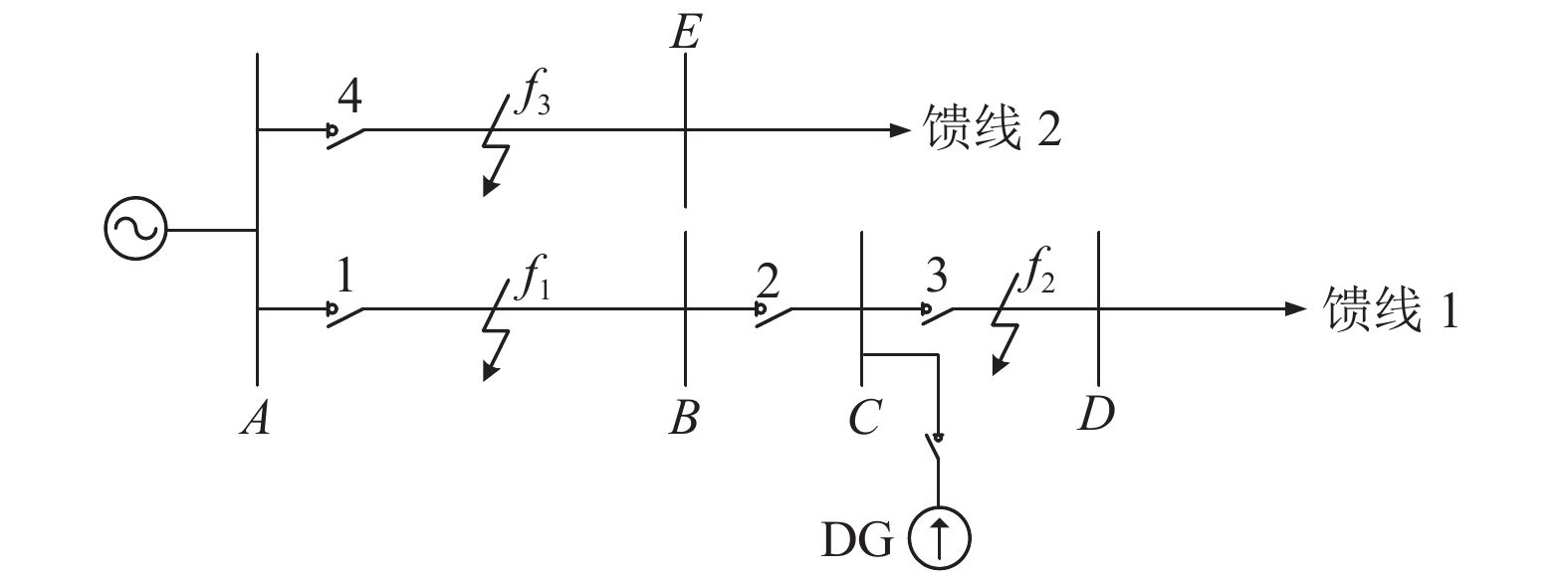
|
图 2 DG接在馈线非末端母线C示意图 |
1.1 DG接在馈线末端母线
(1)线路AB末端发生故障
当线路AB末端f1处发生故障时, 如果配电网没有DG接入, 保护装置1正常启动, 切除故障; DG接入配电网后, 向故障点f1提供电流, 电流经过保护2和保护3, 保护灵敏度度提高, 将有可能导致保护误动作.
(2)线路AE末端发生故障
当线路AE末端f2处发生故障时, 由于DG位置与故障点f2距离相差较远, 对保护4的影响较小.
1.2 DG接在馈线非末端母线(1)线路AB末端发生故障
当AB末端f1处发生故障时, 为了更直观地分析流经各个保护的电流大小, 可将故障线路等效成如图3所示的电路图进行分析.
| I1=USZS+ZAf1 | (1) |
| (1ZCD+1ZBf1+ZBC)UDG=PUDG | (2) |
| UDG=√P⋅ZCD(ZBf1+ZBC)ZCD+ZBf1+ZBC | (3) |
| I2=UDGZBf1+ZBC=√P⋅ZCD(ZCD+ZBf1+ZBC)⋅(ZBf1+ZBC) | (4) |
其中, I1为流经保护1的电流, I2为DG向故障点f1输出的反向电流, Us为系统基准电压, Zs为系统电源阻抗, ZCD为线路CD的阻抗, ZBC为线路BC的阻抗,
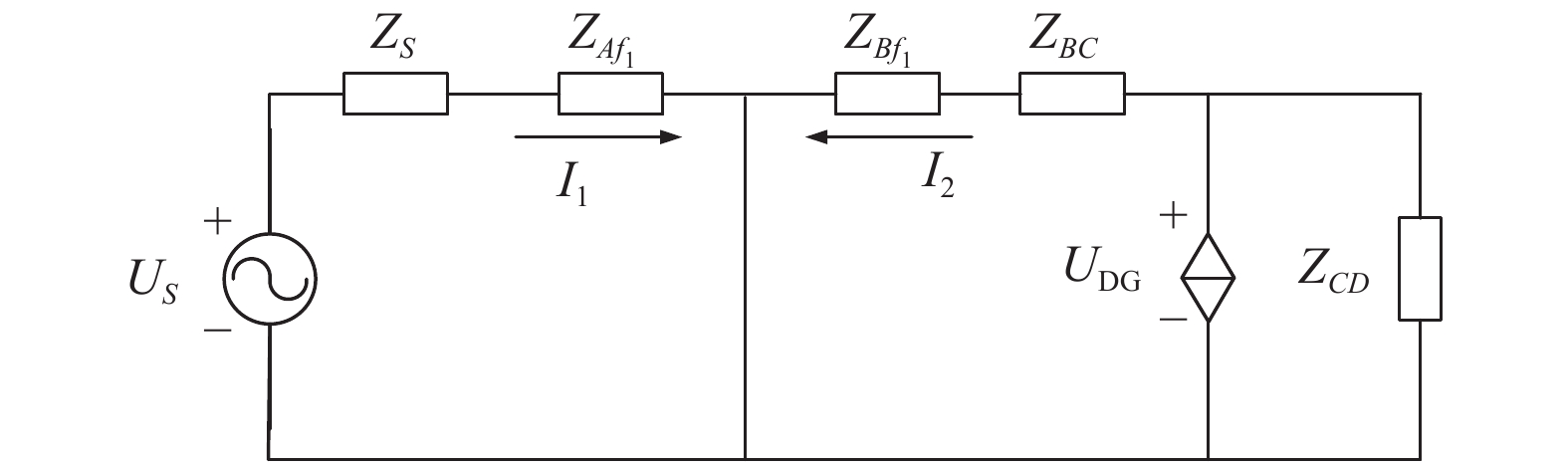
|
图 3 线路AB末端发生故障等效电路图 |
由式(1)–式(4)可知, 当AB末端f1处发生故障时, DG向故障处提供故障电流, 使得流过保护2的电流增大, 这将导致保护2误动作, 有可能导致线路断电范围延长, 而保护1的电流不受DG接入的影响, 仍然能够正常动作切除故障.
(2)线路CD末端发生故障
当线路CD末端f2处发生故障时, 可将线路等效为如图4所示的简化电路模型.
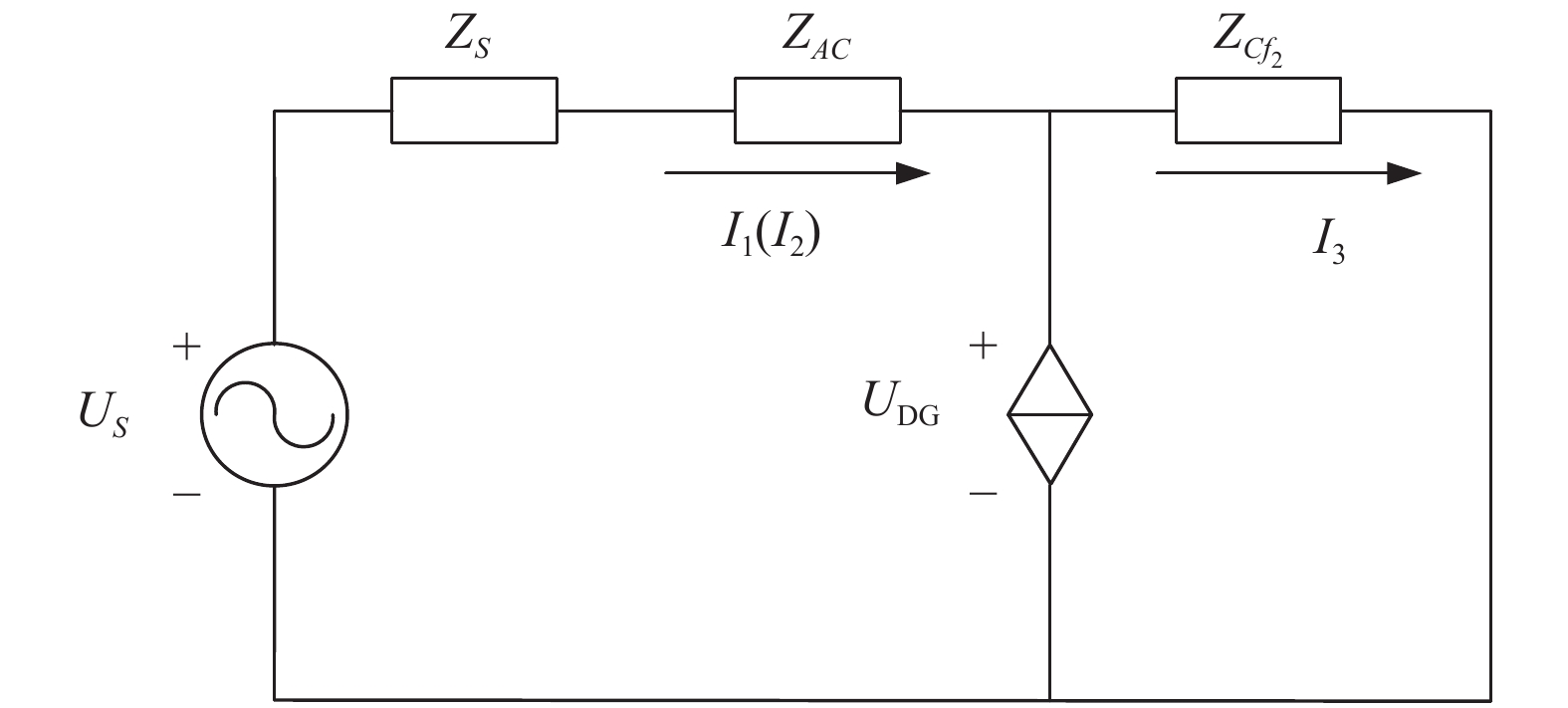
|
图 4 线路CD末端发生故障等效电路图 |
根据简化电路模型图, 可得到流经保护1、保护2以及保护3的电流I1、I2、I3.
| I1=I2=US−UDG|ZS+ZAC| | (5) |
| I3=UDG|ZCf2| | (6) |
其中, Us为系统基准电压, Zs为系统电源阻抗, ZAC为线路AC的阻抗,
| (1ZS+ZAC+1ZCf2)UDG=USZS+ZAC+PUDG | (7) |
| UDG=USZCf2+√US2ZCf22+4(ZCf2+ZS+ZAC)PZCf2(ZS+ZAC)2(ZS+ZAC+ZCf2) | (8) |
所以, 当CD末端f2处发生故障时, 先由保护3动作, 保护2延时动作, 而DG接在母线C上, 使得流经保护3的电流增大, 保护3的灵敏度得到提高, 流经保护2的电流减小, 保护2的灵敏度降低.
(3)线路AE末端发生故障
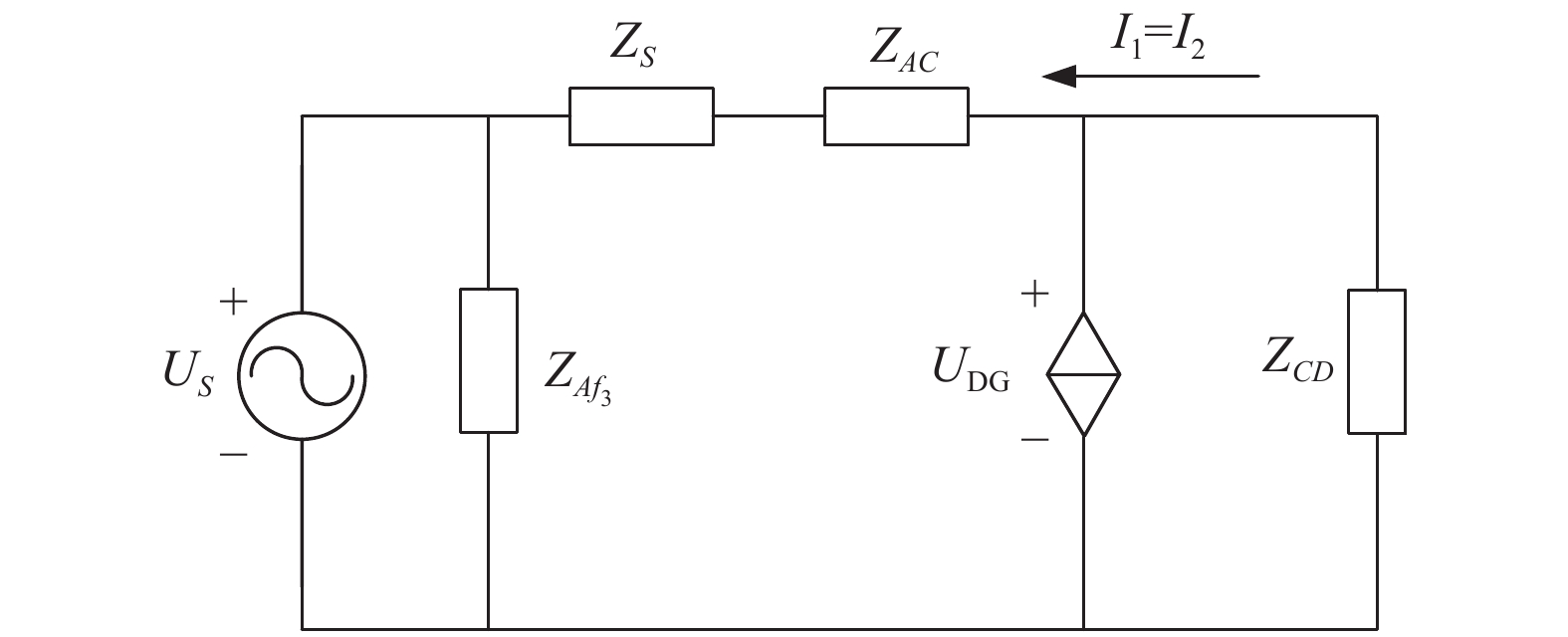
当AE末端f3处发生故障时, 可将故障线路等效成如图5所示的电路图进行分析.
|
图 5 线路AE末端发生故障等效电路图 |
| (1ZCD+1ZS+ZAC)UDG=PUDG+USZS+ZAC | (9) |
| UDG=USZCD+√U2SZ2CD+4(ZS+ZAC+ZCD)(ZS+ZAC)⋅ZCD⋅P2(ZS+ZAC+ZCD) | (10) |
| I1=I2=US−UDGZS+ZAC=[2(ZS+ZAC)US+USZCD−√U2SZ2CD+4(ZS+ZAC+ZCD)(ZS+ZAC)⋅ZCD⋅P]/2(ZS+ZAC+ZCD)(ZS+ZAC) | (11) |
其中, Us为系统基准电压, Zs为系统电源阻抗, ZAC为线路AC的阻抗, ZCD为线路CD的阻抗,
当AE末端f3处发生故障时, 在DG接入前, 由保护4动作即可切除故障, 当DG接入后, DG向故障点输出反向故障电流, 保护1和保护2都可能误动, 但如果DG距离故障点足够远, 提供的故障电流就不足以造成保护的误动作.
1.3 DG接在馈线首端母线当DG接入到配电网馈线首端母线上时, DG与系统原有电源共同为线路供电, 相当于增大了系统电源的容量, 无论是当线路CD末端或者线路AE首端发生故障时, 相较于DG接入前, 对线路中各个保护的影响都是较小的. 如图6所示.
2 DG对配电网电流保护影响仿真分析在PSCAD平台建立如图7所示的仿真模型, 仿真的具体参数配置如下:
(1)系统侧仿真参数
配电网系统的基准电压值为10.5 kV, 系统侧的阻抗值为j0.35 Ω.
(2)线路参数
配电网的线路AB、BC、CD、AF均采用架空线路, 其参数设置为: R=0.26 Ω/km, X=0.355 Ω/km, 由图7可知, 配电网络为两条馈线, 其参数分别为:
馈线1: AB的长度为3 km, 其阻抗值为ZAB=0.78+j1.065 Ω; BC的长度为3 km, 其阻抗值为ZBC=0.78+j1.065 Ω; CD的长度为10 km, 其阻抗值为ZCD=2.6+j3.55 Ω.
馈线2: AF的长度为4 km, 其阻抗值为ZAF=1.04+j1.42 Ω.
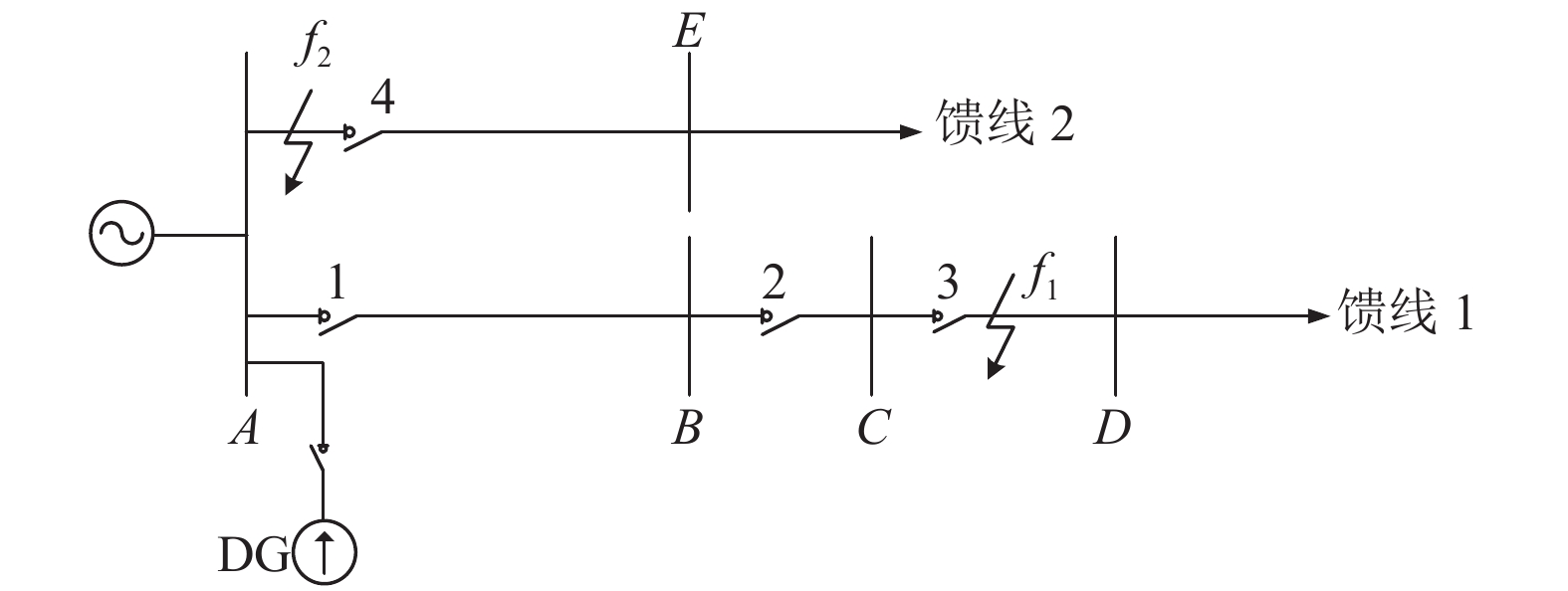
|
图 6 DG接在馈线首端母线A示意图 |
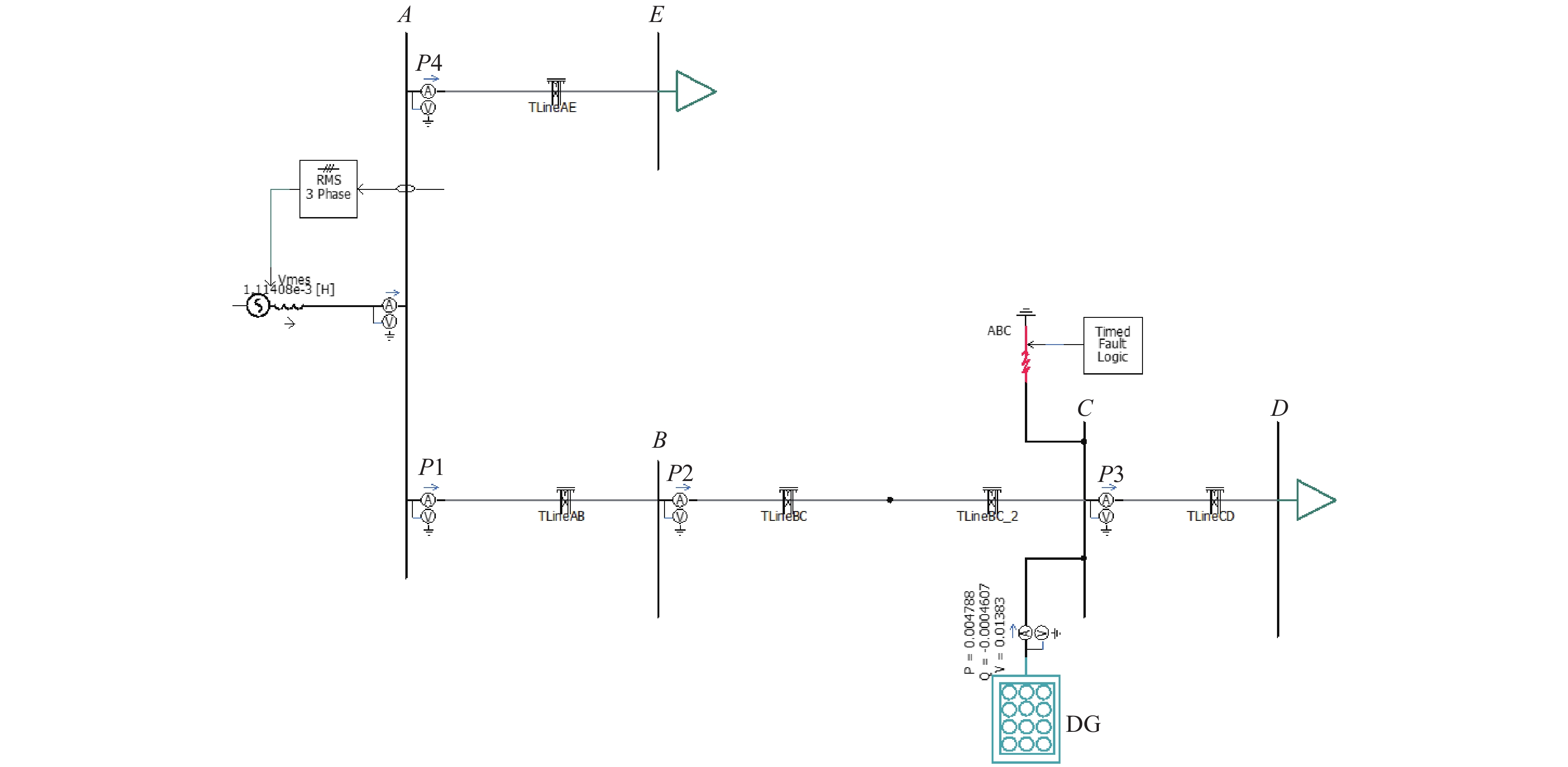
|
图 7 分布式光伏电源接入配电网PSCAD仿真模型 |
馈线1和馈线2末端的负荷的容量均为6 MVA, 功率因数为0.85.
PV输出功率在0–10 MW可调.
2.1 馈线末端接分布式电源仿真结果对比DG接在BUSD上, 设置DG出力为8 MW, 故障类型为ABC三相短路, 故障发生在仿真1 s, 为永久性故障.
(1)线路AB末端发生故障
如图8所示, 根据仿真结果可以看出, 无DG时系统保护1 (P1)动作正常, 但在馈线末端接入DG后, 由于DG向故障点倒送电流, 会造成保护2 (P2)和保护3 (P3)的Ⅲ段保护误动作.

|
图 8 线路AB末端故障时线路保护动作逻辑与A相电流 |
(2)线路AE末端发生故障
如图9所示, 由仿真结果可以看出, 馈线末端接入DG后, 保护4正常动作, 其他保护不误动.
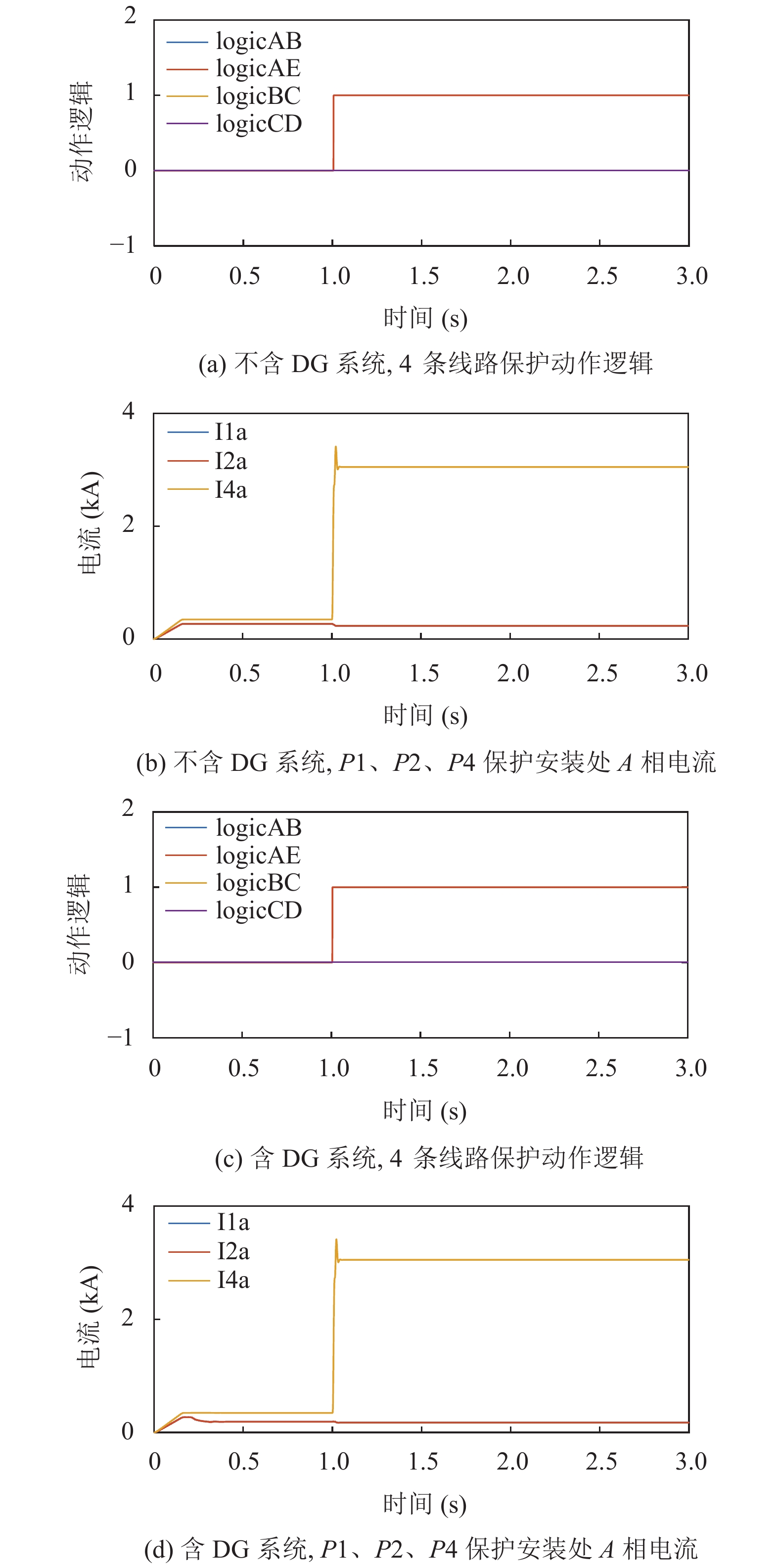
|
图 9 线路AE末端故障时线路保护动作逻辑与A相电流 |
2.2 馈线非末端母线接分布式电源仿真结果对比
DG接在BUSC上, 设置DG出力为8 MW, 故障类型为ABC三相短路, 故障发生在仿真1 s, 为永久性故障.
1)线路AB末端发生故障
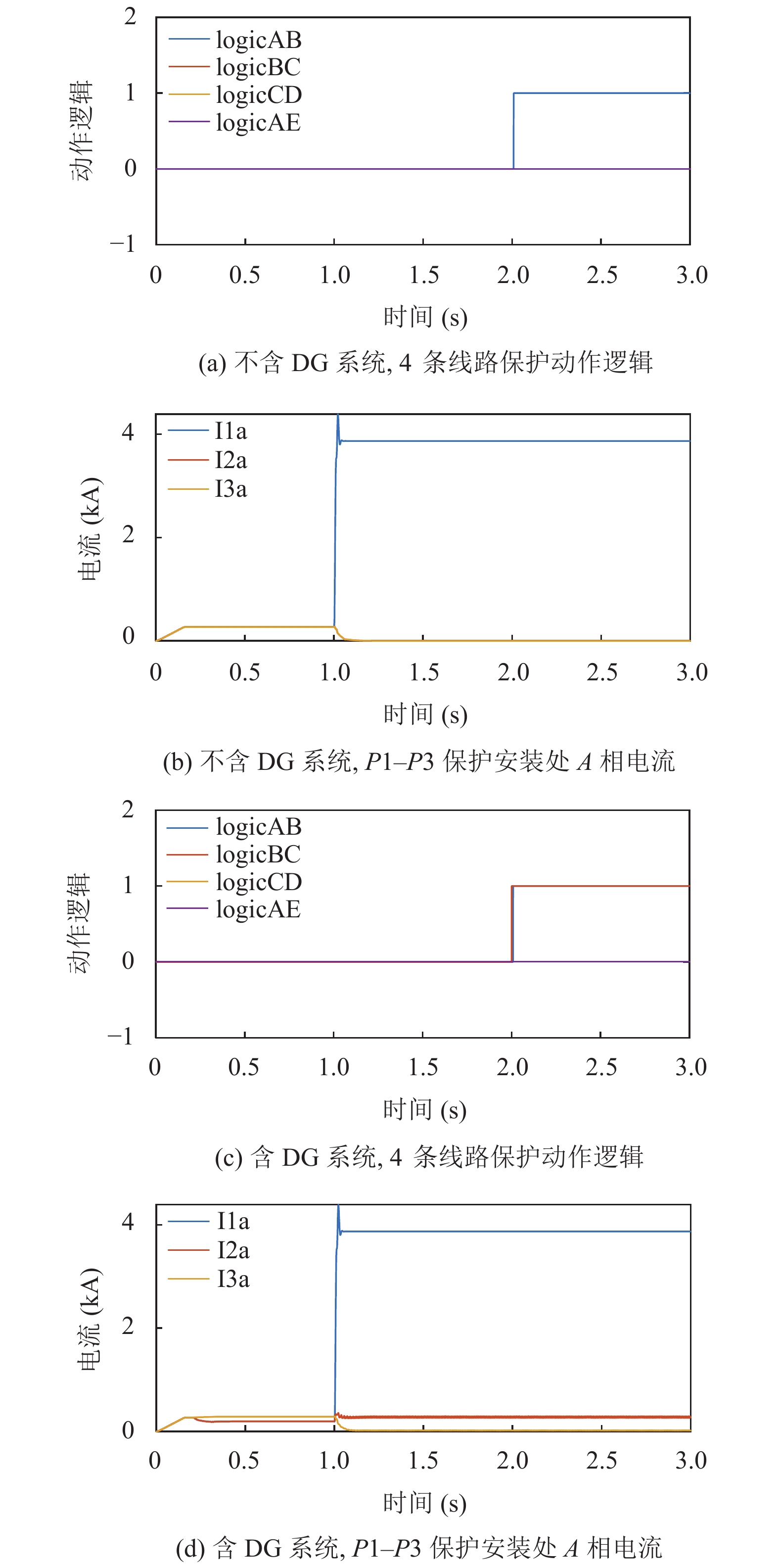
如图10所示, 由仿真结果可以看出, 在AB线路末端故障时, P1的Ⅰ段不能保护线路全长, 只能通过P1的Ⅱ段延时切除故障, 其他保护不动作, 保护选择性正确. 而在C点加入DG时, 会使P2的Ⅲ段发生动作, P2误动作, 这是由于AB线路末端故障时, DG会向故障点倒送电流, 导致P2误动作.
2)线路CD末端发生故障
如图11所示, 由仿真结果可以看出, CD末端发生故障时, 保护不误动, 这是因为虽然含DG的系统功率方向发生改变, 但是故障后流过P2的电流依然达不到P2过流Ⅱ段保护的整定值, 所以保护不误动.
|
图 10 线路AB末端故障时线路保护动作逻辑与A相电流 |
3)线路AE末端发生故障
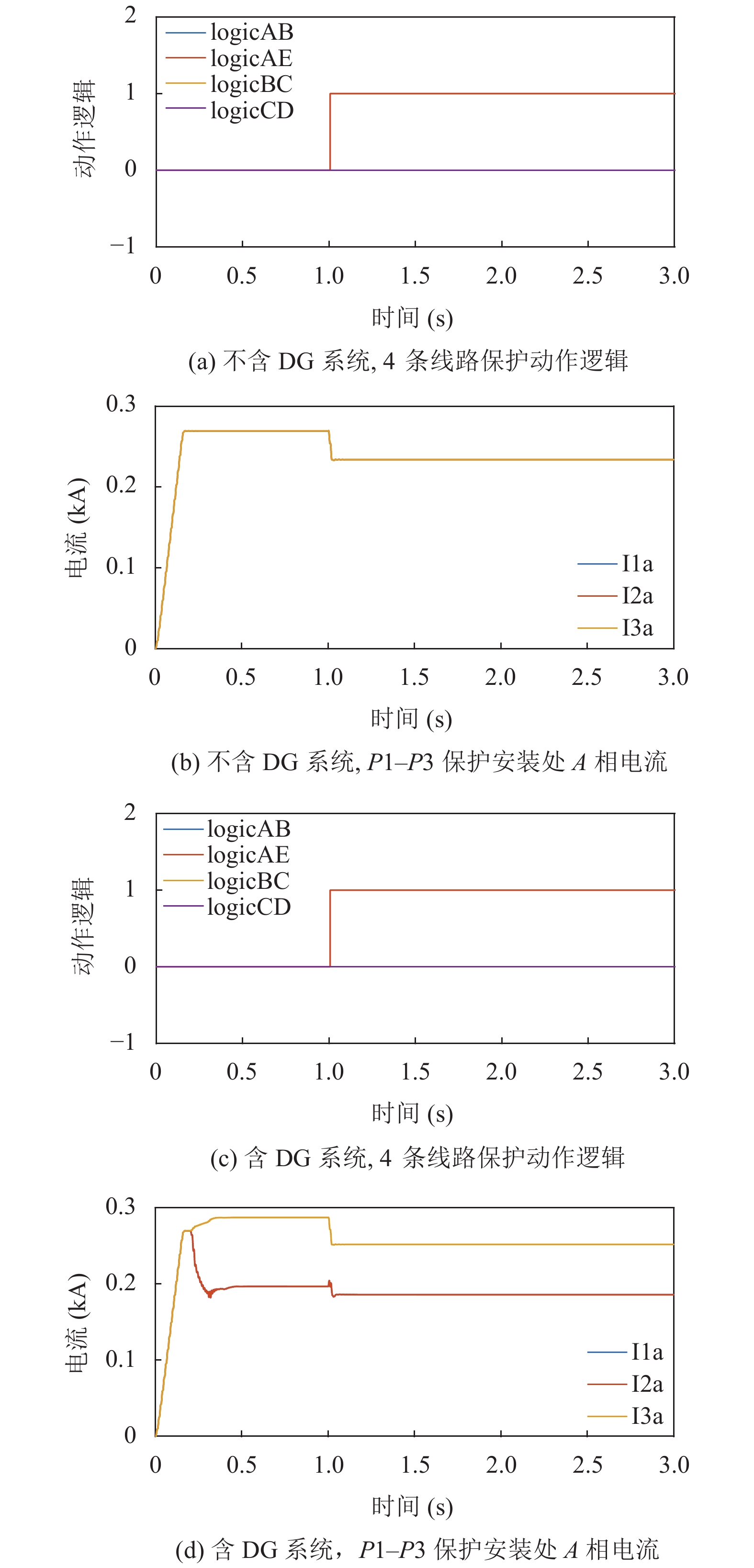
如图12所示, 由仿真结果可以看出, 在AE末端发生故障时, 无DG系统只有P4动作, 其他保护不误动, 在含DG的系统中, 由于DG接入位置距离故障点较远, 倒送的短路电流较小, 所以对配网的电流保护影响不大.

|
图 11 线路CD末端故障时线路保护动作逻辑与A相电流 |
2.3 馈线首端母线接分布式电源仿真结果对比
DG接在BUSA上, 设置DG出力为8 MW, 故障类型为ABC三相短路, 故障发生在仿真1 s, 为永久性故障.
1)线路CD末端发生故障
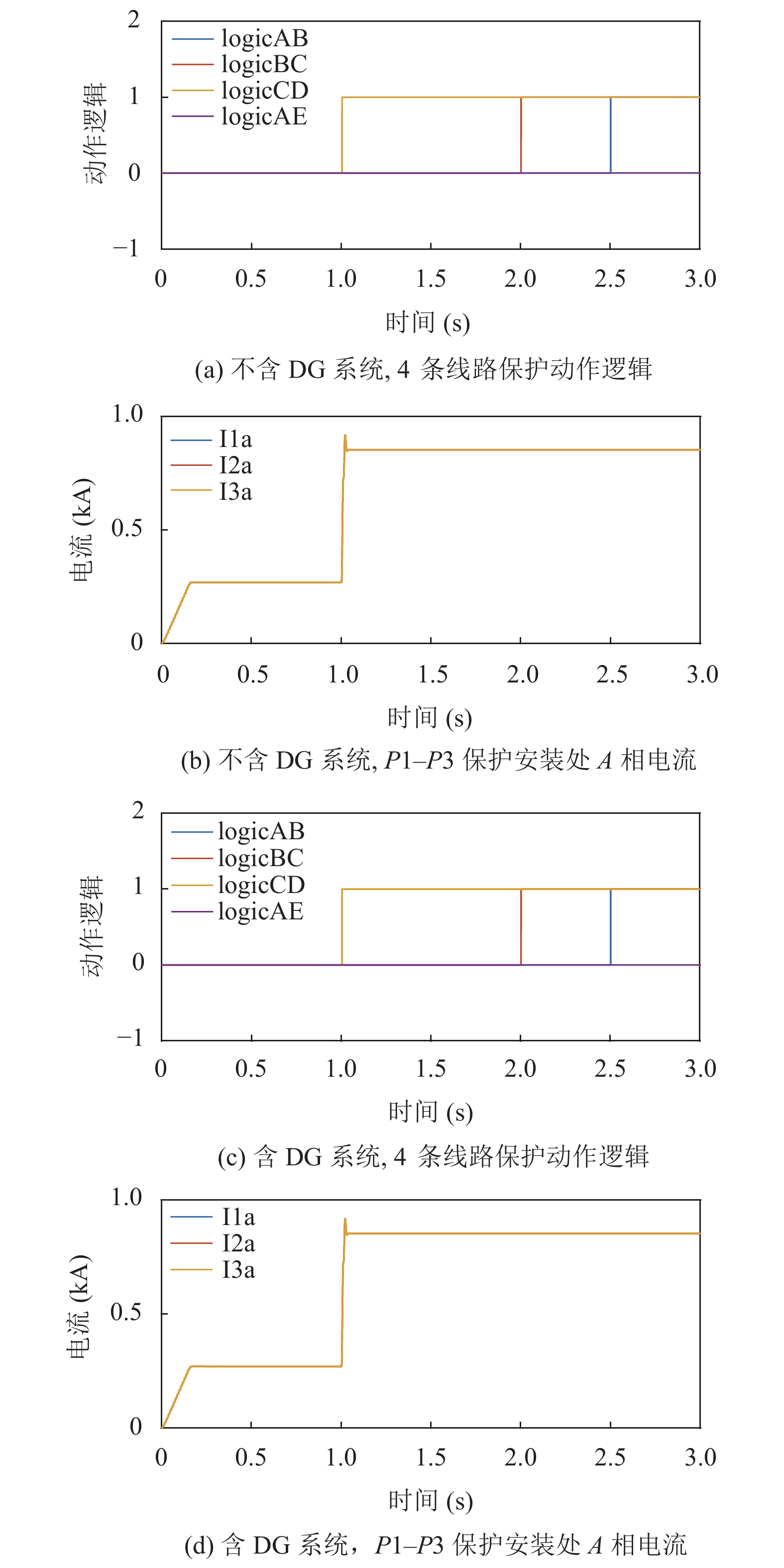
如图13所示. 由仿真结果可以看出, 分布式电源接入馈线首端后, 保护动作正常, 无误动. 这是因为分布式电源接在馈线始端的母线上时, 仅相当于增大了系统的容量, 虽然馈线上发生故障时短路电流会增大, 但由于分布式电源与系统相比容量依旧很小, 因此下游故障时DG对各个保护的影响都很小.
|
图 12 线路AE末端故障时线路保护动作逻辑与A相电流 |
2)线路AE末端发生故障
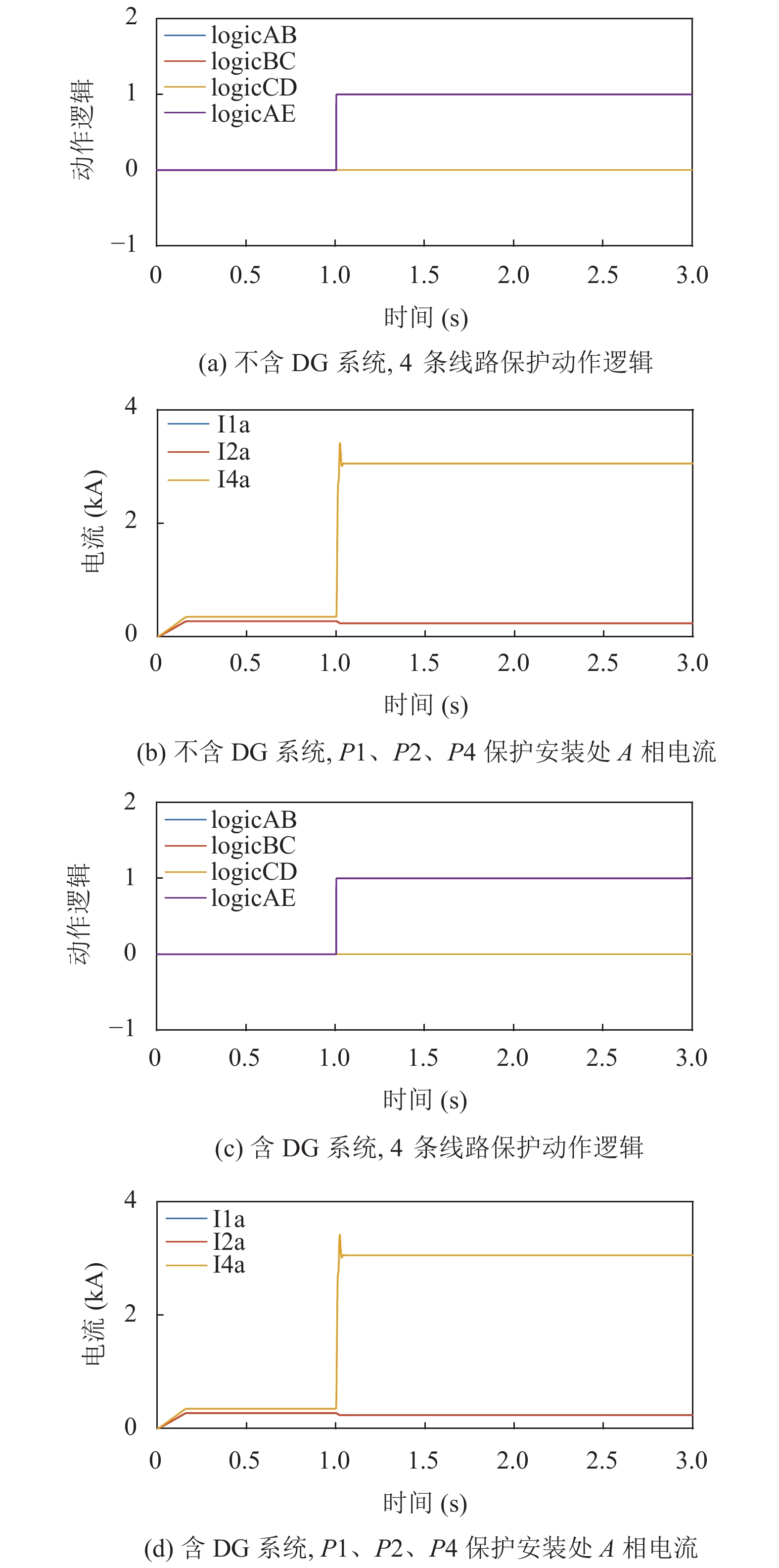
如图14所示. 由仿真结果可以看出, DG接入系统后保护动作正常, 无误动, 与CD末端发生故障时相同, 分布式电源的加入仅相当于增大系统容量, 对系统故障的保护动作影响很小.
|
图 13 线路CD末端故障时线路保护动作逻辑与A相电流 |
3 基于矩阵算法的含DG配电网故障定位 3.1 算法原理
通过上文对含DG的配电网电流保护影响分析可知, 当大规模DG接入配电网运行, 系统由原来的单电源线路变为复杂的多电源网络, 发生短路故障时DG对各段线路的电流保护造成了不同程度的影响, 各个保护动作值整定工作也随之变得困难, 而使用矩阵算法故障判据所需信息量少, 可适用于多电源网络, 尽可能地减少DG接入造成的不良影响. 当前, 配电网线路中大部分都装设有可以采集测量点电流、电压等信息的智能电子设备IED, 各IED通过将信息上传到决策子站, 数据信息在子站中经过处理统一发送到决策中心, 决策中心可实时监控区域内的线路运行情况, 并可根据上传的数据信息结合预设的算法判断线路是否发生故障, 给子站下发命令切除故障, 为本文的矩阵算法提供了现实基础.
|
图 14 线路AE末端故障时线路保护动作逻辑与A相电流 |
(1)网络描述矩阵D
将馈线上的IED作为节点进行编号, 与各个节点相连的馈线部分作为区域进行编号, 假设配电网共有i个区域与j个节点, 则可以构造一个i行j列的网络描述矩阵D, 矩阵D每个元素的值根据式(12)来确定, 当区域i与节点j相连且潮流方向为由i指向j, 则元素dij的值为1; 相反地, 当区域i与节点j相连且潮流方向为由j指向i, 则元素dij的值为−1; 当区域i与节点j不相连, 则元素值为0.
| dij={1,节点j与区域相连且潮流方向为由指向j0,节点j没有与区域相连−1,节点j与区域相连且潮流方向为由指向i | (12) |
(2)故障信息矩阵G
当节点j有故障电流经过其方向与规定正方向相同时, 则元素gjj的值为1; 当节点j有故障电流经过其方向与规定正方向相反时, 则元素gjj的值为−1; 若节点j没有检测到故障电流经过, 则gjj为0; 除了对角线外的其他元素统一为0, 形成故障信息矩阵G.
| gjj={1,节点j有正向故障电流经过0,节点j没有故障电流经过−1,节点j有反向故障电流经过 | (13) |
(3)故障判断矩阵P
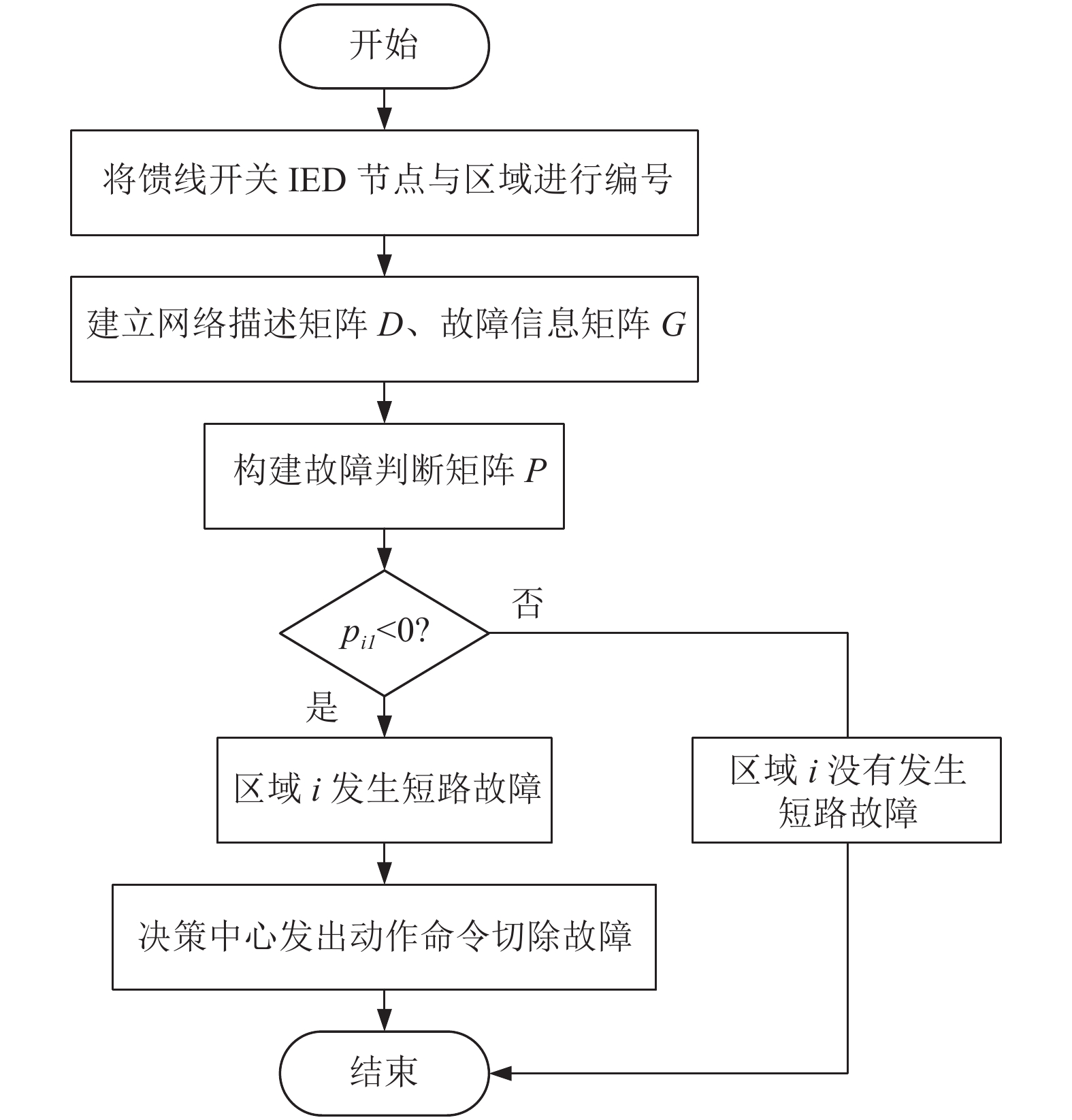
故障判断矩阵P的构造方法为, 先将网络描述矩阵D与故障信息矩阵G相乘得到一个n×n的矩阵P*, 然后分别对P*每行元素进行求和, 得到如式(15)所示n×1的故障判断矩阵P, 当P中某元素pi1<0, 表示流出该区域的短路电流小于流入的短路电流, 则可以判断在该区域内发生故障; 当pi1=0, 表示流入该区域的短路电流与流出的短路电流相等, 则该区域没有发生故障; 当pi1>0, 表示该区域为T型区域或者与系统主电源或DG直接相连, 区域内流过了电源产生的反向电流, 所以该区域也没有发生短路故障. 故障定位判别流程如图15所示.
| P∗=DG | (14) |
| P=[p11,p21,⋯,pi1]T=[n∑j=1p∗1j,n∑j=1p∗2j,⋯,n∑j=1p∗ij]T | (15) |
| {pi1⩾0, 区域i无故障pi1<0, 区域i发生故障i=1,2,⋯,n | (16) |
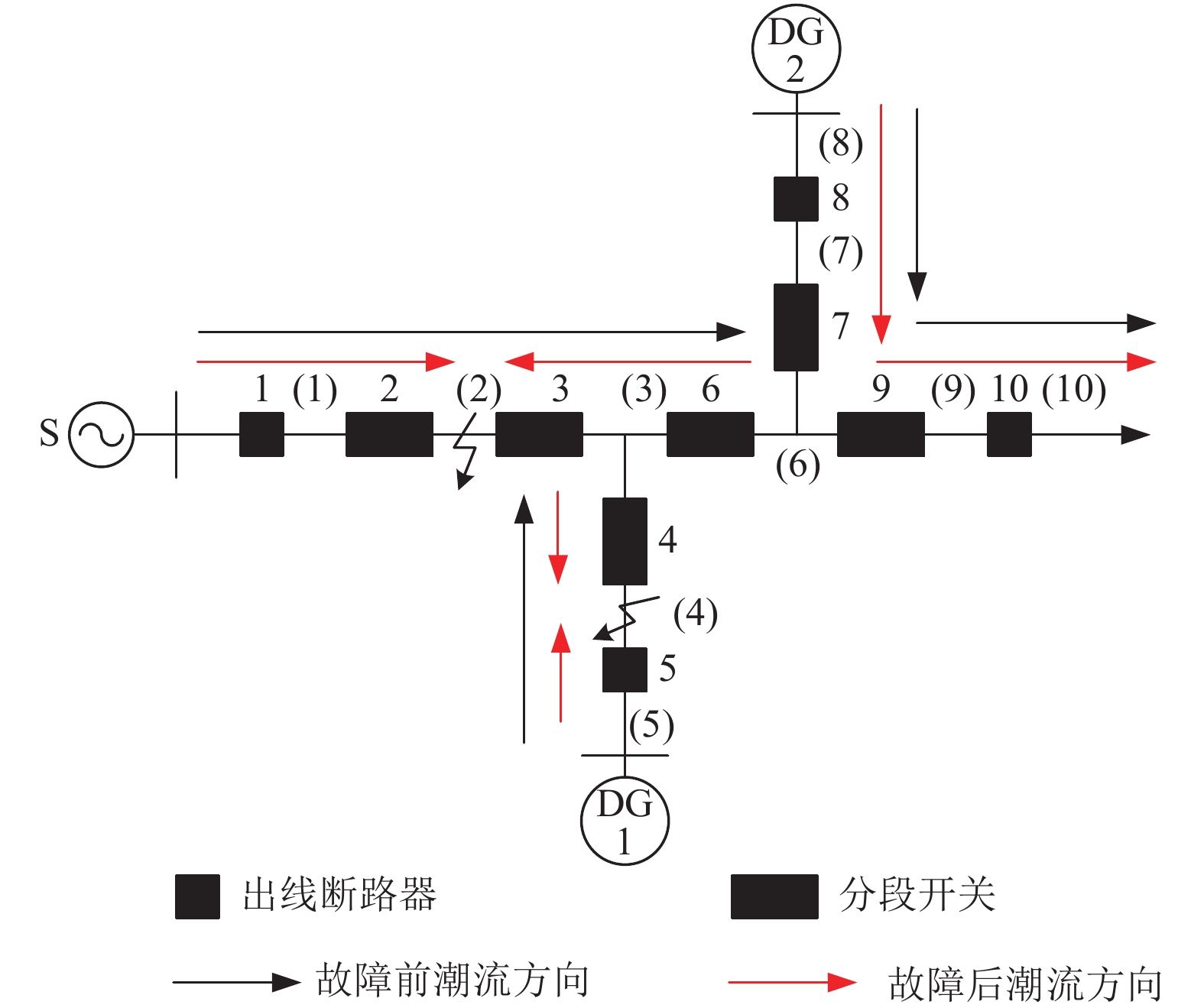
下面以如图16所示的配电网模型来验证算法的正确性与有效性, 规定箭头方向为每个开关节点的正方向.
|
图 15 故障定位判别流程图 |
假设区域(2)与区域(4)发生三相短路故障, 配电网的潮流方向会发生改变. 根据装设在各个开关上的IED采集的故障信息, 首先建立网络描述矩阵D与故障信息矩阵G分别为:
| D=[−11000000000−11000000000−1−10100000001−100000000010000000000−1−10100000001−100000000010000000000−11000000000−1] | (17) |
| G=diag[11−1−11−11100] | (18) |
由式(14)、式(15)计算得到
通过对配电网不同区域设置短路故障并运用矩阵算法进行故障定位验证算法的普遍性, 得到验证结果如表1所示, 无论是单一故障还是多重故障, 该算法都能准确定位故障区域.
此外, 配电网在实际运行过程中有可能因为检测设备故障或者通信原因导致线路中的部分故障信息无法传递到决策中心, 从而影响故障判断矩阵的建立, 此时应根据信息漏报的节点所处位置做出相应的应对措施, 当与信息漏报节点相邻的两个节点故障信息为1时, 则将漏报故障信息记为1; 当与信息漏报节点相邻的两个节点故障信息为−1时, 则漏报故障信息记为−1, 通过上述方法仍然可以得到准确的故障定位结果. 例如, 当区域(5)发生故障时, 如果节点7号节点故障信息漏报, 因与之相邻的6、8号节点故障信息都为0, 则可以将漏报故障信息置0, 最后得出短路故障发生在区域(5). 而当与信息漏报节点相邻的两个节点故障信息为互不相同时, 无法对漏报信息进行修正, 需要通过智能电子设备重新采集故障信息, 所以在配电网实际工作中, 保证设备之间能够进行正常通信极为重要.
|
图 16 含分布式电源的配电网模型 |
4 结论与展望
本文分析了在线路不同位置发生三相短路故障时, 分布式光伏电源接入不同位置, 对线路中流经各个保护的短路电流大小影响. 当故障发生在DG上游, 会造成故障位置保护误动作; 当故障发生在DG下游, 处于DG上游的保护有可能拒动, 处于DG下游的保护会误动作; 当故障发生在DG相邻馈线位置, DG所在馈线上游的保护灵敏度提高, 有可能会误动作, 但是当故障位置距离DG较远时, 对各个保护的影响较小. 针对DG接入后电流保护动作值难以整定的问题, 提出了运用IED采集故障信息的矩阵算法来进行故障区段定位, 该算法具有普遍适用性, 可实现故障区段的精确定位, 对确保配电网安全运行具有实际意义.
| 表 1 矩阵算法故障定位验证结果 |
| [1] |
余鹏, 王勇, 王相, 等. 配电网自动化DTU终端的103规约的安全性分析. 计算机系统应用, 2021, 30(5): 262-268. DOI:10.15888/j.cnki.csa.007890 |
| [2] |
范心明, 孙广慧, 彭元泉, 等. 智能配电柔性多状态开关在主动配电网中的应用. 广东电力, 2020, 33(12): 40-48. DOI:10.3969/j.issn.1007-290X.2020.012.005 |
| [3] |
赵杨竹雨. 多类型分布式电源接入配电网优化及保护研究[硕士学位论文]. 天津: 天津大学, 2019.
|
| [4] |
汤拓. 计及分布式电源的交流配电网保护方案研究[硕士学位论文]. 南京: 东南大学, 2019.
|
| [5] |
杨志强. 分布式电源接入配电网的电流保护方案研究[硕士学位论文]. 长沙: 湖南大学, 2019.
|
| [6] |
段之英. 分布式电源接入配电网保护方案研究[硕士学位论文]. 西安: 西安科技大学, 2018.
|
| [7] |
郭清元, 莫超, 吴杰康, 等. 分布式电源接入的配电系统多类型无功源出力优化方法. 电力工程技术, 2020, 39(5): 211-219. DOI:10.12158/j.2096-3203.2020.05.030 |
| [8] |
袁智勇, 徐全, 徐刚, 等. 含大容量分布式电源接入的配电网电流保护优化方案. 电网技术, 2021, 45(5): 1862-1868. |
| [9] |
李晶, 李鑫, 马越, 等. 分布式电源容量对配电网保护的影响分析. 电力系统及其自动化学报, 2016, 28(2): 98-102. DOI:10.3969/j.issn.1003-8930.2016.02.016 |
| [10] |
Cui SJ, Zeng P, Wang ZF, et al. Research on intelligent protection technology for distribution network with distributed generation. 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC). Chongqing: IEEE, 2021. 1549–1554.
|
| [11] |
邓景松, 王英民, 孙迪飞, 等. 基于配电网电流保护约束的分布式光伏电源容量分析. 电工技术学报, 2019, 34(S2): 629-636. |
| [12] |
Farkhani JS, Zareein M, Soroushmehr H, et al. Coordination of directional overcurrent protection relay for distribution network with embedded DG. 2019 5th Conference on Knowledge Based Engineering and Innovation (KBEI). Tehran: IEEE, 2019. 281–286.
|
| [13] |
李腾, 葛少云, 梁文举, 等. 考虑环境效益的含分布式电源配电网概率可靠性评估. 电力系统及其自动化学报, 2019, 31(1): 117-123, 131. DOI:10.3969/j.issn.1003-8930.2019.01.019 |
| [14] |
张兆云, 林璞, 王星华. 交直流混合配电网继电保护研究综述. 电力系统保护与控制, 2019, 47(5): 179-187. DOI:10.7667/PSPC180561 |
| [15] |
Alalamat FM, Feilat EA, Haj-Ahmed M. Performance assessment of distance protection of PV-integrated microgrids. 2021 6th International Conference on Renewable Energy: Generation and Applications (ICREGA). Al Ain: IEEE, 2021. 173–177.
|
| [16] |
王训哲, 曹昂, 盛逸标. 分布式电源对配电网电流保护的影响. 电测与仪表, 2017, 54(18): 37-41, 78. DOI:10.3969/j.issn.1001-1390.2017.18.006 |
| [17] |
王静, 李泽滔. 配电网故障定位算法研究综述. 智能计算机与应用, 2020, 10(3): 228-231, 235. DOI:10.3969/j.issn.2095-2163.2020.03.048 |
| [18] |
王一非, 贾燕冰. 含分布式电源配电网故障定位改进矩阵算法. 计算机仿真, 2018, 35(4): 58-64. DOI:10.3969/j.issn.1006-9348.2018.04.012 |
| [19] |
张孟琛, 牛益国, 宣文华. 含DG配电网分层分区协同故障定位隔离技术. 电力系统保护与控制, 2019, 47(23): 115-121. |
| [20] |
吴乐鹏, 黄纯, 曾照新. 分布式发电配电网故障区间定位的自适应矩阵算法. 电工电能新技术, 2012, 31(4): 52-57. DOI:10.3969/j.issn.1003-3076.2012.04.012 |
| [21] |
郭利爽, 李凤婷, 赵新利, 等. 基于子网络划分的含DG配电网故障区段定位. 电力系统保护与控制, 2020, 48(7): 76-84. |
| [22] |
李开文, 袁荣湘, 邓翔天, 等. 含分布式电源的环网故障定位的改进矩阵算法. 电力系统及其自动化学报, 2014, 26(12): 62-68. DOI:10.3969/j.issn.1003-8930.2014.12.010 |
| [23] |
张波, 郑涛, 黄予园, 等. 基于改进矩阵算法的含分布式电源配电网故障定位. 智能电网, 2019, 9(6): 227-235. |
 2022, Vol. 31
2022, Vol. 31



