云存储和云服务器技术的迅猛发展, 将数据搬上云, 已是大势所趋, 这样不仅可以使存储容量实现动态扩容, 方便及时应对如“双11”购物节等用户数据激增的情况, 还可以降低初创公司前期的投入成本, 实现只需按需按量采购云服务器. 同时, 惠于当前各云厂商推出的个人免费云盘服务, 对于普通用户只需注册就可以使用, 这极大地方便了人们的日常生活. 然而, 数据存储在第三方云端, 无论是对于企业用户, 还是对于个人用户, 安全问题[1]始终困扰着他们.
与传统存储相比, 目前的云存储的数据都被放在云端, 由云服务器统一计算管理. 但云端存放的数据就可能处在一种不安全的状态[2], 一方面, 有的企业会将全部数据上云, 而这些数据中可能会有很多的秘密信息, 例如一些企业隐私和用户信息等; 另一方面, 用户不可能会完全信任提供云存储和云计算的服务商. 无论是企业还是个人用户在使用云存储时都会担心数据的安全性, 所以对于用户不信任和数据安全问题急需解决.
为了保证数据安全, 我们可以先将数据加密后再上传到云端, 但当存储的数据越来越多时, 对于数据的检索又成为一大问题. 传统方式是先将数据解密后再检索, 但这样的检索效率非常低, 无法满足实际需求. 所以我们需要设计出一种无需解密就能检索的方案, 而同态加密可以实现密文间的计算[3, 4], 所以使用同态加密技术, 这样既能保证数据的安全性也能提升检索效率. 同态加密的概念是由Riverst等人[5]于1978年首次提出, 同年Riverst等人[6]又提出了基于大整数分解难题的RSA公钥加密算法, 该算法具有乘法同态性; 1999年, Paillier提出了基于合数阶剩余类的Paillier公钥密码算法[7], 该算法具有加法同态性和乘法同态性; 2009年Gentry构造出首个全同态加密方案[8], 该方案基于理想格, 之后Gentry等人又在2010年和2013年分别提出DGHV方案[9]和GSW13方案[10], 前者基于近似最大公因子问题(approximate greatest common divisor, AGCD)[11], 后者基于LWE (learning with error)问题; 2012年以后, 文献[12, 13]中提出BGV12方案和Bra12方案, 前者通过模交换和密钥交换技术实现无需bootstrapping就能建立层次型同态加密方案(Leveled-FHE)方案, 后者无需使用模交换就可建立Leveled-FHE方案. 但全同态加密算法的效率很低[14], IBM在其开源库HElib中尝试使用了BGV方案设计了一个基于全同态加密的密文检索实验[15], 实验结果表明, 目前将全同态方案直接用于密文检索会大大限制检索效率, 实用性较弱. 此外国内外学者也做出了很多研究, 文献[16]提出一个基于LWE和AGCD问题的新型密文同态加密方式, 根据逐个计算密文相似度, 进而排序选出相似度最大者即为检索结果, 但其中密文排序增加了云端计算量; 文献[17]利用加法同态性提出一种在密态数据库上的可搜索加密方案; 文献[18]以整数向量加密技术为基础, 通过建立向量空间模型, 进而在密文下计算检索向量与文件向量的相似度进行检索, 但在建立空间向量模型和计算相似度时会增加计算量; 文献[19]给出了一种基于改进的同态加密算法的全文密文检索方案, 但也需要排序、查找后才能达到检索的目的;文献[20]提出了一个基于新型同态密文检索方案CRSHE, 但同样需要通过排序反映文档与关键词之间的相关性去实现检索. 从上面可以看出同态加密技术在云存储中实现密文检索大有可为, 但大都需要一些额外的计算, 例如排序、查找、计算相似度等, 增加系统开销.
而本文针数据存储的安全和密文检索的高效需求, 首先设计一个新的密文检索模型, 在此基础上提出一种混合加密技术, 即使用成熟的ElGamal算法和安全的国密SM4算法设计了一种高效的云端同态密文检索方案, 并给出了该方案的具体流程. 其次, 通过理论证明和实验仿真的方式分析了方案的正确性与安全性. 最后, 对实验数据进行分析, 实验数据表明, 在保证检索结果正确的前提下, 能有效提高检索效率.
1 预备知识 1.1 检索模型在该方案设计的检索模型如图1所示, 主要参与方: 用户、云服务器、可信第三方. 方案的主要功能分为用户录入数据(1)和用户检索数据(2–7).

|
图 1 密文检索系统模型 |
(1) 用户
用户首先将加密数据上传至云服务器, 当需要检索时, 上传检索密文关键词, 下载所需加密文档, 然后解密得到所需文件.
(2) 云服务器
云服务器作为存储和计算数据的平台, 在密文数据中检索计算, 将计算结果发送给可信第三方, 解密得到检索序号, 根据检索序号返回最终的加密文档给用户.
(3) 可信第三方
可信第三方首先产生同态加密的公私钥, 并公布公钥; 然后将云服务器发送过来的密文通过私钥解密, 筛选出检索序号, 并发送给云服务器.
1.2 ElGamal同态加密算法ElGamal算法[21]是国际上公认的公钥密码体制, 其加密算法是基于Diffile-Hellman密钥交换算法[22], 是由Taher ElGamal在1985年提出, 其安全性基于计算有限域上的离散对数难题, 相比于RSA算法, ElGamal算法能抵抗重放攻击. 该算法由参数设置、密钥生成、加密、解密和同态乘法5部分组成:
(1) 参数设置
随机选择一个大素数
(2) 密钥生成
随机选取
(3) 加密
发送者对于明文消息
(4) 解密
接收者收到密文消息
(5) 同态乘法
若对于两个明文消息m1, m2, 加密后的密文分别为:
如图2所示, 是该方案中云端密文检索系统的整体框架, 同态计算和求逆在云服务器中进行实现.
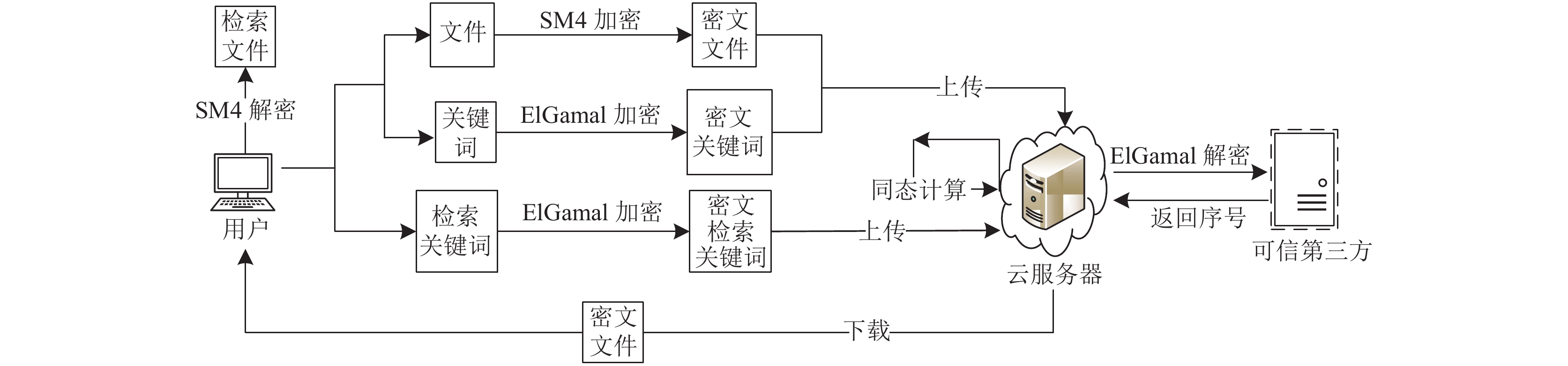
|
图 2 密文检索系统整体框架 |
(1) 初始化
可信第三方生成ElGamal的公私钥对, 并将公钥公开; 用户在客户端生成SM4算法的密钥.
(2) 录入数据
用户使用同态公钥将关键词加密, 使用SM4密钥将文件内容加密, 然后将加密后的关键词和加密后的文档一起上传至云服务器存储, 即录入数据.
(3) 检索数据
用户使用同态公钥加密检索关键词, 再向云服务器提交检索请求, 即检索数据.
(4) 同态计算
云服务器接收到检索请求后, 首先将密文检索关键词先求逆, 然后逐个与密文关键词相乘, 最后将结计算结果发送给可信第三方; 可信第三方收到后使用同态私钥进行解密, 返回给云服务器一个结果; 云服务器根据结果, 返回给用户相应的检索结果.
(5) 解密数据
用户在客户端收到云服务器发送的加密文件后, 用SM4密钥解密, 得到检索关键词所对应的明文文件.
2.2 系统具体结构下面具体介绍整个方案的流程结构, 整个方案主要可以分成两部分, 第1部分是录入数据, 第2部分是检索数据, 且每个角色都有不同的功能, 图3是方案检索成功的详细序列图.

|
图 3 方案序列图 |
下面分别详细介绍这两部分.
(1) 用户录入数据
用户待上传n个明文文件(1≤i≤n), 如表1所示.
| 表 1 待上传的明文数据 |
本方案支持多关键词检索, 设关键词个数为m个(1≤j≤n), 但关键词数量增加会增加同态计算的次数, 引起时间复杂度的增加, 因此在保证检索的效果和减少时间开销的前提下, 我们应当控制关键词数量, 所以在下面的实验中, 我们取m=2.
用户生成的密钥有: 用于ElGamal算法加解密公私钥对{PK, SK}, 以及SM4分组密码算法的密钥{K}.
该方案采用的混合加密, 关键词用ElGamal算法加密, 文件内容使用国密SM4算法加密, 然后合并一起上传服务器. 每个用户拥有自己上传文件的密钥, 可信第三方拥有所有加密关键词的密钥, 具体如表2所示.
| 表 2 角色和密钥分配 |
用户上传文件流程如图4所示.
1) 可信第三方生成同态加密公私钥
随机取一个较大的素数p, 构造一个模p的有限域
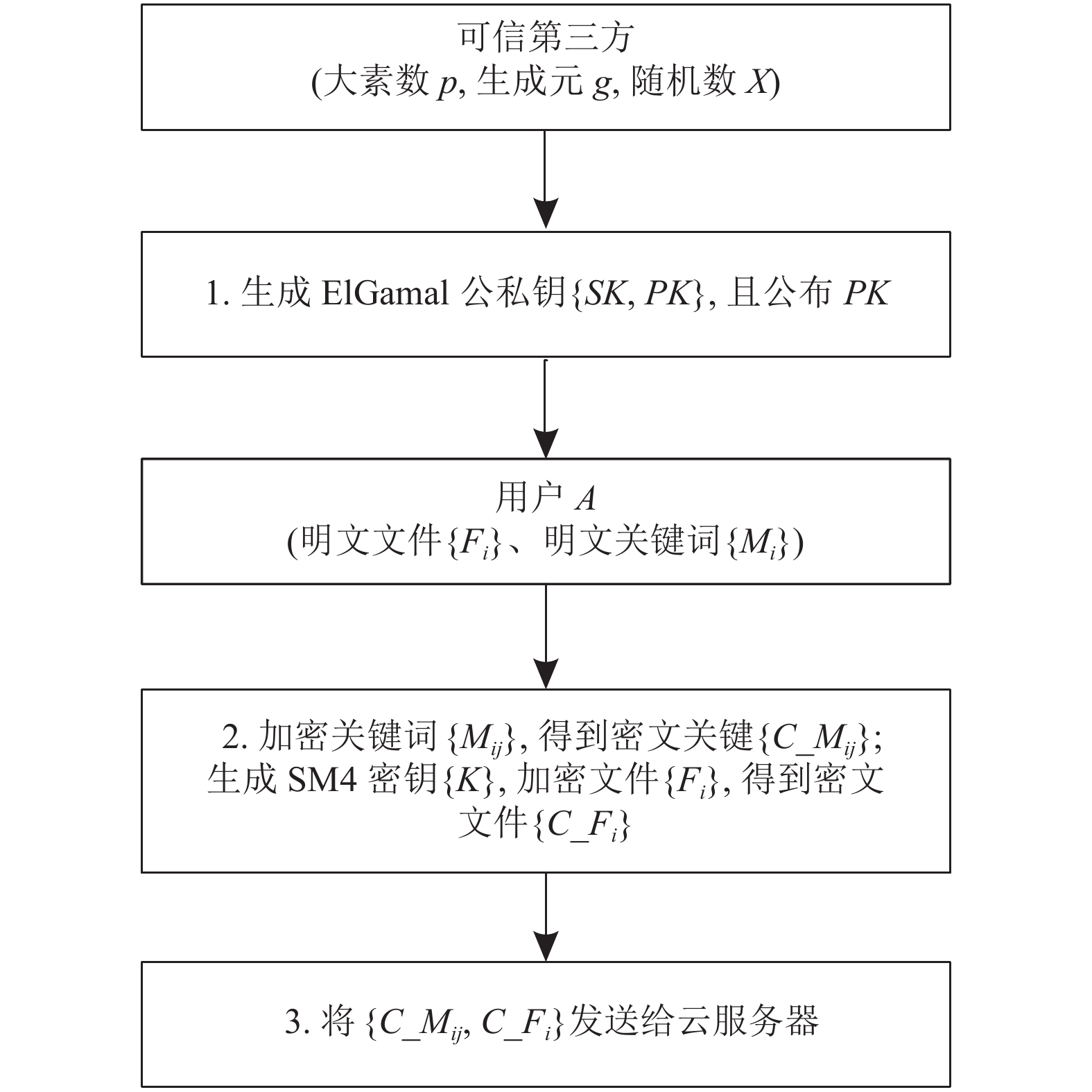
|
图 4 文件上传 |
2) 用户生成对称加密的密钥并加密数据
在客户端取随机数
3) 用户上传密文数据.
将
| 表 3 云端中的密文数据 |
(2) 用户检索数据
用户检索数据的流程如图5所示, 该部分包含5个阶段.
1) 加密检索关键词
假设密文数据库中的密文文件有n个, 用户先将检索关键词Q通过Unicode编码为十六进制字符串, 并转为整数形式得到
2) 同态计算
云服务器收到密文检索关键词
| (C_Q)∗ij=C_Mij×(C_Q∗)−1={c1ij,c2ij}={γij×γQ,βij×βQ} | (1) |
3) 可信第三方解密
云服务器将同态计算的结果
| {Q^*}_{ij} = {{D(}}{(C\_Q)^*}_{ij}{{) = }}{\delta _{{{ij}}}}{({\gamma _{ij}}^X)^{ - 1}}\bmod p | (2) |
4) 云服务器返回检索结果
云服务器根据收到可信第三方返回的解密结果来判断是否将密文文件发送给用户: 若返回的是一个非0的结果

|
图 5 用户检索文件 |
5) 用户解密
用户从云服务器下载到密文文件
本节通过一个具体的案例来验证本方案, 加密原文件可以是图书内容, 图书数量n=4, 关键词个数m=2, 关键词M1和M2分别是书名和作者, 实验环境为Intel(R) Core i5-6200U @ 2.30 GHz双核16 GB内存, Microsoft Visual Studio Community 2019.
(1) 假设用户有待加密上传的文件如表4, 以明文形式展示.
| 表 4 明文数据 |
上面的明文数据使用混合加密, 即关键词{书名、作者}使用ElGamal算法加密, 文件内容使用SM4算法加密.
(2) 将关键词用Unicode编码为十六进制字符串, 并转为整数形式, 见表5.
将关键词(整数形式)使用ElGamal加密, 参数设置:
| 表 5 关键词 |
| 表 6 密文数据 |
(3) 若用户输入检索关键词Q=“史记”, 先用Unicode编码为十六进制字符串, 并转为整数形式
| 表 7 检索关键词 |
(4) 云服务器收到检索关键词的密文
|
表 8 同态乘法运算密文相乘结果
|
云服务器将计算的结果发送给可信第三方, 可信第三方收到消息后, 使用私钥SK逐个解密得到
|
表 9 第三方解密结果
|
(5) 云服务器收到可信第三方发来的s=2, 将
在该方案中, 用户首先要将加密后的文件和关键词上传至云端, 然后从云端检索出关键词对应的加密文件, 解密即可得到检索的文件, 所以本方案的安全性可分为数据存储安全性和检索模型安全性.
(1) 数据存储安全性
关键词是采用ElGamal算法加密的, 相比于RSA算法, ElGamal算法能抵抗重放攻击, 另外根据计算有限域上的离散对数困难, 攻击者很难根据公钥PK去计算或推导出私钥SK, 这就使得用户在密文检索过程中, 攻击者就算得到公钥PK, 也不能作为云服务器和可信第三方之间的中间者去解密云服务器发送的同态计算结果, 这就保证了用户在检索过程中检索数据不可篡改.
再者就是文件采用的是国密SM4分组算法. 加解密过程均由用户在客户端完成, 云服务器无法获知其密钥K. SM4保证了文件的安全性[23], 可以抵抗穷举攻击、差分攻击、线性攻击等攻击手段, 具有较高的安全性, 使得攻击者即使获得加密文件, 也无法作为用户和云服务器之间的中间者解密出原文件.
(2) 检索模型安全性
密文检索过程满足乘法同态性. 方案中同态加密的公私钥均由可信第三方生成, 用户将关键词和文件加密上传至云端, 都是以密文形式存储. 用户将加密的检索关键词上传至云端, 利用同态加密的性质, 将加密的检索关键词与云端中存储的密文关键词做乘法同态运算, 再利用可信第三方解密来求出检索号, 以此完成密文检索. 由于整个过程均是在密文下进行的, 所以说云端是无法获知任何有关密钥和明文数据的, 且只有用户才能获得明文数据, 这就保证了检索过程中的数据是安全的, 所以说检索模型是安全的.
3.3 性能分析(1) 效率分析
在本方案中的密文检索只使用了乘法同态, 也就是只用部分同态来实现, 当然也可以使用全同态来实现密文检索, 但目前全同态效率比较低, 难以广泛使用. 以下面的例子为例, 来证明本文使用部分同态比全同态效率更高. 如表10, 加密1000数字1000次, 取10次试验的平均时间; 将1000和2000的密文相乘, 取10次试验的平均耗时, 明显可以看出使用ElGamal在加密和乘法同态运算上速度更快. 另外表11展示与其他方案的对比, 可以看出本方案更加轻量高效 这里BGV算法和CKKS算法的测试程序采用的是IBM的开源库fhe-toolkit-linux[15]; BFV算法的测试程序采用的是微软的开源库SEAL[24].
| 表 10 测试时间(ms) |
(2) 精确度分析
本方案针对个人用户就是在云端构建单用户的密文数据, 进而在云端进行安全检索, 因为一个文件可以有多个关键词, 所以用户在检索时, 既可以实现单个关键词检索, 也可以实现多关键词检索.
单个关键词检索时, 检索结果只有两种: 找到文件或者是未检索到; 多关键词检索时, 若输入的是一个文件对应的多个关键词, 那么只要有一个匹配上, 则检索成功, 若输入的是多个文件对用的关键词, 则返回多个匹配上的文件, 进而实现多文件检索, 这样效率会更加高, 其精确度和效率远高于逐个关键词检索.
| 表 11 方案对比 |
4 总结与展望
本文利用同态加密的性质, 设计出新的密文检索模型, 再结合安全的国密算法, 提出了一个基于同态加密的云端密文存储检索方案. 该方案能够在保证数据安全的前提下进行数据检索, 即检索过程中云端无法获知任何有关密钥信息和明文数据. 与其他方案相比, 具有轻量级和高效性, 可以应用于小型个人云端U盘的场景, 有较好的实用价值. 经实验数据分析表明, 本文方案检索结果正确、安全性好、效率高、实用性强. 在下一步的研究中, 将尝试设计一种高效的全同态加密算法, 并将其应用在云端密文检索中, 使之具有更好的安全性.
| [1] |
冯朝胜, 秦志光, 袁丁. 云数据安全存储技术. 计算机学报, 2015, 38(1): 150-163. DOI:10.3724/SP.J.1016.2015.00150 |
| [2] |
黄保华, 黄丕荣, 赵伟宏, 等. 云存储中支持属性撤销的多关键词可搜索加密方案. 计算机工程, 2021, 47(11): 29-36. DOI:10.19678/j.issn.1000-3428.0061050 |
| [3] |
杨亚涛, 赵阳, 张卷美, 等. 同态密码理论与应用进展. 电子与信息学报, 2021, 43(2): 475-487. DOI:10.11999/JEIT191019 |
| [4] |
刘钦菊, 路献辉, 李杰, 等. 全同态加密自举技术的研究现状及发展趋势. 密码学报, 2021, 8(5): 795-807. DOI:10.13868/j.cnki.jcr.000477 |
| [5] |
Rivest RL, Adleman L, Dertouzos ML. On data banks and privacy homomorphisms. Foundations of Secure Computation, 1978, 4(11): 169-179. |
| [6] |
Rivest RL, Shamir A, Adleman L. A method for obtaining digital signatures and public-key cryptosystems. Communications of the ACM, 1978, 21(2): 120-126. DOI:10.1145/359340.359342 |
| [7] |
Paillier P. Public-key cryptosystems based on composite degree residuosity classes. International Conference on the Theory and Applications of Cryptographic Techniques. Berlin: Springer, 1999. 223–238.
|
| [8] |
Gentry C. Fully homomorphic encryption using ideal lattices. Proceedings of the 41st Annual ACM Symposium on Theory of Computing. Bethesda: ACM, 2009. 169–178.
|
| [9] |
van Dijk M, Gentry C, Halevi S, et al. Fully homomorphic encryption over the integers. International Conference on the Theory and Applications of Cryptographic Techniques. Monaco and Nice: Springer, 2010. 24–43.
|
| [10] |
Gentry C, Sahai A, Waters B. Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster, attribute-based. Annual Cryptology Conference. Santa Barbara: Springer, 2013. 75–92.
|
| [11] |
Howgrave-Graham N. Approximate integer common divisors. International Cryptography and Lattices Conference. Providence: Springer, 2001. 51–66.
|
| [12] |
Kiran K. (Leveled) Fully homomorphic encryption without bootstrapping. Computing Reviews, 2015, 56(10): 613-613. |
| [13] |
Brakerski Z. Fully homomorphic encryption without modulus switching from classical GapSVP. Advances in Cryptology—CRYPTO 2012. Berlin: Springer, 2012.
|
| [14] |
陈智罡, 宋新霞, 郑梦策, 等. 全同态加密文献计量分析研究. 计算机工程与应用, 2022, 58(4): 40-51. DOI:10.3778/j.issn.1002-8331.2107-0038 |
| [15] |
IBM. FHE-toolkit-linux, 2020. https://github.com/IBM/fhe-toolkit-linux. [2021-10-01].
|
| [16] |
刘家森, 王绪安, 王涵, 等. 云服务器中基于同态加密的关键词检索方案. 科学技术与工程, 2021, 21(8): 3180-3185. DOI:10.3969/j.issn.1671-1815.2021.08.029 |
| [17] |
孙僖泽, 周福才, 李宇溪, 等. 基于可搜索加密机制的数据库加密方案. 计算机学报, 2021, 44(4): 806-819. DOI:10.11897/SP.J.1016.2021.00806 |
| [18] |
韩邦, 李子臣, 汤永利. 基于同态加密的全文检索方案设计与实现. 计算机工程与应用, 2020, 56(21): 103-107. DOI:10.3778/j.issn.1002-8331.1909-0049 |
| [19] |
程帅, 姚寒冰. 基于同态加密的密文全文检索技术的研究. 计算机科学, 2015, 42(S1): 413-416. |
| [20] |
付伟, 李墨泚, 赵华容, 等. CRSHE: 基于同态加密的新型密文检索方案. 计算机工程与科学, 2018, 40(9): 1540-1545. DOI:10.3969/j.issn.1007-130X.2018.09.003 |
| [21] |
ElGamal T. A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Transactions on Information Theory, 1985, 31(4): 469-472. DOI:10.1109/TIT.1985.1057074 |
| [22] |
Boneh D. The decision Diffie-Hellman problem. International Algorithmic Number Theory Symposium. Portland: Springer, 1998. 48–63.
|
| [23] |
李子臣. 密码学: 基础理论与应用. 北京: 电子工业出版社, 2019, 66-77. |
| [24] |
Microsoft. Microsoft SEAL, 2020. https://github.com/micro-Soft/SEAL. [2021-10-01].
|
 2022, Vol. 31
2022, Vol. 31



