轻量级的安全跨域去重方案

引用本文

温琳雅, 仪张倩, 刘行. 轻量级的安全跨域去重方案. 计算机系统应用, 2022, 31(1): 338-343.http://www.c-s-a.org.cn/1003-3254/8316.html

Wen LY, Yi ZQ, Liu H. Lightweight Security Cross-domain Deduplication Scheme. Computer Systems and Applications, 2022, 31(1): 338-343(in Chinese).http://www.c-s-a.org.cn/1003-3254/8316.html

轻量级的安全跨域去重方案

温琳雅, 仪张倩, 刘行

长安大学信息工程学院, 西安 710064

收稿日期：2021-03-31; 修改日期：2021-04-29; 采用时间：2021-06-02; csa 在线出版时间：2021-12-17

通讯作者：温琳雅, E-mail: 1753566917@qq.com.

摘要：云存储为用户提供文件外包存储功能, 然而随着数据外包数量的激增, 数据去重复变得至关重要. 目前数据压缩非常有效也是很常用的一个手段是去重, 即识别数据中冗余的数据块, 只存储其中的一份. 以前的方案可以满足不同的用户将相同的文件加密为相同的密文, 这样暴露了文件的一致性, 随后的方案提出基于集中式服务器作为去重辅助的方案, 随着用户的增加, 数据去重效率也随之降低. 针对目前云存储的安全性及数据去重效率低等问题, 本文提出了跨区域的重复数据删除方案. 所提方案为每个数据生成随机标签和固定长度的随机密文, 确保多域重复数据消除下的数据机密性及抵抗暴力攻击、保护信息平等信息不被披露. 同时, 对所提方案的实施情况和功能比较进行了仔细分析, 安全性分析表明, 所提方案在抵抗蛮力攻击的同时, 实现了数据内容、平等信息和数据完整性等隐私保护, 性能分析表明, 所提方案展示了优于现有方案的重复搜索计算成本及时间复杂度, 可实现轻量级特色.

关键词: 云存储消息锁加密跨区域数据去重访问控制

Lightweight Security Cross-domain Deduplication Scheme

WEN Lin-Ya, YI Zhang-Qian, LIU Hang

School of Information Engineering, Chang’an University, Xi’an 710064, China

Abstract: Cloud storage provides users with outsourcing file storage. However, as the number of data outsourcing surges, deduplication has become critical. At present, a quite effective and commonly used method for data compression is deduplication, that is, to identify redundant data blocks in the data and store only one copy of them. The previous scheme can satisfy different users to encrypt the same file into the same ciphertext, which exposes the consistency of the file. Later, another scheme is proposed in which a centralized server is taken as a deduplication aid. However, with the increase in the number of users, the deduplication efficiency also reduces. In view of the current security and low deduplication efficiency of cloud storage, this study proposes a cross-domain deduplication scheme. The proposed scheme generates random tags and fixed-length random ciphertext for each data to ensure data confidentiality in the case of cross-domain deduplication, resist violent attacks and protect the information equality from being disclosed. In addition, the implementation of the proposed scheme and its function are analyzed. The safety analysis shows that the scheme realizes the privacy protection regarding data content, equality information and data integrity while resisting brute force attacks. The performance analysis demonstrates that it outperforms the existing scheme in terms of repeated search calculation cost and time complexity, which enables lightweight characteristics.

Key words: cloud storage message lock encryption cross-region data deduplication access control

云存储服务在个人和组织环境中, 随着云用户数的增加, 冗余数据量也随之增加. 众所周知, 云服务提供商通常利用跨用户数据去重复来尽量减少存储开销, 允许云服务器检测两个或多个用户上传同一文件的副本, 并且只存储该文件的一个副本.

云服务提供商自由访问用户数据, 这就要求云用户充分信任云服务提供商做正确的事情. 传统的加密算法将文件的相同副本加密成完全独立的密文, 这使得重复删除的工作复杂化. Douceur等人^[1]提出的收敛加密(CE)的技术, CE是一种确定性加密方案, 使得文件的相同副本被加密成相同的密文.

虽然CE提供了一种简单而有效的方法来在数据隐私和加密重复数据消除的功能要求之间取得平衡, 但它有安全性和性能限制. 利用CE的概念, Bellare等人^[2-4]构建了一个名为消息锁定加密(MLE)的新加密原语, 以方便在加密数据上的重复数据消除, 他们还为MLE定义了两个安全要求: 隐私性和标签一致性.

在本文中, 我们提出了一种随机、安全、跨用户重复数据消除方案, 请求上传文件的用户需要与云服务器进行交互, 以确保同一文件的副本被加密到同一密文中, 同时实现抵抗暴力攻击. 具体地说, 拥有相同文件副本的不同用户通过共享相同的随机值生成文件加密密钥, 因此只有具有该文件相同副本的用户才能获得随机值并计算正确的加密密钥.

1 背景知识 1.1 椭圆曲线

Millier^[5]基于椭圆曲线提出了椭圆曲线密码体制, $ {F_p}$ 被设定为阶为 $ q$ 有限域, 有限域 $ {F_p}$ 上的椭圆曲线 $ E$ 被定义为满足等式 $ {y^2} = {x^3} + ax + b\boldsymbolod p$ 上所有点 $ (x,y)$ 集合; 其中 $ a,b \in {F_p}$ 且 $ 4{a^3} + 27{b^2} \ne 0$ . 无穷远点 $ O$ 和椭圆曲线 $ E$ 上其他点形成一个循环加法群 $ {\mathbb{G}}$ , 则椭圆曲线上的标量乘是 $ kP=P+P+\cdots +P(k\ times)$ , 这里 $ k \in {\mathbb{Z}}_q^*$ .

1.2 布谷鸟滤波器

Fan等人在2014年提出布谷过滤器(Cuckoo filter), 这是一种用于近似集合查询的新型数据结构^[6].

本文提出了动态布谷鸟滤波器(DCF), 以支持可靠的删除操作和弹性容量的动态集. 影响DCF设计的效率有两个因素, 首先, DCF数据结构是可扩展的, 使动态集空间的表示更有效. 其次, DCF使用垄断指纹来表示一个项, 并保证可靠的删除操作. 实验结果表明, 与现有的先进设计相比, DCF的内存成本降低了75%, 构建速度提高了50%, 会员查询速度提高了80%.

布谷鸟滤波器一般是成对的哈希函数, 一个是记录的位置, 另一个是备用位置, 这个备用位置是处理碰撞时用的.

使用 $ {H}_{A}:G\to {\left\{\text{0}, \text{1}\right\}}^{L}$ 和 $ {H}_{B}:G\to {\left\{\text{0}, \text{1}\right\}}^{L} $ ( $ L$ 一般为64 bits)计算文件对应的位置.

此外, 在迁移过程中, 存储的是原始数据的哈希值 $ {\xi _x}$ 而不是原始数据 $ x$ 带来了挑战. 为了解决这个问题, 利用了一种新的散列方法, 称为部分密钥布谷鸟散列, 它通过根据当第一个阵列地址和要踢出的哈希值进行异或操作来计算替代位置的地址. 具体来说, 两个阵列的地址可计算为:

$\left\{ { \begin{array}{l} loc1 = Hash(x) \\ loc2 = loc1 \oplus Hash({\xi _x}) \end{array} } \right.$

如果在添加新元素时, 两个哈希列表均被偶然的占据, 则会导致假阳性的结果. 可计算假阳性概率的上限为:

$ \rho = 1 - {\left(1 - \frac{1}{{{2^f}}}\right)^\lambda } \approx \frac{{{2^\lambda }}}{{{2^f}}} $

1.3 椭圆曲线群上困难问题假设

椭圆曲线离散对数问题(ECDLP): 给定 $ P,Q\in {\mathbb{G}}$ 为椭圆曲线上 $ E$ 的点, $ P$ 是 $ {\mathbb{G}}$ 的生成元, 这里 $ a \in {\mathbb{Z}}_q^*$ 且未知, 满足 $ Q=aP$ , ECDL问题是计算 $ a \in {\mathbb{Z}}_q^*$ .

1.4 系统模型

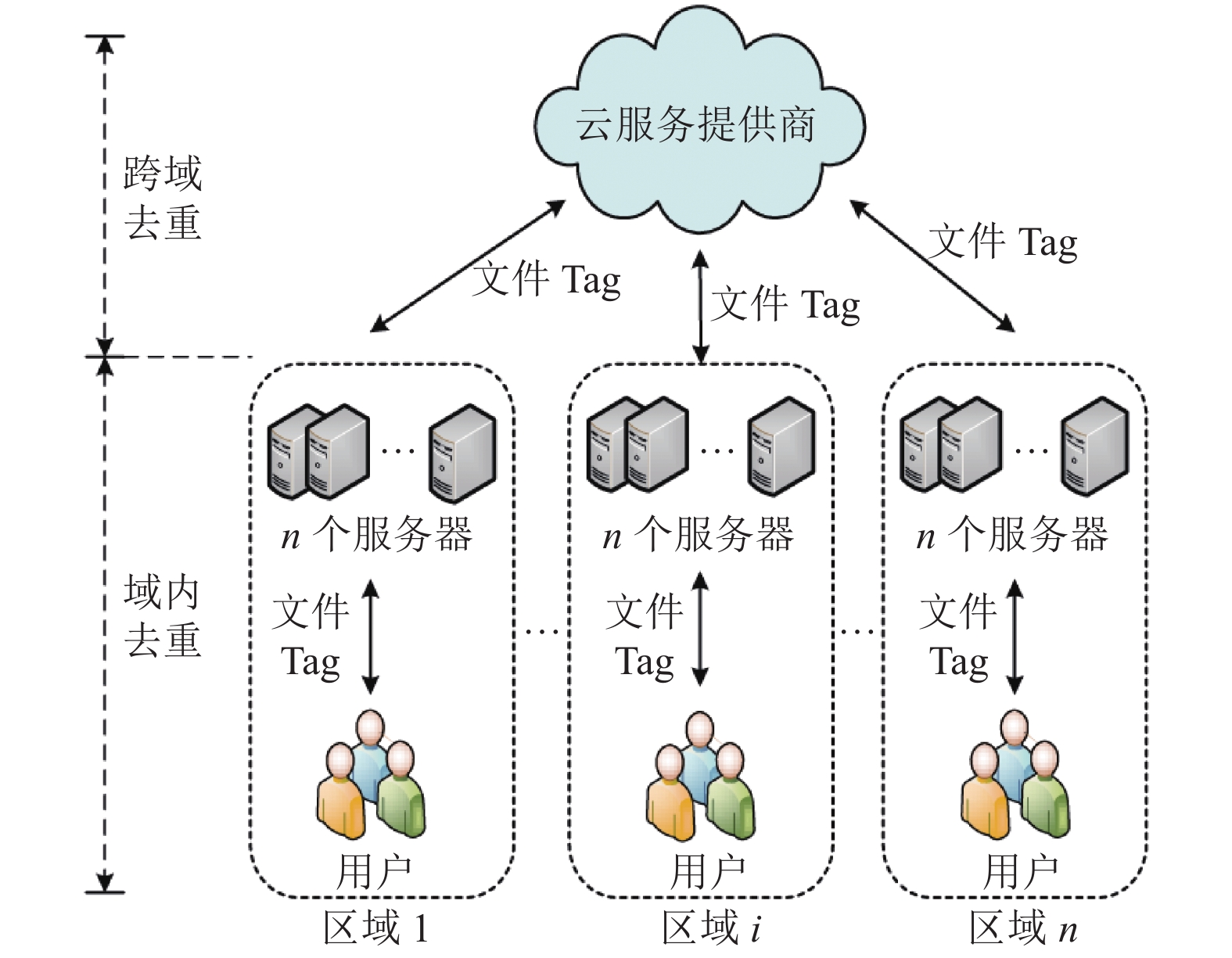
该系统模型图如图1所示, 参与者包括3个实体: 云服务器(CSP), 域服务器(KS), 用户(U).

图 1 网络模型

云服务提供商 $ CSP$ : 表示诚实又好奇的实体机构, 负责系统参数的生成.

区域服务器 $ KS_i$ : 表示诚实又好奇的实体机构, 负责生成用户的文件标识和区域内部去重.

用户 $ U_i$ : 生成文件标识进行去重.

1.5 安全属性

我们的目标是在所提方案中实现以下安全目标.

(1)数据机密性: 任何对手, 包括未经授权的用户 $ U$ 、 $ CSP$ 或 $ KS$ , 都不能获得加密数据的明文信息, 除非他们获得加密数据的密钥^[7].

(2)数据完整性^[8]: 所提方案应保护数据完整性免受对手的影响. 也就是说, 它应该允许 $ U$ 验证从云存储器下载的数据是否没有被更改.

(3)可扩展性: 所有的密钥服务器都不应参与收敛的密钥生成过程, 这会导致系统的性能下降.

2 本文方案 2.1 系统建立

所提方案包含6个阶段: 系统初始化阶段、用户注册阶段、用户文件标签产生阶段、去重阶段、数据完整性校验、用户动态更新.

系统初始化: 该算法由 $ CSP$ 执行.

(1)给定一个安全参数 $ \lambda$ , 基于定义在有限域 $ F_p$ 上的椭圆曲线 $ E$ , 选择一个阶为 $ q$ 的循环加法群 $ {\mathbb{G}}$ , $ P$ 是群 $ {\mathbb{G}}$ 的生成元.

(2) $ CSP$ 随机选取3个单向哈希函数 $ {H_1} : {\left\{ {0,1} \right\}^*} \to {\mathbb{Z}}_q^*$ , $ {H_2} : {\mathbb{G}} \to {\mathbb{Z}}_q^*$ , $ {H_3} : {\mathbb{G}} \to {\mathbb{Z}}_q^*$ . 公开系统参数 $params = \{ q,{\mathbb{G}}, $ $ P,{H_1},{H_2},{H_3} \}$ .

区域服务器参数生成: 区域服务器 $ K{S_i}$ ( $ i \in (1,N)$ , 共有 $ N$ 个区域)随机选择 $ {s}_{i}\in {{\mathbb{Z}}}_{q}^{*}$ 作为私钥, 计算公钥 $ {\rm{p}}{{\rm{k}}_i} = {s_i}P$ , 并将公钥公开.

用户注册: 用户选择 $ {x}_{i}\in {{\mathbb{Z}}}_{q}^{*}$ 作为用户的密钥, 并计算公钥 $ {{\rm{X}}_i} = {x_i}P$ , 并将公钥公开.

2.2 用户文件标签产生阶段

给定系统参数 $ params$ , 区域公钥 $ p{k_i}$ 、用户的数据 $ m_i$ , 执行以下步骤生成文件标签.

(1)用户 $ U_i$ 随机选择 $ {a_i} \in {\mathbb{Z}}_q^*$ , 计算 $ {M_1} = {a_i}{s_i}P + {H_1}{\text{(}}{m_i}){\rm{P}}$ , $ {A_i} = {a_i}\cdot P$ . 用户 $ U_i$ 将 $ \left( {{M}_{1}},{{A}_{i}},{{X}_{i}}) \right.$ 发送给所在区域的服务器 $ K{S_i}$ .

(2)区域服务器 $ K{S_i}$ 随机选择 $ {r_i} \in {\mathbb{Z}}_q^*$ , 计算 $ {M_2} = $ $ {M_1} - {s_i}{A_i} = {H_1}{\text{(}}{m_i}){\rm{P}}$ . 在用户区域内去重过程中, 区域服务器 $ K{S_i}$ 限制规定时间内进行有限次询问, 例如十分钟内进行20次询问. 为了防止区域服务器发生单点故障, 我们在一个区域内部署3个服务器.

(3)生成标签: 区域服务器 $ K{S_i}$ 计算: $ {H_3}({M_2})$ , 哈希值 $ {H_3}({M_2})$ 将用于去重工作.

2.3 去重阶段

去重工作包含两个阶段, 区域内部去重、跨区域去重. 区域内部去重由区域服务器执行, 跨区域去重由 $ CSP$ 执行.

(1)区域内去重阶段区域服务器 $ K{S_i}$ 将 $ {H_3}(Ta{g_i})$ 与本区域保存的哈希列表进行对比. 区域内去重工作存在两种情况:

第1类: 本区域内存在重复, 即本区域内存在 $ Ta{g_i}$ 满足 $ Ta{g_i} = Ta{g_j}$ , 意味着在之前已经有处在同一个区域的用户上传了与用户 $ U_i$ 相同的文件, 则用户 $ U_i$ 为后续上传者, 因此, 用户 $ U_i$ 不需要上传密文.

区域服务器 $ K{S_i}$ 向用户 $ U_i$ 发送‘同区域重复文件存在 $|| $ 不需要上传文件’的指令, 区域服务器 $K{S_i}$ 计算: $ {T_i} = {H_3}({M_2})$ . 区域服务器 $ K{S_i}$ 将用户公钥、用户文件标识: ‘ $ ({X_i},{T_i})||$ 重复’提交给 $ CSP$ , $ CSP$ 将用户 $ U_i$ 的公钥 $ X_i$ 添加到文件第一个上传者的密文列表中.

第2类: 如果本区域内文件不存在重复, 意味着在同一个区域的用户没有上传过与用户 $ U_i$ 相同的文件, 区域服务器 $ K{S_i}$ 将 $ {H_3}(Ta{g_i})$ 保存在本域的哈希列表中, 区域服务器 $ K{S_i}$ 将‘ $ (i,{X_i},{T_i})||$ 去重’提交给 $ CSP$ 进行跨区域去重.

(2)区域间去重阶段, $ CSP$ 收到来自区域服务器 $ K{S_i}$ 的‘ $ ({X_i},{T_i})||$ 去重’指令, $ CSP$ 计算哈希值 $ {H_A}({T_i})$ 、 $ {H_B}({T_i})$ , $ CSP$ 利用布谷鸟服务器进行对比查询这两个哈希值在滤波器列表中映射的位置是否为空, 如果映射位置为空则该文件属于无重复文件, 任选一个位置插入 $ T_i$ , 如果映射的位置不都为空则与 $ T_i$ 进行对比, 存在与 $ T_i$ 相同数值, 则该文件在云上已有重复存在. 去重后存在两种情况:

第1类: 跨区域不存在重复文件, 则表示用户 $ U_i$ 为其文件的第一上传者, 用户需要加密文件并上传. 云向区域服务器发送‘ $ {T_i}||$ 上传文件’指令, 由区域服务器 $ K{S_i}$ 转发给用户.

第2类: 跨区域存在重复文件, 意味着在之前已经有处在不同区域的用户上传了与用户 $ U_i$ 相同的文件, 则用户 $ U_i$ 为后续上传者, 不需要上传加密文件.

$ CSP$ 向区域服务器 $ K{S_i}$ 发送‘ $ {T_i}$ ||文件重复’, $ CSP$ 添加用户 $ U_i$ 的公钥 $ X_i$ 添加进第一上传者的密文条目. 用户去重工作完成后, $ CSP$ 向发生重复的用户发送‘不需要上传文件’指令时, 并向用户发送文件第一上传者的密钥辅助参数 $ C_{i2}$ .

用户 $ U_i$ 在完整性校验过程中利用已保存的 $ H_1(m_i)$ 计算: ${{a}_{i}}=De{{c}_{{{H}_{1}}\left( ~{{{m}}_{i}} \right)}}\left( {{C}_{i2}} \right)$ , $ ck_i^{\prime} = {H_2}\left( {{a_i}} \right)$ . 用户 $ U_i$ 保存对称密钥 $ ck_i^{\prime}$ . 用户 $ U_i$ 保存对称密钥 $ ck_i^{\prime}$ , 形如: $ \left( {ck_i^{\prime} ,{H_1}\left( {{m_i}} \right),name} \right)$ .

2.4 文件上传

用户 $ U_i$ 收到上传文件指令后, 计算对称加密密钥、文件密文、辅助密文:

$ c{k_i} = {H_3}({a_i}),{C_{i1}} = En{c_{c{k_i}}}({m_i}), {C_{i2}} = En{c_{{H_1}{\text{(}}{{{m}}_i}{\text{)}}}}({a_i}) $

其中, $ c{k_i}$ 用于加密文件 $ m_i$ , $ {C_{i2}}$ 用于辅助后续去重工作中与用户 $ U_i$ 具有重复文件的用户生成解密的对称密钥. 用户 $ U_i$ 将密文 $ ({C_{i1}},{C_{i2}},{{\rm{T}}_i})$ 发送给区域服务器 $ K{S_i}$ , 服务器 $ K{S_i}$ 将 $ ({C_{i1}},{C_{i2}},{T_i})$ 转发给 $ CSP$ . 云将 $ ({C_{i1}},{C_{i2}})$ 添加到去重阶段已保存的条目 $ (i,{T_i},{X_i})$ 中, 保存为 $ (i,{C_{i1}},{C_{i2}}, $ $ {T_i},{X_i})$ .

2.5 文件下载阶段

用户 $ U_i$ 向云服务器提交‘下载|| $ T_i$ ’, 云检查 $ T_i$ 相对应的密文列表是否具有用户的公钥 $ X_i$ , 云随机选择 $ r\in {{\mathbb{Z}}}_{a}^{*}$ 计算 $ Enc_{X_i}(r)$ , 发送给用户 $ U_i$ . 用户收到 $ Enc_{X_i}(r)$ 后利用自己的进行解密得到 $ r$ , 用户将 $ r$ 发送给云, 云收到 $ r$ 后进行检验, 相等的情况下云将密文发送给用户. 云服务器向用户发送相应的 $ ({C_{i1}},{C_{i2}})$ .

2.6 文件解密阶段

用户在下载请求后将收到密文 $ ({C_{i1}},{C_{i2}})$ , 用户 $ U_i$ 可以利用已保存的私钥 $ c{k_i}$ , 下载文件进行解密: $ {{{m}}_i} = $ $ De{c_{c{k_i}}}({C_{i1}})$ .

2.7 用户删除文件:

当有用户想要删除文件时, 需要进行密钥的更新, $ CSP$ 从 $ T_j$ 对应的密文条目中删除用户公钥 $ X_j$ .

3 实施情况和功能比较 3.1 安全性分析

数据的保密性和完整性是对加密数据的重复数据消除研究中重要的安全问题. 因此, 在这部分, 我们讨论如何实现更高层次的安全性, 且比其他方案的设置更简单.

内部攻击通常被定义为服务器试图获得明文^[9-11], 在我们的方案中, 由于服务器和云是半信任的, 它们将按指定的方式执行数据的去重复, 但出于好奇, 他们试图获得明文. 具体地, 区域服务器为每个数据存储哈希值 $ {H_3}(Ta{g_i})$ , 云服务器存储密文 $ ({C_{i1}},{C_{i2}})$ . 基于椭圆曲线离散对数难题, 服务器无法通过 $ {M_2} = {M_1} - {s_i}{A_i} = {H_1}{\text{(}}{m_i}) {{P}}$ , $ {A_i} = $ $ {a_i}\cdot P$ 获得文件的哈希值 $ {H_1}{\text{(}}{m_i})$ 和加密密钥 $ a_i$ , 从而服务器无法解密文件密文.

3.2 安全属性比较和效率分析

本节与以前的去重方案的安全属性和计算成本方面的比较.

(1) 安全属性比较

方案的安全属性比较如表1.

表 1 安全属性比较

(2) 计算代价比较

本节将比较所提方案与现有去重方案的计算代价和通信代价.

基于MIRACL Crypto SDK, 仿真实验在CPU为英特尔i7 (2.53 GHz), 内存为8 GB的64位Window 7操作系统下进行. 平均运行时间如表2所示. 表3和表4给出了文献[12–16]和本文提出的方案计算代价比较.

表 2 基本操作的执行时间

由表3可知, 在文件标签上传阶段, 所提方案计算代价为1.16 ms, 与已有的数据去重方案[12-16]相比, 计算代价最小, 分别降低了59.15%, 95.70%, 95.70%, 95.97%和72.76%.

在文件加密阶段中, 所提方案加密文件计算代价为0.0048 ms, 与已有的数据去重方案[12-14, 16]相比, 分别降低了99.91%, 99.96%, 99.96%和99.96%, 与方案[15]相比, 计算代价近乎相同, 但方案[15]不能满足访问控制和用户的动态更新.

密文解密阶段, 在非上传者解密2 KB文件过程中, 所提方案解密文件计算代价为0.39 ms, 与已有的数据去重方案[12-14,16]相比, 分别降低了86.26%, 96.31%, 98.33%和99.96%, 尽管方案[15]的非上传者在文件解密阶段具有更低的计算代价, 但所提方案在功能方面优于方案[15].

由图2可知, 在文件标签上传阶段, 所提方案通信代价为320 bits, 与已有的数据去重方案[12-16]相比, 通信代价最小, 分别降低了68.75%, 79.17%, 79.17%, 68.75%和68.75%.

表 3 该方案与其他方案用户计算代价比较

方案	Ti产生阶段	文件加密阶段	文件解密阶段
[12]	$2{T_{\textit{e-BP}} } = 2.84$	$\begin{array}{l} {\text{4} }{T_{ {\textit{e} } {\textit{-BP}}} } + {T_{\textit{Enc-A}} } = 5.68 \end{array}$	① $\begin{array}{l} {T_{\textit{e-BP} } }{\text{ + } }{T_{\textit{Dec-A}} } {\text{ = 1} }{\text{.42} } \end{array}$ ② $\begin{array}{l} 2{T_{\textit{e-BP}} }{\text{ + } }{T_{\textit{Dec-A}} } {\text{ = 2} }{\text{.84} } \end{array}$
[13]	$\begin{array}{l} {T_{mtp} } + {\text{2} }{T_{BP} } + {\text{3} }{T_{\textit{e-BP}} } = 27.04 \end{array}$	$\begin{array}{l} (N{\text{ + } }1){T_{ {\text{e} } {\textit{-BP}}} } + {T_{BP} } + {T_{\textit{Enc-A}} } = 1.42N + {\text{11} }{\text{.73} } \end{array}$	① ${T_{\textit{Dec-A}} }$ ② $\begin{array}{l} {T_{BP} }{\text{ + } }{T_{ \textit{Dec-A} } } {\text{ = 10} }{\text{.31} } \end{array}$
[14]	$\begin{array}{l} {T_{mtp} } + {\text{2} }{T_{BP} } + {\text{3} }{T_{\textit{e-BP}} } = 27.04 \end{array}$	$\begin{array}{l} {T_{BP} } + 2{T_{\textit{e-BP}} } + {T_{\textit{Enc-A}} } = 13.15 \end{array}$	① ${T_{\textit{Dec-A}} }$ ② $\begin{array}{l} 2{T_{BP} }{\text{ + } }2{T_{\textit{e-BP}} } {\text{ + } }{T_{\textit{Dec-A}} }{\text{ = 23} }{\text{.46} } \end{array}$
[15]	$\begin{array}{l} {T_{\textit{e-BP}} } + {T_{\textit{Enc-R}} } = 28.8 \end{array}$	${T_{\textit{Enc-A}} } = 0.0024$	${T_{\textit{Dec-A}} } = 0.0028$
[16]	$3{T_{\textit{e-BP}} } = 4.26$	$\begin{array}{l} 2{T_{\textit{e-BP} } } + {T_{\textit{E-BP} } } + {T_{BP} } + {T_{\textit{Enc-A} } } = 1{\text{3} }{\text{.67} } \end{array}$	① ${T_{\textit{Dec-A}} }$ ② $\begin{array}{l} 2{T_{BP} } + {T_{\textit{Dec-A}} } {\text{ = 2} }0.62 \end{array}$
本文	$3{T_{\textit{m-ECC}} } = 1.16$	$2{T_{\textit{Enc-A} } } = 0.0048$	① ${T_{\textit{Dec-A}} }$ ② $\begin{array}{l} 2{T_{\textit{Dec-A}} }+ {T_{\textit{m-ECC}} } = 0.39 \end{array}$
注: ①为第一个上传者解密所需做的计算, ②为后续上传者解密所需做的计算, 时间单位为ms. $N$ 为区域数量.

表 3 该方案与其他方案用户计算代价比较

表 4 通信代价比较 (bits)

图 2 通代价比较

文件密文上传阶段, 在密文大小相同的情况下, 对辅助参数的通信代价进行比较. 由图2所知, 与已有的数据去重方案[12-16]相比, 所提方案在密文上传阶段的通信代价最小, 所提方案分别降低了89.58%, 84.38%, 87.50%, 68.75%和72.97%.

文件密文下载阶段, 与已有的数据去重方案[12-16]相比, 所提方案的通信代价最小, 所提方案分别降低了84.38%, 84.38%, 87.50%, 68.75%和72.97%.

由以上分析表明, 所提方案在实际应用中具有更好的适用性.

4 总结

本文提出了一种随机、安全、服务器端去重方案. 通过共享用于为持有相同文件副本的用户生成加密密钥的随机值, 可以抵抗来自恶意云服务器和用户的暴力攻击. 在所提方案中, 昂贵和复杂的计算由云服务器处理, 因此在客户端发生的计算开销较少. 安全性分析表明, 该方案提供了一个更简单的去重复框架, 具有更高的安全性. 性能评估的结果表明, 本文方案在客户端产生最小的计算开销, 这是足够轻量级的.

参考文献

[1]	Douceur JR, Adya A, Bolosky WJ, et al. Reclaiming space from duplicate files in a serverless distributed file system. Proceedings of the 22nd International Conference on Distributed Computing Systems. Vienna: IEEE, 2002. 617–624.
[2]	Bellare M, Keelveedhi S. Interactive message-locked encryption and secure deduplication. Proceedings of the 18th IACR International Workshop on Public Key Cryptography. Gaithersburg: Springer, 2015. 516–538.
[3]	Bellare M, Boldyreva A, O’Neill A. Deterministic and efficiently searchable encryption. Proceedings of the 27th Annual International Cryptology Conference. Santa Barbara: Springer, 2007. 535–552.
[4]	Bellare M, Keelveedhi S, Ristenpart T. Message-locked encryption and secure deduplication. Proceedings of the 32nd Annual International Conference on the Theory and Applications of Cryptographic Techniques. Athens: Springer, 2013. 296–312.
[5]	Miller VS. Use of elliptic curves in cryptography. Williams HC. Advances in Cryptology (CRYPTO ’85). Berlin, Heidelberg: Springer, 1986. 417–426.
[6]	赵晓永, 陈晨. 面向云平台的二代测序数据近似去重方法研究. 计算机工程与应用, 2017, 53(23): 1-5. DOI:10.3778/j.issn.1002-8331.1706-0449
[7]	Yuan HR, Chen XF, Jiang T, et al. DedupDUM: Secure and scalable data deduplication with dynamic user management. Information Sciences, 2018, 456: 159-173. DOI:10.1016/j.ins.2018.05.024
[8]	Duan Y. Distributed key generation for encrypted deduplication: Achieving the strongest privacy. Proceedings of the 6th Edition of the ACM Workshop on Cloud Computing Security. Scottsdale: ACM, 2014. 57–68.
[9]	Miao YB, Ma JF, Liu XM, et al. Lightweight fine-grained search over encrypted data in fog computing. IEEE Transactions on Services Computing, 2019, 12(5): 772-785. DOI:10.1109/TSC.2018.2823309
[10]	Koo D, Hur J. Privacy-preserving deduplication of encrypted data with dynamic ownership management in fog computing. Future Generation Computer Systems, 2018, 78: 739-752. DOI:10.1016/j.future.2017.01.024
[11]	Katz J, Lindell Y. Introduction to Modern Cryptography. Boca Raton: Chapman and Hall/CRC, 2007.
[12]	Guo C, Jiang XR, Choo KKR, et al. R-Dedup: Secure client-side deduplication for encrypted data without involving a third-party entity. Journal of Network and Computer Applications, 2020, 162: 102664. DOI:10.1016/j.jnca.2020.102664
[13]	Shin Y, Koo D, Yun J, et al. Decentralized server-aided encryption for secure deduplication in cloud storage. IEEE Transactions on Services Computing, 2020, 13(6): 1021-1033.
[14]	Nayak SK, Tripathy S. SEDS: Secure and efficient server-aided data deduplication scheme for cloud storage. International Journal of Information Security, 2020, 19(2): 229-240. DOI:10.1007/s10207-019-00455-w
[15]	Yan JJ, Wang XX, Gan QQ, et al. Secure and efficient big data deduplication in fog computing. Soft Computing, 2020, 24(8): 5671-5682. DOI:10.1007/s00500-019-04215-9
[16]	Yang X, Lu RX, Choo KKR, et al. Achieving efficient and privacy-preserving cross-domain big data deduplication in cloud. IEEE Transactions on Big Data, 2017, 32(2): 1344-1354.