空中交通作为一种现代化交通方式, 在世界各地被广泛应用, 各型号民航客机常包含货舱部分, 由于空中运行的特殊性, 为了保障空中交通的安全性, 对航空器重心有着严格要求, 因此航空器配载是飞机运行的关键步骤之一. 随着现代化水平提高, 国内外对于机场智能化管理已经有了明确的发展方向, 引入信息共享系统参与机场管理, 该类系统最早由欧洲提出并实施部署, 将其命名为airport cooperative decision management system, 简称为A-CDM, 用于完善空管系统内部运行信息通报和协同决策机制, 近年来国内正在着手推进机场信息管理系统建设, 2017年8月, 民航局发布了《关于进一步统筹推进机场协同决策(A-CDM)建设的通知》, 要求行业各单位进一步统筹推进A-CDM建设.
配载业务是航空调度的关键组成部分, 该操作长期以来依靠配载员的经验手工完成, 每个机型有单独的配载表, 学习成本高, 配载效果受配载员工作状态影响大. 由飞机负载平衡问题引发的安全事故时有发生, 其根源在于飞机的运作性质, 配载重心超出前限航空器的前起落架及支撑结构会受到损坏, 起飞时难以拉起机头; 落地时会损坏前起落架及支撑结构; 配载重心太过靠后, 起飞过程中可能发生机尾触地的“沉尾”安全事故; 该类问题还会导致飞机可操作性下降、容错率降低, 在遭遇涡流及强风等恶劣情况时会有失速的危险. 随着机型越来越复杂, 航班量越来越大, 航空公司对安全、准点的要求越来越高, 该项工作已经成为提升配载操作效率的瓶颈, 配载业务作为飞机运行关键步骤, 其智能化、统一化势在必行.
目前已经有辅助性的配载系统投入使用, 但仍不完善, 没有较好地适应民航客机配载的多约束、多变动环境, 非常依赖地勤工作人员进行手动调整或者直接进行手动配载操作. 有资料指出当前配载过程含义混杂[1], 指向多种业务过程, 解决方法耦合性高.
本文首先对算法当前存在的问题进行了分析, 并根据分析结果将配载业务过程和涉及模型进行了抽象设计, 选取遗传算法作为基础理论进行针对性优化和模块化设计, 提出约束回报动态计分方法来适应多变、多配载需求的民航货舱配载算法结构, 在不同货物组合中保持相对稳定的重心优化结果, 使得货物在规格、标签和经停装载优先级等约束条件下配载重心接近或达到理论偏移最优值, 并达到秒级实时配载计算的目标, 取得了较好的测试结果. 最后对后续发展方向进行了讨论.
1 问题分析 1.1 算法问题分析算法设计是配载系统开发的核心组成部分, 该问题从性能方面又可分为执行效果和执行效率两部分.
飞机负载平衡问题被认为是一种NP难箱包装载(bin packing)问题[2, 3]的分支, 研究人员对此进行了算法研究.在此基础上, Kaluzny等人针对军事应用[4]提出了一种飞机负载平衡方案, 由于在军用运输机使用中涉及到的货物包括军用装备、车辆等大型物体, 其体积大、重心位置与物品型心位置差距明显等问题, 实现了4个方向正交旋转物体进行配平的方法; 线性规划模型常用于最优化计算, Verstichel等人应用混合整数线性规划[5]进行配载最优化计算; 还有研究人员[6]采用相似的分支定界法来进行配载方案搜索, 取得了不错的配载效果; CLPA系统设计[7]改进了整数线性规划方法, 从最小化剩余空间而不是最大化装载空间的角度来进行问题求解, 在此基础上不同类型的货物划分为不同优先级来辅助计算. 还有研究人员从其他角度[8, 9]和特定应用场景[10]对配载问题进行了讨论.
各类重心相关算法可分为3类, 第1类算法只关心基本的配载重心约束, 如飞机平衡检测器内置系统, 侧重于重心状态实时监测; 第2类算法在第1类算法基础上提升了约束覆盖面, 减轻人工调整工作量, 但是泛化能力差, 在面对机型变动等特殊情况时不能较好地适应, 如前文中介绍的线性规划计算法, 需要针对特定飞机型号推导公式参数; 第3类算法在第2类算法基础上, 继续增大约束覆盖面积, 能适应各种特殊情况, 在少量人工参与下既能完成配载计算, 分支定界搜索法在一定程度上能够有较好的的可扩展性, 但是算法搜索时间较长难以实时配载, 不能做到实时响应.
1.2 系统问题分析从架构方面分析, 当前配载系统有泛化能力差、模块化差的问题.
本文中提到的算法泛化性是指使用一种解决方案能否应对多种机型的配载问题. 由于飞机型号对配载过程影响大, 部分飞机配载系统出现定制化, 系统设计者从单一型号飞机配载方面出发, 形成的系统在一类问题上表现较好, 但是当飞机机型出现新的需求的时候则需要重新进行公式推导, 泛化能力差, 不利于飞机信息的系统性管理. 例如, 有研究人员[3]提出的方案采用2维建模, 且默认货物不可重叠, 当飞机出现双层货舱时则需要重新进行理论推导.
模块化问题指的是部分系统设计将飞机配载业务过程与算法过程混杂, 使得代码可读性和扩充性差, 在航空公司出现新机型、新需求时, 难以调整, 导致算法需要全盘重构, 增加了使用成本.
2 算法设计为了应对以上问题, 提高配载算法的性能和泛化能力, 本文实现一种基于遗传算法的动态分值计算配载算法, 抽象解耦约束计算机制, 提升应对新需求的能力.
2.1 业务建模飞机重心[11, 12]是影响飞机运行过程的关键参数之一, 将飞机在机翼常规状态下平稳运行过程中产生升力的等效点作为理想重心位置, 以下用CGidea指代, 飞机配载完成后实际重力等效点为实际重心, 用CG指代.理想状态为CG与CGidea重合, 不需要进行额外力辅助;实际状态多为CG与CGidea有相对距离且在飞机运行可接受范围内, 飞机需要通过调整机翼及其他手段产生除正常运行的升力以外的力进行辅助平衡, 部分资料将其称为配平力. 将飞机可接受的重心位置集合称为包线范围, 每架飞机有固定的包线范围, 由飞机硬件决定.
就该目标分析可将影响配载效果的属性分为固有属性和可变属性两类. 模型固有属性为飞机各项运行指标及其座位、货舱相关属性, 该类属性在多次配载过程中, 对于同一飞行器不会变动或极少变动; 可变属性为配载过程中旅客及货品相关参数, 包括数量、重量和规格等, 在各次配载过程中会发生改变, 优化配载过程实际上是优化可变属性的装载参数.
根据飞机受力规则, 以机头为纵轴正方向, 右翼指向方为横轴正方向, CGidea为原点进行二维建模, 如图1.

|
图 1 受力约束建模 |
配载目标主要为货品, 同时乘客力矩也会纳入计算以获得飞机整体力矩, 对其建模采用几何中心作为重心. 乘客位置选择主要受到客舱等级lh和重量wh两个属性影响, 货物除了基本的重量限制外, 还收到诸如规格、优先级和标签等属性影响.
飞机结构中与配载相关组件首先与配载可变属性对应, 包括座位和抽象舱位; 其次, 油箱、水箱作为飞机液体容器, 其属性在飞机配载过程中有很大影响; 最后, 飞机本身的整机重量和重心也是其固有属性的一部分.
2.2 相关参数当前设置算法考虑了重量约束、重心约束、装载顺序约束、规格约束、货物种类约束等.在业务建模中介绍了飞机运行配平力的概念, 飞机配平力的产生会导致燃油消耗量增大, 相同负载重量情况下, CG与CGidea相对距离越大, 耗油量越高, 因此燃油节约约束转换为最优化中心位置[13].
为了能更好地对约束进行表达, 在当前模型下, 参数标识方法如表1所示, 可得相关公式.
| 表 1 配载关键参数表 |
| $ \mathop w{_{{\text{mtow}}} } \ge \sum\nolimits_1^{\textit{i}} {\mathop {\textit{wh}}{_i} } + \sum\nolimits_1^{\textit{j}} {\mathop {\textit{ws}}{ _j } } + \sum\nolimits_1^{\textit{k}} {\mathop {\textit{wta}}{ {}_k } } +w_{\text{oew}}$ | (1) |
| $ \mathop w\nolimits_{{\text{mlw}}} \ge \sum\nolimits_1^{\text{i}} {\mathop {\textit{wh}}{_i}} + \sum\nolimits_1^{\textit{j}} {\mathop {\textit{ws}}{_j} } + \sum\nolimits_1^{\textit{k}} {\mathop {\textit{wtb}}{_k}}+w_{\text{oew}} $ | (2) |
| $ \mathop w\nolimits_{{\text{mzfw}}} \ge \sum\nolimits_1^{\textit{i}} {\mathop {\textit{wh}}{_i}} + \sum\nolimits_1^{\textit{j}} {\mathop {\textit{ws}}{_j} } +w_{\text{oew}} $ | (3) |
| $ x = {\rm{ }}\frac{{\displaystyle\sum\nolimits_1^i {({w}{{h}_{i}} \times hs{t_i})} + \displaystyle\sum\nolimits_1^j {({w}{{s}_{j}} \times h{s_j}) + \displaystyle\sum\nolimits_1^k {({wt}{{b}_{k}} \times h{t_k}) + {w_{\rm{oew}}} \times ha} } }}{{\displaystyle\sum\nolimits_1^i {{w}{{h}_{i}}} + \displaystyle\sum\nolimits_1^j {{w}{{s}_{j}}} + \displaystyle\sum\nolimits_1^k {{wt}{{b}_{k}}} + {w_{\rm{oew}}}}} $ | (4) |
| $ y = {\rm{ }}\frac{{\displaystyle\sum\nolimits_1^i {({w}{{h}_{i}} \times ls{t_i})} + \displaystyle\sum\nolimits_1^j {({w}{{s}_{j}} \times l{s_j}) + \displaystyle\sum\nolimits_1^k {({wt}{{b}_{k}} \times l{t_k}) + {w_{\rm{oew}}} \times la} } }}{{\displaystyle\sum\nolimits_1^i {{w}{{h}_{i}}} + \displaystyle\sum\nolimits_1^j {{w}{{s}_{j}}} + \displaystyle\sum\nolimits_1^k {{wt}{{b}_{k}}} + {w_{\rm{oew}}}}} $ | (5) |
| $ \begin{split} \\ \mathop {\textit{e}}\nolimits_{{\text{lpos}}} \ge y \ge \mathop {\textit{e}}\nolimits_{{\text{lneg}}} \end{split} $ | (6) |
| $ \mathop {\textit{e}}\nolimits_{{\text{hpos}}} \ge x \ge \mathop {\textit{e}}\nolimits_{{\text{hneg}}} $ | (7) |
| $ \mathop {\textit{fm}}\nolimits_{\textit{i}} \in \mathop {\textit{fms}}{ _i } $ | (8) |
| $ \mathop {\textit{lb}}\nolimits_{\textit{i}} \in \mathop {\textit{lbs}}{_i } $ | (9) |
| $ \mathop {\textit{lvh}}\nolimits_{\textit{i}} \in \mathop {\textit{lvst}}{_i } $ | (10) |
| $ 1 \ge \sum\nolimits_1^{\textit{j}} {\mathop s\nolimits_{ij} } $ | (11) |
| $ 1 \ge \sum\nolimits_1^{\textit{j}} {\mathop {s{\text{t}}}\nolimits_{ij} } $ | (12) |
| $ sc = \prod\nolimits_1^i {\mathop k\nolimits_i } \times \prod\nolimits_1^j {\mathop r\nolimits_j } $ | (13) |
由上述条件函数可得目标为:
| $ \max \;sc $ | (14) |
其中, 式(1)–式(3)体现配载过程基本的重量约束, 式(4)–式(7)用于保证配载重心约束, 式(8)–式(12)用于满足配载其他约束, 用于进行性质判别, 并通过式(13)计算分值系数辅助决策.
公式的使用方法将在第4节系统实现中进行举例说明, 后续算法以以上公式为基础, 在面临不同工作环境时, 可以通过增减约束函数对算法决策分值进行适应性调整.
2.3 算法流程部分传统算法基于搜索算法, 对于效率难以保证, 并且由于其算法结构, 难以进行效率优化, 处理时间随约束量、配载量上升而急剧增大.
本文算法基于遗传算法, 结合飞机配载建模设计, 采用高度模块化的方法进行分值计算, 在遗传算法基础上调整回报策略, 使用约束系数模块和回报系数模块共同完成配载方案分值计算工作, 为策略模块提供决策依据;并且由于该算法高度模块化的特点, 也可用于其他决策过程, 大大提高算法使用灵活性, 即使在不同工作环境下, 也可通过适应性调整调度策略来进行协调.
遗传算法使用优胜劣汰的思想, 在一代代种群更替的过程中, 选择较优的表现型, 并将基因向下一代遗传, 最终靠近最优值. 其关键步骤为: 1)编码; 2)初始化种群; 3)评估种群个体适应度; 4)选择; 5)交叉; 6)变异, 其中步骤3)–6)持续迭代, 达到预定迭代数或表现型. 在经前几小节建模后, 上述步骤已经比较清晰, 以23舱位货舱一种布局为例, 如图2所示.
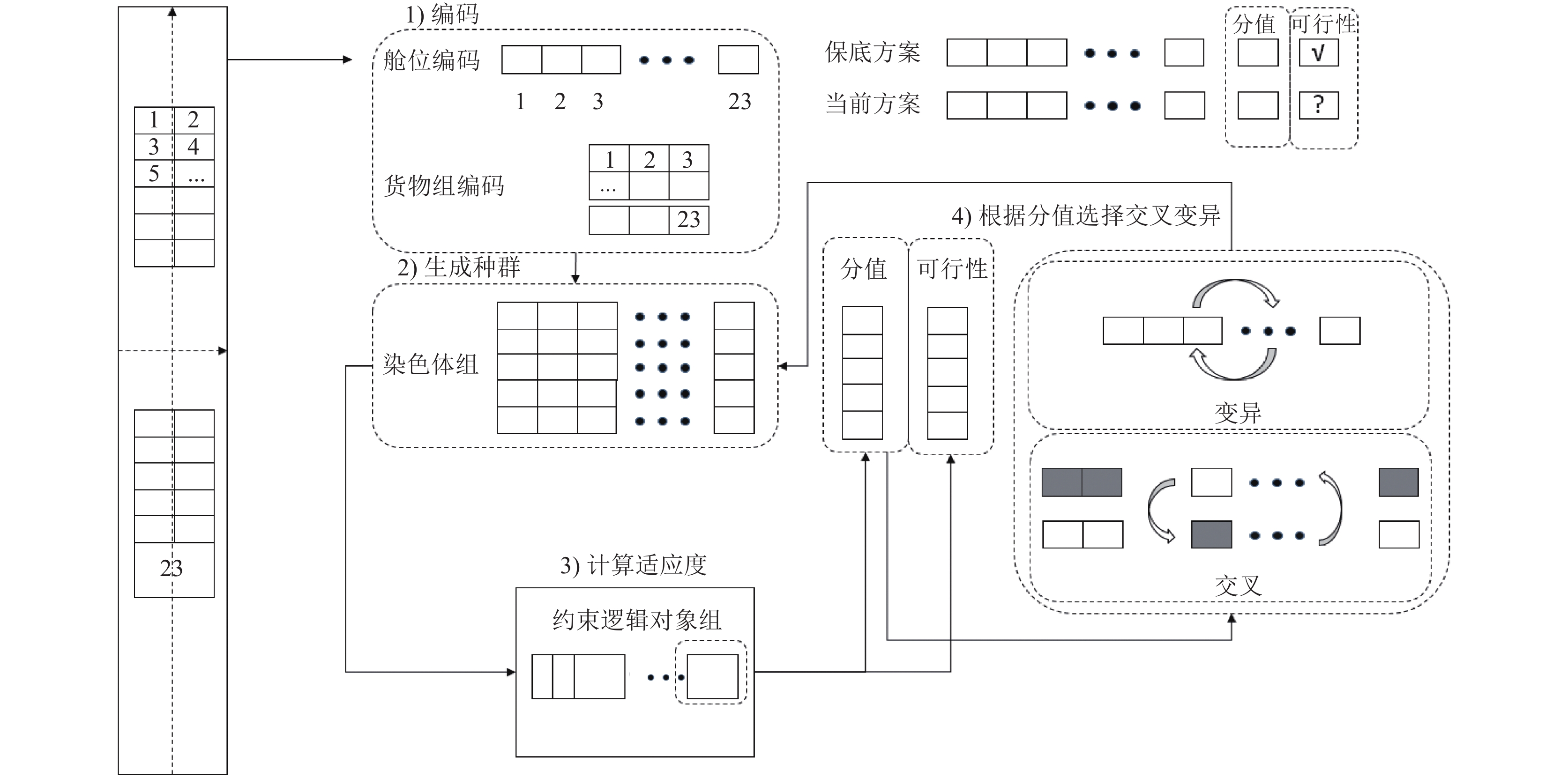
|
图 2 算法流程图 |
配载问题实际上是装载物品对装载空间的占用过程, 属于典型空间资源调度排列问题, 因此使用排列编码, 将所有装载空间抽象为一个数组对象, 数组位置为装载物体, 该数组对象则为一个基因个体.
由于没有使用指导性的公式规范装载位置, 初始化种群时采用随机放置的方式; 需要注意的是, 装载物体数量可能少于装载空间, 为了不对空舱位进行特殊处理, 因此虚构空物品补足数量, 采用同样方式编码.
本文在个体适应度计算方面, 针对飞机货物装载多约束、可变约束的需求, 设计了动态计分的解决方案. 由于不同班次的航班在载客、载货方面都有不同, 没有一个确定的标准, 因此采用信号量分值最大化的方式进行优化遗传. 将每一个约束模型的属性单独划分得到一个约束组, 每个划分中维护自己的影响因子计算方法, 通过影响因子乘积的方式对个体进行组合打分, 如图3所示.

|
图 3 约束组下方案适应度分值计算流程 |
该方案能够引入选定约束的影响, 并且有较好的可扩展性. 需要注意的是, 由于算法需要保证最终方案的可用性, 因此在该过程中加入保障机制, 打分过程中同时进行可用性监测, 会保留一个分值最高的可用方案.
选择和变异时, 由于飞机配载不是严格的最优化问题, 并不要求重心绝对小, 而对计算效率要求更高, 因此不需要过度担心陷入局部最优解的问题, 使用按比例最佳保留和均匀交叉变异的方法进行基因变换, 保证快速收敛.
约束(limit)模块用于处理禁止性质的配载规则, 回报(reward)模块用于处理鼓励性质的配载规则, 首先通过回报模块获取基础分值, 然后通过约束模块增减系数. 各模块的整体调用流程如图4所示.
本文通过调整遗传算法决策值计算法法对配载处理方法进行优化, 通过预处理模块对数据进行结构化, 确定reward、limit和strategy等流程数据出入接口, 通过实现以上接口保证数据流完整性和正确性. Load作为调度器, 根据传入参数构造上述模块并进行组装调用, 处理输入模型获取配载结果.
3 系统设计实现前文对当前配载过程所面临的问题进行了梳理, 然后针对上述问题提出了相应的解决方案, 为了证明上述算法的可用性, 本文对该算法和系统进行了实现, 本节对实现细节进行介绍. 在第3.1节、第3.2节中介绍系统结构和开发框架选取, 便于读者了解实现的整体思路, 第3.3节介绍实现算法功能的各模块, 其中第3.3.2节对公式的使用方法进行了详细介绍.

|
图 4 调用流程图 |
3.1 总体架构
系统架构设计致力于解决系统完善设计问题部分, 部分飞机配载系统长期存在的问题仅考虑业务问题[1], 配载处理泛化能力差, 在面对不同机型需要设计专属配载算法, 复用能力差; 同时, 算法研究常采用单一模型, 难以协调生产条件下复杂的应用环境, 产学不匹配, 进一步加剧系统泛化能力差、可用性低的问题.
本优化技术关注后端架构设计, 可分为交互层、配载逻辑层、实体模型层、配载组件层和数据层等, 通过交互层为前端调用提供接口, 如图5所示, 本节对配载系统架构进行讨论.

|
图 5 总体架构图 |
3.2 开发语言框架选择
本后端配载优化方法采用Java语言开发.希望实现一个泛化能力较好的飞机配载组件, Java语言具有良好的跨平台性, 在所有具有JVM的平台上都能良好运行, 包括目前各种主要的操作系统, 如Windows, MacOS和Linux; 同时, Java在多年的发展下, 出现了适用于后端开发的规范和设计模式, 并且由研究人员提供了强大的后端开发框架. 因此认为Java语言适合进行本系统开发.
使用Maven进行版本管理, 采用SpringBoot框架完成系统架构搭建.
数据管理方面本系统采用MongoDB和MySQL共同进行数据存储管理. MongoDB作为NoSQL型数据库, 有数据可读性强、查询速度快等优点, 但是有数据存储空间难以管理的问题, 因此试用其存储多查询而少变更的飞机模型数据, 保证模型结构化生成效率; 对于多变、多增删的配载货物和人员信息使用MySQL数据库进行存取, 保证数据存储空间能够较好管理.
3.3 模块设置除交互层和数据持久化层外, 本系统从下到上分为实体模型、配载组件和配载逻辑等模块, 本小节对其实现逻辑和内部接口进行详细介绍.
3.3.1 实体模块实体模块根据数据建模部分建立, 本文认为配载过程中相关实体模型分别是飞机、舱位、座位、油箱、货物以及乘客, 其关系如图6所示.
图6中飞机、座位和舱位间有固定层级关系, 每个型号的民航客机都包含一组油箱、一组货物固定位置和一组座位, 因此开发者不需要为每一个型号的飞机单独进行配载实物建模, 将几项实体模型的各项属性录入系统, 根据航行信息调用不同的飞机实体模型即可, 可以对配载模型进行增删而不是重新建模, 来适应变更的机型要求; 并且如果在实际应用中有新的组件需要加入, 只需要对组件计算规则进行建模即可.

|
图 6 实体结构层次关系 |
3.3.2 配载组件模块
配载组件模块目前被划分为3个小模块, 分别是约束系数模块、回报系数模块和策略模块, 它们分别提供如表2所示的操作接口.
| 表 2 模块内部接口设计表 |
配载逻辑模块通过对这3个模块的组合, 调用其接口完成配载计算工作.
提出约束模块和回报模块的目的是通过各个约束公式得到用于遗传算法或其他基于最大最小值进行决策的最优化方法的分值, 实现过程中, 根据公式实现多个装载检测逻辑类, 形成列表进行循环打分.
以式(4)–式(7)为例, 其它公式同理, 这4个公式是针对飞机重心位置的不等式, 用于飞机装载CG是否在保险约束范围内的性质判别, 形成一个CGChecker. 在机器学习算法中, 计算机根据选取更优的策略来进行迭代更新, 而不是通过布尔值来进行取舍, 因此在该类中需要对公式进行转化.
由于约束形式多种多样, 数据代表的意义也不相同, 难以直接对其进行归一化处理, 为了防止出现各约束在计算过程中涉及数值差距过大导致影响因子难以调整的问题, 需要一个类对不同约束进行处理.
约束系数模块提供check接口, 输入配载映射数组, 返回布尔值, 用于表示当前配载映射关系是否满足该约束规则. 每一个约束系数对象只负责一个约束规则的检查工作, 由此可见, 每一个禁止规则至少需要对应一个约束逻辑对象, 因为不满足禁止规则的配载方案是不能作为最终方案的, 即使该方案经计算后能够得到最高的分值, 该判定过程与配载整体数据而不是当前策略模块返回的数据有关, 在进行计算时, 需要联合预处理过程中传递的数据进行综合评判.
除性质检查外, limit对象中还维护一个大于1的正项系数和一个0到1之间的负向系数, 该系数通过乘式的方式影响初始分值, 在经约束模块检测后可行的方案取正项系数, 不可行则取负向系数. 根据不同约束在计算过程中检测规则不同, 会被划分为单一状态约束和组合状态约束, 在获取系数时也有所不同, check接口作为策略模块的服务接口, 传递的是约束整体满足与否, 但是在实际计算中存在单一约束的情况, 需要对每子配载问题进行状态划分, 以保证分值的区分度. 在上述例子中, 重心约束模块通过式(4)计算出当前配载方案导致的横向重心偏移值, 然后使用式(7)进行重心性质判别, 如果符合需求, 则返回一个正向系数, 否则返回一个负向系数.
使用时, 通过计算不同配载方案重心给出分值, 该分值影响遗传算法过程染色体适应度, 结合方式如图3所示, 以此影响算法迭代过程.
3.3.3 配载逻辑模块第3.3.2节介绍的3个模块通过逻辑接口进行信息交互, 只要系统设置了相应接口, 即使有不同配载需求, 只需要通过替换模块即可完成组合, 极大的提高了系统的可扩展性和灵活性.
配载逻辑模块起到了调配小模块的作用, 该对象中包含了3个模块对象的工程类, 通过传入参数对子模块进行拼装, 完成配载计算, 其结构如图7所示.
4 测试在第3节中介绍了系统的实现过程, 本节对上述实现进行验证.
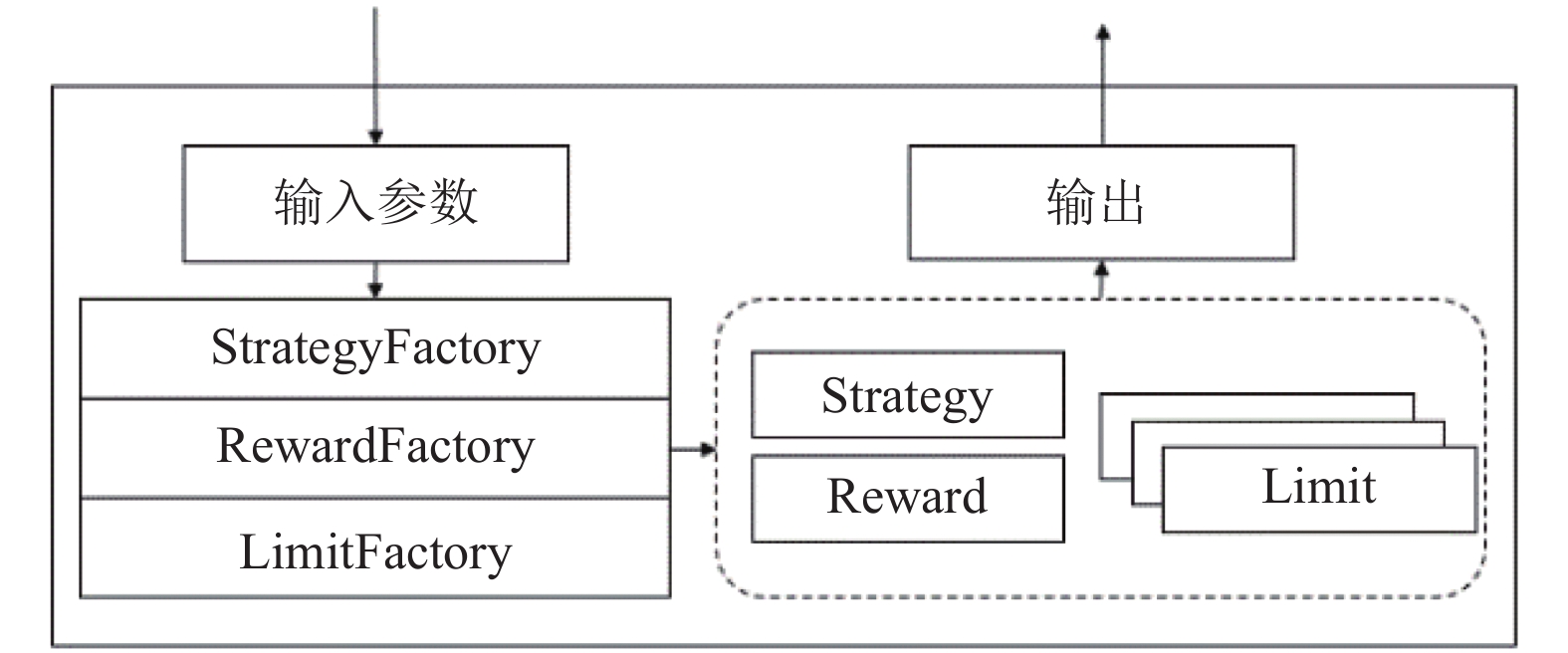
|
图 7 Load模块组成图 |
针对算法效果方面, 由于本系统结构和算法应用目标与第2节中介绍的解决方法有明显区别, 难以在统一条件下模拟, 因此没有采用相关工作进行对比, 转而使用最优解对比验证算法效果.本次测试使用的对比方法为全排列算法, 在一定时间内必然可以获得当前条件下的最优配载方案, 因此可以验证当前算法效果.
算法效率方面, 通过测试本系统配载时间来验证能否实时计算.
4.1 测试数据设置根据上文相关参数及实体模型设计部分介绍, 本优化方法涉及数据主要包括民航客机机型参数和配载相关测试数据.
通过资料调研, 发现美国波音公司生产的民机产品在我国民航客机领域有相对广泛的应用, 因此选取大型宽体飞机波音767作为基础机型生成测试模型数据, 内置模型包含座位230个、货物装载舱位23个, 采用双精度浮点型数据表示坐标位置.
配载货物以航空用统一装载单元为基础结构进行重量、规格、目的地等参数可用范围内随机数据生成模拟需要配载的货物信息, 例如Example1模式下, 可以指定组数随机生成货物, 降低人为测试数据集设定带来的特殊模式匹配问题.
为了测试方法性能, 除以上述模型外, 分别以8、11和14舱位构造module2、module3和module4, 按照飞机货舱比例构建测试模型, 进行运行时间测试.
4.2 测试结果分析测试模型编号为使用的飞机建模编号, 测试数据编号为使用一个测试数据类型随机生成多组测试数据进行测试; 时间属性记录为服务过程中配载算法运行时间, 没有对网络传输延迟时间进行统计; 每次配载完成, 通过约束模块进行配载状态可用性检测.本次测试通过算法性能对比、重心偏移对比、自身收敛情况测试和约束去除自对照来验证算法可用性.
表3为性能对比, 由于搜索空间随舱位数变化指数增长, 因此搜索算法在不同舱位数下配载方案计算表现差距极大, 以搜索为基础即使对其进行剪枝等优化, 也难以从搜索根部直接剪枝, 应对舱位数变化的泛化性差; 当前方法基于遗传算法实现, 其时间复杂度随舱位数线性增长, 因此可以做到实时配载.
表4中使用构造模型将默认遗传算法与搜索算法进行对比, 表明在小量配载时, 遗传算法有很大概率找到当前约束参数下的最优解, 可靠性较高. 验证了通过公式形成的约束模块的可用性.
表5中数据为收敛情况测试, 根据性能对比测试可以得知, 当前数量级搜索空间过大, 因此不适用搜索算法, 采用多次运行自对比的方法, 使用2类模型, 5组测试数据进行遗传算法收敛测试, 测试过程中每个测试用例进行20次运行, 由于篇幅关系, 选取其中两次作为关键数据. 由该数据可得, 算法收敛状况稳定, 坐标偏移极小, 在厘米甚至毫米级, 靠近理论最优值, 总能收敛到打分策略最优值; 配载时间达到秒级, 验证了strategy模块可用性.
表6表示将货物规格约束从约束列表中去除后重心偏移变化, 每组测试用例重心偏移均较去除后更小, 该测试结果表明约束系数变化能够有效引导算法方法像预定目标理论最优值靠近, 证明了模块化拆分约束分值的可用性.
| 表 3 性能对比 |
| 表 4 方法CG对照测试 |
| 表 5 收敛状态关键数据表 |
| 表 6 format约束去除对比 |
4.3 测试小结
当前测试方案通过多组随机配载数据下进行测试汇总, 首先能够证明优化方案的可用性和功能可靠性. 该测试各测试数据组都能保证秒级配载计算速度; 通过上文介绍的配载约束系数模块检测, 方法给出的各配载方案均能够满足飞机正常航行的各项约束目标, 且重心位置、装卸信号量通过回报模块在效率协调状态下逼近了理论最优值.
其次, 该测试还能证明该优化方法的泛化性和可扩展性.
本测试过程中飞机模型构建流程为: 利用本框架提供的模式化构建方法选取适用类; 根据机型图纸注入数据值获得对象; 使用数据层服务进行飞机模型持久化. 测试中货物数据通过模式化构建模块进行数据注入生成, 同样是在进行持久化的状态下通过查询完成后续配载流程, 因此实际使用中可以通过修改数据库查询配置或直接进行数据转储的方法导入配载数据, 以提供服务的模式进行业务处理. 因此该优化方法受机型变动影响小、受原始系统状态影响小; 此外, 当业务中有需求变化时, 可以通过调整约束组合、重新实现约束计分方案等方法进行针对性优化, 有较好的泛化性.
同时本优化方法为后续开发优化提供了接口, 测试用的两种方法均在本方法内部框架下实现, 使用策略设计模式采用同样的调用接口, 通过传递方法名称即可控制方法, 有较强的的可扩展性.
5 总结与展望配载算法的主要指标为配载效果和效率, 本文描述的算法方案基于遗传算法实现, 通过构建约束系数表影响决策值状态, 满足飞机配载约束.
本文旨在从多方面优化飞机自动配载技术, 推动产学结合, 希望通过优化算法和架构设计保证算法在复杂多变的生产环境中得到更好的应用. 基于上述算法实现的系统通过高度结构化的约束模块设计, 通过确定模块接口、提供模板类等方式, 实现可拆装的策略、约束和回报方式, 在保证算法可用性的情况下, 提高系统的可扩展性和灵活性.
本文认为在该架构下进行算法针对业务环境的特性优化还有一定空间. 基于该算法设计和系统架构, 可以通过实现接口应用其他配载策略、改换约束组合等方式对方法结构进行业务针对性调整; 同时, 由于本算法采用约束组合打分的方式, 还可以调整系统策略算法参数、根据目标调整回报函数和根据配载实际需求调整约束正负系数等方法进行优化; 此外, 还可以通过对约束模块进行划分来优化计算过程, 如划分运行时优化约束计算、运行前基础约束检测和运行后可用性约束检测等.
后续会从以上方面进行自动配平优化, 扩大应用范围和业务覆盖面, 进一步减轻人工工作压力.
| [1] |
Brandt F, Nickel S. The air cargo load planning problem-a consolidated problem definition and literature review on related problems. European Journal of Operational Research, 2019, 275(2): 399-410. DOI:10.1016/j.ejor.2018.07.013 |
| [2] |
Falkenauer E. A hybrid grouping genetic algorithm for bin packing. Journal of Heuristics, 1996, 2(1): 5-30. DOI:10.1007/BF00226291 |
| [3] |
Johnson DS. Fast algorithms for bin packing. Journal of Computer and System Sciences, 1974, 8(3): 272-314. DOI:10.1016/S0022-0000(74)80026-7 |
| [4] |
Kaluzny BL, Shaw RHAD. Optimal aircraft load balancing. International Transactions in Operational Research, 2009, 16(6): 767-787. DOI:10.1111/j.1475-3995.2009.00723.x |
| [5] |
Verstichel J, Vancroonenburg W, Souffriau W, et al. A mixed integer programming approach to the aircraft weight and balance problem. Procedia-Social and Behavioral Sciences, 2011, 20: 1051-1059. DOI:10.1016/j.sbspro.2011.08.114 |
| [6] |
Mongeau M, Bes C. Optimization of aircraft container loading. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(1): 140-150. DOI:10.1109/TAES.2003.1188899 |
| [7] |
Fok K, Ka M, Chun A, et al. Optimizing air cargo load planning and analysis. Proceedings of International Conference on Computing, Communications and Control Technologies. Austin, 2004. 14–17.
|
| [8] |
Carlson NJ, Reiman AD, Overstreet RE, et al. Load planning processes to enhance cargo compartment utilization. Journal of Defense Analytics and Logistics, 2017, 1(2): 137-150. |
| [9] |
Krichen S, Dahmani N. A particle swarm optimization approach for the bi-objective load balancing problem. Electronic Notes in Discrete Mathematics, 2010, 36: 751-758. DOI:10.1016/j.endm.2010.05.095 |
| [10] |
Son DH, Kim HJ. An algorithm for the loading planning of air express cargoes. Journal of the Society of Korea Indus-trial and Systems Engineering, 2016, 39(3): 56-63. DOI:10.11627/jkise.2016.39.3.056 |
| [11] |
庄景堂. 飞机载重与平衡的工程问题. 航空维修与工程, 2004(4): 54-55. DOI:10.3969/j.issn.1672-0989.2004.04.031 |
| [12] |
杨德林, 张铮, 刘曦. 飞机配载平衡及装载过程优化的力学逻辑. 航空科学技术, 2016(1): 11-14. DOI:10.3969/j.issn.1007-5453.2016.01.003 |
| [13] |
郭玉涛. 飞机重心节油原理研究和案例分析. 空运商务, 2018(11): 57-59. DOI:10.3969/j.issn.1671-3095.2018.11.029 |
 2022, Vol. 31
2022, Vol. 31



