近年来, 随着深度学习的飞速发展, 深度学习技术被大规模地运用到推荐系统领域[1]. 深度学习技术能够有效地捕获非线性和特殊性的用户和项目之间的关系, 并通过引用神经网络, 将其作为更高层中的数据表示, 来表达更复杂抽象的数据形式以克服数据稀疏性的问题[2]. 因此, 许多研究人员都通过将深度神经网络与传统协同过滤算法结合, 改善传统推荐算法的推荐性能.
2017年, He等首次提出了神经协同过滤模型(neural collaborative filtering, NCF)[3], 同时在此框架下融合了广义矩阵分解和多层感知机模型, 广义矩阵分解通过利用线性内核来建模用户与项目潜在特征向量之间的交互关系. 多层感知机则是使用非线性内核学习交互函数, 进一步优化推荐模型.
近几年, 许多研究人员也根据NCF模型做出了改进以进一步提升推荐效果. 例如刘晶[4]在2019年提出基于Inception-ResNet网络的外积交互协同过滤算法, 将NCF中的神经网络层定义为Inception网络, 复杂的Inception对特征的非线性映射能力更强, 同时添加ResNet结构解决训练中梯度弥散的问题, 使模型具有更好的效果. 王骏等[5]在2020年提出将多层感知机与贝叶斯个性化排序算法融合, 提取所需要的排序信息, 使模型性能得到提高. 纪强[6]在2020年提出基于循环神经网络的序列推荐模型, 通过循环神经网络来学习用户交互的序列历史中的短期用户偏好.
然而这些都不能很好地同时捕捉用户的短期偏好和长期偏好, 针对这个问题, 本文提出融合长短期记忆网络和广义矩阵分解的神经协同过滤模型, 这对实现更好的推荐性能有很重要的意义.
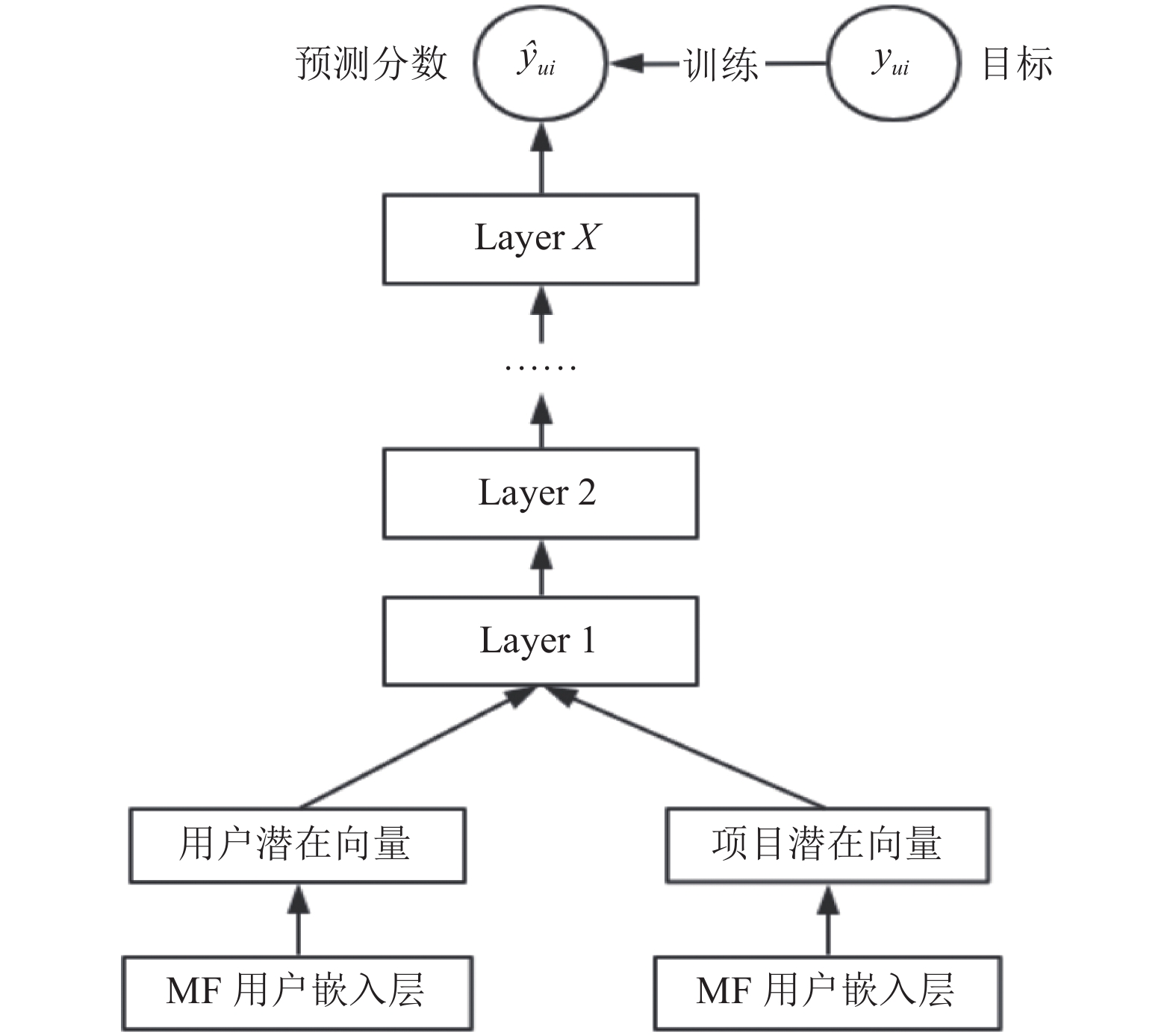
1 相关知识 1.1 神经协同过滤神经协同过滤模型基于隐式反馈数据, 利用深度神经网络结构来学习任意交互函数, 为每个用户生成一个推荐列表, 其框架结构如图1所示. NCF将传统矩阵分解模型中的内积操作替换为“多层神经网络+输出层”的结构, 这样可以使用户和项目向量之间进行更充分的交叉, 从而获得更多的特征组合信息, 而这种非线性特征的加入也将使模型的表达能力获得提升.
1.2 矩阵分解推荐算法中传统的协同过滤算法存在着一定的局限性, 例如头部效应较明显, 泛化能力较弱[7]等问题. 针对这个问题, 矩阵分解(matrix factorization, MF)算法[8]被提出. MF在协同过滤算法中“共现矩阵”的基础上, 加入了隐向量的概念, 加强了模型处理稀疏矩阵的能力, 解决了协同过滤存在的主要问题[9].
矩阵分解算法为每一个用户和项目生成一个隐向量, 然后将用户和项目定位到隐向量的表示空间上, 距离相近的用户和项目表明兴趣特点接近, 在推荐过程中, 距离相近的项目表明相似度更高, 更应该被推荐给目标用户.
|
图 1 NCF框架 |
计算用户u对项目i的预估评分如式(1)所示.
| $ {\widehat r_{ui}} = {q_i}^{\rm T}{p_u} $ | (1) |
其中,
式(2)是求解矩阵分解的目标函数, 该目标函数的目的在于最小化实际评分
| $ \mathop {\min }\limits_{q*,p*} \sum\limits_{(u,i) \in K} {{{({r_{ui}} - {q_i}^{\rm T}{p_u})}^2}} $ | (2) |
长短期记忆网络(long short-term memory, LSTM)[10]是针对循环神经网络(recurrent neural networks, RNN)产生的梯度消失和梯度爆炸问题而进行改进的, 它的结构[11]如图2所示.
LSTM状态更新满足以下公式:
| $ {f_t} = \sigma ({W_f}[{h_{t - 1}},{x_t}] + {b_f}) $ | (3) |
| $ {i_t} = \sigma ({W_i}[{h_{t - 1}},{x_t}] + {b_i}) $ | (4) |
| $ {c_t} = {f_t} \cdot {c_{t - 1}} + {i_t} \cdot \tanh ({W_c}[{h_{t - 1}},{x_t}] + {b_c}) $ | (5) |
| $ {o_t} = \sigma ({W_o}[{h_{t - 1}},{x_t}] + {b_o}) $ | (6) |
| $ {h_t} = {o_t} \cdot \tanh ({c_t}) $ | (7) |
其中,

|
图 2 LSTM结构 |
2 长短期记忆网络矩阵分解模型 2.1 总体框架
每个用户对项目的浏览顺序是推荐系统中的一项重要数据, 随着时间的不同, 用户的喜好也会有着一定的变化. 然而, 传统的推荐算法默认用户的喜好是一成不变的, 仅仅对用户的偏好进行全局预测, 通过静态的方式建模用户与项目之间的交互, 这样忽略了用户兴趣动态变化的过程.
而在实际的推荐场景中, 由于用户所处的上下文不同应该进行不同的推荐. 一个好的推荐系统不能仅仅捕捉用户的长期偏好, 而应该把时效特性考虑其中. 对时间序列数据有很强拟合能力的循环神经网络就刚好可以做到这一点, 捕捉用户的短期偏好, 进一步改善推荐效果.
但是, 通常在进行推荐时, 推荐的预测目标与实际所需要的信息并不是连续的, 甚至会出现超长间隔, 而普通的循环神经网络难以学习这种长依赖关系[12]. 所以在类似电影推荐这种行为建模场景中, 普通的RNN难以建模这种关系. 于是, LSTM被提出, 它是一种特殊的RNN, 专门针对数据的长短期依赖关系, 对于实际推荐系统中序列间的这种长依赖关系进行很好地建模.
因此本文对NCF中的神经网络结构进行了改进, 通过LSTM学习用户的短期偏好信息, 捕捉序列的长依赖关系, 同时通过广义矩阵分解学习用户的长期偏好信息, 然后在NCF框架下构建两个模型, 并把他们进行融合得到预测数据. 本文把这个改进模型称为长短期记忆网络矩阵分解(LSMF)模型, 结构如图3所示.

|
图 3 LSMF模型 |
2.2 嵌入层
嵌入层的作用在于将数据映射成为特征向量. 本文中, 它将输入层的用户ID和项目ID进行了one-hot编码后, 分别通过MF嵌入层和LSTM嵌入层映射成输入到MF层和LSTM层的用户和项目特征向量. 其中, 用户ID和电影ID需要通过时间排序后再输出到嵌入层.
2.3 神经网络层 2.3.1 广义矩阵分解通过嵌入层得到了用
| $ {\phi _1}({p_u},{q_i}) = {p_u} \odot {q_i} $ | (8) |
其中, ⊙表示向量的点积, 然后将向量映射到输出层.
| $ {\widehat y_{ui}} = {a_{\rm {out}}}({h^{\rm T}}({p_u} \odot {q_i})) $ | (9) |
其中,
模型通过LSTM来捕获用户和项目的时间依赖性, 对时序信息循环计算以挖掘上下文关系, 通过构造用户状态和电影状态进行自回归计算, 对推荐系统中的用户行为序列进行分析.
模型通过上一时刻的用户和项目状态预测此时的用户和电影状态[14], 然后预测此时用户和项目进行交互地可能性.
| $ {u_{u,t + 1}} = g({u_{ut}},\{ {r_{ui\left| t \right.}}\} ) $ | (10) |
| $ {m_{i,t + 1}} = h({m_{it}},\{ {r_{ui\left| t \right.}}\} ) $ | (11) |
基于用户评分行为预测评分问题表示为:
| $ {\widehat r_{ui\left| t \right.}} = f({u_{ut}},{m_{it}}) $ | (12) |
其中,
将GMF层和LSTM层输出的向量进行拼接.
| $ {\widehat y_{ui}} = \sigma ({h^{\rm T}}[{\phi _{\rm {GMF}}},{\phi _{\rm {LSTM}}}]) $ | (13) |
本文使用Sigmoid作为激活函数. 由于本文专注于隐式反馈的研究, 所以将LSMF视为概率模型, 把推荐作为一个二分类任务. 因此本文使用对数损失函数(log loss)学习h进行优化.
3 实验分析 3.1 实验数据集本文选择MovieLens-1M作为实验数据集, 其中包含users.dat, movies.dat和ratings.dat三个表. 它拥有来自6 040位在2000年加入MovieLens的用户对3 706部电影的100多万条从1星到5星评级信息, 其中每个用户评级过的电影数据均大于20.
3.2 实验评估标准为了验证模型的推荐效果, 我们选用留一法(leave-one-out)进行验证. 把每个用户最新的评分信息作为测试集, 把其他的交互信息作为训练集. 为了避免对所有项目排序造成的耗时过长, 所以实验是从所有的项目样本中随机选择99个没有评分的电影, 然后将测试集中的电影与这些电影一起输入到模型进行排序.
本文将命中率(hits ratio, HR)和归一化折损累积增益(normalized discounted cumulative gain, NDCG)[15]作为性能评估标准.
| $ HR@K = \frac{{NumberOfHits@K}}{{\left| {GT} \right|}} $ | (14) |
| $ NDCG@K = Z\sum\limits_{i = 1}^K {\frac{{{2^{{x_i}}} - 1}}{{\log (1 + i)}}} $ | (15) |
在式(14)中, GT所表示的是所有用户测试集合中的项目总数, 分子表示推荐列表中属于其测试集合的项目总数. 式(15)中, Z是归一化因子, 表示理想推荐列表的折损累计增益.
本文对5种不同的模型进行对比, 这些模型分别为NCF框架下的广义矩阵分解模型(GMF), 多层感知机模型(MLP), 神经网络矩阵分解模型(NueMF), 长短期记忆网络模型(LSTM)和长短期记忆网络矩阵分解模型(LSMF). 训练50轮, 取不同模型的性能平均值, 得出结果如表1所示.
| 表 1 不同模型的HR和NDCG对比 |
图4和图5显示了广义矩阵分解(GMF)模型, 长短期记忆网络(LSTM)模型以及两者融合后的长短期记忆网络矩阵分解(LSMF)模型的性能对比, 从图中可以看出, 前10个迭代的更新是最有效的. 从以上实验数据可以明显看出, LSTM模型的收敛速度较慢, 但收敛后的推荐性能比GMF要好, 而融合了LSTM和GMF的LSMF模型, 不仅收敛速度比较快, 而且推荐性能也是最好的.

|
图 4 各个模型在HR上的表现 |
从以上实验结果中, 我们可以清楚地得到结论, 这5种模型在推荐性能上的优劣对比为LSMF> LSTM> NueMF> MLP> GMF. 因此本文提出LSMF模型在推荐性能上有了一定的提高.

|
图 5 各个模型在NDCG上的表现 |
4 结论
本文首先介绍了神经协同过滤模型, 然后针对模型中没有考虑时间因素, 无法同时捕捉用户的短期偏好和长期偏好的问题, 提出了长短期记忆网络与广义矩阵分解相结合的神经协同过滤模型, 通过长短期记忆网络学习用户的短期偏好信息, 捕捉序列的长依赖关系, 同时通过广义矩阵分解学习用户的长期偏好信息. 最后在MovieLens-1M数据集上与其他模型进行对比, 根据实验结果发现在命中率和归一化折现累积增益这两个指标上, 本文提出的改进模型有明显的提升, 收敛速度更快, 而且具备更好的推荐性能.
| [1] |
李同欢. 基于深度学习的推荐模型研究[硕士学位论文]. 重庆: 西南大学, 2019.
|
| [2] |
王喆. 深度学习推荐系统. 北京: 电子工业出版社, 2020.
|
| [3] |
He XG, Liao LZ, Zhang HW, et al. Neural collaborative filtering. Proceedings of the 26th International Conference on World Wide Web. Australia: ACM, 2017. 173–182.
|
| [4] |
刘晶. 基于深度学习的协同过滤算法的研究[硕士学位论文]. 北京: 北京邮电大学, 2019.
|
| [5] |
王骏, 虞歌. 基于改进神经协同过滤模型的电影推荐系统. 计算机工程与设计, 2020, 41(7): 2069-2075. |
| [6] |
纪强. 基于循环神经网络的深度推荐模型研究[硕士学位论文]. 合肥: 安徽大学, 2020.
|
| [7] |
郭辰. 基于概率矩阵分解的协同过滤推荐[硕士学位论文]. 大连: 大连理工大学, 2019.
|
| [8] |
Koren Y, Bell R, Volinsky C. Matrix factorization techniques for recommender systems. Computer, 2009, 42(8): 30-37. DOI:10.1109/MC.2009.263 |
| [9] |
袁志远. 基于协同过滤的个性化推荐算法研究[硕士学位论文]. 南京: 南京邮电大学, 2018.
|
| [10] |
Devooght R, Bersini H. Long and short-term recommendations with recurrent neural networks. Proceedings of the 25th Conference on User Modeling, Adaptation and Personalization. Bratislava: ACM, 2017. 13–21.
|
| [11] |
高茂庭, 徐彬源. 基于循环神经网络的推荐算法. 计算机工程, 2019, 45(8): 198-202, 209. |
| [12] |
Song Y, Elkahky AM, He XD. Multi-rate deep learning for temporal recommendation. Proceedings of the 39th International ACM SIGIR Conference on Research and Development in Information Retrieval. Pisa: ACM, 2016. 909–912.
|
| [13] |
李川. 基于改进神经网络协同过滤的研究[硕士学位论文]. 西安: 西安电子科技大学, 2019.
|
| [14] |
Wu CY, Ahmed A, Beutel A, et al. Recurrent recommender networks. Proceedings of the 10th ACM International Conference on Web Search and Data Mining. Cambridge: ACM, 2017. 495–503.
|
| [15] |
武海龙. 基于卷积神经网络的协同过滤算法研究[硕士学位论文]. 武汉: 华中科技大学, 2019.
|
 2022, Vol. 31
2022, Vol. 31



