图结构数据已广泛应用于许多现实世界的应用程序中, 例如社交网络(Facebook和Twitter), 生物网络(蛋白质或基因相互作用)以及属性图(PubMed和Arxiv)等^[1-3]. 节点分类任务是图结构数据上最重要的任务之一, 即给定一个节点子集及其标签, 预测其余节点的标签. 对于节点分类任务, 基于图的深度学习模型——图神经网络已实现了最先进的性能^[4], 而图卷积网络(GCN)作为一种特殊的图神经网络, 在此任务上取得了更好的结果.

目前的研究更多的是将重点放在如何提高GCN的性能上, 却很少有人关注GCN模型的鲁棒性. 但是, 研究表明, GCN是极易受到对抗攻击的. 例如, 只须对图数据的拓扑结构或者节点的特征进行微小的修改就能使GCN得到错误的分类结果^[5]. 目前的攻击方法中, 绝大多数是通过修改图数据的拓扑结构和节点属性来进行攻击的, 然而, 这样的攻击在现实场景中是不适用的. 例如, 在社交网络应用程序中, 攻击者必须登录用户的帐户才能更改现有的连接和功能, 而获得登录访问权限几乎是不可能的. 相比之下, 在实践中添加与用户相对应的伪节点(fake node)会容易得多.

TUA就是一种通过添加伪节点进行攻击的针对性通用攻击方法. 在针对GCN的所有攻击方法中, 通用攻击方法是一种特殊的攻击方法, 此方法要求GCN将所有的受害节点都错误分类, 而不是某个单独的节点^[6-8]. 针对性通用攻击则要求GCN将所有受害节点都错误地分到某一个指定的类别^[9]. 本文则是基于TUA算法, 通过引入梯度选择的方法, 使得本文方法在所有类别的实验中都取得了与TUA方法相当甚至优于TUA方法的结果, 平均ASR相对TUA得到了1.7%的提升.

1 相关知识介绍 1.1 图卷积网络 (GCN)^{[4, 10]}

给定属性图 $ G(A,X) $ , 其中 $ A \in {\left\{ {0,1} \right\}^{N \times N}} $ 为邻接矩阵, $ X \in {\left\{ {0,1} \right\}^{N \times d}} $ 为特征矩阵, 即图G有N个节点, 且每个节点伴随一个 $ d $ 维的特征. 令 $ V = \left\{ {{v_1},{v_2}, \cdots ,{v_N}} \right\} $ 为节点集, $ C = \left\{ {{c_1},{c_2}, \cdots {c_k}} \right\} $ 为类别集. 节点分类任务的目标就是通过在含有节点标签的训练集上学习从而成功预测测试集节点的标签. GCN首先通过聚合邻居节点的信息来得到节点的嵌入表示(第 $ l $ 层如下):

$ {H^{(l + 1)}} = \sigma ({\tilde D^{ - \frac{1}{2}}}\tilde A{\tilde D^{ - \frac{1}{2}}}{H^{(l)}}{W^{(l)}}) $

(1)

其中, $ \tilde A = A + {I_N} $ , $ {\tilde D_{ii}} = \displaystyle\sum\nolimits_j {{{\tilde A}_{ij}}} $ 分别是添加自连接之后的邻接矩阵和度矩阵, $ {W^{(l)}} $ 是权重矩阵, $ \sigma (x) $ 是激活函数. 初始状态 $ {H^{(0)}} = X $ , $ {H^{(l)}} $ 则是第 $ l $ 层的嵌入输出. 根据Kipf等^[4], 仅用一个隐藏层, 最后GCN的输出为:

$Z = f(A,X) = {\textit{Softmax}} (\hat A{\textit{ReLU}}(\hat AX{W^{(0)}})X{W^{(1)}})$

(2)

其中, $ \hat A = {\tilde D^{ - \frac{1}{2}}}\tilde A{\tilde D^{ - \frac{1}{2}}} $ .

1.2 图对抗攻击

在过去的几年中, Zungner等^[6]和Dai等^[5]首先发现了GCN容易受到对抗性攻击的特性. 而根据攻击的不同阶段, GCN中的对抗攻击分为两种类型: 投毒攻击(训练期间的攻击)和逃避攻击(测试期间的攻击). 通常, 投毒攻击的重点是通过干扰训练数据来降低GCN模型的性能, 而逃避攻击则通过修改属性或拓扑结构来构造对抗性样本, 从而使GCN模型的性能降低. 另外, 根据攻击的不同目的, 对图结构化数据的对抗攻击可分为节点分类攻击, 链接预测攻击和图分类攻击.节点分类攻击的目的是使某些节点被GCN误分类. 链接预测攻击的重点是减少节点之间的关联, 从而导致GCN提供错误的预测结果. 图分类攻击则旨在增强指定图与目标分类之间的相关性, 以使GCN无法正确分类给定图样本. 本文提出的GTUA可以归为逃避攻击和节点分类攻击.

在对图结构数据的所有对抗攻击中, 伪节点攻击是一种常见的攻击方法, 通过将一组伪节点注入到图中来实现, 从而可以避免对原始图进行拓扑或属性修改. 例如, GreedyAttack和GreedyGAN通过将伪造的节点直接添加到受害节点来进行目标节点攻击^[11]. Wang等^[12]引入近似快速梯度符号法, 该方法在受害节点和其他节点之间添加了一个恶性节点, 从而导致受害节点被错误分类. 但是, 大多数现有的伪节点攻击并非旨在进行普遍的对抗攻击. 而在本文提出的GTUA中, 伪节点充当受害节点的2跳邻居. 由于GCN的攻击过程, 伪节点特征的影响通过攻击节点传递到受害节点, 从而进行针对性通用对抗攻击.

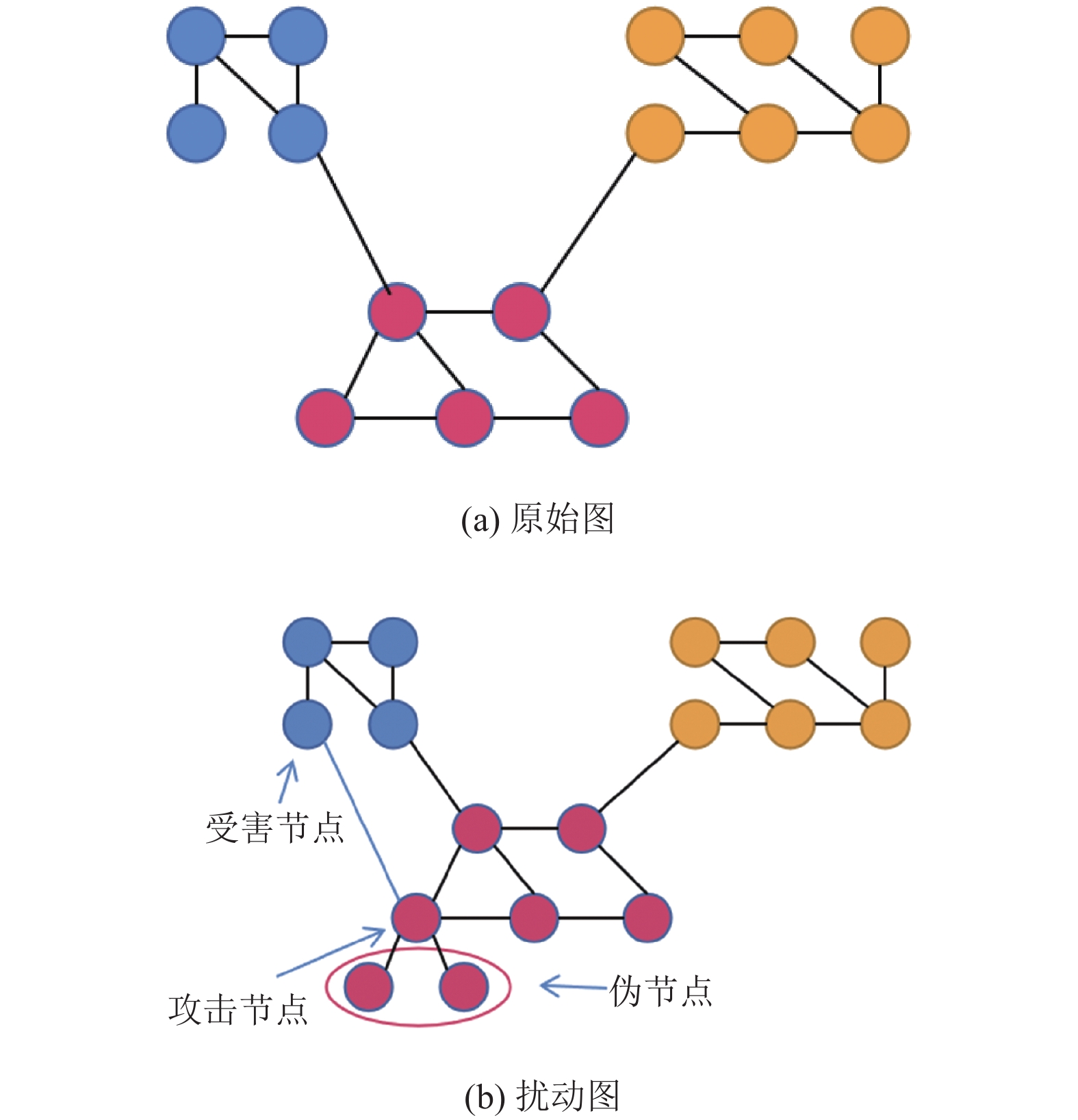
2 基于梯度选择的图卷积网络针对性通用对抗攻击

基于梯度选择的图卷积网络针对性通用对抗攻击(GTUA)的目标是使得每一个与攻击节点(从标签为目标类别的节点集中随机选择)连接的受害节点都得到与攻击节点相同的标签(如图1所示). 主要由3个步骤完成: 添加伴随0特征的伪节点; 计算目标函数关于伪节点特征矩阵的梯度矩阵; 按梯度矩阵元素大小进行梯度选择并确定扰动特征. 下面分别详细介绍每一个步骤.

2.1 添加伴随0特征的伪节点

在添加伪节点之前, 先简单介绍几步预处理过程: 对于给定的图 $ G(A,X) $ , 首先选定一个类别 $ {c_o} $ 作为目标类别, 随后在标签为 $ {c_o} $ 的节点集中随机选择 $ {N_A} $ 个节点作为攻击节点 ${V_A} = \{ v_A^1,v_A^1, \cdots, v_A^{{N_A}}{\text{\} }}$ , 同时为了简便起见, 规定为每个攻击节点连接相同数量 $ {N_F} $ 个伪节点. 即, 给定图 $ G(A,X) $ , 目标类别 $ {c_o} $ , 攻击节点 $ {V_A} $ , 每个攻击节点的伪节点数目 $ {N_F} $ , 通过给每个攻击节点连接特征为0的伪节点得到新图 $ G' = (A',X') $ , 其中,

$ A' = \left[ {\begin{array}{*{20}{c}} A&E \\ {{E^{\rm T}}}&P \end{array}} \right] ,\;\; X' = \left[ {\begin{array}{*{20}{c}} X \\ {{X_F}} \end{array}} \right] $

(3)

其中, $ E \in {\left\{ {0,1} \right\}^{N \times \left( {{N_A} \cdot {N_F}} \right)}} $ , $ P \in {\left\{ {0,1} \right\}^{\left( {{N_A} \cdot {N_F}} \right) \times \left( {{N_A} \cdot {N_F}} \right)}} $ , $ {X_F} \in $ $ {\left\{ {0,1} \right\}^{\left( {{N_A} \cdot {N_F}} \right) \times d}} $ , 且初始化为全0, 本文的目的就是通过给伪节点添加某些特征, 也就是 $ {X_F} $ 的某些元素由0改为1, 从而使得下面的目标函数取得最大值.

2.2 计算目标函数关于伪节点特征矩阵的梯度矩阵

在此首先明确本文的目的是, 对于给定的图 $ G(A,X) $ , 目标类别 $ {c_o} $ , 攻击节点 $ {V_A} $ , 希望每一个标签不是 $ {c_o} $ 的节点, 当其与 $ {V_A} $ 连接时, 能够使得GCN为其得到 $ {c_o} $ 的标签, 这也就是针对性通用攻击的含义. 由此含义, 首先给出一个随机选定的辅助节点集 ${V_T} = \left\{ {v_T^1,v_T^2 ,\cdots, v_T^{{N_T}}} \right\}$ 来帮助建立目标函数, 其中 $ {N_T} $ 表示辅助节点的数量, 要求 $ {V_T} $ 中的每一个节点都不属于标签 $ {c_o} $ , 因此有下面的目标函数:

$ \left\{ \begin{split} &\mathop {\arg \max }\limits_{{X_F}} \sum\limits_{v \in {V_T}} {F\left( {A',X',v} \right)} \hfill \\ & {\rm {s.t.}}\;{\left\| E \right\|_0} + {\left\| {{X_F}} \right\|_0} \le \Delta \hfill \\ \end{split}\right. $

(4)

其中, $ {\left\| E \right\|_0} $ 表示伪节点与攻击节点之间的连边的数量, $ {\left\| {{X_F}} \right\|_0} $ 表示给伪节点添加的特征的数量, 二者都受到参数 $ \Delta $ 的限制, 因为扰动必须是微小的. 其中,

$ \begin{gathered} F\left( {A',X',v} \right) = {\left[ {f\left( {A{'_{\left( {v,{V_A}} \right)}},X'} \right)} \right]_{v,{c_o}}} - {\left[ {f\left( {A{'_{\left( {v,{V_A}} \right)}},X'} \right)} \right]_{v,{c_v}}} \hfill \\ \end{gathered} $

(5)

式(5)是关于每一个辅助节点的目标函数部分, $ v \in {V_T} $ , $ A{'_{\left( {v,A} \right)}} $ 表示辅助节点v与攻击节点 $ {V_A} $ 连接之后的新的邻接矩阵, $ {[f\left( \cdot \right)]_{v,{c_o}}} $ 和 $ {[f\left( \cdot \right)]_{v,{c_v}}} $ 分别表示GCN将节点v判定为目标类别和其当前类别的输出概率. 而制定此目标函数的依据是: 如果本文的攻击或者说扰动能够使得GCN将这些非 $ {c_o} $ 的辅助节点在连接到 $ {V_A} $ 后被分类到 $ {c_o} $ , 那么对于所有的非 $ {c_o} $ 的节点, 当其与 $ {V_A} $ 连接后, 就会有很大的概率被分类为 $ {c_o} $ , 并且如果考虑一种极端情况: 将所有非 $ {c_o} $ 节点作为辅助节点, 那么就能更好地理解此目标函数.

前面确定了目标函数, 那么如何计算扰动？在这里首先介绍基于梯度的方法. 因为只考虑对 $ {X_F} $ 进行扰动, 因此只需要先计算目标函数关于 $ {X_F} $ 的梯度:

$ Grad = {\nabla _{{X_F}}}\sum\limits_{v \in {V_T}} {F\left( {A',X',v} \right)} $

(6)

2.3 按梯度矩阵元素大小进行梯度选择并确定扰动特征

以往的基于梯度的方法基本都是采用一种贪婪式的选择方法^[13]: 在每一次迭代中只改动一个元素, 因此找到每一次迭代中的梯度矩阵中的最大元素作为修改的对象即可. TUA也是采用这样一种方式, 首先找到 $ Grad $ 中的最大元素 $ Gra{d_{\max }} $ :

$\left\{ \begin{split} &Gra{d_{\max }} = \mathop {\arg \max }\limits_{i,j} Grad(i,j) \hfill \\ &i \in 1,2, \cdots ,{N_F};j \in 1,2, \cdots ,d \hfill \end{split}\right. $

(7)

然后找到 $ Gra{d_{\max }} $ 在 $ {X_F} $ 对应哪一个伪节点的哪一个特征, 再找到它在 $ X' $ 中的对应位置, 将该位置的元素由0置为1, 这样就完成了一次迭代, 直到到达一定的阈值就结束扰动. 需要提到的一点是: 如果某一次迭代时最大梯度对应的位置已经是1, 那么就寻找第二大的梯度位置, 依次下去.

本文提出的GTUA也是采用一种基于梯度的贪婪式方法, 但是在这个过程中加上一个梯度选择的过程. 具体做法就是在得到 $ Grad $ 之后, 选出其中从大到小前k个元素:

$\left\{ { \begin{split} &Gra{d_1} = \max \left\{ {Grad(i,j)} \right\} \hfill \\ &Gra{d_2} = \max \left\{ {\left\{ {Grad(i,j)} \right\}\backslash \left\{ {Gra{d_1}} \right\}} \right\} \hfill \\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\vdots \hfill \\ &Gra{d_k} = \max \left\{ {\left\{ {Grad(i,j)} \right\}\backslash \left\{ {Gra{d_1}, \cdots ,Gra{d_{k - 1}}} \right\}} \right\} \hfill \end{split} } \right.$

(8)

然后分别计算将其在 $ X' $ 中对应位置的特征值由0置为1后的损失函数值:

$ \left\{ \begin{split} &{\textit{Loss}}_1 = \sum\limits_{v \in {V_T}} {F\left( {A',{X_1}',v} \right)} \hfill \\ &{\textit{Loss}}_2 = \sum\limits_{v \in {V_T}} {F\left( {A',{X_2}',v} \right)} \hfill \\ &\;\;\;\;\;\;\;\;\;\;\;\vdots \hfill \\ &{\textit{Loss}}_k = \sum\limits_{v \in {V_T}} {F\left( {A',{X_k}',v} \right)} \hfill \end{split}\right. $

(9)

其中, $ {X_1}',{X_2}', \cdots ,{X_k}' $ 分别是对 $ Gra{d_1},Gra{d_2}, \cdots ,Gra{d_k} $ 位置进行扰动后的新的特征矩阵. 最后再选择其中得到最大损失函数值的特征修改作为这一次迭代的扰动:

$ Gra{d_{\rm{obj}}} = \mathop {\arg }\limits_{i,j} \left\{ {\mathop {\arg \max Los{s_n}}\limits_n } \right\} $

(10)

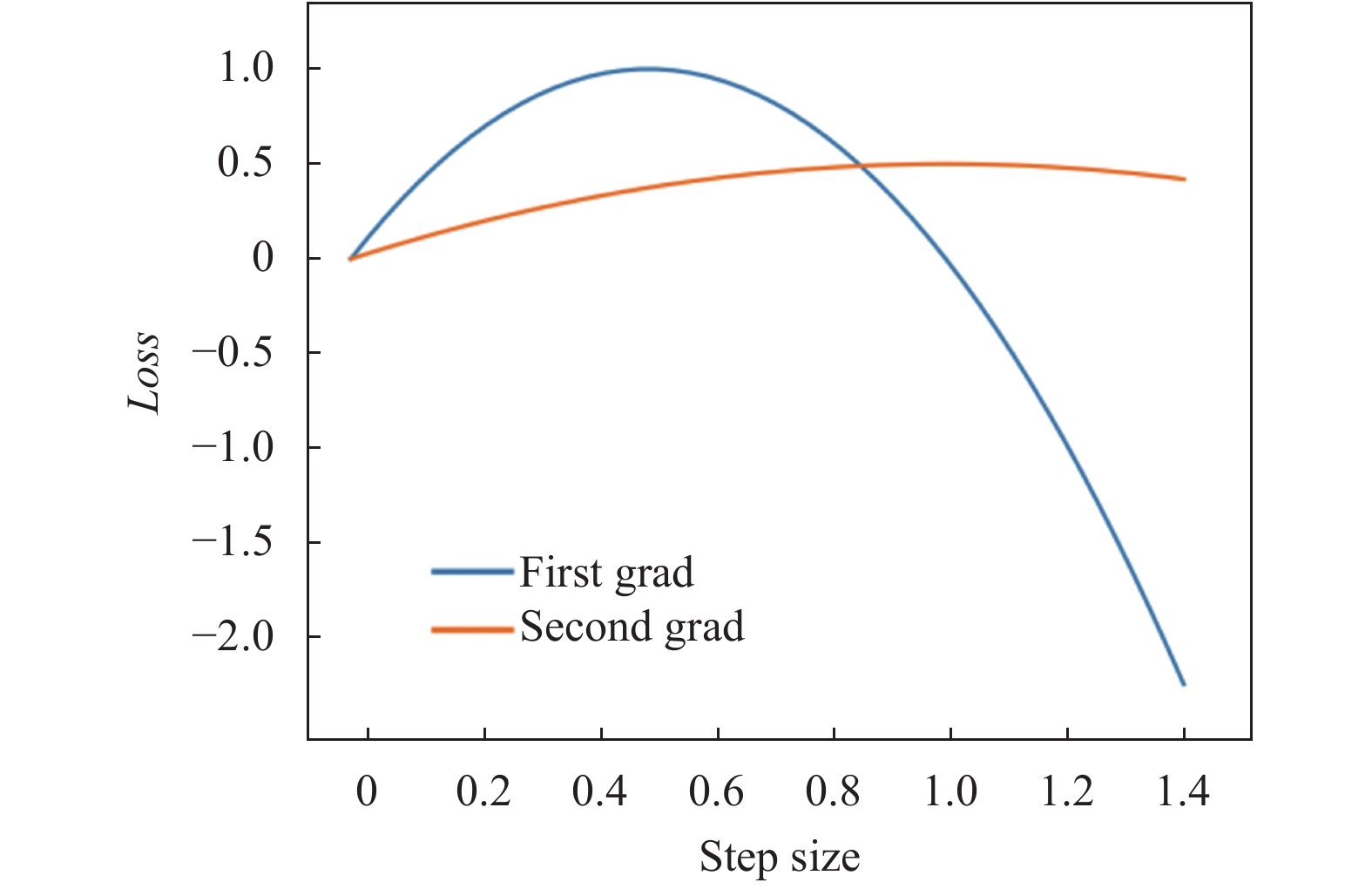
加入这样一个梯度选择的过程, 是出于以下思考: 因为考虑A和X都是取值为0或1的离散数据类型, 因此在选择 $ Grad $ 中最大元素 $ Gra{d_{\max }} $ 对应的位置并由0置为1的时候相当于是选择了长度1的步长, 并且每一次迭代都是固定步长1. 因此, 就很可能出现一种情况, $ Grad $ 中第二大元素 $ Gra{d_{\sec }} $ 对应的位置由0置为1会得到更大的损失函数, 如图2所示.

3 实验分析 3.1 数据集和评价指标

本文在3个常用的属性图数据集上进行实验: Cora (2 708节点, 5 429边, 1 433特征, 7类别), Citeseer (3 312节点, 4 732边, 3 703特征, 6类别) 和 PubMed (19717节点, 44338边, 500特征, 3类别)^[14-16]. 此外, 根据Kipf&Welling的设置, 在3个相应的数据集上训练GCN模型. 最后用平均攻击成功率(ASR)作为模型性能的评价标准, ASR越高, 表明模型的攻击效果越好.

3.2 实验设置

首先按照TUA的方法加快微扰计算. 因为大多数基于梯度的攻击都存在时间和内存成本高的问题, 为了解决这个问题, Li等^[16]提出了一种有效加速攻击的框架, 该攻击框架攻击由目标节点的k跳邻居组成的较小子图(k取决于GCN层数), 从而可以避免不必要的图信息存储和计算^[17]. 因为本文是基于Kipf&Welling的设置来训练GCN, 也就是一个2层的GCN, 因此只需要关注以目标节点为中心, 以其一阶邻居和二阶邻居组成的子图即可. 根据TUA的实验发现, 当 $ {N_F} $ , $ {N_T} $ 固定时, 随着 $ {N_A} $ 的取值大于3之后, ASR几乎不再随着 $ {N_A} $ 的增大而增大; 同样的, 固定 $ {N_A} $ , $ {N_T} $ 的取值时, 当 $ {N_F} $ 大于2之后, ASR也不再随 $ {N_F} $ 的增大而增大; 固定 $ {N_A} $ , $ {N_F} $ 时, 当 $ {N_T} $ 达到20后, 随着 $ {N_T} $ 的增大, ASR几乎不再增大. 但是, 无论其中哪一个参数增大, 对计算与存储的消耗都会成倍的增加. 同时, 对GTUA进行了相关参数的实验, 发现与TUA有着相似的规律. 因此在后续的实验中, 规定参数设置 $ {N_A} = 3 $ , $ {N_F} = 2 $ , $ {N_T} = 20 $ .

3.3 实验结果与分析

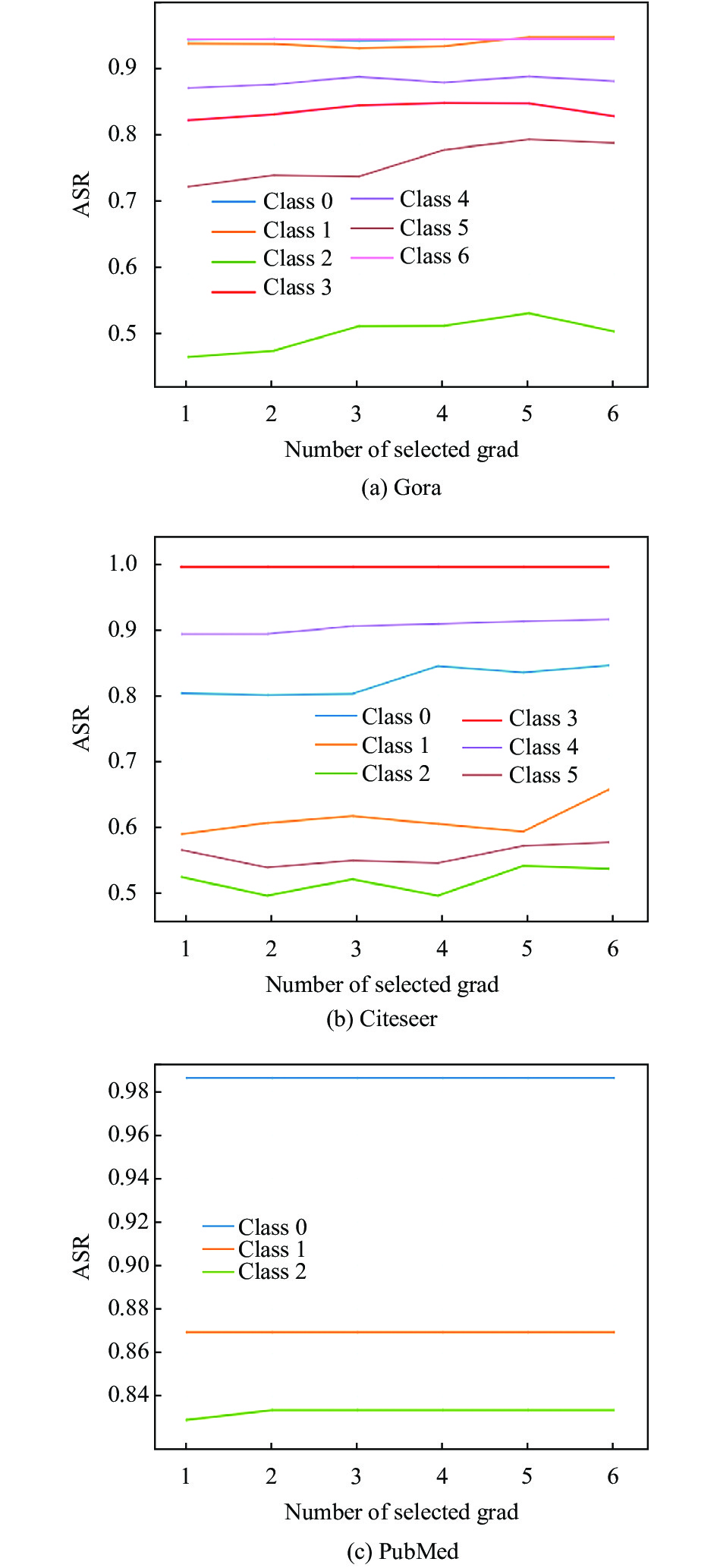
本文进行两组实验, 第一组实验用来查看在梯度选择过程中选择不同数量的梯度值 $ {N_G} $ 对ASR带来的影响, 这里本文考虑 $ {N_G} \in \left\{ {1,2,3,4,5,6} \right\} $ , 实验结果如图3所示. 由图3可知, 当加入了梯度选择的步骤之后, 多数情况下ASR值都是高于原始ASR值的, 且在这里的实验中发现 $ {N_G} $ 取5的时候能在多数情况下得到最大的ASR值, 因此后面的实验就选定 $ {N_G} = 5 $ .

第二组实验选择一个恰当的 $ {N_G} $ 值, 将本文方法GTUA与TUA的ASR值进行对比来验证GTUA的有效性. 由实验一的结果, 本文选择 $ {N_G} = 5 $ . 结果如表1所示, 可以很清楚地看到GTUA在多数情况下优于TUA, 在少量情况下取得与TUA同样的结果, 而取得相同结果的原因是每一次迭代都在梯度最大值处的扰动能得到最大的损失函数值, 表1的最后一行也表明GTUA与TUA相比, 平均ASR提高了1.7%.

表2展示了GTUA与TUA的一次训练加测试的耗时对比, 可以发现: 因为GTUA梯度选择的过程需要计算 $ {N_G} $ 次损失函数, 因此耗时要远大于TUA, 且通过实验发现, 随着图的节点与边的增多, 两者之间的耗时差距越来越大, 因此GTUA比较适用于小图, 而对于大图, 时间成本略高. 但是, 由于GTUA选择梯度的过程, 从而导致它并不依赖于损失函数对特征矩阵的最大梯度, 而TUA则严重依赖于上述最大梯度, 所以一些微小的改动并不会对GTUA模型的结果造成影响, 却会大大影响到TUA的结果, 所以GTUA相比TUA有更好的鲁棒性.

4 结论与展望

本文提出了一种基于梯度的图卷积网络针对性通用对抗攻击GTUA, 实验结果表明, 与当前流行的方法TUA相比, GTUA最差能够达到与其一样的结果, 但在多数情况下优于TUA, 由此可以看出梯度选择的过程确实提升了扰动的质量. 另外, 本文也留下了一个后续的研究方向: 对于离散数据类型上的基于梯度的方法, 都可以尝试加入梯度选择的过程, 由本文的结果可以大胆地预测, 其在很大程度上可能会带来效果上的提升.