2. 太原科技大学 机械工程学院, 太原 030024
2. School of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China
刀具是机械加工中十分重要的工具, 在加工过程中刀具会受到材料的挤压、摩擦以及腐蚀等诸多因素的干扰, 从而会使得加工精度降低, 不合格产品数量增多[1]. 有效的刀具寿命预测可以提高加工效率, 保证加工精度, 因此具有重要的研究价值[2, 3].
目前, 针对刀具寿命预测的问题, 许多学者都做了很多的研究. 丁怡等在BP神经网络的基础上建立刀具寿命预测模型, 通过实验仿真验证了模型的可靠性[4]. 侍红岩等分析了影响刀具寿命的主要因素, 然后以支持向量回归机算法为基础建立了刀具寿命预测模型, 并通过实验验证了模型的适用性[5]. Benkedjouh等提出一种基于非线性特征简约和支持向量回归的方法来进行刀具状态的评估, 进而预测刀具寿命[6]. 夏颖怡等利用改进的遗传算法来优化BP神经网络, 用优化后的BP神经网络模型实现刀具寿命预测, 最后经过实验验证了与传统的BP神经网络模型相比, 其预测精度更高[7]. 王虎等分析了刀具寿命的影响因素和刀具寿命之间的关系, 根据两者之间的高度非线性关系, 采用PSO算法优化BP神经网络, 最终建立刀具寿命预测模型[8]. Kovac等利用工具工作温度的测量值确定了扩展的泰勒函数关系, 该方法可以将获取的刀具表面的温度作为输入信号, 从而进行刀具寿命的预测[9]. 曾晓雪等将混沌理论加入PSO-BP神经网络算法中, 提出了CPSO-BP的刀具寿命预测算法, 通过仿真表明CPSO-BP神经网络算法比之前的PSO-BP神经网络算法的预测效果更好[10]. Hosseinkhani等提出了一种使用混合有限元方法结合经验磨损率方程估算刀具寿命的方法[11]. 但是上述方法都不同程度地存在一些不足, 例如BP神经网络的网络层数、节点数以及连接权值等参数较多, 需要人为反复调试, 优化工作量复杂, 使得预测模型构建的难度增大. 像基于泰勒公式的物理模型, 由于实际生产过程中刀具会受到材料属性、加工类型等多因素的影响, 使得模型参数过于复杂, 难以设计和计算, 因此很难适用于实际生产中.
针对以上所述的问题, 本文提出了基于PSO-RBF神经网络的刀具寿命预测方法. RBF神经网络与BP神经网络不同, RBF的泛化能力在很多方面要优于BP, 同时在网络的训练过程中, 不需要调整神经元之间的连接权值, 完全通过样本数据进行学习, 而且RBF神经网络的学习速率很快. 与BP神经网络模型、传统物理模型相比, RBF神经网络构建的模型不是过于复杂, 适用性很好. 所以本文以RBF神经网络模型为基础, 利用PSO算法对RBF神经网络的主要参数进行优化, 最终建立预测精度较高的模型.
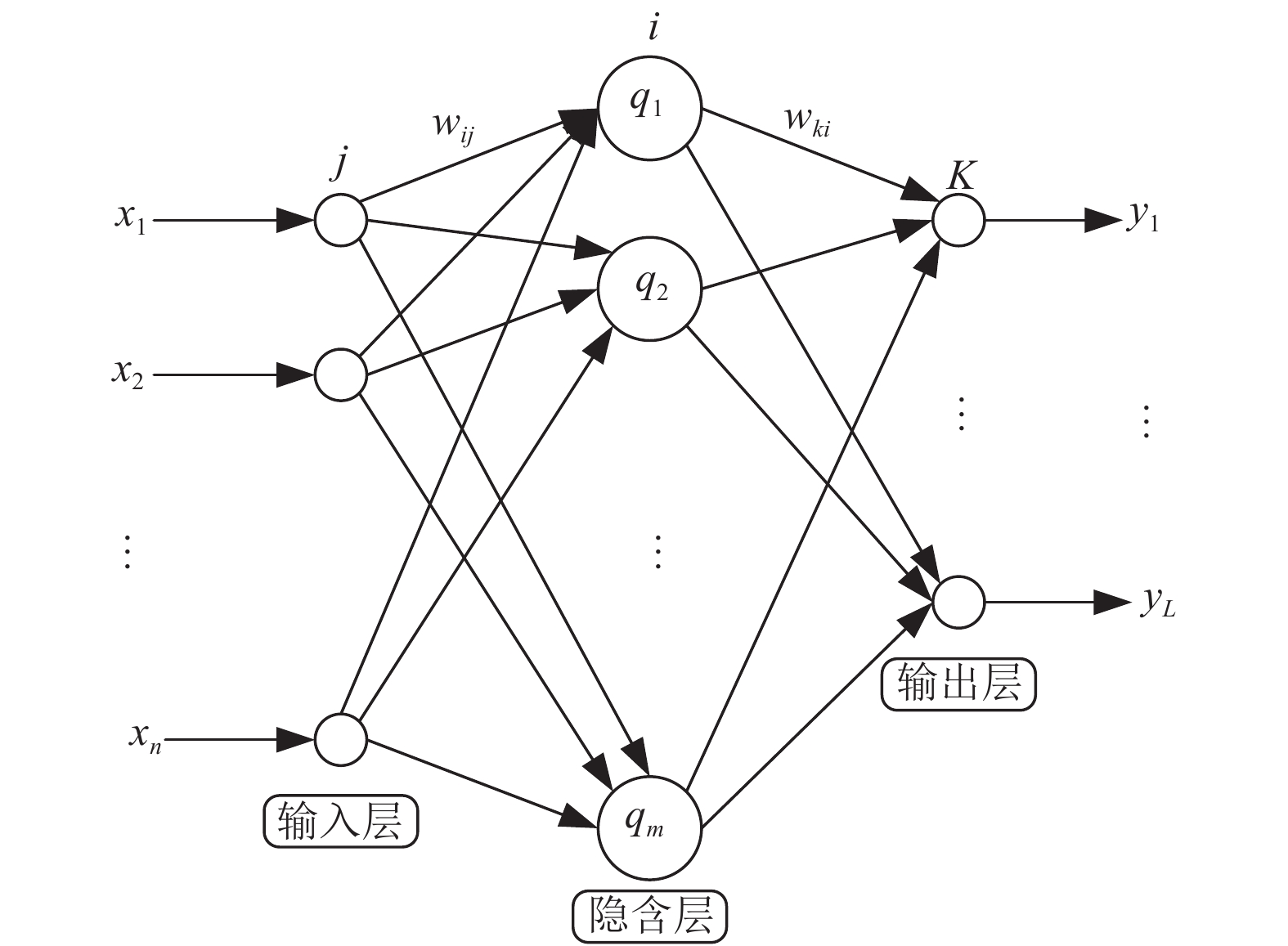
1 相关研究 1.1 RBF神经网络RBF神经网络的原理是利用径向基函数作为隐含层单元的“基”构成隐含层空间, 隐含层对输入向量进行变换, 将低维空间的输入数据映射到高维空间, 使得在低维空间线性不可分的问题在高维空间实现线性可分[12-14]. 图1为RBF神经网络的结构.
|
图 1 RBF神经网络结构 |
图1中, x1, x2,…, xn为n维输入向量, q1, q2,…, qm为输入的m维向量, y1, y2,…, yL为L维输出向量, wij为输入层加权系数, wki为隐含层到输出层的加权系数, 隐含层的输出为:
| $ Q({{{x}}_i}) = {\rm{exp}}\left( - \frac{1}{{2{\rm{\delta }}_i^2}}\left\| {{{{X}}_{{M}}} - {{{C}}_i}} \right\|\right) $ | (1) |
其中, δi为对应隐节点的标准化常数, XM为输入向量, Ci为对应的高斯函数的中心向量. 输出层的输出为:
| $ Y = \sum\limits_{j = 1}^q {{w_i}} Q({{\rm{X}}_i}) $ | (2) |
其中, wi为加权系数. 总误差为:
| $ J = \frac{1}{2}\sum\limits_{p = 1}^N {\sum\limits_{k = 1}^L {{{\left({{t}}_k^p - y_k^p\right)}^2}} } $ | (3) |
其中, N为输入输出样本数, L为输出节点数,
RBF神经网络虽然可以很好地处理非线性问题, 具有良好的泛化能力, 但是由于其隐含层径向基函数中心、标准化常数以及隐含层到输出层的加权系数等几个重要参数难以确定, 导致了RBF神经网络的盲目性较高[15, 16].
1.2 PSO算法20世纪末, Kennedy与Eberhart受到鸟类种群寻找食物传递信息规律的启发, 提出了PSO算法[17]. 该算法的基本思想是将优化问题的解抽象为粒子, 通常会有一个被优化的函数确定每个粒子的适应值, 同时粒子移动的方向和距离由一个速度来确定. 每一个被初始化的粒子根据当前最优粒子的信息在解空间进行迭代搜索, 而在每一次的迭代中, 粒子都是通过本身目前所找的最优解和全部粒子目前所找的最优解来更新自己[18].
在M维空间中, 初始化一群数目为N且随机移动的粒子, xi(i=1,2,…,N)为粒子的初始位置, vi(i=1,2,…,N)为粒子的速度, pbesti(i=1,2,…,N)为个粒子经历过的最好位置, gbesti(i=1,2,…,N)为全部粒子经历过的最好位置. 粒子i根据式(4)和式(5)更新自己的速度和位置:
| $v_{id}^{k + 1} = wv_{id}^k + {c_1}ran{d_1}\left({\textit{pbes}}{{{t}}_{id}} - x_{id}^k\right) + {{{c}}_2}ran{d_2}\left({\textit{gbes}}{{{t}}_{id}} - {{x}}_{id}^k\right)$ | (4) |
| $ x_{id}^{k + 1} = x_{id}^k + v_{id}^k $ | (5) |
式(4)和式(5)中,
PSO算法有着其独特的优点, 首先它拥有很强的全局搜索能力, 其次算法中需要调整的参数不多, 而且它的结构简单, 容易实现. 目前, PSO算法被广泛应用于神经网络的训练、目标寻优以及决策支持等多个方面.
1.3 RBF神经网络模型的优化RBF神经网络的关键问题是径向基函数的中心、宽度和连接权值这3个参数的确定, 而采用PSO算法对RBF神经网络优化就是将这3个参数当做自由运动的粒子, 以向量的形式表示粒子的位置, 通过PSO算法来确定参数合适的值, 最终建立RBF神经网络. 在优化过程中, 根据径向基函数的特点选择均方误差作为PSO算法的适应度函数, 计算方式如下所示:
| $ F = \frac{1}{N}\sum\limits_{i = 1}^N {{{({{{D}}_i} - {{{Y}}_i})}^2}} $ | (6) |
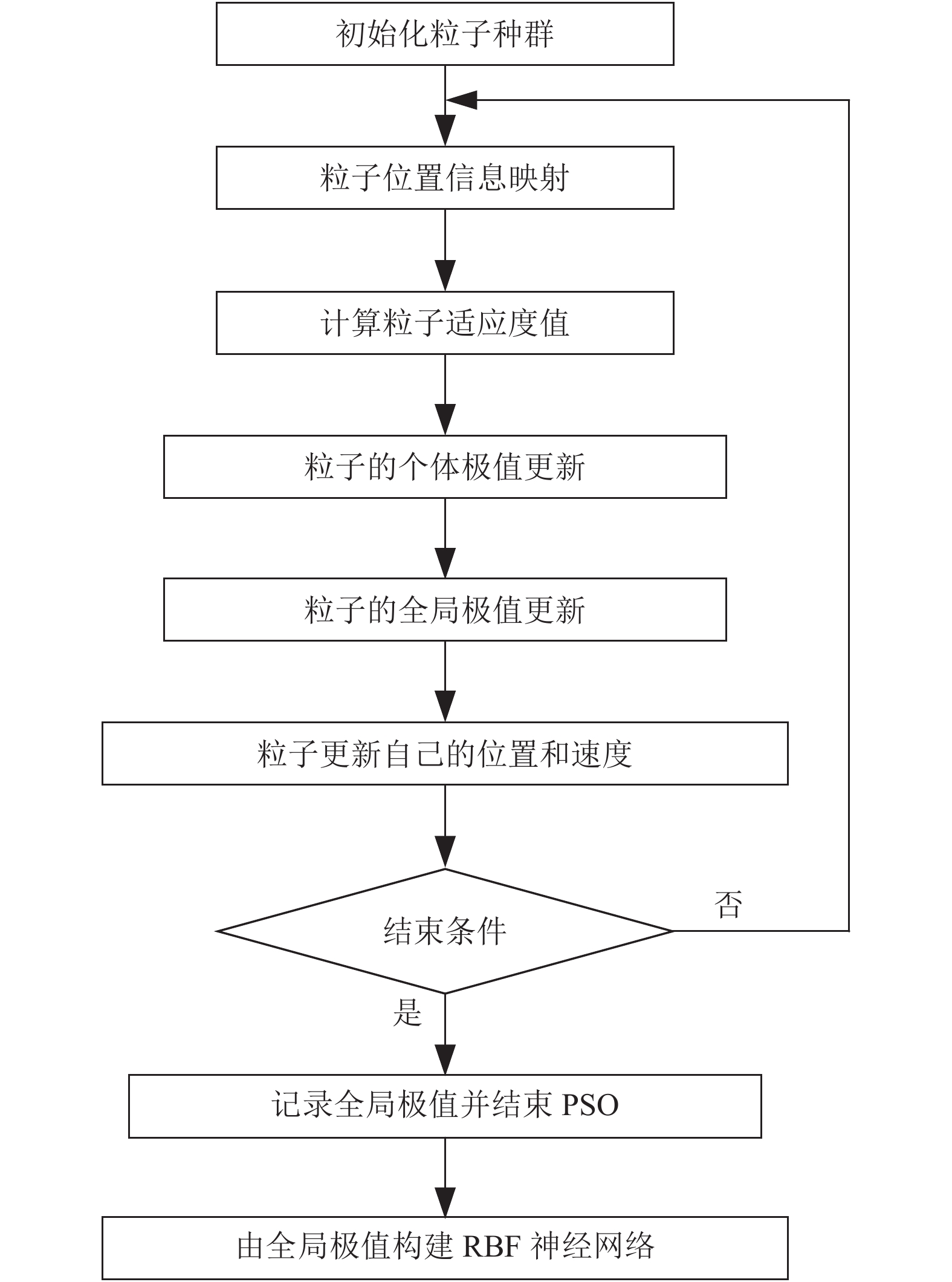
其中, N为训练样本的容量, Di为期望输出值, Yi训练输出值. PSO算法优化RBF神经网络模型的过程如图2所示.
|
图 2 PSO-RBF神经网络框架图 |
Step 1. 随机初始化种群, 确定种群数量、迭代次数以及其他信息, 设定粒子的初始状态, 即位置和速度, 并同时将RBF神经网络的3个参数组成粒子向量.
Step 2. 将所有粒子的位置信息映射到RBF神经网络中, 建立神经网络模型.
Step 3. 按照式(6)计算粒子的适应度值.
Step 4. 比较粒子当前适应度值和上一次的适应度值, 好的话就将当前适应度值作为新的个体极值.
Step 5. 比较当前的全局极值和上一次的全局极值, 好的话就将当前的全局极值作为新的全局极值.
Step 6. 所有粒子根据当前最新的个体极值和全局极值, 按照式(4)和式(5)来更新自己的位置和速度.
Step 7. 根据结束条件来判断是否需要迭代更新, 需要的话返回第Step 2.
Step 8. 记录最新的全局极值, 并且结束PSO算法.
Step 9. 根据所得到的最新全局极值来构建RBF神经网络.
2 刀具寿命预测模型 2.1 分析刀具寿命影响因素通常来说, 刀具寿命是指刀具从投入使用到报废为止的切削时间[19], 如果想高效准确地预测刀具寿命, 就必须要分析影响刀具寿命的因素. 传统刀具寿命计算公式如下所示:
| $ T = \frac{{{C_r}D_0^q}}{{{v_c}a_p^x{f^y}a_w^u{Z^p}}} $ | (7) |
其中, T为刀具使用寿命, Cr为刀具寿命系数, D0为刀具直径, vc为切削速度, ap为背吃刀量, f为进给量, aw为切削宽度, Z为刀具齿数, q、x、y、u、p为各相应参数的指数值.
由此可见, 影响刀具寿命的因素是众多而且复杂的, 主要有刀具寿命系数、刀具直径、切削速度、背吃刀量、进给量、切削宽度以及刀具齿数等, 此外还有加工材料、切削温度以及振动等因素, 传统刀具寿命预测方法难以准确反映以上因素和寿命之间的非线性关系.
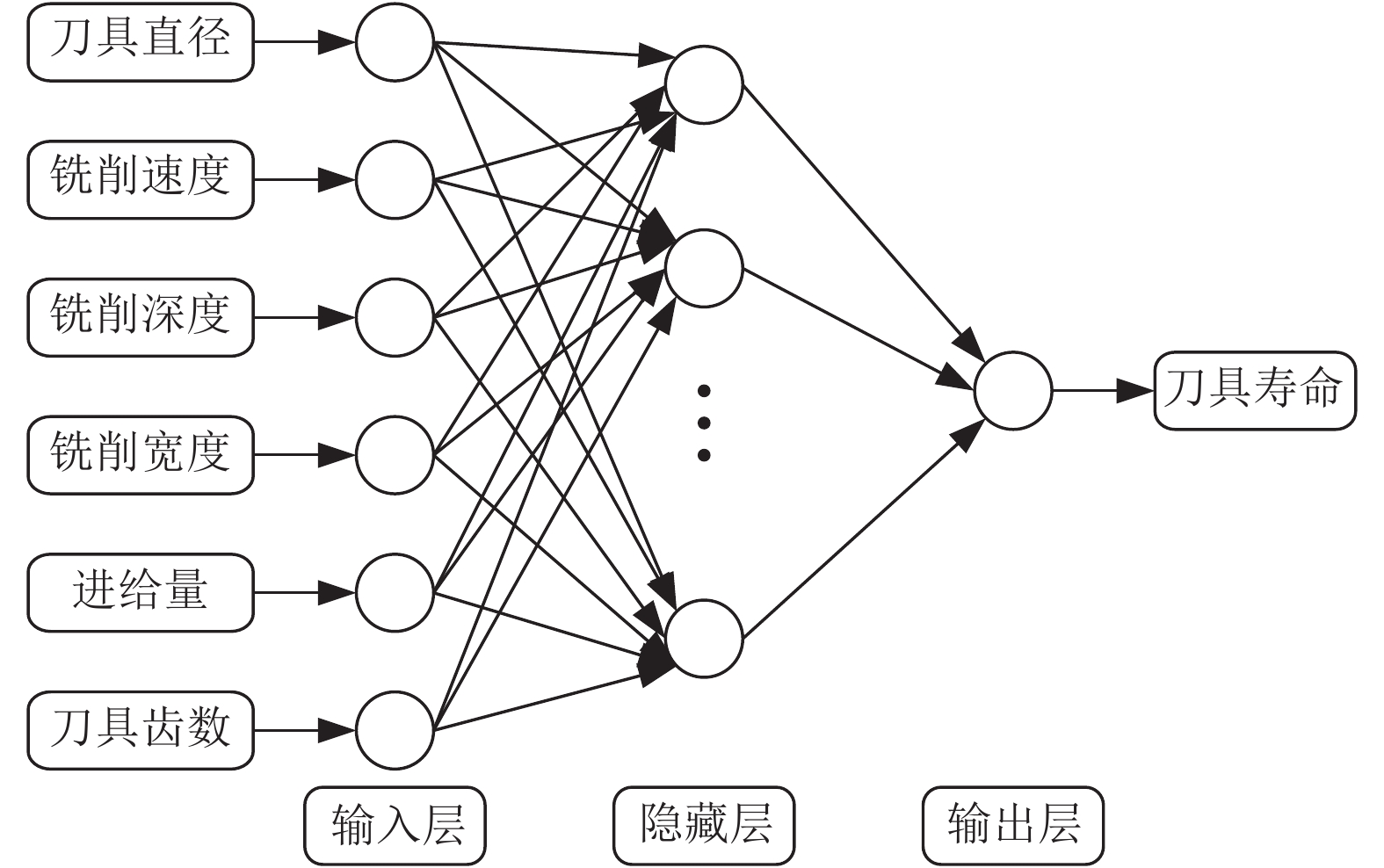
2.2 建立刀具寿命预测模型本文的刀具寿命预测模型是以RBF神经网络为基础建立的, 选择刀具直径、铣削速度、铣削深度、铣削宽度、进给量以及刀具齿数作为输入神经元, 刀具寿命作为输出神经元. 而对于隐含层, 则是采用PSO算法对径向基函数中心、宽度和连接权值进行合理确定, 目的是为了提高预测精度. 刀具寿命预测的神经网络模型如图3所示.
|
图 3 刀具寿命预测的神经网络模型 |
为了避免模型过于复杂, 图3所示的神经网络模型选择刀具直径、铣削速度、铣削深度、铣削宽度、进给量以及刀具齿数这6个主要因素作为输入神经元. 通过多次实验确定当隐含层神经元的个数为10个时, 模型的预测效果最好. 采用PSO算法优化RBF神经网络模型参数时, 经过反复地测试, 当PSO算法中的学习因子c1=c2=1.4945, 惯性因子w=0.2时, 模型的预测结果比较稳定, 而且更加接近真实值.
3 实验验证 3.1 实验环境以及条件本文使用Matlab 2018b实现PSO-RBF神经网络模型, 并进行实验, 同时所使用的系统参数如表1所示.
| 表 1 系统参数表 |
3.2 实验过程
实验选择文献[20]中的实验数据作为刀具寿命预测模型的原始数据, 以此来验证所提出模型的有效性. 实验样本选用的是硬质合金立铣刀, 加工材料为45钢, 加工方式和加工要求分别是为立铣和粗铣. 刀具寿命预测原始样本数据如表2所示.
| 表 2 刀具寿命预测原始样本数据 |
由样本数据可知, 刀具直径、铣削速度、铣削深度、铣削宽度、进给量以及刀具齿数的度量单位是不同的, 为了避免参数之间的纲量影响和提高模型精度, 实验前先将样本数据进行归一化处理, 计算方式如下所示:
| $ {x_{\text{scale}}} = \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} $ | (8) |
其中,xscale为归一化后的值, x为实际样本值, xmax和xmin分别为实际样本中的最大值以及最小值.
根据第1节和第2节所述, 在Matlab 2018b中搭建PSO-RBF神经网络模型, 然后将处理后的数据代入模型进行实验. 为了排除实验的随机性和偶然性, 采用的是十折交叉验证法, 具体来说就是原始样本数据有10组, 每次取其中的9组作为训练样本, 取剩下的1组作为测试样本, 总共进行10次实验. 同时, 为了验证PSO-RBF神经网络模型的预测性能, 本文也采用标准的RBF神经网络模型进行了实验, 并将两者的结果进行对比.
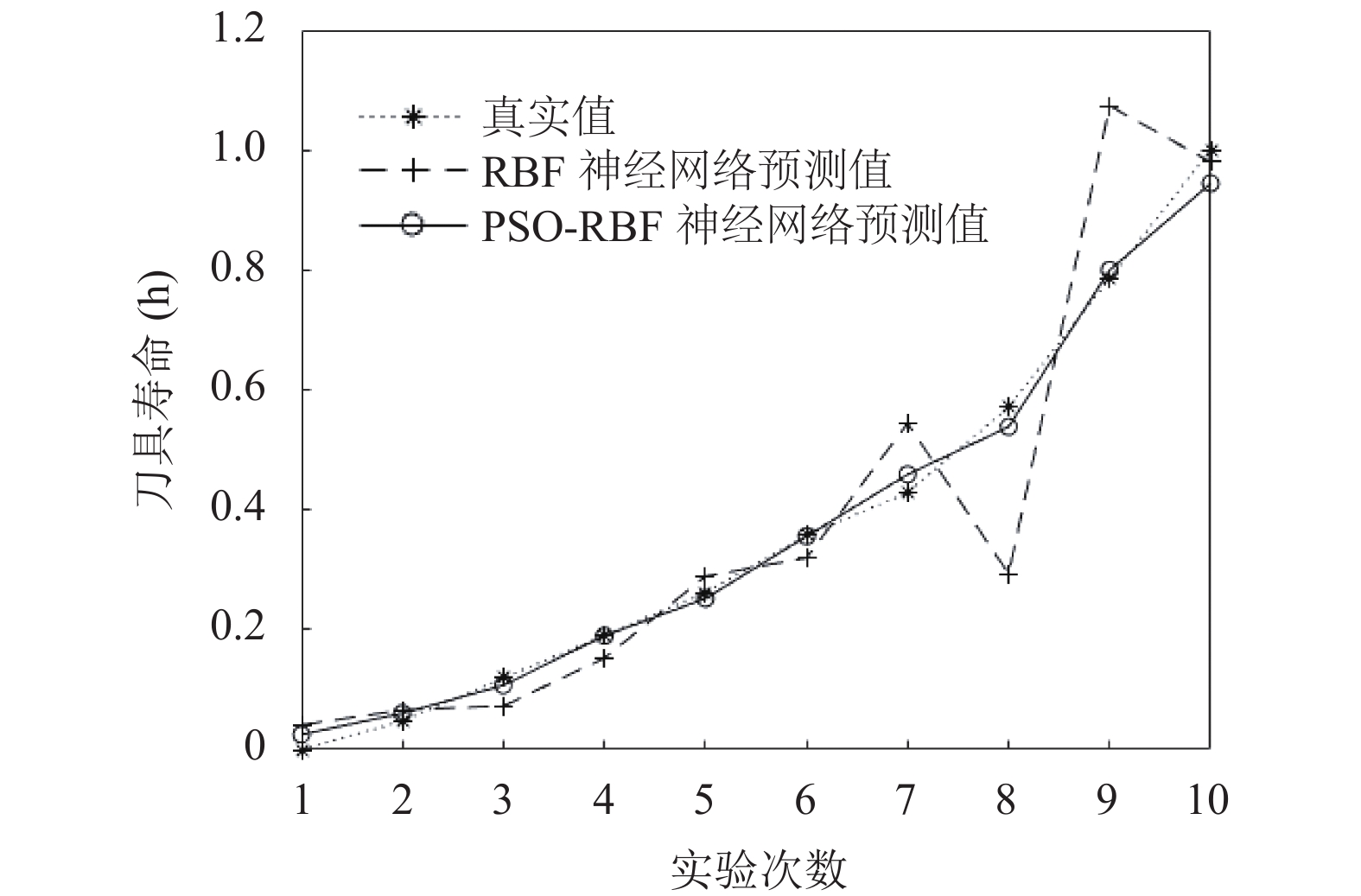
3.3 实验结果分析实验后两个模型的刀具寿命预测结果对比如图4所示.
|
图 4 刀具寿命预测结果对比 |
由图4的曲线拟合度可知, PSO-RBF神经网络模型要比RBF神经网络具有更高的预测精度和更好的预测效果.
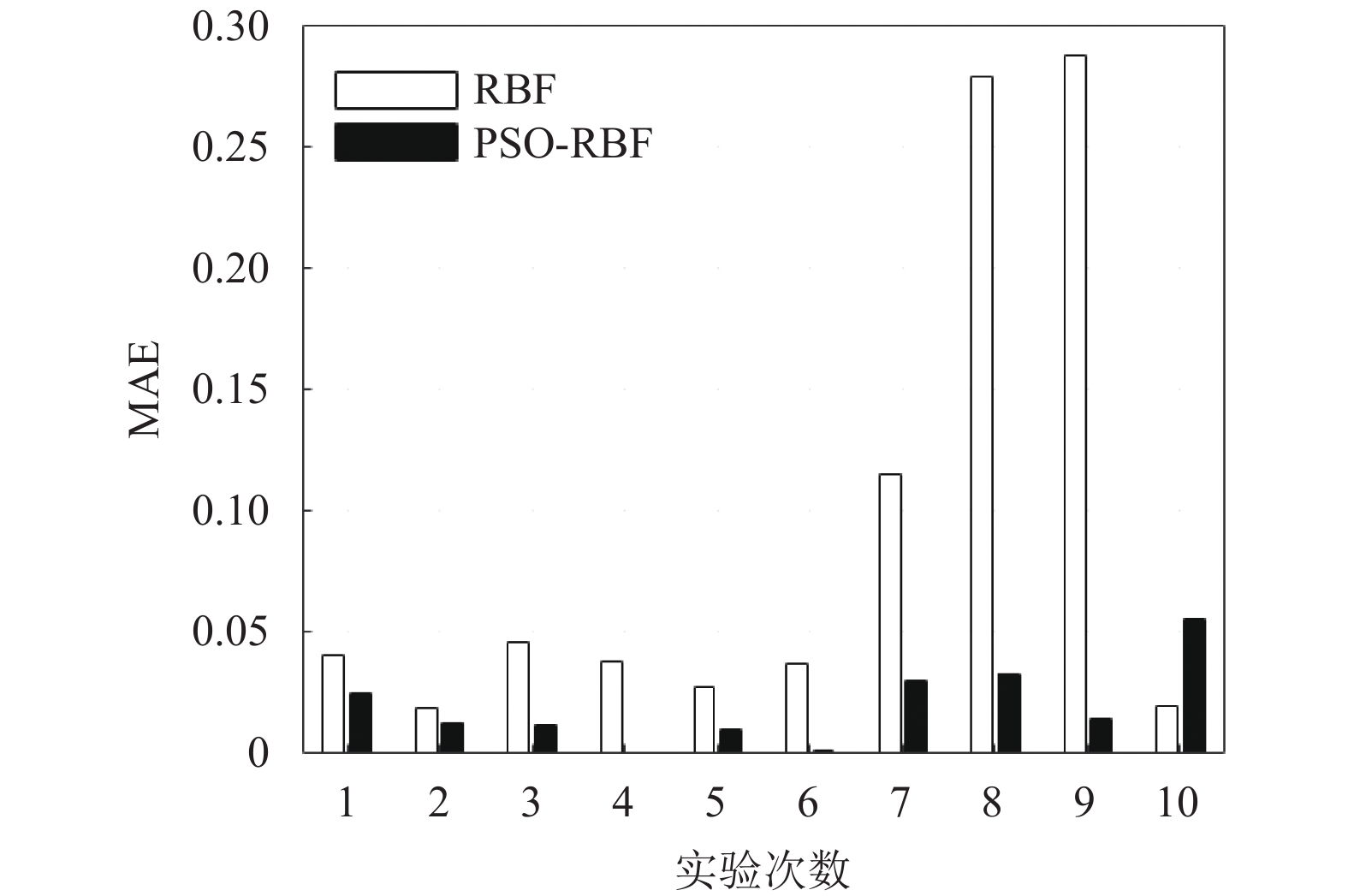
实验结束后, 计算每次实验预测值和刀具实际寿命之间的误差, 进而求得相对误差, 然后求10次实验的平均相对误差, 同时也计算每次实验的MAE (平均绝对误差)和MSE (均方误差), 也将其作为预测模型精度的评价标准. 两个模型的平均相对误差、MSE以及MAE的计算结果对比分别如图5、图6、图7所示.
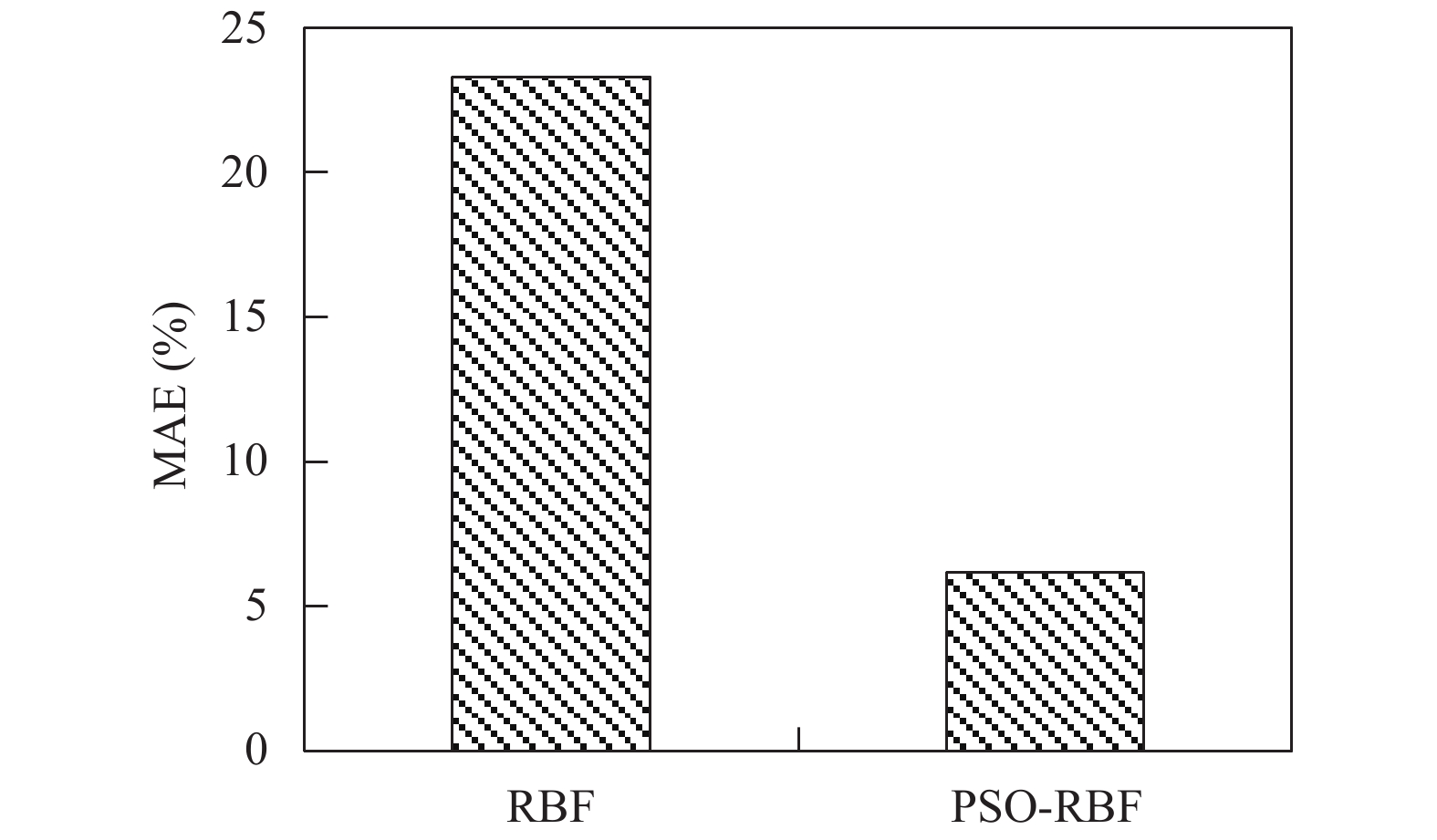
由图5可以看出, RBF神经网络的平均相对误差为23.30%, 而PSO-RBF神经网络模型的平均相对误差为6.16%, 后者比前者降低了17.14%. 由图6和图7可以看出, 在全部10次实验中, PSO-RBF神经网络模型预测结果的MSE均小于RBF神经网络模型, 同时PSO-RBF神经网络模型预测结果的MAE在9次实验中均小于RBF神经网络模型. 由此可见, PSO-RBF神经网络模型拥有更高的的预测精度, 而且预测的误差也更小, 能够获得很好的刀具寿命预测效果.
4 结论本文针对刀具寿命预测受到多种因素影响的特点, 建立了一种PSO-RBF神经网络预测模型, 并采用PSO算法对RBF神经网络的中心值c、宽度σ以及连接权值w进行了优化, 提高了模型的预测精度. 通过实验结果表明PSO-RBF神经网络模型预测结果的平均相对误差为6.16%, 比RBF神经网络模型的23.30%要低17.14%, 进一步验证了该神经网络模型的可行性.
|
图 5 MAE对比 |

|
图 6 MSE对比 |
|
图 7 MAE对比 |
| [1] |
王国锋, 董毅, 杨凯, 等. 基于深度学习与粒子滤波的刀具寿命预测. 天津大学学报(自然科学与工程技术版), 2019, 52(11): 1109-1116. DOI:10.11784/tdxbz201810024 |
| [2] |
Sun HB, Liu Y, Pan JL, et al. Enhancing cutting tool sustainability based on remaining useful life prediction. Journal of Cleaner Production, 2020, 244: 118794. DOI:10.1016/j.jclepro.2019.118794 |
| [3] |
Boing D, Castro FL, Schroeter RB. Prediction of PCBN tool life in hard turning process based on the three-dimensional tool wear parameter. The International Journal of Advanced Manufacturing Technology, 2020, 106(1–2): 779-790. DOI:10.1007/s00170-019-04509-0 |
| [4] |
丁怡, 何卫平, 张维, 等. 基于BP神经网络的刀具寿命预测模型. 航空制造技术, 2010(8): 93-96. DOI:10.16080/j.issn1671-833x.2010.08.019 |
| [5] |
侍红岩, 吴晓强, 张春友. 基于支持向量回归机的刀具寿命预测. 工具技术, 2015, 49(11): 47-50. DOI:10.16567/j.cnki.1000-7008.2015.11.018 |
| [6] |
Benkedjouh T, Medjaher K, Zerhouni N, et al. Health assessment and life prediction of cutting tools based on support vector regression. Journal of Intelligent Manufacturing, 2015, 26(2): 213-223. DOI:10.1007/s10845-013-0774-6 |
| [7] |
夏颖怡. 基于GA-BP神经网络的刀具寿命预测研究. 精密制造与自动化, 2017(2): 9-11. DOI:10.16371/j.cnki.issn1009-962x.2017.02.003 |
| [8] |
王虎, 刘佩松, 叶润章, 等. 基于PSO-BP神经网络的刀具寿命预测. 现代制造技术与装备, 2017(11): 53-54, 60. DOI:10.16107/j.cnki.mmte.2017.1064 |
| [9] |
Kovac P, Gostimirovic M, Rodic D, et al. Using the temperature method for the prediction of tool life in sustainable production. Measurement, 2019, 133: 320-327. DOI:10.1016/j.measurement.2018.09.074 |
| [10] |
曾晓雪, 吉卫喜, 徐杰. 基于CPSO-BP的刀具寿命预测算法. 组合机床与自动化加工技术, 2020(8): 57-59, 63. DOI:10.13462/j.cnki.mmtamt.2020.08.014 |
| [11] |
Hosseinkhani K, Ng EG. A unique methodology for tool life prediction in machining. Journal of Manufacturing and Materials Processing, 2020, 4(1): 16. DOI:10.3390/jmmp4010016 |
| [12] |
Guan XM, Fan FX, Zhu YR, et al. Application of RBF neural network optimized globally by genetic algorithm in intelligent color matching of wood dyeing. Journal of Intelligent & Fuzzy Systems, 2017, 33(5): 2895-2901. DOI:10.3233/JIFS-169340 |
| [13] |
张居设. 基于GA优化RBF神经网络的英语教学质量评价. 计算机系统应用, 2020, 29(3): 167-172. DOI:10.15888/j.cnki.csa.007302 |
| [14] |
Yang L, Chen HX. Fault diagnosis of gearbox based on RBF-PF and particle swarm optimization wavelet neural network. Neural Computing and Applications, 2019, 31(9): 4463-4478. DOI:10.1007/s00521-018-3525-y |
| [15] |
Dong J, Zhao YX, Liu C, et al. Orthogonal least squares based center selection for fault-tolerant RBF networks. Neurocomputing, 2019, 339: 217-231. DOI:10.1016/j.neucom.2019.02.039 |
| [16] |
杜秀丽, 周敏, 吕亚娜, 等. 基于RBF神经网络优化的装备保障系统效能评估. 计算机工程, 2021, 47(9): 282-287, 296. DOI:10.19678/j.issn.1000-3428.0058710 |
| [17] |
Kennedy J, Eberhart RC. Particle swarm optimization. IEEE International Conference on Neural Networks. 1995. 1942–1948.
|
| [18] |
高鹤元, 甘辉兵, 郑卓, 等. 粒子群优化神经网络在船舶辅锅炉故障诊断中的应用. 计算机应用与软件, 2020, 37(8): 137-141, 148. DOI:10.3969/j.issn.1000-386x.2020.08.024 |
| [19] |
薛宏. 企业级刀具全生命周期管理系统研发[硕士学位论文]. 重庆: 重庆大学, 2015.
|
| [20] |
李浩平, 欧阳俊, 谢雪媛. 基于AGA-GRNN神经网络的刀具寿命预测研究. 三峡大学学报(自然科学版), 2018, 40(6): 84-87. DOI:10.13393/j.cnki.issn.1672-948X.2018.06.019 |
 2022, Vol. 31
2022, Vol. 31



