自然环境的展现在许多应用中是必不可少的, 如地理信息系统^[1], 飞行模拟或视频游戏等. 地形是这些室外环境的关键部分, 其表示方式已在文献中得到广泛分析^[2,3]. 一些研究试图提取真实数据^[4], 但结果受到真实世界的限制, 无法总是能够获得所有真实数据来表示它们. 因此自动地形生成非常重要, 仍是一个活跃的研究领域. 利用Mandelbrot^[5], Prusinkiewicz等人^[6]提出的分形维数, 出现了许多研究, 这些研究主要使用过程建模来解决其创建过程的自动化^[7]. 这种建模方法已被用于表示许多与地形有关的特征, 包括道路、树木、村庄、城市景观^[8-10]等, 甚至用于表示大气现象^[11]. 根据Smelik等人^[12]的工作, 过程建模最初是基于细分过程, 其中高程图是迭代创建的, 为了创建高程, 在每次迭代中添加了受控量的随机性. 基于过程建模的第一个细分算法称为中点偏移方法^[13,14], 其中每次迭代都会生成一个新点, 该新点的高程是通过其邻居高程的平均值获得的, 并添加了随每次迭代而减小的随机位移. 许多其他研究, 主要是基于噪声发生器, 如Perlin方法^[15], 其中高程图是通过湍流函数获得的. Perlin噪声很快, 而且会创建均匀且随机的地形, 通常需要进行大量的后处理才能添加有趣的特征. 例如Parberry^[16]提出的一项工作, 它使用Perlin噪声的一种变体——值噪声, 根据从地理信息系统(geographic information system, GIS)数据中提取的高程数据的空间分析来生成典型的程序地形. 基于噪声发生器的方法的优点在于, 由于每个点都可以独立于其邻域进行计算, 因此计算成本较低.

在国内, 张润花等^[17]利用随机中点位移法绘制地形, 但由于算法随机性, 使网格细分的范围难以选择, 容易产生地形的失真现象; 李玉娟等^[18]利用基于数字高程模型(digital elevation model, DEM)的方法, 但该方法数据量较大, 绘制效率较低; 马海凤^[19]对 GeoMipMapping 算法进行改进, 利用LOD算法绘制地形, 在效率上有了提高, 但未考虑动态地形的情况; 郑顾平等^[20]利用WebGL 标准进行动态地形绘制, 是一种基于Web技术下动态调用OpenGL等图形库进行地形绘制, 但只是实现了几何剪切图算法.

综合对上述论文的研究, 本文利用改进的Perlin噪声算法生成高程图, 导入OpenCV库对图像信息进行读取, 采用网格生成算法生成模型数据, 地形模型以及贴图数据, 在OpenGL环境下生成仿真地形图像, 解决了随机中点位移法构建地形中产生的失真及仿真效果较差的问题. 并且优化了光照系统, 在保持其随机性, 低成本计算的同时, 使绘制出的地形网格图细节更为丰富, 成像效果更为真实.

1 Perlin噪声介绍

图形噪声, 是计算机图形学中一类伪随机算法, 经常用于模拟自然界中的各种纹理材质, 如云^[21]、波浪^[22]、水面^[23]、湍流^[24]、雪花^[25]、场景渲染^[26,27]等. 通过伪随机算法计算出的伪随机数是属于[0, 1]均匀分布的随机数序列, 并不真正的随机, 但具有类似于随机数的统计特征. Perlin^[15]在1985年的SIGGRAPH大会上首次提出Perlin函数. 后又在2001年, 提出了Simplex噪声算法来减小计算复杂度. 目前已经被广泛应用于计算机仿真领域及三维游戏制作中. Perilin噪声是一种基于晶格的梯度噪声, 随机数的创建过程包括定义晶格结构, 输入多维点坐标, 使用缓和曲线来计算他们的权重和3个过程. 以Perlin噪声为基础, 后续利用分形, 湍流等手段, 可以生成多种不同有趣的噪声图.

2 3D地形仿真的总体设计

本文主要通过Perlin噪声生成随机高程图, 以读取高程图单通道颜色值映射为地形高程图为主要思路, 形成三维地形网格图. 在构建三维地形网格图时, 选择以TRIANGLES方式^[28]绘制, 因此对于顶点数组的构造方式决定了程序处理的快慢. 假设地图大小为n×m, 以全顶点绘制需要构建(n–1)(m–1)×6个顶点, 而以索引方式来构建, 仅需n×m个顶点, 减小了约83%的内存占用率, 提高了运行效率. 在仿真视觉成效方面, 对不同高度的位置采用不同的贴图进行覆盖. 在贴图交界处, 以模糊函数进行叠加计算, 使过渡效果更加平滑. 光照效果往往能提高整体的视觉体验, 在最终成像结果中加入光照系统, 以提升对整体细节的优化. 总结各项工作, 形成总体流程图如图1所示.

3 3D地形仿真的生成

将3D地形生成仿真分为高程图的生成与改进、数据集生成、贴图策略设计与光照系统设计几个部分.

3.1 基于柏林噪声的高程图生成

假设要生成一个 $N\times N$ 的高程图, 首先使用式(1)与式(2)初始化索引表P与随机矩阵G. 式(1)中随机数赋值为0到N之间无重复任意值, 式(2)中随机矩阵用于对晶格进行赋值. 基于随机矩阵的做法, 与Perlin于2002年的改进算法^[29]相比, 在计算量方面有所增加, 但能够提高生成噪声图像的随机性.

$ P[2N] = [{i_0},{i_1}, \cdots, {i_{N - 1}},{i_0},{i_1}, \cdots, {i_{N - 1}}] $

(1)

其中, ${i_j}(j = 0,1,2,\cdots,N-1)$ 是0到N–1之间无重复随机整数.

$G[2N][3]{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{J_{0,0}}}&{{J_{0,1}}}&{{J_{0,2}}}\\ {{J_{1,0}}}&{{J_{1,1}}}&{{J_{1,2}}}\\ \cdots & \cdots & \cdots \\ {{J_{N-1,0}}}&{{J_{N-1,1}}}&{{J_{N-1,2}}}\\ {{J_{0,0}}}&{{J_{0,1}}}&{{J_{0,2}}}\\ {{J_{1,0}}}&{{J_{1,1}}}&{{J_{1,2}}}\\ \cdots & \cdots & \cdots \\ {{J_{N-1,0}}}&{{J_{N-1,1}}}&{{J_{N-1,2}}} \end{array}} \right] $

(2)

其中,

$ {J}_{p,q}=Random() {\text{%}}2N/N-1,p=0,1,2,\cdots, N-1, q = 0,1,2. $

如图2所示, 假设输入点 $ S(x,y,{\textit{z}}) $ , 通过该点可计算得到 ${S_1},{S_2}, \cdots, {S_8}$ , 共8个晶格值. 首先通过输入点 $ x $ 值, 计算 $ b{x_0},b{x_1},r{x_0},r{x_1} $ . 其中, $b{x_0} = {\rm{int}} (x){\text{%}} N,b{x_1} = $ $ ({\rm{int}} (x)\% N + 1)\% N$ , $r{x_0} = (x - {\rm {int}} (x)){\text{%}} N,r{x_1} = (x - {\rm{int}} (x)) $ $ {\text{%}} N - 1$ . 同理可得, $ b{y_0},b{y_1},r{y_0},r{y_1},b{{\textit{z}}_0},b{{\textit{z}}_1},r{{\textit{z}}_0},r{{\textit{z}}_1} $ .

结合索引表和随机矩阵, 计算出晶格各点的权重值.

$ \left[ {\begin{array}{*{20}{c}} {{{{u}}_0}}&{{v_0}} \\ {{{{u}}_1}}&{{v_1}} \\ {{{{u}}_2}}&{{v_2}} \\ {{{{u}}_3}}&{{v_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {G'[P[b{x_0} + b{y_0}] + b{{\textit{z}}_0}]\left[ {\begin{array}{*{20}{c}} {r{x_0}} \\ {r{y_0}} \\ {r{{\textit{z}}_0}} \end{array}} \right]}&{G'[P[b{x_1} + b{y_0}] + b{{\textit{z}}_0}]\left[ {\begin{array}{*{20}{c}} {r{x_1}} \\ {r{y_0}} \\ {r{{\textit{z}}_0}} \end{array}} \right]} \\ {G'[P[b{x_0} + b{y_1}] + b{{\textit{z}}_0}]\left[ {\begin{array}{*{20}{c}} {r{x_0}} \\ {r{y_1}} \\ {r{{\textit{z}}_0}} \end{array}} \right]}&{G'[P[b{x_1} + b{y_1}] + b{{\textit{z}}_0}]\left[ {\begin{array}{*{20}{c}} {r{x_1}} \\ {r{y_1}} \\ {r{{\textit{z}}_0}} \end{array}} \right]} \\ {G'[P[b{x_0} + b{y_0}] + b{{\textit{z}}_1}]\left[ {\begin{array}{*{20}{c}} {r{x_0}} \\ {r{y_0}} \\ {r{{\textit{z}}_1}} \end{array}} \right]}&{G'[P[b{x_1} + b{y_0}] + b{{\textit{z}}_1}]\left[ {\begin{array}{*{20}{c}} {r{x_1}} \\ {r{y_0}} \\ {r{{\textit{z}}_1}} \end{array}} \right]} \\ {G'[P[b{x_0} + b{y_1}] + b{{\textit{z}}_1}]\left[ {\begin{array}{*{20}{c}} {r{x_0}} \\ {r{y_1}} \\ {r{{\textit{z}}_1}} \end{array}} \right]}&{G'[P[b{x_1} + b{y_1}] + b{{\textit{z}}_1}]\left[ {\begin{array}{*{20}{c}} {r{x_1}} \\ {r{y_1}} \\ {r{{\textit{z}}_1}} \end{array}} \right]} \end{array}} \right] $

(3)

其中, $ G'[i] = \left[ {\begin{array}{*{20}{c}} {G[i][0]}&{G[i][1]}&{G[i][2]} \end{array}} \right] $ .

以Perlin光滑函数^[29]为权重函数(4), 以 $ r{x_0}, $ $ r{y_0},r{{\textit{z}}_0} $ 为参数, 计算得到 $ {\omega _x},{\omega _y},{\omega _{\textit{z}}} $ . 通过线性插值函数(5)及晶格点的权重值(3), 得到两个晶格点的线性插值, 如 $ {S_1} $ 与 $ {S_2} $ 的线性插值 $ {a_0} $ , 如式(6)所示. 同理可以得到插值 $ {b_0},{a_1},{b_1} $ , 如式(7)–式(9)所示. 最终再对4个插值 $ {a_0},{b_0},{a_1},{b_1} $ 再进行二次插值, 可得三维Perlin噪声函数, 如式(10)所示.

$ \omega (x) = 6{x^5} - 15{x^4} + 10{x^3} $

(4)

$ \begin{split}\\ Lerp(a,b,c) = (1 - a)\times b + a\times c \end{split} $

(5)

$ {a_0} = Lerp({\omega _x},{u_0},{v_0}) = (1 - {\omega _x}){u_0} + {\omega _x}{v_0} $

(6)

$\begin{split} \\ {b_0} = Lerp({\omega _x},{u_1},{v_1}) = (1 - {\omega _x}){u_1} + {\omega _x}{v_1} \end{split} $

(7)

$ {a_1} = Lerp({\omega _x},{u_2},{v_2}) = (1 - {\omega _x}){u_2} + {\omega _x}{v_2} $

(8)

$ {b_1} = Lerp({\omega _x},{u_3},{v_3}) = (1 - {\omega _x}){u_3} + {\omega _x}{v_3} $

(9)

$ \begin{split} &PerlinNoise(X,Y,Z) \\ &= (1 - {\omega _{\textit{z}}})Lerp({\omega _u},{a_0},{b_0}) + {\omega _{\textit{z}}}Lerp({\omega _y},{a_1},{b_1}) \\ & = (1 - {\omega _{\textit{z}}})((1 - {\omega _y}){a_0} + {\omega _y}{b_0}) + {\omega _{\textit{z}}}((1 - {\omega _y}){a_1} + {\omega _y}{b_1}) \end{split} $

(10)

以要生成 $N\times N$ 的高程图中的每个像素点的坐标为 $ x,y $ 坐标值, 以当前系统时间为z坐标值, 利用Perlin噪声函数(10), 计算图片中每个像素点对应的高度值, 可得基础高程图, 如图3所示, 其中取N = 1024.

3.2 高程图改进

经过经典Perlin噪声算法得到的高程图冲突效果较差, 可以利用分形(Fbm)与湍流(Turbulence)算法进行改进. 分形布朗运动算法主要对不同频率和振幅的噪声函数进行叠加, 如式(11)所示.

$ Fbm={\sum\limits _{i}^{}PerlinNoise(F_i\times \text{(}X,Y,Z\text{)})\times A_i} $

(11)

$ F_{i+1} = F_i\times L $

(12)

$ A_{i+1} = A_i\times G $

(13)

其中, A表示每一次噪声叠加的权值, F表示叠加噪声的比例, A与F的初始值为1. i为循环次数, 表示多张高程图的叠加效果, 通过测试, 令i为4可取得较好的效果. L和G表示每次迭代中修改A和F值的乘系数, 分别赋值为2与1/2, 使每次叠加的噪声权值和大小不同. 最终得到高程图如图4所示.

在利用Fmb进行改进的基础上, 运用式(14)进行Turbulence计算, Turbulence对噪声函数取绝对值, 使噪声值等于0处发生突变, 产生湍流纹理, 最终得到高程图如图5所示.

$ Turbulence={\sum\limits _{i}^{}\left|PerlinNoise(F_i\times \text{(}X,Y,Z\text{)})\right|}\times A_i $

(14)

其中, 字符含义与式(11)一致.

为验证算法的有效性, 在相同条件下, 与相晓嘉等^[30]提出的基于Perlin噪声的高分辨率地形仿真方法(PNB_HRTDS方法)进行比较, 结果如图6、图7、表1所示. 图6与图7分别是本文方法与PNB_HRTDS方法生成的大小为1024×1024的地形仿真图. 两图相比, 可以看出: PNB_HRTDS方法生成的地形仿真图的效果过于平整, 山体表面褶皱缺少, 山体之间的细节不够充分. 由表1可知, 在不同大小高程图中, 本文方法的高程值的均值有较大提升, 且标准差较大, 说明高程图中冲突效果明显, 山体的表现效果有所提升.

假设要生成 $n\times n$ 大小的高程图, 两种算法均需申请大小为 $ n $ 的float类型数组作为索引表P与大小为 $ 6n $ 的float类型数组作为随机矩阵G, 即需要 $ 7n $ 个float类型的存贮空间, 所以两种算法的空间复杂度为均 ${\rm O}({{n}})$ . 对于 $n\times n$ 大小的高程图中的每一点, PNB_HRTDS方法均需要调用Perlin噪声函数一次, 生成该点的高程, 所以其时间复杂度为 ${\rm O}({{{n}}^2})$ ; 本文方法生成一个点的高程需要调用4次Perlin噪声函数, 所以其时间复杂度也为 ${\rm O}({{{n}}^2})$ , 但实验生成时间要比PNB_HRTDS方法慢一点.

3.3 数据集生成 3.3.1 网格数据生成

通过OpenCV库, 对前述所生成的高程图以单通道模式进行读取, 存入图像信息矩阵 $ A $ 中. 以像素点颜色值映射为高度值, 生成方式如图8所示.

在图8中, ${\rm {Width}}{\text{、}}{\rm {Height}}$ 表示高程图的宽度与高度, $ {\rm {vertices}} $ 表示网格数组, $ I{\text{、}}J{\text{、}}K $ 表示宽高度与数组的递增索引, $ {A_{ij}} $ 表示高程图中读出的高度值, 此外还加入了 ${\rm {verticeScale}}{\text{、}}{\rm {yScale}}$ , 用于控制地图大小的缩放比例与地图高度的缩放比例.

在网格数组的基础上, 可以使用索引的方式, 优化网格数据结构, 加快运行效率, 建立与顶点数据对应的索引数组 $ {\rm {indices}} $ , 如图9所示, 字符含义与图8一致.

3.3.2 法线数据生成与优化

OpneGL以TRIANGLES方式绘制图形, 三角形是绘制的最小图元, 故可基于三角形的数据, 计算垂直于该平面的垂直向量. 一般情况下通过三角图元的各顶点位置信息单独计算, 如刘鹏程等^[31]进行的隧道仿真系统的研究与开发, 使用glNormal3fv () 函数进行法线计算. 在本文的计算方法中, 由于网格数组的优化, 同一顶点复用, 会产生单个顶点包含多个垂直向量问题. 本文以多次二分平均算法优化该问题, 使垂直单位向量变化更加平滑.

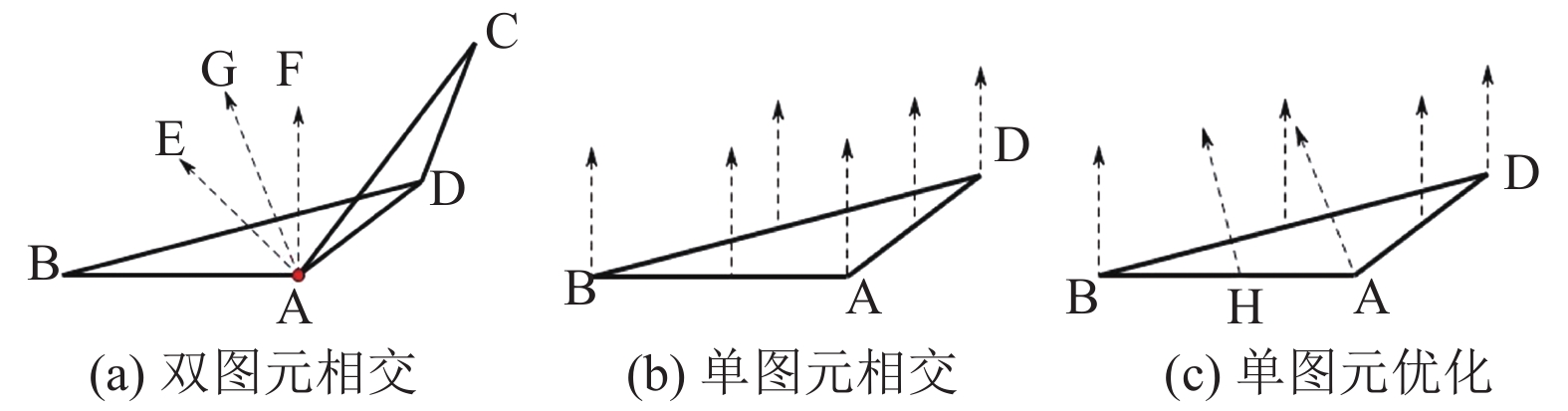
如图10(a)所示, 存在两个三角图元ABD与ACD, A、D两点处是索引情况下的复用点. 虚线AF是ABD图元中顶点A的法线, 虚线AE是ACD图元中A点的法线. 此处以A点为例, 由于A点是复用顶点, 只能存在唯一法线. 在不复用情况下, 每一顶点都属于唯一图元, 如图10(b)所示, 图元中任意处的法线都与顶点一致. 使用多次二分平均法处理后, 使用AE与AF的平分线AG作为A点的法线, 作为解决冲突的手段. 在顶点被多次复用的情况下, 进行多次二分即可. 在法线修正后, 如图10(c)所示, A点的法线由AF替换为AG, 从而AB线段中的位置, 也会依据比例进行调整, 如AB中点H, 法线的方向指向A点与B点法线方向的折中方向.

根据本文提出优化方案, 与刘鹏程等^[31]方案中使用glNormal3fv () 函数进行法线计算进行对比, 图11(a)为本文方案, 图11(b)为常规方案. 从图中可知, 在使用光照计算后, 在最小图元的交界处的左右两侧产生亮度的跳跃性变化. 而本文优化方案下, 不仅保持了光线的漫反射效果, 并且在山体光线的呈现上有更加圆滑的效果.

3.4 贴图策略设计

数据集构建完成后, 可以依照网格数组来生成三维地形的网格模型. 但单纯的模型只能反映山体的地形结构, 不能模拟真实的仿真效果. 因此可以通过三维纹理贴图方法增强仿真效果. 三维纹理贴图指将二维纹理图像张贴到三维模型的表面上, 从而得到逼真的三维图形的过程. 然而, 对于复杂三维模型的纹理贴图还没有找到直接贴图的方法^[32]. 通常情况下会使用一种适合场景的纹理进行贴图, 如图12所示, 但效果会显得较为单一. 本文依据对空间高度的划分, 使用雪、岩石、草坪3种图像进行分层采样. 将高度以一定比例划分为3个区域, 在该区域内, 使用对应的图像进行贴图: 如图13所示, 在红色框标示区域, 不同层次交界处有较强的截断感. 可以使用平滑函数在不同层次之间增加渐变层进行优化, 使效果更为平滑: 如图14所示, 红色框标示区域内, 渐变层的仿真效果更为真实, 整个山体的层次更加自然.

3.5 光照系统设计

现实世界的光照是极其复杂的, 而且会受到诸多因素的影响, 这是我们有限的计算能力所无法模拟的. 因此本文对光照使用冯氏光照模型(Phong lighting model)^[33]对整体进行光照添加. 冯氏光照模型的主要结构由3个分量组成: 环境(ambient)、漫反射(diffuse)和镜面(specular)光照. 环境分量主要取决于物体的颜色, 以一定亮度百分比进行模拟. 漫反射与镜面光照是产生光线效果的关键, 设计如图15展示. 在漫反射中, 如图15(a)所示, $ \stackrel{\rightharpoonup }{N} $ 是法向量, $ \stackrel{\rightharpoonup }{L} $ 是光源方向向量, 将两向量化为单位向量之后, 进行点乘运算, 得到0~1之间的数值A, 为了防止光线从后背穿过, 则取A与0之间的最大值, 该值表示漫反射的强弱程度, 越接近1, 则越接近物体原来的颜色. 在镜面反射中, 如图15(b)所示, $ \stackrel{\rightharpoonup }{N} $ 是法向量, $ \stackrel{\rightharpoonup }{L} $ 是光源方向向量, $ \stackrel{\rightharpoonup }{M} $ 是 $ \stackrel{\rightharpoonup }{L} $ 经过平面反射之后的射线, $ \stackrel{\rightharpoonup }{K} $ 为视线的方向向量. 将 $ \stackrel{\rightharpoonup }{M} $ 与 $ \stackrel{\rightharpoonup }{K} $ 化为单位向量之后, 进行点乘运算, 得到0~1之间的数值B, 其含义与A一致. 最终将物体色值的较低百分比如10%, 及A、B与色值的乘积相加, 得到物体最终在某一视角中应该呈现的颜色.

4 实验结果与分析

本文方法实现的硬件环境为: Intel(R) Core(TM) i7-7700HQ CPU @ 2.80 GHz, 16.00 GB内存, NVIDIA GeForce GTX 1050 Ti显卡, Win10 64位操作系统, Microsoft Visual Studio15编译器. 本文在通过Perlin噪音生成高程图的基础上, 构造了网格数组, 优化了法线计算. 实验程序的运行结果如图14、图16所示. 从图14中观察到, 在不同的高纬度, 有良好的渐变效果, 雪, 岩石, 草坪之间过渡的比较自然. 图16为光源置于图片右侧较高处, 模拟自然界阳光的照射情况, 可以看到山体背阳面有明显的阴影效果, 向阳面有明显的光照效果, 呈现出更贴近现实的仿真效果, 没有过于尖凸的现象出现, 而且山体表面褶皱也表现较好.

5 结束语

本文的工作主要是提出了一种基于OpenGL与Perlin噪声算法来生成不同的随机地形的方法. 在Perlin噪声函数的基础上, 以分形布朗运动为原型, 对噪声进行叠加, 再对冲突部分进行湍流的计算, 最终得到的高程图没有跳跃性与突变型, 显示了良好的效果. 此外, 该方法保持了Perlin噪声的随机性质, 每次运行都会产生不同的高程图. 通过解析高程图来获得点位的高度信息, 并且导入顶点数组中, 并以索引的方式减少了数据冗余和加快了渲染效率. 最后通过多次二分平均算法来计算法线, 结合贴图策略及光照系统完成了3D地形仿真的整体内容. 实验结果表明, 该方法能够创建完整的3D地形, 并且呈现出良好的仿真效果. 本文方法同样适应于火焰, 云朵等的仿真生成.