2. 中国科学院 国家空间科学中心, 北京 100190;
3. 中国科学院大学, 北京 100049
2. National Space Science Center, Chinese Academy of Sciences, Beijing 100190, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
卫星与载荷的运转异常往往不是一蹴而就的, 运转出现异常时, 往往伴随着相关参数的变化, 而这些信息可以通过卫星工程数据反映出来, 例如在近期某个时间段内电压持续偏高、温度持续偏高、姿态发生偏离等. 异常可能由载荷软硬件故障引起, 也可能由单粒子事件等空间环境因素引起, 还可能是由观测到异常目标或者引力波、伽玛暴等特殊空间事件引起. 及时识别数据异常, 并在此基础上挖掘分析出潜在的知识, 进而开展预测分析, 对于判断卫星与载荷健康状态、评估器件寿命、及时有效进行故障处置、快速发现特殊空间事件等都有重要的意义.
空间科学卫星的工程数据是卫星通过地面站传回的关于自身运转工作状态的遥测参数, 是地面数据处理系统判断卫星平台及载荷在轨运行健康状态的依据, 其异常检测是地面数据处理系统研究的重点技术, 是增强卫星在轨可靠性和安全运行的重要依据.
空间科学卫星的工程数据与其他所有类型航天器的工程数据具有通用的特点, 数量大、维度高、参数相关性复杂, 此外, 由于空间科学卫星搭载的有效载荷工作模式和科学实验具有高度的特殊性、多样性和创新性, 载荷的工程数据具有更强的专业性, 为高检测率、低误检率、强解释性的工程数据异常检测实现带来了严峻的挑战.
1 卫星异常检测方法综述在国内外的卫星数据处理领域, 异常检测的传统方法是统计学方法, 近十几年来人工智能方法也有广泛应用[1].
1.1 基于统计学的卫星异常检测方法基于统计学的卫星异常检测方法最常用的有阈值门限法、协方差分析和数据相关性分析. 工程数据的维度通常较为庞大, 一方面, 每个维度的卫星工程数据可以看作一条时间序列, 在统计计算过程中可将其看作一个向量, 通过分析各个维度参数变化趋势进行单通道或者多通道联合检测; 另一方面, 某些维度的参数可能具有相关性, 可使用多元回归分析法, 通过对每一个维度的参数构建多元非线性回归模型, 实现对多个参数之间的相关关系的深层次分析[2].
阈值门限法的优点是设定的阈值与载荷设计一致, 工程实现简单, 而且对于具有固定阈值的参数来说准确率是最高的, 但是也有明显的缺点: 适用范围仅限于可用阈值规则表达的参数, 然而很多类型的异常并不会引起变量的超限, 因此不能表征全部的异常类型, 对于某些参数正确率和某些参数的漏检率不能兼得; 不具备普遍适应性, 可扩展性差, 且当卫星载荷发生性能变化时, 需要不停地重新设定阈值来适应载荷的变化; 阈值有时候会出现设置不合理的情况, 阈值太宽容易发生漏检, 阈值太窄容易发生大量虚假报警, 导致真正的异常事件被埋没忽视[3].
协方差分析法是针对周期内变化趋势相同的数据来进行异常检测的, 通过参数之间的协方差构造卡方统计量, 在一定的置信水平上判断数据是否出现异常. 该方法的优点是可以有效地检测出周期性数据的异常, 但是对于周期时间长、数据量大的数据, 耗时较长, 且对于局部异常数据不敏感[4, 5].
相关性分析法是针对多个参数之间的相关关系建立的, 通过挖掘其相关系数或关联规则来判定数据是否异常. 该方法的优点是对卫星中存在相互影响的遥测数据有很好的检测效果, 排除了单一参数因素产生的误判漏判干扰, 但是对于一些参数同时发生变化的数据来说, 检测效果并不是很理想[6].
1.2 基于人工智能的卫星异常检测方法人工智能及计算机技术的飞速发展, 为卫星异常检测技术提供了新的理论基础, 产生了基于知识的智能诊断方法, 并显示出强大的生命力和优越性. 比较成熟的方法是专家系统, 其采用产生式规则来表示专家的知识, 较适合于复杂系统的分析, 在国际众多空间科学卫星任务中均有应用, 其局限在于准确且完备的专家知识、系统模型的构建很难通过自动化的方式实现, 人工知识获取与模型构建过程耗时、费力, 专家的知识来源也成为其诊断能力的瓶颈, 此外一旦航天器设计发生变化, 知识和模型往往需要推倒重建[7].
近年来, 一些新的研究都尝试利用机器学习算法进行卫星异常检测, 主要有聚类方法、神经网络算法、支持向量机算法和决策树算法等[8].
聚类算法有基于距离、基于密度、基于子空间等多种类型[9]. 例如, 典型的增量聚类算法是通过学习构建反映各参数之间关系的正常数据模型, 根据模型匹配返回的系统偏离值监测系统异常行为, 可以有效地检测出阈值检测方法中在阈值门限之内的异常, 避免漏判错判, 但是需要根据经验确定聚类的数量, 且对离散值比较敏感[10].
长短期记忆网络(long short-term memory, LSTM)是基于循环神经网络的改进算法, 输入门、输出门、遗忘门控制信息在神经元之间的信息传递, 通过迭代更新权重, 最终得到理想的输出值. LSTM相对于深度神经网络和循环神经网络来讲, 能更好的记忆其在过去长时间内的数据相关性, 适合处理序列数据, 但是对于一些在时间序列上相关性不是很强的遥测数据来说, 检测效果并不是很理想[11]. 另外, 网络层数规模往往需通过实验或经验值确定, 存在局部极值问题, 换一个载荷就需要重来一遍, 往往不具有扩展性和普适性.
支持向量机(support vector machine, SVM)算法将边际定义为决策边界和任何样本之间的最小距离, 基于最小二乘支持向量机(LS-SVM)定义最小二乘代价函数, 将二次规划问题转换成线性规划问题, 实现类内距离最小化、类间距离最大化, 具有良好的准确性, 但是由于通常结合主成分分析方法(principal component analysis, PCA)对数据进行预处理降维, 在处理非线性问题方面有局限性, 可能导致异常检测效果不明显[12].
梯度提升决策树(gradient boosting decision tree, GBDT)算法是以决策树为基函数的集成学习方法, 利用加法模型 (即基函数的线性组合) 和前向分布算法实现学习的优化过程, 通过将学习得到的多个树模型进行集成, 可以达到同时减少模型方差和偏差的效果, 而且具有对数据缺失值不敏感、模型易于构建、数据预处理要求低、速度快、效率高的优点, 同时可避免决策树算法的过拟合现象[13]. 目前GBDT算法在电力负荷预测[14]、电路故障诊断[15]、交通流量分析[16]、矿物识别[17]、航班延误分类预测[18]等领域, 均有成熟的应用研究实例, 显示出很好的应用潜力.
2 基于GBDT的卫星工程参数异常检测模型对于空间科学卫星异常检测这一复杂系统, 上文1.2节所述的机器学习方法普遍不够通用, 均需针对具体的样本特性与应用场景构建不同的模型, 在实现方面它们各有优缺点. 如何针对性提高检测的准确率和方法的通用性, 是空间科学卫星数据处理领域长期努力的研究焦点. 本文根据科学卫星的数据特性设计了基于GBDT的卫星异常检测分类模型, 在相对小的调参复杂度下实现了很高的检测准确率, 而且可以灵活处理包括连续值和离散值的各种类型的数据, 通用性更好.
2.1 异常类型分析本文基于量子科学实验卫星(空间科学先导专项系列卫星之一)的长管运行经验, 依据工程数据表现特征从总体上将异常类型归纳为6大类, 包括时间码异常、供电异常、实验控制机异常、星务异常、数传通信异常、测控与姿控异常.
(1) 时间码异常
卫星工程参数数据的时间码字段精确到日内秒, 用“年-月-日T时-分-秒”的格式表达. 时间码错误也为异常. 有的参数采样频率为1次/s, 故时间码逐条递增1 s, 如果有缺失、错误的时间码, 标记为异常. 有的参数为固定间隔采样, 那么设置采样间隔阈值来判定异常. 例如, 对于16 s采样一次的参数, 当其两个样本之间的间隔小于14或者大于18时判为异常. 时间与其他参数之间无相关性.
(2) 供电异常
平台与载荷的所有设备的与电源相关的工程参数, 包括电压、电流以及开关机状态等. 每个参数有自己的阈值, 不同设备的电压、电流阈值不相同, 阈值范围内短期变化剧烈或者长时间不变化均为异常, 同一设备的电流、电压、开关机标志位之间有相关性约束.
(3) 载荷与实验控制异常
各载荷(包括量子密钥通信机、量子纠缠发射机、量子纠缠源、高速相干通信机、载荷温控仪、实验控制机)的所有组成部分(例如通信板、实验板、存储板、电源板、相机等)的工程参数, 包括各种温度、复位计数、工作模式、看门狗屏蔽有效性、极化检测光开关状态、极化检测光档位、泵浦光驱动主备状态、PPS秒脉冲检测状态、各类遥测总线标识、数传数据处理状态、各类电阻、功率、事件表的各类事件数、软件状态、接收/发送帧计数、载荷指令的各类计数、随机数模式、密钥输出状态、量子通信状态、隐形测量状态、各类测量状态、GPS状态、GPS各方向计算角度、粗跟踪状态与角度、精跟踪状态与角度、同步光触发状态、各方向转速、各类单光子计数、各类符合计数、存储容量、存储坏块数、存储错误数、各相机的视场与质心、增益、校正、背景等.
每个参数有自己的阈值设置, 阈值范围内短时间剧烈变化或者长时间固定不动均为异常. 部分参数之间有相关性约束, 例如开关机不同状态下, 温度、电阻有所不同; 不同的工作模式下, 各种触发状态与测量状态有所不同.
(4) 星务异常
卫星平台的星务分系统的工程参数, 包括主控CPU标志、星务模式、星务状态、采集模式、采集状态、遥控模式、遥控状态、遥测模式、遥测状态、轨道模式、轨道状态、姿控模式、姿控状态、载荷模式、载荷状态、软件系统运行模式、进程加载状态等.
(5) 数传通信异常
卫星平台的数传分系统的工程参数, 包括Flash坏块计数、Flash存储错误计数、Flash擦除错误计数、数传CPU复位计数、EDAC纠错计数、数传EEPROM校验和等. 对于某些异常计数类的参数, 阈值内如果发生加1则为异常, 不变化或者一定时间后自动清零均为正常. 对于某些计数, 只要大于0即为异常. 有的参数为固定取值, 一旦出现其他取值即为异常. 部分参数之间有相关性约束.
(6) 测控与姿控异常
卫星平台的测控、姿控、热控分系统的工程参数, 包括单机状态、姿控模式、角度、角速度、轨道GPS、轨道速度、热敏及电阻温度等.
2.2 异常检测流程通过实验找到合适的拟合函数, 在训练得出基于工程数据的分类模型之后, 便可以使用模型对新接收到的工程数据进行分析判断. 正常工程数据预示着卫星有较低的异常风险, 用标签“0”标注; 异常工程数据预示着卫星有较高的异常风险, 用标签“1”标注. 那么可以将异常识别转化为一个分类问题. 检测分类的结果可以为卫星及载荷的异常及时发现与处置干预提供有力的支持.
GBDT是一种串联式模型, 每一层具有低方差高偏差特性, 结合后形成方差和偏差的调和, 使用CART回归树模型, 基于前向分布算法进行迭代计算. 基本思想是在损失函数负梯度的方向上生成若干棵弱回归树, 将这些树组合在一起生成一棵强回归树, 即最终的异常检测模型. 模型检测的时候, 对于输入的一个样本实例, 首先会赋予一个初值, 然后会迭代遍历每一棵决策树, 每棵树都会对预测值进行调整修正, 最后得到预测的结果.
在迭代过程中, 假设前一轮迭代得到的强学习器是
依据机器学习的“数据处理-模型训练-模型评估”标准流程, 结合GBDT算法特性, 依据卫星工程参数特征与异常分布情况, 设计了基于GBDT的卫星工程参数异常检测流程, 如图1所示. 首先选择量子科学实验卫星的工程数据的样本数据, 并对其进行预处理, 整合形成3类样本数据, 将离散变量转为one-hot编码. 之后, 构造出训练集与测试集, 如果已有数据已经覆盖所有异常类型, 则采取分层采样的方法获得训练集; 如果已有数据未覆盖所有异常类型, 需要为训练集插入人造的异常数据, 保证异常特征的覆盖性. 然后确定损失函数和算法模型评价指标, 利用训练集经过多轮弱决策树的遍历迭代生成强决策树, 获得GBDT卫星及载荷工程参数异常检测模型. 最后利用该模型对测试集进行检测, 发现异常并识别异常类型, 再对检测结果进行评价, 输出评价指标供验证分析.

|
图 1 基于GBDT的卫星工程参数异常检测流程图 |
(1) 数据预处理
分类器往往默认数据是连续并且有序的. 如果简单按照数字特征处理, 那么GBDT树学到的是一段一段的值域划分规则. 而属性离散数据值并不是有序的, 而是随机分配的. 本模型中, 将离散变量转为one-hot编码, 可解决分类器不好处理属性数据的问题, 同时在一定程度上也起到了扩充特征的作用.
卫星工程参数数据有很多属性特征采用了多位数字编码, 如“终端A机数据状态”这个特征有初态、发送、空闲、上行4种状态, 原本使用0、1、2、3表示, 使用one-hot编码表示为1000、0100、0010、0001, 每种状态扩充为4种特征来表示, 为后续实验中使用交叉熵损失函数奠定了基础.
(2) 特征参数的选取与优化
在使用卫星参数进行训练建模的环节中, 对于每一类数据, 使用网格搜索寻找最优参数, 调节的参数包括学习率learning_rate、集成的树的数目n_estimators、每棵树的最大深度max_depth等, 需要联合调参以获得最优性能. 为了减少由网格搜索带来的偶然性因素的影响, 采用K折交叉验证法来更加准确有效地评估该模型的泛化能力. 经过测试优化, 设置K值为10, 将数据集分成10等份, 使用其中9份数据作为训练数据, 另外1份数据作为测试数据, 进行模型的训练, 使用准确率作为度量测度来衡量模型的预测性能, 对10个验证结果取平均. 学习率的搜索范围为{0.1, 0.05, 0.01}, n_estimators的搜索范围为{5, 10, 20, 50, 100}, max_depth的搜索范围为{3, 5, 10}.
(3) 损失函数的选取
损失函数可以有多种选择, 比如平方损失函数、指数损失函数等, 其中交叉熵损失函数是分类问题的首选, 因为在分类问题上, 样本输出不是连续的值, 而是离散的类别, 导致我们无法直接从输出类别去拟合类别输出的误差, 而最小化交叉熵实际上等价于极大似然估计, 交叉熵损失函数更容易收敛到泛化能力强的地方. 它将多种类型的异常转化为多个二分类问题的联合, 针对第i类异常, 标签为
| $ - y\log (p) - (1 - y)\log (1 - p) = \log \left(\frac{1}{{1 - p}}\right) + y\log \left(\frac{{1 - p}}{p}\right) $ | (1) |
由于
| $ \log (1 - p) = \log \left(\frac{1}{{1 + {{\rm e}^P}}}\right) = - \log (1 + {{\rm e}^P}) $ | (2) |
| $设\log \left(\frac{p}{{1 - p}}\right) = \log ({{\rm e}^P}) = P $ | (3) |
综上, 二分类损失函数为:
| $ \log (1 + {{\rm e}^P}) - yP $ | (4) |
在量子科学实验卫星任务中原本采用的是“阈值+规则表达式”的卫星异常检测方法, 本文对基于GBDT的卫星异常检测方法与原传统方法二者进行了检测准确率和检测效率方面的比较. 实验所用数据资源由国家科技资源共享服务平台-国家空间科学数据中心提供, 计算资源由中国科学院国家空间科学中心公共技术服务中心提供.
3.1 实验数据本文选取了量子科学实验卫星的3大类工程数据, 合并组织为3类文件作为实验对象, 分别为载荷及实验控制机工程参数(1类样本)、星务/测控/姿控分系统工程参数(2类样本)和数传通信分系统工程参数(3类样本), 每一类样本数据可能存在多种异常.
样本数覆盖卫星在轨运行期间的两年时间, 从2017年1月1日到2018年12月31日. 一个文件包含一天内的数据样本, 每个样本包含几百个参数. 不同文件的采样率为1秒到几秒不等, 所以每个文件的样本数在到几千个到86400个之间, 3类文件总计样本接近八千万(8e+7)条数据, 详情如表1所示.
| 表 1 实验数据说明表 |
3.2 各样本种类的检测准确率
依据模型输出结果, 3类样本的平均准确率(AP, average precision), 即该类样本中分类正确的样本占全部样本的比例如下:
AP (1类样本)=98.11%
AP (2类样本)=98.15%
AP (3类样本)=99.62%
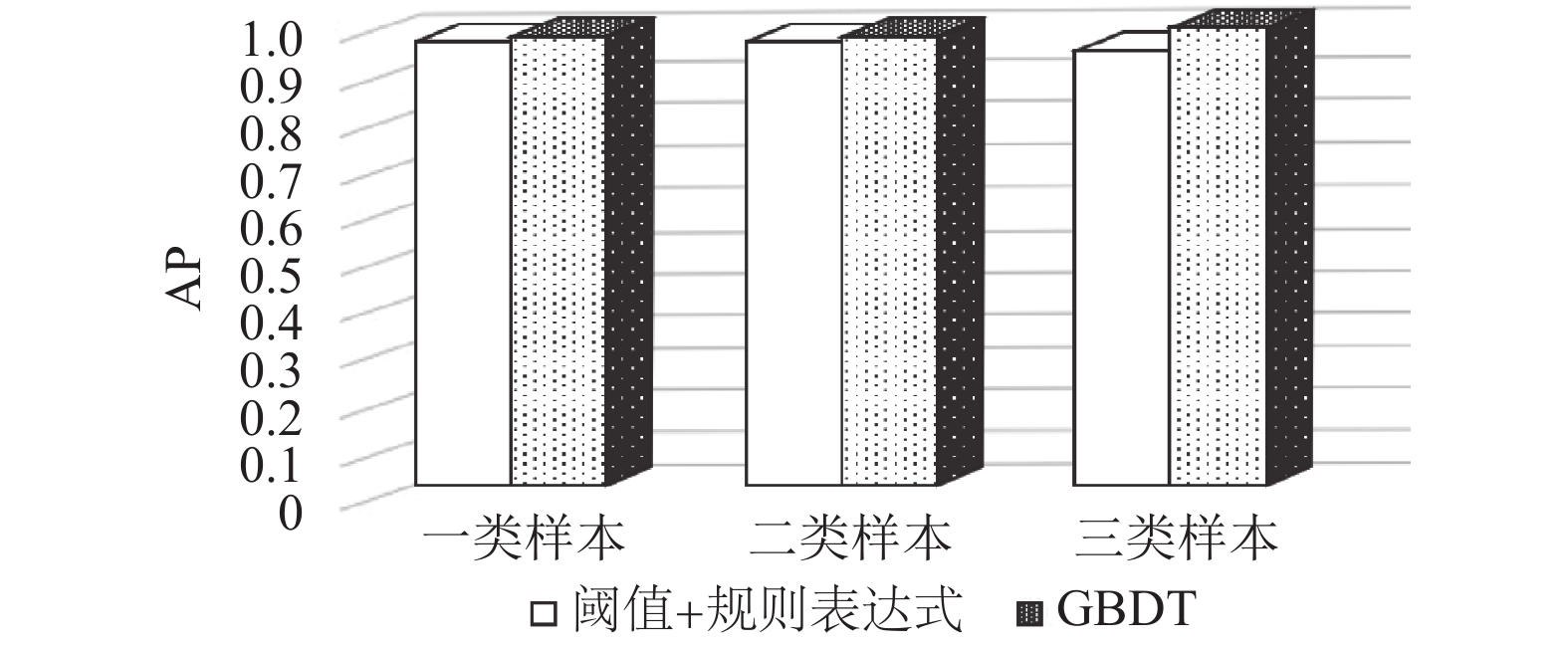
对于同一批实验样本, 使用“阈值+规则表达式”的异常检测方法进行处理, 平均准确率分别为: 96.48%, 96.93%, 94.87%, 如图2所示.
可见, 基于GBDT的卫星异常检测方法可提升平均准确率约两个百分点, 达到98%以上.
3.3 各异常种类的检测准确率在具体的3类样本中, 针对各异常类型绘制其P-R (Precision-Recall)曲线并计算平均准确率(AP), 以评价模型的分类检测效果.
P-R曲线刻画精确率(Precision, 即查准率)和召回率(Recall, 即查全率)之间的关系, 精确率是在所有预测为正例的数据中, 真正例所占的比例, 召回率是预测为真正例的数据占所有正例数据的比例, 将判断阈值从0逐渐调节至1, 即得到P-R曲线. 图3所示为本实验的第1类样本中3类异常各自的P-R曲线, x轴为召回率, y轴为精确率.
|
图 2 两种异常检测方法的平均准确率比较 |

|
图 3 第一类样本中的3类异常的P-R曲线 |
针对各类样本, 计算每一类异常的AP, 可以衡量GBDT学习得到的模型对每个类别的分类能力, 对所有类别异常的AP取平均值得到mAP (mean average precision), 可以衡量模型对所有类别的分类能力.
本实验的3类样本中各异常类型的AP及mAP结果如表2所示, 可见本模型对于不同的异常种类的检测效果都是非常好的.
3.4 检测效率在空间科学卫星任务中, 异常检测是在每次数传站接收数据之后进行的, 也就是针对每一轨接收的数据进行一次检测, 本文针对单轨接收数据进行了检测性能比对. 算法的运行环境为PC单机, Windows 7操作系统, Intel i5处理器@2.6 GHz, 8 GB内存. “阈值+规则表达式”的检测方法与GBDT的运行时间, 如图4所示.
| 表 2 分类检测效果评价表 |

|
图 4 两种异常检测方法的运行时间比较 |
使用基于GBDT的卫星工程参数异常检测方法, 单轨接收的3类样本的异常检测消耗时间分别为2.3 ms、38.6 ms、1.4 ms. 使用原本的“阈值+规则表达式”的卫星异常检测方法, 单轨接收的3类样本的异常检测消耗时间分别为17.6 ms、219.5 ms、11.0 ms. 可见, 采用基于GBDT的卫星异常检测方法使检测速度有了平均6倍以上的提升.
此外, 与深度网络这些计算密集型算法相比, 基于GBDT的卫星工程参数异常检测方法对运行内存等计算资源需求很小, 甚至可以在星载FPGA (field programmable gate array)上使用, 未来可以探讨放到卫星上面执行, 以支持在星上开展实时的工程数据异常分析与数据压缩下行.
4 结论与展望基于GBDT的卫星异常检测方法将多种类型的卫星异常转化为多个二分类问题的联合, 不仅能正确区分正常与异常两种状态的数据, 而且能够准确识别异常类型. 在特征参数的选取与优化过程中采用交叉验证的方式来减少偶然性, 避免了陷入局部极小值的问题. 通过对量子科学实验卫星在轨运行两年的真实工程数据进行验证, 与卫星任务中原本采用的“阈值+规则表达式”异常检测方法相比, 基于GBDT的卫星异常检测方法将平均准确率提升了约两个百分点, 达到98%以上, 并将检测速度提升了大约6倍, 可以更为高效、快速地开展卫星异常检测工作, 在空间科学卫星任务中产生了较大的应用价值. 目前的实验验证只覆盖了主要的异常类型, 后续工作中可针对其它异常类型进行扩展和细化, 以达到更好的异常分类检测效果, 并扩展应用到其他卫星的异常检测中.
| [1] |
彭喜元, 庞景月, 彭宇, 等. 航天器遥测数据异常检测综述. 仪器仪表学报, 2016, 37(9): 1929-1945. DOI:10.19650/j.cnki.cjsi.2016.09.002. |
| [2] |
Liu DT, Pang JY, Song G, et al. Fragment anomaly detection with prediction and statistical analysis for satellite telemetry. IEEE Access, 2017, 5: 19269-19281. DOI:10.1109/ACCESS.2017.2754447. |
| [3] |
杨甲森, 孟新, 陈托, 等. 基于遥测数据相关性的航天器异常检测. 仪器仪表学报, 2018, 39(8): 24-33. DOI:10.19650/j.cnki.cjsi.J1803444. |
| [4] |
Barreyre C, Cabon B, Boussouf L, et al. Detecting abnormal events in multivariate telemetries thanks to covariance analysis. Proceedings of the 2017 Conference on Big Data from Space. Toulouse, 2017. 118–121.
|
| [5] |
Schlag L, O’Meara C, Wickler M. Numerical analysis of automated anomaly detection algorithms for satellite telemetry. International Conference on Space Operations (SpaceOps) 2018. Marseille: AIAA, 2018.
|
| [6] |
Li LS, Hansman RJ, Palacios R, et al. Anomaly detection via a Gaussian Mixture Model for flight operation and safety monitoring. Transportation Research Part C: Emerging Technologies, 2016, 64: 45-57. DOI:10.1016/j.trc.2016.01.007 |
| [7] |
Fuertes S, Picart G, Tourneret JY, et al. Improving spacecraft health monitoring with automatic anomaly detection techniques. International Conference on Space Operations (SpaceOps) 2016. Daejeon: AIAA, 2016. [doi: 10.2514/6.2016-2430]
|
| [8] |
杨琼, 李国通, 冷佳醒, 等. 基于增量聚类的卫星异常遥测监测方法. 电子设计工程, 2018, 26(19): 6-10, 15. DOI:10.14022/j.cnki.dzsjgc.2018.19.002. |
| [9] |
Barreyre C, Boussouf L, Cabon B, et al. Statistical methods for outlier detection in space telemetries. International Conference on Space Operations (SpaceOps) 2018. Marseille: AIAA, 2018. [doi: 10.2514/6.2018-2533]
|
| [10] |
Yairi T, Takeishi N, Oda T, et al. A data-driven health monitoring method for satellite housekeeping data based on probabilistic clustering and dimensionality reduction. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(3): 1384-1401. DOI:10.1109/TAES.2017.2671247. |
| [11] |
Malhotra P, Vig L, Shroff G, et al. Long short term memory networks for anomaly detection in time series. Proceedings of the 23rd European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, ESANN 2015. Bruges: ESANN, 2015. 89–94.
|
| [12] |
Shawe-Taylor J, Žličar B. Novelty Detection with One-class Support Vector Machines. In: Morlini I, Minerva T, Vichi M, eds. Advances in Statistical Models for Data Analysis. Cham: Springer, 2015. 231–257.
|
| [13] |
王小乐, 张玉锋, 袁媛, 等. 基于决策树的卫星故障诊断知识挖掘方法. 电子设计工程, 2018, 26(3): 165-169. DOI:10.14022/j.cnki.dzsjgc.2018.03.037. |
| [14] |
王守相, 刘天宇. 计及用电模式的居民负荷梯度提升树分类识别方法. 电力系统及其自动化学报, 2017, 29(9): 27-33. DOI:10.3969/j.issn.1003-8930.2017.09.005. |
| [15] |
陈宏, 邓芳明, 吴翔, 等. 基于梯度提升决策树的电力电子电路故障诊断. 测控技术, 2017, 36(5): 9-12, 20. DOI:10.19708/j.ckjs.2017.05.003. |
| [16] |
陈俊刚. 基于梯度提升决策树的交通流量预测方法研究[硕士学位论文]. 重庆: 重庆邮电大学, 2017.
|
| [17] |
韩启迪, 张小桐, 申维. 基于梯度提升决策树(GBDT)算法的岩性识别技术. 矿物岩石地球化学通报, 2018, 37(6): 1173-1180. DOI:10.19658/j.issn.1007-2802.2019.38.009. |
| [18] |
刘金元, 丁勇, 李涛. 基于梯度提升决策树的航班延误分类预测. 数学的实践与认识, 2018, 48(4): 1-7. |
 2022, Vol. 31
2022, Vol. 31



