随着智能交通产业发展, 交通视频监控系统被广泛地应用于道路交通信息采集系统中[1, 2], 通过交通监控视频获得车辆的空间信息[3, 4]和行驶信息[5-7], 对于交管部门及交安部门获取交通信息和保障交通安全具有重要的实际意义. 弯道由于其特殊的道路线形特性, 是交通运输中事故易发路段之一, 因此弯道场景的道路空间信息获取是交通监控系统亟待解决的问题.
近年来, 计算机视觉技术大量应用于智能交通中, 相机标定的目的是建立二维平面信息与三维空间信息的映射关系, 是将图像信息转换到真实空间信息的重要环节. Kanhere等[8]基于单消失点和双消失点及道路已知前提信息实现对道路场景标定工作, 从而实现二维三维场景间的转换关系. 对于确定消失点位置, Dubská等[9]通过级联霍夫变换, 将各方向直线转换至钻石空间中进行投票, 获得较为稳定的消失点, López-Martinez等[10]提出一种基于边缘检测和TLBO算法获得方向互相正交的三个准确消失点, 并在检测消失点准确率和速度上找到平衡, Shi等[11]在非标准直道场景下对道路消失点进行提取, 并获得了较高的精度, 宋洪军等[12]在非结构化道路上, 未使用任何先验几何信息, 结合摄像机线性模型与均质雾天, 提出只包含路面以及运动车辆的标定方法, 但模型所需条件过于苛刻, 实用性有待提高. 对于实际高速公路场景, 由于其标准化的修建流程, 有很多先验知识可以使用, Sochor等[13]通过高速公路行驶的车辆所包含的已知信息, 实现了相机的自动标定工作, 并基于文中的标定结果进行了速度检测, 达到了一定的精度, 但车辆的相关模型获取并不容易, 因此存在局限性的问题, Song等[14]通过高速公路场景中的车辆三维包络, 对云台相机进行了自动标定, Zheng等[15]针对交通场景的特点, 提出了由两个消失点和一条消失线组成的最小标定条件, Bhardwaj[16]通过深度学习网络获得车辆关键点空间信息, 结合内参信息, 完成相机标定, 以上算法均能进行自动标定, 并获得了较好的精度.
上述方法均能求得较为准确的标定结果, 进而获得直线坐标系下的道路信息. 但对于真实世界下的道路场景, 通常为直道与弯道并存, 因此传统直线标定方法获取的道路坐标系不能准确描述实际道路信息, 进而无法对交通事件和交通运行状态进行准确分析. 因此本文提出一种基于道路线形的坐标系, 称为里程坐标系(mileage coordinate system, MCS), 简记为MC, 通过单目相机标定获得场景中弯道的线形信息, 进行的多项式拟合, 获得基于道路里程坐标系的交通信息, 如所在车道和里程信息. 相比于传统的世界坐标系, MC可以获得基于道路断面方向和道路线形方向的位置信息, 能够更精确描述道路空间位置, 可为交通管理部门提供更为真实的道路交通信息, 进而可以基于MC判断车辆运行状态和驾驶员行为, 并为全场景跨相机道路空间信息拼接[17]建奠定基础.
1 里程坐标系构建意义及流程 1.1 里程坐标系的构建意义在交通监控场景中, 道路交通信息提取通常是对单个相机进行标定并通过其获得空间映射关系, 进而获得场景中目标的位置信息和运动信息. 传统的相机模型中, 共定义3个右手坐标系: 图像坐标系、相机坐标系、世界坐标系. 图像坐标通过相机标定矩阵转换到传统的世界坐标系, 即从图像平面信息转换到实际三维场景下的空间信息. 以此建立的世界坐标是以监控相机正下方位置为基准的坐标系.
由于世界坐标系的固有特性限制, 世界坐标系仅能表示沿坐标轴方向的真实空间信息, 在弯道场景下, 难以获得车辆所处的车道信息、车辆基于道路断面准确的里程信息, 进而无法得到弯道场景下基于道路线形本身的位置信息, 且交通事故及交通瓶颈路段大多出现在弯道路段. 因此, 基于上述不足, 通过拟合获取弯道路段的道路线形信息, 本文提出基于道路线形的里程坐标系(MC), 如图1所示, 来描述弯道场景下道路及车辆信息. 通过引入道路线形信息, 构建基于道路线性的坐标系统. MC水平方向D轴, 通过计算点到拟合曲线的最短距离描述车道位置信息; MC垂直方向S轴, 通过计算道路上一点投影至道路线性拟合曲线对应点的弧长, 描述道路上一点在路段的道路断面的里程位置, 最终构成道路里程坐标系, 获得弯道下的位置信息. 并可以将MC作为基准, 进行跨相机的道路几何信息拼接融合, 获得全路段的运行信息.

|
图 1 世界坐标与MC空间结构示意图 |
1.2 里程坐标系的构建思路
根据相机模型转换关系, 基于道路线形的里程坐标系需要由世界坐标系转换而来, 若定义世界坐标系为P(x,y,z), 图像坐标系为p(u,v), 两者的映射关系可以通过式(1)表示:
| $ p = KRTP = HP $ | (1) |
其中, K代表相机的内参矩阵, R代表旋转矩阵, T代表相机的平移向量, KRT乘积的结果是一个3×4的矩阵, 将这个矩阵称为相机标定中的映射矩阵H. 基于此矩阵可以建立二维平面与三维空间的转换关系.
为构建道路里程坐标系, 首先需要通过上述相机模型及准确的相机参数, 获得可信的世界坐标信息, 并定义道路平面为世界坐标z=0的平面. 进而通过多项式拟合, 描述弯道线形, 最后可以通过几何关系获得道路上任何一点相对于道路断面的位置关系, 流程如图2所示.
2 基于道路线形的里程坐标系的构建 2.1 基于消失点模型的相机参数求解在道路场景中, 一般只能稳定获取单个消失点, 即沿车流方向的消失点(u0,v0). 本文选用基于VWL[8]的单消失点标定算法. 待求的未知参数为焦距f, 俯仰角ϕ, 偏航角θ和相机高度h. 在真实的高速公路场景中, 根据国标[18], 有如下已知条件: 车道物理宽度w, 车道线物理长度l. 对于道路交通场景下的消失点, 可由道路行车方向的车道线延伸方向等信息提供.
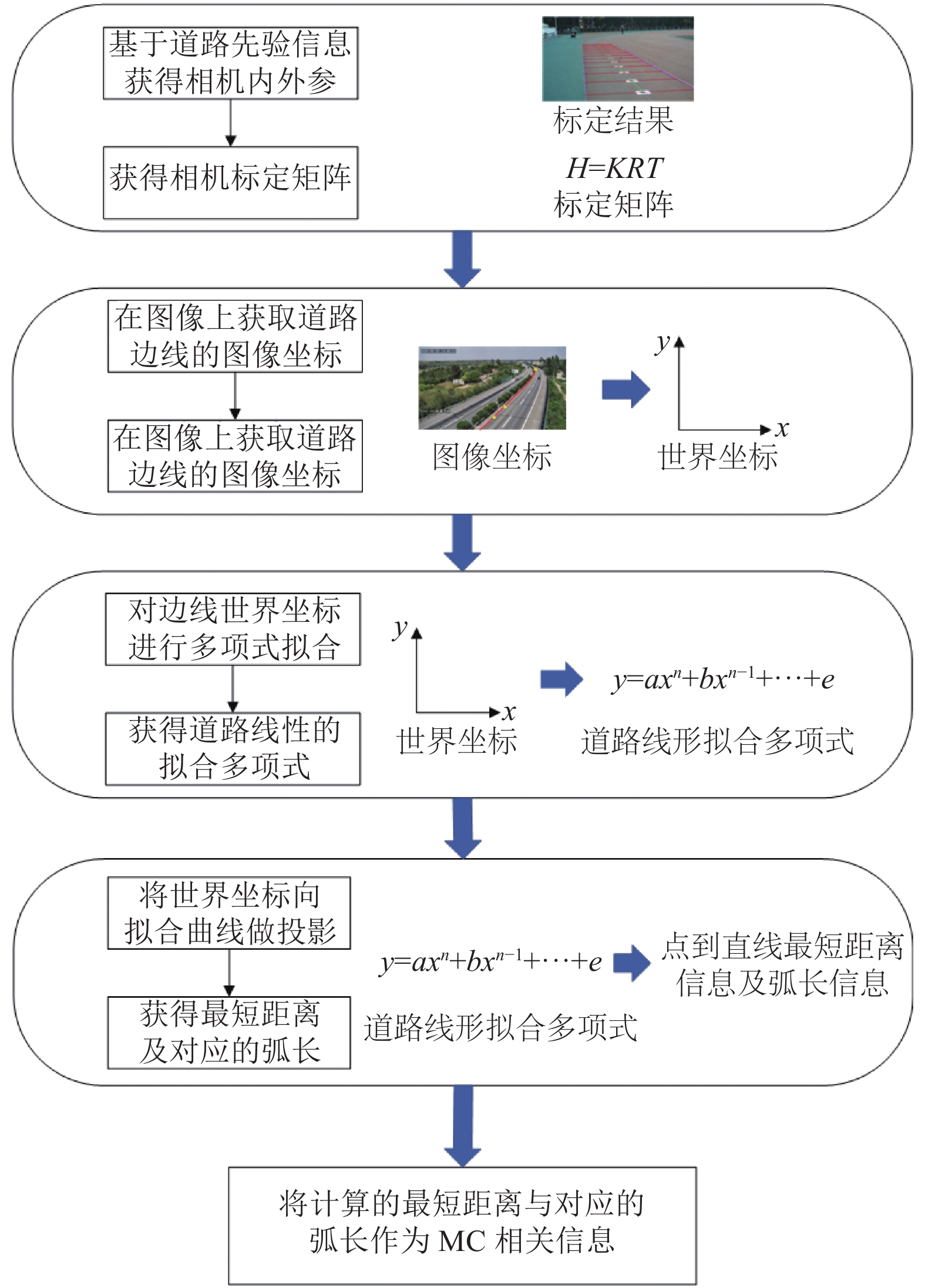
|
图 2 MC构建流程图 |
如图3所示, 在高速公路场景中, θ为相机光轴与道路延伸方向的夹角, ϕ为相机光轴与道路平面的夹角, 消失点的位置位于真实场景无穷远处. 道路的实际宽度为w, 对应图上距离为
| $ \theta = \arctan \left( - \frac{{{v_0}}}{f}\right) $ | (2) |
| $ \phi = \arctan \left(\frac{{{u_0}\cos \phi }}{f}\right) $ | (3) |
对于VWL模型[8]的求解, 需使用到道路已知信息, 根据道路标线的实际长度与图像坐标信息的对应关系, h可以通过式(4)、式(5)求解:
| $ h = \frac{{fw\sin \phi }}{{\delta \cos \theta }} $ | (4) |
| $ h = \frac{{f\tau l\cos \phi }}{{{f^2} + {v_0}^2}} $ | (5) |
其中,
根据所需的参数带入式(4)、式(5)中并联立, 可获得关于焦距f的四次方程:
| $ {f^4} + \left[ {2({u_0}^2 + {v_0}^2) - {k_v}^2} \right]{f^2} + {({u_0}^2 + {v_0}^2)^2} - {k_v}^2{v_0}^2 = 0 $ | (6) |
其中,
根据式(6)求出相机焦距f后, 即可求得相机外参θ、ϕ和h, 并建立起图像世界与真实世界的映射关系, 获得标定映射矩阵H.

|
图 3 交通场景下几何关系图 |
2.2 基于道路标线的相机参数优化
首次标定的结果存在误差, 为了减少由标定引起的基于道路线形的里程坐标系的构建误差, 需对结果进行优化, 本文提出一种通过计算误差的方式寻找对应的标定参数, 以获得最佳标定结果. 高速公路有着较为明显的车道标线, 相关约束可由道路标线实际距离构建, 设图像坐标通过矩阵H获得的世界坐标下的标线长度为Lcalib, 道路真实标线长度为Lreal , 道路虚线的两个端点经标定矩阵获得其世界坐标, 沿车辆行驶方向设置, 起点为Pn(xn,yn,0), 终点为Pn+1(xn+1,yn+1,0), 因此可设下一条道路虚线的起点坐标为Pn+2(xn+2,yn+2,0), 根据道路国标信息可知道路虚线长度Lreal为6 m, 各标线间隔距离Linterval为9 m, 因此存在沿道路方向误差项:
| $ {\Delta _1} = \sqrt {{{({y_{n + 1}} - {y_n})}^2} + {{({x_{n + 1}} - {x_n})}^2}} - {L_{\rm{real}}} $ | (7) |
| $ {\Delta _2} = \sqrt {{{({y_{n + 2}} - {y_n})}^2} + {{({x_{n + 2}} - {x_n})}^2}} - {L_{\rm{real}}} - {L_{{\text{interval}}}} $ | (8) |
高速公路道路宽度的约束由消失点与道路边界形成的道路区域构成, 可由道路虚线端点沿平行于世界坐标x轴正半轴与负半轴做标识线段, 与道路边线分别交于两点, 计算道路虚线端点到两点的距离, 其形成的道路宽度的值为
| $ {\Delta _3} = \left| {w - {\delta _n}} \right| $ | (9) |
因此本文将形成的3项误差进行加权处理, 根据选取约束的车道线端点数量进行累加求和, 则总误差以如式(10)表示:
| $ {\Delta }_{\text{total}}={ \sum \frac{1}{2}(0.5\left|{\Delta }_{1}\right|+0.5\left|{\Delta }_{2}\right|+\left|{\Delta }_{3}\right|)} $ | (10) |
根据式(2)、式(3)、式(4)及式(5), 焦距f的结果将会决定参数θ、ϕ和h, 因此基于初始标定获得的焦距, 在一段区间内, 进行误差计算, 获得整体误差最小时所对应的相机参数, 误差计算条件如下所示:
| $ \left\{\begin{array}{l}\mathrm{min}{\displaystyle \sum \dfrac{1}{2}(0.5\left|{\Delta }_{1}\right|+0.5\left|{\Delta }_{2}\right|+\left|{\Delta }_{3}\right|)}\\ {\rm {s.t.}} {f}_{1}\le f\le {f}_{2}\end{array}\right. $ | (11) |
其中, f1、f2为所设置求解空间的上限与下限.
2.3 基于相机参数的道路坐标系构建在平原地带, 高速公路的弯道最小平曲线半径为650 m, 可将曲线分为多条线段首尾依次连接组成, 并视线段为直线路段. 实际场景应用下, 由于相机可视角度的原因, 相机正下方存在短距离不可见范围, 因此可以假设在相机不可见的范围到场景中第一个标识点之间的路段为直线路段.
定义点集CLp, 设拟合得到的n次多项式为: f(x)=a0+a1x+a2x2+…+aNxn, 其存在点集CLp中各点到曲线拟合的平方误差, 基于此误差为最小的条件, 可求得拟合曲线的各项系数.
获得基于道路线形的拟合曲线f(x)后, 可重建道路上任意一点相对于道路的位置信息. 对于道路上的任何一点Proad_r(xr, yr, 0), 可以根据以下方法对其世界坐标进行重构, 进而获得MC信息, 所提出的具体算法步骤如算法1.
算法1. 基于道路线形的里程坐标系构建算法
Step 1. 根据不同场景的情况, 手动获取n个道路边线点或道路边缘点的世界坐标信息, 构成点集CLp ={p1,p2,p3,…,pn}, 根据表1中实际实验测试发现, 7次多项式附近变化幅度有较大变化, 在拟合高于7次的多项式后, 各指标变化幅度有较为明显的下降, 且7次多项式拟合结果能够较好的描述道路线形, 因此本文选用最高次为7次的多项式作为道路线形拟合曲线进行计算.
Step 2. 提取沿道路方向距离相机最近的待求标识点, 作为后续点求取弧长所用的积分起点, 并将此点的x值记为积分起点, 记作xstrat, 此点的y值记作ystart, 并作为S轴的初始距离, 避免因拟合位置不同造成的“内外圈”误差.
Step 3. 将Proad_r(xr, yr, 0)向拟合曲线做投影, 计算点到直线的欧式距离, 并记为Xmin, 作为道路断面方向的位置信息, 并得到点到直线最短距离所对应的拟合曲线上的点Pcurve=(xcurve, ycurve, 0).
Step 4. 将Proad_r(xr, yr, 0)所对应的曲线投影点Pcurve=(xcurve, ycurve, 0)的x值xcurve作为积分终点, xstart为积分起点, 根据微积分思想求取对应的弧长, Δx为求解时的步长, 弧长L解法如式(12)–式(14):
| $\qquad \qquad \qquad \qquad \scriptstyle {n_{\rm{int} }} = \frac{{\left| {{x_{{\text{curve}}}} - {x_{{\text{start}}}}} \right|}}{{\Delta x}} \qquad \qquad \qquad \qquad\; (12) $ |
| $\qquad \qquad \;\;\;\scriptstyle \left\{ \begin{array}{l} \scriptstyle \Delta {y_n} = f({x_{{\text{start}}}} + (n + 1)\Delta x) - f({x_{{\text{start}}}} + n\Delta x) \\ \scriptstyle {\text{s}}{\text{.t}}{\text{. }}n \in \left[ {0,{n_{\rm{int} }}} \right] \cap n \in Z \\ \end{array} \right. \qquad \qquad (13) $ |
| $\qquad \qquad \qquad \qquad \scriptstyle L = \sum\limits_{n = 0}^{{n_{{\text{int}}}} - 1} {\sqrt {\Delta {y_n}^2 + \Delta {x^2}} } \qquad \qquad \qquad \;\;\;\;\;\; (14) $ |
其中,
Step 5. 将计算获得的弧长L与初始距离ystart求和, 并记为Ls, 作为道路坐标系S轴上的值, 表示沿道路行车方向的里程距离.
Step 6. 通过算法获得道路上各点所对应的欧式距离Xmin与弧长Ls, 将Xmin作为道路坐标系的D轴上的值, 与对应道路坐标系S轴上的值构成新的位置信息点坐标.
| 表 1 多场景拟合多项式评价指标信息 |
将所有待求点完成上述步骤即可构建基于MC的位置信息.
3 实验分析本章基于构建的实验场景以及实际场景对本文提出的MC及其构建的弯道场景位置信息进行实验. 共使用8个场景对算法进行实验, 相关实验图像信息如表2所示, 相关实验场景如图4所示. 其中实验场景1与实验场景2为模拟实际道路的操场弯道场景, 可以通过测量获得准确的实际位置信息; 高速公路场景1至高速公路场景6为实际场景, 无法获得精确的数据, 数据参考国标[18]获得. 由于实际场景测量的不便性, 本文算法的精度由实验场景验证, 实际高速场景侧重于验证算法的可行性与合理性, 计算所得的坐标单位均为米.
| 表 2 场景信息 |

|
图 4 实验场景及实际场景示意图 |
场景中包含右弯与左弯, 且相机位置位于路测或道路中央隔离带, 周围环境及拍摄角度多样且复杂, 对算法的稳定性和算法精度有着很大的挑战.
3.1 实验场景MC构建实验为了验证本文算法精度, 使用上述2个实验场景进行实验, 实验场景选取标准的操场跑道, 经过实际测量获得以下数据: 操场跑道宽1.24 m, 人为设置的标定信息标识点沿跑道标线放置, 各标识点间隔均为1 m, 使用卷尺测量弯道的实际长度, 相机架设高度实测为1.4 m.
通过第2.1节中介绍的方法完成标定及其优化工作, 误差计算由跑道6个标志点对应的宽度(两条跑道宽度为2.48 m, 对应的6个点累计宽度为14.88 m)及标识点间隔(间隔1 m, 共5个累计为5 m)所累积的实际总长度为19.88 m进行评价. 当匹配所得的误差最小时, 确定相机的内参与外参, 标定结果误差由标定所得的标定矩阵计算所得与实际总长度的绝对值所得, 标定结果及相关误差如表3所示.
| 表 3 实验场景标定信息 |
通过表3及图5结果可知, 实验场景1中误差为0.7%, 实验场景2中误差为0.8%, 因此本文提出的标定优化算法具有一定的可行性和准确性, 并为下述的弯道重建提供了有效的支持.

|
图 5 实验场景标定结果 |
基于上述表3中的标定信息的标定矩阵, 对弯道场景进行拟合, 获得跑道线形信息, 并重置标识点位置. 在实验场景1中, 共在弯道处放置6个标识点, 每个标识点间隔3 m; 在实验场景2中, 为了区别场景1实验, 共放置9个标识点, 前4个标识点间隔均为3 m, 从第5个标识点开始间隔变化为4 m.
根据第2.3中提出的算法步骤进行空间信息构建, 此实验中误差由坐标系的两个方向的位置总误差累计所得, 实际世界坐标(x,u,0)转换后的MC数据及对应各位置的误差如表4、表5及图6所示.
| 表 4 实验场景1实验结果 |
| 表 5 实验场景2实验结果 |
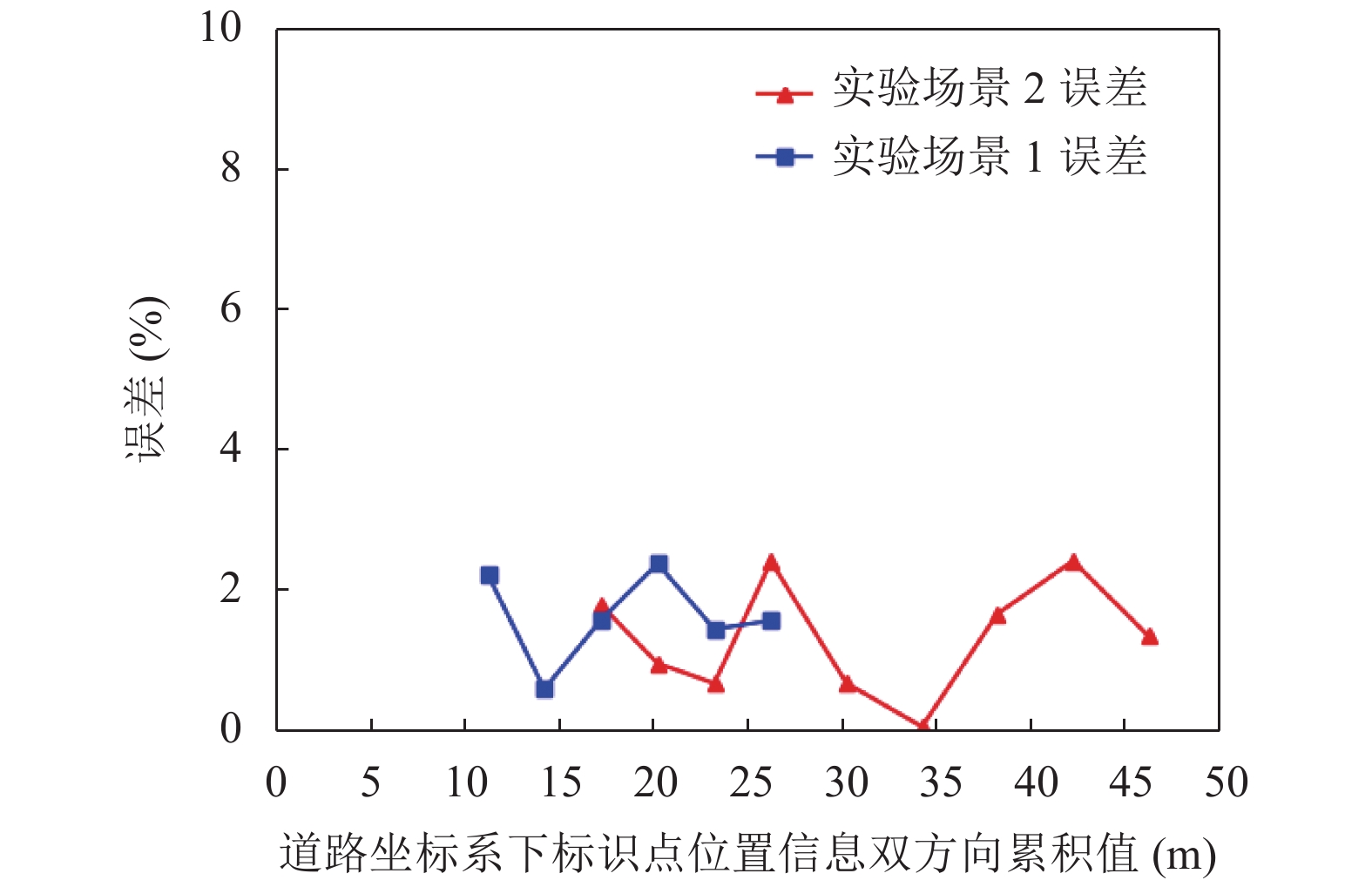
在实验场景下, 最大误差未超过3%. 实验场景1中的位置平均误差约为1.63%, 两个方向距离的平均偏差为0.306 m; 实验场景2中的位置平均误差约为1.33%, 两个方向距离的平均偏差为0.411 m. 误差主要来源于以下3点: 标定误差, 人工选取标识点误差及拟合误差. 结果表明, 标定算法和道路线形拟合算法能有效的重构道路断面位置信息与里程信息, 说明了本文提出的基于单目相机弯道重建算法的有效性与准确性.
3.2 实际场景MC构建实验为了验证实际场景中算法的可行性与相对精度, 使用上述6个实验场景进行实验, 由道路6个标志点对应的宽度(两条道路宽度为7.5 m, 对应的6个点累计宽度为45 m)及标识点间隔(共两个间隔和3条虚线组成, 累计36 m)所累积的实际总长度为81 m进行误差分析. 当匹配所得的误差最小时, 确定相机的内参与外参, 标定结果误差由标定所得的标定矩阵计算所得与实际总长度的绝对值所得, 标定结果及相关误差如表6、图7所示.
|
图 6 实验场景下位置信息误差 |
| 表 6 实际场景标定信息 |
实际场景标定中, 误差评价基于道路标志标线的国标进行描述, 采集3段虚线和虚线间的间隔, 误差计算方法与实验场景相同. 从误差中可见, 实际场景中出现的最大误差为4.9%, 平均误差约为1.64%, 存在较大误差波动的原因是因为部分弯道场景不存在连续的3条两两共线的虚线, 但在实验场景中, 本文提出的优化算法稳定性较高, 因此本文提出的标定优化算法具有一定的可行性和准确性, 并可以为下述的弯道重建提供了有效的支持.
基于表6中的标定信息获得矩阵, 对弯道场景进行拟合, 获得真实高速公路弯道线形信息, 并将虚线两端作为标识点, 共选取8条虚线16个标识点, 根据相机布设的位置不同, 选择一定数量的标识点进行实验, 相关距离均默认为国标: 虚线长6 m、间隔9 m.
根据第2.3节中提出的算法步骤, 高速公路场景1至4选取道路虚线位置信息进行实验, 高速公路场景5和6选取车辆位置信息进行实验, 车辆位置数据的获取方式使用YOLOv4[19]进行检测, 并通过KCF[20]获得车辆轨迹. 实际世界坐标、转换后的MC数据及对应各位置的误差如表7–表10和图8所示.

|
图 7 实际场景标定结果示意图 |
| 表 7 实际场景1实验结果 |
| 表 8 实际场景2实验结果 |
| 表 9 实际场景3实验结果 |
| 表 10 实际场景4实验结果 |

|
图 8 实际场景下位置信息误差分布 |
从实验中的4个场景所获得的结果观察到, 在150 m范围内, 各场景最大误差均未超过7%. 实际场景1的平均误差为1.262%; 实际场景2的平均误差为3.583%; 实际场景3的平均相对误差为1.163%; 实际场景4的平均相对误差为2.54%, 4个实际场景的平均误差为2.137%. 分析上述误差值, 场景2的平均误差要高于其他, 原因可能为实际场景3的弯道曲率较大, 因此拟合重建过程可能会放大误差. 该方案所测得场景的误差均小于10%, 因此该方案具有一定可行性及合理性.
为了获得实际车辆在高速公路场景下的实际位置信息, 本文选取高速公路实际场景5和6进行实验, 选取行驶在不同车道的车辆, 所获得的车辆轨迹点如图9所示, 所提出的方法能有效分辨车辆的车道信息及里程信息.
3.3 结果分析基于本文所提出的算法, 与传统直角坐标系所获得结果进行比较. 由于实验场景可以测量真实距离值, 因此使用实验场景数据进行对比分析, 对比结果如表11所示, 从表中可以得知, 本文方法可以对道路弯道场景进行位置重建, 且结合平均精度及稳定性分析, 可以较好的对道路线形进行拟合构建, 获得道路实际的位置信息.
4 结论与展望本文针对交通监控视频下的弯道场景提出了一种基于道路里程及位置信息的构建方法. 实验结果表明, 本文提出的基于道路线形的道路里程坐标系, 可获取弯道场景下基于道路断面及道路里程的真实信息, 克服了传统世界坐标系无法解决的弯道位置信息准确提取的问题; 本文所使用的相机参数获取方法及优化思路, 可适用于大多带有道路标志标线的场景, 为基于道路线形的里程坐标系构建提供有力支撑; 提高了交通监控应用场景的普适性, 通过里程坐标系可获得车道信息及道路里程信息, 其精度达到90%, 为弯道场景中车辆运行状态及位置信息获取提供了有效的解决方案.

|
图 9 MC下车辆轨迹结果示意图 |
| 表 11 实验场景结果分析 |
后期的研究将通过提取车道线等方式来实现道路信息的提取, 通过优化信息获取方式, 实现系统自动化.
| [1] |
Wan YW, Huang Y, Buckles B. Camera calibration and vehicle tracking: Highway traffic video analytics. Transportation Research Part C: Emerging Technologies, 2014, 44: 202-213. DOI:10.1016/j.trc.2014.02.018 |
| [2] |
赖见辉, 王扬, 罗甜甜, 等. 基于YOLO_V3的侧视视频交通流量统计方法与验证. 公路交通科技, 2021, 38(1): 135-142. DOI:10.3969/j.issn.1002-0268.2021.01.017 |
| [3] |
王伟, 唐心瑶, 宋焕生, 等. 单目视觉下基于三维目标检测的车型识别方法综述. 小型微型计算机系统, 2020, 41(6): 1274-1280. DOI:10.3969/j.issn.1000-1220.2020.06.027 |
| [4] |
Zhang DM, Fang B, Yang WB, et al. Robust inverse perspective mapping based on vanishing point. Proceedings 2014 IEEE International Conference on Security, Pattern Analysis, and Cybernetics (SPAC). Wuhan: IEEE, 2014. 458–463.
|
| [5] |
许燕霞, 杨鸣. 基于地面参考系的视频测速方法. 激光杂志, 2017, 38(11): 97-101. |
| [6] |
巨志勇, 王超男, 何晓蕾. 视频图像的车辆速度实时检测算法研究. 计算机应用研究, 2017, 34(9): 2822-2824, 2853. DOI:10.3969/j.issn.1001-3695.2017.09.057 |
| [7] |
武非凡, 宋焕生, 戴喆, 等. 交通监控场景下的相机标定与车辆速度测量. 计算机应用研究, 2020, 37(8): 2417-2421. |
| [8] |
Kanhere NK, Birchfield ST. A taxonomy and analysis of camera calibration methods for traffic monitoring applications. IEEE Transactions on Intelligent Transportation Systems, 2010, 11(2): 441-452. DOI:10.1109/TITS.2010.2045500 |
| [9] |
Dubská M, Herout A. Real projective plane mapping for detection of orthogonal vanishing points. Proceedings of the 24th British Machine Vision Conference. London: BMVA Press, 2013. 1–10.
|
| [10] |
López-Martinez A, Cuevas FJ. Vanishing point detection using the teaching learning-based optimisation algorithm. IET Image Processing, 2020, 14(11): 2487-2494. DOI:10.1049/iet-ipr.2019.0516 |
| [11] |
Shi JJ, Wang JX, Fu FF. Fast and robust vanishing point detection for unstructured road following. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(4): 970-979. DOI:10.1109/TITS.2015.2490556 |
| [12] |
宋洪军, 陈阳舟, 郜园园. 非结构化道路中基于均质雾天的摄像机动态标定算法. 计算机辅助设计与图形学学报, 2013, 25(7): 1060-1073. DOI:10.3969/j.issn.1003-9775.2013.07.017 |
| [13] |
Sochor J, Juránek R, Herout A. Traffic surveillance camera calibration by 3D model bounding box alignment for accurate vehicle speed measurement. Computer Vision and Image Understanding, 2017, 161: 87-98. DOI:10.1016/j.cviu.2017.05.015 |
| [14] |
Song HS, Li C, Wu FF, et al. 3D vehicle model-based PTZ camera auto-calibration for smart global village. Sustainable Cities and Society, 2019, 46: 101401. DOI:10.1016/j.scs.2018.12.029 |
| [15] |
Zheng Y, Peng SL. A practical roadside camera calibration method based on least squares optimization. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(2): 831-843. DOI:10.1109/TITS.2013.2288353 |
| [16] |
Bhardwaj R, Tummala GK, Ramalingam G, et al. AutoCalib: Automatic traffic camera calibration at scale. ACM Transactions on Sensor Networks, 2018, 14(3–4): 1-27. |
| [17] |
武非凡, 梁浩翔, 宋焕生, 等. 基于相机标定的跨相机场景拼接方法. 计算机系统应用, 2020, 29(1): 176-183. DOI:10.15888/j.cnki.csa.007210 |
| [18] |
中华人民共和国交通运输部. JTG D82-2009 公路交通标志和标线设置规范. 北京: 人民交通出版社, 2009.
|
| [19] |
Bochkovskiy A, Wang CY, Liao HYM. YOLOv4: Optimal speed and accuracy of object detection. arXiv: 2004.10934, 2020.
|
| [20] |
Henriques JF, Caseiro R, Martins P, et al. High-speed tracking with kernelized correlation filters. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596. DOI:10.1109/TPAMI.2014.2345390 |
 2022, Vol. 31
2022, Vol. 31



