2. 合芯科技有限公司, 广州 511365
2. He Xin Technology Co. Ltd., Guangzhou 511365, China
随着人民生活水准的提高, 休闲广场等大型公众区域成为服务人民休闲娱乐的重要场所, 具有服务对象复杂, 承载人群密度高等特点[1]. 我国早已将公共场所突发情况下的人群疏散管理研究作为重点研究项目, 国务院于2006年, 发布《国家中长期科学和技术发展规划纲要》就将“突发公共事件防范与快速处置”列入其中. 即便如此, 据不完全统计, 全球每年因人群聚集而引发踩踏等事故造成人员伤亡的数量还在急剧增加. 例如, 2014年12月31日, 上海外滩广场聚集了一大批因跨年活动而自发到来的人群, 由于疏散管理不到位, 引发大规模人群踩踏事故, 造成近百人伤亡. 成为近些年来, 我国最严重的自发性人群聚集公共安全事故. 苏州市金鸡湖城市广场结合苏州中心商场成为苏州的地标建筑[2], 该广场占地约12000 m2, 2020年国庆期间, 瞬时峰值人数突破120000人次, 密度峰值超过每百平600人次, 一旦发生紧急情况, 将会对人民的生命安全和财产损失产生巨大的影响. 因此, 以金鸡湖城市广场为例, 研究公众开放场所对人群疏散的影响具有指导意义.
目前, 国内外学者对大型公众场所突发情况下的人群疏散进行了大量研究. 其中, 晋良海通过分析建筑空间布局的构成要素, 构建公共建筑疏散空间的拓扑网络, 分析得出疏散路径的人群负荷加载状态对疏散效率的影响[3]. Yang等利用Pathfinder软件仿真模拟和分析得出了地铁站内部障碍物对人群疏散的影响[4]. Helbing等将体育场抽象成分层网络, 分析人员疏散由内向外, 由中心向四周疏散的特点, 确定到安全区域的最佳疏散路线以提高应急疏散效率[5]. 王海红等基于分层和强化学习改进路径搜索算法, 通过合理的减小网络规模, 保证算法求解精度的同时, 改进了算法的效率[6]. 巩青歌等通过分析已有的元胞自动机理论基础, 改进从众吸引力算法, 简化复杂空间欧氏距离算法, 从而提高危险排斥力和出口吸引力的量化效率[7]. 内蒙古工业大学的杨文举等应用元宝自动机和人工智能原理模拟人员的疏散, 分析人群密度达到一定阈值时群体运动的规律, 得出分块划分与出口“群体运动模拟”可以保证疏散的有效性[8].
以上研究都是改进路径规划算法的求解精度和求解速度, 本文将安全出口通行能力因素作为路径规划算法的影响参数, 在路径规划初期就将安全出口条件考虑在内, 实时动态调节分配人群到不同的安全出口, 并且以所有人员最终撤离危险区域时间为算法评估参数, 从而获得最优的人群疏散解. 使用Pathfinder软件仿真, 对比自然疏散条件和传统Dijkstra算法疏散条件的人群疏散结果, 验证改进算法的有效性.
2 现代化广场人群疏散问题的描述及分析 2.1 现代化广场人群疏散问题的描述现代化广场成为城市居民和农村居民的重要休闲娱乐场所. 一般广场具有占地面积大, 出口位置不固定等特点, 从而导致广场中心区域到安全出口距离大的问题. 同时现代化广场, 具有特定时间人群聚集性特点, 特定时段人群数量陡增, 成员复杂, 人群密度高, 因此将现代化广场作为典型的大型公众区域紧急疏散研究对象.
2.2 影响人群疏散的主要因素分析(1)人群与出口距离
现代化广场中心游玩区域距离各出口距离较远. 各游玩区域距离各个出口的距离不一致, 人群与出口的疏散距离成为影响疏散用时的主要因素. 游玩区域和出口区域的距离直接影响到路径疏散中人群出口的选择以及人群奔向出口的耗时.
(2)安全出口通行能力
现代化广场一般具有多个安全出口, 由于各出口的宽度不同, 导致其通行能力具有一定差异, 一定程度造成出口处的人群聚集问题, 直接影响到广场人群的疏散效率.
传统Dijkstra算法以两节点间距离为权值参数, 利用贪心法则遍历所有节点, 最终获取起点和终点的最短距离路径. 本文以传统Dijkstra算法为基础, 首先利用距离参数获取起点与终点的所有路径集合并且排序, 然后引入安全出口通行能力参数, 重新对节点人群科学合理分配至各出口. 最终获取疏散时间更短的规划路径.
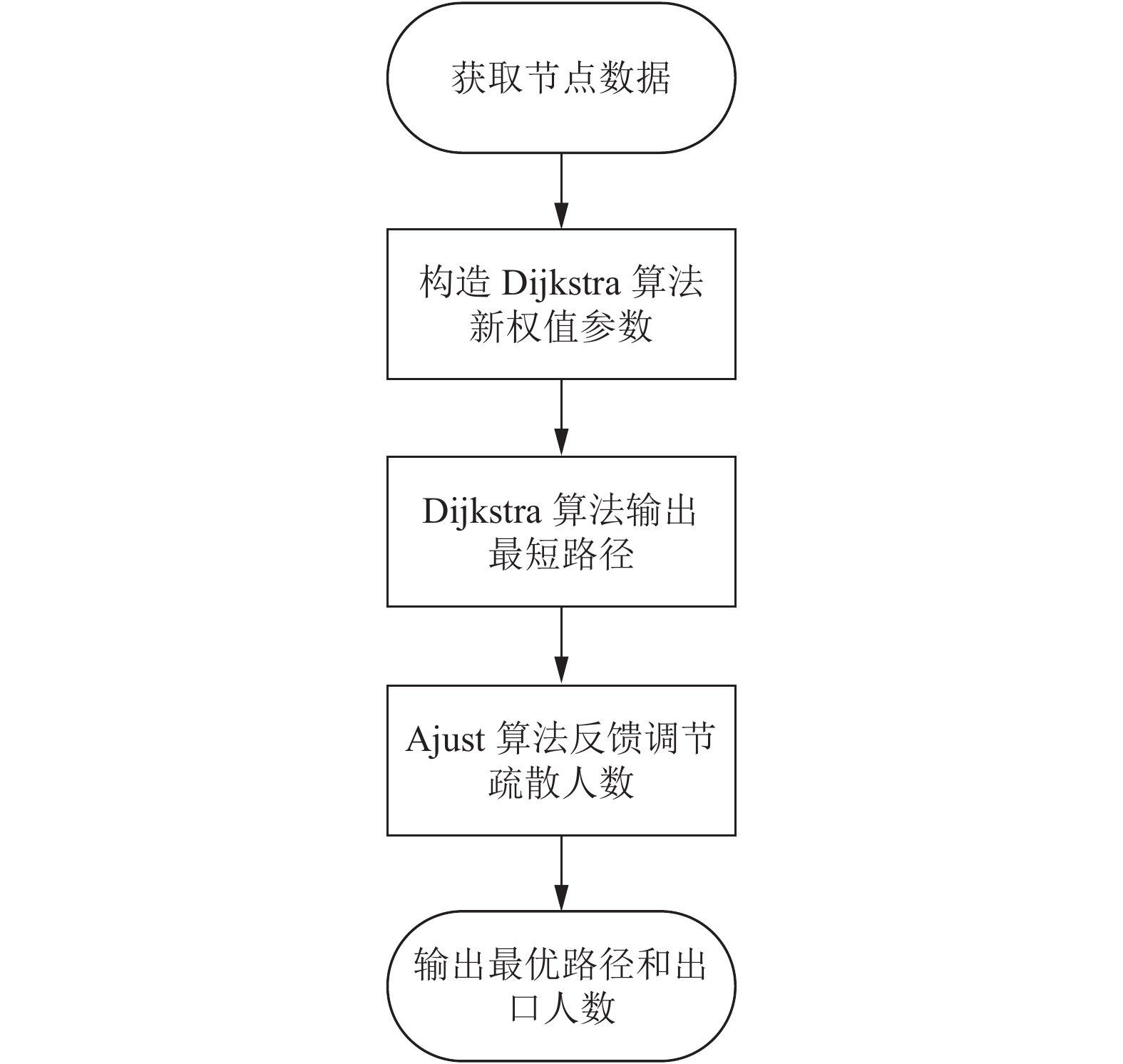
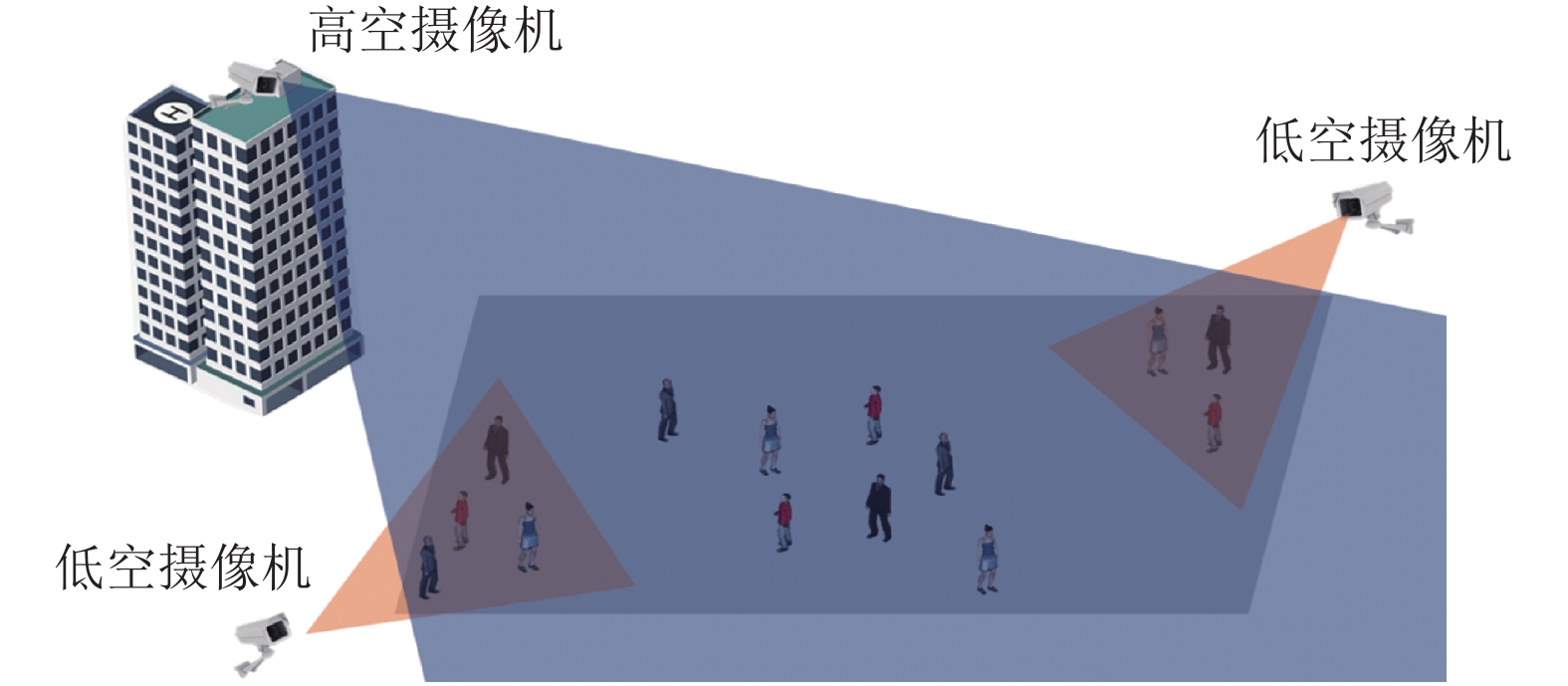
3 基于改进Dijkstra算法的城市广场突发情况下动态人群疏散模型改进Dijkstra算法路径规划流程图如图1所示. 参考柏柳提出的一种多层域异构交通数据融合模型来对动态环境信息中的人群节点位置信息和出口密度信息实时获取[9]. 首先使用多列卷积神经网络(multi column convolutional neural network, MCNN)进行低空视角的人数估计, 然后设计了一种基于高斯混合模型的密度分级算法, 将高空监控视频中的人群密度以关键动点间的距离分级显示[10]. 如图2所示, 结合低空监控和高空监控, 将局部信息和全局信息互补融合, 更加准确的获取上述模型建立的参数信息, 并且构造成Dijkstra算法的新权值参数. 执行Dijkstra输出人群节点到出口节点的最短时间路径. 将输出结果带入自己构造的Ajust算法, 用来调节各条路径的疏散人数. 最终输出最优的路径和对应路径上的行人数量.
3.1 人群疏散模型的建立由于城市广场人群疏散问题较为复杂, 且影响因素较多, 为便于问题的研究, 在此做以下假定:
(1)以每m人划分为一个人群节点. 初始设定为f个人群节点, 共计M = m×f人(m > 0, f > 0);
(2)假定发生意外时, 人群是在同一时间向出口疏散, 且疏散速度μ一致(μ > 0);
(3)假定广场有n个出口, 且各出口通行速率Hk确定 (n > 0, Hk >0);
(4)最后一名人员成功疏散至广场外, 作为疏散完成的判定条件. 以各出口最终疏散完成时间Tk_total的长短来判定疏散算法的优劣.
|
图 1 改进Dijkstra算法路径规划流程图 |
|
图 2 疏散模型参数获取 |
城市广场疏散系统的路网结构用图结构来表示. G = (V, E), 其中V
根据武汉大学与香港城市大学发展的SGEM模型[11], 人群的疏散速度与人群密度的关系可以用式(1)表示:
| $ \mu = \left\{ {\begin{array}{*{20}{l}} {1.4},&{\rho \le 0.75}\\ {0.0412{\rho ^2} - 0.59\rho + 1.867},&{0.75 < \rho \le 4.2}\\ {0.1( \approx 0)},&{\rho > 4.2} \end{array}} \right. $ | (1) |
其中, μ表示不同密度下人群的移动速度(m/s), ρ表示人群密度(人/m2). 整个广场的人数设定为M= m×f (人), 广场移动区域面积为S (m2), 式(2)计算出人群密度ρ. 将ρ带入式(1), 即可得到人群的移动速度μ.
| $ \rho = \frac{M}{S} {\text{人}}/{\rm{m}}^2 $ | (2) |
基于低空摄像, BIM和GIS实时获取人群地理位置信息. 可以获得各个人群节点与出口节点的区域位置和具体距离, 从而构成以距离为权值的邻接矩阵G_dis, 其中dij表示节点i到节点j的距离.
| $ G\_dis = \left({\begin{array}{*{20}{c}} {{{\textit{d}}_{11}}}& \ldots &{{d_{1{\textit{j}}}}} \\ \vdots & \ddots & \vdots \\ {{{\textit{d}}_{i1}}}& \cdots &{{d_{ij}}} \end{array}} \right) $ | (3) |
将式(3)邻接矩阵中的各个参数dij除以式(1)得出的移动速率μ, 整理得出以时间为权值的邻接矩阵GT_road.
| $ G_{T\_road} = \frac{G\_dis}{{\mu }_{} } $ | (4) |
Dijkstra算法原理如下:
Step 1. 设置一个集合S存放已经找到的最短路径顶点, S的初始状态只包含源点, 对Si∈V-S, 假设从源点S到Si的有向边为最短路径.
Step 2. 以后每求得一条最短路径d, …, dj, 就将集合加入S中, 并将路径d, …, dj, Si与原来假设相比较, 取路径长度最小者为最短路径.
Step 3. 重复上述过程, 直到集合V中全部顶点加入集合S中.
对邻接矩阵GT_road执行如上Dijkstra算法.
| $\begin{split} &Dijkstra[v_f,v_k,\;G_{T\_road}]{\rm{ }} = {\rm{ }}T_{fk\_v\_road}\\ &T_{fk\_v\_road} = \sum\nolimits_{{d_{ij}} \in {{ r}}_{{{fk}}}} {\frac{{{d_{ij}}}}{\mu }} \end{split} $ | (5) |
其中, vf表示起点,vk表示终点, GT_road表示存储各节点权值信息的邻接矩阵. rvk表示由Dijkstra算法得到的最短路径. dij表示该最短路径上的分支节点距离. Tfk_v_road表示从人群节点f到出口节点k的最短疏散路径时间.
3.3 疏散出口时间: Tk_exit疏散出口时间Tk_exit表示人群通过安全出口所花费的时间. 参考光海鹏提出的安全出口空间特征对密集人群疏散的影响[12], 获得各安全出口通行能力Hk(人/s).
已知各出口通行能力Hk, 由式(6)计算出每个出口理论通行人数与所有出口通行能力的比值Pk.
| ${P_k} = \frac{{H_k}}{{\displaystyle\sum\nolimits_1^n {H_{\rm{k}}} }}\;\;({\rm{ }}k\{ A,B,C, \cdots \} {\rm{ }})$ | (6) |
由式(7)Pk与疏散总人数M的乘积, 可获得各个出口节点的理论疏散人数Bk, 由式(8)将出口理论疏散人数Bk除以对应出口疏散能力Hk. 获得该出口的疏散出口时间Tk_exit.
| ${B_k} = {\rm{ }}M \times {P_k} $ | (7) |
| $ T_{k\_exit }= \frac{{{B_k}}}{{{H_k}}} $ | (8) |
由式(9)疏散路径时间Tfk_v_road和疏散出口时间Tk_exit相加构成疏散模型总时长Tk_total. 表示在突发情况下, 人群从游玩区域疏散到出口区域的时长Tfk_v_road, 加上在安全出口处排队疏散至广场外安全区域的时间Tk_exit, 构成整个疏散过程的总时长. 将传统Dijkstra算法改进成双目标优化算法.
| $ T_{k\_total }=T_{fk\_v\_road }+ T_{k\_exit} $ | (9) |
| $T_{fk\_v\_road} = \sum\nolimits_{{d_{ij}} \in {{ r}}_{{{fk}}}} {\frac{{{d_{ij}}}}{{\alpha _{{{ij}}}\mu }}} $ | (10) |
| $ \begin{split} T_{k\_exit }&= \dfrac{ M}{\beta (\textit{m},{T}_{fk\_v\_road})} \times \dfrac{{B}_{k}}{{H}_{k}}\\ &= \dfrac{ m\times f}{\beta (\text{m},{T}_{fk\_v\_road})} \times \dfrac{{H}_{k}}{{\displaystyle {\sum }_{1}^{n}{H}_{\textit{k}}}} \end{split} $ | (11) |
式(10)中, αij
式(11)中, β
本文构造了实时人数反馈调节Ajust算法.
输入参数: 各人群节点到各出口节点最短路径rfk,, 路径rfk对应最短疏散时间Tfk_v_road, 路径rfk对应人群节点人数Mf及对应出口节点理论疏散人数Bk.
输出参数为最优路径及对应疏散人数.
Ajust算法如下:
将4个输入参数构造成Python语法中“字典”变量类型. 共计f×k条“字典”. 执行如下Adust算法.
Adust [‘rfk’, Tfk_v_road, Mf, Bk]
Step 1. 以Tfk_v_road由小到大对f×k条“字典”(‘rfk’, Tfk_v_road, Mf, Bk)排序.
Step 2. 当Mf1 < Bk1时:
该人群节点人数小于该出口理论疏散人数:
则删除人群节点为f1的所有“字典”.
更新出口节点k1剩余疏散人数为Bk1—Mf1. 重复Step 1.
Step 3. 当Mf1
该人群节点人数大于该出口理论疏散人数:
则删除出口节点为k1的所有“字典”.
更新人群节点f1剩余人数为Mf1—Bk1.
重复Step 1.
重复以上3个步骤, 直到所有人群节点疏散至出口节点.
Adust [‘rfk’, Tfk_v_road, Mf, Bk] = fk_num
fk_num表示各人群节点疏散至各出口节点具体人数.
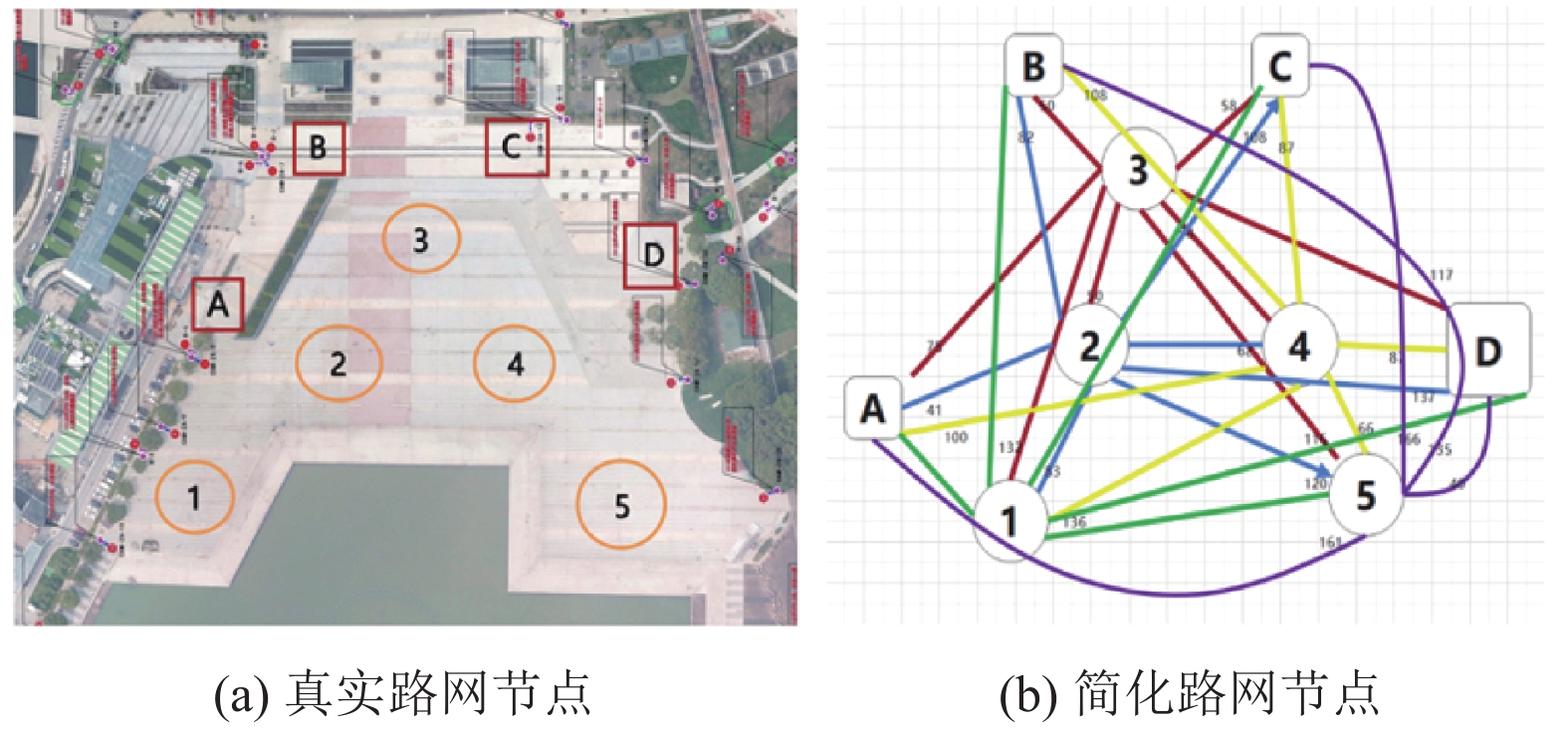
4 案例分析 4.1 地理环境概况苏州市金鸡湖城市广场占地12000 m2, 以每1 200人为一个人群节点, 共设定5个人群节点, 人群总数为6 000人, 导入式(1)中, 获得人群行动速度μ为1.4 m/s. 如图3(a)表示由人群节点Vf{1,2,3,4,5}, 出口节点Vk {A,B,C,D}构成的路网关系图. 由低空摄像, BIM和GIS获得各人群节点和出口节点位置距离(单位: m), 同时用邻接矩阵G_dis构成各节点的距离关系. 导入式(4), 更新为以疏散路径时间为权值的邻接矩阵GT_road.
| $\begin{split} &{G_{{T_ - }road{\rm{ }}}} = \\ &\begin{array}{*{20}{c}} {A}\\ {B}\\ {C}\\ {D}\\ {1}\\ {2}\\ {3}\\ {4}\\ {5}\\ \end{array}\left[ {\begin{array}{*{20}{c}} 0&{60}&{92}&{127}&{46}&{29}&{53}&{71}&{115}\\ {60}&0&{45}&{117}&{105}&{58}&{35}&{72}&{118}\\ {92}&{45}&0&{85}&{134}&{77}&{41}&{62}&{96}\\ {127}&{117}&{85}&0&{148}&{97}&{83}&{55}&{28}\\ {46}&{105}&{134}&{148}&0&{59}&{94}&{97}&{127}\\ {29}&{58}&{77}&{97}&{59}&0&{35}&{44}&{85}\\ {53}&{35}&{41}&{83}&{94}&{35}&0&{35}&{82}\\ {71}&{72}&{62}&{55}&{97}&{44}&{35}&0&{47}\\ {115}&{118}&{96}&{28}&{127}&{85}&{82}&{47}&0 \end{array}} \right] \end{split}$ |
金鸡湖城市广场共有4个出口, 分别为南朝向A出口(宽度1.5 m), 西朝向B出口(宽度2 m)和C (出口宽度2 m), 北朝向D出口(宽度4 m). 表1为不同宽度安全出口通行能力表. 由表1获取A出口通行能力为5.231 人/s. 出口B和出口C通行能力为7.487 人/s. 出口D通行能力为19.031 人/s.
|
图 3 广场节点路网结构图 |
| 表 1 不同宽度安全出口通行能力表[12] |
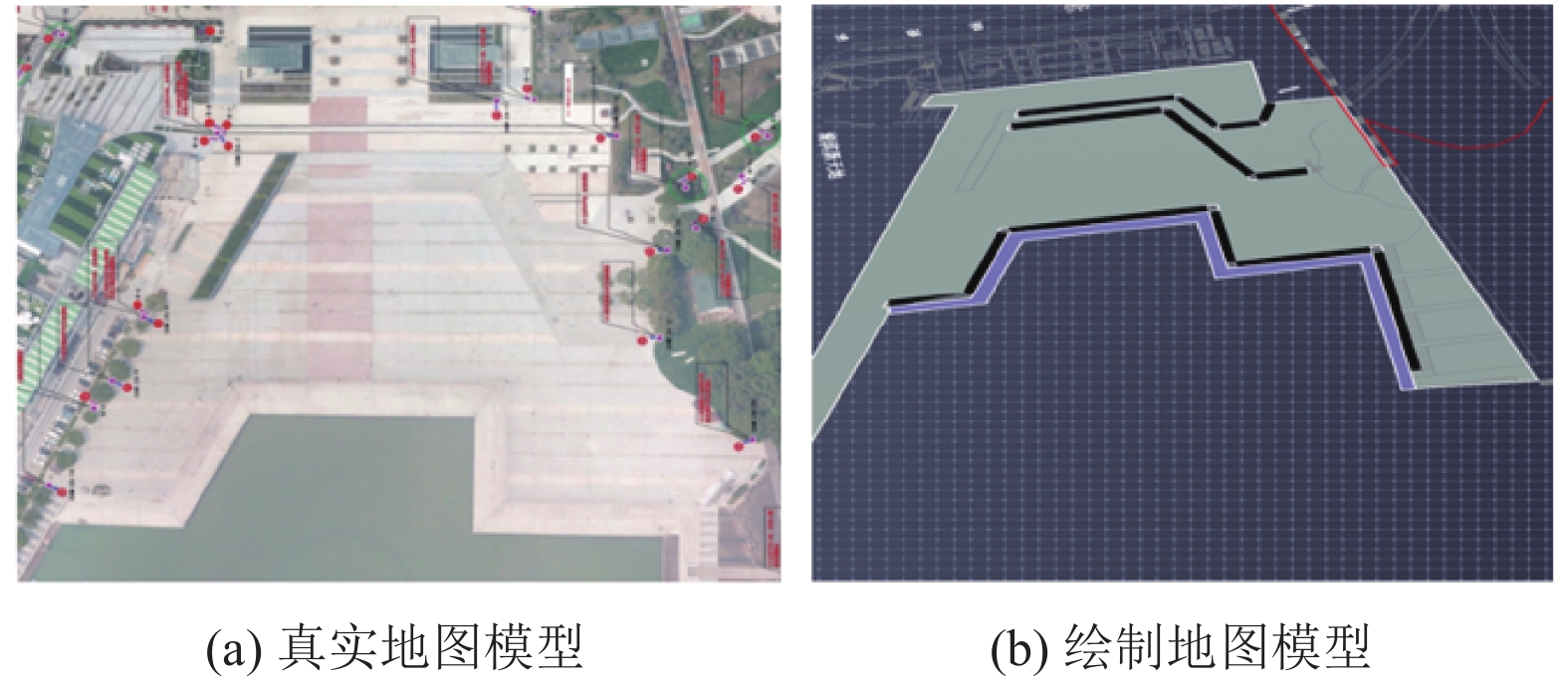
运行Dijkstra算法[13], 获得各个人群节点疏散至各个出口节点结果. 人群节点1,2均奔向出口A, 人群节点3奔向出口B, 人群节点4,5奔向出口D. 同时, 将广场疏散总人数M = 6000人, 带入式(7), 获取各出口理论逃生人数Bk. 数据整理如表2. 如图3所示, 以金鸡湖城市广场为基础构建疏散路网结构图, 图4参考实际环境, 在仿真软件1:1绘制广场疏散环境模型. 图5则展示了Pathfinder软件模拟疏散过程.
|
图 4 城市广场实景图与Pathfinder软件绘制图 |

|
图 5 Pathfinder软件模拟疏散过程 |
| 表 2 多种情况疏散结果表 (s) |
| 表 3 人群节点疏散至出口节点表 |
4.2 人数动态调整
表3可以得出传统Dijkstra算法路径规划结果为TA_exit = 458 s, TB_exit = 160 s, TC_exit = 0 s TD_exit = 126 s. 疏散出口时间Tk_exit差异巨大, 由于C出口没有人群节点疏散, 造成出口资源浪费. 1,2人群节点距离出口A较近, 故疏散至A出口节点, 但是A出口通行能力较差, 造成拥堵, 疏散时间最长. 各出口的理论疏散总人数为A出口疏散804人, B, C出口各疏散1 149人, D出口疏散2 922人.
执行Dijkstra算法, 输出结果如表4, 使用Ajust算法合理分配人数至各出口, 疏散结果如表5所示.
人群节点1转移678人至出口C, 转移522至出口D.
| 表 4 人群动态调整至出口表 |
| 表 5 动态人群出口分配表 |
人群节点2转移804人至出口A, 转移396人至出口C.
人群节点3转移1 149人至出口B, 转移51人至出口C.
人群节点4转移1 200人至出口D, 人群节点5转移1200人至出口D. 式(5)可得疏散路径时间Tfk_v_road:
T2A_v_road = 29 s, T3B_v_road = 35 s, T3C_v_road = 41 s, T5D_v_road = 28 s.
由式(8)得出疏散出口时间: Tk_exit = 153 s.
由式(9)得出疏散模型总时间:
TA_total = T2A_v_road + TA_exit = 182 s, TB_total = T3B_v_road + TB_exit =191 s, TC_total = T3C_v_road + TC_exit = 194 s, TD_total = T5D_v_road + TD_exit = 181 s.
5 软件仿真使用Pathfinder软件仿真模拟3种情况下的人群疏散结果[14]. 情况1: Pathfinder软件自然疏散. 情况2使用传统Dijkstra算法路径规划. 情况3使用改进Dijkstra算法和Ajust人数调节算法结合输出路径规划结果.
情况1 Pathfinder自然仿真结果如图6(a)所示, 最早完成疏散出口为156 s. 最晚完成疏散为A出口209 s.

|
图 6 3种疏散算法仿真对比结果 |
情况2如图6(b)所示, 使用传统Dijkstra算法, 以最短路径为算法的主要参数. 由于C出口无人疏散, 导致模型疏散总时间差异巨大. 最早完成疏散出口为D出口, 用时143 s. 最晚完成疏散出口为A出口, 用时472 s. 相差329 s.
情况3如图6(c)所示, 改进Dijkstra算法结合人群合理分配出口结果. 最早完成疏散为C出口172 s, 最晚完成疏散为D出口185 s. 相差12.9 s, 用时最短, 对比3种算法, 最早完成疏散任务.
改进的Dijkstra算法通过合理的分配人群到各个出口, 完成人群疏散的结果最佳, 比Pathfinder软件模拟自然疏散提升了10 s. 传统Dijkstra算法只考虑最短路径为权值, 没有考虑安全出口的疏散能力, 导致人群大量拥堵在疏散能力差的出口, 浪费了大量时间, 疏散结果最差.
6 总结与展望本文对苏州市金鸡湖城市广场的人群疏散路径规划进行了研究. 改进传统Dijkstra最短路径权值为最短时间权值, 同时加入人群人数反馈调节Ajust算法, 合理分配人群至不同出口, 从而减少人群疏散时间. 通过Pathfinder软件仿真, 对比3种条件下疏散结果, 发现最大化利用所有出口资源对路径规划疏散效率有显著提高.
| [1] |
陆君安, 方正, 卢兆明, 等. 建筑物人员疏散逃生速度的数学模型. 武汉大学学报(工学版), 2002, 35(2): 66-70. |
| [2] |
雷诚, 李锦, 丁邹洲. “双效健康城市”理念下既有公共空间环境更新设计探讨——以金鸡湖环湖绿道为例. 西部人居环境学刊, 2020, 35(3): 1-9. |
| [3] |
晋良海, 易小钰, 殷双萍, 等. 公共建筑人群疏散流线负荷的拓扑解析模型研究. 中国安全生产科学技术, 2020, 16(9): 30-36. |
| [4] |
Yang SG, Jin J, Lu XF. Research on spatial arrangement of metro station floor facilities based on pathfinder. American Journal of Civil Engineering, 2019, 7(6): 147-151. DOI:10.11648/j.ajce.20190706.11 |
| [5] |
Helbing D, Buzna L, Johansson A, et al. Self-organized pedestrian crowd dynamics: Experiments, simulations, and design solutions. Transportation Science, 2005, 39(1): 1-24. DOI:10.1287/trsc.1040.0108 |
| [6] |
王海红, 刘莉. 基于分层和强化学习的改进路径搜索算法. 计算机与现代化, 2020(11): 77-82, 88. DOI:10.3969/j.issn.1006-2475.2020.11.013 |
| [7] |
巩青歌, 沈晓飞, 王文骏. 基于元胞自动机的人群疏散模型. 计算机系统应用, 2013, 22(11): 105-109. DOI:10.3969/j.issn.1003-3254.2013.11.020 |
| [8] |
杨文举, 周洋洋, 常瑜. 模拟疏散中个体及群体运动方法. 计算机系统应用, 2012, 21(6): 182-185. DOI:10.3969/j.issn.1003-3254.2012.06.041 |
| [9] |
Bai L, Wu C, Wang YM, et al. Multiview-fusion-based crowd density estimation method for dense crowd. The Fifteenth International on Conference on Systems (ICONS). Lisbon, 2020.
|
| [10] |
Bai L, Wu C, Wang YM. Overcrowding detection based on crowd-gathering pattern model. Proceedings of SAI Intelligent Systems Conference. London: Springer, 2020. 270–284.
|
| [11] |
Lo SM, Fang Z, Lin P, et al. An evacuation model: The SGEM package. Fire Safety Journal, 2004, 39(3): 169-190. DOI:10.1016/j.firesaf.2003.10.003 |
| [12] |
光海鹏. 安全出口空间特征对密集人群疏散的影响研究. 安徽建筑, 2020, 27(8): 32, 38. |
| [13] |
刘志威, 杨莉琼, 谢永胜, 等. 基于改进Dijkstra算法的川藏铁路站房工程物资动态调运研究. 建筑经济, 2020, 41(S1): 166-170. |
| [14] |
赵金龙, 孙博阳, 王善生, 等. 基于Pathfinder的特殊地铁站点人群紧急疏散模拟. 中国安全生产科学技术, 2020, 16(1): 146-150. |
 2022, Vol. 31
2022, Vol. 31



