2. 工业安全与应急技术安徽省重点实验室, 合肥 230601;
3. 合肥工业大学 软件学院, 合肥 230601
2. Key Laboratory of Knowledge Engineering with Big Data (Hefei University of Technology), Ministry of Education, Hefei 230601, China;
3. School of Software, Hefei University of Technology, Hefei 230601, China
地面沉降是在自然变化和人类活动综合影响下, 引起地壳表面标高缓慢变化的一种局部工程地质现象. 随着全球城市化进展不断加快, 城市扩张和人口快速增长, 城市基础设施的大量修建和地下资源的过度开采, 导致城市地面沉降日益严重. 地面沉降可对建筑物和生产设施造成严重破坏, 不利于城市建设和资源勘测开发, 甚至可能在沿海地区造成海水倒灌, 对人民生命财产安全和基础设施安全造成了重大安全隐患[1, 2]. 传统的调查和侦查方法如全球定位系统(global positioning system, GPS)和水准测量等监测方法虽然精度较高, 但是只能在小范围的点和线进行测量, 难以对大范围区域进行监测, 且对监测点的长期维护也比较困难[3-6]. 因此, 合成孔径雷达干涉测量(interferometric synthetic aperture radar, InSAR)凭借着不受时间气候环境影响和高精度、高分辨率等优点在地面沉降监测中显示出极大的应用潜力[7-9].
InSAR技术最早被应用于地形测绘领域, 文献[10]首次提出合成孔径雷达差分干涉测量(differential inter-ferometric synthetic aperture radar, D-InSAR)技术, 研究表明D-InSAR监测地表形变的精度可以达到厘米级, 自此D-InSAR技术开始被应用于地表形变监测中; 文献[11]利用D-InSAR技术监测伊朗达马内市的地面沉降; 文献[12]利用永久散射体技术(persistent scatterer interferometric synthetic aperture radar, PS-InSAR)对意大利的托斯卡纳滑坡地区进行形变监测研究; 文献[13]利用短基线集技术对克罗地亚的萨格勒布地区进行地面形变分析.
我国将InSAR技术应用于地面形变监测较晚, 但也取得了许多成果. 文献[14]利用PS-InSAR技术对上海高架路进行沉降监测, 分析提取的高架路沉降的空间分布以及时间变化情况; 2019年文献[15]采用时序InSAR技术监测三峡库区藕塘滑坡的稳定性; 文献[16]利用Sentinel-1A影像分别采用PS-InSAR技术和SBAS-InSAR技术监测南京市地面沉降. D-InSAR技术可以达到厘米级的测量精度, 但是难以对同一区域进行时间序列形变监测; PS-InSAR和SBAS-InSAR都可利用大量合成孔径雷达(synthetic aperture radar, SAR)影像(一般多于20幅)进行时间序列分析, 但是在研究SAR影像较少的区域时, 上述两种方法的应用均受到限制.
传统的干涉图叠加方法(interferogram stacking)[17-19]是将地面形变量视为一种线性变化, 将相互独立的干涉图中所包含大气扰动的相位误差在时间上近似为随机量, 将研究区域的地表形变信息视为线性变化, 通过线性叠加, 提高了叠加相位图中形变信息与大气干扰噪声之间的信噪比. 该方法在仅有少量的SAR数据的支撑下也可实现较长时间的形变监测. 但是在没有考虑干涉图质量权重的情况下, 使相干性较低的干涉图参与叠加, 势必会影响监测结果的精度.
综上所述, 本文提出一种面向地面沉降的基于多幅主影像干涉图加权叠加的方法. 该方法通过选取多幅主影像, 并在传统Stacking法上在加入图像质量权重的方法对地表进行形变监测, 相对传统的监测方法提高监测精度.
本文的其余章节将简要安排如下: 第1节介绍研究区域以及数据. 第2节介绍多幅主影像干涉图加权叠加方法的基本原理, 并就所提方法的主要思想、流程及计算公式进行详细介绍. 第3节就监测结果从主观和客观两个方面进行评价并给出分析, 总结部分将在第4节给出.
1 研究概况及数据来源 1.1 研究区域概况美国的加利福尼亚州一直以来存在着不同程度的沉降. 在2014年加利福尼亚州出现了近50年来最严重的地面沉降, 后续预计地面沉降将继续恶化.
选取圣迭戈县作为实验区域, 圣迭戈县的地形较为复杂, 其西侧是蜿蜒的海岸线, 东北侧主要是大雪覆盖的雪峰, 而东部则为大片的金黄色沙漠. 因此这次实验主要选取城区监测沉降, 避开山脉, 沙漠等相干性低的区域.
1.2 数据来源选用的实验数据包括哨兵1A (Sentinel-1A)数据、数字高程模型(digital elevation model, DEM)、以及地下水监测数据, 这一数据来自美国地质调查局(United States geological survey, USGS).
Sentinel-1A卫星是欧洲航天局于2014年发射的首颗地球观测卫星, 载有C波段合成孔径雷达, 可以在各种环境条件下提供影像. 对同一区域的重访周期为12天. Sentinel-1A数据基本参数见表1所列. 本文使用的数字高程数据为SRTM-1 DEM数据, 平面分辨率为30 m, 每个DEM子单元的数据幅宽为经纬度1°.
| 表 1 Sentinel-1A卫星4种工作模式基本参数 |
1.3 数据处理
考虑到多幅主影像干涉图加权叠加方法监测形变的优越性, 选择圣迭戈县城区作为试验区, 避免相干性低的区域, 以提高监测精度. 采用2019年7月至2019年12月Sentinel-1A的9景IW模式的SLC (single looking complex)数据进行试验.
首先从这9幅SAR影像中择优选取3幅作为主影像, 使其余影像与其配准并生成干涉对, 可利用综合函数模型来进行确定.
| $ {d_l} = \frac{1}{n}\sum\limits_{i = 1}^n {\sqrt {{{\left(\frac{{{B_{i,l}}}}{{{B_{\text{c}}}}}\right)}^2} + {{\left(\frac{{{T_{i,l}}}}{{{T_{\text{c}}}}}\right)}^2} + {{\left(\frac{{{f_{i,l}}}}{{{f_{\text{c}}}}}\right)}^2}} } $ | (1) |
其中, dl是以第l幅影像为主影像时正则化距离的平均值, 选取计算出的最小值所对应的影像作为公共主影像[20]; l代表SAR影像序号(按时间前后排序); Bc、Tc和fc分别为垂直空间基线临界值、时间基线临界值和多普勒质心频率差临界值; Bi,l、Ti,l和fi,l分别为第l幅影像作为主影像与第i幅辅影像之间的垂直空间基线、时间基线和多普勒质心频率差. 根据式(1), 计算所有影像的平均正则化距离d, 选取平均值最小的3幅影像作为主影像, 最终确定轨道号为027961、028836、029711的3幅影像作为主影像.
基于D-InSAR的具体工作流程, 首先选取027961、028836、029711共3幅影像作为干涉主影像, 选取027961作为参考影像. 并将所有的图像配准到参考影像上; 接着使用精密卫星轨道数据消除卫星轨道残余相位误差; 选择所有空间垂直基线中小于50 m的11个干涉对进行干涉处理, 以抑制空间去相关引起的相位误差, 生成的干涉像对见表2所列. 主要过程包括相干性计算、去平、滤波和相位解缠. 其中滤波过程采用Goldstein方法对干涉图进行滤波, 这种滤波方法可以提高干涉条纹的清晰度、减少了由空间基线或时间基线引起的失相干噪声. 再将配准的干涉图与STRM1 DEM数据进行差分干涉, 生成差分干涉图集, 选取部分如图1所示. 随后的相位解缠过程使用最小费用流(minimum cost flow, MCF)方法[21]进行, 弱化低相干区域对实验结果的影响, 最终得到各解缠相位.
| 表 2 Sentinel-1A影像和其构成的干涉像对 |

|
图 1 差分干涉图集 |
2 多幅主影像干涉图加权叠加方法 2.1 基本原理及流程
多幅主影像干涉图加权叠加方法是选择较优的多幅主影像, 剩余的影像与主影像进行配准, 对配准到同一主影像生成的干涉像对筛选出时空基线较短的干涉对生成不同的集合, 各个集合之间的基线较长, 通过最小二乘法得到每个集合的地面形变信息, 再使用奇异分解法将各个集合联合后求解. 这种方法可以在数据集较少的基础上获得较高的监测精度.
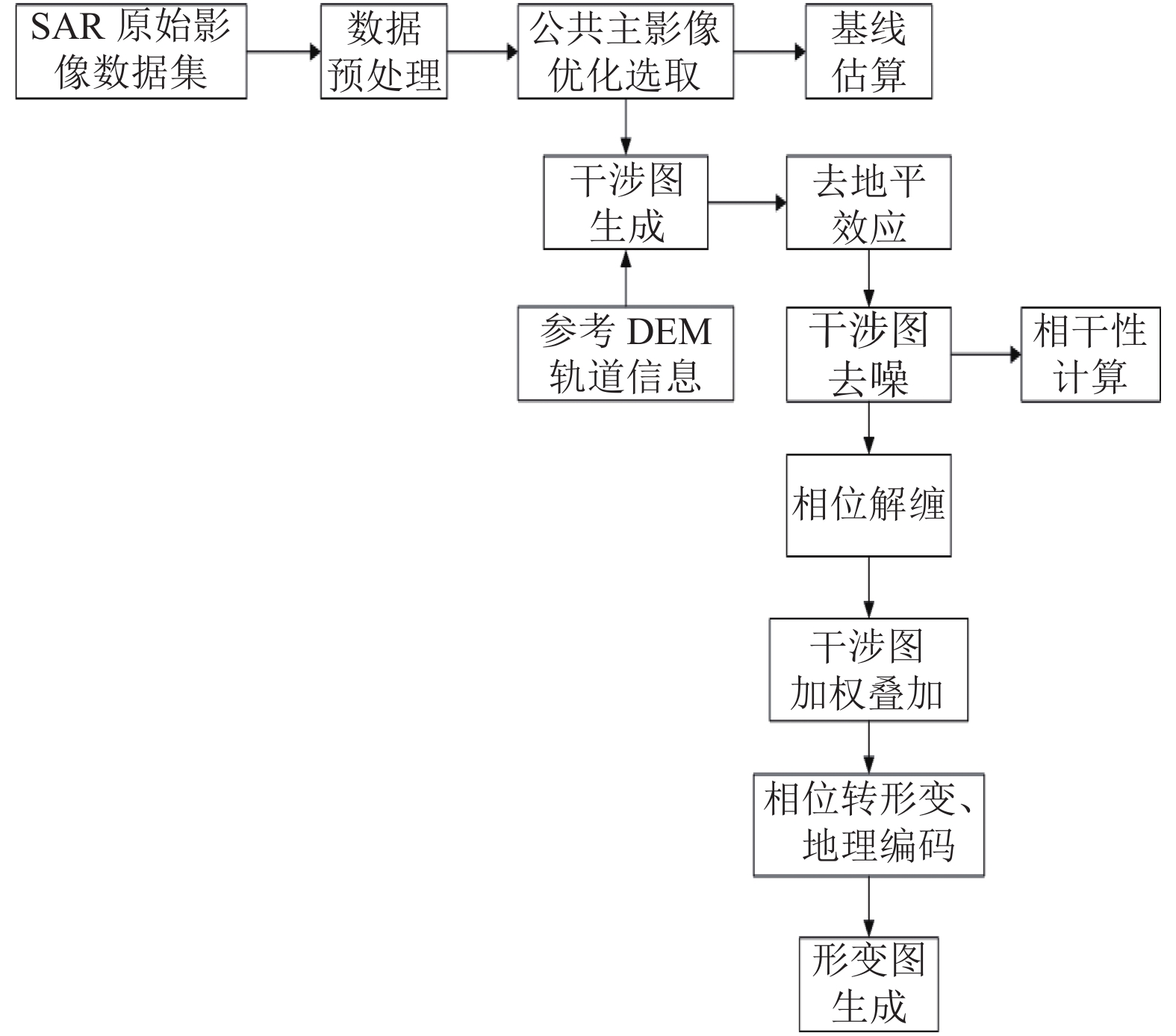
多幅主影像干涉图加权叠加方法数据的处理流程如图2所示, 主要包括: 数据预处理、选取多幅主影像; 基线估算生成连接图, 参考DEM和轨道数据生成干涉图; 干涉图滤波, 并计算相干性; 相位解缠; 剔除相干性差的像对, 干涉图加权叠加; 相位转形变, 地理编码; 生成形变图.
2.2 干涉图加权叠加方法的函数模型在地表形变速率计算过程中, 对于任一幅经过相位解缠的干涉图, 其干涉相位可表示为:
| $ {\phi _{\rm{int} }} = {\phi _{\rm {topo}}} + \phi {}_{\rm{defo}} + {\phi _{\rm {obj}}} + {\phi _{\rm {orb}}} + {\alpha _{\rm {atmos}}} + {n_{\rm {noise}}} $ | (2) |
其中,
在D-InSAR处理过程中,
|
图 2 多幅主影像干涉图加权叠加方法流程图 |
在干涉图叠加过程中, 会将所有经过解缠后的干涉图进行相位叠加, 但这样也会让相干性差的干涉图参与相位叠加过程, 导致解算出的形变量产生较大误差, 降低监测精度. 因此, 需要对干涉图叠加时各图像的权重进行合理的设定, 以剔除相干性差的干涉图. 首先需要基于干涉处理过程中生成的相干图来统计相干点的数量, 然后计算相干图中各相干点的相干值, 根据平均相干值来设置权重. 将平均相干值最大的相干图权重
干涉图相位叠加的数学模型可表述为:
| $ {\overline V _{\rm {defo}}} = \frac{{\lambda \cdot {\phi _{\rm {cum}}}}}{{4\pi \cdot {t_{\rm {cum}}}}} $ | (3) |
其中,
经过干涉叠加后的累积相位值
| $ {\phi _{\rm {cum}}}{\text{ = }}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {\phi _{i,j}^k} } $ | (4) |
时间累积值
| $ {t_{\rm {cum}}}{\text{ = }}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {\Delta {T_{i,j}}} } $ | (5) |
根据平均相干值给干涉图设定权重
| $ {\phi _{\rm {cum}}}{\text{ = }}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {w_{i,j}^k\phi _{i,j}^k} } $ | (6) |
时间累积值
| $ {t_{\rm {cum}}}{\text{ = }}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {w_{i,j}^k\Delta {T_{i,j}}} } $ | (7) |
多幅主影像的干涉图加权叠加方法得到的平均形变相位变化速率
| $ {\overline{V}}_{\rm {defo}}^{k}=\frac{\lambda \left(\displaystyle\sum\limits_{i=1}^{M}\displaystyle\sum\limits_{j=1}^{N}{w}_{i,j}^{k}{\phi }_{i,j}^{k}\right)}{4\pi \left(\displaystyle\sum\limits_{i=1}^{M}\displaystyle\sum\limits_{j=1}^{N}{w}_{i,j}^{k}\Delta {T}_{i,j}\right)} $ | (8) |
其中, M为主影像的个数, N为第i幅主影像参与生成的干涉图的个数;
由于SAR影像中的大气延迟相位是随机分布, 干涉像对经差分处理生成的干涉图中大气延迟相位也随机分布. 根据误差传播定律, 在对所有干涉图进行叠加后, 高质量的相干点受到的大气延迟影响可表示为:
| $ \Delta {\phi ^k}{\text{ = }}\sqrt {MN} \sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {w_{i,j}^k\phi {{_{i,j}^{k'}}}} } $ | (9) |
其中,
将所有干涉图加权叠加后, 对于高质量相干点, 大气延迟对线性形变速率的影响可表示为:
| $ {\overline{V}}_{\rm {atm}}^{k}=\frac{\lambda \Delta {\phi }^{k}}{4\pi \left(\displaystyle\sum\limits_{i=1}^{M}\displaystyle\sum\limits_{j=1}^{N}{w}_{i,j}^{k}\Delta {T}_{i,j}\right)} $ | (10) |
由式(8)和式(10)可得, 像元k经过干涉图加权叠加后的平均速率可表示为:
| $ {\overline{V}}^{k}=\frac{\lambda \left(\displaystyle\sum\limits_{i=1}^{M}\displaystyle\sum\limits_{j=1}^{N}{w}_{i,j}^{k}{\phi }_{i,j}^{k}\text+\Delta {\phi }^{k}\right)}{4\pi \left(\displaystyle\sum\limits_{i=1}^{M}\displaystyle\sum\limits_{j=1}^{N}{w}_{i,j}^{k}\Delta {T}_{i,j}\right)} $ | (11) |
从式(11)可以看出, 叠加后平均形变速率中, 形变相位信息与大气延迟间的信噪比得到了提高.
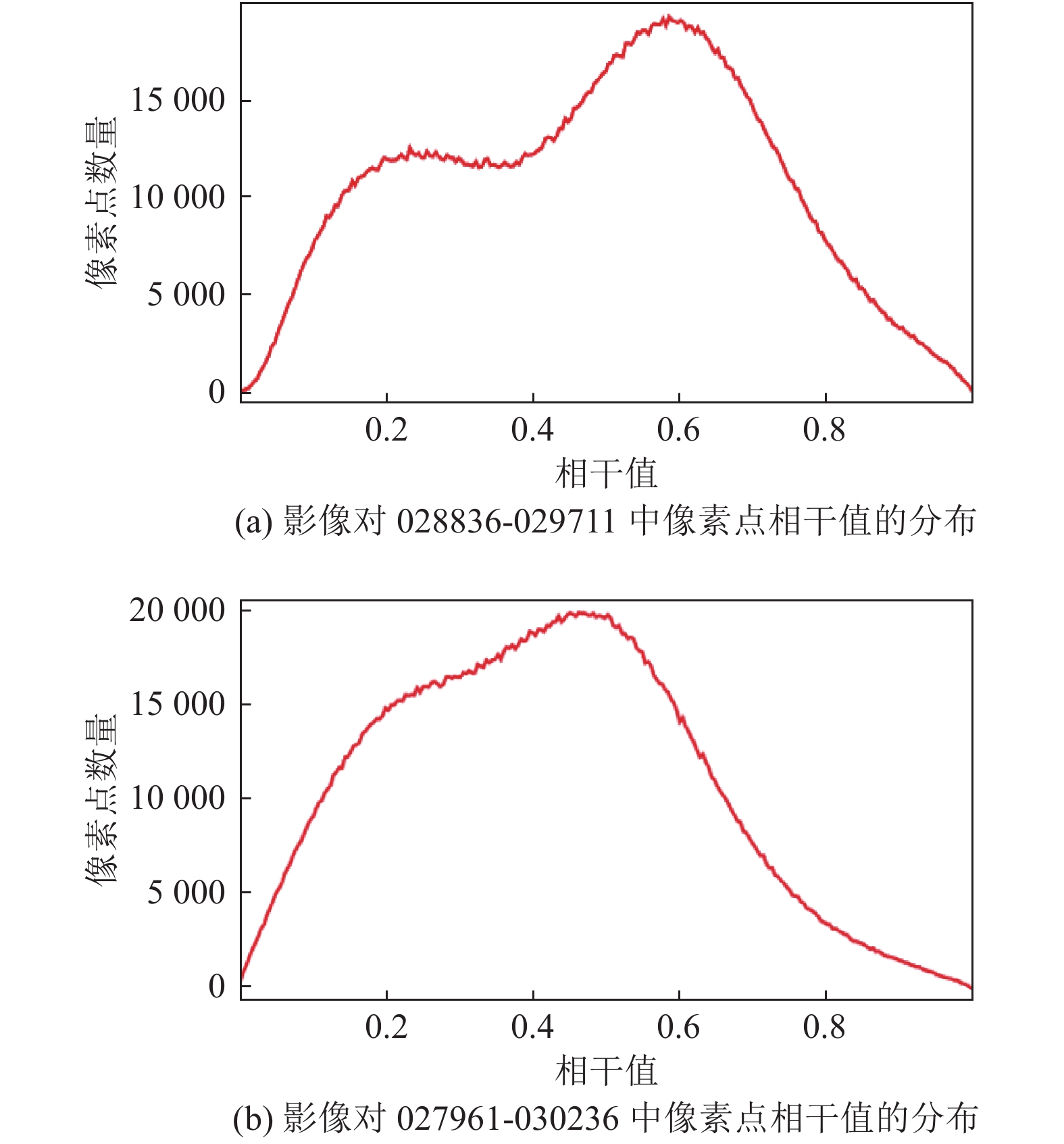
3 实验及结果分析 3.1 实验结果及对比分析为了验证方法的有效性, 收集相干图制成相干图集, 如图3所示. 根据前文所述设置权重的理论, 计算相干图集中的平均相干值, 将相干性低的权重设置为0. 因为研究区域左下角是低相干性的大片水域, 在相干图中显示为黑色, 因此只需研究主城区的相干性. 对比图3中的11幅图可知, 相干图028836-029711在主城区的黑色区域最少, 相干图027961-030236在主城区的黑色区域最多, 统计其像素点相干值的分布, 如图4所示, 并计算出像对028836-029711的像素点平均相干值为0.50, 该像对相干性最好; 像对027961-030236的像素点平均相干值为0.37, 该像对相干性最差, 且占相干性最好像对的平均相干值的比重小于3/4, 因此需将该相干图的权重设置为0, 避免其相干图参与叠加解算, 降低最终的监测精度.
将以上符合要求的相位解缠图叠加解算, 解算得到平均沉降速率图并叠加在Google Earth上, 如图5所示. 从图5可以看出, 在监测过程中, 该地区的地表整体上处于稳定状态, 这与选取的SAR影像时间间隔较短有一定关系. 结果表明在圣迭戈县中心区域的地表有较大抬升, 年均地面抬升速率在10 mm/a左右, 局部区域的最大抬升速率能达到30 mm/a. 在圣迭戈县的北部以及周边区域都呈现出了不同程度的沉降, 大部分区域的年均地面沉降速率在−16 mm/a, 引起沉降的主要原因是该地区持续的农业灌溉和城市建设用水来源于含水层储水, 导致对地下水过度开采, 造成了地下水位的下降, 含水层透支且难以恢复, 从而进一步恶化地面沉降. 后来由于当地对于地下水的一系列政策保护, 总体上城区的形变基本保持稳定, 与历史监测结果相比, 地表形变速率具有明显减缓的特征, 说明该地区的地面沉降已经得到缓解.

|
图 3 相干图集 |
|
图 4 像素点相干值分布图 |
为了验证结果的准确性, 采用传统的D-InSAR方法对2019年7月4日和2019年12月31日两景SAR数据进行形变监测, 结果如图6所示. 从图6中可以看出, 传统的D-InSAR方法得到的监测结果并不准确. 以左下角区域为例进行分析, 左下角实验区域为海平面, 是低相干区域, 却产生了不符实际的异常形变, 监测误差较大. 而本文提出的多幅主影像加权叠加方法结果相较而言更加准确. 此外, 传统的D-InSAR方法是监测起始时间之间的累积形变量作为最终的形变结果, 用这种结果代表监测期间的平均形变速率有失结果准确性和代表性. 本文通过选取多幅主影像, 在采用D-InSAR处理流程的基础上, 对得到的干涉图集进行加权叠加. 这不仅可以代表监测时间序列的沉降速率, 又可同时获得时间序列内部包含各个时间段的形变速率, 结果更具代表性.
3.2 精度分析地下水监测结合了不同类型的水位观测测量(周期的、连续的和实时的), 并结合这些记录来提供井底随时间变化的响应的评估, 所以使用USGS网站地下水网络数据进行验证. 图7(a)是多幅主影像加权叠加方法在地下水监测点的时间序列变化图, 可以看出该点的形变量先减小再增加, 这意味着该区域地表先沉降又抬升, 本文采用SPSS软件中的Analyse模块对地下水位与地面沉降的关系进行分析, 分析得到地下水水位与地面沉降量相关系数为0.941, 两者具有非常高的相关程度, 如图7(b). 以地下水监测点为基础建立深层地下水位与地面沉降量关系的数据见表3, 可以看出本文方法得到的地表形变趋势与地下水水位的变化基本保持一致, 两者最大误差为1.13 mm, 由此证明本文方法用于监测地表形变是可靠的, 监测精度可达毫米级别.

|
图 5 年平均形变速率图 |
因城市地下水的抽取而引起地下水位的变化不是产生地表形变的唯一因素, 同时还有人类活动和其他因素也会对地表形变造成影响, 使得实验结果在数值上同地下水观测数据具有一定的偏差.
4 结论本文在传统D-InSAR监测方法的基础上, 提出一种基于较少影像实现时间序列监测的多幅主影像干涉图加权叠加方法.

|
图 6 传统D-InSAR监测结果图 |

|
图 7 地下水数据精度验证 |
| 表 3 地下水位监测点水位与地面沉降数据表 (mm) |
该方法首先综合考虑了垂直空间基线、时间基线和多普勒质心频率差异的影响, 利用综合函数模型选取3幅主影像, 削弱主影像大气延迟影响, 为后续干涉图加权叠加过程提供更多数量的相干图, 然后对相干图质量(依据平均相干值)进行定权, 解决低相干影像图对监测结果的负面影响, 通过加权叠加后, 提高了相位图的形变信息与大气噪声之间的信噪比, 最后提取形变信息, 实现对目标区域的时序形变监测.
综上所述, 本文提出的方法通过采用圣迭戈县城区的9景Sentinel-1A影像与传统监测方法进行对比分析, 实验结果表明, 本文所提方法所得地表形变监测结果与地下水监测数据的线性拟合程度为0.941, 监测结果明显优于传统D-InSAR方法得到的结果. 这种方法弥补了D-InSAR技术不能进行时间序列监测的缺点, 解决了时序InSAR技术对数据量要求较多的问题, 降低了传统Stacking方法中低相干影像参与叠加带来的不利影响, 提高了监测精度, 方法有效可行. 同时, 本文方法在长时间序列形变监测中具有重要研究意义, 后续将会收集更多资料进行进一步研究.
| [1] |
Rahmati O, Golkarian A, Biggs T, et al. Land subsidence hazard modeling: Machine learning to identify predictors and the role of human activities. Journal of Environmental Management, 2019, 236: 466-480. DOI:10.1016/j.jenvman.2019.02.020 |
| [2] |
Zhou CF, Gong HL, Chen BB, et al. Quantifying the contribution of multiple factors to land subsidence in the Beijing Plain, China with machine learning technology. Geomorphology, 2019, 335: 48-61. DOI:10.1016/j.geomorph.2019.03.017 |
| [3] |
刘欢欢, 张有全, 王荣, 等. 京津高铁北京段地面沉降监测及结果分析. 地球物理学报, 2016, 59(7): 2424-2432. DOI:10.6038/cjg20160709 |
| [4] |
Hung WC, Hwang C, Chang CP, et al. Monitoring severe aquifer-system compaction and land subsidence in Taiwan using multiple sensors: Yunlin, the southern Choushui River Alluvial Fan. Environmental Earth Sciences, 2010, 59(7): 1535-1548. DOI:10.1007/s12665-009-0139-9 |
| [5] |
秦同春, 程国明, 王海刚. 国际地面沉降研究进展的启示. 地质通报, 2018, 37(2): 503-509. DOI:10.3969/j.issn.1671-2552.2018.02.028 |
| [6] |
Bawden GW, Thatcher W, Stein RS, et al. Tectonic contraction across Los Angeles after removal of groundwater pumping effects. Nature, 2001, 412(6849): 812-815. DOI:10.1038/35090558 |
| [7] |
Hooper A, Bekaert D, Spaans K, et al. Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics, 2012, 514–517: 1-13. DOI:10.1016/j.tecto.2011.10.013 |
| [8] |
张路, 廖明生, 董杰, 等. 基于时间序列InSAR分析的西部山区滑坡灾害隐患早期识别——以四川丹巴为例. 武汉大学学报·信息科学版, 2018, 43(12): 2039-2049. |
| [9] |
Massonnet D, Rossi M, Carmona C, et al. The displacement field of the Landers earthquake mapped by radar interferometry. Nature, 1993, 364(6433): 138-142. DOI:10.1038/364138a0 |
| [10] |
Zebker HA, Goldstein RM. Topographic mapping from interferometric synthetic aperture radar observations. Journal of Geophysical Research: Solid Earth, 1986, 91(B5): 4993-4999. DOI:10.1029/JB091iB05p04993 |
| [11] |
Ghazifard A, Akbari E, Shirani K, et al. Evaluating land subsidence by field survey and D-InSAR technique in Damaneh City, Iran. Journal of Arid Land, 2017, 9(5): 778-789. DOI:10.1007/s40333-017-0104-5 |
| [12] |
Rosi A, Tofani V, Tanteri L, et al. The new landslide inventory of Tuscany (Italy) updated with PS-InSAR: Geomorphological features and landslide distribution. Land-slides, 2018, 15(1): 5-19. DOI:10.1007/s10346-017-0861-4 |
| [13] |
Govorčin M, Pribičević B, Wdowinski S. Surface deformation analysis of the wider Zagreb area (Croatia) with focus on the Kašina fault, investigated with small baseline InSAR observations. Sensors, 2019, 19(22): 4857. DOI:10.3390/s19224857 |
| [14] |
王茹, 杨天亮, 杨梦诗, 等. PS-InSAR技术对上海高架路的沉降监测与归因分析. 武汉大学学报·信息科学版, 2018, 43(12): 2050-2057. |
| [15] |
史绪国, 徐金虎, 蒋厚军, 等. 时序InSAR技术三峡库区藕塘滑坡稳定性监测与状态更新. 地球科学, 2019, 44(12): 4284-4292. |
| [16] |
高二涛, 范冬林, 付波霖, 等. 基于PS-InSAR和SBAS技术监测南京市地面沉降. 大地测量与地球动力学, 2019, 39(2): 158-163. |
| [17] |
Williams S, Bock Y, Fang P. Integrated satellite interferometry: Tropospheric noise, GPS estimates and implications for interferometric synthetic aperture radar products. Journal of Geophysical Research: Solid Earth, 1998, 103(B11): 27051-27067. DOI:10.1029/98JB02794 |
| [18] |
Strozzi T, Wegmuller U, Werner C, et al. Measurement of slow uniform surface displacement with mm/year accuracy. IGARSS 2000. IEEE 2000 International Geoscience and Remote Sensing Symposium. Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment. Proceedings (Cat. No. 00CH37120). Honolulu: IEEE, 2000. 2239–2241.
|
| [19] |
Raucoules D, Maisons C, Carnec C, et al. Monitoring of slow ground deformation by ERS radar interferometry on the Vauvert salt mine (France): Comparison with ground-based measurement. Remote Sensing of Environment, 2003, 88(4): 468-478. DOI:10.1016/j.rse.2003.09.005 |
| [20] |
陈强, 丁晓利, 刘国祥. PS-DInSAR公共主影像的优化选取. 测绘学报, 2007, 36(4): 395-399. DOI:10.3321/j.issn:1001-1595.2007.04.007 |
| [21] |
Kampes BM. Radar Interferometry: Persistent Scatterer Technique. Dordrecht: Springer, 2014.
|
 2022, Vol. 31
2022, Vol. 31



