1 概述

近几年, 随着云计算技术的发展, 在云上部署应用服务有利于降低成本和提高效率, 但却引出了资源利用率低、部署和重启应用服务等待时间长等问题, 而Docker作为容器技术的代表, 为应用程序提供了更加轻量级和易于部署的解决方案, 如今已是云计算领域的热点.

Kubernetes是容器编排技术的代表, 是Google公司Borg项目的一个开源版本, 它基于Docker容器技术, 目的是实现资源管理的自动化, 以及跨多个数据中心的资源利用率最大化. Kubernetes具有完备的集群管理能力, 包括多层次的安全防护和准入机制、多租户应用支撑能力、透明的服务注册和服务发现机制、可扩展的资源调度机制等^[1]. 在Kubernetes集群中, 以Pod作为资源调度的基本单位, 而Pod中可以容纳多个容器, 集群根据其生命周期进行管理, 满足了产品内运行程序的需求, Kubernetes已成为大规模容器化应用程序部署的事实标准^[2]. 近年来, 大多数互联网公司的相关技术人员相继把Kubernetes运行在重要业务上, 同时越来越多的微服务也使用Kubernetes进行部署和管理.

Kubernetes资源调度是其核心的模块, 不合理的资源调度策略会造成云平台整体资源利用率低, 用户的部署请求得不到快速响应, 服务质量下降, 同时也提高服务商的软硬件设施成本.

Kubernetes调度策略首先根据用户提交的Pod应用的最小资源需求过滤掉不符合要求的节点, 其次以节点剩余CPU和内存的资源利用率为评分指标, 对候选节点评分, 选择得分最高的节点进行部署. 该策略存在两处不足: (1) 只考虑了CPU和内存两种资源指标, 无法满足各异的应用需求; (2) 采用相同权重计算候选节点得分, 易造成资源使用的过度倾斜.

关于Kubernetes资源调度问题, 已经有学者在优化节点负载、提高集群资源利用率和减少资源成本等方面做了大量研究. Menouer等^[3]在Docker Swarm中利用TOPSIS多属性决策方法结合Spread和Bin Packing原理优化了多个资源指标下容器的调度问题; El Haj Ahmed等^[4]通过容器应用的时间线和执行的历史信息来优化容器应用的部署; Imdoukh等^[5]提出了一种基于多目标遗传算法进行优化的调度算法MOGAS (many-objective genetic algorithm scheduler), 该调度算法与基于蚁群算法优化的调度算法相比较效果更佳; Zhang等^[6]通过结合蚁群算法和粒子群优化算法改进了Kubernetes调度模型, 不仅减少了总的资源成本和节点最大负载, 也使得应用部署更加平衡; 孔德瑾等^[7]提出一种基于资源利用率进行指标权重自学习的调度机制, 提升了集群资源均衡度和资源综合利用率; Li等^[8]提出BDI (balanced-disk-IO-priority)算法来动态调度容器应用以改善节点间磁盘I/O平衡, 提出BCDI(balanced-CPU-disk-IO-priority)算法动态调度容器应用以解决单节点CPU和磁盘I/O负载不平衡的问题; 吴双艳^[9]通过灰色预测算法对资源负载进行预测, 对容器云平台弹性伸缩系统优化来提高服务质量; Dua等^[10]提出一种可供选择的任务调度算法, 为特定类型任务打上标签, 并基于标签将任务迁移实现集群负载均衡; Zheng等^[11]提出一种基于Docker集群的自定义Kubernetes调度器调度策略, 使用优化的预选算法模型和优选算法模型改进Kubernetes默认调度策略, 提高集群调度的公平性和调度效率.

虽然国内外学者针对Kubernetes资源调度的研究已经取得了较多的成果, 但在异构环境下兼顾资源指标权重和资源指标本身都有些欠缺. 针对此问题, 本文主要在崔广章等^[12]、龚坤等^[13]的基础上, 选择CPU、内存、带宽、磁盘容量和IO速率的实时资源利用率作为评价指标, 并将基于层次分析法和熵权法得到的组合权重应用到TOPSIS多属性决策算法中, 致力于将Pod应用部署到最合适的节点上.

2 Kubernetes默认调度策略

Kubernetes Scheduler是Kubernetes集群的调度器, 用于将用户创建的Pod按照特定的调度算法和调度策略绑定到集群中某个合适节点上. 其调度过程可以分为两个阶段, 分别是预选和优选阶段.

预选阶段主要是根据用户提交Pod应用的最小资源需求过滤掉不满足需求的节点, Kubernetes也提供了多种预选策略供用户选择, 如PodFitsResources、PodsFitsPorts等.

优选阶段主要是在预选阶段的基础上, 采集剩下节点上CPU和内存的空闲利用率进行评分, 选择评分最高的节点作为部署节点, 最后将Pod应用绑定到该节点上. 同样的, Kubernetes也提供了几种优选策略:

1) LeastRequestedPriority, 该策略用于从候选节点中选出资源消耗最小的节点, 即CPU和内存空闲资源越多, 评分越高, 其计算公式如下:

$ score = \left[\frac{{({\textit{Scpu}} - {\textit{Ncpu}})}}{\textit{Scpu}}\times 10 + \frac{{({\textit{Smem}} - {\textit{Nmem}})}}{\textit{Smem}}\times 10\right]\Bigg/2 $

(1)

2) BalancedResourceAllocation, 该策略用于从候选节点中选出CPU和内存使用率最均衡的节点, 即CPU和内存使用率越接近, 评分越高, 其计算公式如下:

$ score = 10 - abs\left(\frac{\textit{Ncpu}}{\textit{Scpu}} - \frac{\textit{Nmem}}{\textit{Smem}}\right)\times 10 $

(2)

上述两种策略, 均只考虑了CPU和内存, 且策略中CPU和内存利用率是由Pod应用的需求来衡量调度的优先级的, 无法准确反映节点实际资源使用情况, 也会影响节点的整体资源均衡性.

3) SelectorSpreading, 该策略将相同标签选择器选取的Pod应用尽可能散开部署到多个节点上, 节点上该标签选择器匹配的Pod应用数目越少, 则该节点的评分越高, 使用标签选择器的资源对象有: Service, Replication Controller, ReplicaSet等.

此外, 调度策略还包括NodePerferAvoidPods, InterPodAffinity, NodeAffinity, TaintToleration等.

上述公式中, Scpu和Smem分别表示节点上总的CPU和内存容量, 而Ncpu和Nmem分别表示节点上已被使用的CPU和内存的容量加上将要部署的Pod应用的CPU和内存的容量之和.

3 组合权重的TOPSIS调度策略

由于Kubernetes默认调度算法仅仅考虑CPU和内存, 没有考虑到带宽、IO速率、磁盘容量等资源的需求, 无法对带宽敏感型、IO速率敏感型等Pod应用进行合理的资源调度, 同时两个评分指标都采用相同权重, 无法满足Pod应用各异的资源需求, 当Pod应用部署的数量逐步增加时, 可能会造成其他指标如带宽、IO速率等资源过度浪费.

在评价指标方面, 考虑到评价指标应该有效且有代表性, 因此本文选择CPU、内存、带宽、磁盘容量、IO速率作为评价指标.

在权重方面, 本文利用熵权法^[14]对层次分析法^[15]得到的主观权重进一步优化, 有效避免了层次分析法权重的主观性和熵权法权重的客观性.

最后将组合权重应用到TOPSIS^[16]多属性决策方法中, 来计算Pod应用调度方案解和理想最优解及最劣解之间的距离, 通过理想贴合度的大小排序, 为Pod应用选择最合适的节点进行部署.

3.1 资源信息获取

本文主要采集两种资源信息:

(1) 节点当前的各个资源指标的资源利用率.

(2) 已部署的Pod应用在节点上占用的资源份额.

通过在集群中每个节点上部署Proxy监控代理, 用于采集上述两种资源信息, 具体流程如图1所示. 首先准备两个数据库, 分别用于存储监控节点的资源利用率和Pod的CPU、内存、带宽、磁盘、IO速率占用率信息. 在控制器模块逐个分析节点Node标识和Pod应用标识, 控制器可获取到Proxy代理的IP、端口, 向Proxy代理发送监控命令, 之后采集实验需要的监控信息存放到对应的数据库中.

3.2 层次分析法求权重

层次分析法是一种使人们的思维过程和主观判断实现规划化的方法, 可以使因素的不确定性得到很大程度降低, 不仅简化了系统分析与计算工作, 而且有助于决策者保持其思维过程和决策过程原则的一致性, 是一种确定权重的科学方法, 其计算步骤如下:

Step 1. 构造资源指标判断矩阵

假设集群中有m个资源指标, 通过两两比较确定指标重要程度, 进而得出判断矩阵 $ A = {({a_{ij}})_{m \times m}} $ , i=1, 2, …, m; j=1, 2, …, m, 重要程度的定义如表1所示.

$ A = \left( {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}& \ldots &{{a_{1m}}} \\ {{a_{21}}}&{{a_{22}}}& \cdots &{{a_{2m}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{a_{m1}}}&{{a_{m2}}}& \cdots &{{a_{mm}}} \end{array}} \right) $

(3)

矩阵中, m表示资源指标的个数, $ {a_{ij}} $ 表示相对于第j个资源指标, 第i个资源指标的重要程度, 且 $ {a_{ii}} = 1 $ .

本文以5种资源指标CPU, 内存, 带宽, 磁盘, IO速率为基础, 给出判断矩阵如下, 选取理由如表2所示.

$ A = \left( {\begin{array}{*{20}{c}} 1&3&5&7&5 \\ {1/3}&1&3&5&3 \\ {1/5}&{1/3}&1&3&1 \\ {1/7}&{1/5}&{1/3}&1&{1/3} \\ {1/5}&{1/3}&1&3&1 \end{array}} \right) $

(4)

Step 2. 一致性检验

判断矩阵客观反映了不同资源指标之间的相对重要性, 但是并不能保证每个判断矩阵都是一致的. 例如, 指标A₁比指标A₂重要, 指标A₂比指标A₃重要, 那么指标A₃比指标A₁重要就不合理, 因此需要通过计算一致性检验CI(consistency index) 和一致性比例CR(consistency ratio)来衡量判断矩阵是否完全一致, 具体计算公式如下:

$ CI = \frac{{{\lambda _{\max }} - m}}{{m - 1}} $

(5)

$ CR = \frac{{CI}}{{RI}} $

(6)

其中, $ {\lambda _{\max }} $ 为判断矩阵的最大特征根, m为矩阵的阶数, RI为平均一致性指标, 其取值如表3所示. 若 $ CR < 0.1 $ , 则通过一致性检验, 否则判断矩阵需要修正.

Step 3. 计算资源指标权重

本文选择常用特征值法来计算权重, 只需要计算符合 $ A \cdot W = {\lambda _{\max }} \cdot W $ 的特征向量, 然后 $ {W{{\lambda _{\max }}}} $ 将归一化, 即可得到权重 $ {w_{Aj}} $ , 具体权重信息如表4所示.

3.3 熵权法求权重

熵权法基本思路是根据指标变异性的大小来确定客观权重. 该方法可以深刻反映出指标的区分能力, 若某个指标的信息熵越小, 表明指标值的变异程度越大, 提供的信息量越多, 在综合评价中所能起到的作用也越大, 其权重也就越大. 其计算步骤如下.

Step 1. 数据预处理

假设集群中有n个节点, m个资源指标, 通过监控代理Proxy采集到的资源利用率的实时数据, 构造矩阵 $ X = {\left( {{x_{ij}}} \right)_{n \times m}} $ , i=1, 2, …, n; j=1, 2, …, m, $ {x_{ij}} $ 表示第i个节点上第j个资源指标的资源利用率.

$ X = \left[ {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}& \ldots &{{x_{1m}}} \\ {{x_{21}}}&{{x_{22}}}& \cdots &{{x_{2m}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{x_{n1}}}&{{x_{n2}}}& \cdots &{{x_{nm}}} \end{array}} \right] $

(7)

Step 2. 资源指标归一化处理

考虑到每个资源指标的计量单位不同, 有必要在计算综合资源指标前, 进行标准化处理, 即把资源指标的绝对值转化为相对值.

正向型资源指标归一化, 用于处理效益型决策参数, 这类决策参数的特点是值越大效果越好, 其计算公式如下:

$ {x^{'}_{ij}} = \frac{{{x_{ij}} - \max \left( {{x_j}} \right)}}{{\max \left( {{x_j}} \right) - \min \left( {{x_j}} \right)}} $

(8)

负向型资源指标归一化, 用于处理成本型决策参数, 这类决策参数的特点是值越小效果越好, 其计算公式如下:

$ {x^{'}_{ij}} = \frac{{\max \left( {{x_j}} \right) - {x_{ij}}}}{{\max \left( {{x_j}} \right) - \min \left( {{x_j}} \right)}} $

(9)

其中, $ \max \left( {{x_j}} \right) $ 和 $ \min \left( {{x_j}} \right) $ 分别表示第j个资源指标的最大值和最小值, i=1, 2, …, n; j=1, 2, …, m.

Step 3. 计算第j个资源指标下第i个节点的值所占该资源指标的比重 $ {P_{ij}} $ , i=1, 2, …, n; j=1, 2, …, m.

$ {P_{ij}} = \frac{{{x^{'}}_{ij}}}{{\displaystyle\sum\limits_{i = 1}^n {{x^{'}}_{ij}} }} $

(10)

Step 4. 计算第j个资源指标的熵值 $ {e_j} $ , j=1, 2, …, m.

$ {e_j} = - k\sum\limits_{i = 1}^n {{P_{ij}}In} \left( {{P_{ij}}} \right) $

(11)

其中, $ k = 1/In\left( n \right) > 0 $ , 满足 $ {e_j} \ge 0 $ .

Step 5. 计算资源指标的差异系数 $ {d_j} $ , j=1, 2, …, m.

$ {d_j} = 1 - {e_j} $

(12)

Step 6. 计算各指标的权重 $ {w_{{{E}}j}} $ , j=1, 2, …, m.

$ {w_{Ej}} = \frac{{{d_j}}}{{\displaystyle\sum\limits_{j = 1}^m {{d_j}} }} $

(13)

3.4 计算组合权重

将熵权法得到的权重与层次分析法得到的权重结合, 用于避免层次分析法的主观影响和熵权法的客观影响, 其计算公式如下:

$ {w_j} = \frac{{\sqrt {{w_{Aj}} \cdot {w_{Ej}}} }}{{\displaystyle\sum\limits_{j = 1}^m {\sqrt {{w_{Aj}} \cdot {w_{Ej}}} } }} $

(14)

其中, $ {w_j} $ 为第j个资源指标的组合权重, $ {w_{Aj}} $ 和 $ {w_{Ej}} $ 分别表示通过层次分析法和熵权法得到的第j个资源指标的权重.

以表4得到的AHP权重为基础, 监控代理Proxy采集到的某个时间段的5种资源指标的实时利用率如表5所示, 根据表5的数据计算出熵权权重, 最后根据式(14)计算得到组合权重, 具体权重信息如表6所示.

3.5 TOPSIS确定最优节点

逼近理想解排序方法(TOPSIS)是一种有效的多属性决策方案, 通过从归一化的数据矩阵中构造出决策问题的正负理想解, 计算出方案与正负理想解的距离, 最终得到贴合度作为评价方案的优劣依据. 其计算步骤如下.

Step 1. 构造决策矩阵

假设集群中有n个节点, m个资源指标, 通过监控代理Proxy采集到的资源利用率的实时数据加上Pod部署所占用的资源利用率, 构造决策矩阵 $ X = {\left( {{x_{ij}}} \right)_{n \times m}} $ , i=1, 2, …, n; j=1, 2,…, m.

$ X = \left[ {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}& \ldots &{{x_{1m}}} \\ {{x_{21}}}&{{x_{22}}}& \cdots &{{x_{2m}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{x_{n1}}}&{{x_{n2}}}& \cdots &{{x_{nm}}} \end{array}} \right] $

(15)

其中, $ {x_{ij}} $ 表示第i个节点上第j个资源指标的资源利用率.

Step 2. 归一化决策矩阵

采用极差标准化方法对决策矩阵进行归一化处理, 目的是消除决策参数不同量纲之间的影响.

$ {x^{'}_{ij}} = \frac{{\max \left( {{x_j}} \right) - {x_{ij}}}}{{\max \left( {{x_j}} \right) - \min \left( {{x_j}} \right)}} $

(16)

其中, $ \max \left( {{x_j}} \right) $ 和 $ \min \left( {{x_j}} \right) $ 分别表示第j个资源指标的最大值和最小值, i=1, 2, …, n; j=1, 2, …, m.

Step 3. 构造加权决策矩阵

各异的Pod应用对节点资源指标的需求敏感程度不同. 大体上可以分为内存倾向型、CPU倾向型、IO速率倾向型, 带宽倾向型等等, 若是每个资源指标都采用相同权重, 无法满足各异需求的Pod应用, 因此有必要分别为节点的资源指标设置不同的权重.

基于此, 在考虑资源指标的差异性, 和避免了层次分析法人为的主观影响和熵权法带来的客观影响下, 本文通过结合层次分析法与熵权法得到组合权重, 并应用到决策矩阵中, 构造了加权决策矩阵 $ Z = {\left( {{{\textit{z}}_{ij}}} \right)_{n \times m}} $ , i=1, 2, …, n; j=1, 2, …, m.

$ {{\textit{z}}_{ij}} = \frac{{x^{'}_{ij}}}{{\sqrt {\displaystyle\sum\limits_{i = 1}^n {x^{'}{{_{ij}}^2}} } }} \cdot {w_j} $

(17)

其中, $ {w_j} $ 是第j个资源指标的组合权重.

Step 4. 计算正负理想解

$ {Z^ + } = \left( {{Z_1}^ + {\text{,}}{{\text{Z}}_2}^ + ,\cdots,{Z_m}^ + } \right) = \left( {\max \left\{ {{{\textit{z}}_{1m}},{{\textit{z}}_{2m}},\cdots,{{\textit{z}}_{nm}}} \right\}} \right) $

(18)

$ {Z^ - } = \left( {{Z_1}^ - {\text{,}}{{\text{Z}}_2}^ - ,\cdots,{Z_m}^ - } \right) = \left( {\min \left\{ {{{\textit{z}}_{1m}},{{\textit{z}}_{2m}},\cdots,{{\textit{z}}_{nm}}} \right\}} \right) $

(19)

其中, $ {Z^ + } $ 表示加权决策矩阵的正理想解, 由所有候选节点上每种资源指标参数的最大值构成; $ {Z^ - } $ 表示加权决策矩阵的负理想解, 由所有候选节点上每种资源指标参数的最小值构成.

Step 5. 计算每个候选节点到正、负理想解的距离

$ {D^ + } = \sqrt {\sum\limits_{j = 1}^m {{{\left( {{Z_j}^ + - {{\textit{z}}_{ij}}} \right)}^2}} } $

(20)

$ {D^ - } = \sqrt {\sum\limits_{j = 1}^m {{{\left( {{Z_j}^ - - {{\textit{z}}_{ij}}} \right)}^2}} } $

(21)

其中, $ {D^ + } $ 和 $ {D^ - } $ 分别代表各候选节点到正负理想解的欧式距离.

Step 6. 计算每个候选节点与最优候选节点的相对贴合度 $ {S_i} $

$ {S_i} = \frac{{{D_i}^ - }}{{{D_i}^ + + {D_i}^ - }} $

(22)

其中, 相对贴合度 $ {S_i} $ 越大, 说明该候选节点越适合当前需要部署的Pod应用.

以表5和表6的数据为基础, 结合TOPSIS多属性决策算法可以得到相对贴合度S, 如表7所示, 可以看出节点1的相对贴合度S最大, 因此将Pod应用部署到节点1最合适.

4 实验验证与分析

为测试本文提出的Kubernetes调度算法的性能, 进行实验验证. 所有实验均由PyCharm 2020.2编程实现, 并基于平台: Windows 10, Intel(R) Core(TM) i7-8565U CPU 1.80 GHz, 16 GB内存.

4.1 实验环境

在仿真环境下, 模拟一个包含60个节点的Kubernetes集群, 集群中节点分为3种类型, 每种类型20个来模拟异构的环境, 节点具体信息如表8所示.

同样的, 鉴于容器应用资源多样化的需求, 本文按照CPU敏感型、内存敏感型、带宽敏感型、存储敏感型、IO速率敏感型以及无倾向类型6类容器应用构造了Pod资源需求, 表9为部分Pod资源需求.

4.2 实验评价指标

假设Kubernetes集群中有n个节点, 每个节点上有m种资源. 资源的实时利用率是通过监控代理Proxy采集获取得到的. $ U\left( {i,j} \right) $ 表示节点i上资源j的资源利用率; ${U_{\rm{avg}}}\left( i \right)$ 表示节点i上各个资源利用率总和的平均值; $ S\left( i \right) $ 表示节点i上各个资源利用率的标准差, 即资源失衡度; ${S_{\rm{avg}}}$ 表示所有节点的平均资源失衡度. ${S_{\rm{avg}}}$ 的值越小, 代表集群中各个资源的利用率越平衡, 就不容易出现资源倾斜, 如此就可以部署更多的Pod应用, 具体计算公式如下:

$ {U_{\rm{avg}}} = \sum\limits_{j = 1}^m {\frac{{U\left( {i,j} \right)}}{m}} $

(23)

$ S\left( i \right) = \sqrt {\sum\limits_{j = 1}^m {{{\left( {U\left( {i,j} \right) - {U_{\rm{avg}}}\left( i \right)} \right)}^2}} } $

(24)

$ {S_{\rm{avg}}} = \sum\limits_{i = 1}^n {\frac{{S\left( i \right)}}{n}} $

(25)

4.3 实验结果和分析

在上述Kubernetes集群中, 分别采用Kubernetes的LeastRequestedPriority (LRP)策略与BalancedResource-Allocation (BRA)策略和本文提出的组合权重TOPSIS调度算法(CWT), 从资源平衡度、CPU、内存、带宽、IO速率角度来对比3种算法的表现.

1) 集群资源失衡度

集群失衡度变化曲线如图2所示, 当Pod数量小于1 200时, 此时集群负荷相对较低, LRP和BRA策略与CWT算法的资源失衡度相差不大, 但随着部署的Pod应用数量越来越多, 可以很明显的发现CWT算法开始发挥作用, 它的资源失衡度明显好于LRA策略.

在集群资源整体快达到饱和时, CWT算法优于BRA策略. 这是由于CWT算法不仅考虑了集群节点的5种资源指标, 还分别考虑了各个资源指标的权重情况, 这就降低了集群中单个节点出现单个资源用尽而其他资源大量剩余的可能. 尤其是在集群资源整体饱和的情况下, CWT算法的资源失衡度比LRA策略整体下降18%, 比BRA策略整体下降7.7%, 这说明CWT算法在集群资源饱和的情况下可有效的调节集群资源平衡度.

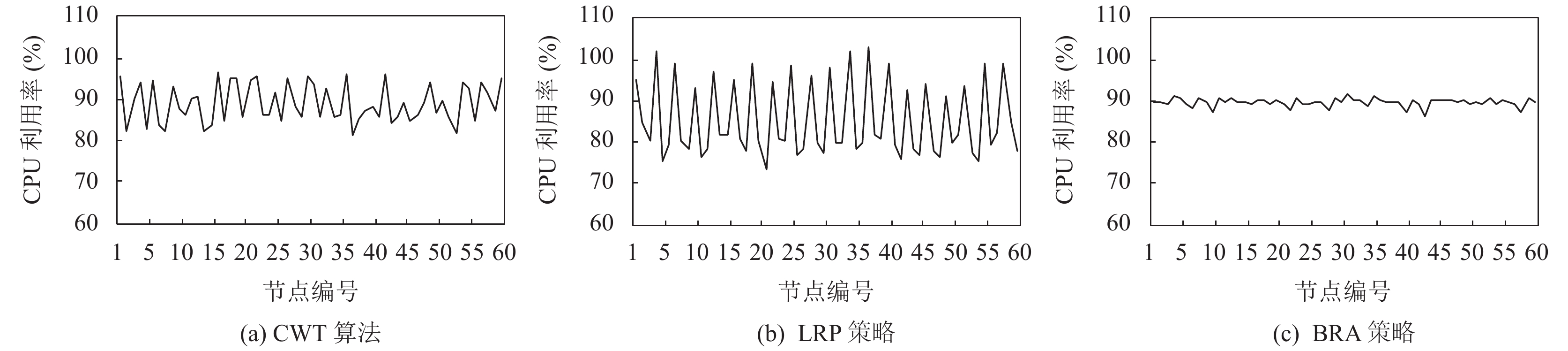
2) CPU、内存资源利用率

图3和图4反映了在Pod应用数量为7 200时, CWT算法、LRP策略和BRA策略下各个节点的CPU和内存资源利用率的情况. 在BRA策略下, CPU资源利用率和内存资源利用率好于CWT算法, 且远远好于LRP策略, 这是由于BRA策略会选取CPU和内存资源使用率最接近的节点进行部署. 而在LRP策略下, 有3个节点CPU资源已经饱和, 1个节点的内存资源已经饱和, 饱和率达到6.7%, 这意味着这4个节点上所有Pod应用的处在资源受到限制的环境, 严重影响了集群的整体健康. 在CWT算法下, CPU和内存的资源利用率波动比BRA策略稍微大一些, 这是由于CWT算法综合考虑了5种资源指标, 相较于BRA策略只考虑CPU和内存两种资源指标, CWT算法则考虑的更加全面, 更加能适应实际生产环境的需求.

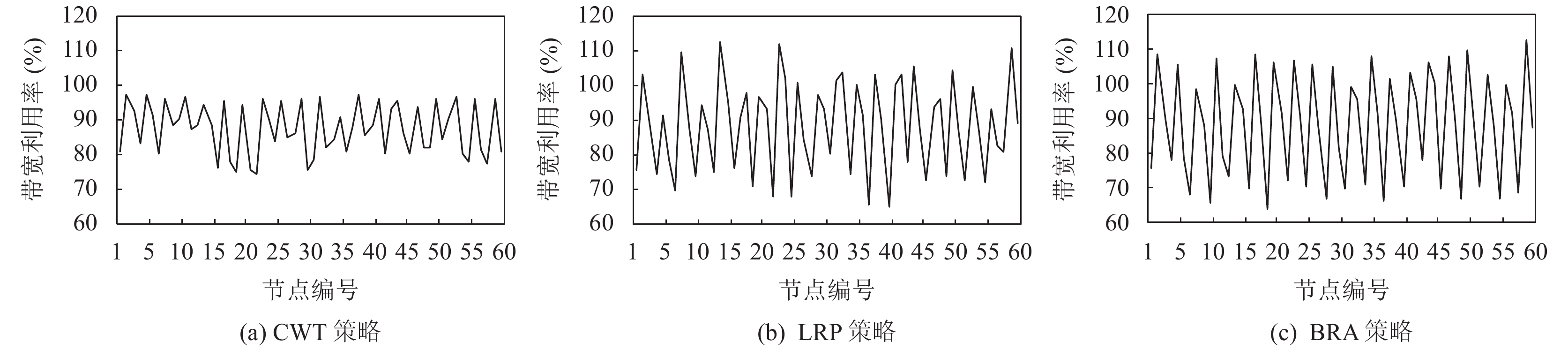
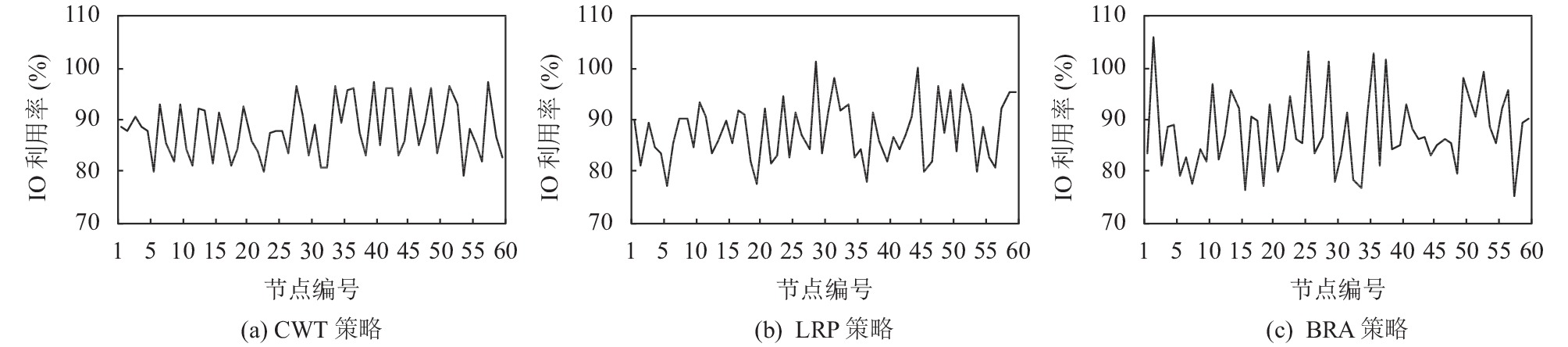
3) 带宽、IO速率资源利用率

图5和图6反映了在Pod应用数量为7 200时, CWT算法、LRP策略和BRA策略下各个节点的带宽和IO速率资源利用率的情况. 由于LRP策略与BRA策略只考虑CPU和内存, 未考虑带宽和IO速率等因素, 随着Pod应用数量增加, 在这两种策略下资源失衡度上升, 集群中部分节点出现资源倾斜, 尤其是带宽和IO资源利用率, 很明显可以看出集群中节点之间利用率波动较大.

在LRP策略下, 带宽利用率最大的节点与利用率最小的节点相差48%, IO资源利用率最大的节点与利用率最小的节点相差24%, 而在BRA策略带宽利用率最大的节点与利用率最小的节点相差47%, IO资源利用率最大的节点与利用率最小的节点相差41%, 甚至有多个节点的带宽和IO资源利用率已超过100%, 这说明这些节点的带宽和IO资源已经完全饱和, LRP策略下饱和率达到25%, BRA策略下饱和度达到18.3%. 若是带宽和IO速率敏感型的Pod应用被部署在这些带宽和IO资源饱和的节点上, 会带来网络和IO读写的拥堵.

在CWT算法下, 全部节点的带宽和IO资源利用率都在75%到95%的区间内震荡, 没有出现带宽资源利用率超过100%的情况, 相较于LRP策略和BRA策略, CWT算法更加保障了集群的带宽稳定.

5 结论与展望

本文针对Kubernetes默认调度算法仅考虑CPU、内存两种资源指标, 且对需求各异的Pod应用采用相同权重的调度策略进行了改进, 通过增加带宽、磁盘、IO速率3项指标, 结合层次分析法与熵权法得到每个资源指标的组合权重, 并应用到TOPSIS多属性决策方法中, 为Pod应用选择合适的节点进行部署, 有效提高了集群整体的资源平衡度, 避免了集群中节点上单个资源耗尽而其他资源尚有剩余的情况, 通过实验验证, 证明了组合权重TOPSIS调度算法的有效性和合理性. 下一阶段将考虑集群的动态调度与多租户情况相结合, 使得集群资源调度更加高效, 集群资源更加平衡, 集群资源利用率更高.