随着科学技术的进步, 不同领域的数据都呈现出网络连接的趋势, 许多科学领域都涉及某种形式的网络研究, 例如人际关系研究、学术论文合著和引用、蛋白质相互作用模式等. 20年前, 关于网络的流行书籍及其研究开始出现[1], 而像Facebook、MySpace和LinkedIn这样的在线网络社区在近10年间也是蓬勃兴起, 这更加增强了人们对网络数据的研究兴趣. 网络连接数据由节点和边组成, 社交网络是此类网络模型的一个典型代表. 社交网络中, 每个节点代表一个人, 边代表人与人之间的沟通交流, 此外, 还有商业网络、基因网络等.
目前关于网络连接数据的研究主要分为两个方面. 一方面是关于网络结构的研究. 另一方面主要是将网络连接数据中的结构信息与统计学习中常用的经典模型结合起来研究.
在网络结构方面, 最早被应用于社区检测. 社区检测兴起于物理学和计算机科学领域, 而后开始应用于统计领域. 其中一类社区检测算法是通过在节点的所有可能分区上优化启发式全局准则来检测社区[2, 3]. 基于概率模型的方法[4, 5]是另一类社区检测算法. 一些学者从观察到的邻接矩阵中检测社区或潜在结构[6-8], 从其他节点之间的信息估计特定节点之间的边缘概率[9]. 社交网络是此类网络模型的代表, 因此针对社交网络的研究也受到了大量的关注[10, 11].
在与经典模型结合方面, 一般是与常用的模型相结合. 例如, 时间序列模型[12], 线性模型[13], 变系数模型[14], 随机效应模型[15], 变化点检测问题[16], 自回归模型[17, 18]等.
线性回归模型是统计学习中的经典模型之一, 应用十分广泛, 关于网络数据的回归模型也开始引起学者的关注. 例如, Asur等[19]将网络数据应用于预测模型, 通过研究网络结构来预测现实生活中某一现象的结果. Li等[13]将网络连接数据应用于回归预测模型, Zhu等[17]和Tang等[18]将网络连接数据与自回归模型相结合, 都表明网络连接数据在回归模型中的研究价值. 随着科技的发展, 数据的采集变得更加容易, 高维数据也越来越受到研究学者的关注, 但是高维数据中存在大量的冗余信息, 如何选出有研究价值的数据?变量选择领域应运而生. 故将网络连接数据应用到变量选择领域是一个值得研究的课题.
对于线性回归模型, 超高的维度使得传统的普通最小二乘法不再适用. 正则化是稀疏建模和变量选择的有效方法, 通过在目标函数上添加惩罚函数来降低模型的复杂度. 根据惩罚函数的不同, 正则化方法一般可以分为凸正则化和非凸正则化.
凸正则化方法主要包括岭回归、LASSO、弹性网以及Dantzig Selector等. 虽然凸正则化的研究已经很成熟, 但由于惩罚函数的凸性, 使得凸正则化估计量都是有偏的. Fan等提出了一个非凸正则化方法—SCAD(smoothly clipped absolute deviation)[20], 并证明了其Oracle性质. 非凸惩罚函数回归的渐进无偏估计, 能进一步降低模型的预测总误差. 此后, 非凸惩罚受到了广泛的关注, 例如MCP (minimax concave penalty)[21]、限制Capped-
关于网络连接数据的变量选择问题近年来也有学者做过相关研究[24, 25]. 例如Li等[24]和Kim等[25]考虑样本系数之间的网络凝聚效应, 即网络中连接节点表现出相似的行为, 对系数同时施加了
本文的目标是对因网络凝聚效应而产生个体效应的组异质性的网络连接数据进行变量选择, 我们对组内样本间个体效应的差异性
本文中所有的向量都是列向量. 考虑一般的线性回归模型,
| $ {\boldsymbol{Y}} = {\boldsymbol{\alpha}} + {\boldsymbol{X\beta}} + {\boldsymbol{\varepsilon}} $ | (1) |
其中,
Li等[13]提出了网络连接数据的预测方法(the regression with network cohesion, RNC), 其主要思想是最小化如下损失函数:
| $ {\boldsymbol{L}}({\boldsymbol{\alpha}} , {\boldsymbol{\beta}} ) = ||{\boldsymbol{Y}} - {\boldsymbol{\alpha}} - {\boldsymbol{X\beta}} |{|^2} + {\boldsymbol{\mu}} {{\boldsymbol{\alpha}} ^{\rm T}}{\boldsymbol{L\alpha}} $ | (2) |
其中,
RNC中假设各样本的个体效应不相等, 惩罚项
令
| $ Q({\boldsymbol{\alpha}} , {\boldsymbol{\beta}} ) = \frac{1}{{2n}}||{\boldsymbol{Y}} - ({\boldsymbol{X}}, {\boldsymbol{I}}){\boldsymbol{\theta}} ||_2^2 + {p_\lambda }(|{\boldsymbol{H}}{\boldsymbol{\theta}} |) $ | (3) |
在本文中, 对
将SNC方法的估计结果与没有对节点个体效应的差异进行惩罚的情况下进行对比, 能够提高估计和预测的精度.
2 算法直接最小化目标函数(3)很难求解出估计量的值, 因为惩罚函数对于每个
| $\left\{ \begin{array}{l} Q({\boldsymbol{\theta}} , {\boldsymbol{\gamma}} ) = \dfrac{1}{{2n}}||{\boldsymbol{Y}} - ({\boldsymbol{X}}, {\boldsymbol{I}}){\boldsymbol{\theta}} ||_2^2 + {p_\lambda }(|{\boldsymbol{\gamma}} |)\\ {\rm {s.t.}}\;\;\;\;\;\;{\boldsymbol{H\theta}} - {\boldsymbol{\gamma}} = {\boldsymbol{0}} \end{array} \right.$ |
基于文献[26]中的思路, 利用增广拉格朗日方法, 通过最小化如下损失函数得到参数的估计:
| $ L({\boldsymbol{\theta}} , {\boldsymbol{\gamma}} , {\boldsymbol{\varphi}} ) = Q({\boldsymbol{\theta}} , {\boldsymbol{\gamma}} ) + {{\boldsymbol{\varphi}} ^{\rm T}}({\boldsymbol{H\theta}} - {\boldsymbol{\gamma}} ) + \rho /2||{\boldsymbol{H\theta}} - {\boldsymbol{\gamma}} ||_2^2 $ | (4) |
其中, 对偶变量
| $ \rho /2||{\boldsymbol{\tau}} - {\boldsymbol{\gamma}} ||_2^2 + {p_\lambda }(|{\boldsymbol{\gamma}} |) $ |
其中,
| $ \hat {\boldsymbol{\gamma}} = ST({\boldsymbol{\tau}} , \lambda /\rho ), $ |
其中,
对于MCP罚函数
| $ {\hat{\gamma} _{ij}} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} ST({{{\tau}} _{ij}}, \lambda /\rho ), \\ {{{\tau}} _{ij}}, \end{array} &\begin{array}{l} |{{{\tau}} _{ij}}| \le a\lambda \\ |{{{\tau}} _{ij}}| > a\lambda \end{array} \end{array}} \right. $ |
对于SCAD罚函数
| $ {\hat{\gamma} _{ij}} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} ST({{{\tau}} _{ij}}, \lambda /\rho ), \\ \dfrac{{ST({{{\tau}} _{ij}}, a\lambda /(a - 1)\rho )}}{{1 - 1/((a - 1)\rho )}}, \\ {{{\tau}} _{ij}}, \end{array} &\begin{array}{l} |{{{\tau}} _{ij}}| \le \lambda + \lambda /\rho \\ \lambda + \lambda /\rho < |{{{\tau}} _{ij}}| \le a\lambda \\ |{{{\tau}} _{ij}}| > a\lambda \end{array} \end{array}} \right. $ |
算法步骤如算法1.
算法1. ADMM算法
输入: 预测变量
输出:
目标: 迭代求解获得
初始化
While
If
then
Break;
Else
End
End
对ADMM算法过程中的原始变量进行追踪,
下面考虑ADMM算法的收敛性.
命题1. 对于MCP和SCAD函数, ADMM算法的原始残差
命题1表明该算法实现了原可行性和对偶可行性, 证明材料见附录. 因此, 它收敛于一个局部最优点. 当采用非凸惩罚函数, 如MCP和SCAD罚函数时, 此最优点是目标函数的局部最优解. 综上, 算法收敛性和稳定性得到证明. 因为
在数值模拟中, 主要比较本文提出的SNC方法和没有对个体节点效应的差异性进行惩罚的LASSO、MCP、SCAD方法在变量选择和预测方面的效果. 网络凝聚效应下的变量选择方法就是考虑了样本之间的连接关系网络的方法, 即我们的SNC方法.无网络凝聚效应下的变量选择方法, 就是不考虑样本之间的连接网络的惩罚方法. 在这里, 我们首先定义几个效果评估指标:
(1)预测损失(prediction error, PE):
(2)
(3)均方误差(MSE(
(4)假阳性数(false positives, FP): 真实为反例却被预测为正例的个数;
(5)假阴性数(false negatives, FN): 真实为正例却被预测为反例的个数;
(6)真阳性数(true positives, TP): 真实为正例预测也为正例的个数;
(7)真阴性数(true negatives, TN): 真实为反例预测也为反例的个数;
(8)
对于式(1)中的线性回归模型, 我们从该模型中随机生成100个数据集. 训练样本的大小考虑两种情况
为了生成含有组异质性样本间的邻接矩阵
表1展示了两种方法在预测评估指标上的结果对比. 与没有利用相连节点的网络凝聚效应对个体效应进行惩罚的LASSO、MCP和SCAD结果相比, SNC-LASSO、SNC-MCP和SNC-SCAD都明显改善了估计和预测误差. 这表明将网络凝聚效应加入变量选择模型中, 可以改善模型变量选择、估计和预测的精度.
表2展示了两种方法在100次模拟实验下变量选择评估指标结果. 我们可以看出各项指标下, SNC方法的变量选择效果都明显优于没有利用网络凝聚效应进行惩罚的方法. 另外, SNC-MCP和SNC-SCAD都要优于SNC-LASSO. 尤其对于假阳性数FP, 100次模拟中, SNC-LASSO的FP平均为15.41 (
模拟1中的结果表明网络凝聚效应惩罚能够改善变量选择、估计和预测效果, 网络凝聚效应主要与邻接矩阵中个体之间产生联系的概率
| 表 1 不同方法下预测评估指标结果 |
| 表 2 不同方法下变量选择评估指标结果 |
图1和图2分别展示了
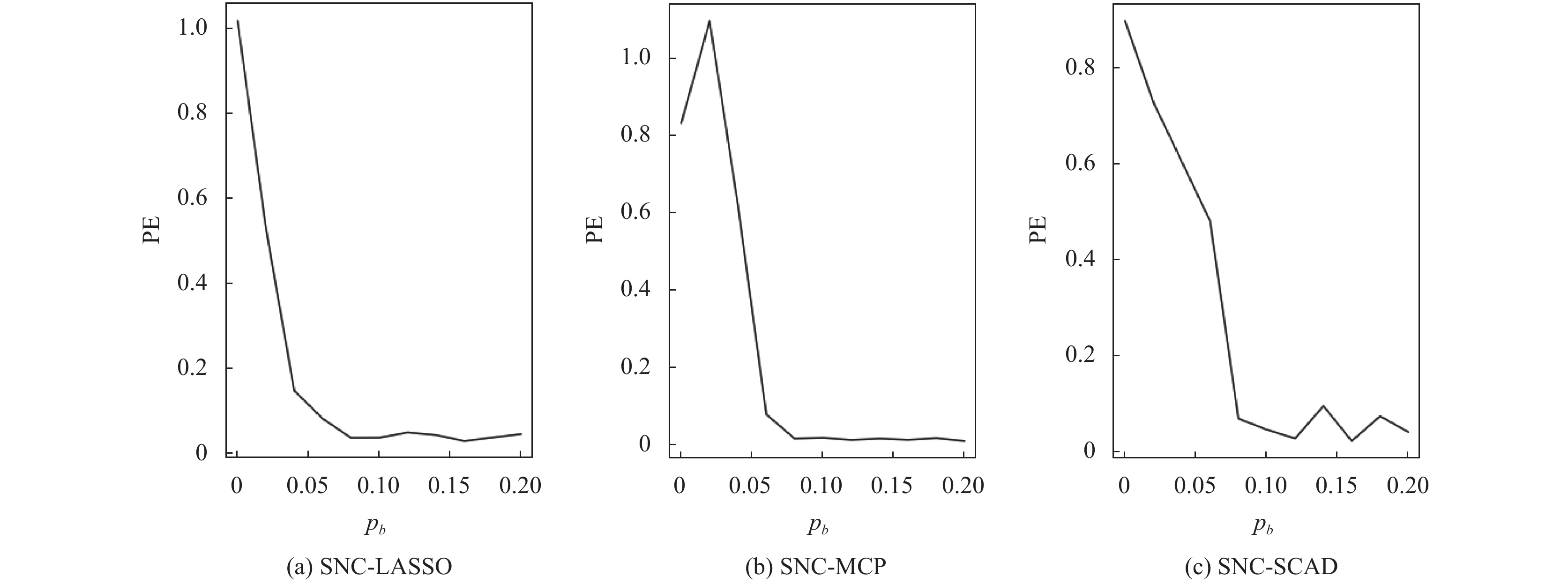
|
图 1 |
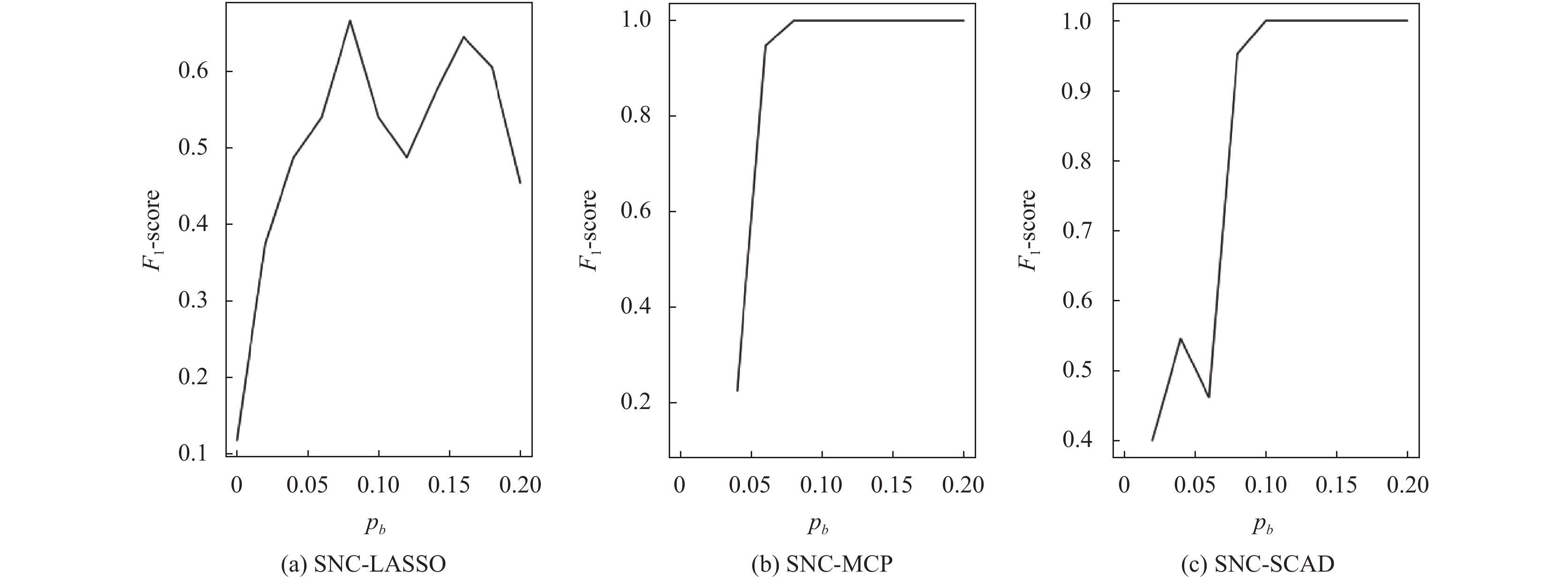
|
图 2 |
4 实际数据分析
我们研究的真实数据案例来自于Teenagers Friends and Lifestyle Study[27]. 这项研究主要是青少年友谊网对他们自身某些行为的影响. 该实际数据与本文中的模型设定保持一致, 因青少年时期学生喜爱团体活动, 故凝聚效应使得网络之间存在组异质性.
Teenagers Friends and Lifestyle Study旨在确定在青少年早期到中期不良习性的变化过程. 实验记录了3个时间点
本文使用的数据集
时间点
分别选取alcohol、tobacco和cannabis作为响应变量来研究影响青少年酗酒、吸烟和吸毒的因素. 将样本随机分成两份: 训练集和测试集, 重复实验100次. 由于不知道真实情况下的参数设定, 无法像模拟实验中那样对比假阴性数、假阳性数等指标. 因此, 主要从预测损失和变量选择两个方面来验证SNC方法的有效性.
表3展示了SNC方法SNC-LASSO、SNC-MCP、SNC-SCAD与无网络凝聚效应下的变量选择方法LASSO、MCP和SCAD对青少年不良习性(酗酒、抽烟以及吸食大麻)的预测损失, 从结果中可以看出SNC方法预测的相对更准确一点. 青少年时期大家都是团体活动, 生活习惯很容易相互影响而慢慢趋同, 而网络凝聚效应正是考虑了这一点, 团体内个体的表现行为更具相似性, 惩罚团体内个体效应的差异性, 提高了个体效应的预测精度, 从而降低了整个模型的预测误差.
为了使挑选出来的变量更具可解释性, 下面我们不考虑特征之间的交互作用, 用SNC方法和无网络凝聚效应下的变量选择方法来挑选变量, 并重复实验100次, 计算100次实验下挑选出来的变量的比例.
表4中我们看到, LASSO、MCP和SCAD挑选出更多的冗余变量. 显然, 两种方法下, 特征变量parent smoking, sibling smoking, “I hang round in the streets”, “I play computer games”和“I go to dance clubs or raves”是最显著的. 青少年时期他们的世界观、人生观和价值观还在形成阶段, 易受他人或团体的影响, 在街上闲逛、经常打电脑游戏、参加俱乐部以及兄弟姐妹抽烟等行为都容易使青少年沾染上不良习性. 通过研究分析, 我们知道了青少年时期朋友以及家人行为的重要性, 家人、朋友以及整个社会需要给青少年营造一个良好健康的成长环境, 给他们树立积极向上的榜样.
针对各种方法挑选出来变量之后的模型进行回归, 我们得到回归后各变量系数的显著性检验以及调整可决系数
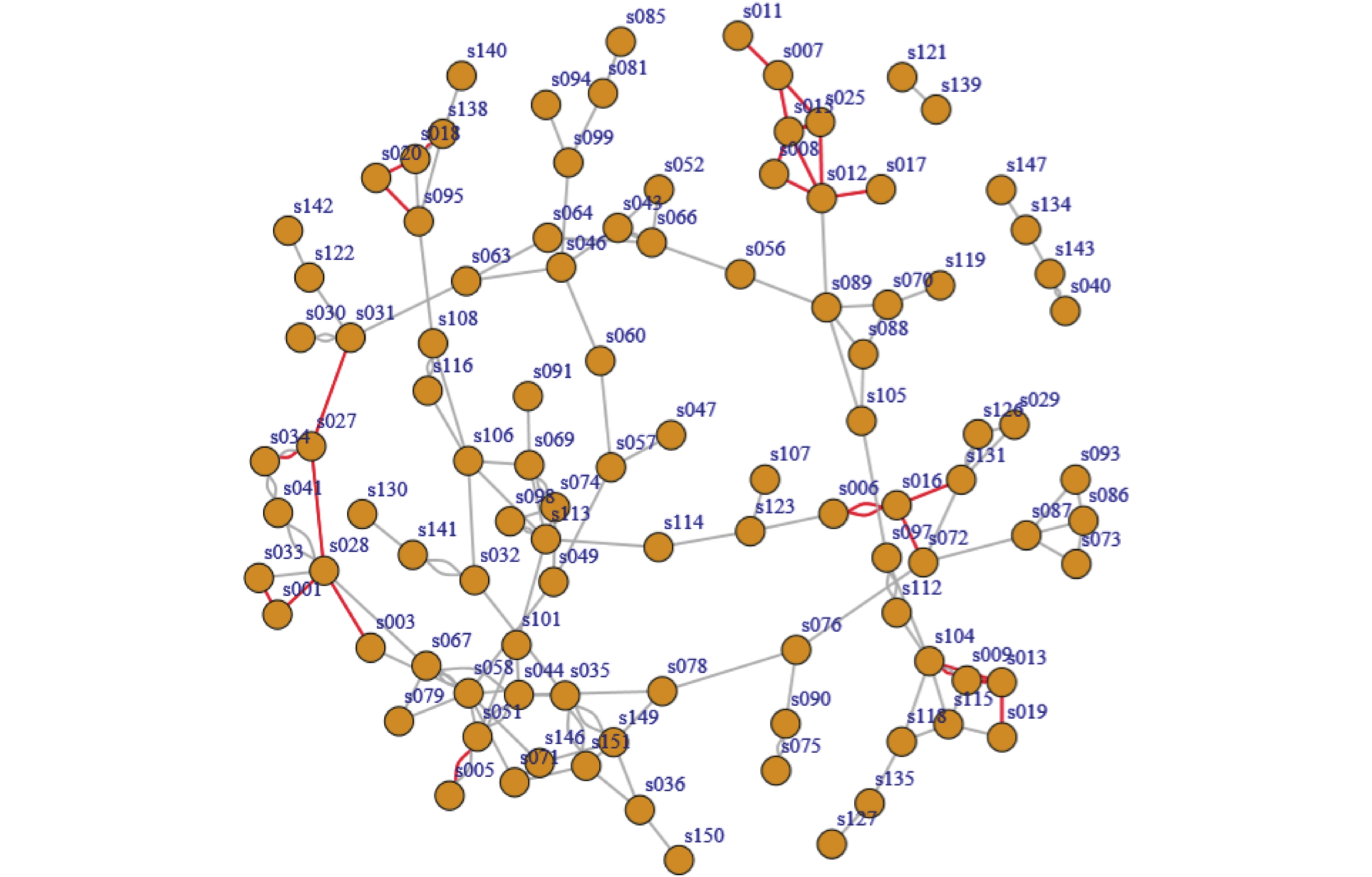
|
图 3 青少年友谊连接网络 |
| 表 3 青少年不良习性的预测损失 |
由表5可知, SNC方法选取了sex.F、I hang out in the streets、I play computer games、money、parent.smoking和sibling.smoking 6个变量, 根据值可以看出这些变量都通过了显著性检验. 而LASSO、MCP和SCAD方法选出了少许的冗余变量. 另外, 从表中的调整可决系数和标准误差来看, SNC方法的效果也是优于没有网络凝聚效应下的变量选择方法.
5 总结本文主要对线性回归模型中因网络凝聚效应而产生个体效应的组异质性的网络连接数据进行变量选择, 使用非凸惩罚MCP和SCAD罚函数同时惩罚变量系数
针对本文提出的方法, 我们运用ADMM算法进行求解, 并证明了算法的收敛性. 针对SNC方法, 本文进行了相关模拟, 从变量选择和预测两个方面来衡量该方法的效果. 从实验结果来看, 无论是预测损失还是变量选择的准确性都有明显改善. 实例分析中, 我们将SNC方法应用于青少年友谊网络和生活方式的研究, 分析预测青少年吸烟等不良习性的活动频率以及挑选出影响青少年吸烟等不良习性的特征变量.
| 表 4 不同方法下挑选出的变量及其比例 |
| 表 5 不同方法下挑选出变量的显著性检验 |
本文提出的方法, 为含有组异质性网络连接数据的变量选择问题提供了一种解决思路. 我们将变量选择方法进一步拓展了应用领域, 对于基因网络、交通网络、公司网络等网络连接数据, SNC方法都能适用.
| [1] |
Barabási AL, Crandall RE. Linked: The new science of networks. American Journal of Physics, 2002, 71(4): 409-410. DOI:10.1119/1.1538577 |
| [2] |
Wei YC, Cheng CK. Towards efficient hierarchical designs by ratio cut partitioning. 1989 IEEE International Conference on Computer-Aided Design. Digest of Technical Papers. Santa Clara: IEEE, 1989. 298–301.
|
| [3] |
Shi JB, Malik JM. Normalized cuts and image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(8): 888-905. DOI:10.1109/34.868688 |
| [4] |
Mariadassou M, Robin S, Vacher C. Uncovering latent structure in valued graphs: A variational approach. The Annals of Applied Statistics, 2010, 4(2): 715-742. DOI:10.1214/10-AOAS361 |
| [5] |
Karrer B, Newman MEJ. Stochastic blockmodels and community structure in networks. Physical Review E, 2011, 83(1): 016107. DOI:10.1103/PhysRevE.83.016107 |
| [6] |
Zhao YP, Levina E, Zhu J. Consistency of community detection in networks under degree-corrected stochastic block models. Annals of Statistics, 2012, 40(4): 2266-2292. DOI:10.1214/12-AOS1036 |
| [7] |
Geng JX, Bhattacharya A, Pati D. Probabilistic community detection with unknown number of communities. Journal of the American Statistical Association, 2019, 114(526): 893-905. DOI:10.1080/01621459.2018.1458618 |
| [8] |
Zhang Y, Levina E, Zhu J. Community detection in networks with node features. Electronic Journal of Statistics, 2016, 10(2): 3153-3178. DOI:10.1214/16-EJS1206 |
| [9] |
Zhao YP, Wu YJ, Levina E, et al. Link prediction for partially observed networks. Journal of Computational and Graphical Statistics, 2017, 26(3): 725-733. DOI:10.1080/10618600.2017.1286243 |
| [10] |
郑永广, 岳昆, 尹子都, 等. 大规模社交网络中高效的关键用户选取方法. 计算机应用, 2017, 37(11): 3101-3106. DOI:10.11772/j.issn.1001-9081.2017.11.3101 |
| [11] |
张书旋, 康海燕, 闫涵. 基于Skyline计算的社交网络关系数据隐私保护. 计算机应用, 2019, 39(5): 1394-1399. DOI:10.11772/j.issn.1001-9081.2018112556 |
| [12] |
Krampe J. Time series modeling on dynamic networks. Electronic Journal of Statistics, 2019, 13(2): 4945-4976. DOI:10.1214/19-EJS1642 |
| [13] |
Li TX, Levina E, Zhu J. Prediction models for network-linked data. The Annals of Applied Statistics, 2019, 13(1): 132-164. DOI:10.1214/18-AOAS1205 |
| [14] |
Lee J, Li G, Wilson JD. Varying-coefficient models for dynamic networks. Computational Statistics & Data Analysis, 2020, 152: 107052. DOI:10.1016/j.csda.2020.107052 |
| [15] |
Hoff PD. Additive and multiplicative effects network models. arXiv: 1807.08038, 2018.
|
| [16] |
Cheng JJ, Chen MJ, Zhou MC, et al. Overlapping community change-point detection in an evolving network. IEEE Transactions on Big Data, 2018, 6(1): 189-200. DOI:10.1109/TBDATA.2018.2880780 |
| [17] |
Zhu XN, Pan R, Li GD, et al. Network vector autoregression. The Annals of Statistics, 2017, 45(3): 1096-1123. DOI:10.1214/16-AOS1476 |
| [18] |
Tang YM, Bai Y, Huang T. Network vector autoregression with individual effects. Metrika, 2021, 84(6): 875-896. DOI:10.1007/s00184-020-00805-y |
| [19] |
Asur S, Huberman BA. Predicting the future with social media. 2010 IEEE/WIC/ACM International Conference on Web Intelligence and Intelligent Agent Technology. Toronto: IEEE, 2010. 492–499. [doi: 10.1109/WI-IAT.2010.63]
|
| [20] |
Fan JQ, Li RZ. Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American Statistical Association, 2001, 96(456): 1348-1360. DOI:10.1198/016214501753382273 |
| [21] |
Zhang CH. Nearly unbiased variable selection under minimax concave penalty. The Annals of Statistics, 2010, 38(2): 894-942. DOI:10.1214/09-AOS729 |
| [22] |
Zhang T. Analysis of multi-stage convex relaxation for sparse regularization. Journal of Machine Learning Research, 2010, 11: 1081-1107. |
| [23] |
Zheng ZM, Fan YY, Lv JC. High dimensional thresholded regression and shrinkage effect. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2014, 76(3): 627-649. DOI:10.1111/rssb.12037 |
| [24] |
Li CY, Li HZ. Network-constrained regularization and variable selection for analysis of genomic data. Bioinformatics, 2008, 24(9): 1175-1182. DOI:10.1093/bioinformatics/btn081 |
| [25] |
Kim S, Pan W, Shen XT. Network-based penalized regression with application to genomic data. Biometrics, 2013, 69(3): 582-593. DOI:10.1111/biom.12035 |
| [26] |
Ma SJ, Huang J. A concave pairwise fusion approach to subgroup analysis. Journal of the American Statistical Association, 2017, 112(517): 410-423. DOI:10.1080/01621459.2016.1148039 |
| [27] |
Pearson M, Michell L. Smoke rings: Social network analysis of friendship groups, smoking and drug-taking. Drugs: Education, Prevention and Policy, 2000, 7(1): 21-37. DOI:10.1080/713660095 |
| [28] |
Teng P. Convergence of a block coordinate descent method for non differentiable minimization. Journal of Optimization Theory and Applications, 2001, 109: 475–494.
|
 2022, Vol. 31
2022, Vol. 31



