2. 初速度(苏州)科技有限公司, 苏州 215100
2. Momenta (Suzhou) Technology Co. Ltd., Suzhou 215100, China
在学生学习过程中, 大多数学生都是需要练题来提升自己的能力. 在如今教育信息化时代, 有海量的试题可以给学生练习, 要想在海量的试题中选择合适的试题必须要知道学生知识点掌握情况[1,2], 因此帮助教师挖掘出学生知识点熟练度是教育中急需解决的问题.
随着计算机技术的不断发展, 传统教育模式已经得到了很大的改变, 一些教师的工作可以让计算机去做, 像试卷批改, 学生知识点诊断分析等. 现有的学生知识点诊断分析大多数采用认知诊断模型[3-7], 它是认知心理学[5]与教育测量学相结合的产物, 主要通过学生的答题记录来挖掘出学生的潜在信息[8], 例如DINA模型[8]结合Q矩阵[3,8]来挖掘出学生对试题所考察知识点的掌握情况, 由于Q矩阵只能给出试题考察知识点的离散化信息(即考察的知识点只有考察和未考察), 因此也只能预测出学生知识点的离散化程度(即学生对知识点只有掌握和未掌握).
在实际做题过程中, 知识点熟练度在0.9和1.0的情况下解决难题就可能体现出差距, 这一点在数学等理科上体现的非常明显. 针对上述问题本文提出了通过特征嵌入[9]来预测学生的知识点熟练度的方法, 对学生和试题分别以知识点作为特征嵌入, 分别建立对应知识点的向量, 并通过神经网络[2,10,11]来训练和调整学生知识点熟练度.
1 问题描述无论是传统的线下教育还是线上的智能教育[12,13], 我们的最终目的都是让学生能够提高自己的知识能力. 然而光靠课上听讲并不能完全应对考试, 学生更多的还是需要课下练习试题, 学生选择的试题必须紧密结合学生自身知识点掌握情况, 否则就是事倍功半, 让学生失去学习的信心.
大多数的教师在对学生知识点熟练度做出判断时基本上按照这些要求来判定: 如果学生能够答对试题(排除猜测), 说明该学生知识点熟练度是达到了试题对知识点考察的要求, 甚至高于试题知识点考察要求; 相反如果学生答错该试题或者没有拿到全部分数(排除失误)说明该学生在试题考察的知识点上至少有一个没有达到要求. 也就是说学生知识点熟练度是可以通过答题情况来反应的, 教师判断的准确性取决于对试题考察知识点难度[14]的精准分析, 因此如果在清楚试题考察知识点的难度和学生在该试题上的得分的情况下, 预测出学生知识点熟练度并不难.
在教育领域中, 给定学生的答题记录为R, R中包含以下信息: 学生集合D={d1,d2,…,dN},试题集合T={t1,t2,…,tM},知识点集合C={c1,c2,…,cK}. 每条答题记录由(dn, tm, snm)组成, 其中snm表示学生dn在试题tm上的得分(得分已经转化为百分比, 即得分率). Q为试题关联知识点矩阵, 由相关领域专家标记, 表示为Q=[qmk]M×K, qmk=1表示试题tm考察了知识点ck, 否则qmk=0.
问题定义: 给定答题记录R和试题知识点关联矩阵Q, 如何精确地预测出学生知识点熟练度.
2 学生知识点熟练度预测方法为了解决上述问题, 本文提出了一种基于特征嵌入的学生知识点熟练度预测方法FE-SKP (feature embedding-student knowledge proficiency), 利用神经网络强大的功能来捕捉学生与试题之间的关系, 其中第2.1节给出了 FE-SKP方法的框架, 第2.2节将会介绍具体做法.
2.1 FE-SKP框架本节提出的FE-SKP方法包含两个步骤: 第1个步骤是构造嵌入模块, 其目的是构建学生和试题的知识点向量; 第2个步骤是构建网络模型, 其目的是通过输出学生的得分预测来检验对其知识点熟练度预测是否准确, 如果与实际得分有差距则在训练过程中进行调整.
嵌入模块: 嵌入模块主要包括学生知识点嵌入和试题知识点嵌入, 学生知识点嵌入是将学生构建成在每个知识点上掌握程度的向量, 试题知识点嵌入是将试题构建成对每个知识点考察难度的向量. 构造过程如下:
1) 学生知识点嵌入: 首先给定一组学生的集合, 嵌入模块首先将其单独在相应的空间下进行初始嵌入, 从而获得由固定知识点数量维度构成的学生知识点向量. 我们将学生知识点向量用SnP表示, 含义为学生dn的知识点熟练向量, 该向量包含学生在所有知识点上的熟练度, 类似于认知诊断中的学生向量, 不同之处在于学生在每个知识点的熟练度都具体量化而并非离散, 例如SnP=(0.1, 0.5)表示该学生dn在知识点1上的熟练度为0.1, 在知识点2上的熟练度为0.5.
2) 试题知识点嵌入: 试题知识点嵌入学生知识点嵌入类似, 嵌入模块首先将其单独在相应的空间下进行初始嵌入, 从而获得由固定知识点数量维度构成的试题知识点向量, 再结合Q矩阵的信息计算出试题的权重. 我们将试题知识点向量用
网络模块: 网络模块主要用于检验学生知识点熟练度预测是否正确, 由于学生知识点熟练度没法直接给出, 因此我们通过学生知识点熟练度预测他们在试题上的得分来检验. 这里选用卷积神经网络模型, 在训练期间, 如果输出了错误的预测, 则优化算法会根据实际情况调整学生知识点熟练度, 如果输出正确说明学生知识点熟练度达到试题考察要求甚至还要高于试题考察要求.
2.2 FE-SKP具体方法(1) 嵌入模块
学生知识点嵌入: 首先我们输入学生集合D={d1,d2,…,dN}, 将每个学生单独进行初始嵌入, 从而获得维度为K的序列A=(a1,a2,…,aN), 操作为Emb1, Emb1和an计算方法如下:
| $ Em{b}_{1}=\text{ }embedding\text{ }(1\times K) $ | (1) |
| $ {a_n} = embedding\left( {{d_n}} \right) $ | (2) |
接着使用Sigmoid函数让学生的知识点熟练度在0–1之间, 得到学生dn知识点熟练SnP∈[0, 1]1×K, SnP计算方法如下所示:
| $ {S_n^P} = Sigmoid\left( {{a_n}} \right) $ | (3) |
试题知识点嵌入: 为了让考察知识点的难度具体化, 我们首先需要计算知识点的权重, 知识点的权重计算分为两步, 第1步是它在该试题考察的知识点中占的比重, 第2步是它在所有试题考察的知识点中占的比重. 我们分别用wmk和Lk表示知识点ck在试题tm中所占的比重以及在所有知识点中所占的比重, 知识点ck的权重用tck表示, 如下所示:
| $ t{c_k} = {w_{mk}} \times {L_k} $ | (4) |
用向量TCm=(tc1, tc2,…, tcK)表示试题tm中所有知识点的权重, 接着计算每道试题难度Diffm∈[0, 1], 试题难度通过学生得分计算, 如下所示:
| $ {\textit{Diff}}{_m} = 1 - \frac{{\displaystyle\sum\limits_{n = 1}^N {{S_{nm}}} }}{{N \times 1}} $ | (5) |
接着输入试题集合T={t1,t2,…,tM}, 将每个试题单独进行初始嵌入, 从而获得维度为K的序列B=(b1,b2,…,bM), 操作为Emb1, bm计算方法如下所示:
| $ {b_m} = Em{b_1}\left( {{t_m}} \right) $ | (6) |
将知识点权重向量乘以bm后, 再乘以该试题难度Diffm, 使用Sigmoid函数将每个知识点难度控制在0–1之间, 最后再乘以Q矩阵得到试题tm考察知识点难度
| $ {E_m^{{\rm{Know }}}} = {\textit{Sigmoid}}\left( {T{C_m}\circ {b_m} \times {\textit{Diff}}{_m}} \right)\circ {q_m} $ | (7) |
其中,
(2) 网络模块
该网络模型包括嵌入层, 输入层, 卷积层, 池化层, 全连接层和输出层, 其结构如图1所示.
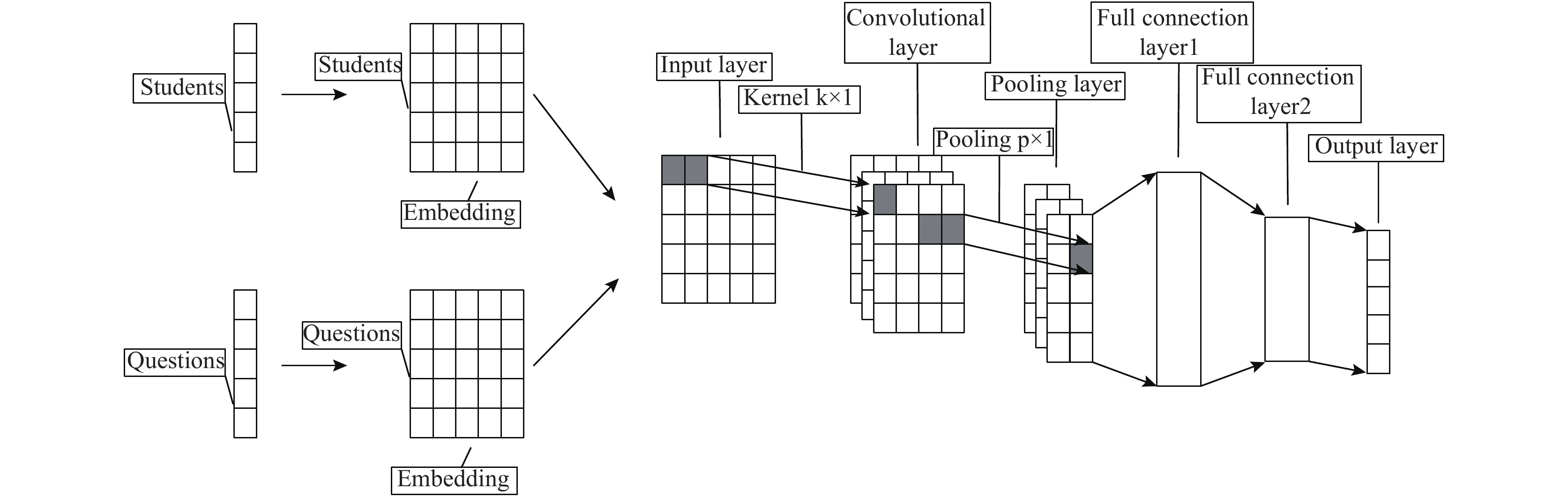
|
图 1 FE-SKP方法结构 |
嵌入层为学生知识点熟练度SnP 和试题知识点考察难度
| $ x = S_n^P - E_m^{\text{Know}} $ | (8) |
x通过卷积层执行卷积操作获得隐藏层
| $ h_n^{cp} = \max \left( {h_{(n - 1)p + 1}^{cp}, \cdots ,h_{n \times p}^{cp}} \right) $ | (9) |
最后新的隐藏层Hcp经过两个全连接层和一个输出层, 得到最后的得分预测y, 计算方式分别如下所示:
| $ {f_1} = {\rm{ }}{\textit{Sigmoid}}{\rm{ }}\left( {{w_1} \times h_n^{cp} + {b_1}} \right) $ | (10) |
| $ {f_2} = {\rm{ }}{\textit{Sigmoid}}{\rm{ }}\left( {{w_2} \times {f_1} + {b_2}} \right) $ | (11) |
| $ y = {\rm{ }}{\textit{Sigmoid}}{\rm{ }}\left( {{w_3} \times {f_2} + {b_3}} \right) $ | (12) |
其中, w为权重参数矩阵, b为偏移量.
FE-SKP方法的损失函数是输出学生得分预测y和真实标签学生实际得分s之间的交叉熵, 计算方法如下所示:
| $ loss=-\sum\limits_{n}\left({s}_{n}\log{y}_{n}+\left(1-{s}_{n}\right)\log\left(1-{s}_{n}\right)\right) $ | (13) |
本节主要验证FE-SKP方法的有效性, 其中第3.1节介绍数据集信息, 第3.2节为数据处理过程, 第3.3节给出评价指标, 最后第3.4和第3.5节给出实验结果并且对实验结果进行分析.
3.1 数据集我们使用一组真实的数据集ASSIST (ASSISTments 2009–2010 skill builder)进行实验, 该数据集是ASSISTments在线辅导系统收集的开放数据集, 包含了学生的答题日志. 每个学生答题日志学生的编号, 试题编号, 试题考察的知识点编号以及学生在该试题上的得分, 一共有4 163个学生, 17746道试题和123个知识点(每个知识点用不同编号表示, 例如知识点1表示函数), 324572条答题日志, 详细信息如表1所示.
| 表 1 数据集信息 |
3.2 数据预处理
由于我们需要输入Q矩阵, 学生和试题编号, 因此我们需要将日志中的信息提取出来. 首先我们将答题日志进行改进, 原本是一个学生编号对应他所做的所有试题信息, 我们将每条日志改为一个学生编号, 一道试题信息.
接着是Q矩阵的构造, 因为答题日志只有试题考察知识点的编号, 因此我们需要先构造一个全为0的矩阵, 维度是试题数乘以知识点数, 接着将试题考察的知识点编号对应矩阵中的位置, 将0改为1即可构造每道试题的Q矩阵. 具体处理过程如图2所示.

|
图 2 数据处理流程 |
最后选择80%作为训练集, 20%作为测试集.
3.3 实验评价指标由于学生知识点熟练度我们无法直接判断预测结果是否准确, 因此我们通过预测学生在试题上得分来判断知识点熟练度预测的效果. 在本次实验中, 我们使用准确率(Accuracy)、均方根误差(RMSE)、ROC曲线下的面积(AUC)作为评价指标, 其计算公式分别如下所示:
| $ {\textit{RMSE}} = \sqrt {\frac{1}{M}\sum\limits_{m = 1}^M {{{\left( {{y_m} - {s_m}} \right)}^2}} } $ | (14) |
| $ {\textit{Accuracy}} = \frac{{TP + TN}}{{TP + FP + FN + TN}} $ | (15) |
| $ {\textit{AUC}} = \frac{{\Sigma I\left( {{P_{\text{正样本}}},{P_{\text{负样本}}}} \right)}}{{{U^*}V}} $ | (16) |
其中, TP表示正确预测学生答对试题的数量, FP表示错误预测学生答错试题的数量, FN表示错误预测学生答对试题的数量, TN表示正确预测学生答错试题的数量. U表示正样本数量, V表示负样本数量, I(P正样本, P负样本)计算方法如下所示:
| $ I\left( {{P_{\text{正样本}}},\;{P_{\text{负样本}}}} \right) = \left\{ {\begin{array}{*{20}{l}} {1,\;{P_{\text{正样本}}} > {P_{\text{正样本}}}}\\ {0.5,\;{P_{\text{正样本}}} = {P_{\text{负样本}}}}\\ {0,{P_{\text{正样本}}} < {P_{\text{负样本}}}} \end{array}} \right. $ | (17) |
为了验证本实验的有效性, 我们对比了传统的一些方法, 其中包括认知诊断模型(DINA, IRT[15], MIRT[16,17])和概率矩阵(PMF)[18]. 对比方法的原理介绍如下:
DINA方法: 根据学生在每道试题上的得分情况来诊断出学生的知识状态, 其中用0表示学生未掌握考察的知识点, 用1表示学生掌握了考察的知识点, 再结合知识点关联矩阵对学生进行得分预测.
IRT方法: 在已知试题的难度、区分度、猜测系数的情况下建立能力参数的极大似然函数, 得到学生的能力参数后, 通过3PL模型计算出学生答对试题的概率.
MIRT方法: 在IRT模型的基础上, 将学生完成一道试题需要的多种能力(即需要掌握的多个知识点)、试题特征与答对概率进行模型化.
PMF方法: 通过学生在每道试题上的得分以及试题知识点关联矩阵, 分别建立学生和试题的知识点潜在向量, 假设学生和试题潜在向量服从高斯分布, 通过已知的学生得分矩阵得到学生和试题的特征矩阵, 用特征矩阵预测学生在试题上的得分.
介绍完对比实验方法后, 我们在该数据集上进行了实验, 结果如表2所示.
| 表 2 实验结果 |
3.5 实验结果分析
根据实验结果, 我们可以发现FE-SKP方法在各项评价指标中效果最好, 主要原因在于以下几点:
DINA模型主要适用于客观题, 对于一些得分不是0分就是满分的题目处理的是比较好的, 因为客观题只要有一个知识点不熟练基本上就是不得分, 是可以将学生的知识点熟练度视为未掌握, 但是对于一些连续性得分像主观题效果并不是很好, 因为主观题只要学生答对一个得分点就可以获得相应的分数, DINA模型无法将学生和试题的知识点量化, 在测试主观题时只要学生有一个知识点不会该试题得分就是0分, 导致主观题的准确率不高, 均方根误差比较大; IRT模型认为学生的单维能力与测试得到的分数是线性关系的, 但是在实际情况中往往不成线性关系, 比如我们在进行考试时, 想要从50分考到60分很容易, 但是想要从90分考到100分却很难, 因为90分与100分的差距主要体现在难题上, 难题涉及到的知识点非常多, 并不是单个能力就能体现出来, 所以在进行一些区分度大的题目上进行测试效果并不是很好; PMF对于学生的得分预测结果缺乏一定的解释性, 因为潜在变量的维度可以任意设置, 很难说明潜在变量一定是知识点, 另一方面它难以融合更多的有用特征, 例如像试题知识点的考察难度. 因此, 这3种传统的方法的效果并不是很理想.
相对于传统的3种方法, MIRT的效果还是比较好的. MIRT相对于IRT的区别主要是潜在向量的建模, IRT潜在向量是一维的, 而MIRT潜在向量是多维, 即一道试题会测试K种能力, 而学生在做这道试题时最后的得分对应了K种能力, 但是仍然存在IRT模型中能力与得分线性关系的缺陷. 而FE-SKP方法利用了卷积神经网络强大的拟合能力, 提取更具有决定性的特征, 使其能够捕捉到学生与试题之间的关系, 并且在构建试题知识点嵌入是考虑了试题考察的知识点权重以及试题的难度, 提高了预测试题知识点考察难度的准确性, 从侧面提升了学生知识点熟练度预测的准确性和分类效果, 并且能够减少均方根误差.
4 结论与展望本文将知识点作为特征嵌入到学生与试题之中, 并且通过卷积神经网络来捕捉学生与试题之间的联系, 从提升试题知识点考察难度准确率来增加学生知识点熟练度预测的准确率. 虽然较传统方法上准确率有所提高, 但是准确率并没有达到教育上完美要求, 教师面对的是一个班级甚至是几个班级的学生, 对每个学生都需要负责. 因此希望在后面的工作中, 可以继续提升准确率, 大大减轻教师和学生的压力.
https://sites.google.com/site/assistmentsdata/home/assistment-2009-2010-data/skill-builder-data-2009-2010
| [1] |
胡庆. 基于决策树的试卷知识点掌握程度分析研究 [硕士学位论文]. 南昌: 江西财经大学, 2014.
|
| [2] |
苏喻, 张丹, 刘青文, 等. 学生得分预测: 一种基于知识图谱的卷积自编码器. 中国科学技术大学学报, 2019, 49(1): 21-30. DOI:10.3969/j.issn.0253-2778.2019.01.004 |
| [3] |
朱天宇, 黄振亚, 陈恩红, 等. 基于认知诊断的个性化试题推荐方法. 计算机学报, 2017, 40(1): 176-191. DOI:10.11897/SP.J.1016.2017.00176 |
| [4] |
陈秋梅, 张敏强. 认知诊断模型发展及其应用方法述评. 心理科学进展, 2010, 18(3): 522-529. |
| [5] |
高旭亮, 汪大勋, 王芳, 等. 基于分部评分模型思路的多级评分认知诊断模型开发. 心理学报, 2019, 51(12): 1386-1397. |
| [6] |
Zhang SJ, Liu J, Huang S, et al. Study of priority recommendation method based on cognitive diagnosis model. Qin PL, Wang HZ, Sun GL, et al. Data Science. Singapore: Springer, 2020. 638–647.
|
| [7] |
Wang JT, Shi NZ, Zhang X, et al. Sequential gibbs sampling algorithm for cognitive diagnosis models with many attributes. Multivariate Behavioral Research, 2020. [doi: 10.1080/00273171.2021.1896352]
|
| [8] |
De La Torre J. DINA model and parameter estimation: A didactic. Journal of Educational and Behavioral Statistics, 2009, 34(1): 115-130. DOI:10.3102/1076998607309474 |
| [9] |
王天时. 基于特征嵌入表示的文本分类方法研究[硕士学位论文]. 济南: 山东师范大学, 2020.
|
| [10] |
李彦冬, 郝宗波, 雷航. 卷积神经网络研究综述. 计算机应用, 2016, 36(9): 2508-2515, 2565. DOI:10.11772/j.issn.1001-9081.2016.09.2508 |
| [11] |
任鸽, 杨勇. BP神经网络在高校学生成绩预警中的应用. 数字技术与应用, 2020, 38(10): 63-65. |
| [12] |
刘淇, 陈恩红, 朱天宇, 等. 面向在线智慧学习的教育数据挖掘技术研究. 模式识别与人工智能, 2018, 31(1): 77-90. |
| [13] |
黄荣怀, 周伟, 杜静, 等. 面向智能教育的三个基本计算问题. 开放教育研究, 2019, 25(5): 11-22. |
| [14] |
佟威, 汪飞, 刘淇, 等. 数据驱动的数学试题难度预测. 计算机研究与发展, 2019, 56(5): 1007-1019. DOI:10.7544/issn1000-1239.2019.20180366 |
| [15] |
De Jong MG, Steenkamp JBEM, Fox JP. Relaxing measurement invariance in cross-national consumer research using a hierarchical IRT model. Journal of Consumer Research, 2007, 34(2): 260-278. DOI:10.1086/518532 |
| [16] |
孙佳楠, 杨武岳, 陈秋. 应用多维项目反应理论模型探索分数减法测验的维度识别. 数学的实践与认识, 2017, 47(21): 291-296. |
| [17] |
王鹏, 朱新立, 王芳. 多维项目反应理论的计量模型、参数估计及应用. 心理学进展, 2015, 5(6): 365-375. |
| [18] |
Koren Y, Bell R, Volinsky C. Matrix factorization techniques for recommender systems. Computer, 2009, 42(8): 30-37. DOI:10.1109/MC.2009.263 |
 2022, Vol. 31
2022, Vol. 31



