在中国互联网迅猛发展的大背景下, 网络视频的需求量激增, 各大网站已经纷纷采用CDN网络架构以应对在运营中遇到的各种难题, 比如网站访问量激增问题、如何提升网站的访问速度问题、以及网站带宽严重不足导致用户无法正常访问等问题. 本文的研究目标是根据带宽时间序列数据, 可以准确地预测下一时刻的带宽值, 依此对时间序列中的每个时间节点进行实时监控, 发现并反馈异常点及其异常情况, 及时向运维人员发出告警, 从而帮助运维人员采取相应后续措施, 进而有效地避免和解决运营中出现的各类问题和带宽成本不可控制等难题.
本文提出了一个新的带宽预测时序模型—局部加权回归串行长短期记忆网络(long short term memory network, LSTM)预测模型. 针对原始带宽数据具有的长时间依赖和数据单一等特点, 使用按时序插值采样的方法构造数据集, 拟合局部加权最小二乘法回归模型, 将其预测结果作为训练集串行LSTM时序模型进行最终带宽异常值预测. 使用4sigma原则判断某时刻带宽是否为异常, 并按等级标准发出异常告警. 通过实验证明, 本文提出的模型泛化能力较强, 可以较准确地预测异常时刻, 并按异常值的级别向运维人员发出准确告警.
1 相关算法原理与分析目前异常值的检测方法有统计的方法、聚类的方法以及一些专门的异常值检测算法[1]: 基于概率分布模型[2]的异常值检测, 它把具有低概率的数据点判断为异常值, 该算法对于多元高维数据的异常检测效果较差; 基于K近邻(KNN)的离群点检测, 它依据数据点的距离以及K值判断出异常值[3], 该算法过度依赖K值的选择, 对密度不均衡的样本数据不适用; 基于密度的离群点检测方法, 使用DBSCAN聚类算法[4]计算密度, 依据密度定义异常值, 该算法同样依赖参数的选择, 且时间复杂度相对较高; 基于聚类的方法判断异常值, 如果一个数据不强属于任何一个簇, 则该数据点为异常值, 该算法对离群点的判断依赖簇的个数和质量; 基于滑动窗口的异常检测方法, 该方法使用滑动窗口对原始时间序列进行分割, 利用扩展的 Frobenius 范数来判断异常子序列, 但面对大数据量的时间序列, 算法的时间复杂度过高[5]. 这些异常值的检测方法均不适用于本研究的数据异常值检测情况.
在时间序列预测中, 循环神经网络RNN是一种非常强大的对序列数据进行建模和预测的神经网络工具[6]. 本研究尝试使用RNN模型进行训练, 但是在实际训练过程中, 发现RNN模型随着其模型深度的不断增加, 会发生梯度爆炸或者梯度消失的现象.
LSTM算法是误差反向传播算法[7], 包括3个步骤: 前向计算每个神经元的输出值、反向计算每个神经元的误差项、根据相应的误差项计算每个权重的梯度[8]. 在LSTM的3种门中, 遗忘门是LSTM的关键组成部分, 它决定了上一时刻的单元状态Ct–1 有多少信息可以保留到当前时刻 Ct. 遗忘门的权重Wf的权重梯度, 可以根据其相应的误差项δf,t计算获得[9]. 通过反向调整误差机制, LSTM算法可以有效地解决循环神经网络的梯度消失或者梯度爆炸的问题.
1.1 最小二乘法线性回归是利用数理统计中回归分析, 来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法[10]. 其表达形式为
局部加权lowess (locally weighted regression)[12]是一种用于局部回归分析的非参数方法. 之所以我们这里采取加权最小二乘法, 是因为我们发现离拟合点越近的样本点, 它的取值对拟合线的影响应该更大, 损失函数的定义应该优先降低与拟合直线距离近的点的误差.
1.3 时间序列算法LSTM长短期记忆网络LSTM是一种特殊的递归神经网络, 它能够学习长期依赖性, 尤其是在长序列预测问题中表现不俗[13]. 标准LSTM由遗忘门、输入门、输出门和隐藏状态组成[14]. LSTM的单元结构如图1[15]所示. LSTM对时间序列的前期信息的存储和更新是由这些门控来决定的. 门控由Sigmoid函数和点乘运算实现, 实质是一个全连接层, 它的一般公式为式(1)[16]:
| $ g\left( x \right) = \sigma \left( {Wx + b} \right),\sigma \left( x \right) = \frac{1}{{1 + {{\rm e}^{ - x}}}} $ | (1) |
其中, σ(x)是Sigmoid函数, 即非线性激活函数[17], 可以将计算结果映射到[0, 1]的区间中, 当它为0时, 代表没有信息可以通过, 当它为1时, 代表所有信息都可以通过. W表示权重矩阵[7], b表示偏置值.

|
图 1 LSTM单元结构图 |
2 局部加权回归LSTM时序算法设计
带宽异常值预测是高度依赖长距离时刻数据的时序问题, 采用LSTM作为模型进行预测最为合适. LSTM框架中每一时刻的输出误差可以反向传递给前一时刻, 使用梯度下降调整网络参数[7]. 但是在实践中我们发现带宽预测中原始数据是真实带宽值, 其中包含异常值, 异常值如果作为训练集会让机器误以为是正常值进行学习, 因此非常有必要找到这些异常值, 也就是噪点, 并对他们进行处理, 处理后的数据再使用LSTM进行训练, 会得到更为准确的异常检测结果. 为此, 本文提出了一个新的带宽预测时序模型框架: 首先采局部加权最小二乘法回归拟合初始模型, 使用初始模型的预测结果作为LSTM的训练集, 真实值作为LSTM的验证集, 串行LSTM时序算法进行预测, 然后使用4sigma方法比对原始真实值和现在的预测值的偏差, 判断异常等级, 做出相应级别的异常告警, 包括以下几个步骤:
1) 数据预处理;
2) 插值采样生成回归模型样本点;
3) 对样本点数据进行lowess局部加权;
4) 最小二乘法回归拟合模型得出预测结果;
5) 调整回归系数λ优化模型;
6) 将预测结果作为LSTM的输入进行训练;
7) 采用4sigma原则判断带宽异常值;
8) 根据实际偏差与训练偏差的比例等级标准发出相应异常警告. 局部加权回归LSTM时序算法活动图如图2所示.

|
图 2 局部加权回归LSTM时序算法活动图 |
2.1 插值采样
本文在带宽预测时, 将训练集数据按照每43个时刻点为一组进行采样, 在每组时间序列 中, 前42列作为训练集样本点的特征, 第43列为其对应的y, 之后的样本点均采用按时间梯形重叠的方法进行插值采样, 具体过程如下:
1) 原始数据的带宽值是每间隔3 s的真实数据, 本文对处理后的4万多原始数据每间隔15 min进行一次插值采样;
2) 采样过程使用时序重叠的方法: 用第1个时刻到第42个时刻的带宽数据作为预测模型的训练集样本点的特征值, 即x1, 第43个时刻的带宽数据作为这个样本点对应的结果真实值y1; 然后用第2个时刻到第43个时刻的带宽数据作为第2个训练集样本点x2的特征值, 第44个时刻的带宽数据作为第2个样本点对应的真实值y2. 以此类推, 一共采样出1 000个样本点, 即1 000行42列的X和1 000行1列的y, X具有42个特征, X矩阵如式(2).
| $ X = \left( {\begin{array}{*{20}{c}} {{x_{11}}}& \ldots &{{x_{1n}}} \\ \vdots & \ddots & \vdots \\ {{x_{m1}}}& \cdots &{{x_{mn}}} \end{array}} \right) $ | (2) |
其中, m为1 000, n为42. 插值采样获取时间序列如图3所示.

|
图 3 插值采样获取时间序列示意图 |
2.2 局部加权最小二乘法拟合模型
局部加权最小二乘法拟合模型流程如下:
1) 使用每组时间序列(x1,x2,…,xn)(n=43)的前42个时刻点作为一个拟合点的特征向量;
2) 采用lowess算法为拟合点数据局部加权, 距离拟合点远的样本点权重低, 距离近的样本点权重高. 距离公式为:
| $ \sqrt {{{\sum\limits_1^n {\left( {{x_i} - {x_j}} \right)^2} }}} $ | (3) |
其中,
| $ B\left( x \right) = \left\{ \begin{array}{l} {\left( {1 - {x^2}} \right)^2},\left| x \right| < 1 \hfill \\ 0,\left| x \right| \ge 1 \hfill \\ \end{array} \right. $ | (4) |
3) 对数据进行归一化处理;
4) 使用最小二乘法拟合模型[19], 公式为:
| $ \hat Y = X{\left( {{X^{\rm T}}\omega X} \right)^{ - 1}}{X^{\rm T}}\omega Y $ | (5) |
其中,
5) 对模型进行测评, 评估指标MSE不满足要求则调整回归系数λ优化模型[20].
上述过程完成后, 调用LSTM模型进行后续操作.
2.3 异常值判断算法和告警等级标准设计 2.3.1 异常值判断算法设计本文算法框架对带宽值的预测依赖带宽时序, 对于带宽预测这一独立事件其结果影响因素单一, 偏差是异常值的判断依据, 偏差值属于正态分布, 目前对于此类情况通常采用“正态分布3sigma原则”作为异常值判断依据[21]. 偏差是指预测结果与真实值之间的差异. 根据正态分布我们知道, 测量值范围在[x–σ, x+σ]的概率为0.682 7. 在[x–3σ, x+3σ]的概率为0.997[21], 其中x表示测量的平均值, σ表示偏差. 本文经过调节参数, 最终采用“4sigma原则”作为异常值检测方法: 将4个标准差作为基准, 用验证集的差值和测试集的4个标准差相比, 如果大于1, 则说明这个值是异常值, 表示带宽异常, 发出告警.
2.3.2 告警等级设计实际的偏差与训练的偏差之间的绝对偏差表示了是否异常. 而异常的程度可以用相对偏差表示, 也就是实际偏差与训练偏差的比例, 根据该比例值的大小设置了8个告警级别, 告警级别用变量 表示, 告警级别如表1所示.
| 表 1 异常告警级别 |
3 实验结果和分析
在局部加权最小二乘法模型预测部分, 使用Matlab R2016a作为开发平台; 在LSTM时序模型部分, 使用Keras+TensorFlow框架, Spyder+Python编程环境.
3.1 插值采样数据集原始数据是真实带宽值, 约为45000个数据. 首先进行数据处理将数据单位转换为GB, 然后进行插值采样. 每隔15 min采样一次.
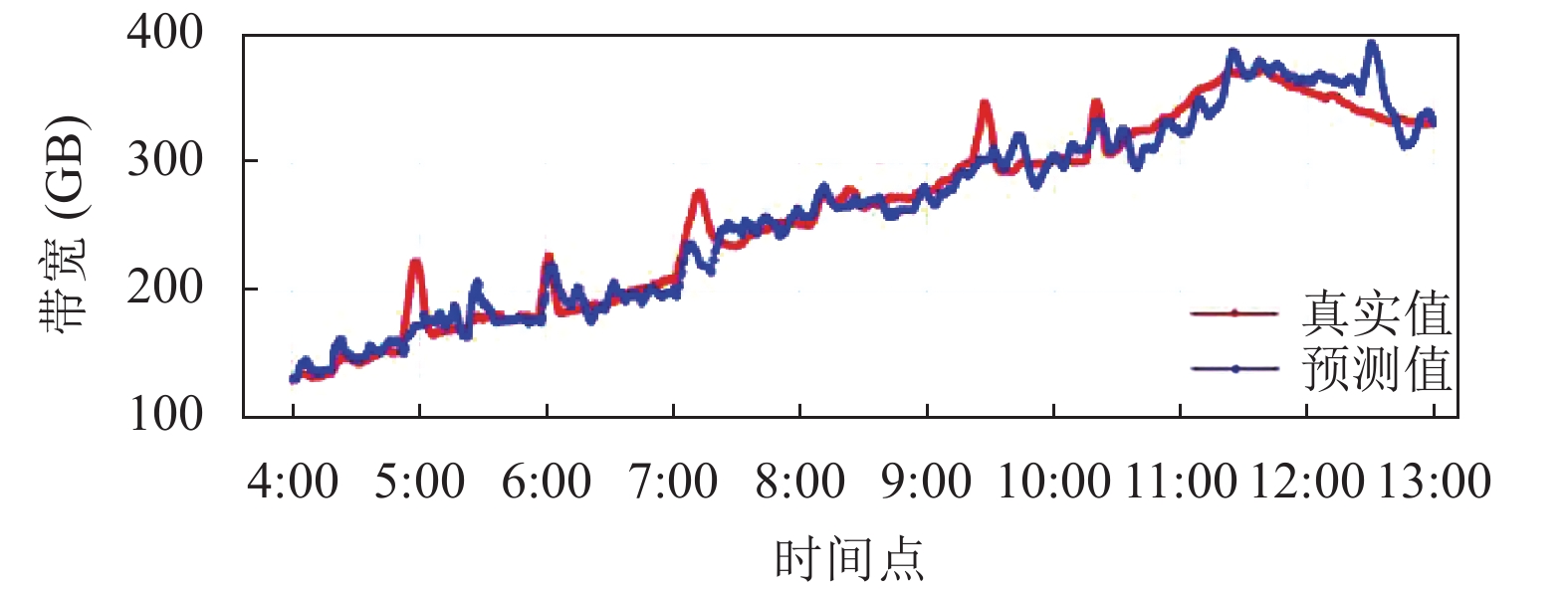
3.2 局部加权最小二乘法拟合模型实验局部加权最小二乘法拟合模型预测结果如图4所示, 图中红色有“陡峭波峰”的曲线为真实值, 蓝色曲线为模型预测值. 我们可以认为明显高于预测值的“凸点”为异常值, 在模型中我们将他们作为噪点, 用此刻的预测值进行替代, 作为LSTM的训练集和测试集.
|
图 4 局部加权最小二乘法拟合模型预测结果 |
3.3 LSTM训练实验
设置LSTM网络隐藏层神经元个数为100, 输入特征维度为1, 激活函数使用linear, 样本训练次数设置为 100 次, 网络使用 Adam 优化器, 每批次处理100条样本, validation_split训练集验证集的分割值为0.33. LSTM网络结构部分代码如图5所示.
3.3.1 模型评价本文采用loss曲线对模型进行评价, 并给出算法的时间复杂度对算法可行性加以说明.
使用loss曲线作为评价标准, 损失函数loss使用均方误差MSE (mean squared error), 其公式为:
| $ MSE = \frac{1}{n}{\sum\limits_{i = 1}^n {\left( {{y_i} - \hat y} \right)} ^2} $ | (6) |
图6是模型的100次完整训练过程, 可以看出从第1次完整训练到第100次完整训练, 训练集loss值从0.016 4降到了4.65e–04.

|
图 5 LSTM网络结构 |

|
图 6 LSTM执行过程 |
图7是100次训练过程模型训练集和验证集损失loss的对比图, 其中蓝色(靠下)曲线是训练集loss值随着迭代过程的变化曲线, 橙色(靠上)曲线是验证集loss值的变化曲线, 可以看出训练集数据在大约第10次训练之后loss值已经迅速降至趋近于0的数值, 之后的训练其loss均平缓趋近于0, 训练集loss和验证集loss都已经收敛并且它们之间相差不大, 说明既没有过拟合也没有欠拟合, 模型学习充分, 效果良好.
模型算法主要包括局部加权最小二乘和LSTM两个部分. 最小二乘法的时间复杂度正比于n2×k, 其中n是特征数, k是样本数量. LSTM算法的时间复杂度为n×d2, 其中n为时间序列长度, d为向量长度. 两个部分的时间复杂度数量级都是O(n2), 取两个部分值大的作为模型的时间复杂度. 因此按LSTM进行计算, 模型时间复杂度为42×1002. 经过实验, 1728个样本数据的执行时间稳定在0:01:05.942850左右, 约1 min. 1728个样本数据是取的3天的带宽监测值, 在实际应用中, 数据池维持在9天的带宽数据进行预测, 系统采用IntelR710服务器, 还可以提高约20%的执行效率, 该算法在实际应用中具有可行性.

|
图 7 训练集loss和验证集loss对比 |
图8是使用测试集对模型进行准确度计算的结果, 模型预测准确度为0.77419, 即约为77%.

|
图 8 模型准确度 |
3.3.2 参数调整
(1) 调整参数batch_size
如果batch_size值设置过大, 比如200, 那么代码执行速度会快很多, 但是预测精确度会降低; 如果该值设置过小, 比如5, 精确度会较高但是代码执行速度会变慢. 因此设置batch_size为100.
(2) 调整参数epochs
从图9可以看出, epochs为200时, 模型在第10次训练之后训练集loss值降为9.2092e–04. epochs为100时, 模型在第10次训练之后训练集loss值也已到达9.0460e–04, 说明epochs为100已经足够, 模型训练已经非常充分, 不需要增至200.
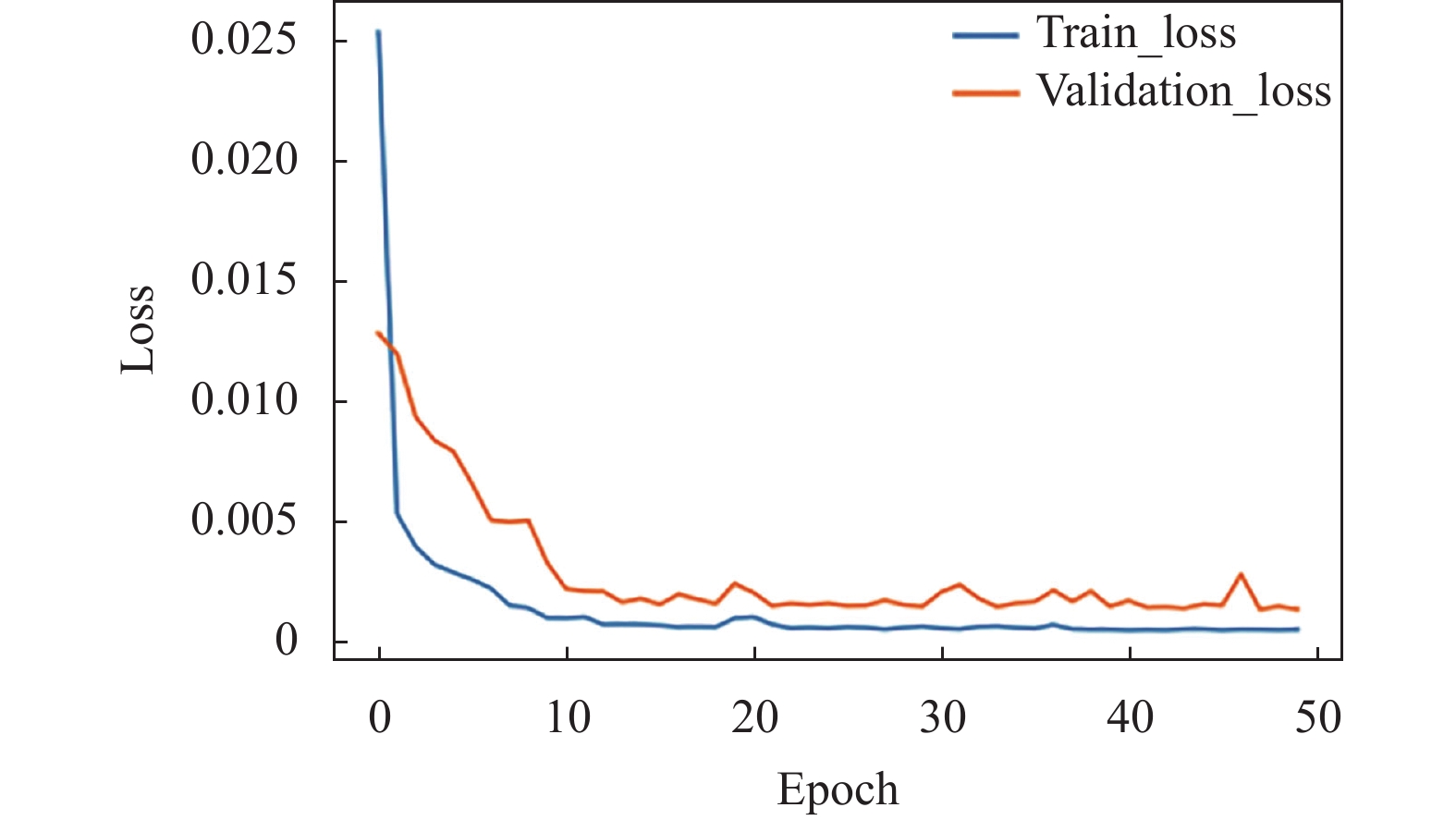
图10是epochs设置为50时的验证集loss和训练集loss(高线)对比曲线图. 可以看出验证集loss和训练集loss曲线间距generalization gap增大, 且训练集loss在第14次才降至8.6938e–04, 后续仍有起伏, 说明模型训练不充分, 出现欠拟合的风险比较大, 因此epochs值最后设置为100.
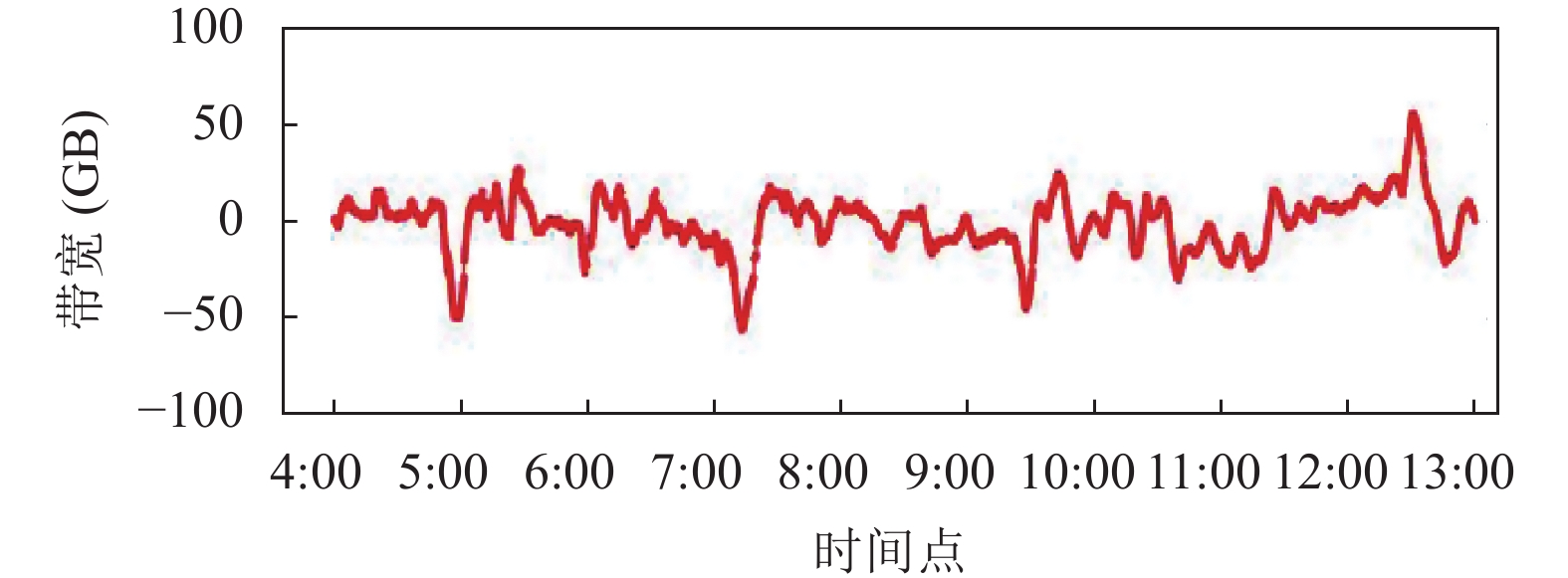
在异常值的判断中结合预测值和真实值的偏差. 图11是每时刻预测结果和真实值的偏差, 该值接近于0说明偏差小. 从图中可见约在5:00、7:10、9:25、12:30几个时刻出现了明显偏差, 根据4sigma原则判断这4个时刻为异常值, 结果见图12. 除此4个时刻外, 其他时刻也有出现偏差的情况, 比如在6:00时刻也发生了偏差, 但是其不符合4sigma的异常定量, 所以模型判断该时刻带宽正常.

|
图 9 Epochs设置为200和100执行过程 |
|
图 10 Epochs设置为50验证集和训练集loss |
根据异常时刻实际偏差与训练偏差的比例Rela_BiasLevel按值的大小分为8个告警级别, 值越大告警级别越高. 图12是模型测评的3个异常时刻点的Rela_BiasLevel定量告警示意图.
|
图 11 预测值和真实值的偏差 |
4 结论与展望
本文以带宽异常值预测为目标, 从解决实际问题出发, 构造了一套适用于研究目标的异常值预测算法. 该算法将局部加权lowess融入最小二乘法回归模型, 使模型曲线更为平滑, 有效的解决了回归模型的欠拟合问题. 该算法将局部加权最小二乘法拟合模型的输出结果作为LSTM的训练集, 起到了剔除噪点的作用, 使得LSTM预测结果更为准确. 从实验结果来看, 本文提出的异常值预测模型算法具有很高的实用价值, 异常值预测结果较为准确, 有效地避免和解决了网络运营中带宽异常带来的各类问题和带宽成本不可控制等难题.

|
图 12 异常值告警示意图 |
另外, 本文的研究尚未结束, 算法中仍有一些内容有待研究. 第一, 局部加权回归模型产生的误差和LSTM模型产生的误差, 会不会有叠加放大的情况, 要如何消化这些误差. 第二, 局部加权回归模型的预测结果是否可以和原始样本按一定比例合成数据作为LSTM的训练集. 第三, 可否在LSTM每次反向传播调整网络参数时, 加入局部加权的思想干预网络参数的调整尤其是遗忘门的权重函数Wf. 本课题将针对上述这些内容展开后续研究.
| [1] |
崔泽潇. 基于异常值检测和K均值聚类的太阳射电频谱图像自动检测方法研究[硕士学位论文]. 昆明: 云南大学, 2019.
|
| [2] |
王萌, 王福龙. 基于端点检测和高斯滤波器组的MFCC说话人识别. 计算机系统应用, 2016, 25(10): 218-224. DOI:10.15888/j.cnki.csa.005425 |
| [3] |
彭艳兵, 冯利容. 基于网格概率的离群点检测算法. 计算机系统应用, 2016, 25(4): 215-220. |
| [4] |
Hermawati R, Sitanggang IS. Web-based clustering application using shiny framework and DBSCAN algorithm for hotspots data in peatland in Sumatra. Procedia Environmental Sciences, 2016, 33: 317-323. DOI:10.1016/j.proenv.2016.03.082 |
| [5] |
宁进. 离群点检测及其参数优化算法研究[博士学位论文]. 成都: 电子科技大学, 2020.
|
| [6] |
刘京麦野, 刘新, 郭炳元, 等. 基于循环神经网络的语义完整性分析. 计算机系统应用, 2019, 28(9): 203-208. DOI:10.15888/j.cnki.csa.007085 |
| [7] |
冯晨, 陈志德. 基于XGBoost和LSTM加权组合模型在销售预测的应用. 计算机系统应用, 2019, 28(10): 226-232. DOI:10.15888/j.cnki.csa.007091 |
| [8] |
郭蕴颖, 丁云峰. 基于CNN和LSTM联合预测并修正的电量缺失数据预测. 计算机系统应用, 2020, 29(8): 192-198. DOI:10.15888/j.cnki.csa.007580 |
| [9] |
游皓麟. Python预测之美: 数据分析与算法实战. 北京: 电子工业出版社, 2020. 336–340.
|
| [10] |
Cohen J, Cohen P, West SG, et al. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences. 3rd ed. Mahwah: Lawrence Erlbaum Associates, 2003.
|
| [11] |
田垅, 刘宗田. 最小二乘法分段直线拟合. 计算机科学, 2012, 39(S1): 482-484. |
| [12] |
Yen HPH, Pham BT, Van Phong T, et al. Locally weighted learning based hybrid intelligence models for groundwater potential mapping and modeling: A case study at Gia Lai province, Vietnam. Geoscience Frontiers, 2021, 12(5): 101154. DOI:10.1016/j.gsf.2021.101154 |
| [13] |
Wielgosz M, Skoczeń A, Mertik M. Using LSTM recurrent neural networks for monitoring the LHC superconducting magnets. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2017, 867: 40-50. |
| [14] |
丁宇阳, 李明悦, 谢柠宇, 等. 双LSTM的光场图像去雨算法研究. 计算机工程与应用, 2021, 57(18): 227-237. DOI:10.3778/j.issn.1002-8331.2009-0225 |
| [15] |
杨青, 王晨蔚. 基于深度学习LSTM神经网络的全球股票指数预测研究. 统计研究, 2019, 36(3): 65–77.
|
| [16] |
刘明进, 王珏, 蔡玉芳, 等. Zernike矩结合Sigmoid曲线拟合边缘检测方法. 计算机工程与应用, 2014, 50(1): 149-152, 174. DOI:10.3778/j.issn.1002-8331.1204-0323 |
| [17] |
Huang L, Chen SJ, Ling ZX, et al. Non-invasive load identification based on LSTM-BP neural network. Energy Reports, 2021, 7 Suppt 1: 485-492. |
| [18] |
Liu JH, Wang YZ. 3D surface reconstruction of small height object based on thin structured light scanning. Micron, 2021, 143: 103022. DOI:10.1016/j.micron.2021.103022 |
| [19] |
徐继刚, 冯新泸, 管亮, 等. 多态偏最小二乘法模型. 计算机系统应用, 2012, 21(6): 178-181. DOI:10.3969/j.issn.1003-3254.2012.06.040 |
| [20] |
杜伟, 傅游. 基于GPU的最小二乘蒙特卡罗算法期权定价. 计算机工程与应用, 2020, 56(4): 225-229. DOI:10.3778/j.issn.1002-8331.1810-0410 |
| [21] |
包汉, 祝海涛, 刘迪. 基于±3σ正态概率区间分族遗传蚁群算法的移动机器人路径规划研究. 控制与决策, 2021, 36(12): 2861–2870.
|
 2022, Vol. 31
2022, Vol. 31



