1 引言

近年来, 强化学习在解决一系列顺序决策问题上取得了巨大的成功. Minih等人^[1]将深度学习和强化学习结合起来, 提出了深度强化学习, 在众多领域都得到了广泛的应用. 比如机器人控制^[2], 生命科学^[3], 自动驾驶^[4], 5G通信^[5], 物联网^[6], 车联网^[7]等. 在深度强化学习的基础上众多研究者提出了多项改进来提升算法的收敛速度和稳定性. 然而这些算法的研究和应用大多集中在单智能体领域. 现实世界中的任务和场景通常更加复杂, 涉及到多个智能体之间的合作和竞争. 比如工厂中的协作机器人, 交通控制系统和自动军事系统等. 将单智能体强化学习算法简单地移植到多智能体场景中通常会带来一些问题和挑战^[8]. 比如单智能体深度强化学习算法无法表征智能体之间的合作与竞争关系以及智能体之间共同进化导致环境非平稳性的问题. 并且多智能体与复杂场景会带来计算量大幅提升, 算法收敛速度明显下降等挑战.

目前, Self-play^[9]被证明是一种有效的多智能体训练范式, 并成功的应用在了围棋, 象棋以及博弈竞争场景中. Palmer等人^[10]提出了一种基于宽容的DQN算法, 对同伴不合理的行为给予一定的容忍度. Foerster等人^[11]提出了反事实的思想, 解决了多智能体合作场景中信用分配的问题. 这些算法在多智能体场景中都取得了很好的效果. 但是只能应用在离散动作空间中, 并且Self-play还增加了智能体之间动作集完全一致的限制. Lowe等人^[12]提出了一种集中式训练, 分散式执行的算法(multi-agent deep deterministic policy gradient, MA-DDPG), 解决了多智能体场景中环境非平稳的问题. 并且该算法可以同时应用在连续和离散控制的多智能体场景中, 使得应用场景更加灵活.

然而对于复杂的多智能体场景, 目前的多智能体深度强化学习算法还有很多问题没有解决. 智能体动作策略的更新质量非常依赖于预期回报的估计, 但是多个智能体与环境交互时, 其内在的随机性会导致预期回报具有不确定性, 现有的方法将预期回报简单地平均为期望值则会丢失完整的分布信息, 导致智能体不能进行有效的学习. 并且现有的方法主要基于单步回报, 智能体只考虑当下的收益而忽略未来的信息, 从而引发算法不稳定. 此外现有方法中经验数据生成往往和网络更新耦合在一起, 导致只能串行处理, 难以有效利用更多的计算资源. 为此, 本文提出了基于值分布的多智能体分布式深度确定性策略梯度算法(multi-agent distributed distributional deep deterministic policy gradient, MA-D4PG), 引入值分布的思想^[13]对预期回报的分布建模, 避免分布信息丢失, 使得智能体能够获得更加准确的梯度更新, 保证学习的有效性; 引入多步回报使得智能体能够从未来的经验中学习, 增加智能体的预见能力, 提高算法的稳定性; 引入分布式数据生成框架(APE-X)^[14], 将智能体与环境交互生成经验数据部分与网络更新解耦, 使得经验数据生成过程和网络更新能够并行进行, 充分利用更多的计算资源.

在多个不同的连续/离散控制的多智能体场景中本文算法的稳定性和收敛速度都有了极大的提升, 智能体的决策能力也有了明显的增强. 最后本文还做了消融实验展示每个改进各自的贡献以及相互作用.

2 相关工作 2.1 多智能体马尔可夫决策过程

多智能体马尔可夫决策过程是马尔可夫决策过程在多智能体场景下的扩展. 其同样由四元组构成:

$ M = (S,A,Pr ({S^{'}}|S,A),R) $

(1)

其中, $S$ 表示所有智能体的状态集合 $\{ {s_1},{s_2},\cdots,{s_k}\} $ , $k$ 表示智能体的数量. $A$ 表示所有智能体的动作集合 $\{ {A_1},{A_2},\cdots, $ $ {A_k}\} $ . $Pr ({S^{'}}|S,A)$ 表示状态转移函数, $ S \times {A_1} \times \cdots \times {{A}_k} \to $ $ P({S^{'}}) $ . 其中 $P({S^{'}})$ 定义了所有智能体的下一个状态的概率分布. $R$ 表示所有智能体的回报集合 $\{ {r_1},\cdots,{r_k}\} $ . 本文遵循以上符号表示.

对于每一个智能体 $i$ , 学习相应的动作选择策略 ${\pi _i}$ : ${o_i} \to P({A_i})$ . 其中 ${o_i}$ 表示智能体 $i$ 的局部观测, $P({A_i})$ 表示选择动作的概率分布.

智能体的目标是学习一个动作选择策略以最大化预期回报如下, 其中 $\gamma $ 为折现因子.

$ {J_i}({\pi _i}) = {E_{{A_1}\sim{\pi _1},\cdots,{A_k}\sim{\pi _k}}}\left[\sum\nolimits_{t = 0}^\infty {{\gamma ^t}{r_{i,t}}({S_t},{A_{1,t}},\cdots,{A_{k,t}})} \right] $

(2)

2.2 多智能体深度确定性策略梯度

深度策略梯度算法(deep policy gradient, DPG)^[15]是一种非常经典的深度强化学习算法. 该算法使用神经网络模拟动作策略函数, 通过梯度上升法调整网络参数以最大化目标函数, 如式(3)所示:

$ J(\theta ) = Q({S_t},{A_t}) $

(3)

其中, $Q({S_t},{A_t})$ 表示状态动作对的预期回报的期望值. 相应的动作策略网络的梯度公式如式(4)所示:

$ \nabla J(\theta ) = {E_{{s_t},{A_t}}}[{\nabla _\theta }\log \pi (A|{s_t})Q({s_t},{A_t})] $

(4)

其中, $\pi $ 表示智能体的随机动作策略, 输出所有动作的概率分布.

DDPG (deep deterministic policy gradient)^[16]是DPG的一种变体, 其中动作策略输出的是确定性动作而不是所有动作的概率分布. 可以应用于连续控制的多智能体场景中, 相应的动作策略网络梯度公式如式(5):

$ \nabla J(\theta ) = {E_{{s_t},{A_t}}}[{\nabla _\theta }\mu ({A_t}|{s_t},\theta ){\nabla _{{A_t}}}Q({s_t},{A_t})] $

(5)

其中, $\;\mu $ 表示智能体的确定性动作策略.

而多智能体深度确定性策略梯度算法是DDPG在多智能体场景的扩展, 并且与actor-critic框架相结合. 其中actor模拟动作选择策略函数 $\;\mu $ , 根据智能体 $i$ 的局部观测 ${o_i}$ , 输出动作 ${A_i} = {\mu _i}({o_i}|{\theta _i})$ . critic模拟动作价值函数 ${Q_i}$ 以输出智能体 $i$ 某一时刻的状态动作对的预期回报的期望值. ${Q_i}$ 是一个集中式的函数, 考虑了所有智能体的状态动作信息, 解决了多智能体场景中智能体共同学习以及相互作用导致的环境非平稳.

在MA-DDPG算法智能体 $i$ 的actor网络的梯度公式以及critic网络的损失函数分别如式(6)和式(7):

$ \nabla {J_i}({\theta _i}) = {E_{S,A}}[{\nabla _{{\theta _i}}}{\mu _i}({A_i}|{s_i},{\theta _i}){\nabla _{{A_i}}}{Q_i}(S,{A_1},\cdots,{A_k})] $

(6)

$\left\{ { \begin{split} &{L_i}({w_i}) = {{\rm E}_{S,A,r,{S^{'}}}}[{(Q_i^\pi (S,{A_1},\cdots,{A_k}|{w_i}) - y)^2}]\\ &{\rm{ }}y = {r_i} + \gamma \mathop {\max }\limits_{{A^{'}}} \bar Q_i^\pi ({S^{'}},A_1^{'},\cdots,A_k^{'}|{{\bar w}_i}) \end{split}} \right.$

(7)

3 基于值分布的多智能体分布式深度确定性策略梯度算法

本文引入了值分布的思想对预期回报的分布建模, 提出了一种基于值分布的评论家(critic)更新方法; 并在此基础上引入多步回报衡量critic的损失; 最后引入了分布式数据生成架构(APE-X)将智能体与环境交互生成经验数据的部分与网络更新解耦. 这些将会在本节进行详细描述.

3.1 基于值分布的critic更新

基于值的多智能体深度强化学习算法直接对智能体状态动作对的预期回报的期望建模, 不考虑智能体与环境的交互的内在随机性对预期回报的影响. 这种建模方式损失了关于预期回报的完整的分布信息. 本文引入值分布的思想, 强调预期回报的分布信息的重要性, 对预期回报的分布建模, 而非对其期望值建模. 本文将预期回报看作随机变量, 记为 $Z_i^{{\mu _i}}({S_t},{A_t})$ . 定义如式(8)所示:

$ Q_i^{{\mu _i}}({S_t},{A_t}) = {E_{{S_t},{A_t},{S_{t + 1}}}}[Z_i^{{\mu _i}}({S_t},{A_t})] $

(8)

其中, $Q_i^{{\mu _i}}({S_t},{A_t})$ 表示智能体 $i$ 的critic网络输出预期回报的期望值.

本文使用参数化的多分类分布对预期回报的分布建模 $\{ N \in \mathbb{N},{\text{ }}{V_{\min }},{\text{ }}{V_{\max }} \in \mathbb{R}\} $ , 其中 $N$ 表示分类个数, ${V_{\min }}$ 表示最小类别值, ${V_{\max }}$ 表示最大类别值. 以此模拟预期回报的近似分布. 其中一系列的类别值分别如式(9):

$ {{\textit{z}}_j} = {V_{\min }} + j\cdot \vartriangle {\textit{z}},{\text{ }}0 \le j < N,{\text{ }}\vartriangle {\textit{z}} = \frac{{{V_{\max }} - {V_{\min }}}}{{N - 1}} $

(9)

在actor-critic的框架下, 改进的基于值分布思想的critic网络输出预期回报的 $N$ 分类分布 $Z_i^{{\mu _i}}$ , 表示各类预期回报值的概率分布. 记 ${p_{i,j}}({S_t},{A_t})$ 为智能体 $i$ 的critic网络所输出的预期回报属于第 $j$ 类 ${{\textit{z}}_j}$ 的概率.

$ {p_{i,j}}({S_t},{A_t}) = \frac{{{{\rm e}^{{w_j}({S_t},{A_t})}}}}{{\displaystyle\sum\nolimits_{n = 0}^{N - 1} {{{\rm e}^{{w_n}({S_t},{A_t})}}} }},{\text{ }}0 \le j < N - 1 $

(10)

其中, ${S_t} = \{ {s_{1,t}},\cdots,{s_{k,t}}\} $ 表示所有智能体的状态信息, ${A_t} = \{ {A_{1,t}},\cdots,{A_{k,t}}\} $ 表示所有智能体的动作信息.

基于值分布的critic的损失函数定义如式(11)和式 (12):

$\begin{split} &{L_i}({w_i}) = E[d((T\bar Z_i^{{{\bar \mu }_i}})({S_t},{A_{1,t}},\cdots,{A_{k,t}}),Z_i^{{\mu _i}}({S_t},{A_{1,t}},\cdots,{A_{k,t}}))] \end{split} $

(11)

$ \begin{split} &(T\bar Z _i^{{{ \bar \mu }_i}})({S_t},{A_{1,t}},\cdots,{A_{k,t}}) =\\ & \;\;\;\;\;{r_{i,t}} + \gamma E[\bar Z _i^{{{ \bar \mu }_i}}({S_{t + 1}},{A_{1,t + 1}},\cdots,{A_{k,t + 1}})] \end{split} $

(12)

其中, $ {\text{ }}Z_i^{{\mu _i}} $ 表示智能体 $i$ 的critic网络输出的预期回报的近似分布( $Z$ 分布), $\bar Z _i^{{{ \bar \mu }_i}}$ 表示智能体 $i$ 的目标critic网络的输出, $(T\bar Z _{i,t}^{{{ \bar \mu }_{i,t}}})$ 表示值分布的贝尔曼算子. 式(12)将目标critic网络的输出映射成目标 $Z$ 分布, $d$ 表示预期 $Z$ 分布和目标 $Z$ 分布之间距离的度量指标, 本文采用交叉熵损失进行度量.

以上所述引入了值分布的思想对critic的更新进行改进, 相应的actor更新也引入预期回报的分布信息, 本文通过引入 $Z$ 分布的期望来实现, 则actor网络更新的梯度公式如式(13)所示:

$ \left\{ {\begin{split} &\nabla {J_i}({\theta _i}) = {E_{{S_t},{A_t}}}[{\nabla _{{\theta _i}}}{\mu _i}({A_{i,t}}|{o_{i,t}},{\theta _i})E[{\nabla _{{A_{i,t}}}}{Z_i}({S_t},{A_{1,t}},\cdots,{A_{k,t}})]] \\ &{\text{ }}{A_{i,t}} = {\mu _i}({o_{i,t}}|{\theta _i}) \\ \end{split}} \right. $

(13)

3.2 多步回报

本小节在第3.1节所述的基于值分布的critic更新的基础上引入多步回报来计算critic的TD (temporal-difference)误差. 利用多步回报可以使得智能体从未来的经验中学习, 而不是只考虑当下的收益. 多步回报的思想已经广泛的应用在众多单智能体强化学习算法^[17,18]中. 类似的修正也可以应用在多智能体深度强化学习算法中. 基于多步回报的贝尔曼方程定义如式(14)和式(15)所示:

$\begin{split} & (T\bar Z _i^{{{ \bar \mu }_i}})({S_t},{A_{1,t}},\cdots,{A_{k,t}}) = \\ &\;\;\;\;{R_{i,t}} + \gamma E[\bar Z _i^{{{ \bar \mu }_i}}({S_{t + N}},{A_{1,t + N}},\cdots,{A_{k,t + N}})] \end{split} $

(14)

$ {R_{i,t}} = \sum\nolimits_{{t^{'}} = t}^{t + N - 1} {{\gamma ^{{t^{'}} - t}}{r_{i,{t^{'}}}}} $

(15)

其中, ${R_{i,t}}$ 表示时刻 $t$ 智能体 $i$ 的 $N$ 步回报.

3.3 分布式数据生成和网络更新

针对模型耦合度高无法充分利用计算资源的问题, 本文引入了分布式数据生成的框架(APE-X)将多智能体场景中智能体与环境交互生成经验数据和网络更新两部分进行解耦. 负责数据生成的部分称为Actor, 负责从经验回放池中采样数据进行网络更新的部分称为Learner. Actor的网络结构与Learner完全一致, 只负责与环境交互得到经验数据存入经验回放池中, 不执行梯度计算进行参数更新, 而是定期复制Learner的网络参数. Learner只负责从经验回放池中采样数据进行网络更新而不负责与环境进行交互. 本文算法并行运行多个独立的Actor, 分别与环境进行交互得到经验数据 $\{ {S_{t + 1 - N}},{A_{t + 1 - N}},{R_{t + 1 - N}},{S_{t + 1}}\} $ , 写入同一个经验缓冲池中. Learner从该经验缓冲池中随机采样M批经验数据进行网络更新. 具体的算法框架图如图1所示. 其中 ${S_{t + 1 - N}} = \{ {s_{1,t + 1 - N}},\cdots,{s_{k,t + 1 - N}}\} $ , $ {A_{t + 1 - N}} = $ $ \{ {A_{1,t + 1 - N}},\cdots, $ $ {A_{k,t + 1 - N}}\} ,{R_{t + 1 - N}} = \{ {R_{1,t + 1 - N}},\cdots,{R_{k,t + 1 - N}}\} . $

3.4 本文算法小结

本文算法的伪代码如算法1和算法2所示. Learner中actor-critic的网络都采用梯度下降法进行网络参数更新. actor和critic的学习率分别是 ${\alpha _t},\;{\beta _t}$ , 均采用Adam优化器^[19], 利用动量和自适应学习率来加快收敛速度. 该算法伪代码中同时包含了Actor和Learner的伪代码, 多个Actor初始化为相同的多智能体环境, 并行与环境交互生成经验数据并将其存入经验回放池中.

算法1. 经验数据生成-Actor

1)　初始化 $\scriptstyle N$ 值, 智能体数量K, 经验回放池B, 初始化软更新频率TAU

2)　初始化Actor网络参数 $\scriptstyle (\theta _{\rm{Actor}}^{1:k},\omega _{\rm {Actor}}^{1:k} ) \leftarrow (\theta _{\rm{Learner}}^{1:k},\omega _{\rm {Learner}}^{1:k} )$

3)　初始化States, Actions, Rewards, Terminals为大小为 $\scriptstyle N + 1$ 的deque

4)　 For $\scriptstyle j = 1,\cdots,Episode\_num$ do

5)　　Clear (States, Actions, Rewards, Terminals)

6)　　 $\scriptstyle {S_0} \leftarrow $ Env.Reset()

7)　　States.Add( $\scriptstyle {S_0}$ )

8)　　 For $\scriptstyle t = 1,\cdots,\max \_{\text{step}}$ do

9)　　　 $ \scriptstyle {A_{1,t - 1}},\cdots,{A_{k,t - 1}} \leftarrow {\mu _1}({s_{1,t - 1}}),\cdots,{\mu _k}({s_{k,t - 1}}) $

10)　　　 $\scriptstyle {r_{1,t - 1}},\cdots,{r_{k,t - 1}},{S_t},{\text{ter}}{{\text{m}}_t} \leftarrow $ Env.Step( ${A_{t - 1}} + OU$ )

11)　　　States.Add( $\scriptstyle {S_t}$ )

　　　　 Actions.Add( $\scriptstyle {A_{t - 1}}$ )

　　　　 Rewards.Add( $\scriptstyle \{ {r_{1,t - 1}},\cdots,{r_{k,t - 1}}\} $ )

　　　　 Terminals.Add( $\scriptstyle {\text{ter}}{{\text{m}}_t}$ )

12)　　 　 If States.full then

13)　　　　根据式(15)计算 $\scriptstyle N$ 步回报 $\scriptstyle {R_{t - N}} $

14)　　　　B.Add(States[0],Actions[0], $\scriptstyle {R_{t - N}} $

　　　　　　　States[N], Terminals[N–1])

15)　　　　PopLeft(States, Actions, Rewards, Terminals)

16)　　　 End If

17)　　　 If $\scriptstyle {\text{ter}}{{\text{m}}_t}$ break

18)　　 End For

19)　 End For

算法2. 网络更新-Learner

1)　初始化采样批次M, 最大更新步数T

2)　随机初始化网络参数 $\scriptstyle (\theta _{\rm{Learner}}^{1:k},\omega _{\rm {Learner}}^{1:k} )$

3)　初始化目标网络参数 $\scriptstyle (\theta _{\rm {targ et}}^{1:k},\omega _{{\rm {targ et}}}^{1:k} ) \leftarrow (\theta _{\rm {Learner}}^{1:k},\omega _{\rm {Learner}}^{1:k} )$

4)　 For $\scriptstyle t = 1,\cdots,T$ do

5)　　 If len( $\scriptstyle B$ ) < $\scriptstyle M$ break

6)　　从B中随机采样M批数据

7)　　 For $\scriptstyle i = 1,\cdots,k$ do

8)　　　根据式(14)和式(11)计算critic的损失, 使用梯度下降法　　　　进行反向传播更新critic网络参数

9)　　　根据式(13)计算actor的梯度, 其中 $\scriptstyle {A_{i,t}} = {\mu _i}({s_{i,t}}|{\theta _i})$ , 更新actor　　　　网络参数

10)　　 End For

11)　　 $\scriptstyle \begin{array}{l}\scriptstyle (\theta _{\rm {targ et}}^{1:k},\omega _{\rm {targ et}}^{1:k} ) = (1 - TAU) \cdot (\theta _{\rm {targ et}}^{1:k},\omega _{\rm {targ et}}^{1:k} ) {\text{ }} + TAU \cdot (\theta _{\rm {Learner}}^{1:k},\omega _{\rm {Learner}}^{1:k}) \\ \end{array}$

12)　　 If $\scriptstyle t\;\boldsymbolod \; {\rm{actor\_update\_freq}} = = 0$ then

13)　　　Replicate Network Weights to Actors

14)　　 End If

15)　 End For

4 实验分析

本文设置了3个实验场景来测试本文算法(MA-D4PG)的性能, 将在本节依次描述. 在实验中设置了一个额外的Actor. 该Actor只利用, 而不进行探索, 方便在没有噪声的情况下测试本文算法的性能. 其他Actor则负责探索环境, 获得更多关于环境的信息, 并且与环境交互生成经验数据. Learner每更新N步, 将网络参数复制给Actor. 本文将N值设为5. 为了加快训练模型以及更好的利用资源, Learner模型在GPU上进行运算, Actor在CPU进行运算. 强化学习算法性能评价的两个关键指标是算法收敛所需的步数以及最终收敛的Episode Reward值. 收敛所需的步数越少, 表示算法的收敛速度越快, 最终的收敛的Episode Reward值越大, 表示智能体的学习效果越好. 本文将根据这两个指标对本文算法进行评价. 并且本文还做了一些消融实验, 分别删除本文算法中的单项组件, 以确定其特定的贡献.

本文实验中统一使用大小为 $1 \times {10^6}$ 经验重放池存储智能体与环境交互产生的经验数据. 为确保一定的探索性, 在智能体的动作策略中添加Ornstein-Uhlenbeck噪声^[19]. 并且本文实验中actor和critic的学习率以及采样批次大小, 软更新频率统一设置如下:

$ \alpha = 5 \times {10^{ - 5}},\beta = 5 \times {10^{ - 5}},M = 256,TAU = 0.001 $

4.1 实验环境配置

本文算法中实验环境的配置如表1所示. 本文采用了PyTorch作为深度学习框架, 在GPU上使CUDNN加速训练模型.

4.2 实验场景

本文实验包含了3个实验场景, 如图2所示. 这3个实验场景分别是多智能体合作清洁, 多无人机监控, 多智能体救援. 本节将对这3个实验场景进行简单描述.

在多智能体清洁场景中, 两个或者多个智能体将合作打扫一个房间, 实验场景如图2(a)所示. 环境中智能体的任务是在规定的时间内尽量扩大清洁面积, 或者是在最短的时间内尽量清洁完所有的区域. 该任务实际上是一个路径规划任务, 智能体之间应该合作规划具有最小重叠区域的路径. 每个智能体的局部观测由周围8个方块的状态组成, 一共8维. 动作空间是1维, 可以朝上下左右4个方向移动.

多无人机监控实验场景如图2(b)所示. 正方形区域表示地面, 空中有多个无人机使用摄像头监控地面, 无人机可以在给定区域自由飞行. 每架无人机都有一个由半径定义的局部观测区域(如图2(c)所示), 无人机只能观测到该区域内的物体. 在该实验场景中, 多个智能体(无人机)的目标是尽量减少视觉区域的重叠以及监控更多的行人. 每个智能体的动作空间包含朝上下左右4个方向移动以及停留原地5个动作.

多智能体救援实验场景如图2(d)所示. 方形区域模拟地震后的废墟. 多个智能体从安全点出发, 进入该区域, 找到该区域的人并带回安全点. 该任务的目标是智能体尽可能在更短的时间内将更多的人带回安全点. 每个智能体的局部观测范围是其前方90度的扇形区域, 半径为3个方块的长度. 智能体的动作空间维度大小为4, 分别表示沿 $x$ 轴方向行走 $[ - 0.5,0.5]$ , 沿 $y$ 轴方向行走 $[ - 0.5,0.5]$ , 旋转 $[ - 10,10]$ , 背起/放下人 $\{ 0,1,2\} $ .

3个实验场景中的超参数如表2所示.

4.3 实验结果分析

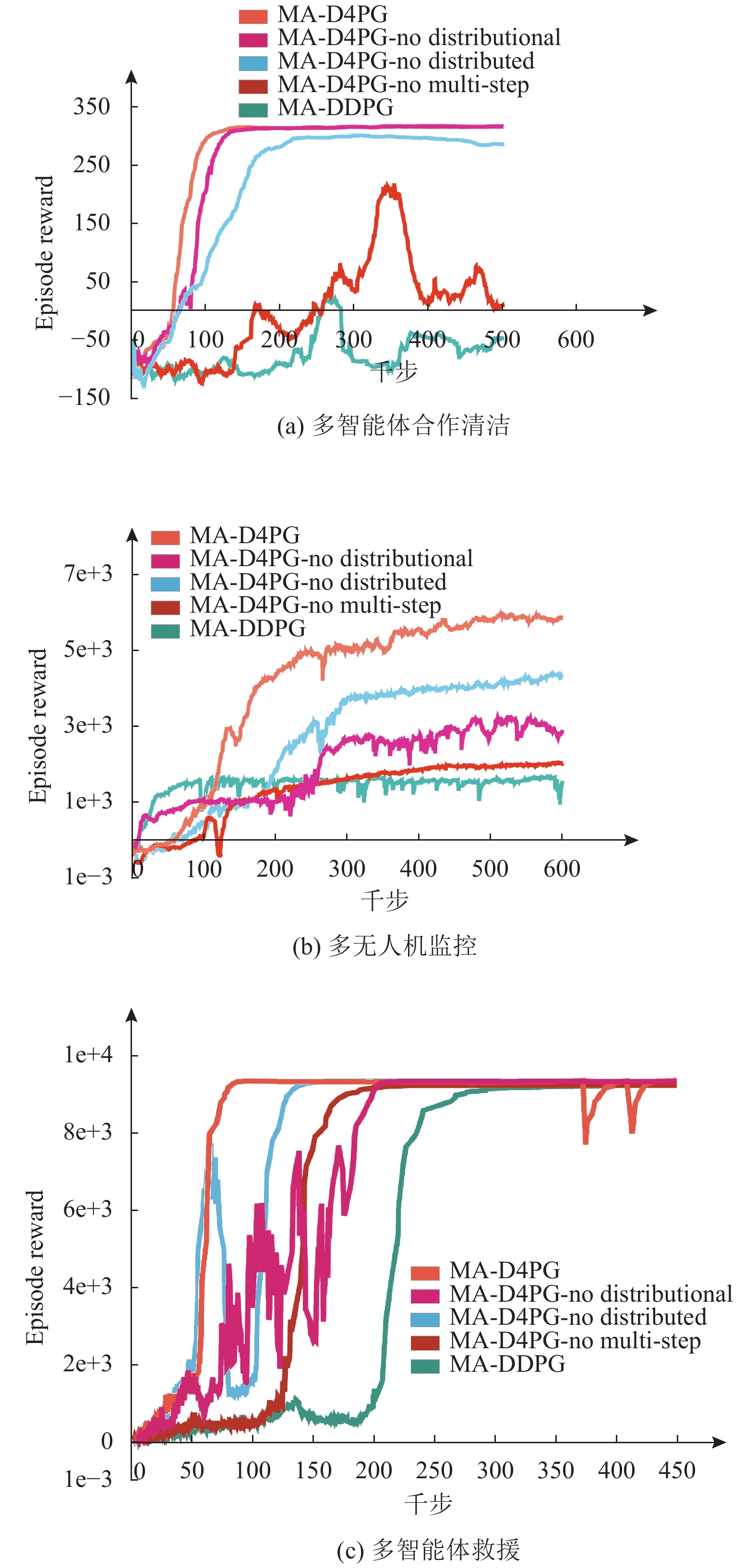
在框架上, 本文较多借鉴了目前性能最好的多智能体深度强化学习算法-多智能体深度确定性策略梯度算法, 因此选择与该算法进行对比实验. 此外还进行了消融实验, 分别确定本文所提每个方法的贡献. 图3展示了本文算法(MA-D4PG)以及3个消融实验和MA-DDPG在该实验环境中的性能. 其中MAD4PG-no distributional所示曲线表示本文算法去掉第3.1节所述改进后的运行效果, MAD4PG-no multistep所示曲线表示本文算法去掉第3.2节所述改进的运行效果, MAD4PG-no distributed所示曲线表示本文算法去掉第3.3节所述改进的运行效果.

从图3(a)中可看到在多智能体合作清洁的场景中, 本文算法MA-D4PG在收敛速度和最终收敛的Episode Reward值这两个指标上都有最好的表现, 并且算法的稳定性更好. 对MAD4PG-no distributional/MAD4PG-no distributed这两条曲线进行分析可看出, 第3.1节和第3.3节所述的改进对算法最后收敛的Episode Reward值的提升虽不太明显, 但是加快了算法的收敛速度.

对图3(b)进行分析可得, 在多人机监控场景中, 相较MA-DDPG算法, 本文算法(MA-D4PG)收敛速度较慢, 但是最终收敛的Episode Reward值约是MA-DDPG的3.6倍, 智能体的决策能力得到了极大地增强. 对MAD4PG-no distributional/MAD4PG-no distributed分析可得, 第3.1节和第3.3节所述改进使得最终收敛的Episode Reward值分别提升了约97%和43%.

对图3(c)分析可得, 在多智能体救援场景中, 本文算法(MA-D4PG)的收敛速度约是MA-DDPG算法的3.75倍. 对MAD4PG-no multistep/MAD4PG-no distributed两条曲线分析可得, 第3.2节和第3.3节所述改进使得算法的收敛速度分别提升了约185%和100%.

对图3(a), 图3(b)的MAD4PG-no multistep曲线联合分析可看出, 去掉多步回报的改进, 算法性能下降最大, 并且去掉该改进会导致算法的稳定性显著下降. 这两个实验场景中智能体只包含一维的离散动作空间, 控制任务相对简单. 从中可看出在离散控制的多智能体场景中, 引入多步回报对算法性能的贡献最大, 而第3.1节和第3.3节所述改进之间的互补作用较小.

对图3(c)的MAD4PG-no distributional曲线分析可得, 去掉值分布的改进, 算法的收敛速度降低最大, 并且算法的稳定性也有一定的下降. 该实验环境中的控制任务比较复杂, 既包含连续动作, 又包含离散动作, 而前两个实验场景中智能体只包含一维的离散动作空间. 从中可看出在复杂的控制任务中, 引入值分布对算法性能的贡献最为突出.

5 结论与展望

本文的主要贡献是提出了一种基于值分布的多智能体分布式策略梯度算法, 利用值分布替代期望值, 进一步区分智能体行为的好坏, 而不是简单地将其平均为期望值; 同时引入了多步回报增加智能体的预见能力, 提高算法稳定性; 此外引入了分布式数据生成框架将多智能体场景中智能体与环境交互生成经验数据和网络更新解耦, 加快算法的收敛. 本文算法在3个实验场景中都实现了最好的性能. 这3项改进都有助于提升本文算法(MA-D4PG)的整体性能, 在前两个实验场景中对性能贡献最大的改进是多步回报. 而在复杂的任务场景中, 值分布的贡献变得更加突出. 本文的实验场景都是基于多智能体合作的场景, 接下来的研究工作是在竞争场景甚至既有合作又有竞争的混合场景中研究本文算法的性能.