复杂性科学是一种新兴的边缘、交叉学科[1], 霍金认为“21世纪是复杂性科学的世纪”. 关于复杂系统的定义, 文献[2]根据组成系统的子系统以及子系统种类的多少和他们之间的关联关系的复杂程度将系统分为简单系统与巨系统两大类, 如果子系统种类很多并且有层次结构, 他们之间的关联关系又很复杂, 将该系统称为复杂巨系统. 从字面上看, 一个复杂的系统是在许多不同组件之间存在多种交互的系统. 复杂系统的发展可以分为两个主线: 以“复杂性”科学的发展历程为主线和以系统科学为主线[3-6]: 钱学森院士引领的“开放的复杂巨系统”的研究.
复杂系统主要具有自适应性、不确定性、涌现性、预决性、演化以及开放性等特征[7-10]. 自适应性体现在组成系统的组件具有自适应、自学习、自组织、自聚集等能力; 不确定性体现在复杂系统中的随机因素不仅影响状态, 而且影响组织结构和行为方式; 涌现性体现在子系统间的相互作用可以产生与单个子系统行为显著不同的宏观整体性质; 系统的预决性是系统对未来状态的预期和实际状态限制的统一; 复杂系统的复杂性体现在复杂系统一般由简单的元素组合, 经过不断的演化而发展为功能和结构更为复杂的系统; 系统与子系统、外部环境之间存在能量、信息或物质的交换, 表现为复杂系统的开放性.
由于复杂系统具有不确定、涌现性等特点所以对复杂系统的整体分析往往是不可能或成本过高的, 其往往涉及到跨时空层次, 多重宏、微观层面的相互关系的子模块. 而各个子系统之间的相互关联使用传统的处理方法很难做出精确的描述, 且系统的不确定性以及多样性使得对复杂系统的建模与仿真比一般的系统要复杂的多, 因此研究复杂系统的建模方式具有巨大的现实意义.
复杂网络是用于描述、分析、理解复杂系统的应用最广泛的方法之一[11,12].
基于复杂网络拓扑结构的建模可以有效的分析复杂系统的结构特征和传播机理. 利用复杂网络来解决交通、电力系统等成为主要的研究课题之一. 但对于复杂系统这样模块间关联度极高的系统来说基于复杂网络的建模存在明显的缺陷: 模型节点表达能力弱, 往往以忽略节点异质性为前提进行研究, 与实际系统存在一定程度的偏差. 在复杂网络的基础上, 2010年Buldyrev等[13]首次提出相依网络建模方法, 其最初的网络被严格假设为两层网络节点数是一致且一对一连接的, 但现实生活中很少存在符合这一严格假设的系统. Parshani等[14]随后提出部分相依网络, 放松了对两层网络节点数一样的限制, 对每层设置随机数量的副本与另一层建立关联. Shao等[15]又进一步提出一对多的依存型多层网络概念, 进一步将相互依存的网络数量由两个推广到多个. 相依网络建模方式能较好的弥补单层网络模型准确度不足的问题, 但当层数大于2时, 建模难度大大提升. 文献[16]提出了基于向量复杂网络的多子网复合网络模型, 该模型在普通复杂网络的基础上通过引入边的关系R将多层网络进行组网, 形成多维向量复杂网络模型. 但该建模方法存在模型过于复杂, 缺少专业的人才来进行准确的建模的难题且模型复杂度过高的问题.
本文通过导入节点间的关系, 提出一个泛化的复杂系统模型-多子网复合复杂向量网络模型. 第1节中对向量复杂网络进行了定义, 并分析了其相应的指标特性; 在第2节中通过八节点模型给出基于业务驱动的向量复杂网络的建模方法; 第3节基于某省电力网络论证了向量复杂网络建模的可行性; 在第4部分进行了分析, 基于向量的复杂复合网络建模为复杂网络拓扑与其上的动力学行为分析提供了一种新颖的思路.
1 向量复杂网络 1.1 术语和符号定义1. 复杂网络[17]. 复杂网络是由点集V和边集E组成的图
定义2. 复合网[16]. 多子网复合复杂网络(简称复合网)是一个四元组
(1)
(2)
(3)
(4)映射
定义3. 向量复合网[16]. 设
| $ \begin{split} & M\left( {\left\langle {{v_h},{v_l}} \right\rangle } \right) = {s^{\left\langle {{v_n},{v_l}} \right\rangle }} \\ &= \left( {{s^{\left\langle {{v_n},{v_l}} \right\rangle }}({r_1})\cdots{s^{\left\langle {{v_n},{v_l}} \right\rangle }}({r_i})\cdots{s^{\left\langle {{v_n},{v_l}} \right\rangle }}({r_n})} \right) \in S,1 \le i \le n \end{split} $ | (1) |
则称三元组
当
当
也就是说, 给定一个复合网与该复合网的关系强度向量空间以及映射M, 则可唯一地确定该复合网的向量复合网.
定义4.向量复杂网络. 复杂网络是一个三元组
(1)
(2)
(3)
命题1. 向量复合网络是向量复杂网络的一种特殊情况.
证明: 要证明向量复合网络是向量复杂网络的一种特殊情况我们采用构造法进行证明. 我们只需要证明向量复合网络是向量复杂网络的真子集即可. 设
向量复合网络是向量复杂网络的一种特殊情况, 但在面对网络规模庞大且节点关系复杂的网络时, 将节点间的关系一一列举并在网络的连接边上进行表达会增加模型的复杂度. 基于扩展节点的向量复杂网络可以降低模型复杂度并提高模型表达能力.
命题2. 一维向量复杂网络是复杂网络.
证明:
复杂网络的指标体现主要涉及: 平均路径长度[18]、聚类系数[19]、点的度数度分布[20,21]、同样对于向量复杂网络, 也具有相应的平均路径长度、聚类系数、度与度分布等指标特性.
定义5. 平均路径长度.
网络的平均路径长度描述了网络种任意两个节点之间的平均最小边的数量, 表示整个网络节点的紧密程度, 用来衡量网络的传输效率. 平均路径越小, 网络越紧密, 传输效率越高.
向量复杂网络的平均路径长度可以反映该网络的传输效率, 研究向量复杂网络的平均路径长度可以分两种情况来研究.
情况1. 异质节点间可以进行传输. 此时, 向量复杂网络的平均路径长度计算等同于复杂网络中平均最短路径.
| $L = \frac{1}{{\dfrac{1}{2}N(N{{ - }}1)}}\sum\limits_{{{i}} \ge j} {{d_i}_j} $ | (2) |
情况2. 异类节点之间无法连通. 网络中两个同类节点间的距离
| ${L^a} = \frac{1}{{\dfrac{1}{2}{N^a}({N^a}{{ - }}1)}}\sum\limits_{{{i}} \ge j} {d_{ij}^a} \;\;(1 \le a \le m)$ | (3) |
向量复杂网络的平均路径长度为所有类型节点平均路径长度的平均值:
| $L = \frac{{{L^a} + {L^b} + {L^c} + \cdots+{L^n}}}{n}$ | (4) |
当网络中服务类型种类数为1时, 即典型的复杂网络, 此时网络中节点的平均最短路径为网络中任意两点间的路径的平均值. N为网络中服务的总数.
定义6. 聚类系数.
聚类系数是评估图中顶点之间结集成团的程度的系数, 我们利用聚类系数来量化网络的传递性. 文献[22,23]研究发现真实世界网络结构, 特别是社交网络结构中, 各个节点之间前向于形成密度相对较高的集群. 小世界性[24]、无标度性[25]的发现进一步促进了复杂网络的发展. 研究表明[26], 规则网络具有较大的聚类系数和大的平均最短路径. 随机网络具有小的聚类系数和小的平均最短路径. 由此可见网络的聚类系数反映了网络的紧密程度, 是网络分类的判定条件之一.
向量复杂网络的聚类系数体现为所有节点聚类系数的平均值. 节点
| ${C_{{i}}} = 2{E_{{i}}}/({k_i}({k_i} - 1))$ | (5) |
| $C = \frac{{{C_1} + {C_2} + {C_3} + \cdots+{C_{{n}}}}}{{{n}}}\;\;(0 \le i \le n)$ | (6) |
定义7. 度与度分布.
节点i的度定义为与该节点连接的其他节点的数目.
向量复杂网络中节点的度与度分布与经典复杂网络相同, 都为与该节点相连的其余节点的数量. 直观上看, 一个节点的度越大就意味着这个节点在某种意义上越“重要”, 定义为
| ${{{p}}_{{k}}} = \sum\limits_{k' = k}^\infty {{p_{k'}}} $ | (7) |
(1)节点表示
(2)边的表示
如图1所示为一个简单的信息物理融合系统的8节点向量复杂网络.
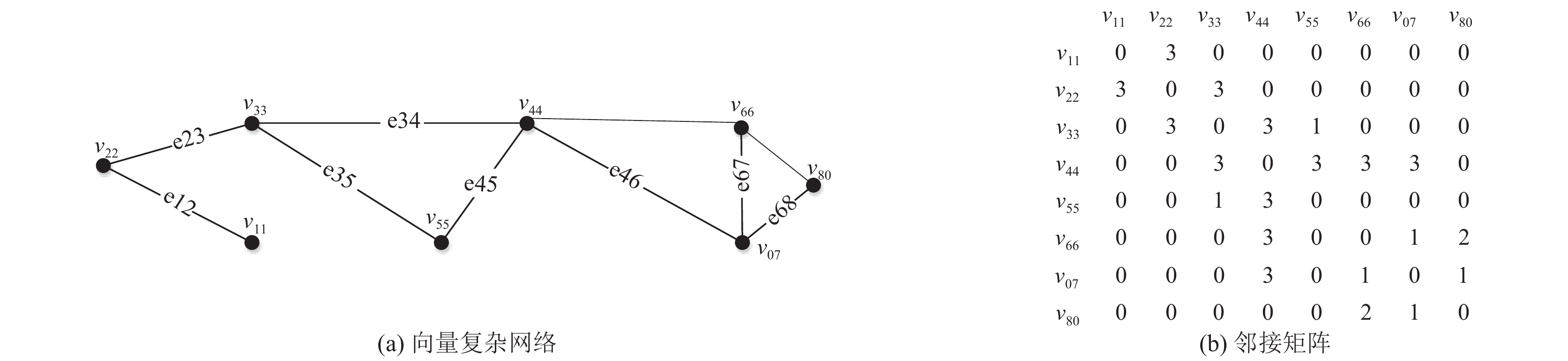
|
图 1 向量复杂网络及其邻接矩阵 |
该网络中默认只有提供相同服务的节点之间可以进行相应服务的传输, 网络中节点的平均路径长度为不同类节点平均路径长度的平均值, 其相应的平均路径长度及聚类系数如表1所示.
| 表 1 8节点向量复杂网络指标特性 |
2 复杂系统的向量复杂网络建模 2.1 基于业务驱动的复杂系统建模方法
基于复杂网络的建模存在一定的难度即规模过于复杂, 缺乏专业的人员进行抽象建模. 针对该问题, 基于复杂网络的向量网络模型提供了解决方案, 通过业务驱动, 将复杂异构系统从不同业务需求角度进行建模, 如在智能电网中, 根据智能电网中的服务类型, 将电网的业务分为物理服务与信息服务, 分别对物理层面及信息层面进行建模, 最后基于一定的组网算法, 将多个异构网络整合为向量复杂网络.
2.2 基于业务驱动的复杂系统建模算法基于业务驱动的复杂系统建模需要对复杂系统有一定的了解, 分析系统中存在的服务类型, 并基于服务分层对系统进行建模. 其建模方法类似于传统复杂网络, 将该服务所涉及到的设备抽象为节点, 设备间的联系抽象为边, 生成该服务对应的网络拓扑模型, 最后基于本文的组网算法对不同服务的网络进行组合进而生成复杂系统的拓扑模型.
设网络
| $ \varPhi :{{v}}_{{i}}\to {{v}}_{{j}}, {{v}}_{{i}}\subseteq {{V}}_{{1}}{{,v}}_{{j}}\subseteq {V}{}_{{2}}$ | (8) |
| $\begin{split} & Z:\{ \left\langle {{v_{i1}},{v_{i2}}} \right\rangle ,\left\langle {{v_{j1}},{v_{j2}}} \right\rangle |{v_{i1}},{v_{i2}} \in {V_1},{v_{j1}},{v_{j2}} \in {V_2}\} \\ & \to (\left\langle {{v_l},{v_s}} \right\rangle |l,s \in V) \end{split} $ | (9) |
| $\varPsi :\{ \left\langle {{v_l},{v_s}} \right\rangle ,{v_l},{v_s} \subseteq V\} \to (T)$ | (10) |
网络1与网络2的加载表明了两个网络中哪些节点间建立一种新的关系, T为节点加载关系, 如果节点间存在该种类型的服务, 则相应位置元素为该关系的值, 否则为0. 在边的耦合中, 只要两个节点间存在任何类型的服务, 即关系
算法实现:
算法1. 向量复杂网络的加载运算
输入:
输出:
步骤:
1.节点以及边的加载:
2. 同层节点间的边直接加载:
如果
3. 不同层节点间边如果存在则直接使用已有连接, 否则进行加载:
如果
否则
4. 节点间关系的加载:
5. 生成节点的向量复杂网络基向量S:
6. 构造节点向量映射M:
当
当
7. 生成对应的边邻接矩阵.
在边的加载过程中, 只要两个节点之间存在服务, 节点之间的边就会被加载到向量复杂网络中, 所以只要
以信息物理融合系统为例, 如图2所示为一个物理层网络
| $\varPhi {{ = }}\left\{ {\left\langle {{{{v}}_{{i}}}{{,}}{{{v}}_{{j}}}} \right\rangle {{|}}{{{v}}_{{i}}} \in {{{V}}_{{1}}}{{,}}{{{v}}_{{j}}} \in {{{V}}_{{2}}}{{,i = j}}} \right\}$ | (11) |
| $Z:\{ \left\langle {{v_{i1}},{v_{i2}}} \right\rangle ,\left\langle {{v_{j1}},{v_{j2}}} \right\rangle |{v_{i1}},{v_{i2}} \in {V_1},{v_{j1}},{v_{j2}} \in {V_2}\} $ | (12) |
| $\varPsi = \left\{ {\left\langle {{v_k},{v_l}} \right\rangle ,({T_1},{T_2})|{V_{{k}}},{V_j} \in V} \right\}$ | (13) |
其中, {0, 1, 2, 3}为对应的
在节点的加载运算中, 我们默认将被加载的节点视为同一个节点, 新节点能提供的服务类型为原来两节点提供服务类型的总和, 节点之间的连边会默认被加载到新的向量复杂网络中且相同节点间的连边仅加载一次. 图2为8节点的信息网络与8节点物理层网络, 采用本文提出的向量复杂网络加载算法进行加载后(默认将相同名称的节点进行加载), 得到如图3所示的向量复杂网络及其邻接矩阵图.

|
图 2 加载前网络连接图 |
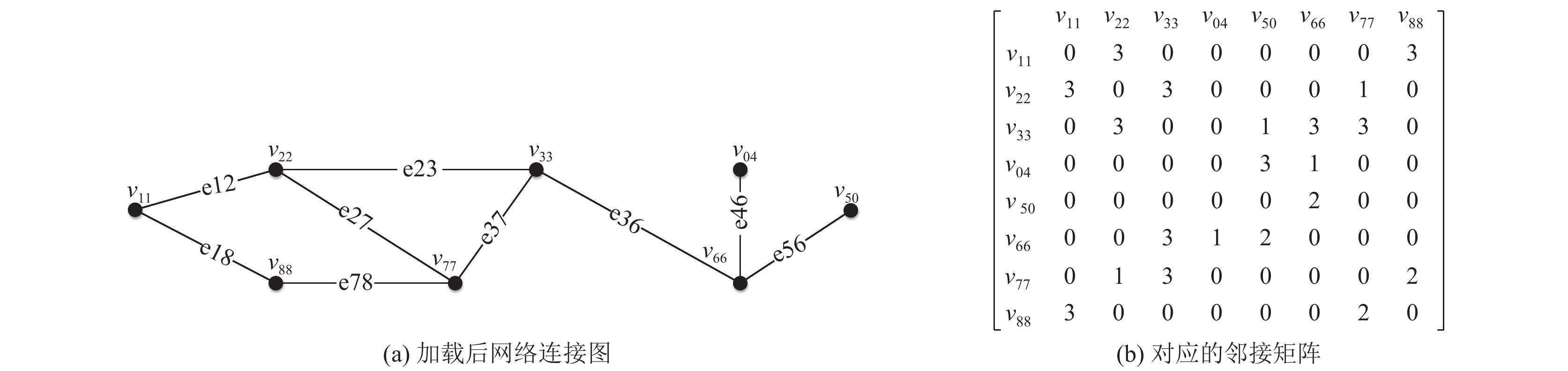
|
图 3 加载后向量复杂网络连接图及邻接矩阵 |
2.3 向量复杂网络模型的还原
向量复杂网络可以从总体的角度分析复杂系统的某些特性, 但有些时候我们只关注复杂系统的局部或者说需要将一个或者几个复杂网络从大型复杂系统中分离出来. 采用基于向量复杂网络的拆分算法可以省去局部建模的工作. 且由于建模人员知识水平差异, 面向服务的单层模型可能存在偏差, 通过将不同建模人员所建模型进行组网整合后可以修正模型中存在的问题, 达到提高准确度的目的. 在子网拆分过程中以服务为导向, 根据服务进行拆分, 可将子网拆分为单个网络或某几个服务的向量复杂网络. 具体的拆分算法将在以下部分进行介绍.
设向量网络
算法2. 向量复杂网络的拆分运算
输入:
输出: 向量复合网关于关系T'的子网
步骤:
1.
2. 将E'中的节点添加至
3. 构造新的节点间关系的加载
4. 生成节点的向量复杂网络基向量S:
5. 构造节点向量映射
当
当
图4(a)为向量复杂网络G, 其组成关系T={
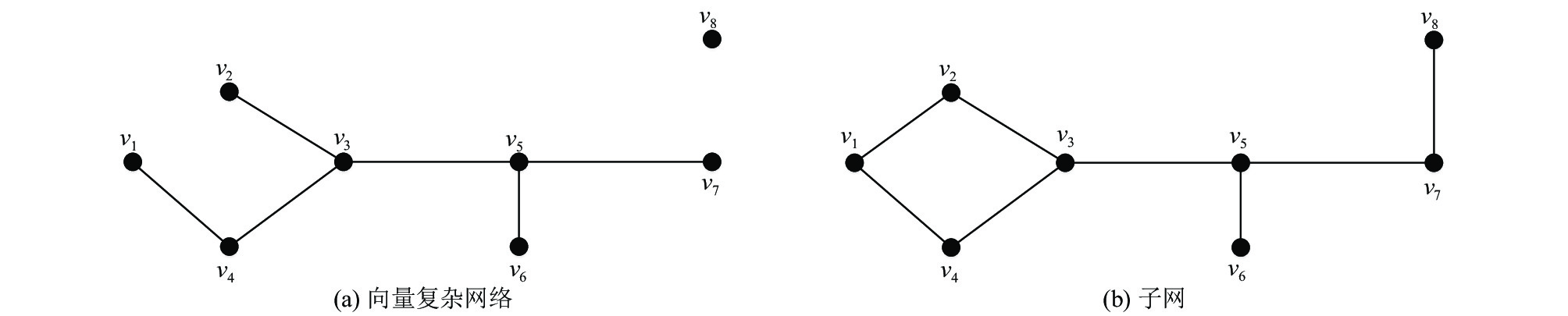
|
图 4 拆分前后对比图 |

|
图 5 向量复杂网络邻接矩阵 |
2.4 向量复杂网络模型分析
本节我们将复杂网络建模、向量复合网络建模、相依网络建模以及向量复杂网络建模4种建模方式从描述能力、建模难度、模型存储空间3个方面进行比较分析, 如表2所示.
3 仿真分析智能电网作为新一代的电网系统, 最大的特点是建立在高效的双向通信网络上, 依赖大量的传感器设备和通信设备进行设备间信息传输, 并通过通信网对接收到的实时信息进行传输, 由信息处理中心对接收到的信息进行处理并通过通信网传输到相应的元件. 以华中地区某省的电力网为例进行分析, 如图4所示为某省电力网的地理接线图, 其中包括220 kV和500 kV层面的变电站、开关站、牵引站以及相应的线路, 为了研究方便, 我们忽略各站点的内部结构, 将220 kV层面的变电站、发电厂抽象为物理节点, 忽略厂内部连接, 将两个厂间的多条物理连边合并为一条, 选取其中的20个节点为例进行研究. 对于信息层面的模型, 我们默认每个物理设备均配有相应的信息设备以实现信息采集、监督、控制等功能, 为简化分析, 我们将信息设备抽象为信息节点, 信息设备之间的连接抽象为节点连边. 电力通信网络为典型的无标度网络, 其高度数节点为网络中具有特定功能的节点, 在通信网络中, 我们默认高度数节点为调度中心, 并基于BA网的生成过程构造出20个节点的信息层.
以20节点为例的电力向量复杂网络拓扑如图6所示.
| 表 2 与其他复杂网络建模方式对照表 |
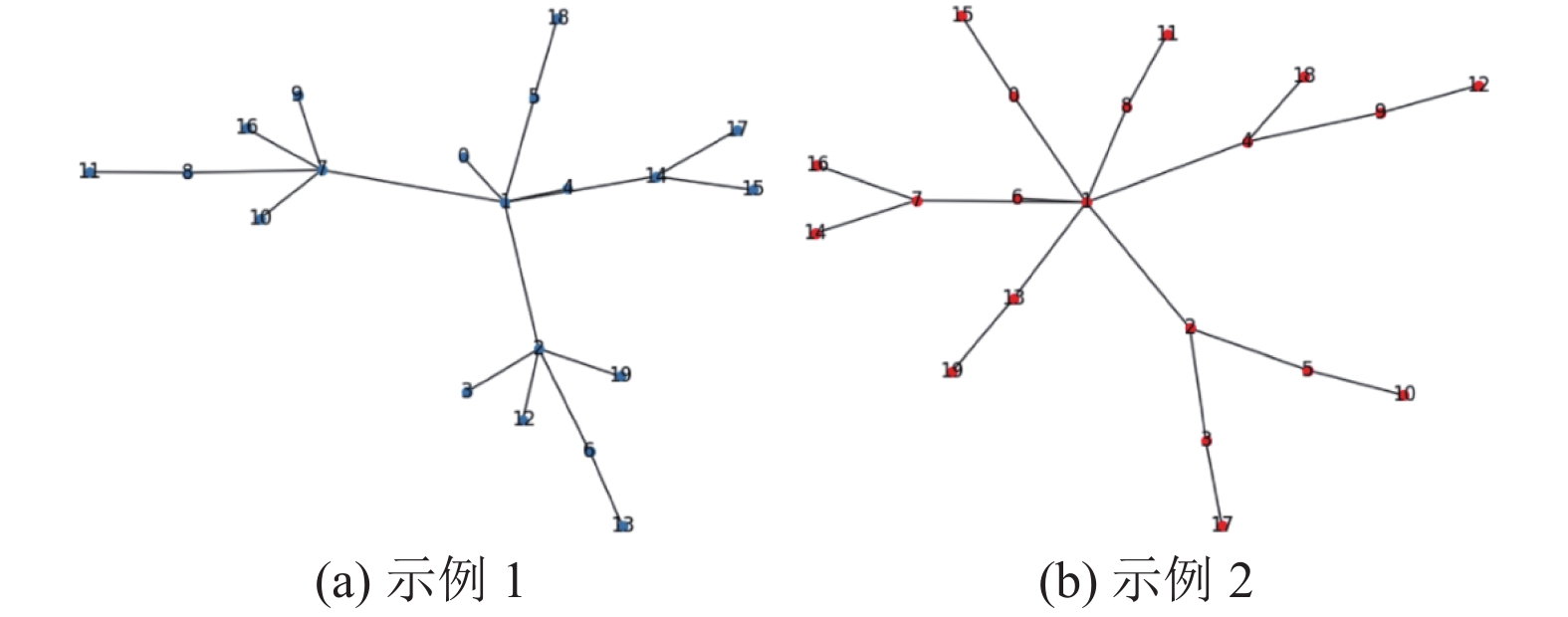
|
图 6 20节点电力向量复杂网络信息物理拓扑图 |
基于本文的业务驱动的复杂系统建模方法, 其加载四元组为:
| $T = \left\{ {{T_1},{T_2}} \right\}$ | (14) |
| $\varPhi :{{{v}}_{{{ic}}}} \to {v_{jp}},{v_i} \in {V_1},{v_j} \in {V_2}$ | (15) |
| $\begin{split} & Z:\{ \left\langle {{v_{i1}},{v_{i2}}} \right\rangle ,\left\langle {{v_{j1}},{v_{j2}}} \right\rangle |{v_{i1}},{v_{i2}} \in {V_1},{v_{j1}},{v_{j2}} \in {V_2}\} \\ & \to (\left\langle {{v_l},{v_s}} \right\rangle |l,s \in V) \\ \end{split} $ | (16) |
| $\varPsi :\left\{ {\left\langle {{{{v}}_{{l}}}{{,}}{{{v}}_{{s}}}} \right\rangle ,{v_l},{v_s} \in V} \right\} \to (T')$ | (17) |
得到加载后的向量复合网络及其度分布图如图7.
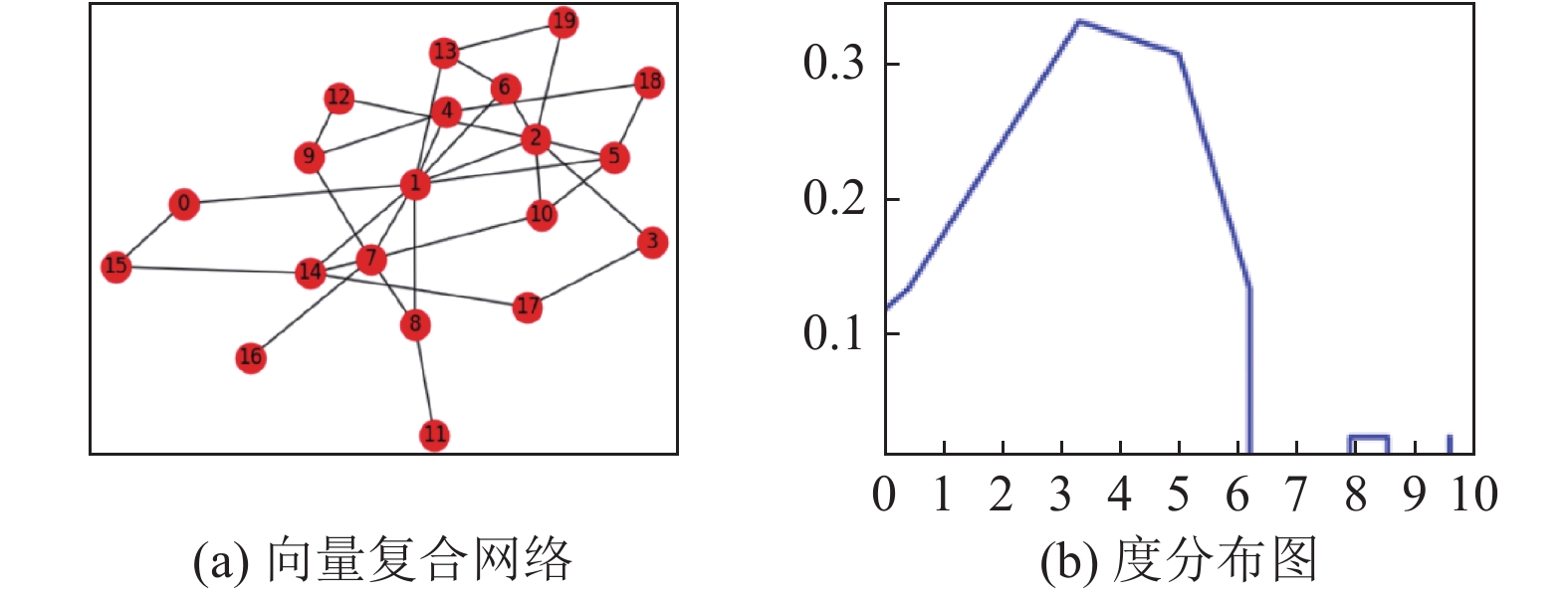
|
图 7 20节点向量复合网络拓扑及度分布图 |
由图7可知, 该省电力系统选取的20个节点中, 传递信息服节点的平均路径长度为: 1.68421052631579, 传输物理服务节点的平均路径长度为: 2.9894736842105263, 所以, 整个网络的平均路径长度为提供信息服务的节点与提供物理服务的节点平均路径长度的平均值为: 2.336842105263158, 聚类系数0.12908730158730158. 度分布图如图7(b). 从图7我们可以发现节点1, 2为高度数节点, 在整个网络中发挥着重要的作用, 在进行资源分配时, 应重点关注这两个节点.
由以上分析可知, 本文方法先将复杂系统按业务拆分为多个业务系统, 分别研究单个系统的网络拓扑, 再重新组合各个业务网络成为完整的复杂系统网络, 适用于大规模且复杂度高的网络, 所建模型的特点:
(1)综合考虑网络整体拓扑结构, 以业务为导向建模增加模型准确度
(2)建模难度低, 不需要对整个复杂系统熟悉的专业人员, 只需涉及单层业务的专业人员分层建模, 降低了对建模人员的要求.
(3)适用于大规模网络. 现有文献再研究大规模复杂系统时, 往往将网络等效为节点数较小的网络, 无法评估网络内部的运行情况. 根据本文建模方法, 将网络基于业务分层建模, 然后分别研究单业务的网络, 再重新组合各个业务网络成为复杂系统的网络拓扑.
4 总结与展望本文建立了一种新的复杂系统建模模型即基于向量复杂网络的建模方法, 与以往复杂系统建模不同的是网络中节点类型复杂, 节点间的连接关系复杂并可以体现在边的邻接矩阵中. 利用复杂网络的组网算法可以克服复杂系统建模复杂度高且缺乏专业人员的问题, 基于向量复杂网络的拆分算法可以实现子网的拆分, 实现复杂系统的局部分析.
采用基于向量复杂网络的建模方式可以充分体现复杂系统内部异质性特点, 且复杂网络的统计指标特性可以很好的分析复杂系统的拓扑特性, 向量复杂网络的建模在现实生活中实用性很强, 它的应用将是下一步研究的重点.
| [1] |
宋学锋. 复杂性、复杂系统与复杂性科学. 中国科学基金, 2003, 17(5): 262-269. DOI:10.3969/j.issn.1000-8217.2003.05.002 |
| [2] |
钱学森, 于景元, 戴汝为. 一个科学新领域——开放的复杂巨系统及其方法论. 自然杂志, 1990, 13(1): 3-10, 64. |
| [3] |
Bertalanffy LV. General system theory. New York: Braziller, 1968.
|
| [4] |
Prigogine I, Stengers I. Order Out of Chaos. New York: Bantam Books, 1984.
|
| [5] |
Haken H. Advanced Synergetics. New York: Springer, 1983.
|
| [6] |
Sastry S. Networked embedded systems: From sensor webs to cyber-physical systems. Proceedings of the 10th International Workshop on Hybrid Systems: Computation and Control. Pisa, Italy. 2007. 1.
|
| [7] |
刘晓平, 唐益明, 郑利平. 复杂系统与复杂系统仿真研究综述. 系统仿真学报, 2008, 20(23): 6303-6315. |
| [8] |
胡晓峰. 战争复杂性与信息化战争模拟. 系统仿真学报, 2006, 18(12): 3572-3580. DOI:10.3969/j.issn.1004-731X.2006.12.063 |
| [9] |
张嗣瀛. 复杂性科学, 整体规律与定性研究. 复杂系统与复杂性科学, 2005, 2(1): 71-83. DOI:10.3969/j.issn.1672-3813.2005.01.012 |
| [10] |
王正中. 基于演化的复杂系统建模与仿真研究. 系统仿真学报, 2003, 15(7): 905-909. DOI:10.3969/j.issn.1004-731X.2003.07.001 |
| [11] |
Kurant M, Thiran P. Layered complex networks. arXiv: physics/0510194, 2005.
|
| [12] |
苏春旺. 复杂系统中的结构与动力学——基于数据的研究[博士学位论文]. 兰州: 兰州大学, 2020.
|
| [13] |
Buldyrev SV, Parshani R, Paul G, et al. Catastrophic cascade of failures in interdependent networks. Nature, 2010, 464(7291): 1025-1028. DOI:10.1038/nature08932 |
| [14] |
Parshani R, Buldyrev SV, Havlin S. Interdependent networks: Reducing the coupling strength leads to a change from a first to second order percolation transition. Physical Review Letters, 2010, 105(4): 048701. DOI:10.1103/PhysRevLett.105.048701 |
| [15] |
Shao J, Buldyrev SV, Havlin S, et al. Cascade of failures in coupled network systems with multiple support-dependence relations. Physical Review E, 2011, 83(3 Pt 2): 036116. |
| [16] |
隋毅, 邵峰晶, 孙仁诚, 等. 基于向量空间的多子网复合复杂网络模型动态组网运算的形式描述. 软件学报, 2015, 26(8): 2007-2019. DOI:10.13328/j.cnki.jos.004697 |
| [17] |
Chen B, Cao L. An optimized algorithm for calculating the average path length of complex network. Proceedings of the 2017 10th International Symposium on Computational Intelligence and Design. Hangzhou, China. 2017. 334–337.
|
| [18] |
Fan LY, Li CF, Zhang LF, et al. Assessing the importance of nodes in the social network based on clustering coefficient. Proceedings of the 2018 IEEE/ACIS 17th International Conference on Computer and Information Science. Singapore. 2018. 229–233.
|
| [19] |
Kartun-Giles AP, Bianconi G. Beyond the clustering coefficient: A topological analysis of node neighbourhoods in complex networks. Chaos, Solitons & Fractals: X, 2019, 1: 100004. |
| [20] |
Pastor-Satorras R, Rubi M, Diaz-Guilera A. Statistical Mechanics of Complex Networks. Berlin: Springer, 2003.
|
| [21] |
汪小帆, 李翔, 陈关荣. 复杂网络理论及其应用. 北京: 清华大学出版社, 2006.
|
| [22] |
Holland PW, Leinhardt S. Transitivity in structural models of small groups. Leinhardt S. Social Networks. Amsterdam: Academic Press, 1977. 49–66.
|
| [23] |
Watts DJ, Strogatz SH. Collective dynamics of ‘small-world’ networks. Nature, 1998, 393(6684): 440-442. DOI:10.1038/30918 |
| [24] |
Barabasi AL, Albert R. Emergence of scaling in random networks. Science, 1999, 286(5439): 509-512. DOI:10.1126/science.286.5439.509 |
| [25] |
周涛, 柏文洁, 汪秉宏, 等. 复杂网络研究概述. 物理, 2005, 34(1): 31-36. DOI:10.3321/j.issn:0379-4148.2005.01.007 |
| [26] |
Kenett DY, Gao JX, Huang XQ, et al. Network of interdependent networks: Overview of theory and applications. In: D’Agostino G, Scala A, eds. Networks of Networks: The Last Frontier of Complexity. Cham: Springer, 2014. 3–36.
|
 2021, Vol. 30
2021, Vol. 30


