互联网的迅速发展使得网络上每天都产生数量惊人的信息, 其在为用户提供丰富的信息化服务的同时, 也让用户越发难以搜索到满足其个人偏好的有效信息, 进而让用户迷失在信息的海洋中, 这就是互联网时代的“信息过载”问题, 推荐系统技术的出现在一定程度上缓解了互联网数据爆炸式增长带给人们的信息过载问题[1-3], 如今, 推荐系统拥有广泛的实际应用场景, 如商品推荐, 影视推荐, 新闻推荐, 社交推荐等.
基于项目的协同过滤算法因简单易行, 目前是推荐系统广泛使用的一种技术, 其基于“物以类聚”的核心思想, 根据用户对项目的评价信息来计算项目相似性, 再利用相似性信息进行后续的推荐步骤, 但是其在实际应用中表现出了一些缺陷, 首先是该算法非常依赖用户评分矩阵的质量, 只有高密度的评分矩阵才能保证项目相似度计算的准确度, 然而用户评分矩阵往往是稀疏的, 因此计算出的项目相似度就会不准确[4,5], 同时, 基于项目的协同过滤算法也并未深入考虑用户的主观偏好情况, 其往往会向单个用户推荐大众喜好的流行项目[6,7], 因此推荐的个性化程度不高, 不能很好地满足用户需求.
本文针对基于项目的协同过滤算法相似度计算不准确和推荐缺乏个性化这两个问题进一步地做了改进工作, 考虑到传统基于项目的协同过滤算法只利用用户评分数据计算相似度, 比较单一, 因此在原有基于评分的项目相似度计算方法基础上, 额外增加了两个维度的项目相似度计算, 可以更全面地评估项目间的相似度, 此外考虑到用户主观偏好挖掘对推荐算法的重要性, 本文使用支持向量机构建用户标签偏好预测模型, 并用于评分预测公式的修正, 可以提供更准确的评分预测.
2 相关工作 2.1 基于项目的协同过滤算法以下是基于项目的协同过滤算法的主要流程[8]:
1)评分矩阵构建
基于项目的协同过滤推荐需要利用用户对项目的评价数据. 用户评价数据可以表示为一个评分矩阵
2)项目相似性计算
项目相似性主要根据评分矩阵来计算, 常用的相似性计算方法有皮尔逊相关系数, 余弦相似度, Jaccard相似度, 这3种计算方式分别如式(1)~式(3)所示:
| $ {SIM(i, j)}_{\rm PCC}=\frac{\displaystyle\sum _{u\in {U}_{i, j}}({R}_{u, i}-\stackrel-{{R}_{i}})\times ({R}_{u, j}-\stackrel-{{R}_{j}})}{\sqrt{\displaystyle\sum _{u\in {U}_{i, j}}{({R}_{u, i}-\stackrel-{{R}_{i}})}^{2}}\times \sqrt{\displaystyle\sum _{u\in {U}_{i, j}}{({R}_{u, j}-\stackrel-{{R}_{j}})}^{2}}} $ | (1) |
| $SIM{(i,j)_{\rm COS}} = \frac{{{R_i} \cdot {R_j}}}{{\left\| {{R_i}} \right\| \times \left\| {{R_j}} \right\|}}$ | (2) |
| $ {SIM(i, j)}_{\rm Jaccard}=\frac{\left|{ U}_{i}\cap {U}_{j}\right|}{\left|{ U}_{i}\cup {U}_{j}\right|} $ | (3) |
其中,
3)项目邻居选择
给定项目
4)项目评分预测
对用户未评分的项目, 根据式(4)来预测评分:
| $ PRED\left(u, i\right)=\stackrel-{{R}_{i}}+\frac{\displaystyle\sum _{{j\in \boldsymbol{N}}_{i}\cap {\boldsymbol{I}}_{u}}{S}_{i, j}\mathrm{*}({R}_{u, j}-\stackrel-{{R}_{j}})}{\displaystyle\sum _{{j\in N}_{i}\cap {I}_{u}}{S}_{i, j}} $ | (4) |
式(4)中,
支持向量机作为一种新兴的机器学习算法, 以其自身在二类分类学习问题上表现出较好的泛化和推广性能, 近年来得到了人工智能和机器学习领域研究者的广泛关注. 基于统计学习理论, 支持向量机的主要目标是借助于核方法来最小化结构风险, 并最终得到支持向量[9].
支持向量机算法的基本理念是, 假设给定一个特征空间上的训练样本数据集
在本文的研究中, 支持向量机将被用于学习并预测用户对给定项目标签的偏好, 而给定一个项目标签实例, 其到分离超平面的距离将被认为是用户对该项目标签的偏好程度.
3 标签相关度与用户偏好预测传统基于项目的协同过滤算法依赖用户的评分来计算项目之间的相似度, 受到用户评分矩阵稀疏的影响, 相似度计算的结果往往不够准确, 因此推荐效果有很大的局限性. 在推荐系统平台中, 除了有用户的评分数据可用, 有时项目本身也有一些描述性的属性信息, 例如标签信息, 那么就可以合理地利用这些信息来进一步地挖掘项目之间的联系以及用户对项目的主观偏好.
3.1 标签相关度标签可以用于概括性地描述项目的内在特征, 比较常见的根据标签信息表征项目的方法是采用独热编码(one-hot encoding)来构造项目的标签向量[10], 其将所有的项目标签考虑进来, 如果一个项目有一个给定的标签, 则该项目标签向量中相对应的值将为1, 否则为0, 之后可以基于余弦相似度公式, 使用标签向量计算项目之间的相似度, 该方法具有简单易行的优点, 但由于忽略了标签之间的关系, 只对两个标签向量中相对应的标签进行了比较, 因此损失了一些有价值的信息.
在电影推荐中, 一部电影通常有多个标签, 有些标签经常同时出现在一部电影中, 这说明标签之间存在一定的关联, 假如电影1有动作标签, 电影2有冒险标签, 并且假设动作标签和冒险标签经常同时出现, 如果用标签向量的方式表征电影, 并用余弦相似度计算电影1和电影2在标签之间的相似度, 那么将得到值为零的相似度, 这意味着系统会认为这两部电影在用户看来是完全不同的, 不幸的是, 对于一个喜欢动作和冒险电影的用户来说, 如果用户曾经对电影 1打过评分, 但由于电影 1和电影2的相似度为零, 那么电影2就没有机会被推荐给那个用户, 但是如果换种方式使用项目标签数据, 具体来说, 可以统计所有不同标签的共现次数, 那么就可以计算出标签之间的相关性, 这样就可以用标签相关性代替标签向量来计算项目之间的标签相似度了, 在前面提到的情况中, 可以利用动作标签和冒险标签之间的相关性来计算两部电影的相似度, 这样得到的电影相似度就不会为零, 而用户可能得到满意的推荐.
3.2 标签相关度计算| $ COR\left({T}_{i},{T}_{j}\right)=\frac{{\displaystyle\sum }_{n=1}^{k}{I}_{\left({T}_{i}\;{\rm{and}}\;{T}_{j}\right)}\left({m}_{n}\right)}{{\displaystyle\sum }_{n=1}^{k}{I}_{\left({T}_{i}\right)}\left({m}_{n}\right)} $ | (5) |
本文根据不同标签的共现次数来计算标签间的相关性, 具体如式(5)所示, 其中
| $ SIMT\left({m}_{i},{m}_{j}\right)=\frac{\displaystyle\sum _{{t}_{{m}_{i}}=1}^{{{k}_{}}_{{m}_{i}}}{\displaystyle\sum }_{{t}_{{m}_{j}}=1}^{{k}_{{m}_{j}}}COR\left({T}_{{t}_{{m}_{i}}},{T}_{{t}_{{m}_{j}}}\right)}{{{k}_{}}_{{m}_{i}}\mathrm{*}{k}_{{m}_{j}}} $ | (6) |
如式(6)所示, 可以计算出项目间基于标签的相似性, 其中,
如前文所述, 基于项目的协同过滤算法仅利用用户矩阵来进行推荐, 两个项目的相似性很大程度取决于有多少用户共同评价过, 这就使传统的协同过滤算法偏向于给单个用户推荐大众流行的项目, 但并未探究用户对特定项目标签的主观偏好, 因此给品味独特的用户的推荐就不够个性化, 考虑到传统算法的这一不足, 本文使用支持向量机构建一种可以预测单个用户对项目标签偏好的模型, 以提高推荐的个性化程度和准确度.
由于要训练预测模型, 因此要根据用户历史评分构建数据集, 设用户
| $x_{ki}=\left\{ {\begin{array}{*{20}{l}} {1,\;\;{t_i} \in T}\\ {\dfrac{{\displaystyle\sum _{j = 1}^lCOR({t_{{j}}},{t_{{i}}})}}{l},\;\;{t_{{j}}} \in T,\;{t_i} \notin T} \end{array}} \right.$ | (7) |
项目标签特征向量包含了所有标签的权值, 这么做的原因和3.1节中所述例子类似, 即若仅考虑用户已评价过的标签, 则学习到的预测模型只会在这个用户历史评价标签范围内做出有效预测, 对一个不在该范围内但和用户历史评价标签高度相关的标签就会一直预测为负向偏好, 这显然是不合理的.
对任意一个用户
| $\min\frac{1}{2}{\left\| \omega \right\|^2}\;\;{\rm{s.t.}}\;\;{y_i}\left( {\omega \cdot {x_i} + b} \right) \ge 1,i = {\rm{1}},{\rm{2}}, \cdots ,K $ | (8) |
式(8)中,
| $f\left( x \right) = \sum\limits_{j = 1}^\mu {{\alpha _j}} {y_j}\varphi \left( x \right) \cdot \varphi \left( {{x_j}} \right) + b$ | (9) |
式(9)中,
在预测阶段, 将项目的标签特征向量输入到预测模型
目前有些研究工作考虑了项目各种属性间的相似度, 并将其与评分相似度相结合, 在一定程度上进一步提高项目相似度计算的准确度[12,13], 然而项目属性信息只能从项目的角度单方面地描述项目的特征, 在电影推荐中, 常识思维认为动画标签的电影是面向低龄用户的, 但是对为有些动画标签电影打过较高评分的用户群体的特征进行分析, 就会发现这些用户不一定是低龄用户, 那么这些动画电影也不一定是面向低龄用户的, 其就不应被和面向低龄用户动画电影等同看待, 更进一步说, 虽然两个项目具有相同的属性信息, 但用户对它们的偏好也有可能是不同的, 具有相同属性信息的项目可能会受到不同用户群体的偏好, 而具有不同属性信息的项目也可能会受到同一用户群体的偏好, 由此可以看出, 分析项目的受众特征信息可以比直接分析项目自身属性信息能更准确地判断项目会受哪类用户偏好, 所以, 不能仅仅根据项目的属性信息来评估两个项目之间的相似性, 因为这可能会导致有偏的推荐, 此外还应该考虑项目的受众类型是否相似.
有研究工作利用了用户特征来提高用户之间相似度计算的精确度[14,15], 但是很少有研究试图利用用户特征来提高项目之间相似度计算的精确度, 本文提出利用受众特征来构造项目的扩充属性, 进而可以从项目受众类型的角度来丰富项目的属性, 是对仅利用项目自身属性计算项目相似度的有效补充, 最终可以更全面地比较项目之间的相似度.
4.2 一个启发性的例子在给出项目扩充属性的计算方式之前, 将列举一个关于电影推荐的启发性例子.
假设有表1所示用户电影评分(0分表示没有评分)和表2所示用户特征信息, 若表1中所列都不是热门电影, 那么本文推测一部电影的受众在某些方面是相似的, 也就是说如果用户有共同的品味, 那么在其他方面应该也有一定的相似性. 在这个例子中, 从直观上来看, 对电影1、2和5这3部电影有正面评价的用户有两个方面比较相似, 其一是用户的年龄, 其二是用户的职业; 再如电影3和电影4, 通过用户评分和用户特征信息可以看出电影3更受女性用户偏好, 电影4更受男性用户偏好.
| 表 1 用户电影评分 |
| 表 2 用户特征信息 |
通过对数据集中每个项目的用户特征信息进行统计分析, 就可以得出每个项目的受众特征, 然后利用这些受众特征构造项目的扩充属性来表示该项目的受众类型, 便可以进一步从受众类型的角度进行项目相似度计算.
4.3 项目属性扩充定义用户的特征集合为
| $ {Attr}_{i}=\frac{\displaystyle\sum _{u\in {Rated}}I\left({uf}_{i}==1\right)\times {R}_{u}}{\displaystyle\sum _{u\in {Rated}}{R}_{u}} $ | (10) |
| $ {Normali{\textit{z}}ed\_Attr}_{i}=\frac{{Attr}_{i}}{\displaystyle\sum _{j}{Attr}_{j}} $ | (11) |
式(10)中,
项目的扩充属性标识项目的受众类型信息, 因此, 如果不同项目的受众类型是相似的, 那么这些项目也可以被认为是相似的, 可用于推荐, 因为它们受到了具有相似特征用户群体的偏好.
通过项目扩充属性计算项目相似性的方法如式(12):
| $ SIMATTR\left({m}_{i},{m}_{j}\right)=2-\frac{2}{1+\exp\left(-\displaystyle\sum _{k}\left|{A}_{{m}_{i}, k}-{A}_{{m}_{j}, k}\right|\right)} $ | (12) |
式(12)中,
在基于评分的项目相似度计算基础上, 本文结合第3节和第4节描述的标签相似度和扩充属性相似度提出综合相似度. 综合相似度考虑项目在3个维度上的相似性, 采用相乘的方式得出, 如式(13)所示:
| $ \begin{split} SIMCOMP\left({m}_{i},{m}_{j}\right)=&SIMATTR\left({m}_{i},{m}_{j}\right)\\ &\mathrm{*}SIMT\left({m}_{i},{m}_{j}\right)\mathrm{*}SIM{\left({m}_{i},{m}_{j}\right)}_{\rm PCC}\end{split} $ | (13) |
对用户
| $ \begin{split} PRED\left(u,{m}_{i}\right)\!\!=&\!\!\frac{\displaystyle\sum _{{{m}_{k}\in \boldsymbol{N}}_{i}\cap {\boldsymbol{M}}_{u}}\!\!SIMCOMP\left({m}_{i},{m}_{k}\right)\mathrm{*}({R}_{{u, m}_{k}}\!\!-\!\!\stackrel-{{R}_{{m}_{k}}})}{\displaystyle\sum _{{{m}_{k}\in \boldsymbol{N}}_{i}\cap {\boldsymbol{M}}_{u}}\!\!SIMCOMP\left({m}_{i},{m}_{k}\right)}\\ &+\stackrel-{{R}_{{m}_{i}}}\\[-11pt] \end{split} $ | (14) |
虽然式(14)使用了项目综合相似度来预测用户评分, 会一定程度提高预测准确度, 但未能直接表达出用户对项目的主观偏好, 因此结合3.4节所述用户标签偏好预测模型, 提出一种用户标签偏好修正因子, 如式(15)所示, 能根据用户主观偏好情况, 调整预测评分计算.
| $ \beta \left({f}_{u}\left(x\right),{x}_{i}\right)=\frac{1}{1+{e}^{-{f}_{u}\left({x}_{i}\right)}} $ | (15) |
式(15)中,
| $\begin{split} & PRED(u,m_i)=\stackrel-{{R}_{{m}_{i}}}+\beta \left({f}_{u}\left(x\right),{x}_{i}\right)\\ &*\frac{\displaystyle\sum _{{{m}_{k}\in \boldsymbol{N}}_{i}\cap {\boldsymbol{M}}_{u}}SIM\_COMP\left({m}_{i},{m}_{k}\right)\mathrm{*}({R}_{{u, m}_{k}}-\stackrel-{{R}_{{m}_{k}}})}{\displaystyle\sum _{{{m}_{k}\in \boldsymbol{N}}_{i}\cap {\boldsymbol{M}}_{u}}SIM\_COMP\left({m}_{i},{m}_{k}\right)} \end{split}$ | (16) |
式(16)中, 最后一个分项即为协同过滤算法评分预测公式中根据待预测项目与用户历史偏好项目的相似性计算出的预测偏差, 修正因子可以调节预测偏差对最终预测评分计算的作用, 若用户偏好该项目的标签, 则最终预测评分就会受到预测偏差的影响, 否则就会削弱预测偏差带来的影响, 即使待预测项目与用户历史偏好项目的相似度很高, 但若偏好预测模型预测出用户的偏好度很低, 则预测评分也不会很高.
5.3 本文算法步骤输入: 用户对项目的评分矩阵
输出: 用户
步骤1. 根据项目类别信息, 根据式(5)计算出项目标签的关联度.
步骤2. 根据式(6)计算出数据集中项目间的标签相似度.
步骤3. 根据项目标签信息和评分信息构建用户标签偏好数据集, 使用支持向量机对数据集中每个用户训练标签偏好预测模型.
步骤4. 根据用户特征, 对数据集中每个项目按式(10)和式(11)计算出项目的扩充属性.
步骤5. 根据式(12)计算出数据集中项目间的扩充属性相似性.
步骤6. 根据式(13)计算出项目间的综合相似度.
步骤7. 对于待预测项目
本文采用在推荐系统研究领域中具有较大知名度的MovieLens-100 k数据集进行实验分析[16], 该数据集包含了由明尼苏达大学GroupLens研究组从MovieLens电影评分网站上收集的943个用户对1652部电影的100000条评分数据、943条用户个人信息以及1652条电影信息. 本文使用用户个人信息中的性别、年龄和职业信息来构造项目的扩充属性, 并利用电影信息中的标签信息来计算项目标签的关联度以及训练用户标签偏好预测模型. 数据集被随机地分成80%的训练数据集和20%的测试数据集.
6.2 评估指标为了评估算法预测的用户评分与实际用户评分之间的差异, 本文采用了均方根误差(RMSE)作为算法性能评估的指标. RMSE的计算如式(17)所示.
| $ RMSE=\sqrt{\frac{1}{\left|TD\right|}{\sum }_{u, i\in TD}{\left({R}_{u, i}-{\widehat{R}}_{u, i}\right)}^{2}} $ | (17) |
式中,
本文根据用户历史评分数据学习并预测用户的标签偏好, 因此合理的用户偏好阈值
由图1实验结果可以看出当
为了验证用户标签偏好修正因子
由图2实验结果可以看出, 用户标签偏好修正因子

|
图 1 阈值
|

|
图 2 用户标签偏好修正因子
|
6.5 扩充属性粒度的影响
本文假设扩充属性的粒度对项目相似度计算有一定的影响, 即用户特征划分地越细, 则项目相似度的计算准确度就越高. 为了验证这一假设, 本文根据用户的年龄特征和职业相似性, 通过适当简化原始数据集中的用户特征构造了一个粒度稍低的用户特征集用于实验, 其中, 使用原始数据集中用户特征的算法记为TP-IAE-1, 使用本文简化用户特征的算法记为TP-IAE-2. 扩充属性粒度对本文算法性能影响的实验结果如图3所示.
由图3实验结果可以看出, 两种算法预测误差率变化趋势一致, 但使用原始用户特征的TP-IAE-1算法的预测误差率低于使用简化用户特征的TP-IAE-2算法, 很显然, 这是因为原始用户特征具有相对更高的粒度, 因此项目受众特征更加丰富, 可以为项目构造更精细的扩充属性, 项目受众类型相似度计算也更加准确.
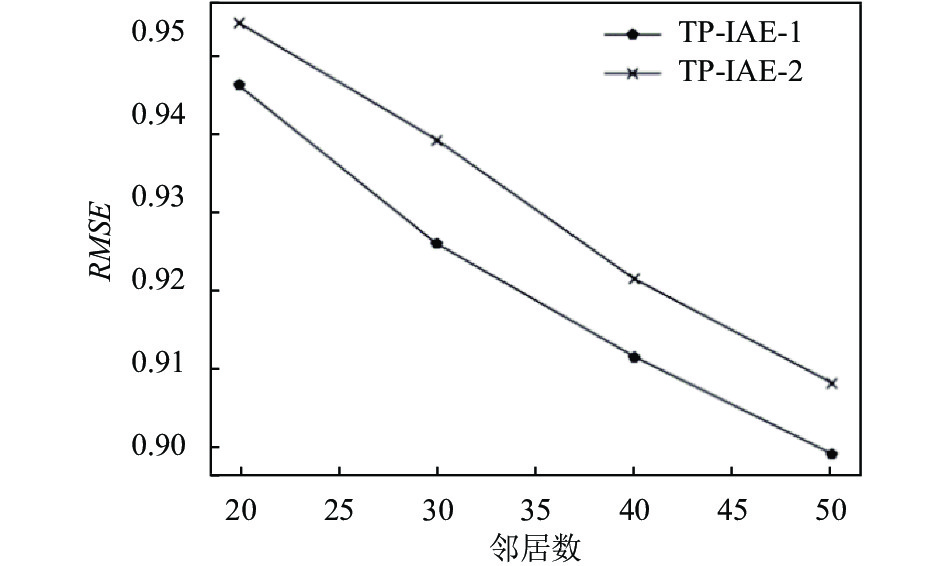
|
图 3 扩充属性粒度对本文算法性能的影响 |
6.6 对比试验
为了验证本文算法对传统基于项目的协同过滤算法做出了有效的改进, 以及相较于其他相关算法的性能改善, 故将本文算法TP-IAE和TP-IAE-

|
图 4 对比实验结果 |
从图4中可以看出, 本文所提算法和其他4种对比算法的预测评分误差率都随着邻居数目的增加而下降, 4种算法的用户预测评分误差率变化趋势也基本相同, 但在邻居数的变化范围内, 本文算法的预测评分误差率相比其他4种算法降低了2%至13%, 显示出良好的推荐效果. 与传统基于项目协同过滤方法相比, 尽管HCF算法在预测效果上有了很大的提高, 因为其不再仅依赖用户的评分信息, 但是, 该方法只是从项目的角度额外地比较项目相似度, 而本文算法不仅考虑了项目的标签属性信息, 另外还考虑了项目的受众特征, 用来判断给定的两个项目是否会得到同一用户群体的偏好, 可以进一步地提高项目相似度计算的准确性, 与UPR和TW-ContentItem算法的对比结果也显示出本文算法预测效果的提升, 且经用户标签偏好修正因子
本文针对传统基于项目的协同过滤算法面临相似度计算不准确和推荐缺乏个性化这两个问题做了相关的改进工作, 提出的方法结合项目的受众特征信息和项目的标签信息对传统基于项目的协同过滤算法的相似度计算方式做出了有效改进, 不仅可以避免项目相似度计算方法过于片面单一, 而且可以在评分数据稀疏的实际场景下提高项目相似性计算的准确度, 提出的方法还考虑了用户的个性化偏好程度, 以进一步提高推荐效果, 实验结果表明, 本文算法相较传统基于项目的协同过滤算法可以显著地降低预测评分的误差率. 基于项目的协同过滤算法的核心是项目相似性计算, 因此下一步的工作是研究从更多的维度来计算项目的相似性以提高推荐算法的性能.
| [1] |
Chen JM, Tang Y, Li JG, et al. Survey of personalized recommendation algorithms. Journal of South China Normal University (Natural Science Edition), 2014(5): 8-15. |
| [2] |
翁小兰, 王志坚. 协同过滤推荐算法研究进展. 计算机工程与应用, 2018, 54(1): 25-31. DOI:10.3778/j.issn.1002-8331.1710-0081 |
| [3] |
Su XY, Khoshgoftaar TM. A survey of collaborative filtering techniques. Advances in Artificial Intelligence, 2009, 2009: 421425. |
| [4] |
Liu HF, Hu Z, Mian A, et al. A new user similarity model to improve the accuracy of collaborative filtering. Knowledge-Based Systems, 2014, 56: 156-166. DOI:10.1016/j.knosys.2013.11.006 |
| [5] |
Anand D, Bharadwaj KK. Utilizing various sparsity measures for enhancing accuracy of collaborative recommender systems based on local and global similarities. Expert Systems with Applications, 2011, 38(5): 5101-5109. DOI:10.1016/j.eswa.2010.09.141 |
| [6] |
张旭, 孙福振, 方春, 等. 引入兴趣稳定性的时间敏感协同过滤算法. 计算机工程与应用, 2018, 54(11): 161-165, 197. DOI:10.3778/j.issn.1002-8331.1701-0332 |
| [7] |
Abdollahpouri H. Popularity bias in ranking and recommendation. Proceedings of 2019 AAAI/ACM Conference on AI, Ethics, and Society. Honolulu, HI, USA. 2019. 529–530.
|
| [8] |
于洪, 李俊华. 一种解决新项目冷启动问题的推荐算法. 软件学报, 2015, 26(6): 1395-1408. DOI:10.13328/j.cnki.jos.004587 |
| [9] |
祁亨年. 支持向量机及其应用研究综述. 计算机工程, 2004, 30(10): 6-9. DOI:10.3969/j.issn.1000-3428.2004.10.003 |
| [10] |
Pham DH, Le AC. Exploiting multiple word embeddings and one-hot character vectors for aspect-based sentiment analysis. International Journal of Approximate Reasoning, 2018, 103: 1-10. DOI:10.1016/j.ijar.2018.08.003 |
| [11] |
Cervantes J, Garcia-Lamont F, Rodríguez-Mazahua L, et al. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing, 2020, 408: 189-215. DOI:10.1016/j.neucom.2019.10.118 |
| [12] |
Zhu L, Hu QH, Zhao L, et al. Collaborative filtering algorithm based on rating preference and item attributes. Computer Science, 2020, 47(4): 67-73. |
| [13] |
王卫平, 王金辉. 基于Tag和协同过滤的混合推荐方法. 计算机工程, 2011, 37(14): 34-35, 38. DOI:10.3969/j.issn.1000-3428.2011.14.009 |
| [14] |
孙龙菲, 黄梦醒. 综合用户特征和项目属性的协作过滤推荐算法. 计算机应用研究, 2014, 31(2): 384-387. DOI:10.3969/j.issn.1001-3695.2014.02.015 |
| [15] |
刘发升, 洪营. 基于用户特征属性和云模型的协同过滤推荐算法. 计算机工程与科学, 2014, 36(6): 1172-1176. DOI:10.3969/j.issn.1007-130X.2014.06.028 |
| [16] |
Harper FM, Konstan JA. The MovieLens datasets: History and context. ACM Transactions on Interactive Intelligent Systems, 2015, 5(4): 19. |
| [17] |
刘宇, 朱文浩. 基于内容和标签权重的混合推荐算法. 计算机与数字工程, 2020, 48(4): 773-777. DOI:10.3969/j.issn.1672-9722.2020.04.008 |
| [18] |
于波, 陈庚午, 王爱玲, 等. 一种结合项目属性的混合推荐算法. 计算机系统应用, 2017, 26(1): 147-151. DOI:10.15888/j.cnki.csa.005490 |
| [19] |
郑小楠, 谭钦红, 马浩, 等. 基于用户偏好矩阵填充的改进混合推荐算法. 计算机工程与设计, 2020, 41(10): 2784-2790. |
 2021, Vol. 30
2021, Vol. 30


