近年来, 在能源危机、环境污染、全球变暖等多重压力之下, 各国纷纷进行能源结构优化和变革^[1]. 我国2020年国务院政府工作报告中也提出全面推进“互联网+”, 打造数字经济新优势. 在能源互联网的背景之下, 充分发挥电、热、气等不同形式能源之间的耦合作用是实现能源“互联网+”的重要途径^[2]. 能量枢纽(Energy Hub, EH)是分析多种能源耦合作用的重要模型, 其主要优点之一就是提高了多能源系统效率, 减少了能源浪费^[3]. 如何利用能量枢纽将可再生能源整合为分布式发电以降低运营成本、增加多能源系统稳定性以及减少碳排放量是今后研究重点.

文献[4]提出了蚁群算法与粒子群优化算法相结合的组合算法, 构建了能源互联微网系统供需多能协同优化策略模型, 并通过实例验证了所提算法与模型的有效性和实用性; 文献[5]基于区域多能量枢纽互联的热电耦合综合能源系统, 提出一种综合考虑静态安全因素与热电最优潮流的综合能源系统联合优化运行模型并结合算例仿真结果验证了所提模型的有效性; 文献[6]基于大规模清洁能源出力的随机性和波动性的问题, 构建了利用多能源优势互补协同运行能量枢纽, 并制定了两阶段优化调度策略, 为解决可再生能源消纳问题提供有效途径. 文献[7]综述了能量枢纽的运行和规划模型及求解方法的研究现状, 并对能量枢纽未来的研究热点和方向进行展望.

上述文章主要是从能量枢纽的优化运行方式开展研究, 对能量枢纽的优化配置方案研究有借鉴意义, 但是考虑CO₂排放量的能源枢纽的优化配置方案研究相对较少. 本文通过建立详细的新型能量枢纽优化设置和运行模型, 对多种能源耦合的运营成本以及社会效益进行估算; 以光伏和风能为例, 考虑了可再生能源的接入对能量枢纽运营的影响; 通过使用Newton-Raphson方法解决了电、热、气网络的流动问题, 以识别状态变量和监测系统的限制; 提出了以CO₂排放量最小, 社会效益最大化为目标的多目标优化模型, 并利用遗传算法对整体问题进行了求解; 本文分析了可再生能源、储能设备和P2G装置对能量枢纽柔性, 稳定性等指标影响, 并基于此提出了一种能量枢纽优化运行配置的方案, 最后通过算例分析比较验证了所提方案的有效性, 为多种能源耦合利用奠定基础.

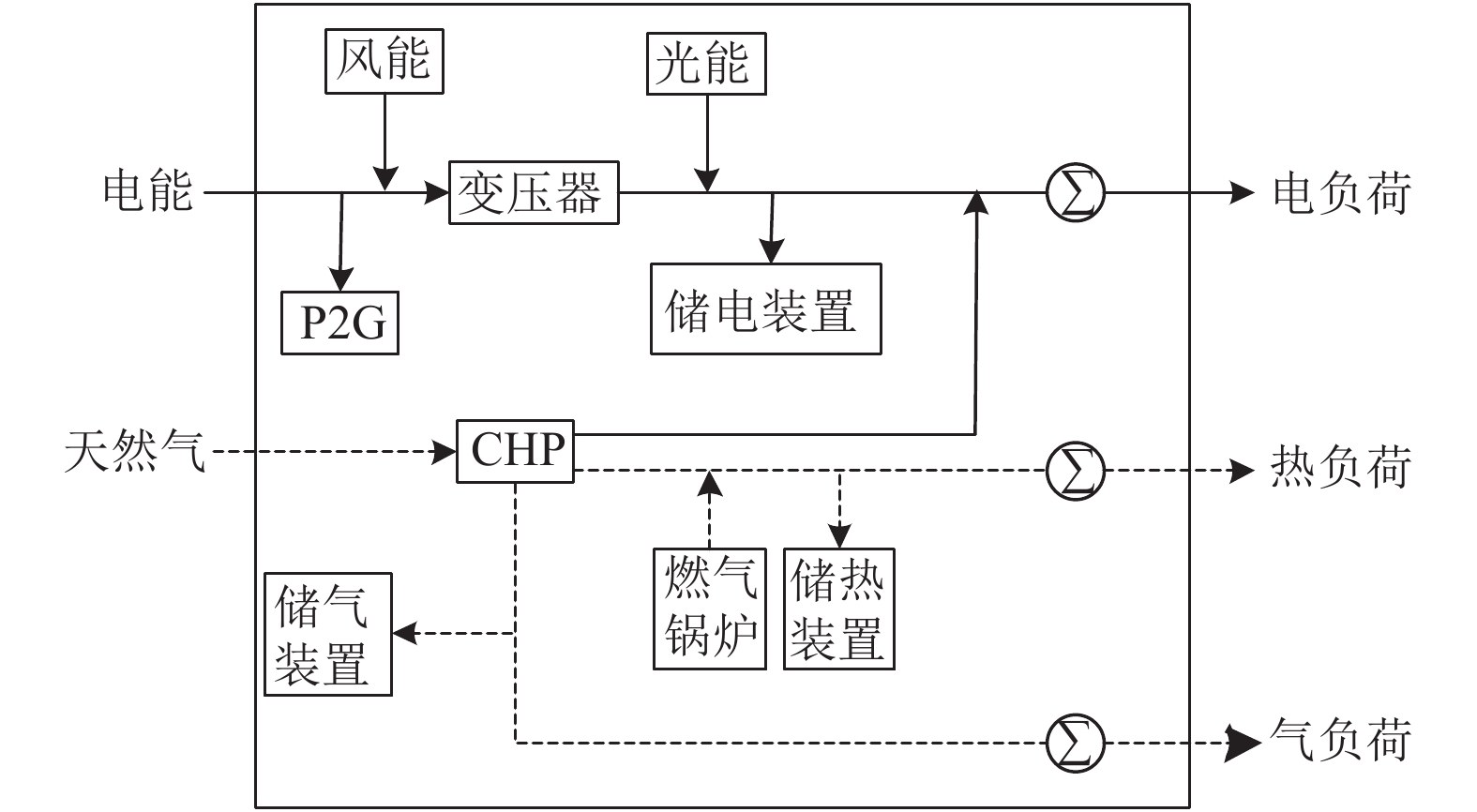
1 能量枢纽模型 1.1 能量枢纽架构

能量枢纽是消费者、生产者、储能设备和传送者之间以不同方式相互连接的框架:直接或通过转换设备管理一个或多个载体^[8]. 转换装置需要将能量载体从一种形式转换成另一种形式. 燃料电池、熔炉、锅炉和热电联产都可以作为转换装置. 在能量枢纽中合并不同的能量载体有许多优点, 如增加系统稳定性、发电灵活性和优化运行潜力^[9-11]. 图1给出了一个能量枢纽的示意图, 枢纽的主要能源是电力和天然气, 而输出端是电能、热能和天然气. 根据枢纽内部的条件, 输入侧的能量载体被转换或直接传输到输出侧. 最终目标是通过直接连接或转换设备在输出端提供不同的负载要求.

1.2 能量转换

能量枢纽实际上描述的是一种多能源系统中输入与输出的耦合关系, 如图2所示. 利用耦合矩阵 $C$ 可以建立一个通用的模型, 该模型由输入和输出之间的耦合因子组成, 耦合矩阵可以表示为:

$ \left[ {\begin{array}{*{20}{c}} {{I_1}}\\ {{I_2}}\\ \vdots \\ {{I_m}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{C_{11}}}&{{C_{12}}}& \cdots &{{C_{1n}}}\\ {{C_{21}}}&{{C_{22}}}& \cdots &{{C_{2n}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{C_{m1}}}&{{C_{m2}}}& \cdots &{{C_{mn}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{L_1}}\\ {{L_2}}\\ \vdots \\ {{L_n}} \end{array}} \right] $

(1)

其中, $ {C}_{ij} $ 是输出量 $ I $ 和输出量 $ L $ 之间的耦合因子, 表示第 $ j $ 种形式能源输出与第 $ i $ 种形式能源输入的比值; $ m $ , $ n $ 分别是输入能源形式和输出能源形式的数量.

1.3 数学模型

由于每个能量系统都具有针对性和特殊性, 所以目前没有涵盖所有能量类型的通用模型, 下面分别给出了交流电网、供热系统和天然气管道的稳态流动数学模型.

1.3.1 交流电网

潮流研究在电力系统的规划和运行中具有重要的意义. 潮流研究的目标是获得电力系统中每个母线在特定负载和发电机功率和电压条件下的电压角和幅值信息. 本文用极坐标形式给出了系统的母线电压V和节点导纳矩阵Y, 如式(2)、式(3)所示:

$ {V}_{i}=\left|{V}_{i}\right|\angle {\theta }_{i}=\left|{V}_{i}\right|(\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{i}+j\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{i}) $

(2)

$ {Y}_{ij}=\left|{Y}_{ij}\right|\angle {\theta }_{ij}=\left|{Y}_{ij}\right|(\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{ij}+j\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{ij})={G}_{ij}+j{B}_{ij} $

(3)

不同母线上的注入的有功功率和无功功率可表示为:

$ {P}_{i}=\left|{V}_{i}\right|\sum\nolimits_{j=1}^{N}\left|{V}_{j}\right|({G}_{ij}\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{ij}+{B}_{ij}\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{ij}) $

(4)

$ {Q}_{i}=\left|{V}_{i}\right|\sum\nolimits_{j=1}^{N}\left|{V}_{j}\right|({G}_{ij}\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{ij}-{B}_{ij}\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{ij}) $

(5)

式中, $ {\theta }_{ij}={\theta }_{i}-{\theta }_{j} $ , $ {P}_{i} $ 表示有功功率, $ {Q}_{i} $ 表示无功功率. 节点功率平衡方程可表示如下:

$ \varDelta {P}_{i}={P}_{g,i}-{P}_{d,i}-\left|{V}_{i}\right|\sum\nolimits_{j=1}^{N}\left|{V}_{j}\right|({G}_{ij}\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{ij}+{B}_{ij}\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{ij}) $

(6)

$ \varDelta {Q}_{i}={Q}_{g,i}-{Q}_{d,i}-\left|{V}_{i}\right|\sum\nolimits_{j=1}^{N}\left|{V}_{j}\right|({G}_{ij}\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{ij}+{B}_{ij}\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{ij}) $

(7)

式中, $ {P}_{g,i} $ 和 $ {P}_{d,i} $ 分别表示母线 $ i $ 上的发电量和消耗量.

1.3.2 供热系统

供热系统通常由以蒸汽或热水形式提供热量的供热和回流管道组成. 通过基于Newton-Raphson方法的热力和水力分析, 可以确定如下变量.

(1)液压模型

任何热节点周围的质量流量等于进入节点的质量流量、离开节点的质量流量和节点处的流量消耗之和. 流动连续性表示为:

$ A\times {m}_{\rm pipe}={m}_{\rm node} $

(8)

式中, ${m}_{\rm pipe}$ 是表示每根管道内的质量流速(kg/s)的向量, ${m}_{\rm node}$ 表示通过的每个节点的质量流速(kg/s)的向量, A表示热网节点关联矩阵. 管道中的水头损失是由于管道摩擦引起的管道压力(以m为单位)的变化.

$ B\times {h}_{f}=0 $

(9)

式中, B是回路关联矩阵, $ {h}_{f} $ 表示闭环总水头损失.

每根管道的水头损失与流量之间的关系用式(10)表示:

$ {h}_{f}=K\times {m}_{\rm pipe}\times \left|{m}_{\rm pipe}\right| $

(10)

式中, K是管道阻力系数矢量, 大小通常取决于管径.

(2)热模型

热功率可以由式(11)计算:

$ HP={c}_{p}{m}_{\rm node}({T}_{s}-{T}_{o}) $

(11)

式中, $ {c}_{p} $ 代表水的比热容(J/(kg·℃)), $ {T}_{s} $ 和 $ {T}_{o} $ 分别代表供应温度和出口温度(℃).

管道出口的温度计算公式如下:

$ {T}_{\rm end}=({T}_{\rm start}-{T}_{a}){e}^{-(\lambda L/{c}_{p}{m}_{\rm pipe})}+{T}_{a} $

(12)

式中, ${T}_{\rm start}$ , ${T}_{\rm end}$ 分别代表管道起点和终点的温度(℃), $ {T}_{a} $ 是环境温度, $ \lambda $ 表示单位长度内每根管子的传热系数(W/(m·℃)), $ L $ 表示管子长度(m).

离开节点时的水温( ${T}_{\rm out}$ )和具有一个以上输入管道的水温( ${T}_{\rm in}$ )可以通过所有输入流的混合温度来计算:

$\left( {\sum {{m_{\rm pipe,out}}} } \right){T_{\rm out}} = \sum {\left( {{m_{\rm pipe,in}}{T_{\rm in}}} \right)} $

(13)

式中, ${m}_{\rm pipe,out}$ 表示流出节点的管道内的质量流量(kg/s), ${m}_{\rm pipe,in}$ 表示流入节点的管道内的质量流量(kg/s).

1.3.3 天然气系统

天然气系统的建模类似于供热系统的分析, 有以下两个假设: (1)假设气体管道的温度没有变化, 所以气体流动温度保持不变. (2)忽略管道高度的差异, 即两点管道为水平管道. 本文给出了天然气通过任意管道的流动方程, 如下所示:

$ {Q}_{mn}={K}_{mn}\sqrt{{P}_{m}^{2}-{P}_{n}^{2}} $

(14)

式中, $ {Q}_{mn} $ 表示 $ m $ 管道和 $ n $ 管道之间的气体流(m³/h), $ {K}_{mn} $ 表示天然气特性因子, $ {P}_{m} $ 和 $ {P}_{n} $ 表示节点 $ m $ 和节点 $ n $ 的压强(PSIA).

2 能量枢纽运营成本及CO₂排放量估算 2.1 能量枢纽运营成本

(1)电网成本

在能量枢纽需求高峰期间, 负荷需求由电网和能量枢纽来满足. 电网发电机组的运营成本可以表示为:

$ {C}_{G}={a}_{G}+{b}_{G}{P}_{{G}_{t}}+{c}_{G}{P}_{{G}_{t}}^{2}+\left|{g}_{G}\times \sin\left({e}_{G}\left({P}_{G}^{\min}-{P}_{{G}_{t}}\right)\right)\right| $

(15)

式中, ${C}_{G}$ 是电网发电机的运营成本, $ {a}_{G} $ , $ {b}_{G} $ , $ {c}_{G} $ 是电网发电机的成本系数, $ {g}_{G} $ , $ {e}_{G} $ 是代表电网发电机的阀点负载效应的系数, $ {P}_{{G}_{i}} $ 表示是公用电网在 $ t $ 时刻处的电能交换量.

(2)燃气发电机成本

燃气发电机成本函数可以表示为:

$ \begin{split} {C_{\rm GF}} =& {a_{\rm GF}} + {b_{\rm GF}}{P_{{G_{tf}}}} + {c_{\rm GF}}P_{{G_{tf}}}^2 \\ &+ \left| {{g_{\rm GF}} \times {\rm{sin}}\left( {{e_{\rm GF}}\left( {P_{\rm GF}^{{\rm{min}}} - {P_{{G_{tf}}}}} \right)} \right)} \right| \end{split} $

(16)

式中, ${C}_{\rm GF}$ 是燃气发电机的运营成本, ${a}_{\rm GF}$ , ${b}_{\rm GF}$ , ${c}_{\rm GF}$ 是燃气发电机的成本系数, ${g}_{\rm GF}$ , ${e}_{\rm GF}$ 是代表燃气发电机的阀点负载效应的系数, $ {P}_{G{f}_{i}} $ 表示是燃气发电机在 $ t $ 时刻处的电能交换量.

(3)天然气供应成本

天然气供应成本函数可以表示为:

$ {C}_{gs}={G}_{pr_i}{Q}_{{S}_{i,t}} $

(17)

式中, $ {C}_{gs} $ 表示天然气供应总成本, $ {G}_{p{r}_{i}} $ 表示第 $ i $ 台天然气供应设备的成本系数, $ {Q}_{{s}_{i,t}} $ 表示第 $ i $ 台天然气供应设备在 $ t $ 时刻的供应量.

(4)风力发电成本

风力发电的成本可以表示为:

$ {C}_{{P}_{w}}={c}_{{w}_{i}}\left({P}_{{w}_{i,t}}\right)+{c}_{p.{w}_{i}}({P}_{{w}_{av_{i,t}}}-{P}_{{w}_{i,t}})+{c}_{r.{w}_{i}}({P}_{{w}_{i,t}}-{P}_{{w}_{av_{i,t}}}) $

(18)

式中, $ {C}_{{P}_{w}} $ 表示风力发电的总成本, $ {c}_{{w}_{i}} $ 表示计划风力发电的成本系数, ${P}_{w_{i,t}}$ 表示第 $ i $ 台风力发电机在 $ t $ 时刻产生的计划功率, $ {c}_{p.{w}_{i}} $ 表示风力涡轮机功率的惩罚成本, $ {P}_{{w}_{a{v}_{i,t}}} $ 表示第 $ i $ 个风电场在 $ t $ 时刻产生的可用功率(MW), $ {c}_{r.{w}_{i}} $ 表示风力涡轮机的备用成本.

(5)光伏发电成本

光伏发电机的运营成本表示如下:

$ {C}_{pv}={c}_{p{v}_{i}}\left(p{v}_{i,t}\right)+{c}_{p.p{v}_{i}}(P{V}_{a{v}_{i,t}}-p{v}_{i,t})+{c}_{r.p{v}_{i}}(p{v}_{i,t}-P{V}_{a{v}_{i,t}}) $

(19)

式中, $ {C}_{pv} $ 表示光伏发电总成本, $ p{v}_{i,t} $ 表示第 $ i $ 台光伏发电机在 $ t $ 时刻产生的电量, $ {c}_{p.p{v}_{i}} $ 表示第 $ i $ 个光伏发电机功率的惩罚成本, $ P{V}_{a{v}_{i,t}} $ 表示第 $ i $ 台光伏发电机在 $ t $ 时刻产生的可用功率, $ {c}_{r,p{v}_{i}} $ 表示光伏发电机的备用成本.

(6)储能设备成本

储能设备的成本可以由下式计算得到:

$ {C}_{\rm SD}=\sum\nolimits_{i=1}^{{N}_{\rm SDD}}{C}_{\rm SDD}{P}_{{\rm SDD}_{i,t}}+\sum\nolimits_{i=1}^{{N}_{\rm SDC}}{C}_{\rm SDC}{P}_{{\rm SDC}_{i,t}} $

(20)

式中, ${C}_{\rm SD}$ 表示储能设备总成本, ${C}_{\rm SDD}$ , ${C}_{\rm SDC}$ 分别表示充电成本和放电成本, ${P}_{{\rm SDD}_{i,t}}$ , ${P}_{{\rm SDC}_{i,t}}$ 分别表示第 $ i $ 台储能设备在 $ t $ 时刻的充放电功率, ${N}_{\rm SDD}$ , ${N}_{\rm SDC}$ 分别表示充放电设备数量.

(7)供热单元成本

供热单元(HOU)在能量枢纽中的作用主要是为区域供热系统提供了大量能量. 在热电联产机组存在的情况下, HOU通常只在高需求期使用, 总成本函数可以表示为:

$ {C}_{\rm HOU}={a}_{{\rm HOU}_{i}}+{b}_{{\rm HOU}_{i}}{Q}_{{\rm HOU}_{i,t}}+{c}_{{\rm HOU}_{i}}{Q}_{{\rm HOU}_{i,t}}^{2} $

(21)

式中, ${C}_{\rm HOU}$ 表示HOU的总运营成本, ${a}_{{\rm HOU}_{i}}$ , ${b}_{{\rm HOU}_{i}}$ , ${c}_{{\rm HOU}_{i}}$ 表示第 $ i $ 个供热单元的成本系数, ${Q}_{{\rm HOU}_{i,t}}$ 表示第 $ i $ 个供热单元在 $ t $ 时刻产生的热能.

(8) CHP成本

CHP装置有一个凸成本函数, 变量为 ${P}_{\rm CHP}$ 和 ${Q}_{\rm CHP}$ , 如下所示:

$ \begin{split} {C}_{\rm CHP}=&{\alpha }_{C{o}_{i}}+{\beta }_{C{o}_{i}}{P}_{{\rm CHP}_{i,t}}+{\gamma }_{C{o}_{i}}{P}_{{\rm CHP}_{i,t}}^{2}+{\delta }_{C{o}_{i}}{Q}_{{\rm CHP}_{i,t}}\\ &+{\xi }_{C{o}_{i}}{Q}_{{\rm CHP}_{i,t}}^{2}+{\xi }_{C{o}_{i}}{P}_{{\rm CHP}_{i,t}}{Q}_{{\rm CHP}_{i,t}}\\[-3pt] \end{split} $

(22)

式中, ${C}_{\rm CHP}$ 表示CHP发电机总成本, $ {\alpha }_{C{o}_{i}} $ , $ \;{\beta }_{C{o}_{i}} $ , $ {\gamma }_{C{o}_{i}} $ , $ {\delta }_{C{o}_{i}} $ , $ {\xi }_{C{o}_{i}} $ 是第 $ i $ 台CHP发电机成本系数.

(9) P2G装置成本

P2G装置的总运营成本包括获得的电力成本减去出售P2G生产的天然气的利润, 如下所示:

$ {C}_{\rm P2G}={c}_{\rm P2G}{P}_{{\rm P2G}_{i,t}}-{G}_{p{r}_{i}}{S}_{{\rm P2G}_{i,t}} $

(23)

式中, ${C}_{\rm P2G}$ 表示P2G装置的总运营成本, ${c}_{\rm P2G}$ 是P2G装置的成本系数. ${S}_{{\rm P2G}_{i,t}}$ 表示第 $ i $ 个P2G装置中电能到天然气的转化量.

2.2 CO₂排放量

在大多数电力公司中, 发电主要是由具有高CO₂排放量的火力发电厂完成. 供风量、煤质、燃烧器性质等参数对火电机组污染物的排放有一定的影响. 火电机组的输出功率会受这些参数变化的影响. 因此, 总污染排放量可以表示为发电量的函数, 如下所示:

$ {E}_{G}={a}_{E}{P}_{{G}_{t}}^{2}+{b}_{E}{P}_{{G}_{t}}+{d}_{E}+{\gamma }_{E}\mathrm{e}\mathrm{x}\mathrm{p}\left({\delta }_{E}{P}_{{G}_{t}}\right) $

(24)

式中, $ {E}_{G} $ 表示总污染排放量, $ {a}_{E} $ , $ {b}_{E} $ , $ {d}_{E} $ , $ {\gamma }_{E} $ , $ {\delta }_{E} $ 是火电机组的排放系数.

3 优化配置建模

能量枢纽是一个物理交叉点, 类似于能源站, 不同形式的能源相互转换以满足当前需求. 因此, 如何实现能量枢纽的最优运行就成为一个重要问题. 最优运行这一过程包括枢纽内的电力调度和能源价格.

3.1 目标函数

系统优化的总体目标是通过减小系统运营总成本来获得更多的社会效益. 除此之外, 还应将总CO₂排放量降至最低. 总运营成本函数可以表示为:

$ \begin{split} cost=&{C}_{G}+{C}_{\rm GF}+{C}_{gs}+{C}_{P_w}\\ &+{C}_{pv}+{C}_{\rm SD}+{C}_{\rm HOU}+{C}_{\rm CHP}+{C}_{\rm P2G} \end{split} $

(25)

通过向消费者出售能源而获得的收益可以表示为:

$ {R}_{D}={\lambda }_{e}{P}_{D}+{\lambda }_{\rm heat}{P}_{\rm heat}+{\lambda }_{\rm gas}{P}_{\rm gas} $

(26)

式中, $ {\lambda }_{e} $ 是消耗的电能成本, ${\lambda }_{\rm heat}$ 是消耗热能的成本, ${\lambda }_{\rm gas}$ 是消耗气体能源的成本, $ {P}_{D} $ , ${P}_{\rm heat}$ 和 ${P}_{\rm gas}$ 分别表示电能需求, 热能需求和天然气需求. 社会效益可由式(27)计算:

$ SW={R}_{D}-cost $

(27)

本文利用惩罚因子 $ h $ 将多目标优化问题转化为单目标优化问题. 惩罚因子 $ h $ 将CO₂排放量转换为排放成本. 因此, 在满足负荷需求和运行约束的前提下, 通过优化问题求解, 使发电厂获得的社会效益最大同时CO₂排放量最小. 最高惩罚价格因子 $ h $ 是社会效益的最大值 $ S{W}^{\mathrm{m}\mathrm{a}\mathrm{x}} $ 和CO₂排放量的最大值 $ {E}_{G}^{\mathrm{m}\mathrm{a}\mathrm{x}} $ 之间的比值, 如下所示:

$ h=S{W}^{\mathrm{m}\mathrm{a}\mathrm{x}}/{E}_{G}^{\mathrm{m}\mathrm{a}\mathrm{x}} $

(28)

与CO₂排放量相对应的成本 $ {C}_{E} $ 可由式(29)计算:

$ {C}_{E}=h{E}_{G} $

(29)

总体目标函数如下:

$ Max\to F=SW-{C}_{E} $

(30)

3.2 约束条件

目标函数 $ Max\to F=SW-{C}_{E} $ 受到以下约束:

(1)有功功率平衡:

$ \begin{split} &\sum\nolimits_{i=1}^{{N}_{G}}{P}_{{G}_{i,t}}+\sum\nolimits_{i=1}^{{N}_{\rm GF}}{P}_{{\rm GF}_{i,t}}+\sum\nolimits_{i=1}^{{N}_{w}}{P}_{{w}_{i,t}}+\sum\nolimits_{i=1}^{{N}_{pv}}p{v}_{i,t}\\ &+\sum\nolimits_{i=1}^{{N}_{\rm CHP}}{P}_{{\rm CHP}_{i,t}}+\sum\nolimits_{i=1}^{{N}_{B}}{P}_{P{b}_{i,t}}\\ &=\sum\nolimits_{i=1}^{{N}_{\rm P2G}}{P}_{{\rm P2G}_{i,t}}+{P}_{Dt}+{P}_{\rm loss}\\[-15pt] \end{split} $

(31)

式中, $ {P}_{P{b}_{i,t}} $ 表示 $ t $ 时刻的电池电量, $ {P}_{Dt} $ 表示 $ t $ 时刻的总电力需求, ${P}_{\rm loss}$ 表示功率损耗, ${P}_{\rm loss}$ 计算公式如下:

$ {P}_{\rm loss}=\sum\nolimits_{j=1}^{{N}_{l}}{G}_{ij}\left({V}_{i}^{2}+{V}_{j}^{2}-2{V}_{i}{V}_{j}\cos{\theta }_{ij}\right) $

(32)

式中, $ {G}_{ij} $ 是母线 $ i $ 和 $ j $ 之间的电导, $ {V}_{i} $ 和 $ {V}_{j} $ 分别表示母线 $ i $ 和母线 $ j $ 上的电压, $ {\theta }_{ij} $ 是相位角.

(2)母线电压和支路潮流约束:

$ \left\{\begin{array}{c}{V}_{i}^{\min}\le {V}_{i}\le {V}_{i}^{\max}\\ \left|{S}_{{\rm{flow}},i}\right|\le {S}_{{\rm{flow}},i}^{\max}\end{array}\right. $

(33)

式中, $ {V}_{i}^{\mathrm{m}\mathrm{a}\mathrm{x}} $ , $ {V}_{i}^{\mathrm{m}\mathrm{i}\mathrm{n}} $ 表示第 $ i $ 条母线电压最大值和最小值, ${S}_{{\rm{flow}},i}$ 表示第 $ i $ 条支路上的潮流分布, ${S}_{{\rm{flow}},i}^{\max}$ 表示第 $ i $ 条支路上的潮流分布的最大值.

(3)爬坡率约束:

$ \left\{\begin{array}{c}{P}_{i,t}-{P}_{i,t-1}<U{R}_{i}\\ {P}_{i,t-1}-{P}_{i,t}<D{R}_{i}\end{array}\right. $

(34)

式中, $ U{R}_{i} $ 和 $ D{R}_{i} $ 分别表示第 $ i $ 台机组的上升速率约束和下降速率约束, $ {P}_{i,t} $ 表示第 $ i $ 台机组在 $ t $ 时刻的功率, $ {P}_{i,t-1} $ 表示第 $ i $ 台机组在 $ t-1 $ 时刻的功率.

(4)输出功率约束:

$ \left\{\begin{array}{l}{P}_{{\rm GF}_{i}}^{\min}\le {P}_{{\rm GF}_{i,t}}\le {P}_{{\rm GF}_{i}}^{\max}\\ {P}_{{\rm CHP}_{i}}^{\min}\le {P}_{{\rm CHP}_{i,t}}\le {P}_{{\rm CHP}_{i,t}}^{\max}\\ 0\le {P}_{{w}_{i,t}}\le {P}_{{w}_{r}}\\ 0\le p{v}_{i,t}\le p{v}_{{\left({K}_{t\max}\right)}_{i}}\\ 0\le {P}_{{\rm P2G}_{i,t}}\le {P}_{{\rm P2G}_{i}}^{\max}\end{array}\right. $

(35)

式中, ${P}_{{\rm GF}_{i}}^{\max}$ , ${P}_{{\rm GF}_{i}}^{\min}$ 分别表示第 $ i $ 台燃气发电机输出功率的最大值和最小值, ${P}_{{\rm CHP}_{i,t}}^{\max}$ , ${P}_{{\rm CHP}_{i}}^{\min}$ 分别表示第 $ i $ 台热电联产发电机输出功率的最大值和最小值, ${P}_{{\rm P2G}_{i}}^{\max}$ 表示第 $ i $ 台P2G装置输出功率的最大值.

(5)热节点平衡约束:

$ \begin{split} &\sum\nolimits_{i=1}^{{N}_{\rm CHP}}{Q}_{{\rm CHP}_{i,t}}+\sum\nolimits_{i=1}^{{N}_{\rm HOU}}{Q}_{{\rm HOU}_{i,t}}+\sum\nolimits_{i=1}^{{N}_{HS}}{Q}_{{H}_{i,t}}\\ &={H}_{D_t}+{H}_{\rm loss} \end{split} $

(36)

式中, $ {Q}_{{H}_{i,t}} $ 表示 $ t $ 时刻的蓄热量, ${H}_{D_t}$ 表示 $ t $ 时刻的热需求, ${H}_{\rm loss}$ 表示热损耗.

(6)热电联产和供热单元的热量约束:

$ \left\{\begin{array}{l}{Q}_{{\rm CHP}_{i,t}}^{\min}\le {Q}_{{\rm CHP}_{i,t}}\le {Q}_{{\rm CHP}_{i,t}}^{\max}\\ {Q}_{{\rm HOU}_{i,t}}^{\min}\le {Q}_{{\rm HOU}_{i,t}}\le {Q}_{{\rm HOU}_{i,t}}^{\max}\end{array}\right. $

(37)

式中, ${Q}_{{\rm CHP}_{i,t}}^{\max}$ , ${Q}_{{\rm CHP}_{i,t}}^{\min}$ 表示第 $ i $ 台热电联产发电机在 $ t $ 时刻产热量的最大值和最小值, ${Q}_{{\rm HOU}_{i,t}}^{\max}$ , ${Q}_{{\rm HOU}_{i,t}}^{\min}$ 表示第 $ i $ 台供热单元机组在 $ t $ 时刻产热量的最大值和最小值.

(7)气体节点平衡约束:

$ \begin{split} &\sum\nolimits_{i=1}^{{N}_{M}}{Q}_{{S}_{i,t}}+\sum\nolimits_{i=1}^{{N}_{M}}{Q}_{{\rm P2G}_{i,t}}+\sum\nolimits_{i=1}^{{N}_{M}}{Q}_{{g}_{i,t}}\\ &=\sum\nolimits_{i=1}^{{N}_{\rm CHP}}{L}_{{\rm CHP}_{i,t}}+\sum\nolimits_{i=1}^{{N}_{\rm GF}}{L}_{{\rm GF}_{i,t}}+{Q}_{D.t}+{Q}_{\rm loss} \end{split} $

(38)

式中, $ {Q}_{{S}_{i,t}} $ 表示第 $ i $ 台设备在 $ t $ 时刻的气体输出量, $ {Q}_{{g}_{i,t}} $ 表示 $ t $ 时刻的气体存储量, $ {Q}_{D.t} $ 表示 $ t $ 时刻的气体需求量, ${Q}_{\rm loss}$ 表示气体损耗.

(8)压强和气流约束

$ \left\{\begin{array}{l}{P}_{m,{n}_{i}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le {P}_{m,{n}_{i,t}}\le {P}_{m,{n}_{i}}^{\mathrm{m}\mathrm{a}\mathrm{x}}\\ 0\le {Q}_{mn}\le {k}_{mn}\sqrt{({P}_{m}^{2}-{P}_{n}^{2})}\end{array}\right. $

(39)

式中, ${P}_{m,{n}_{i}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ , ${P}_{m,{n}_{i}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$ 表示节点 $ m $ 和节点 $ n $ 间压强的最大值和最小值.

(9)充放电功率约束

$ \left\{\begin{array}{l}-{E}_{\max}/4\Delta t\le {P}_{{\rm SDC}_{i,t}}\le 0\\ 0\le {P}_{{\rm SDD}_{i,t}}\le {E}_{\max}/4\Delta t\end{array}\right. $

(40)

式中, $ {E}_{\mathrm{m}\mathrm{a}\mathrm{x}} $ 表示不同存储类型的最大储能设备容量.

(10)储能设备中能量约束:

$ {E}_{{\rm SD}_{i}}^{\min}\le {E}_{{\rm SD}_{i}}^{\rm ini}+{P}_{{\rm SDC}_{i,t}}\varDelta t-{P}_{{\rm SDD}_{i,t}}\varDelta t\le {E}_{{\rm SD}_{i}}^{\mathrm{m}\mathrm{a}\mathrm{x}} $

(41)

式中, ${E}_{{\rm SD}_{i}}^{\max}$ , ${E}_{{\rm SD}_{i}}^{\min}$ 表示储能设备中能量的最大值和最小值, ${E}_{{\rm SD}_{i}}^{\rm ini}$ 表示第 $ i $ 台储能设备的初始能量.

4 算例分析 4.1 算例描述

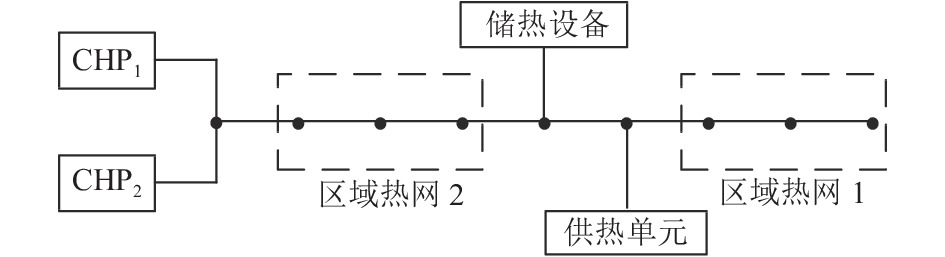
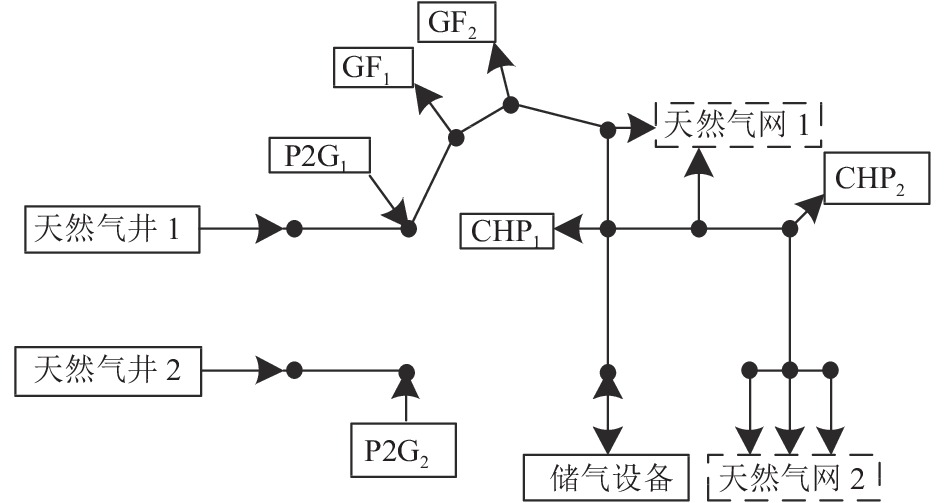
为了验证所提算法的适用性和有效性, 将其应用于IEEE 69节点标准测试系统. 该系统由9个常规发电机、48个负荷和68条支路(输电线路和变压器)组成, 如图3所示. IEEE 69总线测试系统的完整数据在文献[12]中给出. 其中设备参数如表1所示. 此外, 将一个容量为60 MWh的储能设备接到节点60上. 供热系统由两个CHP机组, HOU和储热设备组成, 其中储热设备为区域热网供热, 如图4所示. 天然气系统配置结构如图5所示.

本文考虑了5个算例来说明可再生能源、储能设备和P2G装置在能量枢纽运行中的作用.

算例1: 在不包括任何可再生能源或储能设备的情况下, 对原始能量枢纽配置进行研究.

算例2: 在算例1的基础上加入储能设备进行研究.

算例3: 能量枢纽中包括可再生能源和P2G装置, 但不包含储能设备.

算例4: 能量枢纽中只包含可再生能源.

算例5: 能量枢纽中包含所有能源出力.

4.2 仿真结果分析

本文通过对算例中电压、功率损耗、负荷节点温度以及天然气管道压强等指标的比较分析, 说明了不同配置对能量枢纽运营的影响, 比较结果如图6~图9所示.

5种算例中电压日变化如图6所示. 凌晨1点到下午4点这个时间段, 负荷需求较小, 电压变化也较小. 下午4点到夜间24点这个时间段, 负荷需求较大, 此时功率损耗将随着负荷需求的增大而增大, 随着负荷需求的减小而减小, 如图7所示. 由于没有可再生能源和储能设备支持, 算例1中电压变化和功率损耗变化最大. 在算例5中, 由于能量枢纽包括了所有能源出力, 此时电压变化和功率损耗变化最小.

图8比较分析了不同的能量枢纽配置对热负荷节点处供热系统温度的影响. 由于凌晨1点到下午3点这个时间段热负荷需求比较小, 所以这个时间段内5个算例中温度变化都较小. 其中算例1中温度变化最大, 算例5中温度变化最小.

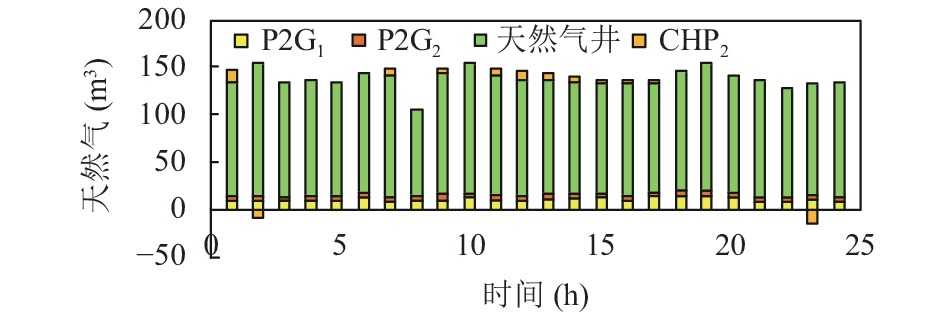
5种算例中天然气管道中压强变化情况如图9所示. 从图中可以看出, 天然气管道压强会随着负载和可用能源的变化而变化. 由于算例1中缺少可再生能源和储能设备, 所以此时出现最高压降. 所以燃气发电机产生了更多的电能来满足电力负荷. 在算例5中, 由于燃气发电机所需功率的减少和P2G机组的存在, 因此其压强变化最小.

4.3 算例比较分析

在每种算例中, 分别计算总运营成本、CO₂排放量以及系统损耗. 以母线2上电、热、气成本为参考, 以各节点的电、热、气成本为指标, 考虑损耗的情况下, 计算各节点的电、热、气成本, 如表2所示.

从表2中可以看出:

(1) 在算例1中, 由于天然气价格较低, CHP机组是白天供电和供热的主要来源, 此外, 由于增加了气体系统的进料路径, 天然气损耗也随之增加. 但是, 随着白天负荷的增加, CHP不能满足这些负荷, 只能向HOU购买, 因此增加了运行成本和碳排放量.

(2) 在算例2中, 随着储能设备的加入, 系统性能得到了较大的提高. 碳排放量和能耗略有减少. 在这种情况下, 能量枢纽中多余的能量会被储存起来, 以供在能源不足时使用.

(3) 算例3与算例1和算例2相比, 由于可再生能源的加入, 社会效益, 碳排放量以及能耗等方面都得到了明显的改善, 但是由于能量枢纽中没有储能设备, 损耗也随之增加.

(4) 与算例3相比, 算例4的P2G装置的缺失使得其在社会效益, 碳排放量和能量损耗方面都有所减少.

(5) 在算例5中, 由于可再生能源, 储能设备和P2G装置同时运行, 从而减少了从电网和火电机组购买的电能. 因此, 能量枢纽的性能参数以及稳定性都得到了改善. 算例5中最优出力的仿真结果如图10~图12所示.

从算例比较分析的结果中可以看出, 当火电机组成为能量枢纽中能量的主要来源时, 运营成本和CO₂排放量都会增加. 当储能设备连接到能量枢纽中后, 能量枢纽在CO₂排放量, 系统损耗和社会效益方面都得到了改善. 同样, 当可再生能源加入到能量枢纽中后, 系统中的各方面性能也得到很大改善. 在没有P2G机组的情况下, 总负载减少, 从而提供给电网的功率增加, 社会效益, CO₂排放量和损耗也随之减少. 在算例5中, 即能量枢纽中包括可再生能源, 储能设备和P2G装置时, 此时能量枢纽的参数和稳定性都得到了较大改善.

5 结论

本文提出了一种考虑CO₂排放的能量枢纽优化运行配置方案, 以满足当今能源互联背景下的电力, 热能和天然气的需求. 在考虑了光伏和风能两种可再生能源的不确定性的基础上建立函数模型以及约束条件, 实现了社会效益最大化, 同时总运营成本和CO₂排放量最小化的目标. 本文通过5种算例的比较分析遗传算法说明了可再生能源、储能设备和P2G装置对能量枢纽运行的作用和影响. 根据电压、功率损耗、压强和温度等指标的对比, 证明了光伏发电机组、风力发电机组、蓄电、蓄热、储气、P2G机组组合的能量枢纽在配置、损耗、CO₂排放量、社会效益以及稳定性等方面的性能优化. 本研究对建设能量枢纽, 促进新能源发电, 以及实现能源可持续发展利用有着重要意义.