随着信息技术的发展, 各领域涌现出大量的数据碎片. 然而, 大数据呈现“大数据、小样本”的问题, 即数据重复性较高, 某些样本数据量较少. 大数据处理方法是建立在充足数据的基础上, 小样本数据会带来信息不完全、不完备问题, 使得算法精度较差, 很难满足实际应用要求^[1]. 因此, 我们需要通过数据生成技术生成较为接近真实数据的虚拟数据, 丰富小样本数据, 从而提高大数据处理算法的准确率^[2].

在实际工业领域中, 机械设备的整个生命周期大多处于正常状态, 很难采集到故障数据^[3]. 数据驱动的故障诊断方法建立在充足的数据基础上, 小样本问题很难概括数据的整体信息, 使得相关机器学习及深度学习算法精度下降^[4].

在工业领域中, 针对故障数据小样本问题, 最直接的方法是重新获取更多的故障数据, 常用的方法包括数据采样和数据生成. 数据采样包括欠采样^[5-7]、过采样^[8,9]. 欠采样与过采样会造成信息的丢失或过拟合. 数据生成方法包括模拟采样^[10]和生成式对抗网络(Generative Adversarial Networks, GAN)^[11]. 模拟采样^[10]通过获取数据的概率分布p(x), 并通过计算机模拟随机采样过程获取生成数据. 该类方法需要获取较为准确的数据概率分布, 构造合理的转移概率函数, 且不能保证生成的数据多样性. 而基于深度学习方法的生成式对抗网络可以有效解决概率分布函数的获取问题, 降低了数据生成难度. 然而GAN需要大量的数据支持, 小样本数据不足以支撑GAN的训练, 且GAN方法学习速度较慢.

近年来, 小样本学习^[12-15]取得了长足发展. 小样本学习试图在有限样本条件下实现分类或拟合任务, 其中基于优化方法的元学习^[14]旨在学习一组元分类器, 并在新任务上微调实现较好的性能. 文献[15]提出了一种模型无关的元学习(Model-Agnostic Meta-Learning, MAML)方法, 该算法能在面对新任务时, 仅通过少步迭代更新就可取得较好的性能.

因此, 本文将元学习和生成式对抗网络相结合, 提出一种基于元学习的生成式对抗网络(Generative Adversarial Networks based on Meta-Learning, ML-GAN). ML-GAN利用元学习训练方式搜寻最优初始化参数得到一个较好的初始化模型, 而后在初始化模型的基础上通过少量某种类别样本快速学习当前任务的数据特性, 获得能够生成某种类别数据的特异性GAN. ML-GAN可以有效减少对样本的需求量, 同时通过微调还能增强生成数据的多样性, 实现了对于小样本数据的生成扩充.

1 相关工作

受益于计算设备的发展, 学习观测样本的概率密度并随机生成新样本的生成式对抗网络成为热点. 文献[16]首次提出生成式对抗网络, 但该方法采用KL散度容易导致模式崩溃. 文献[17]针对模式崩溃问题, 将Wasserstein距离代替KL散度, 并采用Lipschitz约束限制梯度, 基本解决了模式崩溃问题. 文献[18]与文献[19]提出了CGAN与info-GAN, 该方法可以控制数据生成的类别, 但需要大量的数据支撑.

在工业领域数据生成中, 文献[20]提出MAD-GAN数据增强技术用以生成工业水处理数据, MAD-GAN通过优化噪声生成较为真实的数据, 但该方法仅能保证最优噪声附近的数据生成质量, 小样本数据不足以支撑整个噪声空间的训练, 难以保证除最优噪声之外的噪声的数据生成质量. 文献[21]利用先验知识将正常齿轮箱运转数据转化为粗故障数据, 而后利用GAN将粗故障数据转化为较为真实的故障数据, 但该方法没有充分利用噪声的随机性, 生成的故障数据多样性较差. 文献[22]提出一种将GAN和叠加去噪自编码器相结合的方法, 该方法在小样本情况下具有良好的生成效果, 但该方法无法控制生成的数据类别. 文献[23]利用生成式对抗网络进行多场景电力数据生成, 但该方法需要大量数据支持, 不适用于小样本数据.

针对GAN方法不适用于小样本数据的问题, 本文将元学习学会学习特性引入到生成式对抗网络中, 通过元学习的训练策略得到最优初始化模型, 并通过元学习的基学习器快速学习, 从而实现小样本的数据生成工作.

2 基础知识介绍 2.1 MAML算法介绍

MAML是一种与模型无关的元学习算法, 它利用元任务之间的内在知识优化网络初始化参数, 使得网络在新任务上仅需通过较少样本和少步梯度更新便可取得较好的性能, 达到快速学习的效果. MAML网络包括多个基学习器和一个元学习器, 其学习策略是每个基学习器学习当前元任务, 得到一组适合当前任务的模型参数, 元学习器学习多个基学习器之间的通用知识策略, 得到一组适合所有任务的模型通用初始化参数.

MAML网络模型记为 $f$ , 并由参数 $\theta $ 进行描述, 即 ${f_\theta }$ . MAML任务分布记为 $P(T)$ , 随机选取 $batch\_si{\textit{z}}e$ 个元任务 ${T_i}$ 用于基学习器的学习, 元任务 ${T_i}$ 由支持集和查询集组成 ${T_i} = \{ T_i^s,T_i^q\} $ . 每个基学习器在元任务的支持集 $T_i^s$ 上进行梯度更新, 假设梯度更新一次, 其梯度为 ${\nabla _\theta }{L_{T_i^s}}({f_\theta })$ , 其中 $L$ 为损失函数, 更新后的网络参数记为 ${\theta _i}'$ :

$ {\theta _i}' = \theta - \alpha {\nabla _\theta }{L_{T_i^s}}({f_\theta }) $

(1)

当多个基学习器学习完成后, 元学习器在基学习器的基础上进行再次学习, 获取一组适用于所有元任务的初始化参数:

$ \theta = \theta - \beta {\nabla _\theta }\sum\limits_{{T_i} \sim P(T)} {{L_{T_i^q}}({f_{{\theta _i}'}})} {\rm{ }} $

(2)

式(2)中, $\alpha $ 与 $\;\beta $ 为学习率.

2.2 GAN算法介绍

GAN的基本思想源自博弈论的二人零和博弈, 其模型结构如图1所示, 由一个生成器G和一个判别器D构成, 其中, 生成器G将从噪声分布采样得到的数据z映射到样本数据空间中, 判别器D则对生成数据G(z)和真实数据x进行判断. 两模型对抗训练, 当判别器无法准确判断输入的真伪时, 即达到纳什平衡, 此时可认为生成器学习到了原始数据的分布.

GAN的目标函数:

$ \begin{split} &\mathop {\min }\limits_G \mathop {\max }\limits_D V(G,D) \\ &={E_{x \sim p(x)}}\log_2 D(x) + {E_{{\textit{z}} \sim p({\textit{z}})}}\log_2 (1 - D(G({\textit{z}}))) \end{split} $

(3)

式(3)中 $p(x)$ 表示真是样本分布, $p({\textit{z}})$ 表示噪声分布. 其中, 判别器的目标函数为:

$ \begin{split} L(D) =& {E_{x \sim p(x)}}\log_2 D(x)\\ & + {E_{{\textit{z}} \sim p({\textit{z}})}}\log_2 (1 - D(G({\textit{z}}))) \end{split} $

(4)

生成器的目标函数为:

$ L(G) = {E_{{\textit{z}} \sim p({\textit{z}})}}\log_2 (1 - D(G({\textit{z}}))) $

(5)

3 ML-GAN数据生成算法

数据生成模型GAN能够以无监督的形式实现训练, 然而该类方法需要大量的数据支持; MAML算法适用于小样本学习, 能够学习到各项元任务之间可转移的内在表征. 因此, 本文将元学习引入到GAN中, 提出一种适用于小样本问题的数据生成算法ML-GAN.

ML-GAN通过不断优化搜寻最优的初始化参数, 以期在新任务(小样本数据生成任务)上快速收敛, 得到针对新任务的特异性GAN, 实现对于小样本数据的生成扩充. ML-GAN模型由生成器G与鉴别器D组成, 并以基学习器与元学习器交替训练的方法进行. 实际上, ML-GAN是希望找到一组对于任务变化敏感的GAN模型参数, 使得参数的微小变化就可以很大程度上提高新任务的GAN模型的表现性能.

本章节将在3.1节描述ML-GAN的任务设置, 在3.2节与3.3节描述基学习器与元学习器的训练流程, 并在3.4节描述ML-GAN整体训练流程.

3.1 任务设置

ML-GAN以任务为训练数据进行训练, 每一组GAN任务 ${T_i}$ 都由支持集 $T_i^s$ 和查询集 $T_i^q$ 构成, 支持集、查询集均由真实数据与生成数据组成:

$ \begin{split} {T_i} = \{ T_i^s,T_i^q|T_i^s = \{ x \in X,{\textit{z}} \in Z\},\; T_i^q = \{ x \in X,{\textit{z}} \in Z\} \} \end{split} $

(6)

其中, 真实数据来自真实数据集, 即x∈X, 生成数据由生成器生成, 其噪声来自噪声分布, 即z∈Z.

3.2 基学习器

基学习器继承自元学习器, 其模型由生成器G和鉴别器D构成. 生成器是噪声z到数据x的映射, 判别器是数据x到真假类别的映射. 生成器参数为 ${\theta _G}$ , 生成器表示为 ${G_{{\theta _G}}}$ , 鉴别器参数为 ${\theta _{{D}}}$ , 鉴别器表示为 ${D_{{\theta _D}}}$ .

基学习器的生成器和鉴别器在一组元任务 ${T_i} = $ $ \{ T_i^s,T_i^q\} $ 上训练, 鉴别器目标是能够对输入数据进行真假判别, 其目标函数为:

$ \begin{split} L_D^{T_i^s} =& \mathop {\max }\limits_D {E_{x \sim T_i^s}}\log_2 D(x,{\theta _D}) \\ &+ {E_{{\textit{z}} \sim T_i^s}}\log_2 (1 - D(G({\textit{z}},{\theta _G}),{\theta _D})) \end{split} $

(7)

生成器目标是在有限的训练样本和迭代轮次内生成尽量真实的数据, 其目标函数为:

$ L_G^{T_i^s}({\theta _G}) = \mathop {\min }\limits_D {E_{{\textit{z}} \sim T_i^s}}\log_2 (1 - D(G({\textit{z}},{\theta _G}),{\theta _D})) $

(8)

基学习器会根据当前任务损失进行生成器和鉴别器的迭代更新, 生成器参数会由 ${\theta _G}$ 更新为 $\theta _G^{T_i^s}$ , 鉴别器模型参数会由 ${\theta _D}$ 更新为 $\theta _{{D}}^{T_i^s}$ . 假设模型在新任务上进行k次梯度更新, 以一次梯度更新为例:

$\left\{ \begin{split} \theta _D^{T_i^s} =& {\theta _D} - {\alpha _D}{\nabla _{{\theta _D}}}L_D^{T_i^s}\\ \theta _G^{T_i^s} =& {\theta _G} - {\alpha _G}{\nabla _{{\theta _G}}}L_D^{T_i^s} \end{split}\right. $

(9)

上述参数更新公式中, ${\alpha _D}$ 与 ${\alpha _G}$ 分别为学习率.

基学习器所学参数 $\theta _{{D}}^{T_i^s}$ 、 $\theta _G^{T_i^s}$ 仅在当前任务上表现优异, 而不一定适合所有任务, 因此需要元学习器通过各GAN任务最优参数对应的梯度更新初始化参数, 从而搜寻到适合所有任务的最优初始化参数.

3.3 元学习器

基学习器仅能学习到当前任务的数据特性, 不适合其他任务. 元学习器的目的是平衡各基学习器的学习效果, 找到适合于所有任务的最优初始化模型, 从而在面对新任务时仅需少量数据便可取得较好的生成效果.

元学习器在查询集 $T_i^q$ 上通过各元任务最优参数对应的梯度更新初始化参数, 其判别器目标函数为:

$ \begin{split} \mathop {\max }\limits_{{\theta _D}} \sum\limits_{{T_i}\sim P(T)} {L_D^{T_i^q}\left( {\theta _D^{T_i^s}} \right)} =& \mathop {\max }\limits_D \sum\limits_{{T_i}\sim P(T)} {{E_{x\sim T_i^q}}} \log_2 D\left( {x,\theta _D^{T_i^s}} \right)\\ & + {E_{{\textit{z}}\sim T_i^q}}\log_2 \left( {1 - D\left( {G({\textit{z}},{\theta _G}),\theta _D^{T_i^s}} \right)} \right) \end{split} $

(10)

生成器目标函数为:

$ \begin{split} &\mathop {\min }\limits_{{\theta _G}} \sum\limits_{{T_i}\sim P(T)} {L_G^{T_i^q}\left( {\theta _G^{T_i^s}} \right)} = \\ &{\mathop {\min }\limits_G \sum\limits_{{T_i}\sim P(T)} {{E_{{\textit{z}}\sim T_i^q}}\log_2 \left( {1 - D\left( {G\left( {{\textit{z}},\theta _G^{T_i^s}} \right),{\theta _D}} \right)} \right)} } \end{split} $

(11)

元学习器目标函数使用各基学习器参数 $\theta _{{D}}^{{{{T}}_i}}$ 与 $\theta _G^{{{{T}}_i}}$ 计算, 通过评估其在所有任务查询集上的表现性能进行梯度更新, 这样可以获得一个全局最优的模型参数, 其梯度更新公式为:

$\left\{ \begin{split} {\theta _D} =& {\theta _D} - {\beta _D}{\nabla _{{\theta _D}}}\sum\limits_{{T_i}\sim P(T)} {L_D^{{T_i}}\left( {\theta _D^{{T_i}}} \right)} \\ {\theta _G} =& {\theta _G} - {\beta _D}\nabla {\theta _G}\displaystyle\sum\limits_{{T_i}\sim P(T)} {L_G^{{T_i}}\left( {\theta _G^{{T_i}}} \right)} \end{split}\right. $

(12)

3.4 ML-GAN训练策略

ML-GAN以任务为数据进行学习, 其中基学习器重点学习当前任务的数据特性, 其目标是生成接近于当前任务的真实数据; 元学习器学习基学习器的学习结果, 其目标是找到适合所有任务的最优初始化模型. 两者在训练时交替进行, 基学习器继承元学习器, 并利用任务数据进行梯度更新; 元学习器通过各基学习器的最优参数对应的梯度更新初始化参数, 平衡各基学习器的学习效果.

ML-GAN算法流程如算法1.

算法1. ML-GAN算法

1) 随机初始化 ML-GAN 的元学习器;

2) while not done do:

3)　　初始化基学习器参数为元学习器;

4)　　随机选取任务 $\scriptstyle{T_i}$ ;

5)　　for all $\scriptstyle{T_i}$ do:

6)　　　　计算任务 $\scriptstyle{T_i}$ 的鉴别器损失 $\scriptstyle L_D^{T_i^s}$ ;

7)　　　　计算任务 $\scriptstyle{T_i}$ 的生成器损失 $\scriptstyle L_G^{T_i^s}$ ;

8)　　　　更新基学习器参数 $\scriptstyle\theta _G^{T_i^s}$ 和 $\scriptstyle\theta _D^{T_i^s}$ ;

9)　　end for

10)　　计算所有任务的鉴别器损失 $\scriptstyle \sum\limits_{{T_i} \sim {{P}}(T)} {L_{{D}}^{T_i^{{q}}}(\theta _{{D}}^{T_i^{{s}}})}$ ;

11)　　计算所有任务的生成器损失 $\scriptstyle \sum\limits_{{T_i} \sim {{P}}(T)} {L_G^{T_i^{{q}}}(\theta _G^{T_i^{{s}}})}$ ;

12) 　　更新元学习器参数 $\scriptstyle{\theta _D}$ 和 $\scriptstyle{\theta _{{G}}}$ ;

13) end while

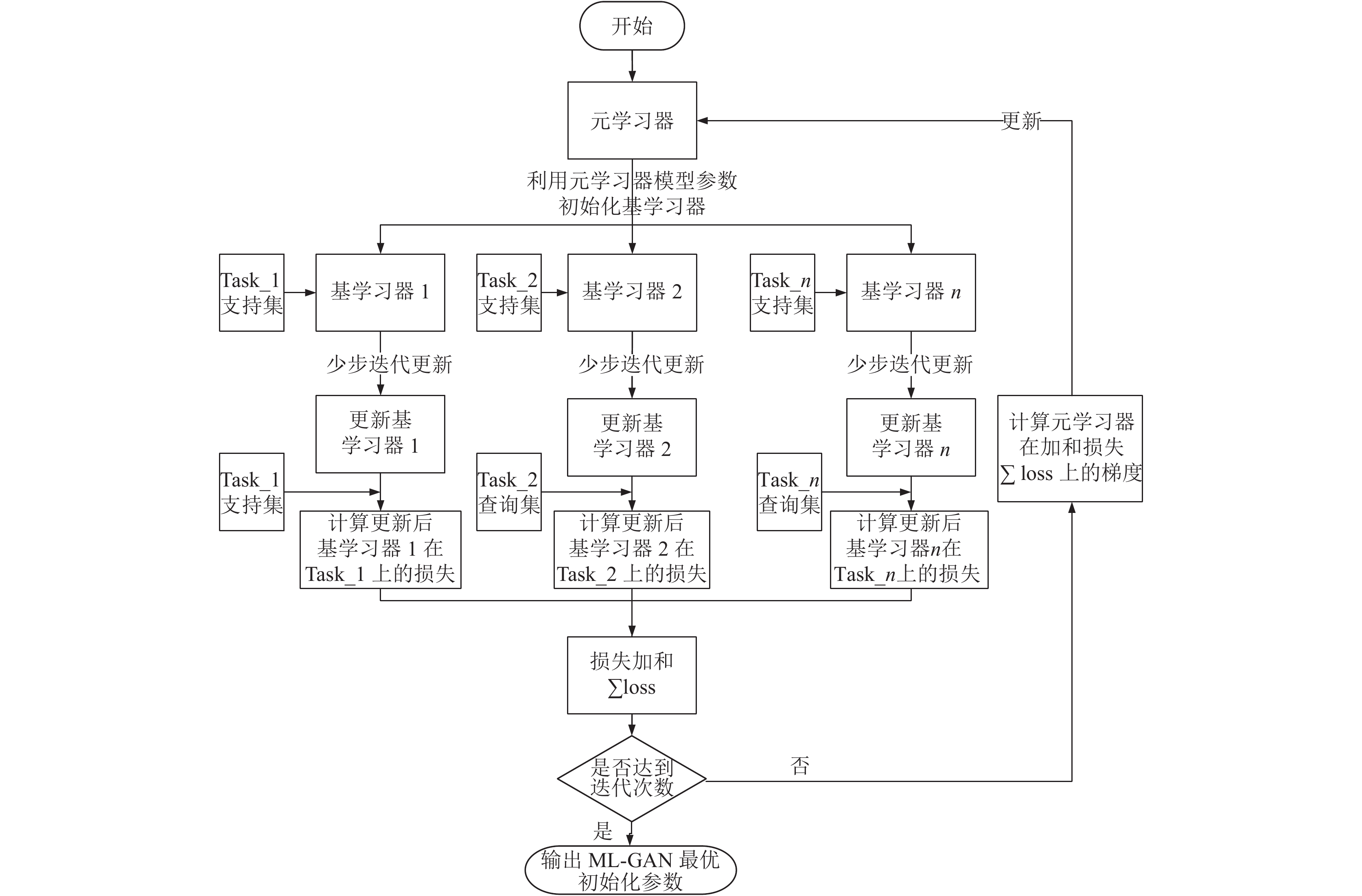
ML-GAN整体训练流程如图2所示, 首先初始化元学习器, 并利用元学习器的模型参数初始化各基学习器模型参数. 各基学习器利用各自任务支持集的数据进行GAN的对抗训练更新, 其损失函数和梯度更新公式如式(7)、式(8)和式(9)所示. 由于更新后的基学习器仅适合于当前任务, 具有较强的特异性, 不适合作为初始化模型, 因此再利用式(10)和式(11)在查询集上计算损失, 并通过式(12)更新元学习器参数.

4 ML-GAN数据生成实验

本章节将对ML-GAN进行深入研究, 详细描述其基学习器损失和元学习器损失的变化形式. 为了展示ML-GAN优异的生成性能, 本文通过海尔水冷磁悬浮数据进行每种故障的数据生成实验, 并利用生成数据与真实数据进行故障分类器的训练, 验证生成数据的有效性.

由第2节可知, ML-GAN算法得到的是一个最优初始化模型, 还需要通过基学习器的快速学习微调模型, 获取到生成某种特定类别数据的特异性GAN. 本文在4.2节与4.3节详细阐述ML-GAN最优初始化模型和特异性模型的训练过程.

4.1 实验数据集

实验数据集选取自海尔水冷磁悬浮机组数据. 海尔水冷磁悬浮机组数据包括蒸发器侧进水温度(℃)、蒸发器侧出水温度(℃)、冷凝器侧进水温度(℃)、冷凝器侧出水温度(℃), 压缩机吸气温度(℃)、压缩机排气温度(℃)、压缩机负荷(%)、故障类别等19维向量. 经过PCA降维^[24]分析, 由表1结果可知前四维数据蕴含的信息量约为91%, 故选取前四维及故障类作为数据集. 海尔数据共包含17327条, 由表2可知, 故障数据类型共占6.3%, 其中电机轴承故障数据最少, 为121条数据.

4.2 ML-GAN训练

ML-GAN超参数设置如下, 内部学习率 ${\alpha _D} = 0.001$ 与 ${\alpha _G} = 0.001$ , 外部循环学习率为 $\;{\beta _D} = 0.01$ 与 $\;{\beta _G} = 0.01$ , 序列长度SeqLen=30, 支持集数据条数n=10, 查询集数据长度q=5, 任务数meta_batch=4. 由于ML-GAN网络是通过对抗方式进行训练, 基学习器循环迭代次数不宜设置较低, 本实验设置基学习器循环迭代次数inner_step=10.

ML-GAN以任务形式训练, 每条任务包含支持集数据n条和查询集数据q条, 每条数据序列长度SeqLen=30. 基学习器训练时, 利用随机噪声与支持集数据进行GAN的对抗训练, 其损失函数与梯度更新公式为式(7)、式(8)和式(9). 基学习器仅适用于当前任务, 具有特异性, 还需进行元学习器优化平衡各基学习器学习效果. 在本实验中, 元学习器训练时利用meta_batch项任务的q条查询集数据进行训练, 其损失函数与梯度更新公式为式(10)、式(11)和式(12).

ML-GAN基学习器损失是针对于特定任务的效果评价, 基学习器迭代更新, 目标是尽可能生成接近支持集的生成数据. 如图3(a)所示, 基学习器进行快速学习, 鉴别器损失快速下降, 生成器损失快速上升, 生成器会根据鉴别器损失快速学习到较为真实的数据形式, 而后生成器损失下降判别器损失上升, 呈现对抗状态.

如图3(b)所示, 在训练过程中, 基学习器中出现了几次生成器与鉴别器损失一起下降的现象, 这是由于元学习器的前几次训练任务与当前任务类型的数据不同, 其鉴别器与生成器具有一定的特定性, 即鉴别器与生成器适合鉴别和生成之前任务的训练数据, 而当面对不同类型数据任务时, 鉴别器将真实数据判断为假可能性较大. 由式(7)可知, 鉴别器对于真实数据的鉴别损失 ${E_{x\sim T_i^s}}\log D\left( {x,q_D^{{T_i}}} \right)$ 较大, 对于生成数据的鉴别损失 ${E_{{\textit{z}}\sim T_i^s}}\log \left( {1 - D\left( {G\left( {{\textit{z}},\theta _G^{{T_i}}} \right),\theta _D^{{T_i}}} \right)} \right)$ 较小, 因此鉴别器损失初始值较大, 由式(8)可知生成器生成数据不贴近当前任务类型数据, 因此生成器损失值也较大. 而当经过训练之后, 生成器与鉴别器性能均得到提升, 鉴别器能够有效识别真实数据, 因此真实数据的鉴别损失 ${E_{x\sim T_i^s}}\log D\left( {x,\theta _D^{{T_i}}} \right)$ 下降幅度较大, 而当前任务开始时, 生成器生成数据较假, 因此它在鉴别器的指导下生成性能提升, 生成器损失 ${E_{{\textit{z}}\sim T_i^s}}\log \left( {1 - D\left( {G\left( {{\textit{z}},\theta _G^{{T_i}}} \right),\theta _D^{{T_i}}} \right)} \right)$ 继续下降. 因此, 鉴别器与生成器损失整体呈现出下降状态.

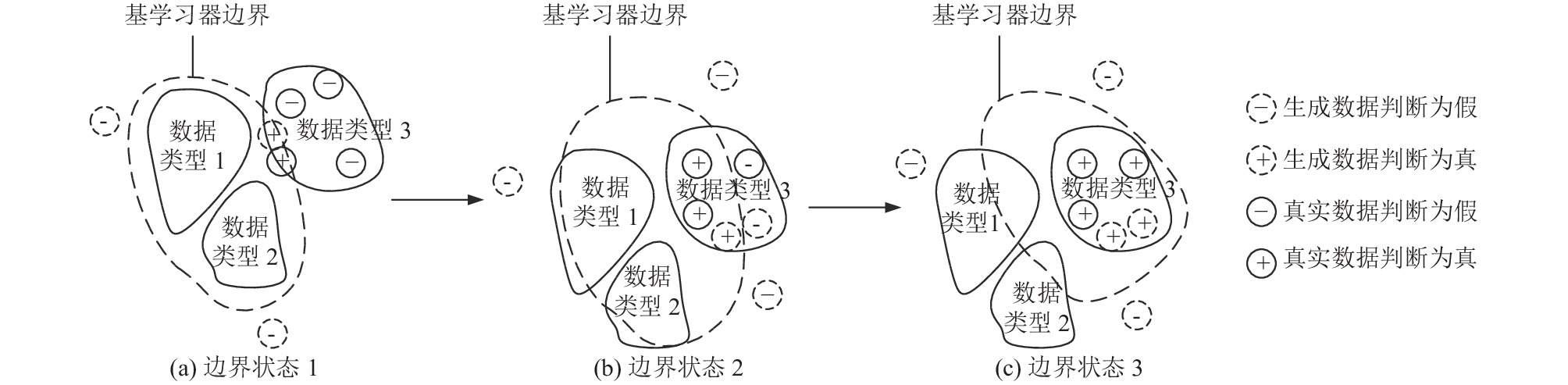
为了更详细描述图3(b)损失变化现象, 图4形象展示了基学习器学习边界变化状态, 当前任务数据为数据类型3. 开始时, 元学习器之前几次的训练任务为数据类型1与2, 如图4(a)所示基学习器边界囊括了数据类型1与2的边界. 在此状态下, 当任务数据类型为3时, 鉴别器将真实数据大部分判断为假, 生成数据部分判断为假. 在经过训练后, 基学习器边接变化到图4(b)状态, 此时真实数据少部分鉴别为假, 生成数据开始贴近数据类型3. 到训练到图4(c)时, 基学习器边接开始接近数据类型3, 之后的训练会呈现对抗状态, 图3(b)的1、3与4损失图在迭代次数为8之后出现对抗状态. 这种现象之所以与常见GAN不同, 是因为常见GAN不会出现将真实数据全部鉴别为假. 而本文这种情况的出现也是由于前几次迭代更新使用的是除数据类型3以外的数据.

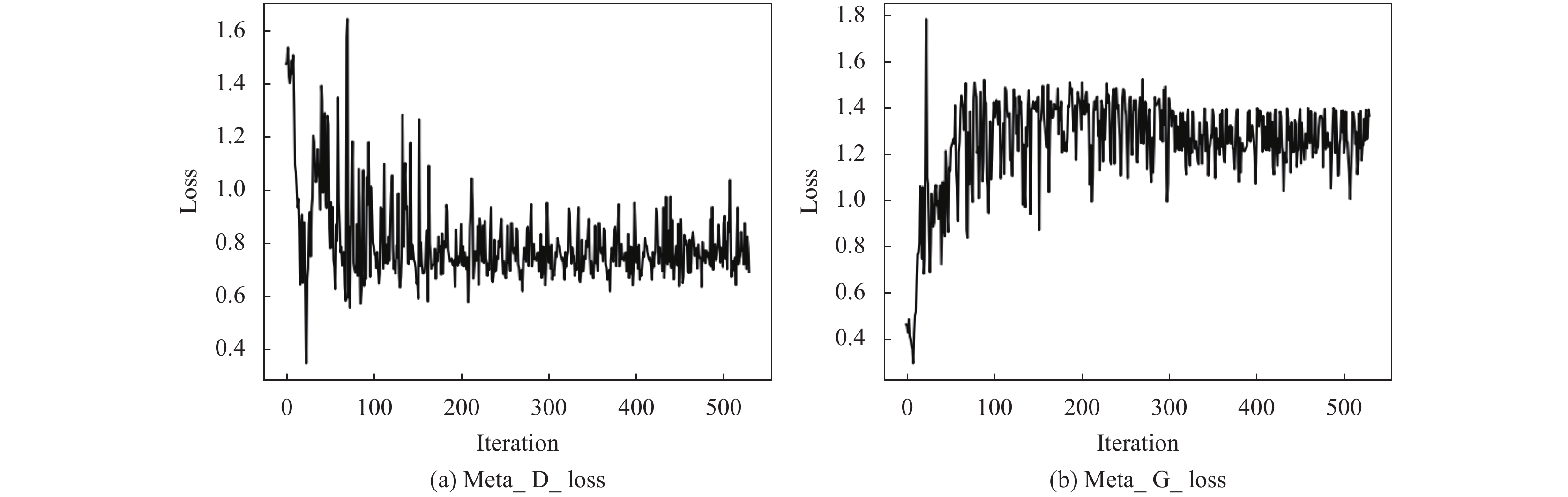
元学习器损失变化如图5所示, ML-GAN的生成器与鉴别器分别呈现出对抗的状态, 震荡较大, 在经过一段时间训练后, 震荡逐渐变小, 生成器与鉴别器损失值开始收敛. 此时, 鉴别器与生成器具有较好的性能, 能够适应与多项任务, 适合作为最优初始化模型.

4.3 数据快速生成实验

ML-GAN训练的目标是找到适合与所有任务的最优初始化模型, 4.2节ML-GAN训练实验已经找到一组最优参数作为初始化模型. 本节实验目的是在4.2节实验的最优初始化模型基础上, 利用ML-GAN的基学习器特异性训练过程, 通过少量数据和少步迭代获取到多个生成不同类别数据的GAN.

基学习器训练超参数如下, 基学习器学习率 ${\alpha _D} = $ $ 0.001$ 与 ${\alpha _G} = 0.001$ , 序列长度SeqLen=30, 支持集数据条数n=30, 任务数meta_batch=7, 基学习器迭代次数inner_step=20. 每个任务分别对应一种故障类型数据, 即7个任务会对应7个故障类型得到7种特异性GAN.

在数据快速生成实验中, 首先导入4.2节实验中的最优初始化模型作为元学习器, 而后用元学习器初始化7个基学习器, 对应7个故障类别. 每个基学习器模型参数相同, 不同的是输入数据. 7个基学习器对应7中故障类别的数据输入, 经过inner_step次迭代快速迭代更新, 获得7个生成器. 而后利用7个生成器生成故障数据.

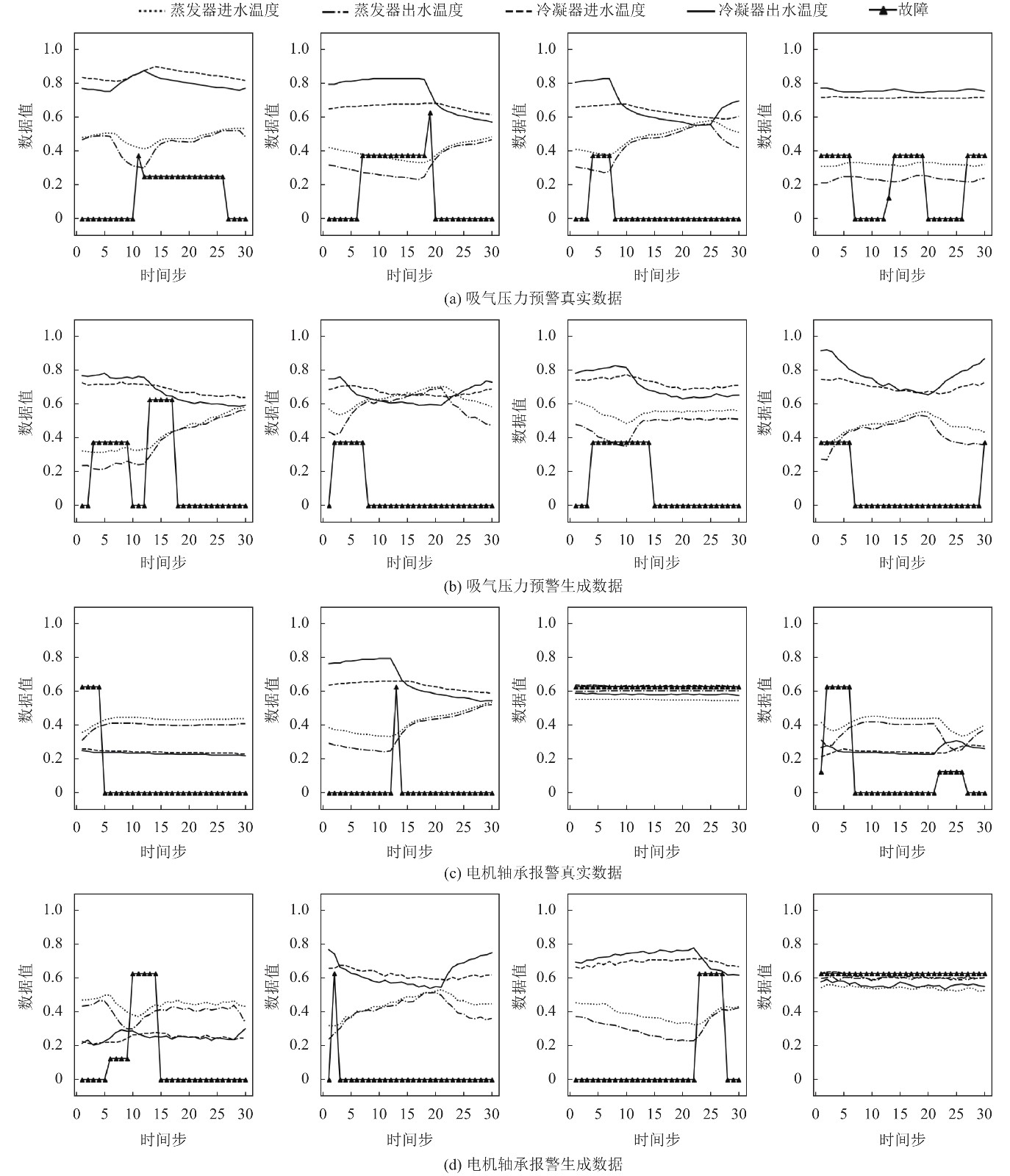
以基学习器1和基学习器2为例, 其输入的真实数据与生成数据如图6所示, 从上到下依次为吸气压力预警故障的真实数据与生成数据和电机轴承报警故障的真实数据与生成数据. 生成数据基本贴近输入数据, 其变化趋势也基本与真实数据相接近, 故障类别与真实数据故障类型基本相同, 表明ML-GAN模型基学习器仅需要使用30条支持集数据微调就可达到较好的数据生成效果, 降低了GAN模型对于数据集大小的需求, 实现了小样本数据的快速生成.

4.4 故障分类实验

为了验证第3节生成数据的有效性, 本节实验将第3节生成的故障数据与真实数据进行混合, 并利用实验室已有模型进行训练, 验证生成数据能够提高分类器的分类性能.

实验室已有分类器采用的是lightGBM, 其超参数设置如下, 学习率 $l = 0.001$ , 最大树深度max_depth=8, 最大叶子数num_leaves=64, bagging_fraction=0.8, lambda_l1=0.1, lambda_l2=0.2. 训练集中, 每类数据分别有Num=100条, 序列长度SeqLen=30包含有真实数据和生成数据. 真实数据和生成数据的混合比例设置为0:1、3:7、5:5、7:3、1:0.

实验结果如表3所示, 由实验结果可知, 当正常数据与生成数据混合比例为7:3时, 分类准确率最高, 较仅采用正常数据高2.7%. 当混合比例超过3:7时, 分类准确率开始下降. 仅采用生成数据时作为训练数据的分类准确率最低为72.7%, 说明生成数据不具有较为准确的分类边界, 但生成数据依然学习到了每种故障的数据特性. 由实验结果可知, 少量生成数据可以提高分类准确率, 当生成数据较多时将导致分类性能下降, 这是由于生成数据不具有较为明显的分类边界, 少量生成数据可以作为分类边界的补充, 大量生成数据将会模糊分类边界, 致使分类性能下降.

5 结论与展望

本文提出一种基于元学习的小样本数据生成算法ML-GAN, 该算法目标是在各数据生成任务上训练一个通用的GAN模型, 确定模型最优初始化参数. 由于训练结果是一组最优初始化参数, 因此可以利用少量样本数据和较少的迭代次数微调通用模型, 自适应输入数据, 从而获取多个特异性生成器, 增强数据的多样性. 该算法有效降低了GAN对数据集大小的要求, 实现了小样本数据的高质量生成.

ML-GAN方法还存在着一些不足之处, 例如噪声的选择与数据生成质量密切相关, 又例如前后时间步数据的因果关系影响. 未来我们将会对ML-GAN进行下一步的优化工作, 引入故障特征的时序性, 控制噪声生成更为真实的数据.