2. 浙江远图互联科技股份有限公司, 杭州 310012
2. Zhejiang Yuantu Internet Technology Co. Ltd., Hangzhou 310012, China
随着当前居民医疗需求的迅速增长[1], 智慧医疗成为大势所趋. 如何通过信息化手段提高医疗管理效率、提升医疗服务质量和安全, 已成为医疗领域最关注的焦点. 流水量是衡量一家医院经营、管理水平的重要指标之一, 准确高效的预测流水数据的长期变化能够为医院的资源分配、工作调度等提供依据, 提高医院资源利用率. 流水量是一种典型的时间序列数据, 可以应用时间序列预测方法进行研究.
时间序列预测方法按照不同研究阶段可以归纳为3类: 传统时序预测方法、基于浅层机器学习的时序预测方法和基于深度学习的时序预测方法.
传统时序预测方法的典型代表为自回归(AutoRegressive, AR)模型、滑动平均(Moving Average, MA)模型、自回归-滑动平均(AutoRegressive Moving Average, ARMA)模型[2]. AR模型用时间序列中的过去值的线性组合加误差项来表示当前值, MA模型用随机噪声的线性组合加误差项来表示当前值, ARMA模型是AR模型和MA模型的结合. 这3种模型都以时间序列平稳为前提, 当时间序列不平稳时, 需引入差分方法[3]使序列变为平稳序列, 即自回归-差分-滑动平均模型[2].
传统时序预测方法受限于固定的模型框架, 且几乎所有模型都是线性的. 但现实中时序数据常常表现为非线性特性, 线性模型无法很好的拟合非线性数据的变化趋势, 使得传统时序预测方法对此类数据的预测效果有限. 随着机器学习算法的发展, 越来越多的机器学习算法被应用于时序预测中, 如支持向量机、贝叶斯算法、各种浅层神经网络等, 机器学习算法能够较好的处理非线性问题. 文献[4]使用神经网络提取特征, 然后使用支持向量机来预测汇率变化, 同时对不同的支持向量机的核函数进行了比较. 文献[5]使用贝叶斯算法来推断金融时间序列数据的波动性从而实现时序预测. 文献[6]提出了一种基于人工神经网络的模型用于海洋涛动指数和海面温度的预测.
基于机器学习的时序预测方法在处理具有高维数的大数据的能力有限, 并且无法实现复杂的功能[7]. 随着深度学习的兴起, 越来越多的深度学习网络被应用到时序预测中. 多层感知器(Multi-Layer Perceptron, MLP)是最早开发的人工神经网络之一, 与浅层网络的区别在于可以包含更多的层, 主要由3层组成: 输入层、隐藏层和输出层. 每个隐藏层具有非线性的激活函数. 为更好的对序列数据进行处理, 20世纪80年代提出了循环神经网络(Recurrent Neural Network, RNN), RNN具有记忆性, 对序列的非线性特征进行学习时具有一定的优势, RNN与普通神经网络的区别在于神经元的输出取决于当前的输入和先前的输入数据. 为了解决RNN只能学到短期依赖关系, 无法学习长时间跨度的非线性关系的问题, 1997 年, Hochreiter和Schmidhuber提出了长短期记忆网络(Long Short-Term Memory, LSTM)[8]. 由于其采用3个门控控制输入、记忆和输出状态的选择, 因此LSTM可以有效的处理和预测长时间依赖的时间序列. 2006年, Hinton等[9]提出了深度置信网络(Deep Belief Network, DBN), DBN通过堆叠受限玻尔兹曼机组成, 通过预训练结合反向传播更新网络参数, 具有更高的精度, 能够有效运用于多维非线性序列的拟合. 2018年, Bai等[10]提出了时间卷积网络(Temporal Convolutional Network, TCN), TCN使用因果卷积提取时序特征, 使用扩张卷积增大感受野, 使用残差卷积加快反馈与收敛. 与传统RNN相比, TCN在参数量上大幅减少, 在结构上更加简洁明了. 文献[11]使用循环神经网络来对空气污染进行预测. 文献[12]提出了一种多层网格搜索的LSTM预测模型. 文献[13]采用基于DBN的模型结构来对交通流进行预测. 文献[14]通过使用TCN网络结构提取数据的时间特征用于交通预测, 取得了较好的应用效果.
现有的医院流水预测方法大多使用ARIMA模型或简单人工神经网络模型, 这些模型只能简单地把握数据的浅层特征, 对于复杂结构的流水数据, 无法挖掘数据的前后大跨度信息, 对数据特征的把握不够全面, 导致模型预测的准确率和效率不佳. 基于以上分析, 为进一步提高医院流水预测模型的准确率和效率问题, 针对流水数据具有长、短期特征、非线性和非平稳性的特点, 本文提出了一种基于时域卷积、残差结构和注意力机制的时序预测模型(A-TCNN). 本文主要的创新点如下: (1)引入时域卷积提取时间关联特征, 残差结构加快网络收敛以及缓解网络深度增加带来的梯度消失问题, 通过使用不同的残差时域卷积模块分别提取时间序列的长、短期特征; (2)引入注意力机制加强模型中对输出影响较重的参数的权重; (3)所提算法在实际医院流水数据集进行测试验证, 与常规网络对比, 比较多种多步预测策略, 证明了本文所提模型的有效性.
2 算法理论基础 2.1 时域卷积卷积神经网络是LeCun等[15]在1998年提出的一种神经网络模型, 它利用卷积层处理多维图像输入, 是一种应用于计算机视觉领域的模型.
卷积层(图1)是卷积神经网络模型的基础, 通过将输入图像与卷积核进行卷积运算来提取输入图像的局部特征, 通过卷积的权重共享来降低参数的数量.

|
图 1 卷积层操作过程 |
时域卷积是一维卷积的一种应用, 将输入按照时间进行卷积, 即在
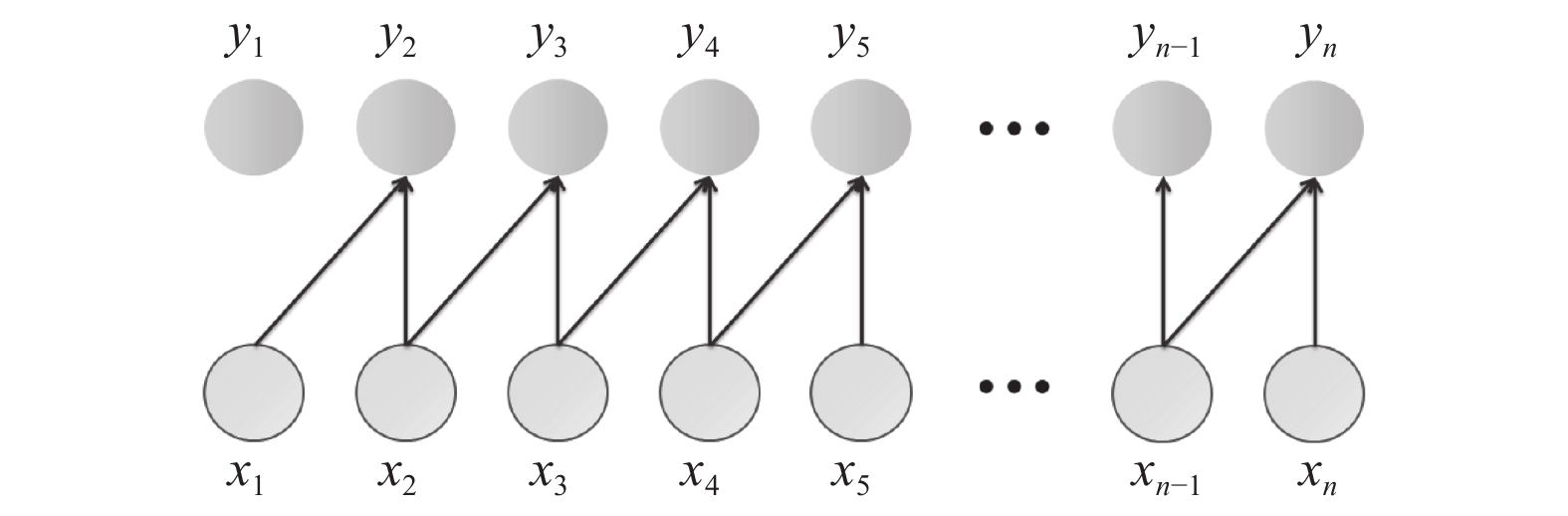
|
图 2 时域卷积 |
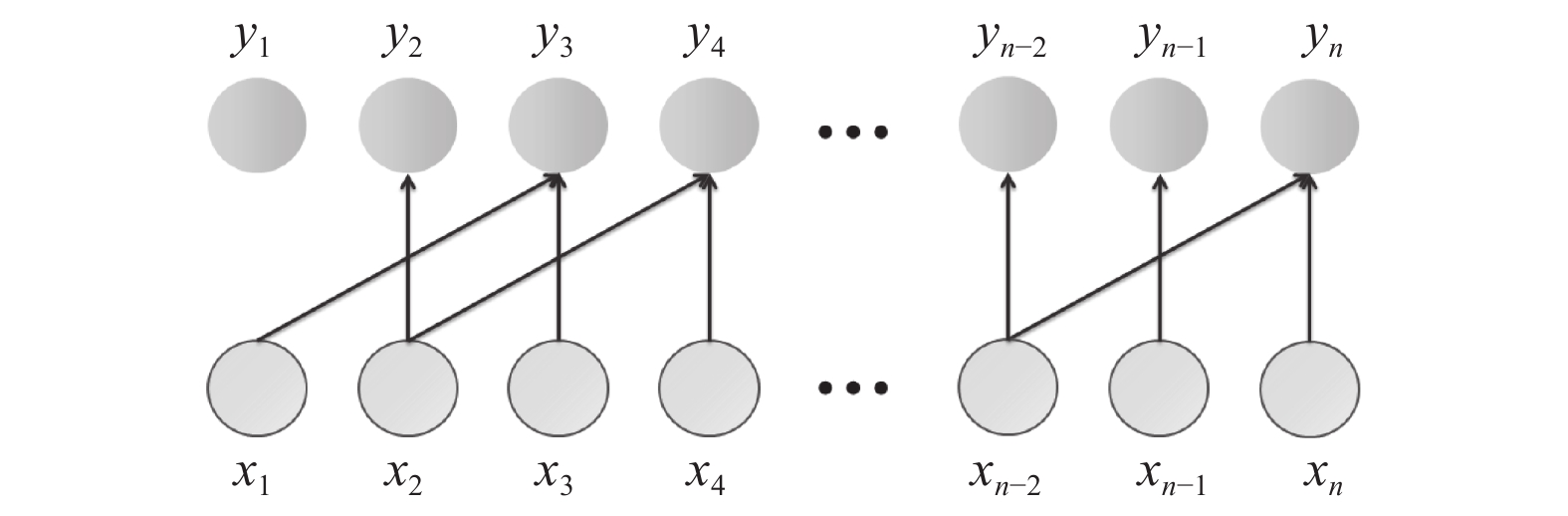
|
图 3 时域膨胀卷积 |
时域卷积的计算公式如式(1)所示.
| ${y_t} = \sum\limits_{k = 1}^m {{\omega _{t - p\times(k - 1), k}}\times{x_{t - p\times(k - 1)}}} $ | (1) |
其中,
注意力机制(Attention Mechanism, AM)[16]通过构建一个注意力矩阵, 使神经网络在训练过程中关注重点特征, 从而降低其他低影响特征的权重. 其计算公式如式(2)所示.
| $Attention(Q, K, V) = softmax\left(\frac{{Q{K^{\rm{T}}}}}{{\sqrt {{d_k}} }}\right)V$ | (2) |
其中,
时序预测可描述为: 给定时序数据
常见的时序预测方法是单步预测(single), 即用长度
针对现有时序预测模型对非线性、非平稳性的数据预测效果不佳, 为进一步提高预测模型的准确率和效率问题, 考虑时域卷积对于提取时间关联特征的有效性和参数的轻量化, 残差结构能够加快网络收敛以及缓解网络深度增加带来的梯度消失问题, 以及注意力机制能够加强模型中对输出影响较重的参数的权重, 本文提出了一种基于时域卷积、残差结构和注意力机制的时序预测模型(A-TCNN). 模型(如图4所示)包含残差时域卷积层、注意力层、融合层和全连接层.
| 表 1 多种预测策略的数学表达 |

|
图 4 A-TCNN模型结构 |
第1层为输入层, 输入向量为给定长度的时间序列数据:
| $X = {({x_{t - d + 1}},{x_{t - d + 2}},\cdots,{x_t})^{\rm{T}}}$ | (3) |
其中,
第2、3层为残差时域卷积层, 共4个残差卷积模块, 每个残差卷积模块包含一个普通卷积Conv和一个时域卷积Temporal Conv, 时域卷积采用不同的膨胀系数
| ${H_{11}} = ({\omega _{c1}}*X + {b_{c1}}) + ReLU({\omega _{t1}}*X + {b_{t1}})$ | (4) |
| ${H_{12}} = ({\omega _{c2}}*X + {b_{c2}}) + ReLU({\omega _{t2}}*X + {b_{t2}})$ | (5) |
| $\begin{split} \\ {H_{21}} = ({\omega _{c3}}*X + {b_{c3}}) + ReLU({\omega _{t3}}*X + {b_{t3}}) \end{split}$ | (6) |
| ${H_{22}} = ({\omega _{c4}}*X + {b_{c4}}) + ReLU({\omega _{t4}}*X + {b_{t4}})$ | (7) |
其中,
第4层为注意力层:
| ${Q_1} = {\omega _{q1}}*{H_{21}}$ | (8) |
| ${K_1} = {\omega _{k1}}*{H_{21}}$ | (9) |
| ${V_1} = {\omega _{v1}}*{H_{21}}$ | (10) |
| ${H_{31}} = softmax\left(\frac{{{Q_1}K_1^{\rm{T}}}}{{\sqrt {{d_{k1}}} }}\right){V_1}$ | (11) |
| ${Q_2} = {\omega _{q2}}*{H_{22}}$ | (12) |
| ${K_2} = {\omega _{k2}}*{H_{22}}$ | (13) |
| ${V_2} = {\omega _{v2}}*{H_{22}}$ | (14) |
| ${H_{32}} = softmax\left(\frac{{{Q_2}K_2^{\rm{T}}}}{{\sqrt {{d_{k2}}} }}\right){V_2}$ | (15) |
其中,
第5层为拼接层, 将前一层得到的两个输出对时间维度进行拼接:
| ${H_4} = concatenate({H_{31}},{H_{32}})$ | (16) |
第6层为全连接层, 得到输出值:
| $Y = {\omega _y}*{H_4} + {b_y}$ | (17) |
其中,
模型采用多层残差结构的时域卷积, 能够有效的对数据的长期和短期关系特征进行提取; 通过注意力机制加强参数的权重, 得到输入数据的特征向量表示; 经过全连接层得到精度较高的输出结果.
模型选择以均方根误差作为目标函数, 用Adam优化算法对模型参数进行更新.
4 实验及结论 4.1 实验仿真为验证算法效果和鲁棒性, 使用杭州市某医院2019年全年的实际流水数据进行测试. 原始数据为百万数量级的每人次消费金额, 现从门诊消费金额和全部消费金额两个角度对数据进行整合, 得到门诊流水和全部流水两个数据集, 两个数据集均表现为非线性、非平稳性, 分别对每个数据集按天进行聚合, 同时对数据进行窗口滑动滤波处理消除随机噪声干扰, 选择前11个月的数据为训练集, 后1个月的数据为测试集. 选择时间步长d为14, 即用14天的时间进行预测, 单输出时预测1天的值(H = 1), 多输出时预测30天的值(H = 30), 分段输出时每段预测6天的值(
本文采用ARIMA模型、MLP网络、LSTM网络、TCNN网络和A-TCNN网络对上述数据进行预测, 分别对5种模型的单步预测和5种多步预测策略的结果进行对比. 其中, MLP网络的结构及参数如图5所示; LSTM网络的结构及参数如图6所示; TCNN网络的结构如图7所示, 该网络为不添加注意力层的A-TCNN网络, 其余参数与图4算法相同. 采用均方根误差(RMSE)和
| $RMSE = \sqrt {\frac{1}{m}\sum\limits_{i = 1}^m {{{({{\hat y}_i} - {y_i})}^2}} } $ | (18) |
| ${R^2} = 1 - \frac{{\displaystyle\sum\nolimits_{i = 1}^n {{{({y_i} - {{\hat y}_i})}^2}} }}{{\displaystyle\sum\nolimits_{i = 1}^n {{{({y_i} - {{\bar y}_i})}^2}} }}$ | (19) |
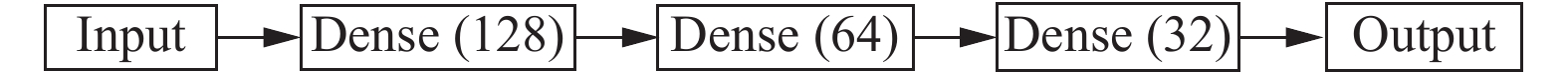
|
图 5 MLP网络结构 |

|
图 6 LSTM网络结构 |

|
图 7 TCNN网络结构 |
4.2 结果分析及讨论
从表2倒数第2行两个数据集单步预测策略的平均指标来看, 与MLP网络相比, TCNN网络和A-TCNN网络的平均均方根误差降低和平均R2分数提升效果不明显; 与LSTM网络相比, TCNN网络的平均均方根误差降低了25.9%, 平均R2分数提升了6.6%; A-TCNN网络的平均均方根误差降低了32.3%, 平均R2分数提升了8.2%.
| 表 2 5种网络多种预测策略在医院流水两个数据集的测试结果对比 |
从最后一行两个数据集多步预测策略的平均指标来看, 与ARIMA模型相比, TCNN网络的平均均方根误差降低了20.8%, 平均R2分数提升了10.8%, A-TCNN网络的平均均方根误差降低了30.0%, 平均R2分数提升了15.0%; 与MLP网络相比, TCNN网络的平均均方根误差降低了18.2%, 平均R2分数提升了9.6%, A-TCNN网络的平均均方根误差降低了27.7%, 平均R2分数提升了13.8%; 与LSTM网络相比, TCNN网络的平均均方根误差降低了23.7%, 平均R2分数提升了14.9%, A-TCNN网络的平均均方根误差降低了32.6%, 平均R2分数提升了19.2%.
对比分析5种网络的不同预测策略: 由于Recursive策略和DirRec策略将模型预测得到的值应用于下一步的预测, 使得每次预测的误差会累积, 因此, 随着预测次数的增加, 误差会越来越大, 所以这两种策略的效果比Single策略和Direct策略差. 同时, Direct策略和DirRec策略需要建立多个模型, 因此当预测步长较长时所花费的时间也成倍增加. MIMO策略由于使用较小的输入步长预测较大的输出步长, 使得输入含有的信息量不足, 导致预测效果较差. DIRMO策略是一种较为折中的策略, 无需训练大量模型的同时, 也能保证准确率. 纵观全部结果可知: 在多步预测的策略上, 基于DIRMO策略的A-TCNN网络取得最佳预测性能, 在门诊流水数据集上的均方根误差为0.190, R2分数为0.903; 在全部流水数据集上的均方根误差为0.162, R2分数为0.940.
以上结果表明, A-TCNN网络使用时域卷积来对医院流水数据进行处理, 能够有效的提取时间关联特征, 加强模型对非线性、非平稳数据的信息挖掘能力, 减少参数的数量级, 以及使用残差结构能够加快网络的收敛速度. 与传统ARIMA模型、MLP网络和LSTM网络相比, 预测能力和效果得到了明显的提升; 同时进一步引入注意力机制来加强影响参数的权重, 优化模型参数, 再次增强模型的预测能力.
5 结束语针对现有模型对时序预测的准确性和效率问题, 本文提出了一种融合时域卷积、残差结构和注意力机制的预测模型, 通过残差时域卷积层来对时间序列数据的长、短期特征进行提取, 同时引入注意力机制强化模型参数, 进一步提升模型的预测能力. 在实际医院流水数据集上, 与传统ARIMA模型、MLP网络和LSTM网络相比, 在参数量上能够大幅减少, 同时能够减少模型的训练时间以及硬件资源的消耗; 在预测效果上, 对于多种多步预测策略都有不同程度的提升, 验证了该模型的有效性. 该模型能够有效的对医院流水数据进行长期预测, 有较好的实际应用效果, 能够为医院的决策提供较好的参考. 在未来研究中, 考虑将其他特征(例如天气、节假日等)引入输入中, 并优化模型结构, 进一步提升模型的预测能力和准确性.
| [1] |
李忠萍, 王建军, 单巍. 基于分级诊疗体系的下转决策及支付机制研究. 系统工程理论与实践, 2019, 39(8): 2126-2137. DOI:10.12011/1000-6788-2018-0055-12 |
| [2] |
Box GEP, Jenkins GM, Reinsel GC. Time Series Analysis: Forecasting and Control. 3rd ed. Englewood Cliffs: Prentice Hall, 1994. 2–45.
|
| [3] |
Rao JNK, Tintner G. On the variate difference method. Australian & New Zealand Journal of Statistics, 1963, 5(3): 106-116. DOI:10.1111/j.1467-842X.1963.tb00289.x |
| [4] |
Moradi A, Alizadeh M, Samadi M, et al. Understanding the characteristics of financial time series through neural network and SVM approaches. International Journal of Electronic Finance, 2019, 9(3): 202-216. DOI:10.1504/IJEF.2019.10020409 |
| [5] |
Van Gestel T, Suykens JAK, Baestaens DE, et al. Financial time series prediction using least squares support vector machines within the evidence framework. IEEE Transactions on Neural Networks, 2001, 12(4): 809-821. DOI:10.1109/72.935093 |
| [6] |
Pérez-Chavarría MA, Hidalgo-Silva HH, Ocampo-Torres FJ. Time series prediction using artificial neural networks. Ciencias Marinas, 2002, 28(1): 67-77. DOI:10.7773/cm.v28i1.205 |
| [7] |
Bengio Y, LeCun Y. Scaling learning algorithms towards AI. Large-scale Kernel Machines, 2007, 34(5): 1-41. |
| [8] |
Hochreiter S, Schmidhuber J. Long short-term memory. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [9] |
Hinton GE, Osindero S, Teh YW. A fast learning algorithm for deep belief nets. Neural Computation, 2006, 18(7): 1527-1554. DOI:10.1162/neco.2006.18.7.1527 |
| [10] |
Bai SJ, Kolter JZ, Koltun V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv: 1803.01271, 2018.
|
| [11] |
范竣翔, 李琦, 朱亚杰, 等. 基于RNN的空气污染时空预报模型研究. 测绘科学, 2017, 42(7): 76-83, 120. DOI:10.16251/j.cnki.1009-2307.2017.07.013 |
| [12] |
王鑫, 吴际, 刘超, 等. 基于LSTM循环神经网络的故障时间序列预测. 北京航空航天大学学报, 2018, 44(4): 772-784. DOI:10.13700/j.bh.1001-5965.2017.0285 |
| [13] |
冯微, 陈红, 张兆津, 等. 基于GBRBM-DBN模型的短时交通流预测方法. 交通信息与安全, 2018, 36(5): 99-108. DOI:10.3963/j.issn.1674-4861.2018.05.013 |
| [14] |
Yu B, Yin HT, Zhu ZZ. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. Proceedings of the 27th International Joint Conference on Artificial Intelligence. Washington, DC, USA. 2018. 3634–3640.
|
| [15] |
LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 |
| [16] |
Mnih V, Heess N, Graves A, et al. Recurrent models of visual attention. Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal, QC, Canada. 2014. 2204–2212.
|
| [17] |
Taieb SB, Bontempi G, Atiya AF, et al. A review and comparison of strategies for multi-step ahead time series forecasting based on the NN5 forecasting competition. Expert Systems with Applications, 2012, 39(8): 7067-7083. DOI:10.1016/j.eswa.2012.01.039 |
| [18] |
Cheng HB, Tan PN, Gao J, et al. Multistep-ahead time series prediction. Proceedings of the 10th Pacific-Asia Conference on Knowledge Discovery and Data Mining. Singapore. 2006. 765–774.
|
| [19] |
Hamzaçebi C, Akay D, Kutay F. Comparison of direct and iterative artificial neural network forecast approaches in multi-periodic time series forecasting. Expert Systems with Applications, 2009, 36(2): 3839-3844. DOI:10.1016/j.eswa.2008.02.042 |
| [20] |
Sorjamaa A, Lendasse A. Time series prediction using dirrec strategy. Proceedings of the 14th European Symposium on Artificial Neural Networks. Bruges, Belgium. 2006. 143–148.
|
| [21] |
Bontempi G, Taieb SB. Conditionally dependent strategies for multiple-step-ahead prediction in local learning. International Journal of Forecasting, 2011, 27(3): 689-699. DOI:10.1016/j.ijforecast.2010.09.004 |
| [22] |
Taieb SB, Bontempi G, Sorjamaa A, et al. Long-term prediction of time series by combining direct and MIMO strategies. Proceedings of 2009. International Joint Conference on Neural Networks. Atlanta, GA, USA. 2009. 3054–3061.
|
 2021, Vol. 30
2021, Vol. 30



