油井在开发和采油过程中会出现某些对油井的常规生产造成干预的现象, 这种现象被称作油井结蜡, 严重时其会造成油流道堵塞, 导致油井开采过程中出油量降低. 更为严重时, 会造成井筒路径被卡死等生产性问题, 甚至会造成油井的停产. 随着油田信息化的提高, 数据采集传感器被广泛应用于油井中, 因此对于每个油井都会产出和记录海量的实时相关数据, 而目前这些数据没有真正利用起来. 影响井筒结蜡的因素很多, 例如原油含蜡系数、载荷、位移、油温、压力等数据, 目前的方法主要依靠示功图等方法对结蜡进行监测分析, 而生成示功图的数据会有大量间接误差导致图形畸变、不正确, 同时人工对示功图的判断和解读会不够全面和精准, 造成对结蜡情况产生较大误判. 所以建立一个以石油专业知识为背景的科学与智能化的油井结蜡预测模型, 提前准确地识别结蜡现象, 降低油田的风险和损失拥有显而易见的价值.
1 相关工作目前大量学者通过现场的操作以及应用, 在对于井筒中结蜡情况的预测模型的构建方面取得了不错的成绩, 并将其顺利应用于油田的生产中. 王利中[1]将数学与石油知识结合, 实现了对于油井结蜡快慢和结蜡形成周期长短的计算; 另外对于实际工作的油井还需要考虑其他现实因素如管内侧本身就沉淀过的结蜡和抽油杆上经过长期工作挺溜的蜡. 孙百超等[2]在石蜡沉积机理的基础上, 结合实际生产中石油油温高、粘度小、热流强度大等特点, 将热、动力学结合, 模拟出了管线长度与结蜡厚度的分布关系模型. 但此模型采用的许多常数仅对个别油管有效, 而对与不同的油流和油井, 参数需要重新进行计算, 不具有普适性. Gawas等提出了单相湍流条件下的沉积预测模型, 对动态循环沉积数据进行了分析之后提出了新的剪切效应关系[3]. 最近几年, 人工智能技术如火箭般突破, 使其迅速成各行业各领域应用的焦点, 在油田领域, 段友祥等[4]利用人工智能的分类算法, 建立了异常工况诊断模型, 对油井工况中的结蜡行为进行判别和诊断; Manshad 等[5]利用人工智能预测算法, 建立了储层流体结蜡量预测模型. 然而, 石油行业的数据集一般是不平衡数据. 针对油井结蜡的问题, 在这种不平衡数据集中, 各类基础以及传统的机器学习算法大多仍局限于均衡的样本训练, 会导致算法将更多的精力用于多数类分类, 从而使得少数类分类错误率较高, 此时即使模型整体的分类结果较好, 但是实际上的结蜡分析效果不理想.
针对类似上述问题, 在机器学习相关的领域出现了许多针对不平衡数据处理的研究方法. 解决不平衡数据的分类问题, 大抵可以归类于两种办法, 一种方法是基于数据集的数据本身, 另一种方法是脱离数据集, 尝试对算法进行创新. 对于数据本身的方法, 大多是采取对不平衡数据中的少数类或多数类样本分别实现过采样或欠采样, 去提升数据集的均衡水平, 使分类器可以在相对平衡的数据集上进行学习. Chawla等[6]突破性得提出了一种SMOTE 的方法, 计算所有的少数类样本情况, 据此再构造一定数量的相似的少数类样本, 完成过采样扩充数据集. 而SMOTE算法所暗藏的问题是没有对少数类样本之间邻近样本的不同进行思索, 对它们以同样的权重进行合成, 可能会造成较大重复. Kermanidis等[7]对于数据不平衡问题采取了一种单边抽样的方法, 并利用抽样技术使得样本分类变得更加准确. Gong等[8]使用一种新的循环神经网络来对少数类样本进行过采样, 使得最后的分类成果十分出色. Giraldo-Forero等提出了基于距离度量的SMOTE类算法[9]. de Souto等[10]提出了一种新的多数类样本欠采样方法, 通过对两种算法Tomek links和CNN进行结合, 最终对分类结果产生了不错的提升. Laurikkala[11]提出了范围清算NCL (Neighborhood CLeaning rule)的欠采样算法. 算法层面主要通过将自己所提出的创新或结合融会于一些基础和传统的机器学习的方法及分类模型, 从而对不均衡数据的分类从另一层面产生提高和进步. Thanathamathee等[12]将自己提出的处理边界数据的方法与传统的AdaBoost算法融会, 此措施同样属于样本的过采样方法的一种. Liang等[13]通过在不平衡数据中使用bagging算法, 对多个底层的分类器进行屡次采样, 提高了二分类模型的预测效果, 也相当有效地提高了模型的分类效果. 徐丽丽等提出了一种基于集成学习的不平衡数据处理方法, 通过将各类别以不同比例进行加权并且将模糊聚类和加权支持向量机模型WSVM结合. 但此方法的缺点是降低不平衡数据集误分类的损失相对较大[14].
基于上述问题, 本文引入ADASYN来代替SMOTE算法的过采样作用, 并改善了SMOTE算法生成新样本中的“傻瓜”操作; 引入ENN进行欠采样来删除大部分邻居中的样本都和自己本身不属于一类的多数类样本, 删除了少部分非常相似的多数类样本, 并将新的采样算法与随机森林算法相结合, 提出ADASYN-ENN-RF (AERF)算法模型来预测油井的结蜡情况. 多组实验结果表明, 本文采样后的样本更能代表数据集, 本文提出的采样算法与所选分类算法的结合对现有的算法进行了提升, 具有更好的分类效果, 证明了此算法的可行和提升.
2 ADASYN-ENN-RF算法 2.1 ADASYN算法ADASYN算法又叫自适应合成采样算法[15]. ADASYN专门针对了SMOTE的缺点并加以改进, 它对少数类样本不再同权重对待, 并利用少数类样本的密度分布来计算少数类样本生成的数量, 使学习困难的少数类样本生成更多的合成样本; 它能根据样本的分布来进行采样, 从而提高了少数类样本在边缘区域的比例, 可以缓解边缘区域类分布不平衡的问题, 来增强分类模型的学习能力. 既能有效地克服SMOTE在生成少数类样本中的盲目性, 又能较好地改善 SMOTE在处理边缘区域对象上的局限性, 从而合理的使样本比例达到相对均衡的效果, 缓解数据不平衡的问题. 因而在提升不平衡样本学习能力上具有非常显著的优势. ADASYN的重点是取得一个概率分布ri, 然后根据ri计算需要构造的样本个数.
对于训练集T包含p个样本{xi, yi},i=1, 2, 3,…, p, 其中xi是n维特征空间X的一个样本, yi∈Y={0, 1}代表不同类别, 其中y=1代表多数类样本, y=0代表少数类样本. 它们的数量分别用pl和ps表示. 所以有ps ≤ pl且pl+ps=p.
算法流程如算法1.
算法1. ADASYN算法
1) 计算不平衡度d = ps / pl, d∈(0, 1];
2) 计算应该构造的样本个数
3)使用欧式距离计算所有少数类样本的邻近样本数量, 设邻近样本为m个, △i为m个邻近样本中多数类样本的个数, 设比值ri为ri = △i/ m, ri∈[0, 1];
4)在3)中获得所有少数类样本的概率分布ri, 用
5)通过公式获得所有少数类样本需要构造的样本个数:
6)在任何一个需要构造的少数类样本周围都有m个邻居, 选取其中一个, 新样本构造计算如下:
7) 持续步骤6)构造样本, 当达到步骤5)所要求构造的样本数量即可停止.
2.2 ENN算法ENN算法即最近邻规则欠采样算法[16], 该算法根据多数类样本的邻近样本是否大部分和其本身一致来对其判断是否进行欠采样, 当它周围的样本中和它类别不同的样本占据主导地位时, 就可以判定此样本点是存在问题的样本, 处理方法为删除. 以邻近样本数量K=5为例子, 具体的ENN步骤如下:
设少数类为S, 多数类为L, 多数类样本点记为p.
算法2. ENN算法
1)从p的邻近样本中, 计算找出5个最近的样本;
2)对于每个点p, 如果5个最近样本中有3个或3个以上的样本点不是多数类样本L, 就删除该样本点, 反之即无操作;
3)遍历计算, 直到没有此种多数类样本即可停止.
2.3 ADASYN-ENN-RF算法ADASYN是基于SMOTE算法的一种改进的算法, 改进了SMOTE在生成少数类样本中的盲目性, 又能较好的改善 SMOTE 在处理边缘区域对象上的局限性. 但只基于ADASYN的RF算法, 利用的是已经存在的少数类样本信息来增加样本数量, 没有产生任何新的不同的知识, 在训练样本严重不平衡时, 可能会因为少数类样本欠缺空间代表性导致分类器学习的决策域变小, 从而出现过学习. ENN算法改善了随机欠采样不考虑每个多数类样本不同且独立的近邻分布, 造成可能会误删某些重要的多数类样本信息的问题. 但只基于ENN的RF算法因为多数类样本本身远多于其他, 它们之间往往也互相紧邻, 所以仅能删除非常有限的多数类样本, 并且可能会忽略掉许多多数类样本中的有用信息, 对不平衡数据集提升有限. 所以, 本文将上述两种采样方法相结合实现数据均衡, 并提出一种基于ADASYN-ENN和Random Forest相结合的算法(AERF).
算法的主要思想是:
1)将不平衡数据集通过ADASYN算法增加少数类样本, 调整ADASYN算法中的β值来确定合成后的新数据集的样本平衡度, β=1时, 代表多数类样本和少数类样本数量一样, 本文中取β=0.5.
2)将1)步中生成的新的数据集, 通过ENN算法减少多数类样本, 最终生成一个多数类样本和少数类样本数量一样的新数据集.
3)将处理完的数据集利用随机森林算法来进行分类, 调整参数使其分类性能达到最佳.
基于AERF的算法如图1所示.
算法描述:
对于训练集T包含p个样本{xi, yi}, i=1, 2, 3,···, p, 其中xi是n维特征空间X的一个样本, yi∈Y={0, 1}代表不同类别, 其中y=0为少数类样本即结蜡数据, y=1为多数类样本即非结蜡数据. 它们的数量分别用ps和pl表示. 所以有ps ≤ pl且pl+ps=p.

|
图 1 基于AERF的算法流程 |
算法步骤如算法3.
算法3. AERF算法
1)计算不平衡度d = ps / pl, d∈(0, 1];
2)计算应该构造的结蜡样本个数
3)使用欧式距离计算所有结蜡样本的邻近样本数量, 设邻近样本为m个, △i为m个邻近样本中属于非结蜡样本的个数, 记比例为ri为ri = △i/ m, ri∈[0, 1];
4)对ri进行标准化:
5)计算出所有结蜡样本需要合成的数据样本:
6)对结蜡样本生成的数据样本
7)使用ENN算法对处理过的样本集进行处理. 找出新样本集中的每个非结蜡样本的距它最近的5个样本点. 当在5个最近样本中有3个及其以上为结蜡样本, 则可判断此样本与周围大部分近邻样本不同, 视该非结蜡样本为噪声样本, 从数据集中删除;
8) 调用RF算法对平衡数据集进行分类.
3 实验结果及分析 3.1 数据来源本文使用的数据集来源于胜利油田某采油厂的一百多万条抽油井生产数据. 原始的数据包括单井基础信息、示功图采集数据、示功图分析数据、油井实时数据、结蜡数据信息、油水分析数据, 数据时间范围是2018年至2019年, 其中单井基础数据主要存储井名、所属区域等信息, 示功图采集数据、示功图分析数据、油井实时数据主要记录各井每个时间点的示功图、油井实时参数, 结蜡数据信息主要对油井出现结蜡异常的情况进行了标记.
尽管以上数据时间跨度大、涵盖油井数量多、数据资源丰富, 但现实情况下提取和记录的数据依然存在以下缺陷: (1)数据存在空缺值; (2)数据存在无效值; (3)数据收集的时间有中断, 存在没有采集到数据的时间; (4)不同数据库字段命名不一致; (5)数据表中存在属性冗余等现象.
因此, 为提高抽油井结蜡预测的准确度, 在建立油井结蜡预测模型之前需要进行数据预处理.
3.2 数据预处理 3.2.1 数据清洗当示功图或油井数据中某一属性即某一列全部为空时, 对整列进行删除. 当示功图或油井数据中某时间一条数据全部为空时, 对该时间段记录进行删除. 对空缺值使用整个属性的平均值进行填补.
3.2.2 数据归一化在模型训练与分类时, 其中的连续变量如果维度不同有可能影响到整个模型的精度. 所以在此之前, 需要对这些变量进行规范化的归一化处理, 将他们全部映射到0~1中. 对于分类变量, 同样需要对其做规范化的离散化处理, 将它们全部映射到0,1的向量空间中.
设xi为来自于总体X的一个样本, 通过式(1)解决归一化, 生成新样本.
| ${x_{\rm new}} = \frac{{{x_i} - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}}$ | (1) |
对数据进行预处理过后, 数据集依然有178个特征. 许多冗余特征对模型的分类不能提供帮助甚至产生了干扰. 因此, 我们使用mutual_info_classif方法来对数据集进行特征选择, 选取15个对模型分类影响最大的特征. 最终我们将提供的结蜡数据信息中所标记为结蜡的时间, 在油井及示功图数据中将对应时间段的数据标记为1, 其他数据标记为0. 如表1所示, 繁杂的数据通过预处理过程, 构成了样本数据集, 我们从中挑选了5口井来进行实验.
3.4 实验设计本文对样本数据集采取分区实验, 所用数据集如上表所示. 实验在4核CPU、1.60 GHz主频、16 GB内存的PC机上进行, 使用Python完成了所有算法. 本文选择使用RF, SMOTE-RF, ADASYN+RF, ADASYN-ENN-KNN, ADASYN-ENN-AdaBoost, ADASYN-ENN-RF六种算法对相同的数据集进行测试, 采用十折交叉运算进行预测. SMOTE、ADASYN算法中领域值K值取5, ADASYN算法中β取0.5. 在不平衡数据集中, 采用Accuracy作为评价指标不能客观的展示出模型的分类效果, 会倾向于多数类样本. 所以针对不平衡数据集, 我们采用评价指标F-value、G-mean和recall来对分类模型做出评价.
| 表 1 数据集基本信息 |
3.5 评价指标
在分类问题中, 使用Accuracy作为分类的评价指标的多是一般的平衡数据集, 但当碰到不平衡数据集[17]时, 它的多数类少数类样本数量之差比较夸张, 所以使用Accuracy判断此类分类器的性能是不精准的. 因此, 本文采用不平衡分类中常用的评价指标F-value、G-mean和recall进行评估(本文中定义少数类为正类, 多数类为负类). 而这3种指标均由混淆矩阵计算得出. 混淆矩阵如表2所示.
| 表 2 二分类的混淆矩阵 |
表2中, TP是指样本预测和实际特征均为正; TN是指样本预测和实际特征均为负; FN是指样本实际是正预测是负; FP则与FN相反.
Recall、F-value、G-mean计算公式如下:
(1)召回率(recall)的计算公式为:
| $recall = \frac{{TP}}{{TP + FN}}$ | (2) |
(2)精确率(precision)的计算公式为:
| $precision = \frac{{TP}}{{TP + FP}}$ | (3) |
(3) F-value值为precision和
| $F {\text{-}} {{value}} = \frac{{(1 + {\beta ^2}) \times recall \times precision}}{{{\beta ^2} + recall + precision}}$ | (4) |
参数β设置为1, 如果precision和recall都高时, 很明显F-value值也会随之提升.
(4) G-mean表示算法在正确正类和正确负类的平均性能:
| $G {\text{-}} mean = \sqrt {\frac{{TP}}{{TP + FN}} \times \frac{{TN}}{{TN + FP}}} $ | (5) |
其值越大分类性能越好, 只有当正、负类样本的分类效果都比较好时, G-mean值才会高.
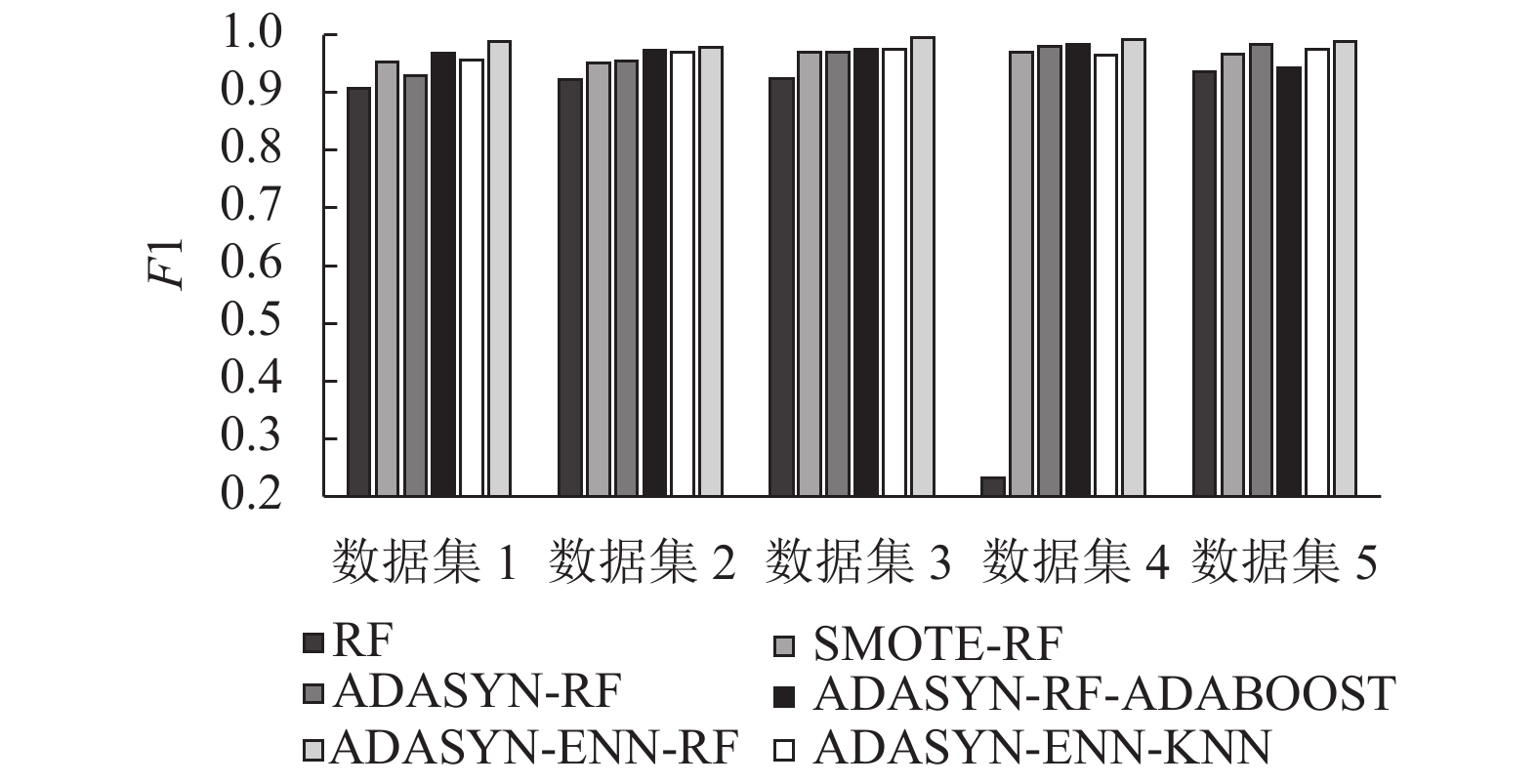
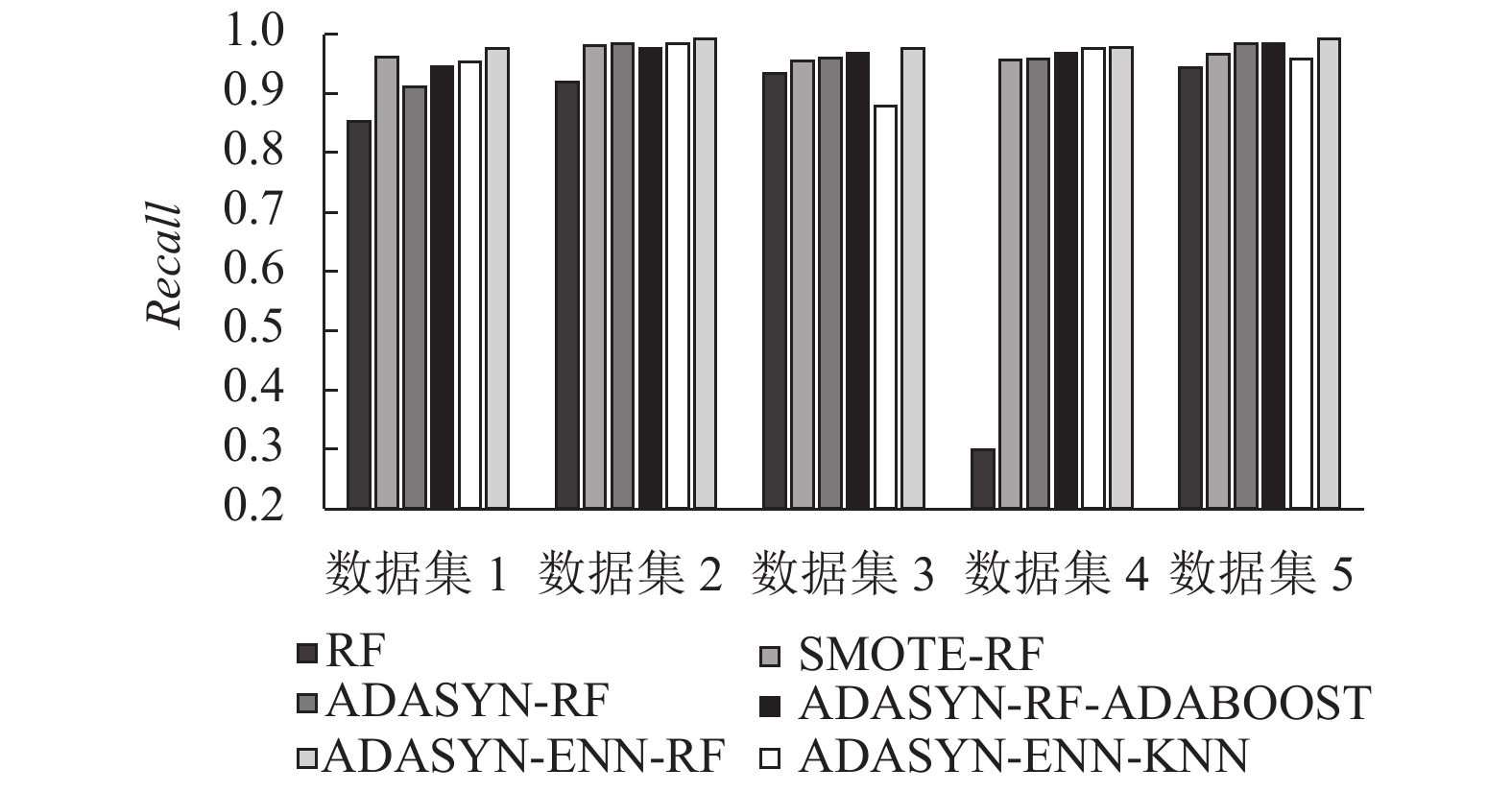
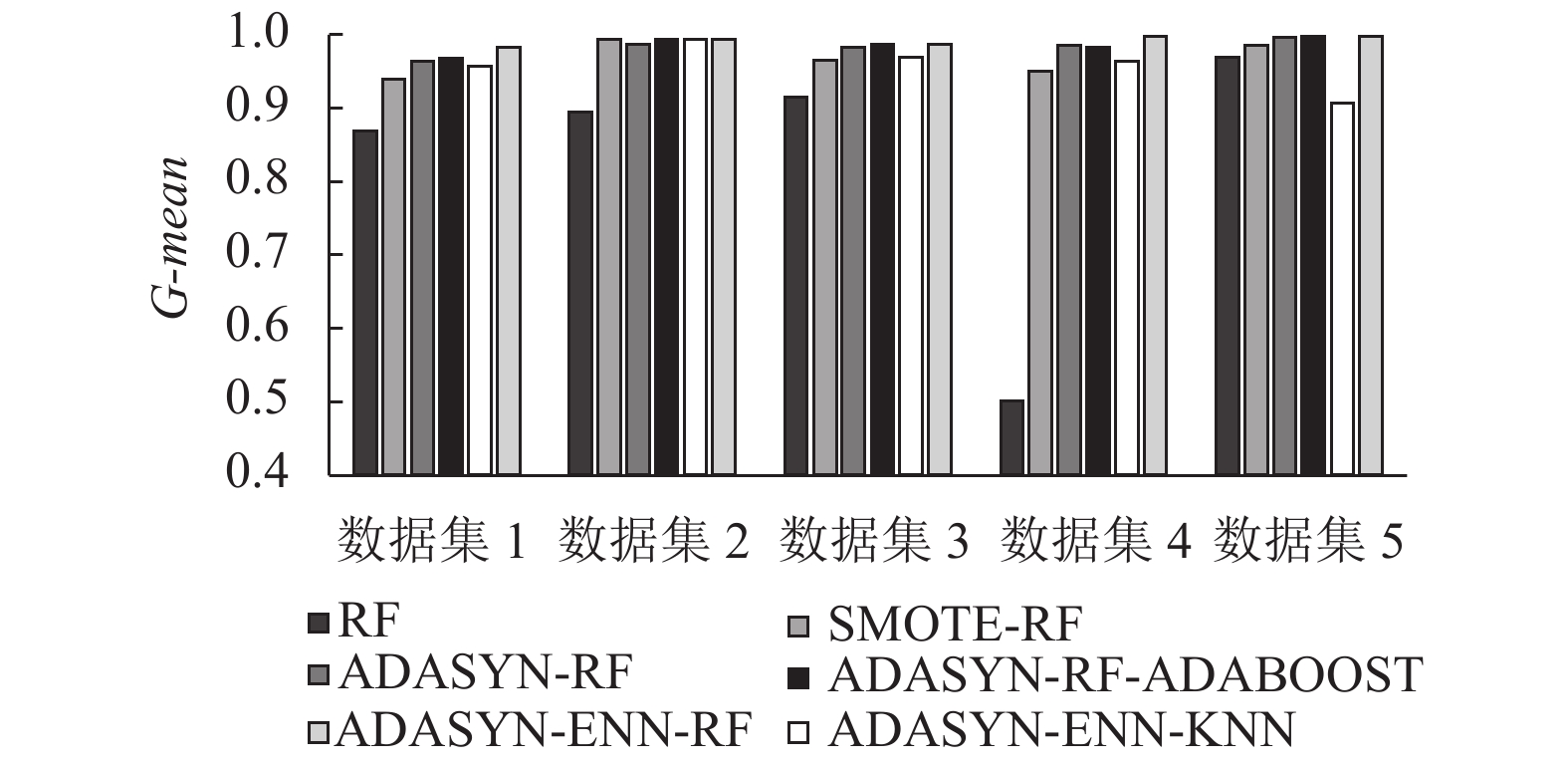
3.6 实验结果使用RF, SMOTE-RF, ADASYN+RF, ADASYN-ENN-KNN, ADASYN-ENN-RF, ADASYN-ENN-AdaBoost六种算法进行分类, 得到分类后的 F1、recall和G-mean值, 从而对不平衡数据采样方法的处理效果以及分类模型的分类效果进行比较. 结果如表3~表5所数据集进行处理的RF算法, ADASYN-ENN-RF算法在5个数据集上的3个指标均拥有5%以上的提升. 对比仅使用了单一过采样算法处理数据集的SMOTE-RF、ADASYN-RF算法, ADASYN-ENN-RF算法同样在5个数据集上的3个指标均产生至少0.1%以上的提升. 对比ADASYN-ENN-KNN, ADASYN-ENN-AdaBoost, ADASYN-ENN-RF三种算法, ADASYN-ENN-RF算法在5个数据集上最终跑出的F1值, 均至少高出了0.05%; 在5个数据集上最终跑出的recall值, 均至少高出了0.01%; 在5个数据集上最终跑出的G-mean值, 均持平或高出. 结果如图2至图4所示.
| 表 3 各个模型在5个数据集上的F1值 |
所以综合对比F1、recall、G-mean值这3个指标发现, AERF算法能够有效地处理不平衡数据集并且在分类性能上有显著的提高.
| 表 4 各个模型在5个数据集上的recall值 |
| 表 5 各个模型在5个数据集上的G-mean值 |
|
图 2 各个模型在5个数据集上的F1值对比 |
|
图 3 各个模型在5个数据集上的recall值对比 |
|
图 4 各个模型在5个数据集上的G-mean值对比 |
4 结束语
油井的运行过程中, 它的各项数据往往是极度不均衡的. 在绝大多数时间产生的都是运行正常时的样本, 而它出现问题造成结蜡的样本甚至几个月才有一次. 这很大程度增加了现在主流分类预测算法对其应用的难度. 主流算法以总体的准确性作为提升目标, 总会偏向于占比较大的类, 反而导致重要样本被忽视. 从而致使结蜡情况的出现难以被预测.
本文针对油井结蜡数据类别不平衡、判断结蜡情况不准确等问题, 提出一种AERF算法, 即使用ADASYN算法和ENN算法相结合的方法处理不平衡数据集, 再配合随机森林算法在平衡样本集中进行训练和学习, 从而得到效果优异的模型. 实验结果表明, 该算法在构造平衡数据集时更加合理, 特别是明显地提升了本来处于绝对弱势的少数类样本的影响力. 本文没有对 ADASYN算法中β参数对于算法性能的影响并且没有对更加多元化的采样方式的组合来进行研究和实验, 这是下一步的研究方向.
| [1] |
王利中. 油井结蜡速度及清蜡周期预测. 石油与矿业工程, 2003, 15(11): 54-55. |
| [2] |
孙百超, 王岳, 尤国武. 含蜡原油热输管道管壁结蜡厚度的计算. 石油化工高等学校学报, 2003, 16(4): 48-51. DOI:10.3969/j.issn.1006-396X.2003.04.013 |
| [3] |
Gawas K, Karami H, Pereyra E, et al. Wave characteristics in gas–oil two phase flow and large pipe diameter. International Journal of Multiphase Flow, 2014, 63: 93-104. DOI:10.1016/j.ijmultiphaseflow.2014.04.001 |
| [4] |
段友祥, 李钰, 孙歧峰, 等. 改进的Alexnet模型及在油井示功图分类中的应用. 计算机应用与软件, 2018, 35(7): 226-230, 272. DOI:10.3969/j.issn.1000-386x.2018.07.041 |
| [5] |
Manshad AK, Ashoori S, Manshad MK, et al. The prediction of wax precipitation by neural network and genetic algorithm and comparison with a multisolid model in crude oil systems. Petroleum Science and Technology, 2012, 30(13): 1369-1378. DOI:10.1080/10916466.2010.499403 |
| [6] |
Chawla NV, Bowyer KW, Hall LO, et al. SMOTE: Synthetic Minority Over-sampling TEchnique. Journal of Artificial Intelligence Research, 2002, 16: 321-357. DOI:10.1613/jair.953 |
| [7] |
Kermanidis K, Maragoudakis M, Fakotakis N, et al. Learning Greek verb complements: Addressing the class imbalance. Proceedings of the 20th International Conference on Computational Linguistics. Geneva, Switzerland. 2004. 1065.
|
| [8] |
Gong ZC, Chen HH. Model-based oversampling for imbalanced sequence classification. Proceedings of the 25th ACM International on Conference on Information and Knowledge Management. Indianapolis, IN, USA. 2016. 1009–1018.
|
| [9] |
Giraldo-Forero AF, Jaramillo-Garzón JA, Ruiz-Muñoz JF, et al. Managing imbalanced data sets in multi-label problems: A case study with the SMOTE algorithm. Proceedings of the 18th Iberoamerican Congress on Pattern Recognition. Havana, Cuba. 2013. 334–342.
|
| [10] |
de Souto MCP, Bittencourt VG, Costa JAF. An empirical analysis of under-sampling techniques to balance a protein structural class dataset. Proceedings of the 13th International Conference on Neural Information Processing. Hong Kong, China. 2006. 21–29.
|
| [11] |
Laurikkala J. Improving identification of difficult small classes by balancing class distribution. Proceedings of the 8th Conference on Artificial Intelligence in Medicine in Europe. Cascais, Portugal. 2001. 63–66.
|
| [12] |
Thanathamathee P, Lursinsap C. Handling imbalanced data sets with synthetic boundary data generation using bootstrap re-sampling and AdaBoost techniques. Pattern Recognition Letters, 2013, 34(12): 1339-1347. DOI:10.1016/j.patrec.2013.04.019 |
| [13] |
Liang G, Cohn AG. An effective approach for imbalanced classification: Unevenly balanced bagging. Proceedings of the 27th AAAI Conference on Artificial Intelligence. Bellevue, WA, USA. 2013. 1633–1634.
|
| [14] |
徐丽丽, 闫德勤. 不平衡数据加权集成学习算法. 微型机与应用, 2015, 34(23): 7-10. DOI:10.3969/j.issn.1674-7720.2015.23.003 |
| [15] |
He HB, Bai Y, Garcia EA, et al. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. Proceedings of 2008 IEEE International Joint Conference on Neural Networks. Hong Kong, China. 2008. 1322–1328.
|
| [16] |
Phua C, Alahakoon D, Lee V. Minority report in fraud detection: Classification of skewed data. ACM SIGKDD Explorations Newsletter, 2004, 6(1): 50-59. DOI:10.1145/1007730.1007738 |
| [17] |
李克文, 杨磊, 刘文英, 等. 基于RSBoost算法的不平衡数据分类方法. 计算机科学, 2015, 42(9): 249-252, 267. DOI:10.11896/j.issn.1002-137X.2015.09.048 |
 2021, Vol. 30
2021, Vol. 30



