2. 广西师范大学 广西多源信息挖掘与安全重点实验室, 桂林 541004
2. Guangxi Key Lab of Multi-source Information Mining and Security, Guangxi Normal University, Guilin 541004, China
流失客户通常是指在一定时期内终止使用企业的服务或产品的客户, 其预测水平是衡量客户保持策略有效性和客户关系管理智能化程度的重要标志. 目前对于客户流失的研究对象主要集中在传统的电信客户流失预测和网络客户流失预测两个方面, 研究方法上主要是从特征向量选择和分类器优化两个角度构建客户流失预测模型.
在特征选择方面, 文献[1]针对于高维度的样本特征属性, 定义了属性满意度和属性集满意度, 通过满意度函数来开展高维特征属性的选择. 文献[2]基于原始特征引入网络客户价值特征和情感特征, 增加了客户流失预测的新的客户特征属性. 文献[3]以网络客户的在线评论信息为依据, 通过技术性的情感分析将其表示为积极与消极情感并作为客户流失预测新属性. 文献[4]针对电信数据集中存在的特征维度过高问题, 结合过滤式特征选择和嵌入式特征选择方法的优点, 提出了一种基于Fisher比率和预测风险准则的分步特征提取方法.
在分类器优化方面, 文献[5]利用分类回归树算法和自适应Boosting算法作为分类算法, 生成通信企业的离网客户的预测模型. 文献[6]改进随机森林中生成每棵树时节点划分的方法, 形成新的随机森林分类模型. 文献[7]将深度学习引入到客户流失预测中, 构造了基于深度神经网络的流失预测模型. 文献[8]通过改进粒子群算法优化支持向量机分类器. 文献[9]区分边界样本和非边界样本, 分别采用K近邻分类法与支持向量机作为分类器.
上述两类方法在不同数据集上都取得了较好的预测效果, 但随着信息管理技术在客户关系管理中的广泛应用, 客户的属性维度和记录数大规模增长, 原始实验中数据样本体量偏小, 对于预测结果科学性的解释问题日益凸显, 文献[3]使用京东运营商手机卡用户的在线评论作为数据源, 将评论星级、会员等级、点赞数作为特征属性, 采集样本共10000余条; 文献[1]使用两个数据集, 第1个数据集通过在UCI中随机抽样, 获得3333个训练样本和1667个测试样本, 第2个数据以国内某电信公司对小灵通客户拆机停号来定义客户流失, 建立1474个训练样本, 966个测试样本; 文献[8]选取UCI最常用的8个数据集, 每个样本集150~1500不等; 文献[6]以某电信公司2013年9月至2014年2月在网和离网的客户样本作为研究对象, 样本数量共计7913个; 文献[5]选取了15个可能影响客户流失的属性, 在18万条数据中, 在网数据和离网数据分别随机抽取3000条数据, 形成研究样本. 由此可见, 当前客户流失预测研究的数据源大部分为小数据集或者大样本集的抽样, 且特征维度较低. 随着大数据技术的发展, 小样本的抽样数据集已经不能满足对于预测的需要, 大样本的高维度数据计算将成为必然.
大样本的高维度数据计算核心算法包括早期的主成分分析(Principal Component Analysis, PCA)[10], 线性判别分析(Linear Discriminant Analysis, LDA)等, 这类算法理论基础坚实, 且易于执行, 很多学者通过使用核技巧, 将这些线性特征提取算法扩展到核领域, 如核独立主成分分析[11]. 另一类非线性特征提取技术是流行学习方法, 例如, 局部保持投影(Locality Preserving Projection, LPP)[12]、局部线性嵌入(Locally Linear Embedding, LLE)[13]等, 文献[14]中Zhai等人在LPP的基础上提出了一种改进的局部保持投影. 局部保持投影(LPP)不但具有简单、快捷等优点, 同时可以考虑到整体数据空间; 此外, LPP算法最大程度保持了数据的局部结构, 因此在低维空间中表示的最近邻搜索极大可能与高维空间中产生的结果类似. 所以, LPP算法在数据降维领域有相当高的实用性. 虽然LPP算法实用性较强, 但是却有一个不可避免的缺点: 在算法的优化过程中包含一个稠密矩阵分解计算. 这是一个非常消耗时间和计算资源的计算过程, 而谱回归(Spectral Regression, SR)[12]将学习嵌入函数的方式转化为一个回归框架, 避免了稠密矩阵分解这一计算过程, 同时提高了优化的效果. 因此本文提出基于谱回归的特征降维更适合大样本高维度数据的计算.
针对以上问题, 本文以网络客户数据集和传统电信客户数据集为研究对象, 从特征向量提取的角度, 提出基于谱回归局部保留投影的客户属性降维算法, 并从特征选择和分类器优化方面与不同的方法做了对比, 实验证明了算法的有效性.
1 基于谱回归的特征降维基于谱回归的特征降维算法是针对流行结构图嵌入式的典型降维算法, 通过特征提取来构造一个能揭示数据流行的结构图, 其结构图的表示方式为一个投影矩阵, 实现将高维数据特征投影到低维子空间中, 以保持高维空间中数据间的邻近结构, 达到降维的目的. 在该算法模型中, 每个顶点都是一个样本点, 两个样本点之间的边权重采用K近邻法计算两个样本点之间的邻接程度, 因此对数据的完整性保持较好.
1.1 局部保形投影局部保形投影算法(LPP)应该被视为PCA的替代方法. PCA是一种经典的线性技术, 他沿着最大方差的方向投影数据. 当高维数据位于嵌入外围空间的低维流形上时, 通过求流行上 Laplace Beltrami算子特征函数的最优特征逼近, 得到局部保持投影. 因此, LPP具有许多非线性技术的数据表示特征.
局部保形投影算法, 属于将图嵌入子空间的学习算法, 其目的是用低维向量表示高维空间中图的节点. 通过求解一个投影矩阵A将空间样本节点投影到低维空间从而实现降维. 图中任意两节点之间的关联性用最近邻图模型表示, 因此较好的保留了子空间中节点局部的结构, 实现了局部降维.
假设构建一个无向加权图Graph有m个节点, 第i个节点用xi表示, 任意两个节点之间采用K近邻法定义是否关联. 选择与xi邻近的k个节点作为xi的邻近点, 若xj在xi的k个邻近点中或者xi在xj的k个邻近点中, 则xi与xj相连; 反之, 则不相连.
根据上述邻接图计算权值. 矩阵W表示权值矩阵, 则两节点xi与xj之间的权值为Wij, 若xi与xj在相互的邻近域中, 则Wij为非0值, 反之, Wij为0. 用径向基函数计算任意两节点的权值, 则权值矩阵Wij可定义为:
| $ {W}_{ij}=\left\{\begin{array}{l}{e}^{\left({\frac{\Vert {x}^{i}-{x}^{j}\Vert }{\sigma }}^{2}\right)}, {\text{若}}{i}{\text{与}}{j}{\text{相连}}\\ 0, {\text{其他}}\end{array}\right.$ | (1) |
最后, 对其做特征分解. 假设总节点数即样本集为m, 样本集矩阵
| $ \min {\sum\limits_j^i {\left( {{y_i} - {y_j}} \right)} ^2}{W_{ij}} $ | (2) |
因线性函数
| $ \begin{split} &\min {\displaystyle\sum\limits_{i,j} {\left( {{a^{\rm{T}}}{x_i} - {a^{\rm{T}}}{x_j}} \right)} ^2}{W_{ij}}\\ & = \displaystyle\sum\limits_{i,j} {\left( {{a^{\rm{T}}}{x_i}{W_{ij}}{x_i}^{\rm{T}}a} \right)} - \displaystyle\sum\limits_{i,j} {\left( {{a^{\rm{T}}}{x_i}{W_{ij}}{x_j}^{\rm{T}}a} \right)} \\ &= \displaystyle\sum\limits_{i,j} {\left( {{a^{\rm{T}}}{x_i}{D_{ii}}{x_i}^{\rm{T}}a} \right)} - \displaystyle\sum\limits_{i,j} {\left( {{a^{\rm{T}}}{x_i}{W_{ij}}{x_j}^{\rm{T}}a} \right)}\\ & = {a^{\rm{T}}}X\left( {D - W} \right){X^{\rm{T}}}a\\ & = {a^{\rm{T}}}XL{X^{\rm{T}}}a \end{split} $ | (3) |
其中, D为
| $ \begin{split} &\mathop {\min }\limits_{{a^{\rm{T}}}XD{X^{\rm{T}}}a = 1} {a^{\rm{T}}}XL{X^{\rm{T}}}a\\ &= \mathop {\min }\limits_{{a^{\rm{T}}}XD{X^{\rm{T}}}a = 1} \frac{{{a^{\rm{T}}}XL{X^{\rm{T}}}a}}{{{a^{\rm{T}}}XD{X^{\rm{T}}}a}}\\ &= \mathop {\min }\limits_{{a^{\rm{T}}}XD{X^{\rm{T}}}a = 1} \frac{{{a^{\rm{T}}}X\left( {D - W} \right){X^{\rm{T}}}a}}{{{a^{\rm{T}}}XD{X^{\rm{T}}}a}}\\ &= \mathop {\min }\limits_{{a^{\rm{T}}}XD{X^{\rm{T}}}a = 1} - \frac{{{a^{\rm{T}}}XW{X^{\rm{T}}}a}}{{{a^{\rm{T}}}XD{X^{\rm{T}}}a}}\\ & = \mathop {\max }\limits_{{a^{\rm{T}}}XD{X^{\rm{T}}}a = 1} \frac{{{a^{\rm{T}}}XW{X^{\rm{T}}}a}}{{{a^{\rm{T}}}XD{X^{\rm{T}}}a}} \end{split} $ | (4) |
用拉格朗日乘数法将式(4)转化为求解下列方程的最大特征向量
| ${a^{\rm{T}}}XW{X^{\rm{T}}}a = \lambda {a^{\rm{T}}}XD{X^{\rm{T}}}a$ | (5) |
其中,
LPP算法实现降维的同时保留了数据节点间的局部空间结构, 具有较好的局部判别能力; 与传统的线性降维方法相比, 该算法能保持数据的流行结构, 克服了非线性方法难以获得新样本低维投影的缺点. 但是LPP算法也存在自身的缺陷, 在求解大规模特征值问题时会导致计算量较大, 计算时间较长. 算法只注重数据的局部结构, 而未考虑到数据样本的类别, 另外在噪声影响下算法不能获得较理想的结果, 因此算法的鲁棒性较差.
1.2 基于谱回归的特征降维为了克服局部保形投影算法计算稠密矩阵的特征值问题, 引入谱回归(Spectral Regression, SR)方法用回归模型处理特征函数, 先将特征函数根据图谱理论进行图的谱分析, 再将数据放入回归模型中处理. 其特征降维的优良特性使得在众多领域中得到了广泛应用[15].
在定义线性函数
| $a = {\min _a}\left( {\sum\nolimits_{i = 1}^m {{{\left( {{a^{\rm{T}}}{x_i} - {y_i}} \right)}^2}} } \right)$ | (6) |
通过对式(6)求偏导可得:
| $a = {\left( {X{X^{\rm{T}}}} \right)^{ - 1}}Xy$ | (7) |
若
| $a = {\min _a}\left( {\sum\nolimits_{i = 1}^m {{{\left( {{a^{\rm{T}}}{x_i} - {y_i}} \right)}^2} + \alpha {{\left\| a \right\|}^2}} } \right)$ | (8) |
当正则化参数
本文在网络客户和电信客户两个大样本数据集上进行实证研究, 预测流程如图1所示, 采用F1值、精确率、召回率、准确率等指标评价模型预测结果, 具体参见表1. 实验所用电脑的内存是16 GB, 处理器是Intel(R) Xeon(R) CPU E5-1603 v3, 操作系统为Win7 64位, 实验环境为Matlab 2018a.

|
图 1 运动目标误判效果 |
2.1 某电子商务网站网络客户数据
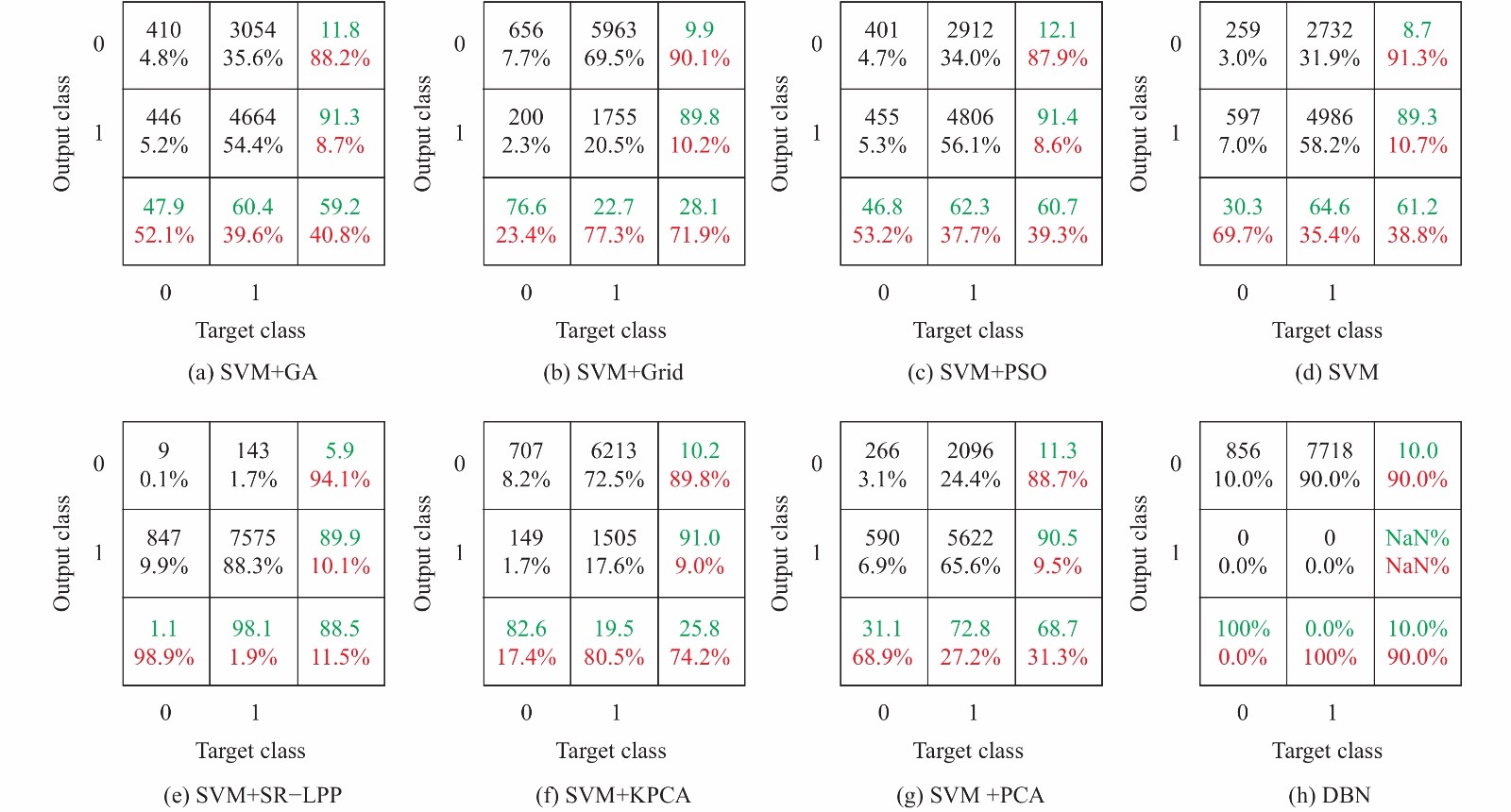
该数据集来源于某电子商务网站. 采用过抽样和随机抽样形成训练数据集和测试数据集, 以自然年度为周期共得到训练样本20006个, 测试样本8574个. 其中训练集中流失客户10002个, 非流失客户10004个. 测试集中非流失客户856个, 流失客户7718个. 非流失客户与流失客户的比例基本为1:9, 主要包括客户首次购买时间、客户关系长度、客户消费新鲜度、客户消费频度、客户消费金额、客户对商品的评分、客户评论情感共7个属性特征[2]. 这里我们从不同特征约简算法和分类器两个层面进行对比. 特征约简算法则包括KPCA、PCA, 分类器包括原始线性核SVM、优化SVM算法(网格算法, 遗传算法, 种群优化算法)和DBN (深度置信网络), 其中KPCA, PCA, SR-LPP的约简维度统一设置为3, DBN设置为3层隐藏层, 每层30节点. 鉴于企业获取新客户的成本是保留老客户成本的数倍, 将流失客户判别为非流失客户称为导致严重后果的第一类错误(FN)[1], 将非流失客户判别为流失客户称为第二类错误(FP). 对于企业而言, 模型导致的第二类错误会增加客户保持成本, 而犯第一类错误则将面临着客户流失的巨大风险, 因此在该实验中添加导致严重后果的第一类错误发生率作为辅助评价指标.
实验结果混淆矩阵如图2所示(其中0代表了非流失类, 1代表了流失类). 基于谱回归的预测方法在精确率、召回率、准确率等方面都优于其他方法. 且第一类错误的发生概率仅为1.7%. 在分类器优化的方法中, 基于遗传算法(GA)和种群算法(PSO)优化的SVM, 并不能显著提高客户流失预测效果, 相比与非优化SVM各项指标基本持平, 但第一类错误发生率在35%左右, 略高于非寻优SVM的32%, SVM+Grid预测效果则更不理想. 而DBN分类器在非流失客户与流失客户明显不平衡的测试集中, 全部将测试集判断为非流失客户. 在特征约简方法中, 除了KPCA外, PCA和本文的SR-LPP都在不同程度上提高了客户流失预测效果, 其中SVM+SR-LPP综合Precision、Recall、Accuracy和第一类错误率4个指标较其他方法最优, 也在一定程度上说明特征层面的选择优化更为重要.
| 表 1 混淆矩阵 |
|
图 2 不同算法的结果混淆矩阵对比 |
2.2 电信客户数据
电信客户数据采用高维度、大样本的美国DUKE大学电信客户行为数据. 数据样本共计151306个, 其中训练集共100000个样本, 包含流失客户49562个, 非流失客户50438个, 两类客户的比例基本为1:1; 测试集共51306个样本, 包含流失客户924个, 非流失客户49514个, 客户流失率为1.8%, 数据类别严重不平衡. 其属性值包含产品特征、客户方案、客户信息3大类, 共计87个初始属性指标. 鉴于数据样本大、维度高, SVM分类器的参数寻优已无法在实验计算机有效时间内的求出结果, 这里重点进行特征选择和约简算法的对比, 采用PCA、KPCA、MCFS[16]、SRLPP算法分别在1–87维度之间做了比对, 分类器统一使用线性SVM.
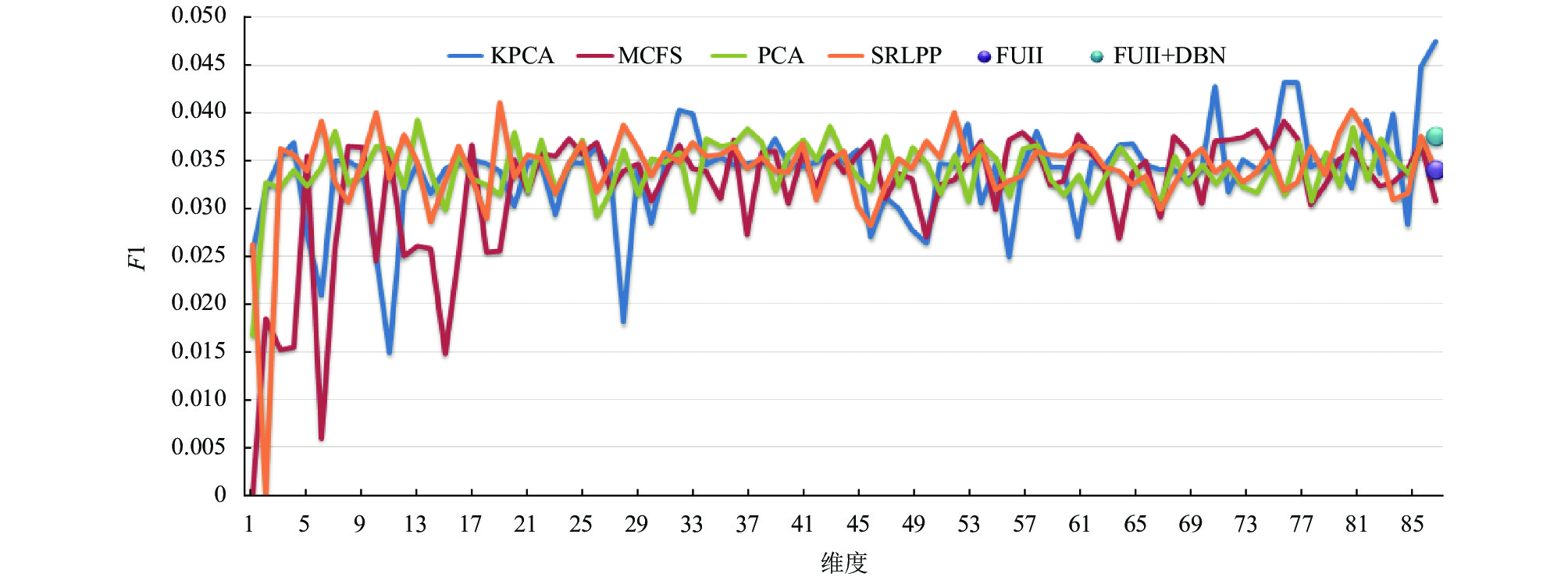
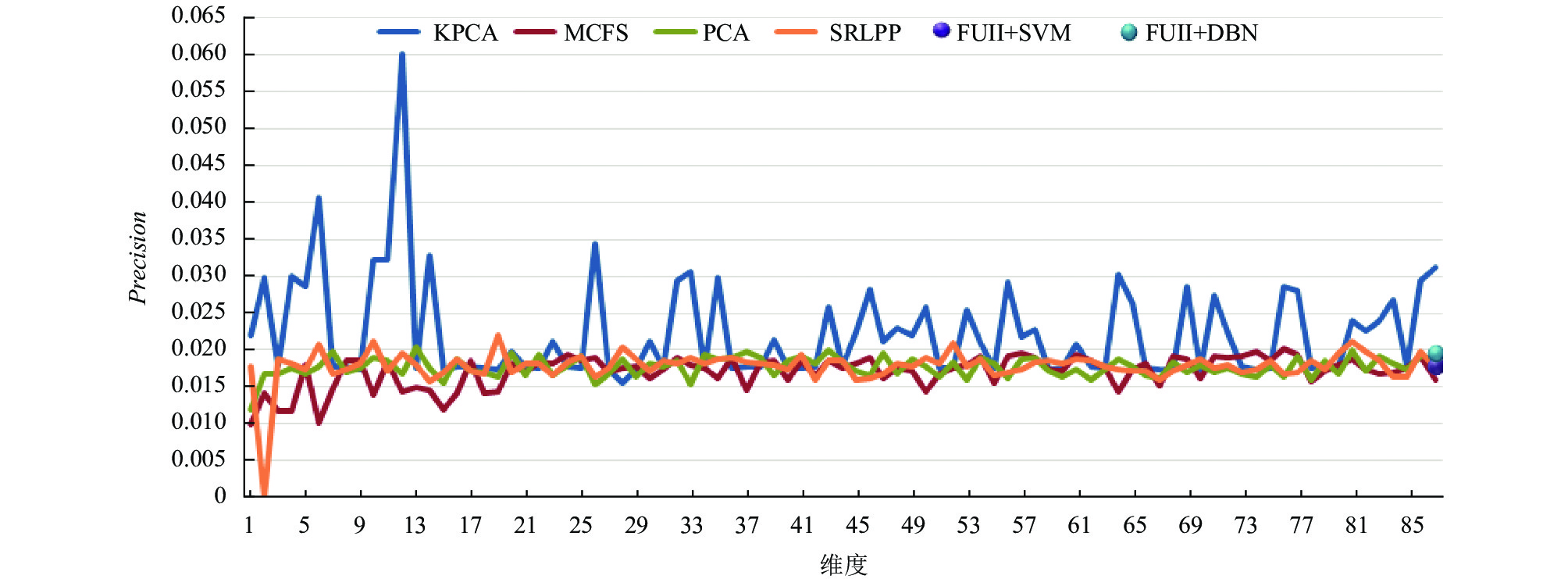
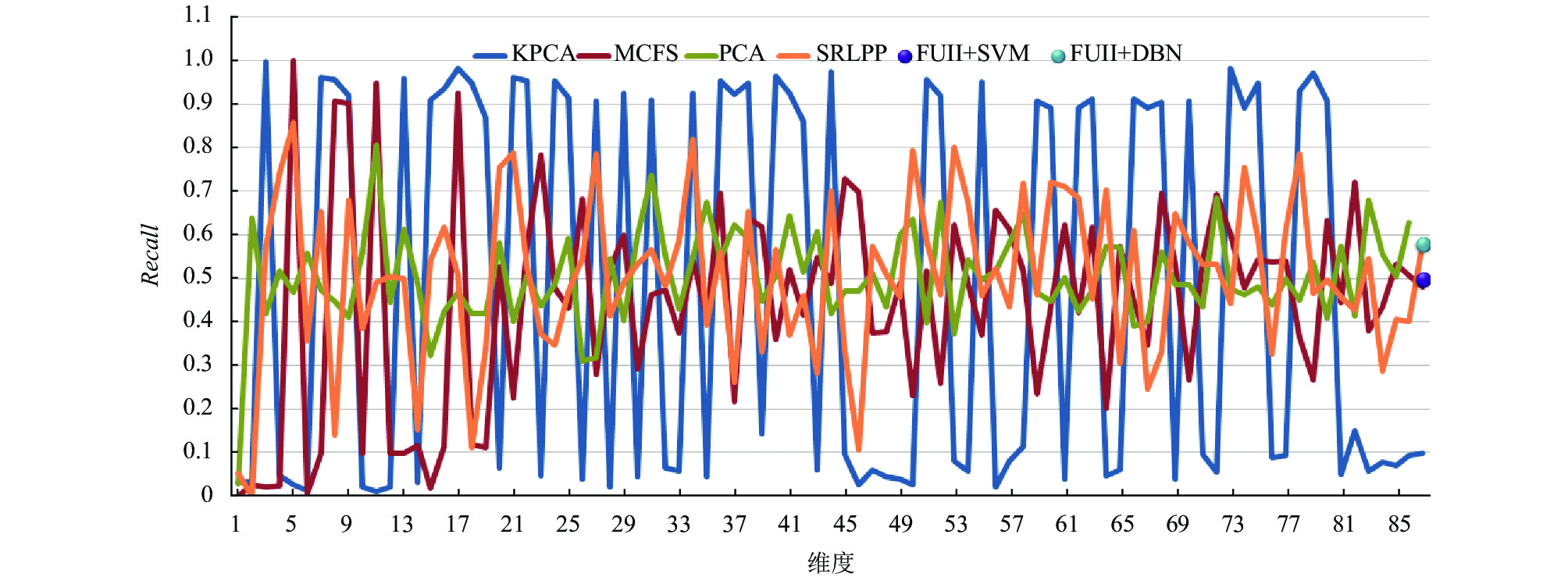
通过图3–图5可见, 降维或选择后的特征在一定程度上优于全部特征作为SVM输入的预测方法, 全部特征虽然包含的信息量大, 但不同属性数据间交叉、重合所产生的信息冗余也容易引起不同类别的误判, 这种特征本质的混淆在上述不同分类器并没有得到良好的解决. 在特征降维和选择的算法中, KPCA对于不同维度稳定性较差, 在不平衡数据中容易将测试集全部预测为流失或非流失, 从而造成大部分实验召回率非0即1, 使得F1和精确度指标失去意义. 同时核函数方法需要对核矩阵计算和特征分解来完成高维空间的映射, 对于大样本数据时间复杂度高. 传统PCA降维, 虽然没有优异的预测效果, 但计算简单, 结果稳定, 不失为一种有效的特征降维方法. 作为特征选择方法代表的MCFS三项指标都略低于其他方法, 说明每一维度的特征都具有一定隐含的语义, 对于单纯维度的剔除难以满足分类的需要. SRLPP方法则3项指标较为稳定, 能够对不同维度特征进行有效的融合, 在87个维度的约简中, 大概率的高于其他方法.
|
图 3 F1 指标值 |
|
图 4 Precision指标值 |
|
图 5 Recall指标值 |
我们求取不同维度下的各方法的均值和标准差, 如表2所示, 其中KPCA平均精度最高, 但是其各指标值偏离程度较大, 尤其是召回率标准差达0.44是PCA方法的4倍, 因此表现出图4中连续的大波峰和波谷. MCFS则综合表现一般, 不如全部特征输入SVM的预测效果. SRLPP平均精度仅次于KPCA, 其他指标在4种特征降维方法中相对最优, 整体表现稳定.
| 表 2 不同维度下各方法指标均值与标准差 |
3 结论与展望
随着互联网+的广泛应用, 无论是客户数量还是属性的数据体量都在指数式增长, 且呈现出数据类型严重不平衡的特点, 传统抽样已经不能满足预测结果的解释性要求, 本文针对于高维度多属性的大规模客户流失预测, 利用基于谱回归的流形降维建立可区分性的低维特征空间, 使用线性支持向量机分类, 相比于参数优化的分类器和不同的特征降维方法, 预测效果有了不同程度的提高.
| [1] |
夏国恩. 基于满意控制的客户流失两类错误. 系统工程, 2016, 34(3): 136-141. |
| [2] |
夏国恩, 马文斌, 唐婵娟, 等. 融入客户价值特征和情感特征的网络客户流失预测研究. 管理学报, 2018, 15(3): 442-449. DOI:10.3969/j.issn.1672-884x.2018.03.016 |
| [3] |
冯鑫, 王晨, 刘苑, 等. 基于评论情感倾向和神经网络的客户流失预测研究. 中国电子科学研究院学报, 2018, 13(3): 340-345. DOI:10.3969/j.issn.1673-5692.2018.03.019 |
| [4] |
徐子伟, 王鹏, 陈宗海. 一种基于Fisher比率和预测风险准则的电信客户流失预测分步特征选择方法. 中国科学技术大学学报, 2017, 47(8): 686-694. DOI:10.3969/j.issn.0253-2778.2017.08.008 |
| [5] |
张玮, 杨善林, 刘婷婷. 基于CART和自适应Boosting算法的移动通信企业客户流失预测模型. 中国管理科学, 2014, 22(10): 90-96. |
| [6] |
丁君美, 刘贵全, 李慧. 改进随机森林算法在电信业客户流失预测中的应用. 模式识别与人工智能, 2015, 28(11): 1041-1049. |
| [7] |
马文斌, 夏国恩. 基于深度神经网络的客户流失预测模型. 计算机技术与发展, 2019, 29(9): 76-80. DOI:10.3969/j.issn.1673-629X.2019.09.015 |
| [8] |
于小兵, 卢逸群. 电子商务客户流失预警与预测. 系统工程, 2016, 34(9): 37-43. |
| [9] |
卢光跃, 王航龙, 李创创, 等. 基于改进的K近邻和支持向量机客户流失预测. 西安邮电大学学报, 2018, 23(2): 1-6. |
| [10] |
Fowler JE. Compressive-projection principal component analysis. IEEE Transactions on Image Processing, 2009, 18(10): 2230-2242. DOI:10.1109/TIP.2009.2025089 |
| [11] |
Zhao CH, Wang YL, Mei F. Kernel ICA feature extraction for anomaly detection in hyperspectral imagery. Chinese Journal of Electronics, 2012, 21(2): 265-269. |
| [12] |
Zhang LM, Qiao LS, Chen SC. Graph-optimized locality preserving projections. Pattern Recognition, 2010, 43(6): 1993-2002. DOI:10.1016/j.patcog.2009.12.022 |
| [13] |
Roweis ST, Saul LK, et al. Nonlinear dimensionality reduction by locally linear embedding. Science, 2000, 290(5500): 2323-2326. DOI:10.1126/science.290.5500.2323 |
| [14] |
Zhai YG, Zhang LF, Wang N, et al. A modified locality-preserving projection approach for hyperspectral image classification. IEEE Geoscience and Remote Sensing Letters, 2016, 13(8): 1059-1063. DOI:10.1109/LGRS.2016.2564993 |
| [15] |
陈朋, 张建华, 文再治, 等. 基于核谱回归与随机森林的脑电情感识别. 华东理工大学学报(自然科学版), 2018, 44(5): 744-751. |
| [16] |
Cai D, Zhang CY, He XF. Unsupervised feature selection for Multi-Cluster data. Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Washington, DC, USA. 2010. 333–342.
|
 2021, Vol. 30
2021, Vol. 30



