噪声污染是当今世界的四大污染源之一. 现代社会、科技工业和城市交通在持续发展, 噪声污染也在不断加重, 城市环境噪声的投诉量已占环境污染投诉量的60%以上. 人们对于生活环境的要求也进一步提高, 相应地促进了噪声监测系统的应用.
噪声监测系统可以在线监测各种环境噪声, 如交通噪声, 机场噪声, 施工场地, 工厂及社会生活等噪声污染源, 可以自动对噪声数据进行采集和处理, 并使用网络传输和共享监测信息. 噪声监测系统可以实行全天候监测, 准确地发现超标噪声, 探测出噪声的强度、所属的分类和出现的规律, 也可以及时通知执法人员进入现场取证或处罚. 完全靠人力的传统方式已经很难处理日益严重的噪声污染. 因此噪声在线监测系统的应用就显得非常重要[1].
声级计是声学测量领域广泛使用的声压级测量仪器, 也是噪声监测系统中最基本的测量仪器. 随着技术的进步, 声级计的功能越来越丰富, 能测量瞬时声级Lp、等效连续声级Leq、脉冲声级 LI、累计百分声级LN、暴露声级Le、最大声级Lmax、最小声级Lmin等多个不同参数[2].
时间计权特性和频率计权特性是检验声级计性能的重要技术指标. 其中, 声级计的频率计权通常有A、B、C、D计权, 这是为了模拟人耳听觉在不同频率处有不同的灵敏度而在声级计的电路内设计的不同的计权网络. 通过计权网络测得的声压级叫做计权声压级, 如A计权声压级, 也称A声级; 不通过计权网络的称为线性声压级, 目前用Z计权声压级表示.
A、B、C计权分别近似地模拟40方、70方和100方3条等响曲线, 由于A计权更能表征人耳的主观特性, 因此在噪声测量中常用A计权声级表示噪声大小, 而C计权声压级和Z计权声压级往往在噪声测量中表示为总声压级, D计权则专用于飞机噪声的测量[3].
1 ENS3000噪声监测系统ENS3000噪声监测系统[4]是自动化、网络化、智能化的在线监测系统. 在线监测系统以不同区域的噪声监测单元为基础组成. 可将本地噪声数据传送到监测中心. 系统各个功能模块高度集成, 性能稳定可靠.
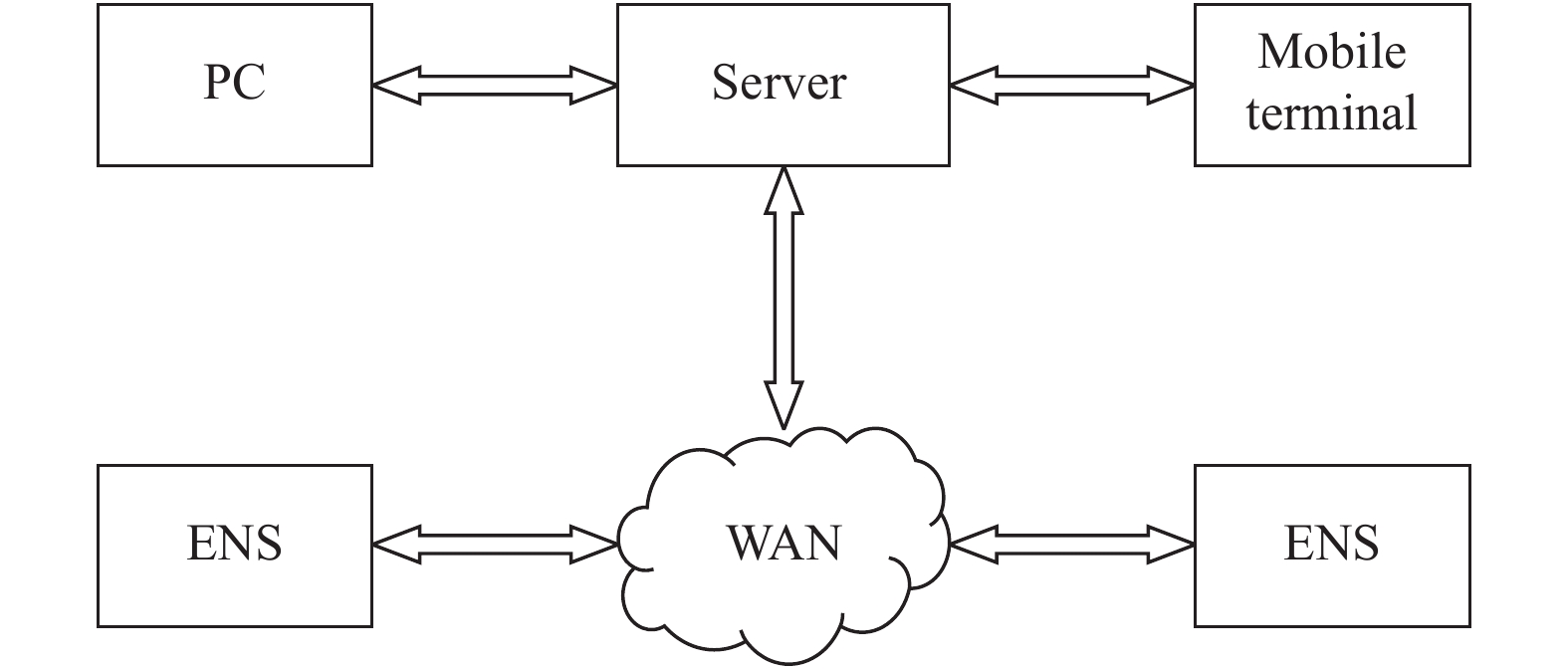
噪声监测的布点方式依据测量内容分为几类. 对于交通噪声, 可以沿着道路分布测量点, 一般使用交通噪声指数TNI来测量噪声; 对于区域噪声, 可以使用网格法分布测量点, 一般使用累计百分声级LN 和昼夜等效声级 Ldn来测量噪声; 对于功能区噪声, 可以在重要位置分布测量点, 使用无线网络进行实时监测[5]. 图1是噪声监测系统的结构.
|
图 1 ENS3000噪声监测系统 |
ENS3000噪声监测系统采用模块化设计. 系统包含分贝数据采集模块、音频数据采集模块、超标噪音处理和传输等模块. 模块可以灵活配置, 模块间使用消息队列进程来进行通信. 每个模块是各自独立的可执行文件, 不同的模块可以作为系统运行时的独立进程而存在于系统中. 从删除或禁用某个模块, 并不会影响其他模块的性能. 系统具有一体化、全功能、实用性强、稳定性高等优点.
2 监测系统自动校正原理自动校正方法结合各种算法, 通过对已测量得到的数据进行回归分析, 再依据现场设备实际测出的温度、湿度、大气压力等数值, 来建立噪声预测模型. 可以利用建立的模型通过网络对声级计进行自动校正, 进而消除误差并提高测量精度.
2.1 误差产生的原因和后果当噪声监测系统使用声级计测量噪声时, 会受到温度、湿度、大气压力和背景噪声等多个因素影响, 测量结果与实际值误差较大[6].
测量噪声分贝值与真实噪声分贝值之差等于声级计本身的误差分贝值, 因此声级计本身误差的产生会影响声级计测量的准确性, 而不同等级的声级计的误差不得超过规定的相应分贝值. 为了满足对声级计精度的规定, 每隔一段时间, 工作人员就要到各个声级计设备安放现场进行校准, 以修正误差.
2.2 误差的消除按照国家规定, 声级计作为计量器具在经历几次维护人员手工校准后, 每年还需要送到当地的相关计量部门重新进行检定, 由专业机构使用规范设备仪器重新进行校准重置后再投入使用. 在两次年检的正常使用过程中间, 传统的声级计误差消除是由维护人员进入现场进行手工校准来实现的.
对比传统的误差消除方法, 使用自动校正方法在误差的消除方面有了很大改进.
首先, 传统校准过程需要多个仪器实现, 既不够标准又费时费力. 不同检测人员的校准仪器和步骤也都有差异, 操作的时候难免会产生测量误差, 测量结果准确度和稳定性都不高. 而自动校正方法可以由相同人员使用统一设备来采集数据, 减少了测量误差.
其次, 当进行手工校准时, 声级计测量值与校准器标准值之间的差值在同一设备安装地点的不同时间段会高低变化, 现场维护人员会相应调整声级计基准使之与校准器标准值一致. 使用一段时间后, 由于温度等各因素改变, 又需要再次进行手工校准. 声级计基准的多次调整可能会放大误差. 而自动校正方法的基准则保持不变, 在两次年检间隔的正常使用过程中间, 不需要手工校准, 因此就能大量地减少检测人员的现场工作量.
2.3 不同环境因素下的性能分析声级计按精度可分为1级和2级声级计. 其中1级声级计的工作温度范围为−10~50 ℃, 2级声级计的工作温度范围为0~40 ℃. 声级计重要的传感部件是电容传声器[7], 电容传声器可以在−50~150 ℃的温度下使用. 在35 ℃时, 短期稳定性为每年0.l dB, 长期稳定性每年小于0.5 dB. 传声器灵敏度受到温度、湿度、大气压力等因素的影响, 其中温度的影响比较大[8]. 电容传声器温度每变化1 ℃, 灵敏度变化约为0.008 dB. 在湿度为0~90%时, 灵敏度总的变化小于0.5 dB; 大气压每变化1 毫米汞柱, 灵敏度变化约为−0.003 dB.
电容传声器作为声级计主要部件, 两者变化规律是相似的. 为了得到声级计在不同因素下的详细变化规律, 可以使用不同的算法来得到不同模型.
3 线性回归在噪声自动校正中的应用 3.1 实验数据处理方法实验测量数据值有4项: 温度、湿度、气压值以及声级计对校准器的实时测量值. 其中, 温度单位为摄氏度℃, 湿度单位为相对湿度%rh, 气压值为实时大气压值减去标准大气压值1013.2, 单位为百帕hPa, 声级计对校准器的实时测量值读数常会有0.1 dB左右小幅变动, 因此测量时可以多测几次求取平均值.
温度、湿度和气压值可由监测系统相应配套设备测出. 校准器在工作时会发出94 dB的恒定标准声源, 校准器的耦合腔对插入其中的1/2英寸声级计会产生0.2 dB衰减, 其值应修正为93.8 dB, 因此声级计的标准读数应为93.8 dB, 但受到温度等各环境因素影响会产生一定量误差. 而这个误差就等于测量噪声分贝值与真实噪声分贝值之差.
在建立回归模型后, 噪声监测系统就可以由系统自动采集的温度、湿度和气压这3项数值来拟合出变化后的标准噪声值, 并与标准读数93.8 dB相减得到误差分贝值, 用于自动修正噪声实时测量值.
3.2 线性回归原理线性回归[9]模型的原理如下:
| $\left\{\begin{array}{*{20}{c}} {{y_1} = {\beta _0} + {\beta _1}{x_{11}} + {\beta _2}{x_{21}} \cdots + {\beta _p}{x_{p1}} + {\varepsilon _1}} \\ {{y_2} = {\beta _0} + {\beta _1}{x_{12}} + {\beta _2}{x_{22}} \cdots + {\beta _p}{x_{p2}} + {\varepsilon _2}} \\ \vdots \\ {{y_n} = {\beta _0} + {\beta _1}{x_{1n}} + {\beta _2}{x_{2n}} \cdots + {\beta _p}{x_{pn}} + {\varepsilon _n}} \end{array}\right.$ | (1) |
| $Y = \left( {\begin{array}{*{20}{c}} {{y_1}} \\ {{y_2}} \\ \vdots \\ {{y_n}} \end{array}} \right)$ | (2) |
| $X = \left( {\begin{array}{*{20}{c}} 1&{{x_{11}}}&{{x_{21}}}& \cdots &{{x_{p1}}} \\ 1&{{x_{12}}}&{{x_{22}}}& \cdots &{{x_{p2}}} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 1&{{x_{1n}}}&{{x_{2n}}}& \cdots &{{x_{pn}}} \end{array}} \right)$ | (3) |
| $\beta = \left( {\begin{array}{*{20}{c}} {{\beta _0}} \\ {{\beta _1}} \\ \vdots \\ {{\beta _p}} \end{array}} \right)$ | (4) |
| $\varepsilon = \left( {\begin{array}{*{20}{c}} {{\varepsilon _1}} \\ {{\varepsilon _2}} \\ \vdots \\ {{\varepsilon _n}} \end{array}} \right)$ | (5) |
因此, Y=Xβ+ε, E(Y|X)= Xβ
3.3 多元线性回归函数和模型在Matlab中, 回归函数可用:
| $ {{[b, bint, r, rint, stats] = regress(}}y{\rm{,}}x{\rm{,}}a{\rm{)}} $ | (6) |
回归结果由5部分组成:
(1) b={β0, β1, β2, ···}是回归系数β的估计值;
(2) bint是回归系数的置信区间;
(3) r是残差向量;
(4) rint为残差向量的置信区间;
(5) stats={R2, F, p, S2}是检验统计量.
其中的stats由4部分组成:
(1) R2为判定系数[10], 越大各因素相关性越高;
(2) F为作F检验统计量的值;
(3) p为对应F的概率, 默认p< 0.05时模型成立;
(4) S2为估计误差的方差.
回归模型如下, y 是噪声监测值, x1 是温度, x2是湿度, x3是气压. 对于简单处理, 忽略随机错误.
| ${y_i} = {\beta _0} + {\beta _1}{x_{1i}} + {\beta _2}{x_{2i}} + {\beta _3}{x_{3i}}$ | (7) |
残差ei是观测值Yi与Xi的预测值
| $Q = \sum\limits_{i = 1}^n {e_i^2} = \sum\limits_{i = 1}^n {{{({y_i} - {{\hat y}_i})}^2}} $ | (8) |
在实验测试中, 噪声值取决于温度、气压、湿度和背景噪声等环境因素的影响, 但是各因素相关程度又有所不同. 可以使用Matlab工具对各因素进行回归分析.
3.4.1 第1次线性回归实验数据为M1={x1, x2, x3, y}, 其中x1是温度, x2是湿度, x3是当前气压与标准大气压的差值, y是噪声监测值, 共54组实测数据.
x1[54]={27.2, 26.7, 26.5, 26.8, 27, 27.60, 27.50, 27.90, 27.80, 26.90, 27.30, 27.4, 28.5, 29.1, 28.8, 28.4, 28.6, 29.3, 30.2, 30.4, 30.2, 27.6, 28.8, 27.3, 26.1, 25.9, 25.3, 24.1, 25.1, 24.8, 24.9, 24.8, 24.6, 24.7, 25.8, 25, 24.6, 25.2, 26, 29.5, 30.4, 30.5, 30.1, 30.4, 29, 29.1, 31.1, 30.8, 31.4, 31.6, 27.8, 27.7, 28.3, 30.5}
x2[54]={51.8, 60.4, 62.4, 58.3, 58.3, 57.40, 56.90, 54.70, 55.30, 58.40, 60.20, 66.9, 67.8, 71.5, 68.8, 69.7, 68, 67.1, 74.8, 73.8, 73.7, 56.7, 75, 59.6, 63.8, 57.5, 60.7, 64.4, 62.7, 67.8, 68.3, 68.2, 70.9, 71.4, 69.4, 71.4, 76.8, 76, 82.4, 81.8, 79.7, 77.6, 77.5, 78.5, 73.5, 71.4, 73.7, 74.9, 73.6, 68.5, 52.3, 50.6, 65.8, 73.8}
x3[54]={−3.99, −2.65, −2.05, −2.49, −2.9, −4.75, −5.25, −5.45, −5.25, −3.75, −3.35, −2.25, −3.25, −4.75, −5.05, −3.95, −3.65, −3.25, −11.15, −11.45, −11.85, −11.25, −7.75, −6.95, −6.25, −2.15, −4.35, −3.75, −4.15, −4.15, −4.05, −4.25, −4.65, −4.65, −7.05, −6.95, −6.15, −5.75, −10.75, −5.65, −6.45, −8.75, −8.95, −8.95, −6.25, −8.25, −9.15, −10.75, −10.25, −10.55, −10.45, −9.95, −10.15, −6.25}
y[54]={93.8, 93.9, 94.1, 94, 93.9, 93.70, 93.70, 93.60, 93.70, 93.80, 93.90, 93.9, 93.8, 93.7, 93.8, 93.7, 93.8, 93.8, 93.7, 93.7, 93.8, 93.6, 93.8, 93.6, 93.7, 93.7, 93.7, 93.6, 93.7, 93.8, 93.9, 93.8, 93.7, 93.6, 93.7, 93.7, 93.7, 93.7, 93.5, 93.9, 93.8, 93.8, 93.8, 93.8, 93.8, 93.7, 93.8, 93.7, 93.8, 93.8, 94.3, 94.2, 93.8, 93.8}
使用Matlab工具对实验数据M1进行线性回归, 得到回归系数估计值b和stats的值为:
b ={93.6135, 0.0217, −0.0059, 0.0063}
stats =0.1507, 2.9564, 0.0412, 0.0178
其中的判定系数R2值仅为0.1507, 远小于1. 则相关系数R相应地大于0.3, 小于0.4. 说明温度、气压、湿度三因素与当前噪声测量值之间的线性相关性较低[12].
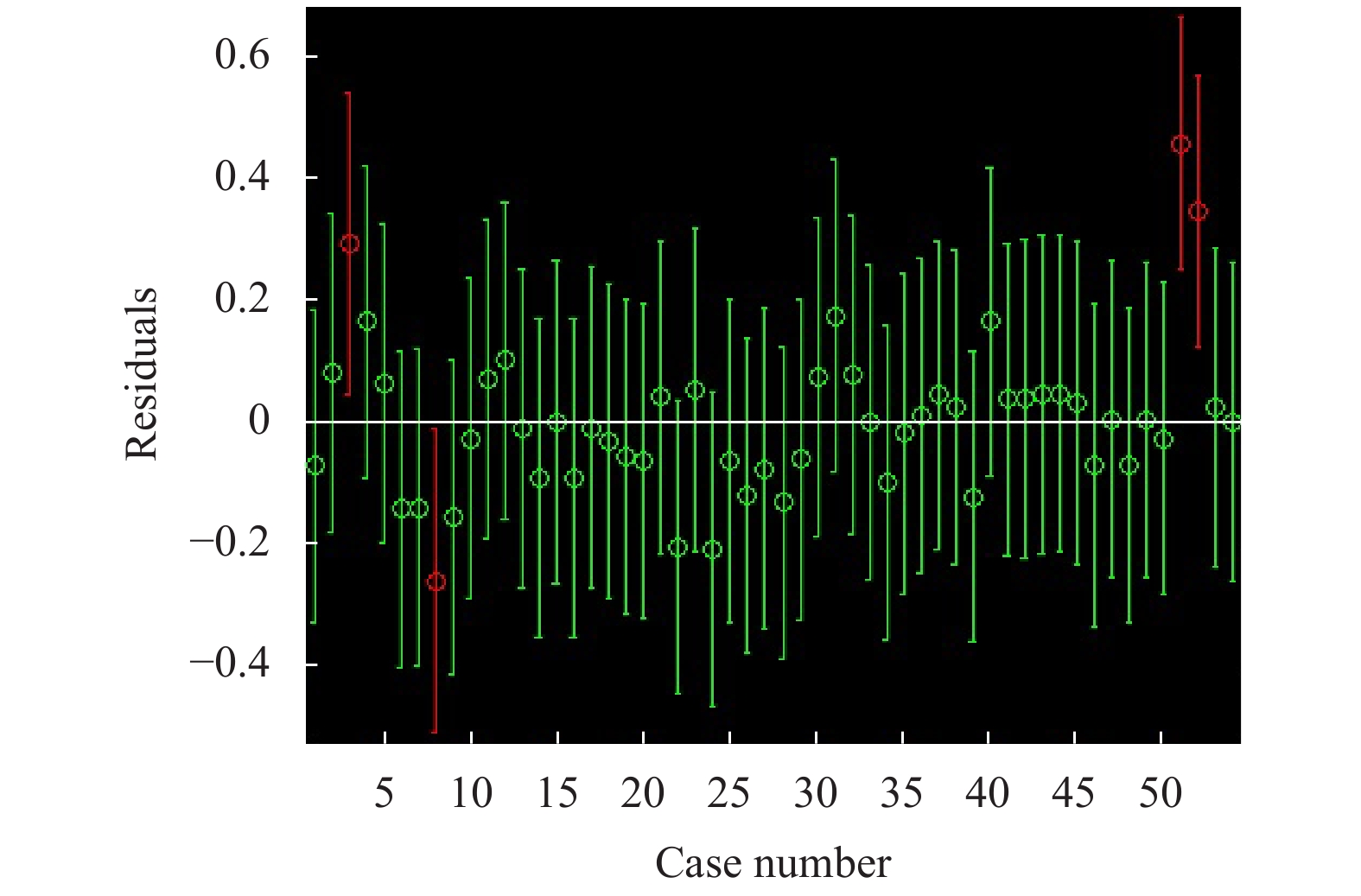
原因可能是测量数据的时间跨度以及背景噪声等其他因素影响, 导致测量数据中出现了个别残差明显过大的测量点[13], 如图2所示. 解决的办法是屏蔽掉残差图上远离中心线外的4组残差异常点, 之后对剩下的数据再进行逐步回归.
|
图 2 线性回归残差图 |
3.4.2 逐步回归
第1次线性回归之后, 根据图2所示, 删除了4组残差明显过大的测量点.
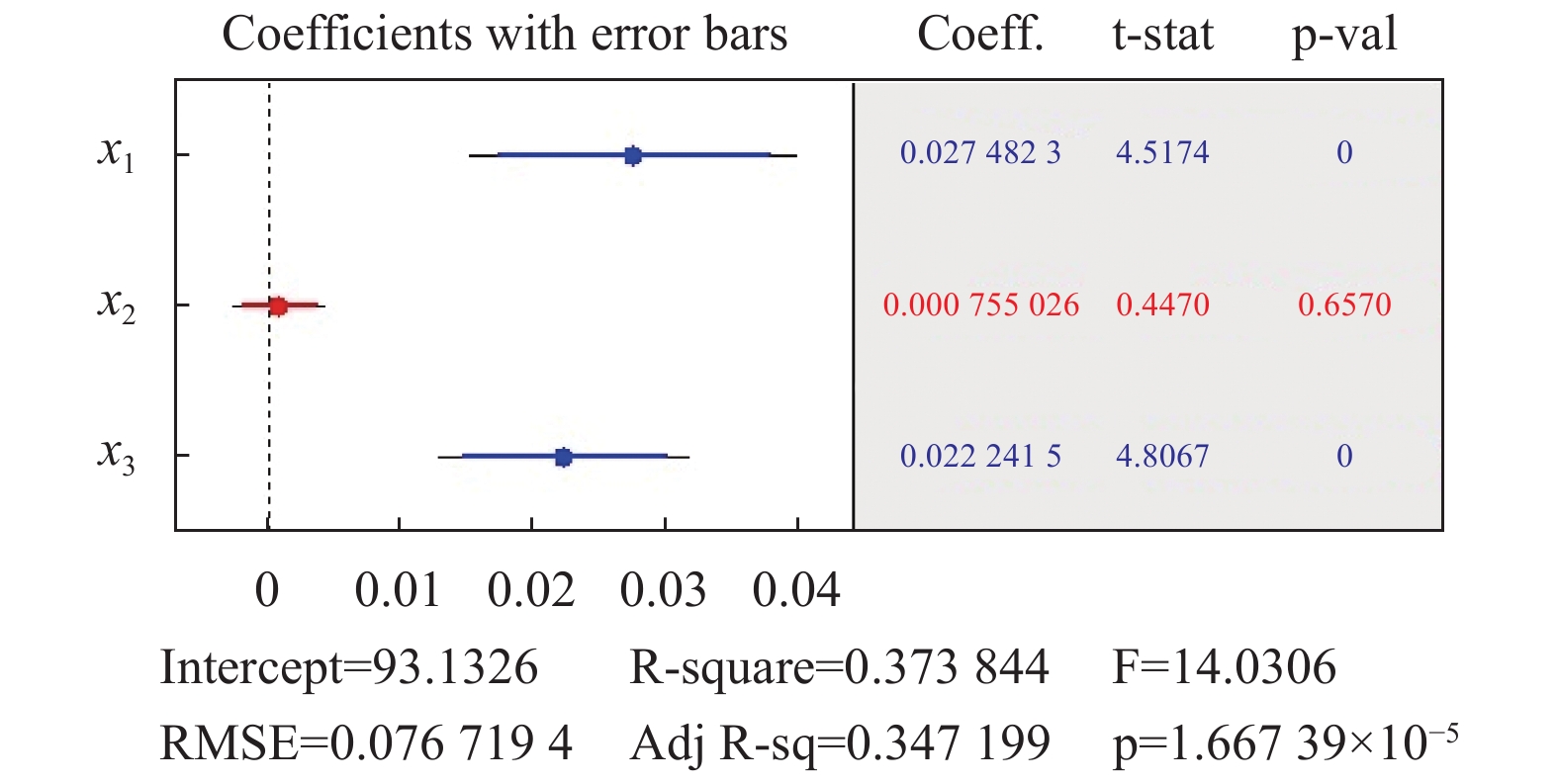
再使用Matlab工具对数据进行逐步回归(stepwise regression), 逐步回归结果表明温度和气压两个因素对噪声的线性相关度相对较大, 如图3所示, 其判定系数R2值为0.373844, 可以说明温度和气压这两个因素与噪声存在一定的线性相关.
|
图 3 双因素逐步回归结果图 |
经过逐步回归分析之后, 比较了各因素的线性相关性, 确定了下一步参与第2次回归的各因素.
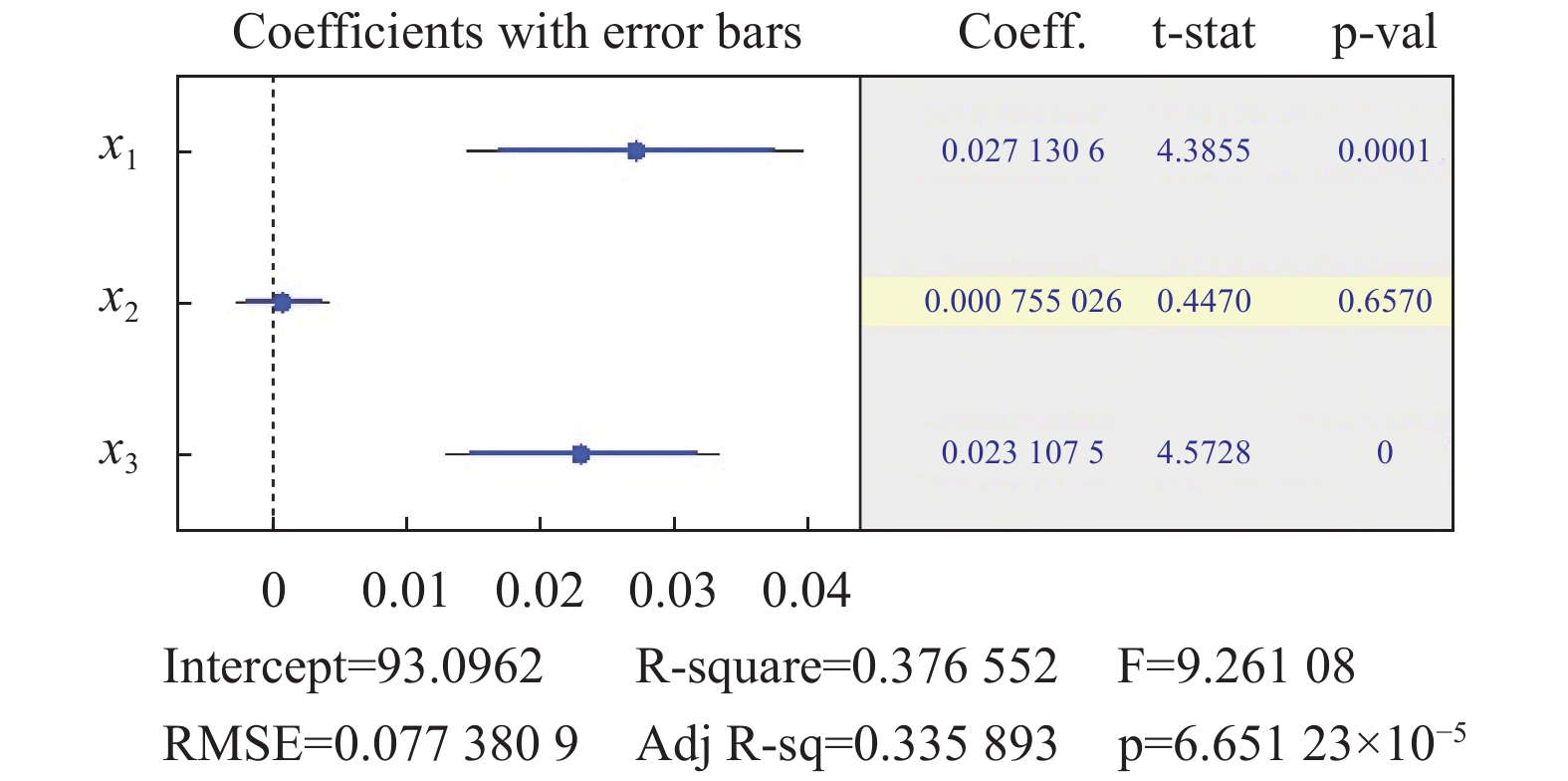
当温度、湿度和气压三因素都参与回归时, 如图4所示, 其判定系数R2值为0.376552, 与温度和气压双因素的判定系数R2值0.373844相比区别不大, 说明湿度因素与噪声的线性相关性比较小.
|
图 4 三因素逐步回归结果图 |
3.4.3 第2次线性回归并确定最终线性回归模型
实验数据为M2={p1, p2, p3, q}, 其中p1是温度, p2是湿度, p3是当前气压与标准大气压的差值, q是噪声监测值, 共50组实测数据.
p1[50]={27.2, 26.7, 26.8, 27, 27.6, 27.50, 27.80, 26.90, 27.30, 27.40, 28.50, 29.1, 28.8, 28.4, 28.6, 29.3, 30.2, 30.4, 30.2, 27.6, 28.8, 27.3, 26.1, 25.9, 25.3, 24.1, 25.1, 24.8, 24.9, 24.8, 24.6, 24.7, 25.8, 25, 24.6, 25.2, 26, 29.5, 30.4, 30.5, 30.1, 30.4, 29, 29.1, 31.1, 30.8, 31.4, 31.6, 28.3, 30.5}
p2[50]={51.8, 60.4, 58.3, 58.3, 57.4, 56.90, 55.30, 58.40, 60.20, 66.90, 67.80, 71.5, 68.8, 69.7, 68, 67.1, 74.8, 73.8, 73.7, 56.7, 75, 59.6, 63.8, 57.5, 60.7, 64.4, 62.7, 67.8, 68.3, 68.2, 70.9, 71.4, 69.4, 71.4, 76.8, 76, 82.4, 81.8, 79.7, 77.6, 77.5, 78.5, 73.5, 71.4, 73.7, 74.9, 73.6, 68.5, 65.8, 73.8}
p3[50]={−3.99, −2.65, −2.49, −2.9, −4.75, −5.25, −5.25, −3.75, −3.35, −2.25, −3.25, −4.75, −5.05, −3.95, −3.65, −3.25, −11.15, −11.45, −11.85, −11.25, −7.75, −6.95, −6.25, −2.15, −4.35, −3.75, −4.15, −4.15, −4.05, −4.25, −4.65, −4.65, −7.05, −6.95, −6.15, −5.75, −10.75, −5.65, −6.45, −8.75, −8.95, −8.95, −6.25, −8.25, −9.15, −10.75, −10.25, −10.55, −10.15, −6.25}
q[50]={93.8, 93.9, 94, 93.9, 93.7, 93.70, 93.70, 93.80, 93.90, 93.90, 93.80, 93.7, 93.8, 93.7, 93.8, 93.8, 93.7, 93.7, 93.8, 93.6, 93.8, 93.6, 93.7, 93.7, 93.7, 93.6, 93.7, 93.8, 93.9, 93.8, 93.7, 93.6, 93.7, 93.7, 93.7, 93.7, 93.5, 93.9, 93.8, 93.8, 93.8, 93.8, 93.8, 93.7, 93.8, 93.7, 93.8, 93.8, 93.8, 93.8}
使用Matlab工具对实验数据M2进行线性回归, 得到回归系数估计值b和stats的值为:
b ={ 93.0962, 0.0271, 0.0008, 0.0231}
stats = 0.3766, 9.2611, 0.0001, 0.0060
最后确定的线性回归模型为:
| $y = 93.0962 + 0.0271*{x_1} + 0.0008*{x_2} + 0.0231*{x_3}$ | (9) |
BP神经网络模型的原理如下:
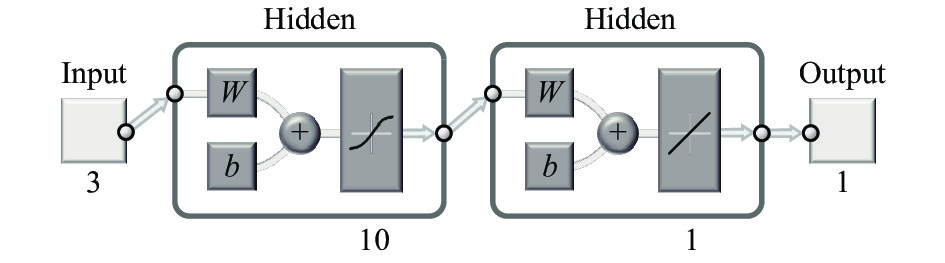
神经网络[14]由输入层(Input)、隐藏层(Hidden)、输出层(Output) 3部分组成, 如图5所示.
|
图 5 神经网络模型 |
数据从输入层, 经过权重值和偏置项的计算后, 再通过激活函数, 得到隐藏层的输出, 同时作为下一输出层的输入; 从隐藏层到输出层又经过权重值和偏置项的计算后, 再通过激活函数, 得到输出层.
BP神经网络[15,16]的基本思想是利用梯度下降法, 使网络的实际输出值和期望输出值的误差均方差为最小. BP算法包括信号的正向传播和误差的反向传播两个过程. 先从输入到输出的方向计算误差, 接着从输出到输入的方向调整权值和阈值. 正向传播时, 若实际输出与期望输出不相符, 则进行误差的反向传播. 误差反向传播过程是将输出误差通过隐藏层向输入层逐层反传, 并调整各单元权值使误差沿梯度方向下降. 最终经过学习训练, 确定最小误差网络的参数.
在图5神经网络模型中各参数为: 输入层是温度、湿度和气压差的三维输入向量x, 隐藏层单元为10, 输入层到隐藏层的权重为w, 偏置项为b, 激活函数为g1(w, b), 隐藏层到输出层的权重值为w', 偏置项为b′, 激活函数为g2(w′, b′), 实际输出值为y, 期望输出值为
| $x = \left( {\begin{array}{*{20}{c}} {{x_1}} \\ {{x_2}} \\ {{x_3}} \end{array}} \right)$ | (10) |
| $w = \left( {\begin{array}{*{20}{c}} {{w_{1,1}}}&{{w_{1,2}}}& \cdots &{{w_{1,10}}} \\ {{w_{2,1}}}&{{w_{2,2}}}& \cdots &{{w_{2,10}}} \\ {{w_{3,1}}}&{{w_{3,2}}}& \cdots &{{w_{3,10}}} \end{array}} \right)$ | (11) |
| $b = \left( {\begin{array}{*{20}{c}} {{b_1}} \\ {{b_2}} \\ \vdots \\ {{b_{10}}} \end{array}} \right)$ | (12) |
| $w' = \left( {\begin{array}{*{20}{c}} {{{w'_1}}} \\ {{{w}_2'}} \\ \vdots \\ {{{w}_{10}'}} \end{array}} \right)$ | (13) |
| $b' = \left( {b'} \right)$ | (14) |
| $y = ( {{y_1}}\;\;{{y_2}}\;\; \cdots \;\;{{y_n}} )$ | (15) |
| $\hat y = ( {{{\hat y}_1}}\;\;{{{\hat y}_2}}\;\; \cdots \;\;{{{\hat y}_n}} )$ | (16) |
期望输出值
| $\hat y = {g_2}\left( {{{w'}^{\rm{T}}}{g_1}\left( {{w^{\rm{T}}}x + b} \right) + b'} \right)$ | (17) |
损失函数
| $E\left( \theta \right) = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} $ | (18) |
实验数据为第1次线性回归方法所使用的数据M1={x1, x2, x3, y}. 其中x1是温度, x2是湿度, x3是当前气压与标准大气压的差值, y是噪声监测值, 共54组实测数据.
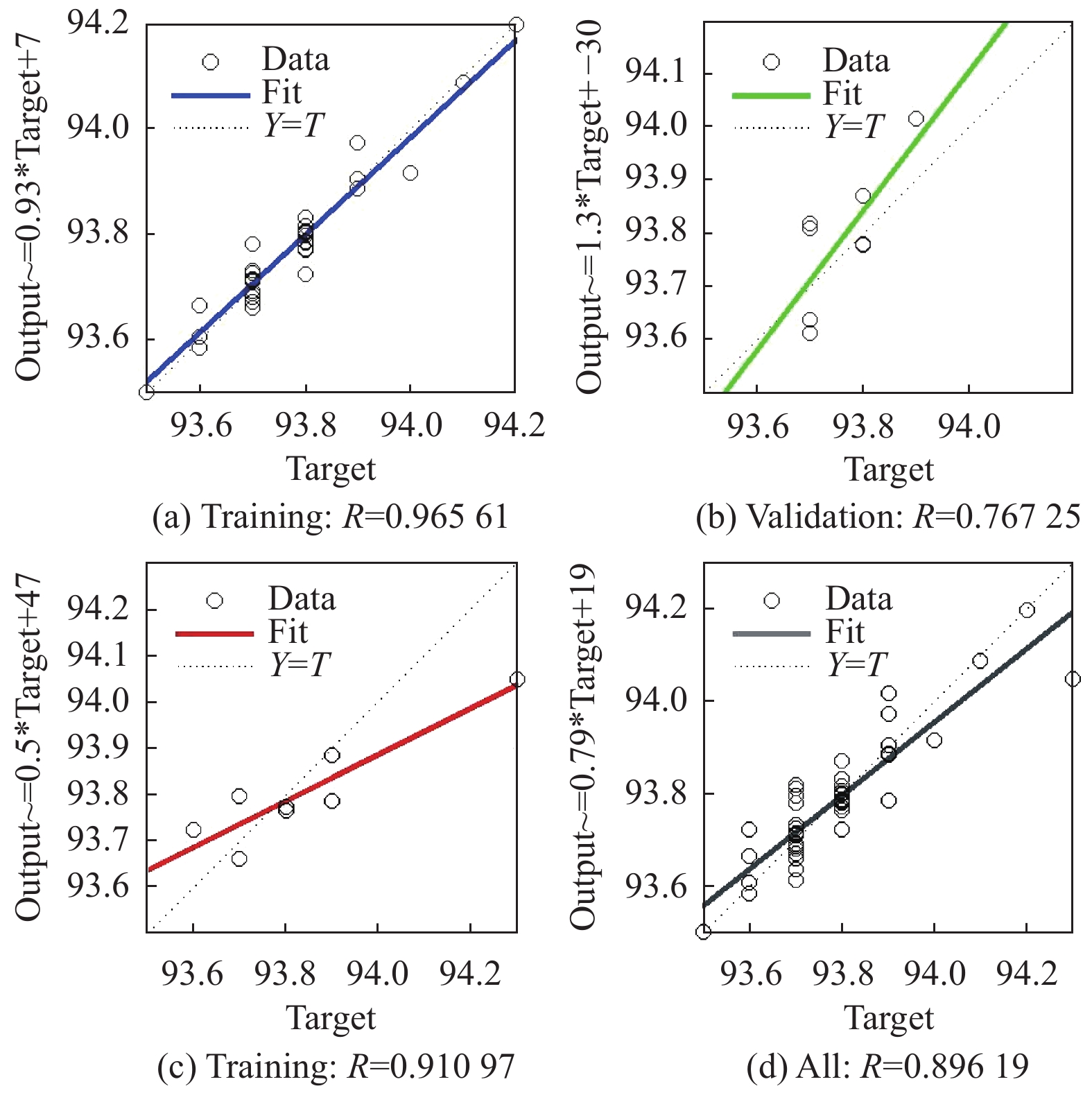
通过Matlab中的BP神经网络工具计算得出实验结果, 如图6所示.
|
图 6 BP神经网络模型结果图 |
实验步骤为: (1)创建BP神经网络; (2)训练神经网络; (3)计算出预测的噪声监测值.
训练出的BP神经网络模型各阈值如下:
输入层到隐藏层的权值w为:
| $\left[ {\begin{array}{*{20}{c}} { - {\text{2.4693 }}}&{ - {\text{0.1280}}}&{ - {\text{1.4486}}}\\ {{\text{0.8020}}}&{{\text{2.4070}}}&{ - {\text{0.7482}}}\\ {{\text{1.0341}}}&{{\text{3.4443}}}&{{\text{0.0986}}}\\ { - {\text{0.7739}}}&{-{\text{3.6847}}}&{2.4399}\\ \text{2.8022}&\text{0.4753}&\text{0.0060}\\ {-1.4424}&{-1.8849}&{3.5153}\\ {-3.9765}&{-0.4528}&{1.1764}\\ {-1.4793 }&{-2.9689}&{-3.9005}\\ {4.8526}&{-0.4672}&{-0.3937}\\ {-1.1197}&{-2.3988 }&{0.6877} \end{array}} \right]$ |
隐藏层各神经元阈值偏置项b为:
| $\left[ {\begin{array}{*{20}{c}} {3.7370}\\ {0.9398}\\ {1.1485}\\ {1.4997}\\ {0.1133}\\ {1.2514}\\ {-1.7257}\\ {-2.5456}\\ {2.7728}\\ {-4.1422} \end{array}} \right]$ |
隐藏层到输出层权值w′为:
| $\left[ {\begin{array}{*{20}{c}} {0.6340}\\ {-1.2380}\\ {1.0986}\\ {-0.6346}\\ {0.3171}\\ {0.5232}\\ {0.4608}\\ {0.9016}\\ {0.3900}\\ {0.1860} \end{array}} \right]$ |
输出层神经元阈值偏置项b′为: −0.0732.
最终回归结果R值如图7所示. 其中, 判定系数R2的值为0.89619×0.89619≈0.8032.
第1次线性回归时判定系数R2的值为0.1507; 第2次线性回归时判定系数R2的值为0.3766; 使用BP神经网络模型进行回归时判定系数R2的值为0.8032, 有了较大的提升.
5 不同时间段相关性分析为了减少因使用不同设备所造成的测量误差, 在每段实验期间使用同一个校准器和声级计相配对.
共使用两个校准器对应两段实验数据:
一段数据时间从12月到5月, 共153组. 平均温度为20.02 ℃(15.51 ℃–28.23 ℃), 噪声值浮动范围略小(93.8 dB–94.1 dB). 使用线性回归方法后得到:
b ={93.4832, 0.0243, −0.0009, 0.0024}
stats =0.8100, 211.7785, 0.0000, 0.0010
另一段数据时间从6月到8月, 共54组. 平均温度为27.76 ℃(24.1 ℃–31.6 ℃), 噪声值浮动范围过大(93.5 dB–94.3 dB). 去除异常点后得到:
b ={ 93.0962, 0.0271, 0.0008, 0.0231}
stats = 0.3766, 9.2611, 0.0001, 0.0060
考虑到校准器误差较小, 当温度升高时, 数据的相关性会相对变小. 通过分析比较不同时间段的不同数据, 结果表明噪声误差主要受温度因素影响, 温度每变化10 ℃, 噪声误差会增加0.2 dB–0.3 dB.
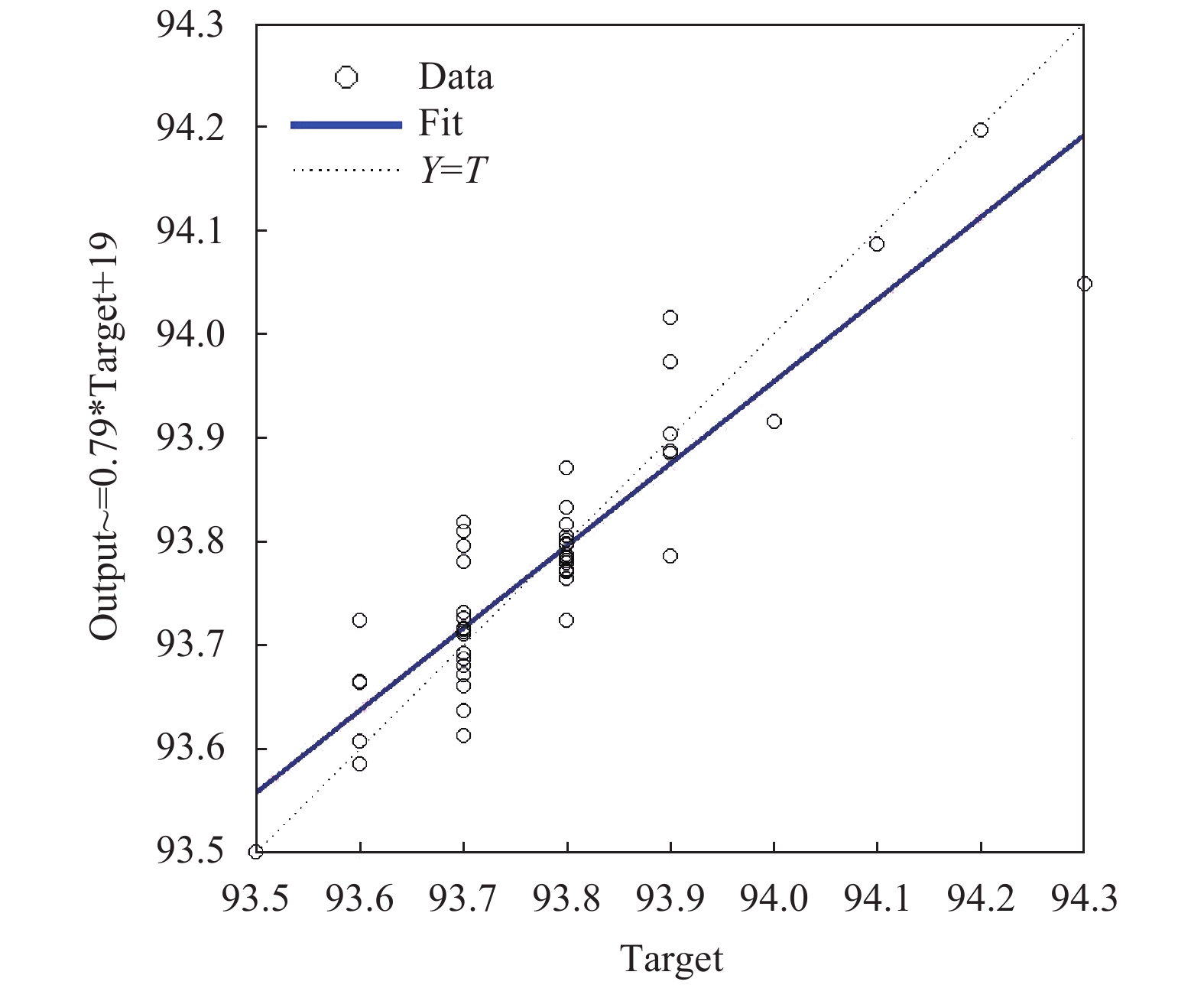
|
图 7 回归结果图 (R=0.896 19) |
6 结论与展望
在建立预测模型的过程中, 分别采用了不同算法来处理相同的实验数据. 实验结果表明, 使用BP神经网络方法相对于使用线性回归算法, 其判定系数R2值有了较大提高. 表明了噪声监测系统实验中涉及的温度、湿度、大气压3因素确实存在一定程度的线性相关, 但从总体上看, 存在更多的是非线性相关. 线性回归算法在处理数据时, 如果去掉少数残差异常点后, 相关系数会有较大提升. 而采用BP神经网络方法可以直接处理数据, 允许存在个别误差较大的异常点. 表明了用BP神经网络建立的模型容错能力更高, 可以更准确地自动校正噪声监测值, 改进了噪声监测的精度.
线性回归和BP神经网络应用于ENS噪声监测系统中, 满足了社会发展需求, 相应地改善了城市噪声环境, 节省大量人力资源.
| [1] |
孟苏北. 环境噪声自动连续监测系统在噪声监测中的作用. 现代仪器, 2006, 12(5): 38-41. |
| [2] |
钟国策. 声级计的工作原理. 电声技术, 2002(1): 65-66. DOI:10.3969/j.issn.1002-8684.2002.01.024 |
| [3] |
陈剑林, 白滢, 牛锋, 等. 声级计的频率计权特性. 计量技术, 2008(6): 47-50. |
| [4] |
浦云明, 汪志华, 乔峰, 等. ENS3000噪声监测系统研究与实现. 集美大学学报(自然科学版), 2015, 20(3): 236-240. DOI:10.3969/j.issn.1007-7405.2015.03.014 |
| [5] |
牛滨, 孙晶华, 丁新心. 噪声监测系统的设计与实现. 哈尔滨理工大学学报, 2009, 14(3): 131-134. DOI:10.3969/j.issn.1007-2683.2009.03.033 |
| [6] |
蒋渭鑫. 测量声级校准器产生的声压级对温度和气压依赖关系的方法. 电声技术, 1995(7): 28-30. |
| [7] |
何龙标, 白滢, 裘剑敏, 等. 实验室标准传声器静压和温度修正系数的测量. 计量学报, 2012, 33(4): 336-339. DOI:10.3969/j.issn.1000-1158.2012.04.11 |
| [8] |
桂桂, 姚小兵, 鄂治群, 等. 噪声监测系统传声器的温度特性实验研究. 中国测试, 2017, 43(10): 123-126. DOI:10.11857/j.issn.1674-5124.2017.10.024 |
| [9] |
王松桂. 线性统计模型: 线性回归与方差分析. 北京: 高等教育出版社, 1999.
|
| [10] |
Groemping U. Relative importance for linear regression in R: The package relaimpo. Journal of Statistical Software, 2006, 17(1): 1-27. DOI:10.1360/jos170001 |
| [11] |
田垅, 刘宗田. 最小二乘法分段直线拟合. 计算机科学, 2012, 39(S1): 482-484. |
| [12] |
谢明文. 关于协方差、相关系数与相关性的关系. 数理统计与管理, 2004, 23(3): 33-36. DOI:10.3969/j.issn.1002-1566.2004.03.008 |
| [13] |
Zeng HP, Li YT, Xu HY, et al. The noise monitoring system and automatic correction algorithm. International Journal of Multimedia and Ubiquitous Engineering, 2016, 11(9): 265-276. |
| [14] |
Bishop CM. Neural networks for pattern recognition. Oxford: Oxford University Press, 1995.
|
| [15] |
Le Cun Y, Boser B, Denker JS, et al. Handwritten digit recognition with a back-propagation network. Proceedings of the 2nd International Conference on Neural Information Processing Systems. Denver, CO, USA. 1989. 396–404.
|
| [16] |
Hecht-Nielsen R. Theory of the backpropagation neural network. Proceedings of International 1989 Joint Conference on Neural Networks. Washington, DC, USA. 2002. 593–605.
|
 2021, Vol. 30
2021, Vol. 30



