2. 复旦大学 智能机器人教育部工程研究中心, 上海 200433;
3. 复旦大学 大数据学院, 上海 200433;
4. 复旦大学 上海智能机器人工程技术研究中心, 上海 200433
2. Engineering Research Center of AI & Robotics, Ministry of Education, Shanghai 200433, China;
3. School of Data Science, Fudan University, Shanghai 200433, China;
4. Shanghai Engineering Research Center of AI & Robotics, Shanghai 200433, China
随着全球经济和金融市场的蓬勃发展, 作为金融市场的前沿领域, 衍生品市场的重要组成部分, 期货市场的健康发展对于国民经济和国家经济安全的重要性越来越高, 具有越来越大的战略意义. 对期货价格的预测可以在宏观层面帮助预研预判经济形势, 改善宏观调控的预见性和有效性, 观察和分析期货市场的价格波动, 可以预测未来某一领域和宏观经济走向的状况, 更有效地揭示和判断宏观经济的运行状况.
期货价格走势的预测主要分为基本面分析和技术分析. 基本面分析是依据期货品种的行业和宏观基本面的情况来预测未来走势. 比如某些事件的发生往往会引起资产价格显著的波动, 相关经济数据的公布也会对市场走势产生明显的影响. 技术分析则是假定历史是相似的或者是可以重演的, 通过数据和因子的挖掘来进行分析预测. 多年来, 随着技术的进步和发展, 各种类型的预测思路被不断地提出, 尤其是深度神经网络产生以来, 因其强大的非线性拟合的能力和较强的适应能力, 逐渐被应用于金融资产价格的分析和预测中[1].
本文旨在从期货的历史数据中捕捉到潜在有用的特征, 并结合相应的模型来对期货走势进行预测, 并提供对比试验分析, 辅助投资策略的制定, 为神经网络模型在金融市场的应用提供一定的理论和实验基础.
1 研究现状时间序列数据预测工作本质上与机器学习方法分类中的回归分析之间存在着紧密的联系, 人工神经网络被看作实现时间序列预测的有效工具[2].
徐浩然等[3]从股票预测研究的主要问题、特征工程和机器学习算法应用等3个方面, 对近年来该领域的主要文献进行总结, 并针对每种算法在应用中的特点与不足进行评述. 围绕目前机器学习在股票预测上遇到的主要问题, 从迁移学习、特征工程、深度学习模型融合等方面进行了深入的分析与展望. 张栗粽等[4]针对Elman神经网络模型, 通过引入时间权重与随机性因素, 提出了改进的Elman神经网络模型, 提高了现有Elman神经网络针对时序数据预测的精度, 实验结果表明, 所提出的模型在金融时序预测中具有更好的准确度. 李秀枝等[5]率先拓展了双权可拓神经网络模型在股指期货预测分析领域的应用研究, 详细描述了两种双权可拓神经网络结构设计、算法过程, 并且通过实验验证了该模型在股指期货预测分析领域的可行性和有效性.
在深度神经网络中, 循环神经网络被认为是一类较好预测时间序列的模型. 由于前馈神经网络的输入只依赖当前输入, 因此难以处理时序数据. 而循环神经网络通过自身反馈神经元, 可以处理任意长度的时序数据. LSTM、GRU是常见的循环神经网络结构. 王婷等[6]采用LSTM来处理长距离的股票时序问题, 构建了一个多类别特征体系作为长短期记忆网络的输入进行训练, 通过实验全面分析了各类特征对股票趋势预测的有效程度, 对比结果表明了多类别特征体系在预测中的良好表现. 黄婷婷等[7]利用堆叠去噪自编码从金融时间序列的基本行情数据和技术指标中提取特征, 将其作为LSTM神经网络的输入, 获得了比较高的预测精度. 刘翀等[8]使用深度LSTM网络对金融数据进行建模, 解决了数据间长依赖的问题, 并能学习到更加复杂的市场动态特征, 该模型引入了注意力机制, 使得不同时间的数据对预测的重要程度不同, 预测更加精准. Qin等[9]结合了注意力机制实现的时间序列的预测, 不仅在解码器的输入阶段引入注意力机制, 还在编码器阶段引入注意力机制, 通过在编码层和解码层都引入双向注意力机制实现时间序列更好的预测. 本文将注意力机制和LSTM相结合起来, 试图提高模型在期货投资策略中的效果.
遗传算法常用于模型参数调节. 武大硕等[10]提出了基于遗传算法改进的LSTM神经网络股指预测分析方法, 分别应用3种模型对纳斯达克数据进行预测, 实验结果表明所提方法较其他两种方法在股票波动较小的阶段准确度得到了显著提升, 在股票波动较大的阶段也可对其基本趋势进行预测. 包振山等[11]利用遗传算法解决调参问题来保证模型预测的平衡性, 实验得出改进模型的各方面指标均优于单独的LSTM模型.
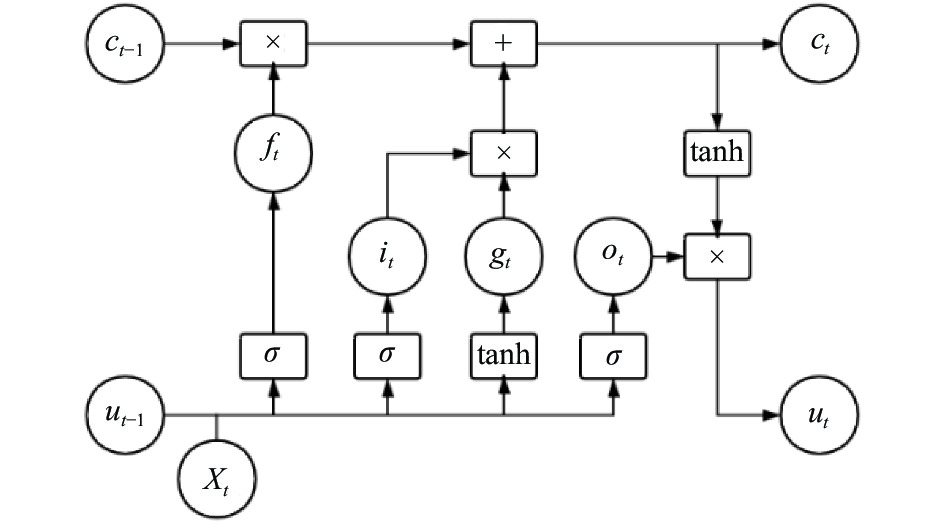
2 相关理论与模型 2.1 LSTM神经网络LSTM神经网络是一种特殊的循环神经网络. LSTM (Long-Short Term Memory)可以解决传统循环神经网络中存在的梯度消失和梯度爆炸问题, 也就是较远的消息间隔难以进行传递的问题. LSTM神经元中设计了许多控制数级的门(gates), 包括输入门(input gates), 遗忘门(forget gates), 输出门(output gates). 输入门控制有多少信息可以流入记忆细胞(memory cell)中, 遗忘门控制有多少上一时刻的记忆细胞中的信息可以流入当前时刻的记忆细胞中, 输出门控制有多少当前记忆细胞中的信息可以流进隐藏状态中. LSTM神经元结构如图1所示.
|
图 1 LSTM神经元结构 |
LSTM网络引入一个新的内部状态
首先利用上一时刻的隐藏状态
| ${i_t} = \sigma ({W_i} * {x_t} + {U_i} * {u_{t - 1}} + {b_i})\;\;$ | (1) |
| ${f_t} = \sigma ({W_f} * {x_t} + {U_f} * {u_{t - 1}} + {b_f})\;\;$ | (2) |
| ${o_t} = \sigma ({W_o} * {x_t} + {U_o} * {u_{t - 1}} + {b_o})\;\;$ | (3) |
| ${g_t} = {\rm{tanh}}({W_g} * {x_t} + {U_g} * {u_{t - 1}} + {b_g})\;\;$ | (4) |
然后根据上一个时刻的记忆单元
| ${c_t} = {f_t} \odot {c_{t - 1}} + {i_i} \odot {g_t}$ | (5) |
| ${u_t} = {o_t} \odot {\rm{tanh}}({c_t})\;\;$ | (6) |
这样, 每一个时间步都接收到了上一个时间步的隐藏状态u, 并将本时间步的输出u和x一起作为下一个时间步的输入, 使得较长时间的信息得以保留并影响输出.
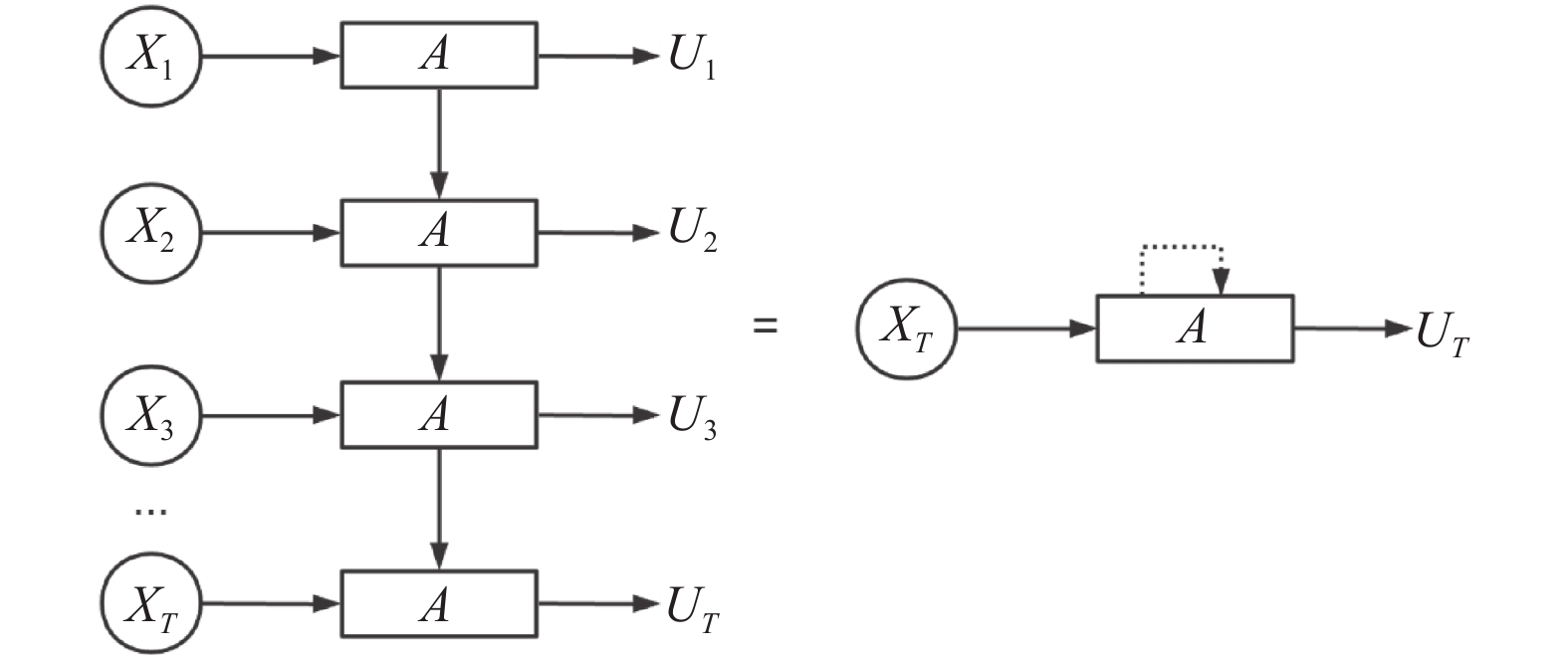
如果按照时间顺序将LSTM展开, 那么时间步为T的时间序列, 输入到LSTM网络中如图2所示. 其中A代表LSTM神经元, 隐藏层的输出记为u.
|
图 2 LSTM按时间步展开 |
2.2 注意力机制
注意力机制是受认知神经学中注意力的启发, 人脑在处理复杂的外部信息时, 会有意或无意地从大量输入信息中选择一小部分重点处理而忽略其他信息, 这种能力称为注意力(attention). 神经网络在处理较多的输入信息时, 也可以借鉴人脑的注意力机制, 只选择一些关键的信息进行处理. 如果选择的信息是所有输入向量在注意力分布下的期望, 那么称为软性注意力机制; 反之, 若只关注其中某一个输入向量, 称为硬性注意力机制[12].
软性注意力机制的计算一般分为两步: 一是计算在所有输入信息上的注意力分布, 即权重; 二是根据注意力分布计算输入信息的加权平均. 通过赋予不同权重来反映各种信息的重要程度.
为了从n个输入向量
首先, 计算在给定q和X下, 选择第i个输入向量的概率:
| $ \begin{split} {a_n} &= P({\textit{z}} = n|X,q)\; = softmax(s({x_n},q))\\ &= \exp (s({x_n},q))\Bigg /\sum\limits_{j = 1}^N {\exp (s({x_j},q))} \end{split} $ | (7) |
其中, z表示选择了第几个输入向量,
1)加性模型
| $s(x,q) = {v^{\rm{T}}}\tanh(W * x + U * q)\;\;$ | (8) |
2)点积模型
| $s(x,q) = {x^{\rm{T}}} * q\;$ | (9) |
3)双线性模型
| $s(x,q) = {x^{\rm{T}}} * W*q\;$ | (10) |
4)缩放点积模型
| $s(x,q) = {x^{\rm{T}}} * q\;/\sqrt D $ | (11) |
其中, W、U、v是可学习的参数, D为输入向量的维度. 加性模型和点积模型的复杂度相当, 双线性模型是一种泛化的点积模型, 缩放点积解决了当输入向量维度较高时点积模型方差较大导致softmax函数的梯度较小的问题.
其次, 根据注意力分布
| $att(X,q) = \sum\limits_{n = 1}^N {{a_n}{x_n}} $ | (12) |
本文模型中对注意力机制部分的具体处理过程将在第3节详细描述.
2.3 遗传算法遗传算法(Genetic Algorithm, GA)是基于自然选择和遗传变异等生物进化机制, 模仿自然界生物进化机制发展起来的随机全局搜索和优化方法. 其本质是一种高效、并行、全局搜索的方法, 能在搜索过程中自动获取和积累有关搜索空间的知识, 并自适应地控制搜索过程以求得最佳解. 遗传算法的实现过程大致分为以下步骤:
初始化种群(population): 先通过编码把要求的问题的可行解表示成遗传空间的染色体或个体.
适应度(fitness): 适应度是个体在种群生存的优势程度, 采用适应度函数或评价函数进行度量.
选择(select): 它定义了为进一步的复制而保留的解决方案. 例如轮盘赌选择法, 锦标赛选择法.
交叉(crossover): 它描述了如何从现有的解决方案创建新的解决方案. 例如n点交叉.
变异(mutation): 它的目的是通过随机交换或关闭解决方案, 将多样性和新奇性引入到解决方案池(solution pool)中. 例如二进制变异.
由于本文采用的是循环神经网络模型, 循环神经网络中的循环的结构使它们难以并行化, 因此训练循环神经网络需要大量的时间. 通过遗传算法来对循环随机网络进行参数调优, 又会更进一步造成整个模型的调优时间增加, 因此, 让遗传算法能够更快速地收敛十分重要.
从上述过程中可以知道, 交叉算子负责组合优化基因, 变异算子负责广泛搜索整个空间, 选择算子负责选出适应值高的解. 交叉与变异均是无指导性的操作, 所以必须由选择算子保证群体朝着预期的目标进化. 通过选择算子, 适应值优秀的个体将会有更多机会被选中成为下一代群体的父代[13]. 基于这一点, 本文对遗传算法中的选择算子部分进行了改进, 以加快遗传算法的收敛速度.
遗传算法常用的选择算子是轮盘赌选择法. 传统的轮盘赌选择法首先将种群中所有个体的适应度值进行累加然后归一化, 然后通过随机数对随机数落在的区域对应的个体进行选取, 类似赌场里面的旋转的轮盘. 各个个体的选择概率和其适应度值成比例, 适应度越大, 选中概率也越大.
为了加快收敛速度, 本文模型采用改进后的轮盘赌选择法. 在传统的轮盘赌选择法中, 由于每次需要对种群中所有适应度进行遍历搜索, 因此算法的时间复杂度依赖于种群数N, 为O(N)或O(logN). 通过使用基于随机接受(stochastic acceptance)的方法来进行轮盘赌选择, 可以将时间复杂度降低为O(1)[14].
3 模型构建模型构建包括: 数据处理, LSTM神经网络层, 注意力机制层, 全连接层, 遗传算法调优. 模型整体流程如图3所示.
3.1 数据处理选择以下5种常用的技术指标作为输入特征:
MA(n): n日移动平均线=n日收市价之和/n.
RSI(n): 相对强弱指标, 一定时期内总上涨幅度和总下跌幅度的比率, 反映了市场在一定时期内的景气程度. n为可调参数.
CCI(n): 顺势指标, 测量资产价格是否已超出常态分布范围. n为可调参数.
WILLER(n): 利用摆动点来度量市场的超买超卖现象, 所以可以此预测循环周期内的高和低点, 找出其有效信号, 可以用于分析市场短期行情走势. n为可调参数.
OBV: 是通过累计每日的需求量和供给量并予以数字化, 制成趋势线, 然后配合证券价格趋势图, 从价格变动与成交量增减的关系上, 来推测市场气氛的一种技术指标.
特征设置完成后, 按照一定比例将总样本划分为训练集(train set), 验证集(validation set)和测试集(test set). 对训练集进行均值方差归一化. 为避免使用未来数据影响到模型效果, 将训练集上得到的包含均值方差的归一化因子用于验证集和测试集的归一化.
设样本数量为batch_size, 表示神经网络每次训练可以处理的样本数量. 设时间步为n_steps, 表示使用过去多少步的数据来对未来进行预测. 设特征数量为n_features, 表示选择多少种特征, 在该模型中就是上述介绍的技术指标的数量. 最后按照LSTM神经网络层的输入格式将样本数据整理成[batch_size, n_steps, n_features]形状.
3.2 LSTM神经网络层LSTM层需要设置的相关参数如下, 在PyTorch包中可以通过hidden_size设置每一层隐藏态神经元的个数, 通过n_layers设置包含多少层, 通过bidirectional参数设置LSTM是否为双向. 本文模型设置n_layers为2层, 单向LSTM.
在单向LSTM情况下, LSTM层的输入数据的维度为[batch_size, n_steps, n_features], 输出数据的维度为[batch_size, n_steps, hidden_size].
3.3 注意力机制层目前各类的注意力机制很多, 由于期货数据属于金融时间序列, 每一时刻的交易行情都会受到历史行情不同程度的影响, 为了更好地体现出历史行情对当前行情的影响程度的不同, 在本文模型中选择对LSTM层的输出数据中的时间步参数n_steps来做注意力机制, 即赋予滞后各时间步的数据以不同的注意力. 算法优化的目标为时间步权重参数W. 具体算法流程如算法1.
算法1. 时间步注意力机制算法
1)获得LSTM神经网络层的输出, 作为注意力机制层的输入x, 即
2)使用Linear线性变换函数和
3)再将样本按照n_steps列输入到
4)将第1)步中的初始样本x和权重向量W相乘得到赋予权重W后的样本
5)最后将样本按照n_steps列进行求和, 得到注意力机制层最终的输出.
本文采用的注意力机制中的查询向量q为对应的因变量, 即下文中数据样本的收盘价(CLOSE). 因此在神经网络训练过程中权重W会随着q得到动态调整.
硬性注意力机制基于最大采样或者随机采样的方式选择信息, 易导致最终的损失函数与注意力分布之间的函数关系不可导, 无法在反向传播时进行训练[12]. Kim等[15]在2018年提出了双线性注意力网络(Bilinear Attention Networks, BAN), 基于VQAv2数据集获得了比之前的方法更好的效果, 证明了双线性打分函数的优越性. 因此本文采用软性注意力机制以及双线性模型打分函数. 使用双线性打分函数作为选择某个时间步的概率计算方法, 在网络设计时用一个全连接层来实现. 在特征维度上, 时间权重是共享的, 即同一时间步上各个特征对应的权重是相同的, 将各个时间步的权重赋给各个特征并求和, 得到每个特征经过时间加权以后的最终特征向量, 作为下一层的输入.
整个注意力机制层的的输入维度为[batch_size, n_steps, hidden_size], 输出维度为[batch_size, hidden_size].
3.4 全连接层全连接层的神经元的个数为1, 输入维度为[batch_size, hidden_size], 输出维度为[batch_size, 1]. 其中hidden_size与之前LSTM层所设置的hidden_size相等. 全连接层使用使用Linear线性变换函数实现.
在全连接层主要实现的功能就是将注意力机制层的输出转换为所预测的目标, 本文模型以收盘价为预测目标, 也就是将注意力机制层的输出转换为收盘价.
3.5 遗传算法调优本文将LSTM超参数n_steps、hidden_size以及所有技术指标中的参数n设置为待优化参数, 随机产生初始种群.
设置模型在验证集(validation set)上的均方根误差(RMSE)为一个适应度值. 计算每个个体的适应度, 并判断是否满足优化准则.
依据适应度选择再生个体, 适应度高的个体被选中的概率高, 反之, 适应度低的个体被选中的概率低, 甚至可能被淘汰. 在选择过程中使用改进后的基于随机接受(stochastic acceptance)的方法来进行轮盘赌选择.
设置交叉概率和交叉方法, 变异概率和变异方法, 生成子代个体.
循环计算适应度, 由交叉和变异产生新一代种群, 定义迭代次数, 在算法运行结束后将产生k个最佳解决方案, 那么就可以很快得到第1个方案作为最佳方案.
4 实验分析 4.1 实验环境实验计算机的配置: AMD Ryzen 9 3950X 4.2 GHz, 内存64 GB, 显卡Nvidia GeForce GTX 1070Ti 8 GB显存. 操作系统: Windows 10 专业版. 软件环境: PyCharm Professional 2020.1. 采用Python 3.7.4编写实验程序. 所使用的深度学习框架为PyTorch 1.5.1, 遗传算法库为Deap 1.3.1.

|
图 3 模型流程示意图 |
4.2 实验数据获取
选取中证500股指期货IC主力合约作为研究对象进行实验, 样本区间跨度从2019年1月3日到2020年5月29日一共340个交易日, 样本时间单位为分钟, 数据源来自万德金融数据库. 将样本的前240个交易日作为模型的训练集和验证集, 后100个交易日作为模型的测试集, 用于测试模型的预测效果. 数据标签即预测对象设置为下一时刻的收盘价(CLOSE), 经过处理后的前240个交易日的样本共计57985条, 其中前80%为训练集, 共46388条, 后20%为验证集, 共11597条. 经过处理后的后100个交易日的样本为测试集样本, 共计24140条. 图4是全样本收盘价走势图.

|
图 4 全样本收盘价走势图 |
4.3 模型训练
模型权重初始化采用随机初始化方法. 学习率(learning rate)设置为0.001, epoch设置为100, batch_size设置为128, 为了降低训练过程中的过拟合, 设置dropout参数并运用早停法(early stopping). 模型采用RMSProp 优化器. 评价函数使用均方根误差(RMSE).
4.4 信号转换在得到收盘价预测值之后, 进行一阶差分得到收益率, 将收益率转换为类别信号, 类别的设置分为3类, 大于0时为1, 小于0时为−1, 等于0为0.
获得信号后, 按照以下规则进行仓位操作: 在连续获得6个下跌信号时进行开多, 之后在获得1个上涨信号时进行平多. 在连续获得5个上涨信号时进行开空, 之后在获得1个下跌信号时进行平空.
4.5 实验结果进行4组对比试验, 分别为LSTM, LSTM-GA, LSTM-Attention, LSTM-Attention-GA, 其中GA代表经过遗传算法优化后的模型, Attention代表模型采用了注意力机制.
图5展示训练后的各模型在测试集上的拟合情况. 由图可知, 随着时间的推移, 虽然各模型预测值与真实值的差距较大, 但是各模型预测的收盘价与真实的收盘价的趋势基本相同. 为提高模型泛化能力, 减少模型在测试集上过拟合, 本文中遗传算法所设置的优化目标是各模型在验证集的RMSE.
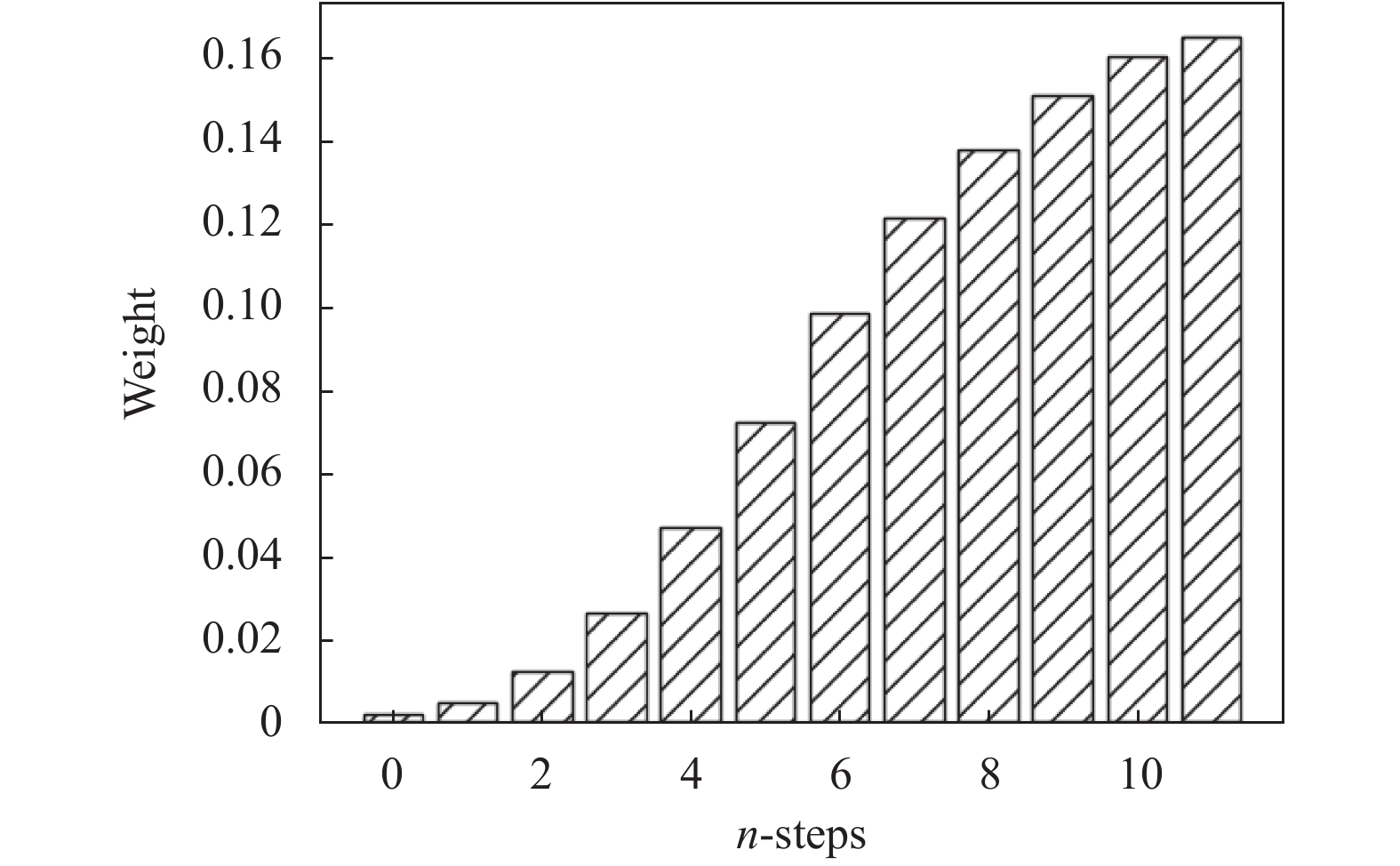
加入注意力机制的模型会对时间步n_steps的权重进行调整, 图6展示测试集第1个交易日(20191227)在时间步n_steps为12的情况下, LSTM-Attention-GA模型调整后的时间步权重的分布情况. 本文数据以分钟为单位, n_steps为12表示使用前12分钟的数据来对下1分钟的数据进行预测. 其中横坐标0表示前12分钟, 11表示前1分钟, 随着时间的推移, 其所占的权重也逐渐增加. 这说明越相近的时间所产生的影响越大, 越相远的时间所产生的影响越小.

|
图 5 各模型在测试集上的拟合图 |
|
图 6 时间步权重分布图 |
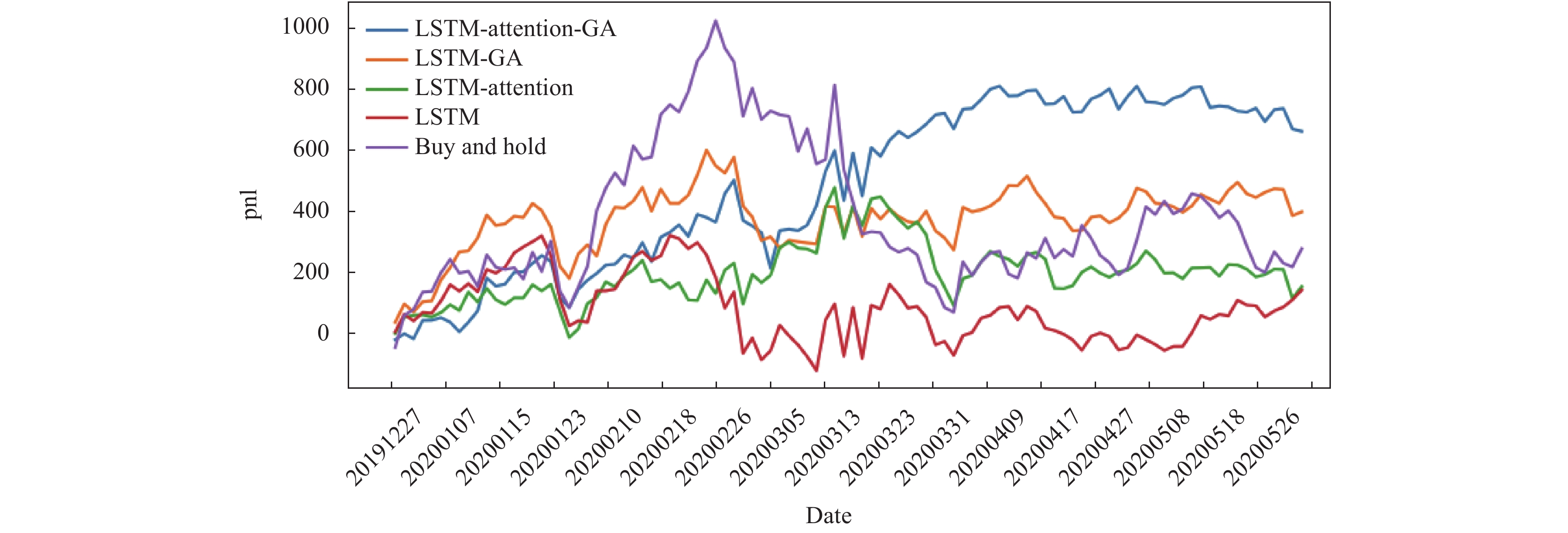
图7展示模型对比实验的回测结果. 为简化实验, 不考虑交易成本, 采用日内交易, 即当天必须平仓. 没有杠杆, 既可以开多仓又可以开空仓. 每次交易单位为1报价单位. 模型评测指标包括: 测试集RMSE, 测试集的整体收益, 测试集的收益的夏普比率, 测试集的最大回撤. Buy and Hold策略表示在每一个交易日都开盘买入收盘卖出. 为更准确对比模型效果, 也将本文模型与Buy and Hold策略进行对比.
通过pnl (profit and loss)曲线可以看出随着时间的延长, 短期时模型之间的区别并不明显, 但是在长期来看LSTM-Attention-GA模型和LSTM-GA模型更加有效, 并且LSTM-Attention-GA模型要比没有引入注意力机制的LSTM-GA模型效果更好, 这说明加入注意力机制层后的模型的长期有效性得到了增强.
以LSTM-Attention模型为例, 表1展示的是在经过遗传算法调优前后的参数对照. 可以看出所有的模型参数都得到了调优. 结合表2的回测结果作为比较, 可以看出经过遗传算法参数调优的模型效果普遍比没有经过参数调优的模型要好, 没有经过参数调优的模型甚至夏普比率和收益都要劣于Buy and Hold策略的效果, 这也说明了通过遗传算法参数调优后, 模型的泛化能力得到增强.
本文还对传统遗传算法的选择算子做了改进, 采用基于随机接受的方法来进行轮盘赌选择, 加快遗传算法的收敛速度. 图8和图9分别展示在迭代过程中, 每一轮优秀子代的最佳适应度收敛曲线对比图和平均适应度收敛曲线对比图. 从图8可以看出, 基于随机接受轮盘赌选择法的遗传算法, 其在训练过程中的收敛速度要明显比基于传统轮盘赌选择法的遗传算法要快, 基于随机接受轮盘赌选择法在第2次迭代后子代最佳适应度就基本趋于收敛, 而基于传统轮盘赌选择法要在第10次迭代后子代最佳适应度才趋于收敛. 这说明了改进后的遗传算法可以提高模型参数调优的收敛速度. 另外, 通过图9可以看出, 基于随机接受轮盘赌选择法的遗传算法在训练过程中的子代平均适应度波动要比基于传统轮盘赌选择法在训练过程中的子代平均适应度的波动要小.
|
图 7 回测结果对比图 |
| 表 1 参数调优对照表 |
| 表 2 回测结果对照表 |
5 结论与展望
本文首先介绍了对于期货价格预测所出现的不同方法, 接着提出一种改进的基于长短期记忆神经网络的LSTM-Attention-GA模型, 该模型结合了注意力机制和遗传算法. 然后介绍了实验所需的软硬件, 数据的获取和处理过程. 最后通过对比实验显示了我们构建的LSTM-Attention-GA模型实现了用于期货投资策略的有效性, 解决了传统LSTM神经网络对金融时间序列预测不佳的问题, 因此对神经网络模型在金融市场的应用具有重大意义.

|
图 8 子代最佳适应度收敛曲线对比图 |
在未来的工作中, 可以拓展的方向包括挖掘更多更有效的因子; 改为使用更高频数据甚至tick级别的数据来进行训练, 因为更多的数据将有利于模型对于数据特征的进一步发掘. 还包括如何构建更优的模型来降低训练中的过拟合, 以及模型训练速度慢的问题. 另外, 遗传算法也可能会陷入局部最优值而非得到全局最优值, 如果防止这种情形以及如何进一步提高预测效果, 也都是接下来所要进一步研究的方向.

|
图 9 子代平均适应度收敛曲线对比图 |
| [1] |
Shah D, Isah H, Zulkernine F. Stock market analysis: A review and taxonomy of prediction techniques. International Journal of Financial Studies, 2019, 7(2): 26. DOI:10.3390/ijfs7020026 |
| [2] |
杨海民, 潘志松, 白玮. 时间序列预测方法综述. 计算机科学, 2019, 46(1): 21-28. DOI:10.11896/j.issn.1002-137X.2019.01.004 |
| [3] |
徐浩然, 许波, 徐可文. 机器学习在股票预测中的应用综述. 计算机工程与应用, 2020, 56(12): 19-24. DOI:10.3778/j.issn.1002-8331.2001-0353 |
| [4] |
张栗粽, 王谨平, 刘贵松, 等. 面向金融数据的神经网络时间序列预测模型. 计算机应用研究, 2018, 35(9): 2632-2637. DOI:10.3969/j.issn.1001-3695.2018.09.017 |
| [5] |
李秀枝, 孟志青. 可拓神经网络模型及其股指期货分析研究. 计算机科学, 2014, 41(S2): 440-446. |
| [6] |
王婷, 夏阳雨新, 陈铁明. 基于多类别特征体系的股票短期趋势预测. 计算机科学, 2020, 47(S2): 491-495. |
| [7] |
黄婷婷, 余磊. SDAE-LSTM模型在金融时间序列预测中的应用. 计算机工程与应用, 2019, 55(1): 142-148. |
| [8] |
刘翀, 杜军平. 一种基于深度LSTM和注意力机制的金融数据预测方法. 计算机科学, 2020, 47(12): 125-130. DOI:10.11896/jsjkx.200700050 |
| [9] |
Qin Y, Song DL, Cheng HF, et al. A dual-stage attention-based recurrent neural network for time series prediction. Proceedings of the 26th International Joint Conference on Artificial Intelligence. Melbourne, Australia. 2017. 2627–2633.
|
| [10] |
武大硕, 张传雷, 陈佳, 等. 基于遗传算法改进LSTM神经网络股指预测分析. 计算机应用研究, 2020, 37(S1): 86-87, 107. |
| [11] |
包振山, 郭俊南, 谢源, 等. 基于LSTM-GA的股票价格涨跌预测模型. 计算机科学, 2020, 47(S1): 467-473. |
| [12] |
邱锡鹏. 神经网络与深度学习. 北京: 机械工业出版社, 2020. 141–143, 193–196.
|
| [13] |
陈有青, 徐蔡星, 钟文亮, 等. 一种改进选择算子的遗传算法. 计算机工程与应用, 2008, 44(2): 44-49. DOI:10.3778/j.issn.1002-8331.2008.02.014 |
| [14] |
Lipowski A, Lipowska D. Roulette-wheel selection via stochastic acceptance. Physica A: Statistical Mechanics and Its Applications, 2012, 391(6): 2193-2196. DOI:10.1016/j.physa.2011.12.004 |
| [15] |
Kim JH, Jun J, Zhang BT. Bilinear attention networks. Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal, QC, Canada. 2018. 1571–1581.
|
 2021, Vol. 30
2021, Vol. 30



