近年来, 电力需求的增长使得包括风能在内的可再生能源变得越来越重要[1]. 风速变化具有很强的随机性和间歇性, 这种不稳定性会严重影响电力系统的安全, 对及时可靠的风速预测提出了严峻的挑战[2].
在过去的几十年中, 科学家们已经提出了各种方法以增强风速预测的性能. 这些方法大致分为以下3类[3]: 物理方法、统计方法以及机器学习方法. 物理方法主要通过利用气象因素和地理因素等物理参数来预测风速. 但是, 物理模型的计算成本高且无法捕获气象因素复杂的动态变化关系, 因此不适用于短期风速预测. 统计方法利用历史时间序列中各个变量的线性关系来构建统计模型, 如时间序列方法[4]、自回归移动平均(ARMA)方法[5]和卡尔曼滤波方法[6]等, 这些方法克服了物理模型的缺点, 但它们只能分析历史时间序列中变量之间的线性关系, 难以处理气象要素之间的非线性关系. 机器学习如支持向量机(SVM)[7]、多层感知器(MLP)[8]和极限学习机(ELM)[9]可以提取风速时间序列中的复杂非线性特征, 并在一定程度上提高预报的准确性. 但这些传统的线性和非线性模型只能提取浅特征, 并且需要进行大量的特征工程, 无法自动提取时间序列特征. Wang等[10]提出了一种基于集成方法的卷积神经网络模型来实现概率性风电功率预测, 并通过案例研究验证了该模型的准确性和稳定性. Ghaderi等[11]使用基于STC的长短期记忆网络模型进行风速预测. Hu等[12]成功设计了基于DBN和传递学习的有效风速模型. Zaytar等[13]使用多个堆叠的LSTM映射相同长度的天气值序列以预测未来24–72小时的风力变化情况, 但仅针对单个城市研究, 并未考虑其相邻地域的影响.
深度学习使用分布式的分层特征表示方法[14]自动提取数据中的从最低层到最高层固有的抽象特征和隐藏不变结构[15]. 为了充分利用单个模型的优点并提高预测性能, 现已提出了许多组合模型. 此外, 最近的一项研究表明目标站点的风速与其相邻站点之间存在显著的互相关[16,17]. 因此, 每个站点的时空相关数据量不断增加, 使用STC时空相关模型探索风速预测的方法已成为研究的热点. STC模型可以有效利用每个站点的地理特征, 解决某些站点缺少风速数据的问题, 并获得良好的预测结果.
如上所述, 现有模型可以在一定程度上改善预报性能, 但未考虑对气象因素的处理也尚未具备同时提取时空特征的能力. 因此, 本文通过结合CNN和LSTM来构建MFSTC(多因素时空相关)模型, 以克服上述缺点并实现更准确、可靠的风速预测. 本文主要工作如下:
(1) 构建了一种基于三维矩阵的数据表示方法, 该矩阵包含每个站点在多个历史时间点的全部特征气象要素的值, 可以有效解决某些站点缺少风速数据的困难;
(2) 提出了一个MFSTC模型, 该模型同时考虑时间、地点和气象因素之间的多种时空相关性, 从多个方面提高风速预报的准确率;
(3) 针对多个站点, 综合PCA-LASSO两种算法提取特征气象要素集, 避免了冗余因素对预测精度的不利影响, 同时也简化了模型计算量;
(4) 为了同时提取风速数据的时空相关性特征, 开发了具有多输入单输出组合结构的CNN-LSTM模型. 该组合模型不仅能够充分利用CNN良好的空间特征提取能力和LSTM出色的时间序列特征提取能力, 还可以有效地解决获取不同站点的复杂地理特征的困难, 从时间和空间上提高风速预报的准确性.
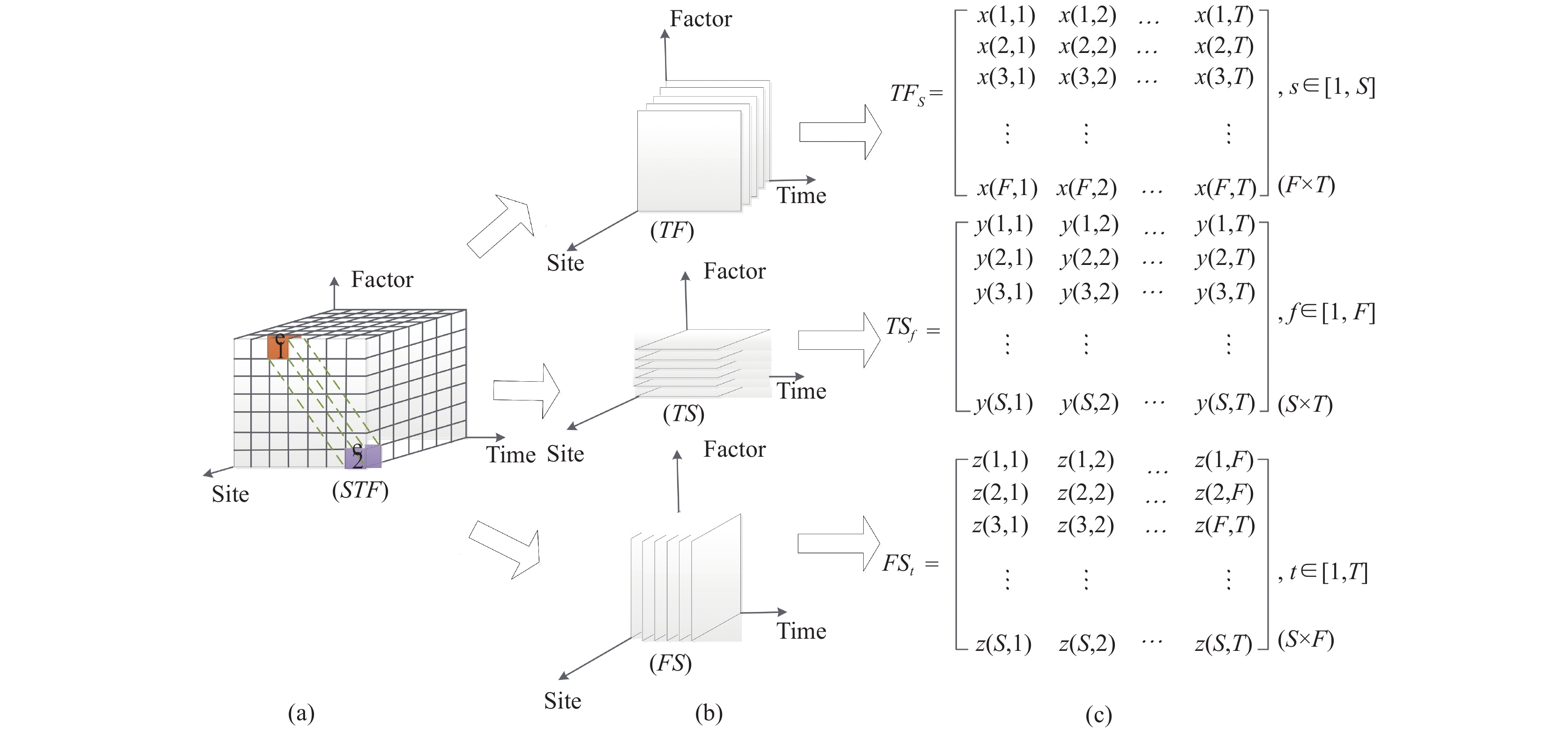
1 三维矩阵模型时空模型的基本思想是, 目标站点的风速特征不仅与本站点的气象要素密切相关, 还与其周围站点的气象要素有关[18], 周围站点的气象要素(如温度、湿度、压强等)变化会对目标站点的风速产生影响. 因此, 充分利用目标站点及其周围站点的气象信息有助于提高风速预报的准确性和可靠性. 基于3D矩阵的MFSTC模型的核心在于, 同时考虑了时间和空间维度中站点和气象因素的多重相关性, 包括多个站点之间的相关性、多个因素之间的相关性以及站点和因素之间的相关性. 模型结构如图1所示, 其中3D矩阵可以用式(1)表示.
| $STF = \left( {TF,TS,FS} \right) = < {E_{sft}} > $ | (1) |
其中, STF表示一个“站点-时间-因素”的3D矩阵, TF, TS和FS分别表示“时间-因素”, “时间-地点”和“因素-地点”的二维平面集. 相应的平面分割操作如图1(b)所示. Esft是一组3D矩阵点, 每个点都可以定义为e(s,f,t), 代表在历史时间点t处第s个站点的第f个特征气象因子的值. 同时, 如图1(c)所示, 每个二维平面可以由二维矩阵表示. 其中, TFs包含站点s在T个历史时间点处随时间变化的F个气象因子的值, TSf包含第f个气象因子在S 个站点的T个历史时间点处随时间变化的值, FSt包含在历史时间点t处S个站点的F个气象因子的值. S, F和T分别代表站点、气象因素和历史时间点的数量. 任意两个点e1(s,f,t)和e2(s,f,t)之间的相关系数
| $R_{{e_2}}^{{e_1}} = { }Corr\left( {{e_1}\left( {s,f,t} \right),{e_2}\left( {s,f,t} \right)} \right)$ | (2) |
基于上述相关系数, 可以根据每个站点在T个历史时间点的全部气象要素值计算出下一时刻目标站点的风速. 该公式定义为:
| ${e_a}\left( {q,wind,t + 1} \right) = \sum\nolimits_{s = 1}^S {\sum\nolimits_{f = 1}^F {\sum\nolimits_{t = 1}^T {\left( {{e_g}(s,f,t)R_{{e_a}}^{{e_g}} + {\xi _{ag}}} \right)} } } $ | (3) |
其中,
|
图 1 基于3D矩阵的MFSTC模型结构 |
2 提出的组合模型
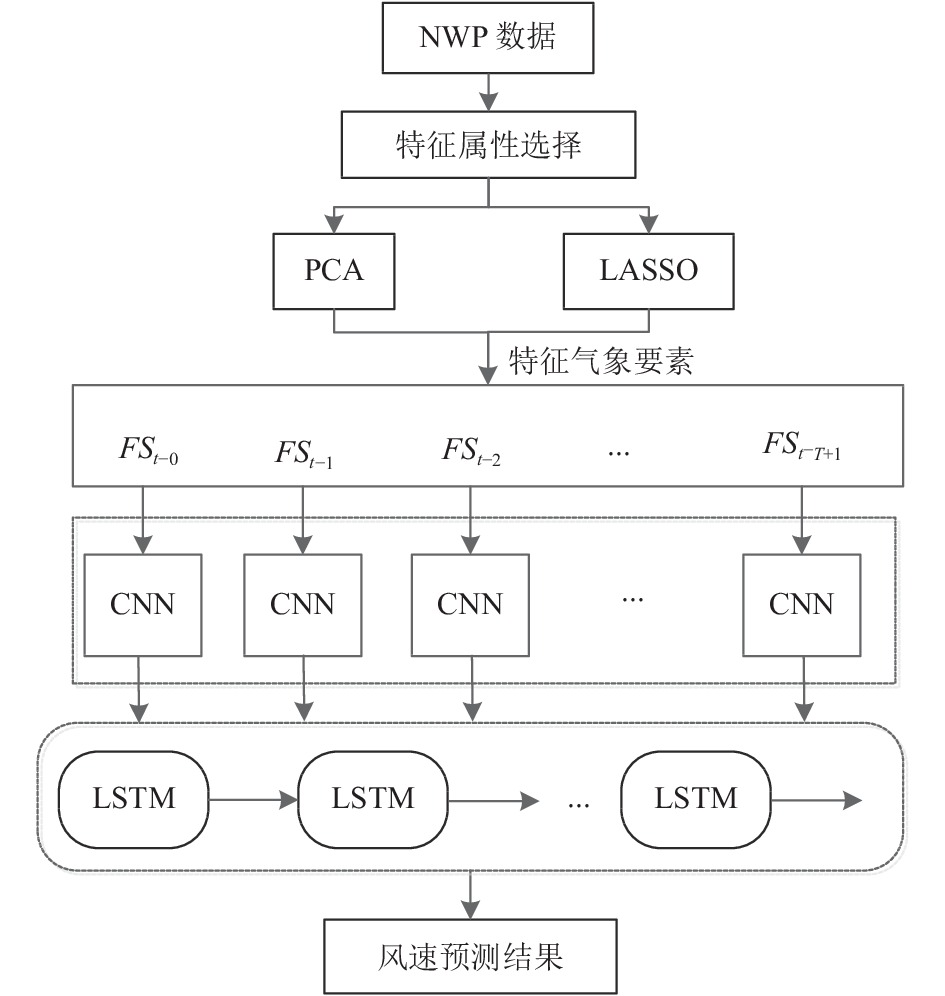
在本文中, 为了提高风速预测的准确率, 提出了一种MFSTC-CNN-LSTM框架, 如图2所示. 该方法同时考虑了风速与气象因素、空间以及时间3个维度方面的相关性, 最终实现对多站点气象因素之间相关特征的深层提取. MFSTC-CNN-LSTM框架的实现过程描述如下:
(1) 针对多个站点, 通过PCA-LASSO提取特征气象要素.
(2) 将特征气象要素的数据在3个维度上进行重构. 模型的每个输入都是一个3D矩阵, 矩阵的3个维度分别对应气象因素F、空间S以及时间T. 矩阵包含S个站点在T个历史时间点的F个特征气象因子的值.
(3) CNN的输入是T个二维矩阵FSt, 每个FSt包含在t时间点处S个站点的F个气象因子的值. 通过CNN的特征提取, 可以获得T个特征向量, 代表在T个预报时次上各个站点的气象因子之间的空间相关性. 然后, 将T个特征向量输入LSTM以提取和分析时间特征关系, 最终获得目标站点的风速预测结果.
2.1 特征属性提取原始气象数据属性复杂、形式多样, 然而并非所有要素都与风速变化是相关的, 过多的预测要素将导致冗余信息并降低泛化性能. 从原始气象要素中进行特征选择[19]以降低风速预测数据集的维度. 经过特征提取, 能够有效减少模型的计算和存储开销并且明显提高可解释性. 基于单个算法无法提取出有效的特征气象要素的问题, 本文结合PCA和LASSO两种算法以形成新的PCA-LASSO技术.
PCA[20]的主要原理是找到适当的线性变换将相关变量转换为彼此独立的新变量, 其中方差较大的变量可以反映原始多个变量中包含的主要信息, 也就是更符合要求的气象要素. 为了进一步简化模型计算量, 同时避免冗余因素对预测精度带来的不利影响, 需要从PCA筛选出的气象要素中进一步提取出能够对风速变化带来显著影响的特征气象要素. LASSO[21]回归是一种缩小变量集的压缩估计方法, 它通过构造一个惩罚函数将变量的系数进行压缩并使某些回归系数变为0, 进而达到特征选择的目的. 在本文中, 设定有m个气象要素的特征向量
| $f\left( x \right){ } = { }{w_1}{x_1} + { }{w_2}{x_2} + { } \cdots { } + {w_m}{x_m}$ | (4) |
式中,
| $loss\left( w \right){ } = { }{\left| {\left| {f\left( x \right){ } - { }y} \right|} \right|^2} + \alpha { }\left| {\left| w \right|} \right|$ | (5) |
其中, y代表风速实际值. 为防止过拟合和提高模型泛化性能引入正则化项α||w||. 通过对损失函数loss(w)的最小值求解得到w, 从而确定LASSO回归的相关参数. 随着超参数α变大, 越来越多的变量系数被收缩为0, 从而得到最终的特征气象要素.
|
图 2 风速预测流程图 |
2.2 CNN提取空间特征
CNN是多层前馈神经网络, 已被证明在提取隐藏的空间特征方面具有突出的性能[22]. CNN具有稀疏连接和权重共享的性质, 这大大减少了模型参数的数量. 使用CNN提取目标站点和其他站点的气象因素之间的潜在空间关系, 以减少风速的预测误差. CNN的计算可以定义为[23]:
| $map_{mn}^{uv} = relu\left( {\sum\limits_l {\sum\limits_{h = 0}^{h - 1} {\sum\limits_{w = 0}^{w - 1} {\omega _{mnl}^{hw}} } } \cdot map_{(m - 1)l}^{(u + h)(v + w)} + {b_{mn}}} \right) $ | (6) |
其中, u和v分别是特征图行和列的索引, h和w分别是卷积滤波器行和列的索引, h′和w′分别是卷积滤波器的行列数, l是特征图在第m-1层的索引,
| $relu\left( x \right){ } = { }\max\left( {0,x} \right)$ | (7) |
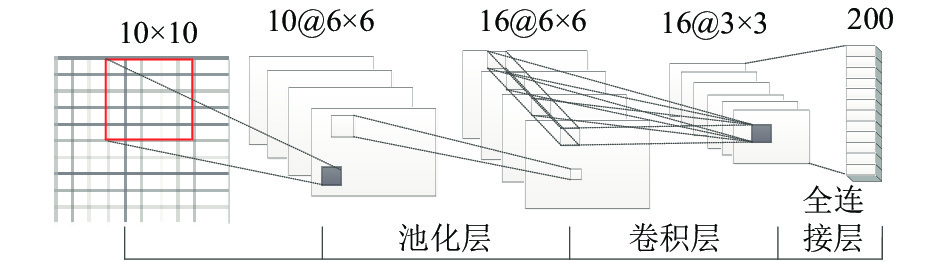
本文需配置T个CNN来处理T个空间风速矩阵, 每个CNN神经网络结构如图3所示, 主要由卷积层、池化层以及全连接层3种类型构成, 通过卷积层和池化层的交替处理, 最终由输出层输出得到的抽象特征. 首先输入10×10个站点在t(t=1,2,…,T)预报时次的特征气象要素数据, 设CNN输入层有10个卷积核, 且每个卷积核的大小均为5×5, 则输入层将产生10个尺寸为6×6的特征图, 每个特征图中的元素与其对应的空间关联域具有一致的排列顺序. 后续的网络层在这些特征图的基础上继续进行上述过程, CNN逐层捕获风速矩阵中的空间信息, 最终得到各个预报时次上的空间特征向量, 并传递给LSTM.
|
图 3 CNN神经网络结构图 |
2.3 LSTM提取时间特征
时间序列[25]是按照时间排序的一组随机变量, 它本质上反映的是某个或者某些随机变量随时间不断变化的趋势. 在数值天气预测模型中, 气象要素数据的后值与初值存在一定的依赖性与相关性. 风速预测不仅依赖气象要素的最新数据, 较早的数据可以帮助模型得到风速变化的总体趋势[26].
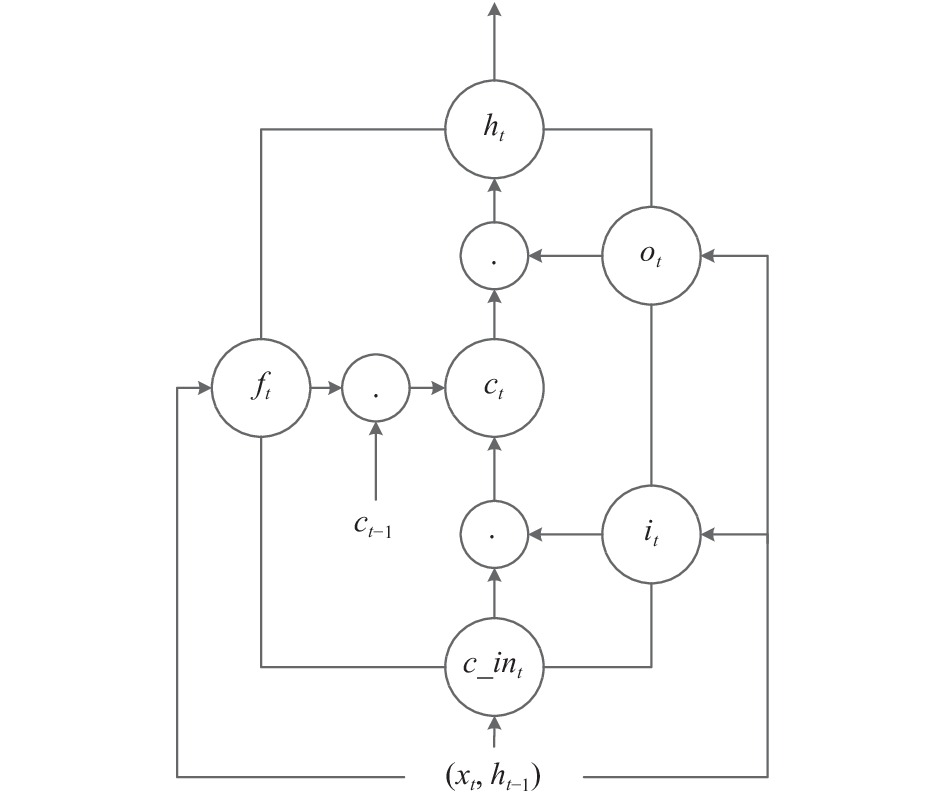
作为循环神经网络的特殊变体, LSTM具有自动存储和删除时间状态信息的能力[27], 可以提取长时间序列的复杂特征关系, 解决传统RNN缺乏建立远程结构连接能力的问题, 从而避免“梯度爆炸”现象的发生[28,29], 如图4为一个“LSTM细胞”单元[30], 该细胞单元由输入门 i、输出门 o 和遗忘门 f组成. 这3种门控是控制信息流的关键, 其对应的函数表达式为:
| ${i_t} = \sigma \left( {\sum {{W_{xi}}} {x_t} + \sum {{W_{hi}}} {x_{t - 1}} + \sum {{W_{ci}}} {x_{t - 1}} + {b_i}} \right)$ | (8) |
| ${f_t} = \sigma \left( {\sum {{W_{xf}}} {x_t} + \sum {{W_{hf}}} {x_{t - 1}} + \sum {{W_{cf}}} {x_{t - 1}} + {b_f}} \right) $ | (9) |
| ${c_t} \!=\! {f_t}{c_{t - 1}} \!+\! {i_t}\tanh\left( {\sum {{W_{xc}}} {x_t} \!+\! \sum {{W_{hc}}} {x_{t - 1}}\! +\! \sum {{W_{cf}}} {x_{t - 1}} \!+\! {b_c}} \right) $ | (10) |
| ${o_t} = \sigma \left( {\sum {{W_{xo}}} {x_t} + \sum {{W_{ho}}} {x_{t - 1}} + \sum {{W_{co}}} {x_t} + {b_o}} \right) $ | (11) |
| ${h_t} = {o_t}\tanh({c_t})$ | (12) |
其中, ct为细胞间激活向量, b是矩阵偏置向量, σ是激活函数Sigmoid. it, ft, ot分别是t时间点输入门、输出门和遗忘门的计算方法. W代表权重矩阵, 根据其下标分别具有不同的含义.
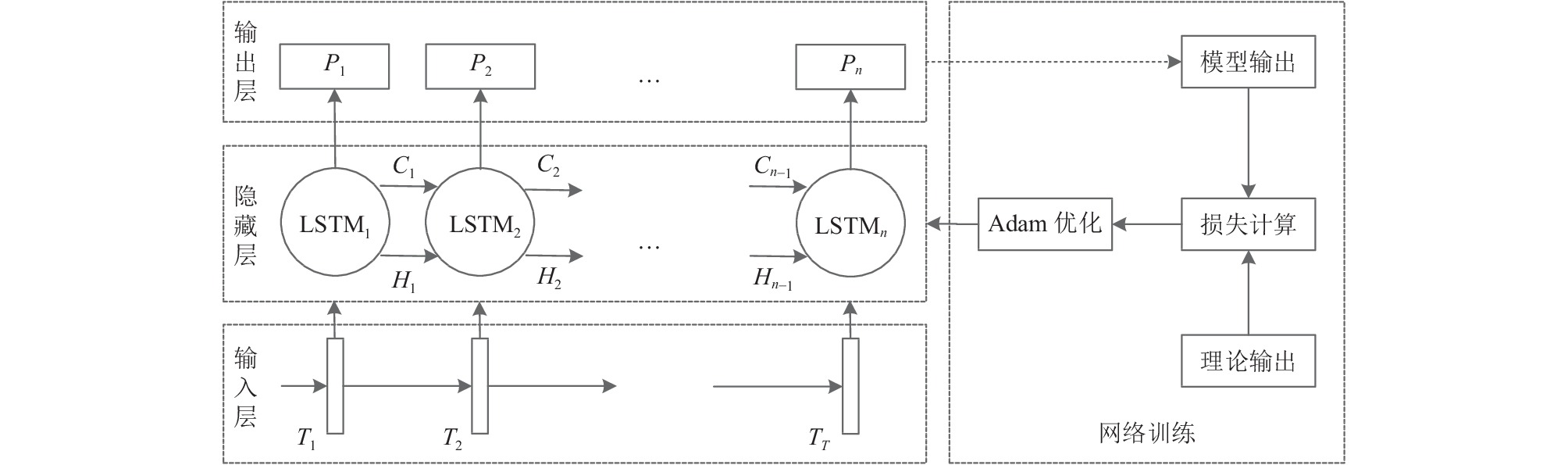
如图5 为LSTM预测模型结构示意图, 由输入层、隐藏层、输出层以及网络训练层4部分组成. 将CNN的空间特征向量输入LSTM各节点, 在中间的隐藏层使用多个 LSTM 细胞单元进行循环连接, 输出层提供预测结果, 网络训练采用Adam算法不断调整参数以优化预测结果. 损失函数的数学公式如式(13)所示.
| $L = \frac{1}{D}\sum\nolimits_{d = 1}^D {{{({y_d} - {{\hat y}_d})}^2}} $ | (13) |
其中, D为测试集中的样本数量,
在固定卷积层和池化层提取的特征信息不变的情况下, 通过逐渐增加LSTM网络记忆单元数和隐含层数来测试不同隐含层的预测效果, 如表1所示. 可以看出适当的增加LSTM的隐含层数可以提高模型的预测能力, 当隐含层数过多如隐含层数为4时, 会出现过拟合现象. 此外, 随着隐含层的增加, 模型的运行时间也会相应延长. 最终确定LSTM网络设置3层隐含层, 其隐含层中LSTM单元数分别为32、20、20.
|
图 4 LSTM 细胞单元结构示意图 |
|
图 5 LSTM神经网络处理层结构图 |
3 实验
本文数据集来自东营气象中心提供的100个站点在2009至2018年共10年的风速相关记录数据, 通过在3个站点数据集上的实验验证所提出MFSTC-CNN-LSTM模型的预测性能, 对目标站点未来5个预报时次的风速进行预测, 并使用RMSE作为衡量模型预测拟合度的指标. 为了确保模型比较的公平性和实验的有效性, 对3个站点的预测模型分配相同的超参数, 学习率设置为0.01, dropout设置为0.1, batch_size设置为32, 时间步长设置为4, 通过多次训练, 迭代次数超过500次时损失值趋于稳定. 另外, 为了提取相应区域中的不同风速特征, 实验分别利用不同的数据集来训练和调整模型的内部参数. 结果如表1所示.
| 表 1 提前0时预报时次不同LSTM层数的实验结果 |
3.1 实验数据
数据集包括100个站点10年间每天39个气象要素(HECA88, HHCA30, HHCA50, HHCA70, HHCA85, HHCA92, HHCA99, HRCA30, HRCA50, HRCA70, HRCA85, HRCA92, HRCA98, HRCA99, HTCA30, HTCA50, HTCA70, HTCA85, HTCA92, HTCA98, HTCA99, HUCA30, HUCA50, HUCA70, HUCA85, HUCA92, HUCA98, HUCA99, HVCA30, HVCA50, HVCA70, HVCA85, HVCA92, HVCA98, HVCA99, HTCA50, HTCA70, HTCA85, HTCA92, HTCA98, HTCA99, HUCA30, HUCA50, HUCA70, HUCA85, HUCA92, HUCA98, HUCA99, HVCA30, HVCA50, HVCA70, HVCA85, HVCA92, HVCA98, HVCA99, HOCA70, HOCA85, HOCA92, HPCA89)在5个预报时次(0时、6时、12 时、18 时以及24 时)的观测数据, 在高度上涵盖1000 hPa、地面、925 hPa、850 hPa、700 hPa、500 hPa、300 hPa 7个不同的层次, 在空间上包括100个网格站点. 3个实验的数据集大小均设置为13340, 模型的训练集、验证集和测试集的比例设置为6:2:2.
3.2 实验设计及分析由于原始数据包含39个气象要素, 根据前期实验, 利用单一方法提取的特征气象要素并不准确, 具有一定的片面性. 因此, 首先利用PCA提取出反映原始变量中所包含主要信息的气象要素, 然后利用LASSO回归对这些要素进行进一步筛选, 从而得到能够真正影响风力变化的特征气象要素.
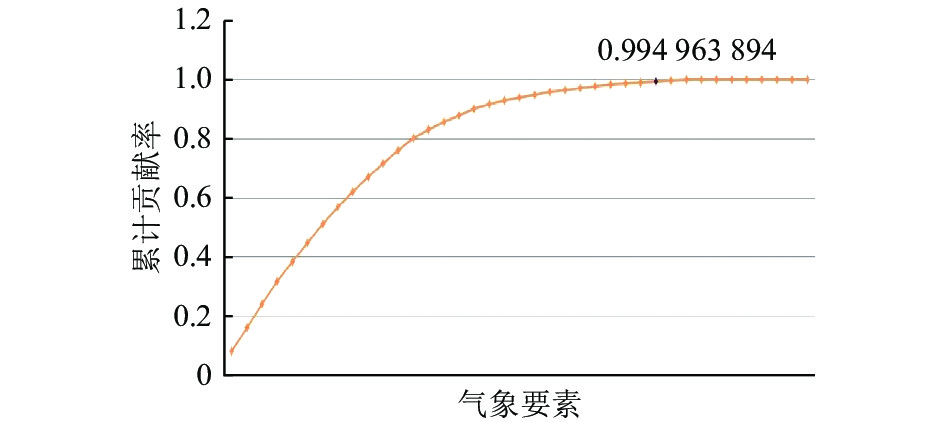
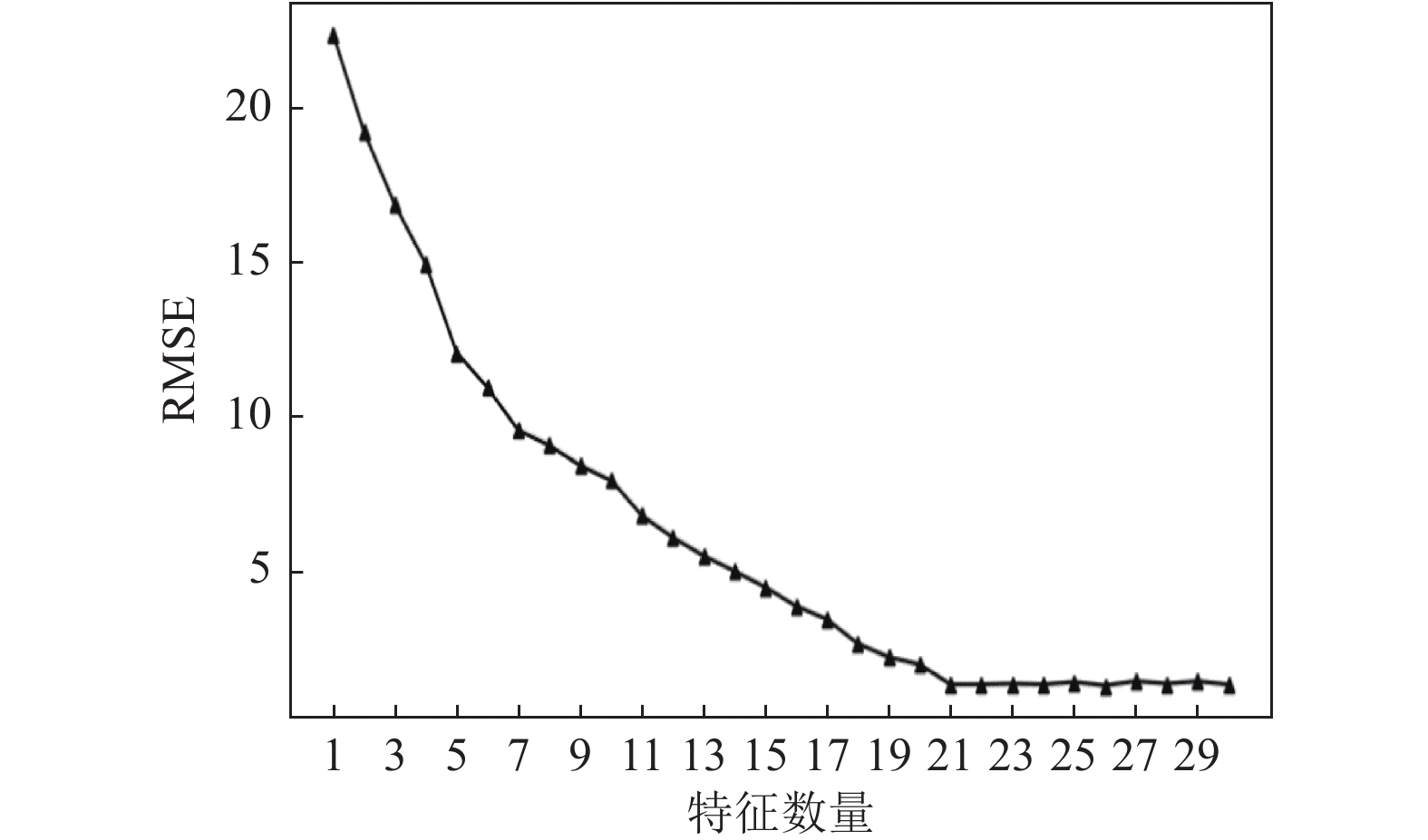
通过PCA得到各气象要素的累计贡献率如图6所示. 从图6分析可得, 当选择其中的30个气象要素时, 对风速变化的累计贡献率高达99.496%, 其他成分可以丢弃. 利用LASSO回归进一步压缩PCA所得的30个气象要素. 如图7所示, 横坐标表示气象要素的数量, 纵坐标表示预测值与真实值的均方根误差. 通过对LASSO中超参数α的设置来控制横坐标的大小. 当LASSO将特征要素的数量设定为21左右时, 可将RMSE稳定在一个较小的值.
|
图 6 气象要素累计贡献率 |
|
图 7 基于LASSO模型的风速预测 |
气象要素的特征权重的大小与其对风速预测的影响程度成正比. 本文在5个预报时次分别进行特征选择, 结果如表2所示. 表中数值是LASSO回归得到的各气象要素在5个预报时次中特征权重的平均值, 本文选取其中前21个作为特征气象要素. 根据先验知识, 海拔越低的气象要素(气象要素英文简称后缀数字越大)对风速变化的影响越大, 而提取到的特征气象要素也符合这个特点, 从而说明PCA-LASSO能够有效筛选出与风速有关的特征气象要素.
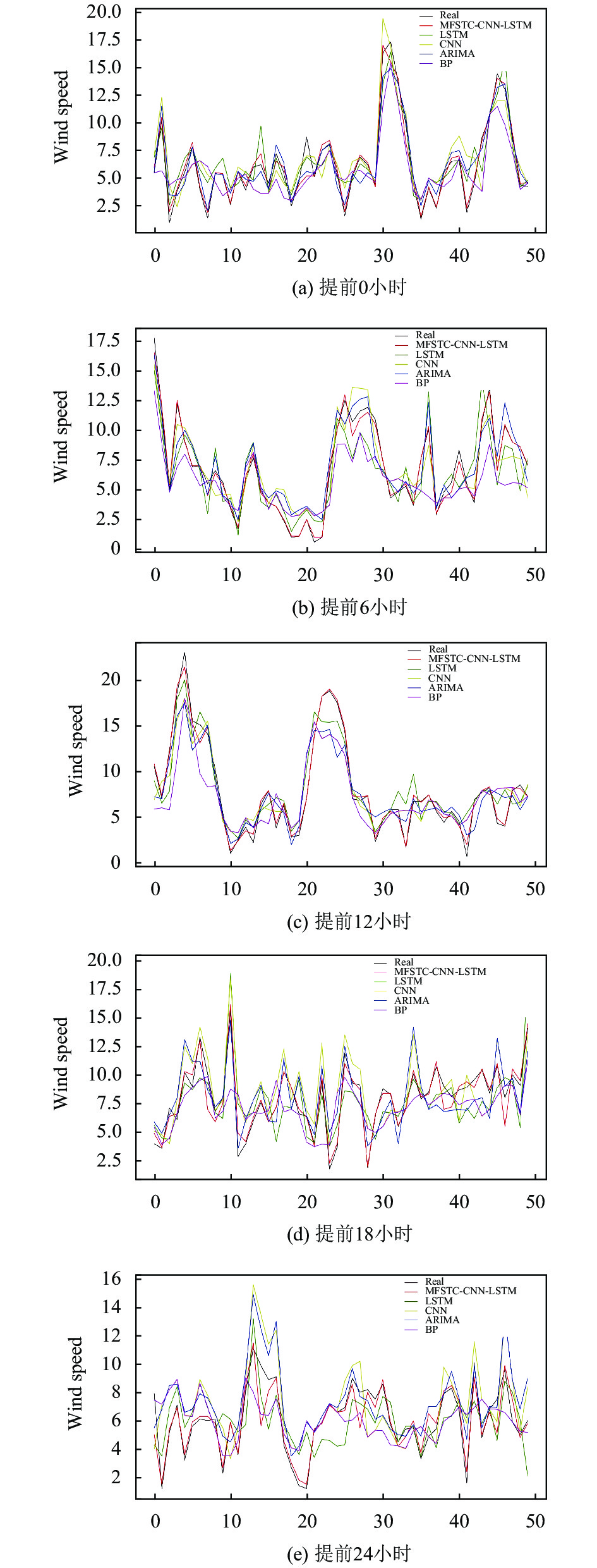
为了验证方法的有效性, 选择了CNN、LSTM、ARIMA以及BP神经网络与提出的MFSTC-CNN-LSTM模型对比并在3个站点的测试集上进行了5个预报时次(共24小时)的预测测试. 为直观展示不同模型间的效果与差异, 本文在3个站点(第21,61,91站点)的测试集上随机选取了100个记录点, 并对5个预报时次的模型预测值与真实值进行对比. 如图 8所示, 分别为 MFSTF-CNN-LSTM、CNN、LSTM、ARIMA 以及BP神经网络5种模型分别在5个预报时次的预测值与真实值的预测效果对比图. 整体来看, 所有模型误差都随预测时间增长呈增大趋势. 由图可知, 在预测时效较短时, 各个模型的预测值与真实值都有较好的拟合度, 但随着预测时效的延长, CNN、LSTM、ARIMA以及BP神经网络预测效果都呈现明显下降态势, 而MFSTF-LSTM-CNN模型的预测结果与真实值依然能够保持较好的拟合度.
| 表 2 各气象要素的特征权重分布图 |
实验结果将预测值和真实值的均方根误差RMSE用作评分函数以评估模型的预测性能. 表3中的数据为各模型在3个站点测试集RMSE的均值. 随着预报时间的推移, 所有模型的均方根误差均呈现上升趋势. 从总体的预测效果来看, 表现最好的是MFSTF-LSTM-CNN, 它能使模型获得最小均方误差值, 证明了提出方法的有效性.
4 总结结合数据挖掘和神经网络技术, 本文提出了一种基于多因素时空相关性和深度学习算法的风速预测模型, 实现了对研究地区站点的风速预测, 提高了预报的时效性和精确度. 提出的PCA-LASSO算法有效减少了参与计算的气象要素的数量, 提高了模型的计算效率. MFSTC-CNN-LSTM模型有效地融合了多种神经网络算法, 具有更强的泛化能力和更高的预测精度, 因此该模型能够在不同站点的具有不同波动程度的风速数据集上依然保持出色的预测质量和稳定性. 同时, 为使数据能够更好的适应模型, 还提出了一种基于三维矩阵的数据重构方法.
|
图 8 不同预测模型在5个时次的预测效果对比图 |
与仅考虑单个站点的气象属性之间关系的模型相比, MFSTC模型充分考虑了不同站点上各种气象因素的时空耦合关系, 并为预测下一时刻的风速提供了更加完整和可靠的基础. CNN-LSTM组合策略在MFSTC模型的基础上, 充分利用了CNN强大的空间特征提取能力和LSTM强大的时间特征提取能力的优势. 通过对两个模型优势的充分利用, 实现了对时空关系特征的深层提取. 在后续研究中, 将数值模型和图像识别模型(例如卫星图像)相结合构成新的天气预报系统的基础是进一步研究的主要目标.
| 表 3 各模型在5个预报时次的RMSE |
| [1] |
赵建利, 白格平, 李英俊, 等. 基于CNN-LSTM的短期风电功率预测. 自动化仪表, 2020, 41(5): 37-41. |
| [2] |
Du P, Wang JZ, Guo ZH, et al. Research and application of a novel hybrid forecasting system based on multi-objective optimization for wind speed forecasting. Energy Conversion and Management, 2017, 150: 90-107. DOI:10.1016/j.enconman.2017.07.065 |
| [3] |
Liu H, Duan Z, Han FZ, et al. Big multi-step wind speed forecasting model based on secondary decomposition, ensemble method and error correction algorithm. Energy Conversion and Management, 2018, 156: 525-541. DOI:10.1016/j.enconman.2017.11.049 |
| [4] |
Billinton R, Chen H, Ghajar R. A sequential simulation technique for adequacy evaluation of generating systems including wind energy. IEEE Transactions on Energy Conversion, 1996, 11(4): 728-734. DOI:10.1109/60.556371 |
| [5] |
Jiang Y, Chen XY, Yu K, et al. Short-term wind power forecasting using hybrid method based on enhanced boosting algorithm. Journal of Modern Power Systems and Clean Energy, 2017, 5(1): 126-133. DOI:10.1007/s40565-015-0171-6 |
| [6] |
Bossanyi EA. Short-term wind prediction using Kalman filters. Wind Engineering, 1985, 9(1): 1-8. |
| [7] |
Yuan XH, Chen C, Yuan YB, et al. Short-term wind power prediction based on LSSVM-GSA model. Energy Conversion and Management, 2015, 101: 393-401. DOI:10.1016/j.enconman.2015.05.065 |
| [8] |
Li S, Wang P, Goel L. Wind power forecasting using neural network ensembles with feature selection. IEEE Transactions on Sustainable Energy, 2015, 6(4): 1447-1456. DOI:10.1109/TSTE.2015.2441747 |
| [9] |
Liu H, Mi XW, Li YF. Smart multi-step deep learning model for wind speed forecasting based on variational mode decomposition, singular spectrum analysis, LSTM network and ELM. Energy Conversion and Management, 2018, 159: 54-64. DOI:10.1016/j.enconman.2018.01.010 |
| [10] |
Wang HZ, Li GQ, Wang GB, et al. Deep learning based ensemble approach for probabilistic wind power forecasting. Applied Energy, 2017, 188: 56-70. DOI:10.1016/j.apenergy.2016.11.111 |
| [11] |
Ghaderi A, Sanandaji BM, Ghaderi F. Deep forecast: Deep learning-based spatio-temporal forecasting. arXiv preprint arXiv: 1707.08110, 2017.
|
| [12] |
Hu QH, Zhang RJ, Zhou YC. Transfer learning for short-term wind speed prediction with deep neural networks. Renewable Energy, 2016, 85: 83-95. DOI:10.1016/j.renene.2015.06.034 |
| [13] |
Zaytar MA, El Amrani C. Sequence to sequence weather forecasting with long short-term memory recurrent neural networks. International Journal of Computer Applications, 2016, 143(11): 7-11. DOI:10.5120/ijca2016910497 |
| [14] |
Wang HZ, Wang GB, Li GQ, et al. Deep belief network based deterministic and probabilistic wind speed forecasting approach. Applied Energy, 2016, 182: 80-93. DOI:10.1016/j.apenergy.2016.08.108 |
| [15] |
Zhao Z, Chen WH, Wu XM, et al. LSTM network: A deep learning approach for short-term traffic forecast. IET Intelligent Transport Systems, 2017, 11(2): 68-75. DOI:10.1049/iet-its.2016.0208 |
| [16] |
Sanandaji BM, Tascikaraoglu A, Poolla K, et al. Low-dimensional models in spatio-temporal wind speed forecasting. Proceedings of 2015 American Control Conference. Chicago, IL, USA. 2015. 4485–90.
|
| [17] |
Hill DC, McMillan D, Bell KRW, et al. Application of auto-regressive models to U. K. wind speed data for power system impact studies. IEEE Transactions on Sustainable Energy, 2012, 3(1): 134-141. |
| [18] |
Zhao YN, Ye L, Pinson P, et al. Correlation -constrained and sparsity-controlled vector autoregressive model for spatio-temporal wind power forecasting. IEEE Transactions on Power Systems, 2018, 33(5): 5029-5040. DOI:10.1109/TPWRS.2018.2794450 |
| [19] |
孙全德, 焦瑞莉, 夏江江, 等. 基于机器学习的数值天气预报风速订正研究. 气象, 2019, 45(3): 426-436. DOI:10.7519/j.issn.1000-0526.2019.03.012 |
| [20] |
Westerhuis JA, Kourti T, MacGregor JF. Analysis of multiblock and hierarchical PCA and PLS models. Journal of Chemometrics, 1998, 12(5): 301-321. DOI:10.1002/(SICI)1099-128X(199809/10)12:5<301::AID-CEM515>3.0.CO;2-S |
| [21] |
Tibshirani R. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B(Methodological), 1996, 58(1): 267-288. DOI:10.1111/j.2517-6161.1996.tb02080.x |
| [22] |
宋海峰, 杨巍巍. 基于Multi-CNN空间特征提取的高光谱遥感影像分类. 测绘工程, 2019, 28(6): 10-16. |
| [23] |
Ji SW, Xu W, Yang M, et al. 3D convolutional neural networks for human action recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(1): 221-231. DOI:10.1109/TPAMI.2012.59 |
| [24] |
Nair V, Hinton GE. Rectified linear units improve restricted boltzmann machines. Proceedings of the 27th International Conference on Machine Learning. Haifa, Israel. 2010.807–814.
|
| [25] |
白玉洁. 改进时间序列模型在降雨量预测中的应用研究. 计算机仿真, 2011, 28(10): 141-145. DOI:10.3969/j.issn.1006-9348.2011.10.035 |
| [26] |
Lorenz EN. Deterministic nonperiodic flow. In: Hunt BR, Li TY, Kennedy JA, et al. The Theory of Chaotic Attractors. New York: Springer, 2004: 25–36.
|
| [27] |
Yao WY, Huang P, Jia ZX. Multidimensional LSTM networks to predict wind speed. Proceedings of the 37th Chinese Control Conference. Wuhan, China. 2018. 7493–7497.
|
| [28] |
Bengio Y, Frasconi P, Simard P. The problem of learning long-term dependencies in recurrent networks. IEEE International Conference on Neural Networks. San Francisco, CA, USA. 1993. 1183–1188.
|
| [29] |
Guo T, Liu R, Yang H, et al. Predict atmosphere electric field value with the LSTM neural network. 2017 International Conference on Computer Systems, Electronics and Control. Dalian, China. 2017. 263–266.
|
| [30] |
Ma XL, Tao ZM, Wang YH, et al. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data. Transportation Research Part C: Emerging Technologies, 2015, 54: 187-197. DOI:10.1016/j.trc.2015.03.014 |
 2021, Vol. 30
2021, Vol. 30



