在受灾地区进行及时的搜救行动是至关重要的. 然而, 由于道路被淹、水路不同以及不安全的航空基础设施, 使得救援人员很难及时到达救援场地搜索受害者^[1], 且一些火灾、洪水等场景对于搜救人员也是具有危险性的. 地面机器人可以代替救援人员达到搜索和救援目的. 然而, 它们价格昂贵, 需要人工操作, 并且轮式和履带式机器人机动性有限, 导致地面机器人并不能保证在市区外的不成型道路上进行搜救^[2].

无人机可以作为解决这些问题的替代方案, 因为无人机比人类和地面机器人具有机动性和高度的双重优势. 首先, 无人机可以通过高分辨率图像序列, 短时间内搜索大面积区域并检测人类. 其次, 无人机可以被发往到任何地方, 而无需事先了解目标区域的实际情况. 最后, 无人机可以将救援人员受伤或死亡的风险降至最低^[3].

Kang等的一项研究提出了一种基于无人机捕获的热图像从空气中检测和跟踪人体对象的技术^[4]. Rudol和Doherty的另一项研究提出了一种基于热像仪和彩色摄像机相结合的技术, 可以让无人机在室外环境中检测到人体^[5]. Rivera等还使用无人机上的热像仪和彩色摄像机的组合来探测幸存者的地理位置^[6]. 然而, 这些研究有几个缺点, 如近程探测、低分辨率、高成本和运动伪影、且没有检测人类生命体征.

在灾区执行救援任务不仅需要探测到人体存在, 还需要检测人是否活着, 以优先抢救和治疗活着的人^[7]. Al-Naji等人最近的研究提出了使用成像光电容积描记法(IPPG)来检测人类的心率^[8]. 然而, 该技术更多地依赖于面部肤色分析, 而不是运动分析, 这意味着当感兴趣区域由于被衣服、碎片、血液遮挡而不清楚时, 或者当受试者面朝下躺着时, 很难应用该技术.

为了应对这些挑战, Al-Naji等于2019年提出使用无人机采集图像进行人体呼吸的检测, 以此判断人的生存状态^[9,10]. 然而, 无人机自身的晃动对于检测结果具有较大影响, 该技术的稳像处理方法很难处理无人机晃动的方向高度复杂性, 尤其在相对物体垂直方向的晃动更是难以处理, 使用的小波变换也需要选取合适的基函数, 因为无人机晃动的频谱的多变性, 很难预先设置统一的小波基函数进行滤除. 因此, 研究如何去除无人机晃动的影响对于精确地测量视频中待测人体的呼吸率具有理论意义和实际意义, 本文的主要贡献是提出一种方法可以使无人机在受光学限制的距离和晃动的情况下准确检测出人体的呼吸率, 对比目前最优的无人机视频呼吸率检测方法Ali Al-Naji 2019^[10], 该方法将变分模态分解(VMD)用于提取呼吸波形, 利用VMD可以自适应地实现信号频谱的划分和各本征模态函数分量的有效分离, 将符合本征模态函数特征的呼吸信号提取出来, 克服了无人机晃动对于呼吸率检测结果的影响.

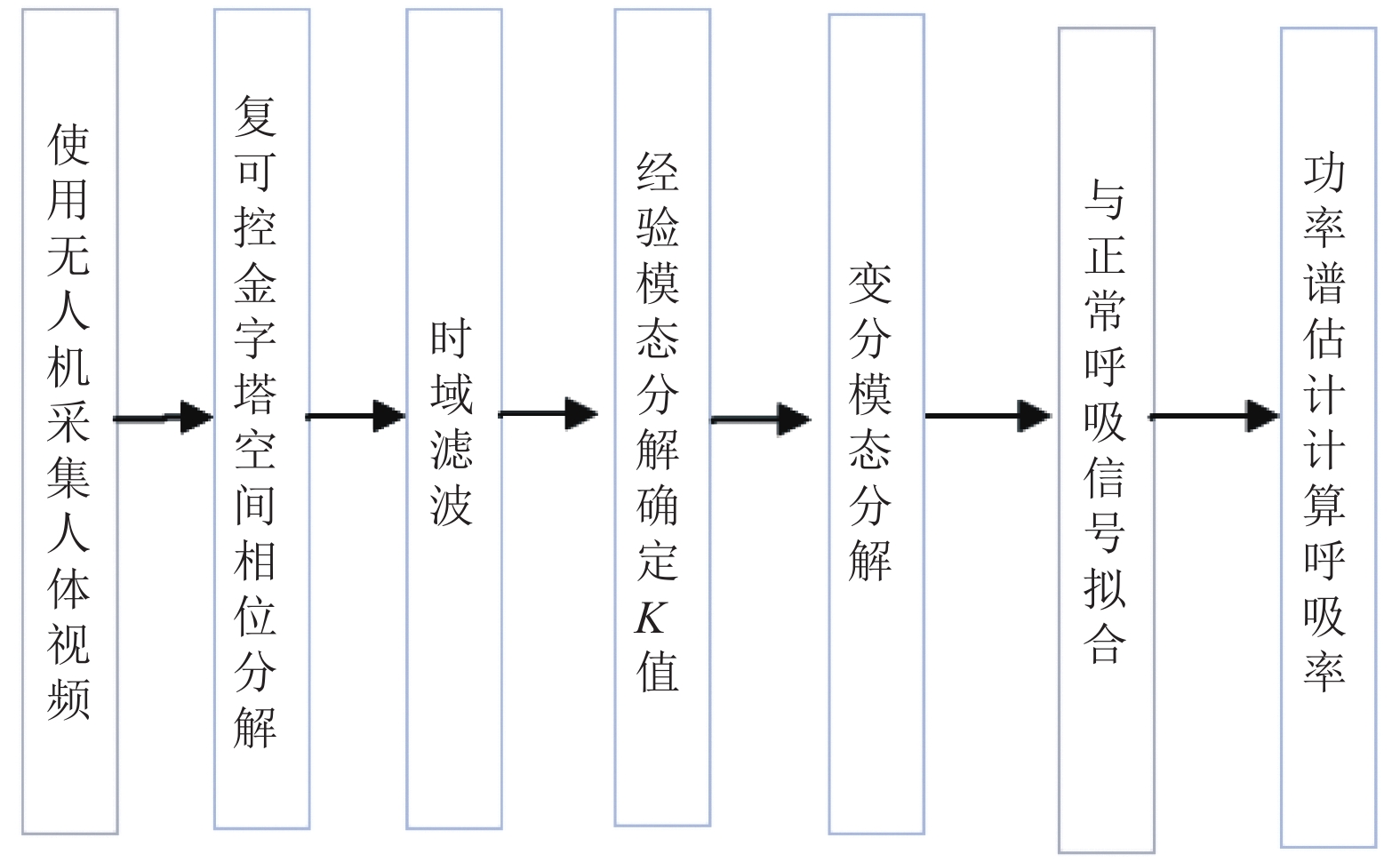
1 本文方法

本文提出了一种基于变分模态分解(Variational Mode Decomposition, VMD)的无人机视频呼吸率检测方法, 该方法主要分为以下4个部分: (1) 选择视频中人体胸腹部作为感兴趣区域(ROI), 进行复可控金字塔方向选择和分解, 得到局部频谱和相位谱, 对相位谱进行计算得到相位差^[11–13]; (2) 利用时域带通滤波选择感兴趣的频段内的相位差信号, 并使用变分模态分解算法^[14–17]分离出人体呼吸和无人机晃动波形; (3) 通过与正常呼吸信号进行拟合, 选择出呼吸信号; (4) 通过对ROI各像素的呼吸信号进行信号平均, 得到呼吸信号波形, 使用功率谱估计法计算呼吸率^[18].

整体方法框架图如图1所示.

1.1 空间相位分解

复可控金字塔的本质就是一个尺度-方向带通滤波器组. 各层带通滤波器(频域)的实现均是通过低通滤波器与高通滤波器相乘的方式来实现, 高通滤波器的实现公式为:

$\begin{split} &{{Hi}}Mask =\\ &\left. {\left\{ \!\!\begin{array}{l} 1,\;rad \ge r \\ \left| {\cos \left( {\dfrac{\pi }{{2 \times twidth}} \times \left[ {\log _2^{rad} - \log _2^r} \right]} \right)} \right|,\;r\!\! \times\!\! {2^{ - twidth}} <\!\! rad\!\! < r \\ 0,\;rad \le r \times {2^{ - twidth}} \\ \end{array} \right.} \!\!\!\!\right. \end{split}$

(1)

低通滤波器的实现公式为:

$LoMask = \sqrt {1 - HiMas{k^2}} $

(2)

其中, $rad$ 表示极径图, r的取值范围为 $r \in {2^ \wedge }[ - MaxHeight: $ $ 0]$ , 步长为1, 用来控制带通滤波的有效范围, $MaxHeight$ 为金字塔层数. $twidth$ 人为设定1, 用来调整高通滤波器的无效频带范围和低通滤波器的有效频带范围.

将视频序列进行复可控金字塔多分辨率分解, 得到不同的空间频率的基带, 并在相位域将每一帧和第一帧做差得到相位差信号.

接着进行时域滤波: 对每个基带进行时域滤波, 先对每个像素点进行时域带通滤波处理, 频带范围根据人体呼吸范围为0.1–1 Hz, (这里因为受伤的人呼吸可能会加快或变慢, 所以这里选取较宽的频带), 滤波器采用无限脉冲响应(Infinite Impulse Response, IIR)滤波器. 但是传统的IIR滤波器无法去除无人机晃动的频带中和人体呼吸频带中混频带来的干扰, 所以此部分干扰我们通过变分模态分解进行去除, 具体方法将在1.2节中详细介绍.

我们得到带通滤波后的相位差信号, 需要用相位差信号模拟腹部运动信号. 假设视频输入信号在时刻t, 以视频中ROI区域内的1个像素点为例, 位置x处的像素, 一维信号的强度表示为 $I\left( {x,t} \right)$ , 根据傅里叶变换的平移性质, 可以得到如下公式:

$\begin{split} I\left( {x,t} \right) &= f\left( {x - \delta \left( t \right)} \right) \\ & = \sum\limits_\omega {{A_\omega }\exp \left( {i{\phi _\omega }} \right)\exp \left( { - i\omega \left( {x - \delta \left( t \right)} \right)} \right)} \\ & = \sum\limits_\omega {{A_\omega }\exp \left( {i\omega \left( {{\phi _\omega } + \omega \delta \left( t \right)} \right)} \right)\exp \left( { - i\omega x} \right)} \end{split} $

(3)

其中, $\delta \left( t \right)$ 位移函数中较小的幅度. 从式(3)可以看出, 位移差已经转换成相位差.

1.2 基于VMD的去除无人机晃动干扰方法

变分模态分解是一种自适应非递归信号处理算法, 该方法通过迭代搜寻变分模型最优解来确定信号的各个频率分量的中心频率和带宽, 能够自适应地实现信号频谱的划分和各本征模态函数分量的有效分离, 呼吸率信号符合本征模态的特征, 所以满足可以被分离的基本条件. 这一点与建立在先验性假设的谐波基函数(或基频)和小波基函数上的傅里叶分解与小波分解方法具有本质性的差别, 不仅改变了信号分解的效率, 更有利于非平稳信号数据处理. 与传统的经验模态分解^[12]等递归算法相比, 变分模态分解有效缓解了模态混叠和边界效应, 具有较高的运算效率和较强的鲁棒性.

以呼吸信号为例, VMD 分解可以将呼吸信号f分解为频谱在各个子信号的带宽稀疏性各不相同的K个离散的子信号 ${u_k}(t)$ 体的步骤如下所示^[16]:

(1) 对呼吸波信号f分解出的模态 ${u_k}(t)$ ,采用希尔伯特变换计算出各个模态的解析信号, 得出 ${u_k}(t)$ 的单边频谱 ${u_k}{(t)'}$

${u_k}{(t)^\prime } = \left( {\delta (t) + \frac{j}{{\pi t}}} \right){u_k}(t)$

(4)

(2) 通过在各个模态 ${u_k}(t)$ 中加入一个移频因子 ${\omega _k}$ 过移频的方式. , 将各解析信号的频谱变换到基带上, 得到 ${u_k}{(t)^{''}}$

${u_k}{(t)^{''}} = \left[ {\left( {\delta (t) + \frac{j}{{\pi t}}} \right){u_k}(t)} \right]{{\rm{e}}^{ - j{\omega _k}t}}$

(5)

(3) 由于各个模态都能紧密围绕在以中心脉冲频率 ${\omega _i}$ 为各个模态的中心频率附近, 这样呼吸波对应的K个模态分量约束变分模型表达式如下:

${\textit{z}} = \mathop {\min }\limits_{\{ {u_k}\} ,\{ {\omega _k}\} } \left\{ {\sum\limits_k {||{\partial _t}\left[ {\left( {\delta (t) + \frac{j}{{\pi t}}} \right){u_k}(t)} \right]{{\rm{e}}^{ - j\omega t}}||_2^2} } \right\} $

(6)

$\sum\limits_{k = 1}^k {{u_k}} = f$

(7)

式中, z是式(6)的解, ${u_k}(t)$ 代表K个模态分量, ${\omega _i}$ 代表各个分量的中心频率.

(4) 引入增广拉格朗日函数式(8), 得到上述K个模态分量约束变分问题的最优解.

$\begin{split} L(\{ {u_k}\} ,\{ {\omega _k}\} ,\lambda ) =& \alpha \sum\limits_k {||{\partial _t}\left[ {\left( {\delta (t) + \frac{j}{{\pi t}}} \right){u_k}(t)} \right]{{\rm{e}}^{ - j\omega t}}||_2^2} + \cdots \\ & +||f(t) \!-\!\! \sum\limits_k {{u_k}} ||_2^2 + \!\! <\!\! \lambda (t),f(t) \!-\!\! \sum\limits_k {{u_k}}\!\!> \\ \end{split} $

(8)

式中, $\alpha $ 是惩罚参数; $\lambda $ 为拉格朗日乘子. 通过式(8) K值的估算得到频带划分清晰的自适应分离的模态分量. 该函数频率域的最优解就是模态分量 ${u_k}(t)$ 的频域表达式, 对应的 ${\omega _k}$ 就是频域中心频率. 模态分量的K设置后, 原始信号能够得到的模态数量就被确定了下来. 在此问题上, 可以使用EMD自适应分解求出K值^[15].

1.3 呼吸信号拟合选择

本文将带通滤波后信号分解为多个模态分量, 还需要确定哪一个模态分量是后续步骤需要的, 对此, 本文采用常人呼吸波形与不同本征模态进行对比, 为了规范化, 不同信号统一进行归一化处理和初始相位同相化, 然后对比信号, 获取其方差:

${u_k}(t) = \frac{{{u_k}(t) - {u_k}{{(t)}_{\min }}}}{{{u_k}{{(t)}_{\max }} - {u_k}{{(t)}_{n{\rm{min}}}} }}$

(9)

${s_n}^2 = \frac{1}{N}\sum\limits_{t = 1}^N {({u_k}(t) - d(t)} {)^2}$

(10)

其中, ${u_k}(t)$ 是第 $k$ 个模态分量, $d(t)$ 是正常人呼吸的波形, ${s_n}$ 是第 $k$ 个模态和正常人呼吸波形的方差, 方差最小对应的本征模态即使我们所选出的呼吸率波形 $B(t)$ .

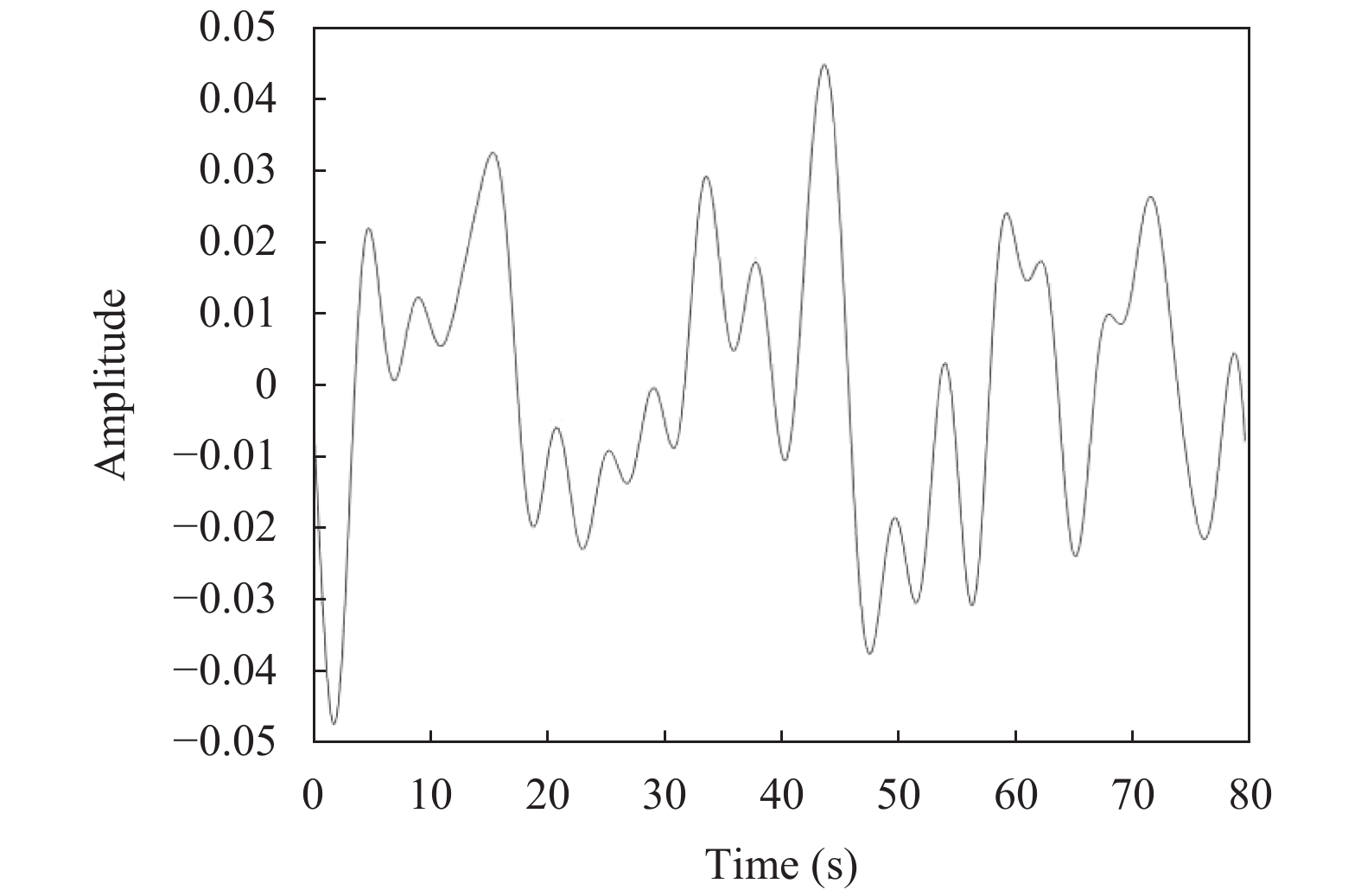
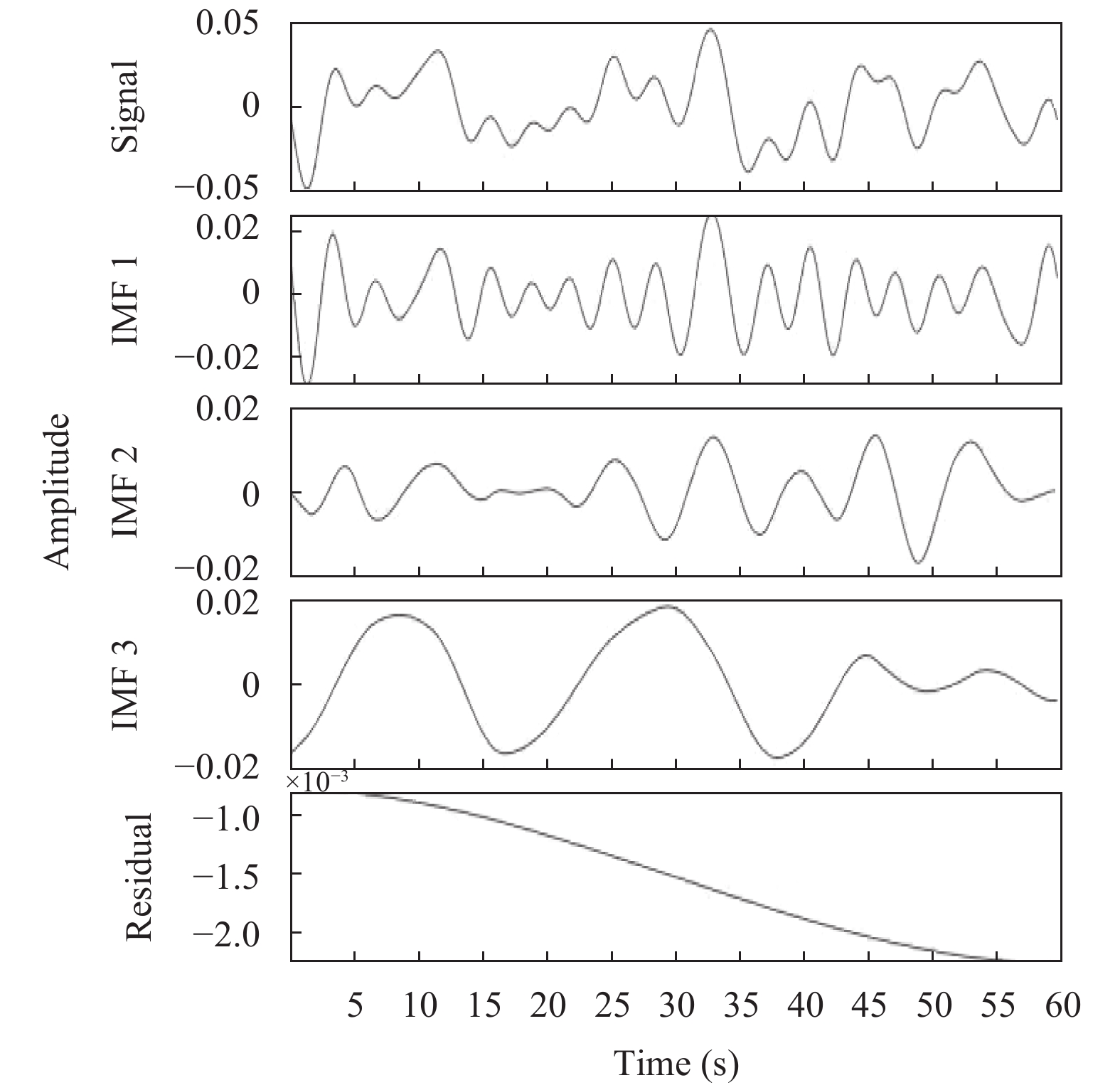
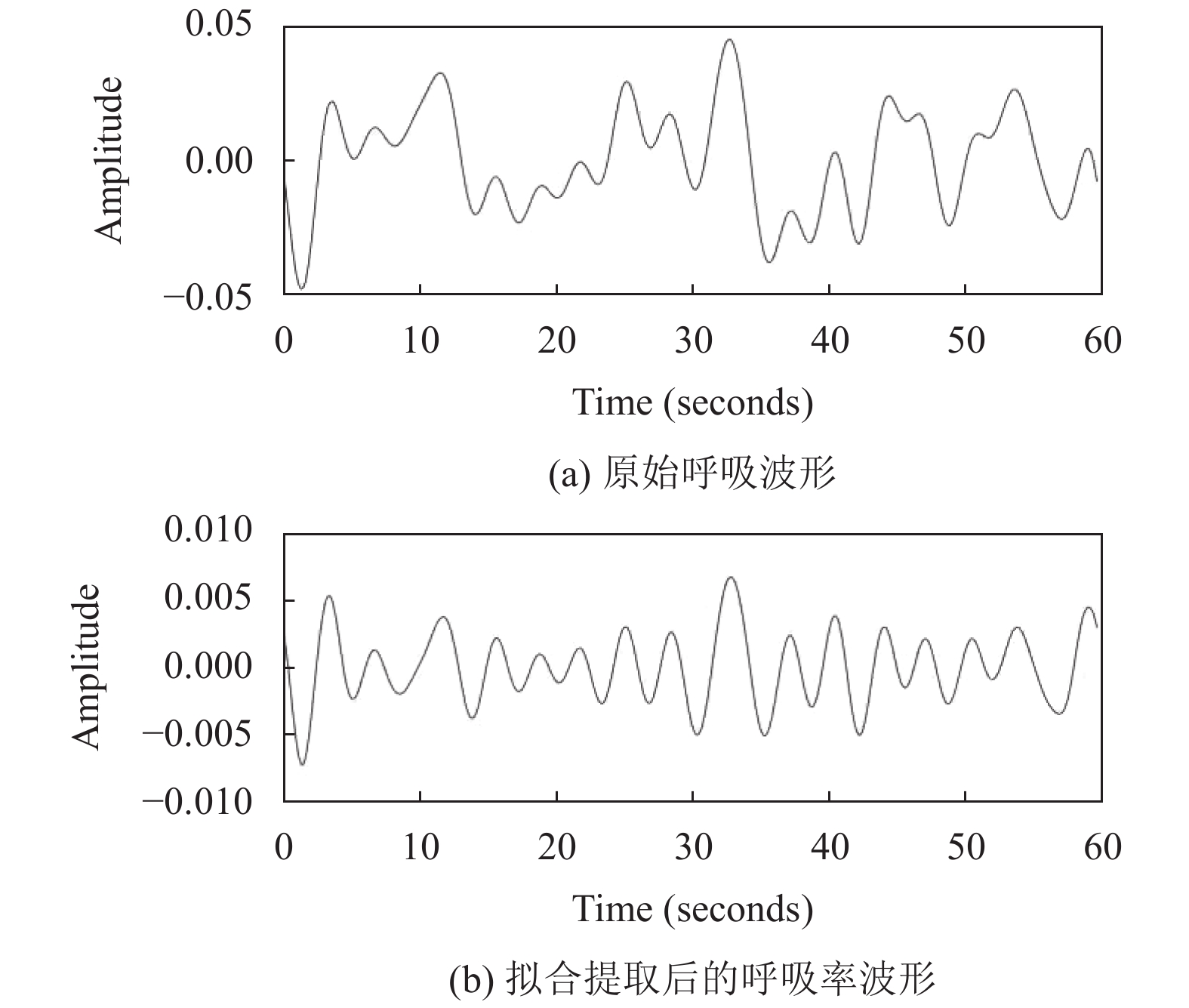
原始呼吸波形如图2所示，经过分解后的多个模态分量结果如图3所示. 进行选择拟合后波形如图4所示.

1.4 呼吸率计算

上文将视频中每一像素位置代表呼吸率的相位差提取出, 对视频每一帧的腹部区域的相位差信号做信号平均, 得到一维信号, 这个一维信号即是我们最后得到的呼吸率波形. 利用波形进行呼吸率估计最常用的方法是用快速傅里叶变换(FFT)分析功率谱, 最大功率对应的频率即为呼吸率. 但是, FFT在大量样本数目的前提下才能取得较高的精度, 同时又增加了时间复杂度. 本文用一种傅里叶系数迭代插值的呼吸率估计算法对呼吸率信号进行分析, 实现了算法精度与复杂度之间的均衡. 主要包括两个步骤:

(1) 计算样本数为N的呼吸信号的功率谱P和功率最大值对应的位置T.

(2) 针对功率谱, 执行迭代的傅立叶系数插法. 首先, 初始化起始偏差 ${e_0} = 0$ 和迭代次数 $Q = 50$ . 统计发现, 迭代50次后傅立叶系数偏差基本稳定.

$\left\{\begin{split} {s_d} &= \displaystyle\sum\limits_{n = 0}^{N - 1} {B(n){e^{\frac{{ - j2\pi (T + {e_k} + d)}}{N}}}} \\ {e_k} &= {e_{k - 1}} + r({e_{k - 1}}) \end{split} \right.$

(11)

其中, $d = \pm 0.5$ , ${e_k}$ 为迭代 $k$ 次后的傅立叶系数偏差, $r({e_{k - 1}}) = 0.5 \times \dfrac{{|{s_{ + 0.5}}| - |{s_{ - 0.5}}|}}{{|{s_{ + 0.5}}| + |{s_{ - 0.5}}|}}$ .

(3)计算最终的呼吸率:

$BR = 60\frac{{T + {e_Q}}}{N}fs$

(12)

其中, ${f_s}$ 为视频采样率, $N$ 为样本数.

2 实验分析

本章将设计4组对比实验来验证本文提取呼吸率方法的准确性和鲁棒性. 我们在无人机轻微晃动和剧烈晃动的情况下分别进行如下实验: 使用手机进行一分钟计时, 期间每隔固定秒数响一次, 同时记录下呼吸次数, 以此作为参考值与本文方法进行对比, 验证本文方法提取呼吸率结果的准确性. 然后再与Ali Al-Naji 2019^[10]的基于稳像技术和小波去噪的无人机视频呼吸率检测方法进行对比, Ali Al-Naji 2019方法是目前最优的无人机呼吸率检测方法, 以此为对比, 可以有效验证本文方法在无人机晃动情况下对人体呼吸率的检测效果.

2.1 实验设计

实验过程如图5所示, 使用无人机的视频采集装置进行视频的采集, 其中无人机距离受测者分别为3米、6米、9米、12米, 同时受测者分别进行了平躺、卧趴姿势的检测. 在采集视频的同时, 我们也使用手机计时方式同步记录受测者呼吸情况. 以此作为本文方法的参考值.

实验装置为惠普笔记本电脑CPU为英特尔 i7, 内存16GB, 操作系统Windows10; 无人机型号为大疆Mavic 2 pro. 采用软件Matlab 2019b进行装置控制, 实验采集视频为RGB彩色空间, 分辨率为1920×1080, 视频帧率 30 帧/s, 每位受测者每次拍摄时长为60 s, 总计3600帧图像. 受测者共计14人, 包括11名男性3名女性. 每位受测者在轻微晃动, 剧烈晃动两种条件下分别进行测试并同时使用手机进行同步呼吸计数.

方法评价采用定量分析的方法进行, 验证本文方法的准确性与鲁棒性. 采用平均绝对误差 ${M_e}$ 、标准差 $S{D_e}$ 、均方误差 $RMSE$ 、平均准确率 $B{R_{ac}}$ 和皮尔森相关系数r作为方法的评价指标. 其中平均准确率 $B{R_{ac}}$ 用来反映测量值 $B{R_{me}}$ 相对参考值 $B{R_{re}}$ 的准确性, N个样本的平均准确率为:

$B{R_{ac}} = 1 - \frac{1}{N}\sum\limits_{n = 1}^N {\frac{{|BR_{me}^n - BR_{re}^n|}}{{BR_{re}^n}}} $

(13)

2.2 实验结果分析

实验过程如图5所示, 使用无人机的视频采集装置进行视频的采集, 其中无人机距离受测者分别为3米、6米、9米、12米.

(1)无人机轻微晃动干扰下的呼吸率检测

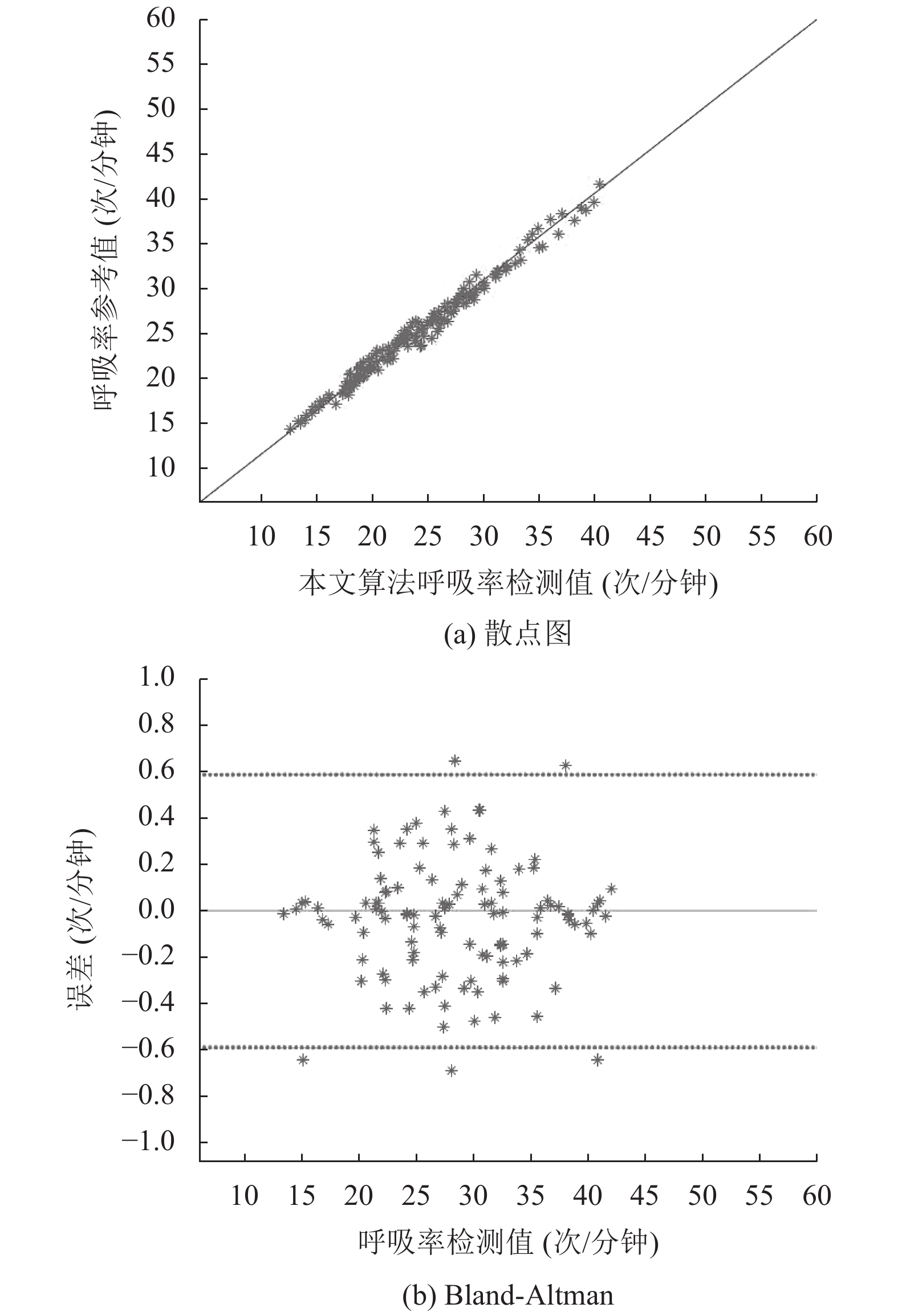
本方法通过对视频中相对人体固定不动的物体进行经典的光流追踪(KLT)^[17], 得到其位移的像素点数, 用其反应无人机的晃动程度, 将最大位移的像素点数小于视频区域的1/30定义为轻微晃动. 14名受测者每人分别进行8组实验, 每组包括手机监测和无人机检测数据. 共计112组数据. 使用散点图与Bland-Altman 图进行数据相关性分析, 结果如图6所示, 图6散点图中, 横坐标表示的是呼吸率检测值, 由本文呼吸率检测方法得出. 纵坐标表示的是呼吸率参考值, 由手机监测结果得出, 每组输入数据对应的是散点图中的一个黑色点(测量值, 真实值), 而参考值应该是图中横贯整个坐标轴斜率为1的黑色实线. 在图6的 Bland-Altman 图中: 横坐标代表由无人机视频利用本文方法检测得的呼吸率, 纵坐标代表呼吸率检测值和手机记录的参考值之间的误差, 黑点是由检测值和误差组成的坐标点, 中间黑线是通过这些坐标点计算出的误差均值, 上下两条黑线代表95%置信范围, 中间黑线越接近于0且上下两条黑线之间的距离越小, 说明呼吸率的测量值和参考值之间的误差越小.

从图6中可以看出, 所有的黑色点都分布在中间黑色实线的附近, 证明了本文方法提取呼吸率的准确性较高, 具有良好的应用性.

为了证明本文方法具有良好的抗无人机晃动干扰能力, 我们将与Ali Al-Naji 2019进行结果对比. Ali Al-Naji 2019使用无人机进行呼吸率的检测, 通过稳像处理和小波去噪去除无人机晃动干扰. 结果如表1, 表格单元格内5个数据单位分别为, ${M_e}$ /bpm、 $S{D_e}$ /bpm、 $RMSE$ /bpm、 $B{R_{ac}}$ (%), $r$ , 其中bpm (breaths per minute)表示为每分钟呼吸次数. 结果表明在无人机轻微晃动场景下, 本文方法和Ali Al-Naji 2019方法都体现了良好的检测性能, Ali Al-Naji 2019的方法检测性能略低于本文方法.

(2)无人机剧烈晃动干扰下的呼吸率检测

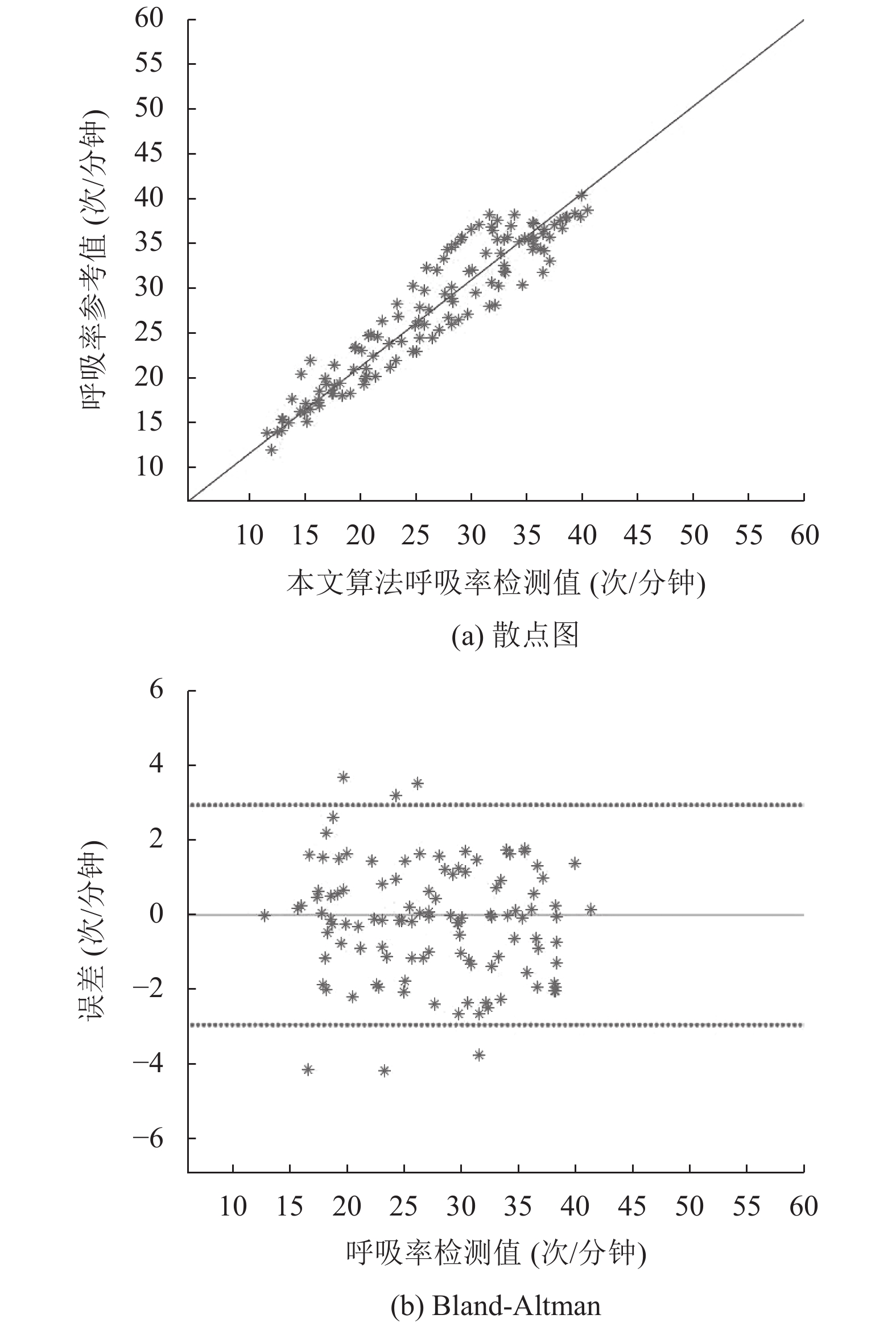
通过对视频中相对人体固定不动的物体进行经典的光流追踪(KLT), 得到其位移的像素点数, 用其反应无人机的晃动程度, 将最大位移的像素点数不小于视频区域的1/30定义为剧烈晃动. 14名受测者每人分别进行8组实验, 每组包括手机监测和无人机检测数据. 共计112组数据. 使用散点图与Bland-Altman图进行数据相关性分析. 从图7中可以看出, 所有的黑色点都分布在中间黑色实线的附近, 证明了本文方法在无人机剧烈晃动的情况下提取呼吸率的准确性也较高.

我们再将其与Ali Al-Naji 2019进行结果对比, 结果如表2所示, 表格单元格内5个数据单位分别为, ${M_e}$ /bpm、 $S{D_e}$ /bpm、 $RMSE$ /bpm、 $B{R_{ac}}$ (%), $r$ , 其中bpm( breaths per minute)表示为每分钟呼吸次数. 结果表明, 在无人机剧烈晃动场景下Ali Al-Naji 2019的方法检测性能和准确率低于本文方法, 本文方法体现了良好的抗无人机晃动干扰性.

(3)结果分析

从上面的结果中, 可以得出结论, 本文的方法可以很好的在无人机轻微晃动和剧烈晃动情况下, 有效的计算出人的呼吸率, 并且本文方法在受测者不同姿势, 无人机不同高度下都可以取得较好的实验结果, 具有较好的稳定性. 而Ali Al-Naji 2019的方法, 在轻微晃动时性能只是略微低于本文方法, 但在剧烈晃动时, 性能指标远低于本文方法, 其主要原因是:

Ali Al-Naji 2019通过无人机进行人体视频的采集, 进行稳像处理, 并通过复可控金字塔进行相位差提取, 然后利用小波变换进行去噪, 然而, Ali Al-Naji 2019的稳像处理方法很难处理无人机晃动的方向高度复杂性, 小波变换也需要选取合适的基函数, 不同场景下很难确定统一的基函数, 且Ali Al-Naji 2019没有对呼吸波形的功率谱执行迭代的傅立叶系数插值算法. 在无人机轻微晃动时, 干扰的影响不是很大, 对于检测结果影响很微小, 本文方法和Ali Al-Naji 2019都取得了很好的结果. 但在无人机剧烈晃动时, Ali Al-Naji 2019方法很难去除此干扰, 本文方法通过VMD依据数据自身的时间尺度特征来进行信号分解特性, 适应了不同场景使用无人机进行呼吸率检测的需求.

3 结论

本文提出了一种基于变分模态分解的无人机视频呼吸率检测方法. 选择视频中人体腹部作为ROI区域, 并进行复可控金字塔相位分解, 得到局部频谱和相位谱, 对相位谱进行计算得到相位差. 然后, 通过对ROI各点的相位差信号进行时域带通滤波选择感兴趣的频段内的相位差信号, 并使用变分模态分解算法分离出人体呼吸和无人机晃动波形. 在此基础上, 通过与正常呼吸信号进行拟合, 选择出呼吸信号. 最后, 对ROI各像素点呼吸信号进行信号平均, 得到一维信号. 使用功率谱估计法计算呼吸率. 本文以手机监测得到的呼吸率作为参考值, 与基于小波变换抗干扰的无人机视频呼吸率检测方法在不同无人机晃动程度下进行对比实验, 实验结果证明本文方法具有较高的抗无人机晃动能力, 提高了无人机视频呼吸检测的鲁棒性.