近年来国内外逐渐兴起的用户画像技术, 为提升电力客户体验, 提高产品和服务的竞争力, 满足客户的用电服务需求^[1]提供了有效支撑.

用户画像是建立在一系列真实数据之上的目标用户模型, 是真实用户的虚拟代表^[2], 用户画像以了解用户预测用户需求为目的^[3], 但相关的文献数量较少^[4].

国网浙江省电力公司在2015年开始探索基于客户标签的用户画像, 2017年在电力营销业务应用系统中启用了客户画像全景视图, 主要应用在电力营业厅. 最初的标签数量多达三百多个, 建设维度包括: 社会属性、交费行为、用电行为、信用评价、风险评估和关联行为, 覆盖浙江省所有用户. 目前基于多项业务的个体画像构建及应用方法, 涉及庞大的标签库和海量的电力用户数据, 存在有效性差和运算速度慢的缺陷, 在各类电力业务推荐时效果欠佳, 未能得到有效应用.

本文提出了一种基于改进的萤火虫优化加权K-means算法的分层聚类画像推荐模型, 仅就单项业务设计标签模型, 减少了标签数量, 提高了运行速度; 通过分层聚类着重构建特征群体画像, 提高了业务推荐的针对性和精准性.

1 算法基本原理

聚类是数据挖掘中一个重要的概念, 其目的是把具有相似特性的数据对象放到一起, 寻找其中隐藏的有价值的信息, 是将没有分类标签的数据集分成若干个簇的过程, 是一种无监督的分类方法^[5,6].

1.1 传统K-means算法简介

1967年提出K-means算法, 是聚类算法中最经典的算法^[7]. 因其思想简单, 速度快, 聚类效果好而应用广泛. 其核心思想是指定初始聚类数目k, 并在数据集中任选k个初始聚类中心, 计算其余数据与聚类中心的相似度, 将数据分配到相似度最高的聚类中心所对应的簇中; 重新计算每个簇中数据平均值作为新的聚类中心, 不断迭代直到算法收敛. 然而, 初始聚类中心的随机选择, 造成了对初始值的敏感和易陷入局部最优解等缺点^[8], 即聚类结果的好坏依赖于初始聚类中心的选择; 对异常样本点较敏感, 只能处理数值型的数据集^[9]. 许多研究者致力于K-means算法的各种改进方法, 主要集中在初始k值的选择、初始聚类中心的选取、离群点的检测和去除、距离和相似性度量等方向上的优化^[10].

1.2 萤火虫算法简介

群智能优化算法是用智能方法来搜索解空间的启发式聚类算法^[9], 是近几十年发展起来的仿生模拟进化算法, , 典型算法如蚁群算法、粒子群算法、萤火虫算法^[11-13]等. 萤火虫算法用搜索空间的点模拟萤火虫, 搜索和优化模拟成萤火虫的吸引和移动. 萤火虫有两个要素: 亮度和吸引度. 萤火虫之间相互吸引、移动, 不断搜索靠近亮度更高, 吸引度更高的邻域位置, 最终使所有样本到相应聚类中心的距离之和最小, 达到分群的目的^[13,14].

萤火虫算法用萤火虫表示聚类问题的解, 亮度大的位置代表最优的聚类中心, 目标函数的解反映位置的优劣^[15]. 具有操作简单、宜于并行处理、鲁棒性强等特点, 但是因为最亮的萤火虫随机移动, 导致该算法聚类时存在收敛速度较慢、后期容易在最优值附近振荡、稳定性较差的问题^[16].

1.3 基于改进的萤火虫优化加权K-means算法基本思路

基于改进的萤火虫优化加权K-means算法利用传统K-means算法和萤火虫算法自身的优点弥补了对方的缺点, 在此基础上又做了局部改进来优化算法性能.

具体思路首先是针对传统K-means算法初始聚类中心选择的随机性等缺点, 本文采用萤火虫算法(Firefly Algorithm, FA)^[17]求得最优解, 作为K-means算法的初始聚类中心; 其次传统K-means算法由于速度快, 聚类效果好又纠正了萤火虫算法收敛慢、易振荡的缺点; 再次考虑采集数据的业务相关度不同, 对传统欧氏距离引入权值以减轻异常点影响; 最后通过改进萤火虫的移动方式和随机扰动方式, 来提高聚类的准确性和稳定性, 以得到稳定的聚类结果^[18].

设待聚类样本数据集X, m为数据维度.

$ X=\left\{X_{1}, X_{2}, \cdots, X_{j}, \cdots, X_{n} ; X_{j}=\left(x_{j 1}, x_{j 2}, \cdots, x_{j m}\right)^{\rm T} \in R^{m}\right\} $

算法相关定义^[16-19]如下:

定义1. 萤火虫i和j之间的距离:

${r_{ij}} = \left\| {{x_i} - {x_j}} \right\| = \sqrt {\sum\limits_{k = 1}^m {{{({x_{ik}} - {x_{jk}})}^2}} } $

(1)

式中, m为数据维度, x_ij为萤火虫i的第j个数据分量.

定义2. 萤火虫的亮度:

$ I=I_{0} \times e^{-\gamma_{i j}} $

(2)

式中, I₀为萤火虫自身r=0处的荧光亮度; $\gamma $ 为光强吸收系数, 通常为常数.

式(2)计算量大, 导致了萤火虫算法收敛速度慢, 而亮度与目标函数相关, 所以本文算法直接采用目标函数J_c反映萤火虫的亮度, J_c由式(11)计算.

定义3. 萤火虫吸引度:

$ \beta (r) = {\beta _0} \times {e^{ - \gamma r_{ij}^2}} $

(3)

其中, $\;{\beta _0} $ 为最大吸引度, 即r=0处的吸引度.

萤火虫被吸引移动, 距离越变越小, 由等价无穷小替换原理, 用式(4)代替式(3), 能减小计算量, 提高运算速度.

$\beta (r) = \frac{{{\beta _0}}}{{1 + \gamma r_{ij}^2}}$

(4)

定义4. 位置更新公式.

萤火虫算法的扰动项 $\alpha \times (rand - 0.5) $ 扰动作用不明显, 容易造成在局部最优值附近波动, 因此在萤火虫算法中引入了扰动算子^[18] $ \alpha \times rand \times {({X_i} - {V_0})^2}$ , 则萤火虫i被吸引向萤火虫j移动的位置更新公式可优化为式(5). 可见位置的更新与吸引度有关, 吸引度决定移动距离大小.

${X_{i + 1}} = {X_i} + \frac{{{\beta _0}}}{{1 + \gamma r_{ij}^2}}({X_i} - {V_0}) + \alpha \cdot rand{({X_i} - {V_0})^2}$

(5)

式中, V₀为目前最优聚类中心,α为步长因子, 是[0, 1]上的常数, rand为[0, 1]上服从均匀分布的随机数.

${V_0} = \frac{1}{{{n_i}}}\sum\limits_{y \in {C_i}} y $

(6)

式中, n_i为聚类簇C_i中的数据个数, y代表聚类簇C_i中的数据数值.

最亮的萤火虫X_*按式(7)移动.

$ {X_{* + 1}} = {X_*} + \alpha \times rand \times {({X_i} - {V_0})^2} $

(7)

扰动算子的优化能有效避免最亮的萤火虫随机移动, 提高算法收敛速度和精度.

定义5. 权值.

考虑到待聚类样本数据的业务相关度和影响程度不同, 在目标函数的计算中引入权值 $\Omega = \{ {\omega _1},{\omega _2}, \cdots ,{\omega _j}, \cdots , $ $ {\omega _n};{\omega _j} = {({\omega _{i1}},{\omega _{i2}}, \cdots ,{\omega _{im}})^{\rm{T}}} \in {R^m}\}$ 来反映数据的整体分布特性.

${\omega _{id}} = \dfrac{{{x_{id}}}}{{\dfrac{1}{n}\displaystyle\sum\limits_{d = 1}^n {{x_{id}}} }}$

(8)

定义6. 目标函数.

亮度和目标函数相关, 用目标函数代表亮度, 亮度越大、萤火虫位置越佳, 目标函数值越小, 聚类效果越好, 即亮度高的萤火虫吸引亮度低的萤火虫, 亮度决定移动方向.

用传统K-means算法求得的聚类中心为 $ V = $ $ \{ {V_1},{V_2}, \cdot \cdot \cdot ,{V_k}\} $

数据对象与聚类中心的欧氏距离为:

$d(X,V) = \left\| {{x_i} - {v_j}} \right\| = \sqrt {\sum\limits_{j = 1}^m {\left| {{X_i} - {{\left. {{V_j}} \right|}^2}} \right.} } $

(9)

式中, V_j表示第j类的中心位置, i=1,2,3,…, n, j=1,2,3,…, k.

$ {V_j} = \frac{1}{{{n_j}}}\sum {{x_i}} $

(10)

式中n_j为V_j中的数据数量, x_j为V_j中的样本数据.

仅用传统K-means算法得到目标函数为:

$J(X,V) = \sum\limits_{j = 1}^k {\sum\limits_{{X_i} \in {G_j}}^{} {d({X_i}} } - {V_j}) = \sum\limits_{j = 1}^k {\sum\limits_{{X_i} \in {G_j}}^{} {\sqrt {\sum\limits_{j = 1}^m {\left| {{X_i} - {{\left. {{V_j}} \right|}^2}} \right.} } } } $

(11)

式中, G_j为j类中的数据集合.

加权后, 数据对象与聚类中心的距离为:

${d_\omega }(X,V) = {\left\| {{x_i} - {v_j}} \right\|_\omega } = \sqrt {\sum\limits_{j = 1}^m {{\omega _{id}}\left| {{X_i} - {{\left. {{V_j}} \right|}^2}} \right.} } $

(12)

在式(11)中引入权值 ${\omega _{id}} $ 后, 突出了数据分布特性, 易于排除异常点, 提高聚类精度, 同时减少迭代次数, 速度更快.

加权后的目标函数为:

$ {J_c}(X,V) \!=\! \sum\limits_{j = 1}^k {\sum\limits_{{X_i} \in {G_j}}^{} {d({X_i}} } - {V_j}) \!=\! \sum\limits_{j = 1}^k {\sum\limits_{{X_i} \in {G_j}}^{} {\sqrt {\sum\limits_{j = 1}^m {{\omega _{id}}\left| {{X_i} - {{\left. {{V_j}} \right|}^2}} \right.} } } } $

(13)

1.4 算法流程

聚类算法流程如图1所示.

(1)参数初始化: 确定群体数据规模n、最大吸引度 $ {\;\beta _0}$ 、光强吸收系数 $ \gamma $ 、步长因子α、最大迭代次数T_max、迭代停止阈值 $ \varepsilon $ ;

(2)位置初始化: 选择k个数据对象作为初始聚类中心V;

(3)距离计算: 由式(12)计算数据对象与聚类中心的距离 ${d_\omega }(X,V) $ ;

(4)划分聚类簇: 根据计算所得距离, 依次将对象划分到距离最近的聚类中心所在的类中;

(5)确定对象移动方向: 由式(13)计算加权后的目标函数J_c(X,V), 以确定对象移动方向. 亮度决定移动方向, 目标函数值越小, 亮度就高, 所处位置就越好;

(6)确定对象移动距离: 由式(5)计算萤火虫移动后的新位置, 确定对象位置;

(7)确定新的聚类中心: 由式(7)计算最亮的萤火虫的新位置, 作为新的聚类中心;

(8)收敛判断: 判断如果达到最大迭代次数或满足停止阈值, 则停止算法, 否则转到步骤(3);

(9)输出聚类结果.

2 用户画像构建和应用

为提高计算速度和精度, 本文提出一种基于改进的萤火虫优化加权K-means算法的分层聚类画像推荐模型. 首先就单项业务, 比如电能替代推广业务, 设计简单的, 针对性强的标签库, 找出具有某些典型共性的特定用户群体, 通过对群体的数据分析, 深度挖掘, 进一步提取出用户的群体特征, 采用基于改进的萤火虫优化加权K-means算法对电力用户进行两层聚类, 分别构建两组不同相似特征的k_Y类和k_N类群体画像模型^[20]. 其次通过计算两组聚类中心的相似度, 将构建得出的电能替代群体画像, 应用到电能替代的业务推荐中. 最后用同样的方法, 拓展到其它新业务的推荐应用中, 以实现电力营销业务的全面推广.

电力用户可划分为高压、低压非居民、低压居民3种, 这3种用户的数据特征分布有较明显差异, 但建模算法等没有差异. 本文仅以高压客户组为例, 介绍了向目标潜力用户推荐电能替代和其它新业务的应用方法.

2.1 用户画像建模流程

(1)数据采集: 对于电力企业最有优势的方法是直接从企业的电力业务系统中获得大量真实可靠的用户数据, 比如电力客户用电信息采集系统、电力营销业务应用系统、95598客户服务系统, 还有网上国网平台. 采集与电能替代密切相关的业务数据, 高压用户数据采集重点应放在用电设备清单、增容减容等业务的办理情况、用电容量、行业分布、能耗情况、用电趋势、经营现状及其前景等方面.

(2)数据特征映射: 假设用户数据集为 $X = \{ {X_1},{X_2}, \cdots , $ $ {X_j}, \cdot \cdot \cdot ,{X_n}\}$ , 将高压用电客户数据进行预处理, 采用向量空间模型(Vector Space Model, VSM)将高压用户的m维特征映射为 $X = \{ {X_1},{X_2}, \cdot \cdot \cdot ,{X_j}, \cdot \cdot \cdot ,{X_n};{X_j} = \left( {{x_{j1}},{x_{j2}}, \cdot \cdot \cdot ,} \right.$ ${x_{jm}}{)^{\rm{T}}} \in {R^m}\}$ .

(3)第一层聚类: 用基于改进的萤火虫优化加权K-means算法提取用户与电能替代密切相关的用电特征, 将用户聚成2类. 识别出办理过电能替代的Y群体和未办理电能替代的N群体两大类.

(4)第二层聚类: 再次用基于改进的萤火虫优化加权K-means算法分别对Y群体和N群体进行聚类, 将Y群体分成K_Y类, 将N群体分成K_N类.

(5)群体特征提取: 经过了两层聚类, 共得到K_Y+K_N个聚类簇和聚类中心. 聚类簇的聚类中心代表该聚类簇的所有对象, 其各个参数即标签反映了该群体的共性特征.

(6)群体画像表达: 将标签可视化, 最终得到了K_Y+K_N个高压用户的群体画像.

画像建模的总体流程如图2所示.

2.2 用户画像的应用 2.2.1 电能替代业务推荐

画像模型构建完成之后, 向目标潜力客户推荐电能替代业务. 检查审视未办理电能替代的目标用户群体 $N = \{ {N_1},{N_2}, \cdot \cdot \cdot ,{N_i}, \cdot \cdot \cdot ,{N_{kn}}\} $ , 通过式(14)逐个计算群体N的聚类中心N_i与群体 $ Y = \{ {Y_1},{Y_2}, \cdot \cdot \cdot ,{Y_i}, \cdot \cdot \cdot ,{Y_{kY}}\} $ 的聚类中心之间的欧氏距离.

$d({N_i},{Y_j}) = \left\| {{N_i} - {Y_j}} \right\| = \sqrt {\sum\limits_{l = 1}^m {{{\left| {{N_{il}} - {Y_{jl}}} \right|}^2}} } $

(14)

对计算所得的 $ d({N_i},{Y_j}) $ 进行排序, 求出N_i与群体Y的最小距离集合 ${D_{NY\min }} = \{ {d_{\min }}({N_1},Y),{d_{\min }}({N_2},Y), \cdot \cdot \cdot , $ $ {d_{\min }}({N_{KN}},Y),\} $ 即目标群体 $N = \{ {N_1},{N_2}, \cdot \cdot \cdot ,{N_i}, \cdot \cdot \cdot ,{N_{kn}}\} $ 的最近邻. 距离越小, 相似度越高, 推荐偏好越一致, 依次按D_NYmin向目标群体N推荐相应的电能替代业务. 由系统自动发送“…的用户已成功办理了电能替代”的信息, 发送“如何办理电能替代”、“现在就办电能替代”的链接. 拉近企业与用户的关系, 使用户从不了解到有意向, 再到成功办理业务.

2.2.2 其它新业务推荐

前文所述, 将画像技术应用在电能替代这一项业务的推荐应用上. 这一推荐方法, 同样适用于开展其它新业务的推荐, 比如分布式光伏发电、节能服务等. 只要按照推荐的新业务类型, 再一次利用基于改进的萤火虫优化加权K-means算法, 由所得的目标潜力群体画像即可推荐又一项新业务. 由系统自动发送“办理了…的用户也成功办理了…”之类的信息, 发送“如何办理…”、“现在就办…”的链接. 照此思路, 可以逐渐将用户画像拓展应用到一项项具体的电力业务中, 提升自身竞争力, 开拓出更大的用户市场.

目前有许多学者致力于大数据处理技术的研究, 数据挖掘技术和用户画像技术日益成熟, 但电力用户数据量巨大, 而且持续增长, 导致海量的交互数据大大超过企业自身的数据抓取、数据存储与数据分析能力, 增大了用户画像的难度^[21]. 为加快运算速度, 提高推荐精准度, 本文通过压缩标签数量, 降低采集数据维度, 在画像建模的数据采集环节, 只关注与推荐业务密切相关的数据, 虽然每项业务推荐都需要用算法分层聚类来完成画像的构建和应用, 但总的来说大大减少了交互数据量, 同时精准度更高.

3 实验例证 3.1 实验数据集

实验数据于2019年6月采集自电力营销业务应用系统, 以某市供电公司的高压用户为实验对象, 选取A、B、C、D、E这5个样本个数依次递增的供电所高压用户集, 数据集的描述如表1所示. 实验的运行环境为Windows10操作系统、8 GB物理内存、CPU速度为3.1 GHz、Matlab2018b.

3.2 实验结果与分析

为验证本文算法在电力用户画像构建和推荐应用中的聚类精度和收敛速度, 设计了实验将本文算法与传统K-means和FA 算法作了对比. 在5个高压用户数据集上分别进行100次实验, 比较目标函数值、运行时间和迭代次数, 实验结果如表2至表4所示. 实验参数设置如下: 最大吸引度 $ \;{\beta _0}$ =1、光强吸收系数γ=1、步长因子α=0.05、最大迭代次数T_max=150、迭代停止阈值ε=10⁵ .

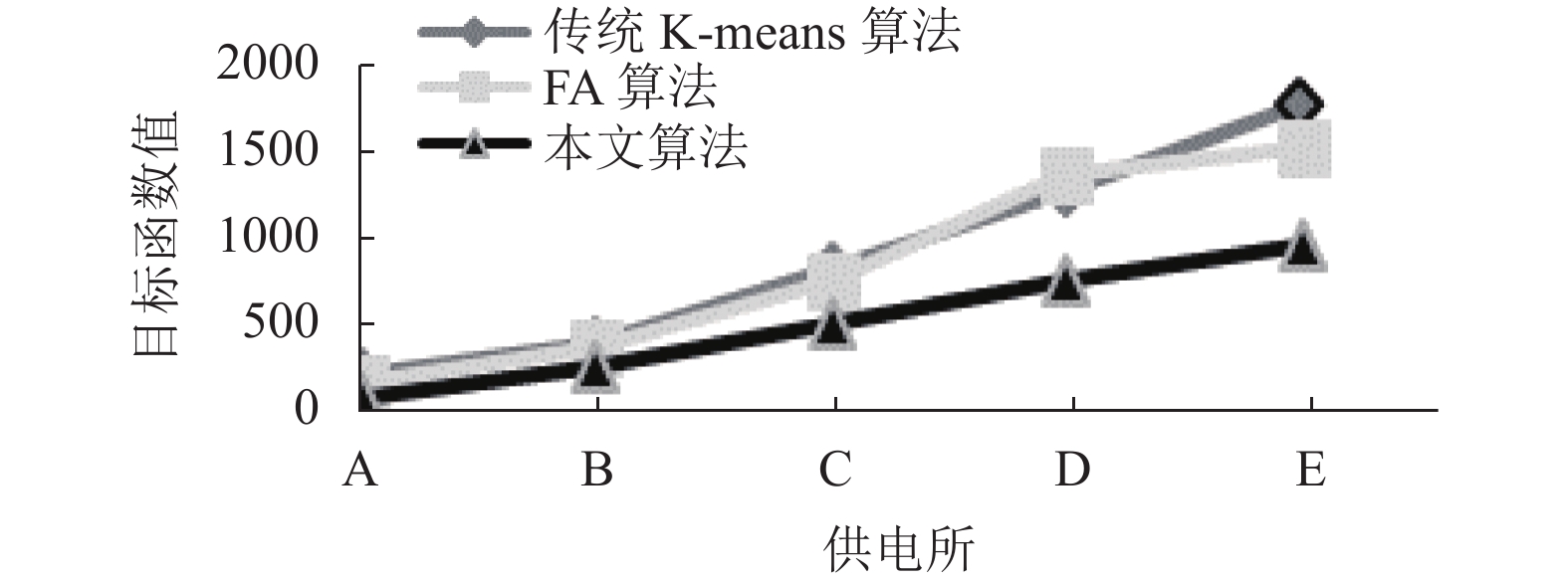
为了方便比较, 将表2至表4的对比结果, 以折线图的形式表示出来, 如图3至图5所示.

通常用目标函数值来衡量聚类效果, 目标函数值越小, 聚类簇越紧凑, 聚类效果越好. 对比本文算法与传统K-means和FA 算法, 由图3可见本文算法的目标函数Jc(X,V)平均值较小, 而传统K-means算法和FA 算法的目标函数值相近, 明显较大, 反映出本文算法的聚类有效性、聚类效果更好. 由图4可见本文算法的平均迭代次数更少, 由图5可见本文算法的运行时间更短, 在数据量增多的情况下优势更明显, 反映出聚类收敛速度的加快. 由于本文算法结合了K-means和FA 算法的优点, 引入了加权的目标函数, 引入了平方项作为扰动算子进行优化, 使得原来分布不明显、不容易分类的数据变得有利于划分, 使算法的每一次迭代更快地接近于真实的数据划分, 进而减少算法的迭代次数, 有效避免了聚类结果的随机性, 提高了算法稳定性和收敛速度. 实验结果表明本文算法构建的用户画像更清晰准确, 快速, 推荐针对性更强,

4 结论

本文针对电力企业用户画像在应用中效果欠佳的现状, 提出一种基于改进的萤火虫优化加权K-means算法的分层聚类推荐模型. 该模型优点如下:

(1)算法结合K-means和FA 算法的优点, 并采用了两层聚类方法, 使得原来分布不明显、不容易分类的数据变得有利于划分, 使算法的每一次迭代更快地接近于真实的数据划分, 进而减少算法的迭代次数, 有效避免了聚类结果的随机性. 算法稳定性和收敛速度的提高, 使用户画像的构建和应用过程更快速更有效, 从而为画像技术在电力业务的推广应用提供有力支撑.

(2)通过就某一项具体业务, 压缩标签数量, 降低采集数据维度的方法, 大大减少了交互数据量, 避免了无关数据和异常数据的干扰, 提高了画像的速度和精准度.

(3)画像重点由个体画像转移到群体画像, 更易于提取出用户的共性特征, 提升了画像构建和应用的效率.

实验阶段, 选取供电公司的5个高压用户样本集设计了仿真实验, 实验表明本文方法有效提高了运算精度和速度, 使画像构建和应用的针对性和精准性得到了提升.