随着能源和电力需求的不断增长, 传统电网完成了向智能电网的转变. 而作为物联网的重要应用场景, 智能电网中接入的智能设备数量呈指数级增长, 其发展高度依赖于通信发展, 并且对于安全性、时延性、可靠性的需求将会越来越大. 同时, 由于智能电网中各种不同的电力服务对于带宽、时延、成本等方面的不同需求, 通信平台的灵活性和适应程度也面临着巨大挑战. 然而, 对于4G网络来说并不能完全满足这种差异化需求, 如更高的数据速率、更低的端对端延迟、更高的可靠性以及庞大的设备连接^[1]. 随着5G网络的发展逐渐成熟以及商业化进程顺利进行, 5G中的新一代移动通信技术, 具有应用于电力服务的可能性.

网络切片是5G的核心技术之一, 基于云计算、网络功能虚拟化、软件定义网络等技术实现对资源的合理配置, 其本质是将物理网络在逻辑上划分为多个虚拟网络, 每个虚拟网络可以根据不同的需求, 如带宽、时延、安全性、成本提供定制服务, 从而灵活且可靠的应对网络中的不同场景^[2]. 对于运营商来说, 网络切片使其可以以不同的价格向不同的客户出售定制的服务. 将网络切片应用于智能电网中, 不仅可以针对电力服务的多样性提供定制服务, 同时相互之间逻辑独立的虚拟化网络也大大增加了智能电网的可靠性和安全性.

但是, 为了提供性能更好且具有成本效益的服务, 针对网络切片的实时资源管理方面成为了亟待解决的问题^[3]. 在智能电网场景中, 主要的问题是资源分配之前的服务类型未知, 需求变化不稳定, 即缺乏用户信息的先验知识. 考虑到有时并不能获取有效和完整的数据以进行可靠资源或流量预测, 本文现阶段面临的挑战是将5G切片应用于智能电网并合理分配资源. 针对这一问题, 许多学者和研究机构给出了解决方案, 比如提出了一种用于切片间资源管理的在线遗传切片策略优化器^[4], 但是这种优化器并没有考虑切片上的资源以及服务水平协议之间的具体关系. 或者使用启发式算法来控制用户的请求准入^[5], 但是在处理紧急事例方面能力不足. 在面向边缘计算^[6]和物联网^[7]之类的具体方案中, 针对网络切片的资源管理这一问题已经取得了突破性的进展, 但是这类研究并没有考虑到一般情况下的解决方案. 强化学习着重于通过尝试所有流体行为以产生更多奖励结果的方式与环境交互, 从而解决这个问题^[8].

深度强化学习(DRL)是深度学习和强化学习的结合, 可以在没有先验知识的条件下, 解决上述问题, 被认为是一种可以根据切片状态实现最佳资源分配的方法^[9]. 深度强化学习也被广泛应用于网络领域, 在许多无线电资源分配方案中表现良好, 例如卫星通信^[10], 任务关键型服务^[11], URLLC (超可靠和低延迟通信)中的多波束场景等^[12].

因此, 综合以上观点, 本文提出了一种基于DRL的智能电网RAN切片策略, 以实现智能电网的资源管理, 主要贡献如下;

(1)将DRL应用于智能电网的RAN切片, 并对场景中的状态, 操作和奖励进行了分析, 并且完成了从智能电网切片资源管理到DRL的映射.

(2)对电力服务进行了分类, 设置了不同的效用函数, 以对弹性和实时应用这两种服务应用进行建模.

(3)提出了一种基于Q学习的DRL策略, 即深度Q网络模型(Deep Q Network, DQN)来解决RAN切片资源分配问题.

仿真结果表明, 本文提出的方法可以在最大化系统效益的前提下降低成本.

1 系统模型

本文所提出的系统模型如图1所示, 从图中可以看出RAN中的射频资源被分为许多网络切片, 用来支持智能电网中相关的电力服务. 用向量 $\lambda $ 表示所有切片的集合为 $ Q=\{{q}_{1}, {q}_{2}, \cdots,{q}_{n}\}$ , 这些切片共享系统总带宽. 而向量 $E$ 则表示智能电网中的电力服务流, 集合为 $ D= $ $ \{{d}_{1}, {d}_{2}, \cdots,{d}_{m}\}$ .

面对智能电网多服务的特点, 每个切片服务需要满足的QoS (服务质量)要求是不同的. 在实际场景中, 系统事先不知道哪种服务流具体代表智能电网中的哪种服务, 并且智能电网场景中服务的实时需求变化是不稳定的. 可以看出 ${d_i}\;(i \in M = \{ 1,2,\cdots,m\} )$ 遵循特定的流量模型.

基于DRL的关键要素, 本文首先定义了RAN的系统状态空间、行为空间以及奖励功能. 切片控制器与无线环境的交互由数组 $\left[ {S,A,P\left( {s,s*} \right),R\left( {s,a} \right)} \right]$ 表示, 其中S代表一组可能的状态, A代表一组可能的动作, $P(s,s*)$ 代表从状态s到s'的转移概率, $R = \{ s,a\} $ 是与状态s中的动作触发相关的奖励, 该奖励被反馈给切片控制器. 下面给出了RAN切片资源管理到DRL的具体映射;

(1)状态

本文中的状态空间定义为数组 $S = \{ \mathop s\nolimits^{\rm slice} \}$ . $\mathop s\nolimits^{\rm slice}$ 是一个用于表明所有切片当前状态的向量, 这些切片被用于承载相关的电力业务, 其中第n个元素定义为 $\mathop s\nolimits_n^{\rm slice}$ .

(2)行为

对于智能电网时变流量模型, 强化学习的智能体需要为相应的电力服务分配合适的切片资源. 智能体可以基于当前切片状态和奖励功能来决定如何在下一时刻执行动作. 动作空间定义为 $A = \{ \mathop a\nolimits^{\rm bandwidth} \}$ , 其中 $\mathop a\nolimits^{\rm bandwidth}$ 表示智能体为每个逻辑独立切片分配适当的带宽以承载相应的服务.

由于网络切片是在虚拟网络之间共享网络资源, 因此网络切片必须彼此隔离, 以便如果一个切片上的资源不足以承载当前服务, 则拥塞或故障不会影响其他切片. 因此, 为了确保切片之间的隔离, 同时最大程度地利用资源分配, 我们假设每个切片最多只能承载一项服务:

$ {\sum _{j=1}^{N}{{a}}_{{d}_{i}}^{{{q}}_{i}}}=1, \;\forall i\in M$

(1)

同时定义二进制变量 $\mathop a\nolimits_{{d_i}}^{\mathop q\nolimits_i } \in \{ 0,1\} $ .

(3)奖励

智能体将特定的切片分配给智能电网服务后, 它将获得详细的奖励, 本文将其用作系统的奖励. 控制电源服务对通信的时延和误码率有严格的要求, 通信的失败或错误可能影响电网的控制执行, 导致电网运行失败. 对于某些移动应用服务(例如巡逻传输视频, 高清视频的回放等), 需要一定的传输速率保证, 并且对通信带宽有很高的要求. 供电可靠性意味着连续, 充足, 高质量的供电. 例如, 当供电可靠率达到99.999%时, 表示该地区用电用户的年度停电时间不会超过5分钟, 而当该数字达到99.9999%时, 用电用户的年度停电时间该区域的时间将减少到30 s左右. 由于RAN中的频谱资源有限, 在分配切片时应选择一种最佳策略, 以最大程度地提高用户的QoS要求.

本文主要考虑下行链路情况, 并使用频谱效率(SE)和延迟作为评估指标. 系统的频谱效率可以定义为:

$SE = \frac{R}{B}{\rm{(bit/s/Hz)}}$

(2)

其中, B是信号带宽, R是传输速率. 根据香农公式 $ R=b{\mathrm{log}}_{2}(1+({g}^{BS\to UE}P)/{\sigma }^{2})$ 可以得出基站对用户的实际速率, 其中 ${g^{BS \to UE}}$ 是基站和设备之间的信道状态信息(CSI), 服从瑞利衰落. b是分配给切片的带宽, $ ({g}^{BS\to UE}P)/{\sigma }^{2}$ 是信噪比.

为了描述用户的QoS要求, 本文引入了效用函数^[13], 它是分配切片服务的带宽与用户感知的性能之间的曲线图. 在本文中, 假设切片所承载的服务可以分为弹性应用程序和实时应用程序^[14].

① 弹性应用程序: 对于这种类型的应用程序, 没有最低带宽要求, 因为它可以承受相对较大的延迟. 灵活流量效用模型使用以下函数:

$ {U}_{e}(b)=1-{\rm e}^{-\frac{kb}{{b}_{\mathrm{max}}}}$

(3)

其中, k是一个可调参数, 它确定效用函数的形式并确保在收到最大请求带宽时, U $ \simeq $ 1. 但是, 即便带宽很高, 该应用程序的用户满意度也很难达到1. 因此, 本文认为即使网络带宽非常大(例如分布式电源, 视频监控, 高级计量等), 分配给此类应用程序的带宽也不应超过最大带宽 ${b_{\max }}$ .

② 实时应用程序: 这种类型的应用程序流量要求网络提供最低级别的性能保证. 如果分配的带宽降至某个阈值以下, 则QoS将变得难以接受. 主要代表类型是URLLC切片服务, 典型示例是配电自动化, 紧急通信等. 使用以下效用函数为实时应用程序建模:

$ {U}_{rt}(b)=1-{\rm e}^{-\frac{{k}_{1}{b}^{2}}{{k}_{2}+b}}$

(4)

其中, k₁和k₂是确定效用函数形式的可调参数. 智能体的奖励定义如下:

$R = \lambda \cdot SE + \mu \cdot U{}_e + \xi \cdot {U_{rt}}$

(5)

其中, $\lambda $ , $\mu $ , $\xi $ 分别是SE, $U{}_e$ , ${U_{rt}}$ 的权重.

因此, 本文提出的问题可以表述为:

$ \begin{split} &\mathop {\arg \max }\limits_b\left\{R(b, D)\right\}\rm=\\ &\mathop {\arg \max }\limits_b\{\lambda \cdot SE(b, D)+\mu \cdot U{}_{e}(b)+\xi \cdot {U}_{rt}(b)\} \end{split}$

(6)

约束于:

$ {C}_{1}: Q=\{{q}_{1}, {q}_{2}, \cdots,{q}_{n}\}$

(7)

$ {C}_{2}: D=\{{d}_{1}, {d}_{2}, \cdots,{d}_{m}\}$

(8)

$ {C}_{3}: {\displaystyle \sum _{j=1}^{N}{{\displaystyle a}}_{{{\displaystyle d}}_{i}}^{{{\displaystyle q}}_{i}}}=1, \forall i\in M,{{\displaystyle a}}_{{{\displaystyle d}}_{i}}^{{{\displaystyle q}}_{i}}\in \{0,1\}$

(9)

其中, ${d_i}(i \in M = \{ 1,2,\cdots,m\} )$ 遵循特定的流量模型.

解决该问题的困难在于, 由于流量模型的存在, 当最初不了解情况时, 即在智能电网场景中服务的实时需求变化未知时, 服务需求的变化是不稳定的. 表1显示了智能网格切片资源管理机制到DRL的映射.

2 基于DQN的切片策略

本节主要介绍的是使用深度Q学习算法训练网络, 通过不断迭代的方式最终得出最优策略的值. 深度Q学习算法简称DQN(Deep Q-Network), DQN主要是在Q-Learning的基础上演变而来的, DQN用一个深度网络代表价值函数, 依据强化学习中的Q-Learning, 为深度网络提供目标值, 对网络不断更新直至收敛.

由于上述的RAN状态集, 动作集和奖励函数的表达式略有不同, 因此在本文中, 基于提出的映射模型, Q学习算法具有通用性. 本文将状态空间定义为 $S = \{ {s_1},{s_2},\cdots,{s_n}\}$ , 动作空间为 $A = \{ {a_1},{a_2},\cdots,{a_n}\}$ , 奖励功能为 $R = \{ s,a\} $ . $P(s,s*)$ 表示从状态s到状态s'的转变概率.

切片控制器的最终目标是找到最佳切片策略 $\pi {\rm{*}}$ , 这是从状态集到操作集的映射, 并且每个状态的预期长期折扣奖励需要最大化:

$ \pi *(s)=\mathrm{arg}\underset{\pi }{\mathrm{max}}{V}_{\pi }(s)$

(10)

状态s的长期折扣奖励是在状态轨迹上获得的奖励的折扣总和, 由式(11)给出:

$R(s,\pi (s)) + \gamma R({s_1},\pi ({s_1})) + {\gamma ^2}R({s_2},\pi ({s_2})) + \cdots$

(11)

其中, $\gamma $ 是折扣因素(0< $\gamma $ <1), 确定与未来奖励相对应的当前值. 式(10)中的优化目标表示任何策略的状态值函数, 可以表示为:

$ \begin{split} {V_\pi }(s) = &{E} \Bigg\{ \sum\limits_{t = 0}^\infty {{\gamma ^t}R} ({s_t},{a_t})|{s_0} = s,{a_0} = a\Bigg \} \\ = & { E}\{ R({s_0},{a_0})|{s_0} = s,{a_0} = a\} \\ & +{E}\Bigg \{ \sum\limits_{t = 1}^\infty {{\gamma ^{t - 1}}R} ({s_t},{a_t})|{s_0} = s,{a_0} = a\Bigg \} \\ \end{split} $

(12)

根据贝尔曼的最优性标准^[15], 在单个环境中至少存在一种最优策略. 因此, 最优策略的状态值函数由式(13)给出:

${V_{\pi *}}(s) = \arg \mathop {\max }\limits_{a \in A(s)} \{ \overline R (s,a) + \gamma P(s,s',a){V_\pi }(s')\} $

(13)

状态转换概率取决于许多因素, 例如流量负载, 流量到达和离开速率, 决策算法等, 所以在无线端或核心网络端获取都不容易. 因此, 无模型强化学习非常适合于推导最优策略, 因为它不需要期望的回报, 并且状态转换概率可以称为先验知识. 在本文中, 从各种现有的DRL算法中选择了深度Q学习^[16].

以RAN切片为例, 切片控制器在较短的离散时间段内与无线环境进行交互. 状态动作二进制数组的动作值函数(也称为Q值)可以表示为 $Q(s,\pi (s))$ . 它被定义为使用策略 $\pi $ 时状态s的预期长期折扣奖励. 本文的目标是找到一种优化策略, 使每个状态s的Q值最大化:

$ \pi *(s)=\mathrm{arg}\underset{a\in A(s)}{\mathrm{max}}Q(s,a),\forall s,\pi $

(14)

根据深度Q学习算法, 切片控制器可以基于已知信息通过迭代学习Q的最佳值. 处于状态s的切片控制器可以随时选择动作a. 然后, 给出即时奖励 ${R_t}$ , 状态s将转换为下一个状态s'. 深度Q学习算法的过程可以通过以下更新公式表示:

$Q(s,a) \leftarrow Q(s,a) + \alpha [\widehat R + {\gamma ^t}\mathop {\max }\limits_{\alpha ' \in A(s)} Q(s',a') - Q(s,a)]$

(15)

其中, α是学习率, $\widehat R$ 是所有即时奖励 ${R_t}$ 的折扣累积:

$\widehat R = \sum\limits_{t = 0}^{T - 1} {{\gamma ^t}{R_t}} $

(16)

通过长时间更新Q值并调整α和γ的值, 可以保证 $Q(s,a)$ 最终收敛到最优策略的值, 即 ${Q_{{\pi ^*}}}(s,a)$ .

整个切片策略由以下算法给出. 最初, Q的值设置为零. 在应用Q学习算法之前, 切片控制器基于每个切片的功率需求估算, 对不同切片执行初始切片分配, 以初始化不同切片的状态. 现有的无线电资源切片解决方案使用基于带宽或基于资源的供应来将无线电资源分配给不同的切片.

由于Q学习是一种在线迭代学习算法, 因此它执行两种不同类型的操作. 在探索模式下, 切片控制器会随机选择一个可能的操作以增强其将来的决策. 相反, 在开发模式下, 切片控制器更倾向于过去尝试并发现有效的操作. 我们假设状态s中的切片控制器以概率ε进行探索, 并以概率1–ε使用先前存储的Q值. 在任何状态下, 并非所有动作都是可能的. 为了维持切片到切片的隔离, 切片控制器必须确保不在RAN中将相同的物理资源块(PRB)分配给两个不同的切片.

简单来说, DQN是神经网络和Q-Learning的融合, 而不管是Q-Learning还是DQN, 都是通过贪婪算法直接获取Q值, 在获取Q值时都会使用到maxQ, 即式(15). 使用这种方法可以使Q值向需要的优化目标快速逼近, 但同时也可能导致过度估计, 导致最终获得的算法模型与实际偏差过大. 为了解决这个问题, 在本文中, 除了上述的DQN算法, 还考虑了其改进算法DDQN与之进行比较.

DDQN通过解耦目标Q值动作的选择和目标Q值的计算这两步, 来达到消除过度估计的问题. DDQN更新函数如下:

$Y_t^{DDQN} = {R_{t + 1}} + \gamma Q({S_{t + 1}},\mathop {\arg \max }\limits_a Q({S_{t + 1}},a;{\theta _t}),\theta _t^ - )$

(17)

在DDQN中, 不再是直接在目标Q网络里面找各个动作中最大Q值, 而是先在当前Q网络中先找出最大Q值对应的动作. 然后利用这个选择出来的动作在目标Q网络里面去计算目标Q值.

DDQN算法使用了一个新的相同结构的目标Q网络来计算目标Q值^[17,18], 但在本文中不过多赘述. 而除了目标Q值的计算方式以外, DDQN和DQN的算法流程完全相同.

3 仿真结果

考虑到服务到达时不仅只有一个基站作为接收点, 因此在本文中建立了两个基站BS1和BS2. 基站BS1的覆盖半径为R=1000, 中心坐标为[0, 0], 而基站BS2的覆盖半径为R=500, 中心坐标为[500, 0]. 实时应用程序和弹性应用程序的生成服从泊松分布, 并且生成速率表示为 ${\lambda _{rt}}$ =3.6和 ${\lambda _e}$ =2.4. 服务的生成坐标是随机生成的, 并且根据服务与两个基站之间的距离来确定对哪个基站的访问. 接入遵循最小距离优先原则. 基站与设备之间的信道状态信息(CSI)服从方差 ${\sigma _r}$ =1.5的瑞利分布, 信道噪声服从平均值 $\;{\mu _g}$ =0且方差为 ${\sigma _g}$ =5的高斯分布, 基站BS1的信道数为BS1_channel=20, 基站BS2的信道数为BS2_channel=10. 为了方便研究, 香农公式中的信道带宽为b = 8 MHz. 基于Q学习, 构造了两个DRL网络, 即深度Q学习(DQL)和双深度Q学习(DDQL). DQL的主要作用在于目标网络和体验回放. DDQL的主要作用是改善最大动作选择操作并解决高估问题. 前者有两个神经网络, 即评价网络的两层结构和目标网络的两层结构, 后者只有一个神经网络, 由两层结构组成.

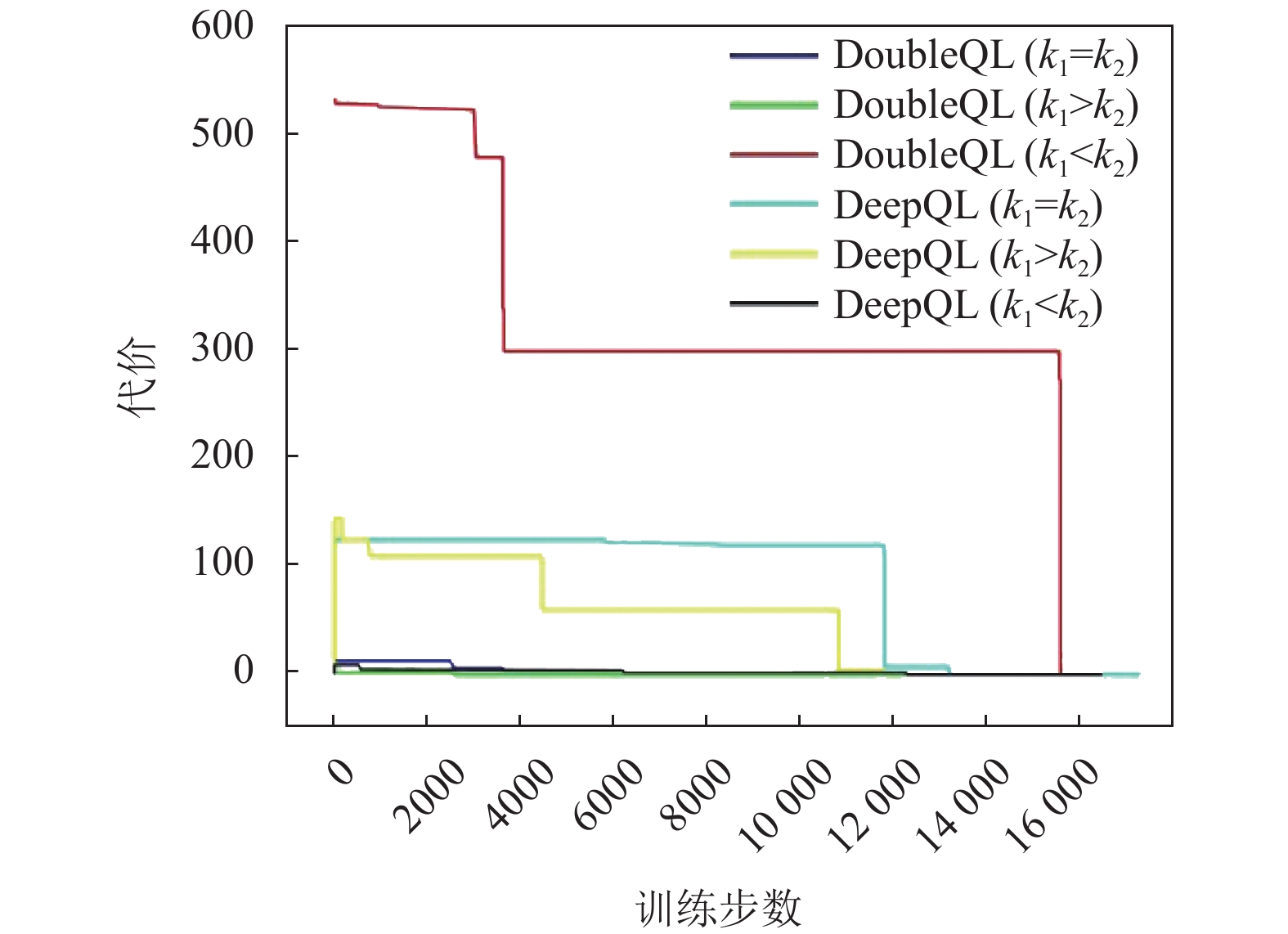
对于弹性应用, 在式(3)中将可变参数设置为k=0.8. 对于实时应用, 在式(4)中讨论了k₁和k₂之间的关系, 即k₁= k₂, k₁<k₂以及k₁>k₂. 由于应用程序会随时间更改位置坐标, 因此生成的应用程序会以 $upv = 3$ 的速率更新基站覆盖范围内的坐标. 基站根据接入应用生成相应数量的切片. 可以在弹性服务中分配最大带宽 $b_{\max }^{rt} = 5\;{\rm{MHz}}$ . 由于本文的算法满足了奖励最大化, 因此可以忽略由于实时服务分配的带宽太小而导致的服务质量无法接受.

累积折扣奖励 $\mathop {\arg \max }\limits_b\left\{R(b, D)\right\}$ 是通过每次迭代生成的奖励的折扣累积而生成的. 图2示出了该算法的奖励函数值. 横坐标表示迭代步骤的数量, 纵坐标表示奖励值. 在图中, 比较了2种算法的3种类型. 从图中可以看出, 在k₁= k₂的情况下, DQL的奖励值大于其他5种情况, 但是这6种情况的奖励值差异很小. 图3显示了算法的成本值, 比较了2种算法的3种类型. 该算法在开始时会产生大量成本, 但是随着算法的进一步更新, 成本逐渐收敛, 最终降低为零. 比较这6个曲线, 可以看出, 在k₁<k₂的情况下, DDQL的收敛速度最慢, 成本值较大. 在k₁>k₂的情况下, 成本收敛速度最快, 成本值最小.

最后, 作为补充, 本节以5G规范标准对所提出的切片方法在系统吞吐量与系统效用方面进行了评估, 并与现有的Q-L (Q-Learning)以及RRA (随机资源分配)方法比较^[19]. 通过对实验结果的分析, 表明了文章所提出的基于深度学习的切片策略能有效提高系统性能.

本节选用Matlab进行数值评估和分析, 具体参数可以参照上文, 这里不过多介绍. 考虑到切片资源的数量和用户请求的增加, 实验中将基站数量增加到10个, 然后不断增加用户请求的数量来评估系统的性能. 图4为DQN、Q-L和RRA的系统吞吐量. 可以看出, 当用户请求数增加到40时, DQN算法的系统吞吐量低于Q-L算法. 当用户持续增加时, DQN系统的吞吐量高于Q-L, 这是因为Q-L算法关注的是短期回报. 除了用户数量在16–24时, RRA算法有着比DQN算法稍高吞吐量, 其余都是最低. 这是因为RRA具有随机性, 当用户数量较少时, 会占用过多的资源, 如果一个切片的剩余资源不足或超过功率限制, 则拒绝用户的请求.

图5是3种算法的总效用比较, 总效用随着用户数量的增加而增加, 并最终达到一个稳定值. 由于整个片的资源是有限的, DQN通过合理地为切片分配用户来充分利用资源. 从图中可以看出, DQN算法总体上优于Q-L和RRA算法.

4 结论

智能电网是物联网的典型应用场景. 论文提出了一种用于智能电网的RAN切片资源分配的深度Q学习策略. 在到达服务未知的情况下, 该算法通过判断应用程序坐标与基站之间的距离来选择接入基站. 通过不断更新Q学习网络的阈值和参数, 可以最大程度地发挥系统的优势, 并使成本逐渐收敛到0. 基于上述, 本文应用了两种不同的神经网络, 并比较了k₁=k₂, k₁<k₂和k₁>k₂的3种情况. 可以看出, 奖励函数最终收敛到某个最大值, 成本最终达到最小值0. 仿真结果表明, 当奖励函数的差较小时, 在k₁>k₂的情况下, DDQL具有最快的成本收敛性和最小的成本值. 因此, 当神经网络层为双层时, 该算法可以更好地满足RAN侧智能电网的资源分配要求. 最后, 通过进一步对本文所提出的切片策略评估, 以及与Q-L以及RRA这两种算法的比较, 表明了本文算法的优势. 在未来的研究中, 将改进Q学习网络的参数, 以使该算法可以更快地收敛并优化服务中每个评估指标的权重.