路面裂缝是由自然应力引起的路面损坏,如果不及时处理, 很可能导致道路塌陷和交通事故. 因此, 对路面进行准确高效的检测尤为重要. 最直接的检测方法是对路面进行目测, 并由专家对其进行准确的评估. 然而, 这种方法涉及到较高的人工成本, 并且可能产生不可靠和不一致的结果, 同时检测人员直接在路面上检测是极其危险的且效率也很低[1]. 因此有必要设计一种精确、自动化的路面裂缝检测系统. 然而路面裂缝的自动检测是一个充满挑战的课题, 因为裂纹不仅拓扑结构复杂, 尺度不均匀, 而且会受低对比度和杂乱背景的影响而降低检测精度[2].
路面裂缝通常具有以下特点:
(1)裂缝的颜色相对于背景较深;
(2)裂缝的延伸方向是线性且宽度可变的;
(3)裂缝边缘的拓扑结构复杂.
传统检测方法中, 基于最大后验分类器, Oliceria等[3]提出一种利用激光成像系统对图像中的裂缝进行检测, 再利用二值区域和几何特征进行分割. Zou等[4]提出采用地面阴影去除法, 通过张量投票法建立裂缝分布概率图, 然后构造随机森林对递归树的边缘进行剪枝以进行裂缝检测. Oliveria等[5]推出一种用于路面裂缝检测与表征的图像处理算法和技术评价算法工具箱. Peng等[6]首次采用Otsu阈值分割法去除路面图像中的道路标志, 然后采用自适应迭代阈值分割算法得到裂缝分割图像.
深度学习方法迅速发展并且已经应用到了路面裂缝检测任务中. 基于深度学习的路面裂缝检测方法可以分为五类: 分割算法, 边缘检测算法, 分类器算法, 生成对抗方法和无监督方法. 文献[7,8]将裂缝检测视为分割任务, 文献[7]提出一种分块阈值分割方法对裂缝进行分割. 文献[8]在SegNet的基础上通过融合同一尺度下编码器和解码器的卷积特性来进行裂缝特征的提取. Yang等[9]将裂缝检测视为边缘检测任务, 以特征金字塔的形式将上下文信息转化为低层特征进行裂纹检测. Dorafshan等[10]基于混凝土图像的裂缝检测比较了深度卷积神经网络和边缘检测器. Zhang等[11]采用基于裂缝修补(CPO)的生成对抗网络模型对路面进行检测并将大尺度裂缝图像输入到非对称U形网络中, 以克服裂缝的产生“全黑”问题. Li等[12]提出了一种基于无监督多尺度融合裂纹检测的(MFCD)算法. 此外, 文献[13,14]将分类算法应用到路面裂纹检测中. 文献[13]提出了深度卷积神经网络(DCNN)实现了自动检测和分类路面裂纹. 文献[14]提出基于概率生成模型(PGM)和支持向量机(SVM)的网络来生成和计算裂纹特征的概率图, 并且提出了一种基于融合概率图的加权展开运算, 增强了算法的有效性.
在一定程度上, 无论是传统方法还是深度学习方法都可以检测到裂缝. 然而, 保证裂缝检测的连续性和裂缝边缘的完整性仍需进一步研究. 一方面, 裂缝沿着其延展方向是连续分布的, 一些比较细的裂缝容易检测不到. 另一方面, 裂缝的边缘拓扑结构复杂, 检测器容易丢失边缘信息, 导致检测裂缝的边缘过于光滑. 如图1所示, 图1(a)中检测结果出现裂缝断裂的现象, 图1(b)中的检测结果丢失了裂缝的边缘信息.

|
图 1 原生SegNet检测结果 |
1 相关方法 1.1 SegNet的发展
我们将路面裂缝检测视为分割任务, 且网络结构是受SegNet的启发. SegNet是一种编码解码模型, 由Badrinarayanan等[15]首次提出, 用于像素级图像分割. 之后, Badrinarayanan等[16]改进了他们之前提出的SegNet模型. 编码器部分和VGG16的13层卷积层相同, 且编码层由上采样和卷积构成, 最后将每个像素通过Softmax激活函数进行分类.
Schmugge等[17]首先将SegNet作为基础框架应用于裂缝检测任务. 他们提出了一种自动检测方法, 以帮助对核电站部件的焊接、划痕和研磨进行远程自动检测, 给出了不同光照条件下多帧图像的层次分类置信度.
1.2 基础框架虽然我们设计的框架是基于SegNet的, 但是, 它与原生SegNet[16]不一样, 我们没有直接在编码器部分使用VGG16模型. 编码器部分分为5层, 前2层是两个卷积, 并且每个卷积层后有1个max-pooling层, 最后3层是3个卷积层, 每个卷积层后有1个max-pooling层.
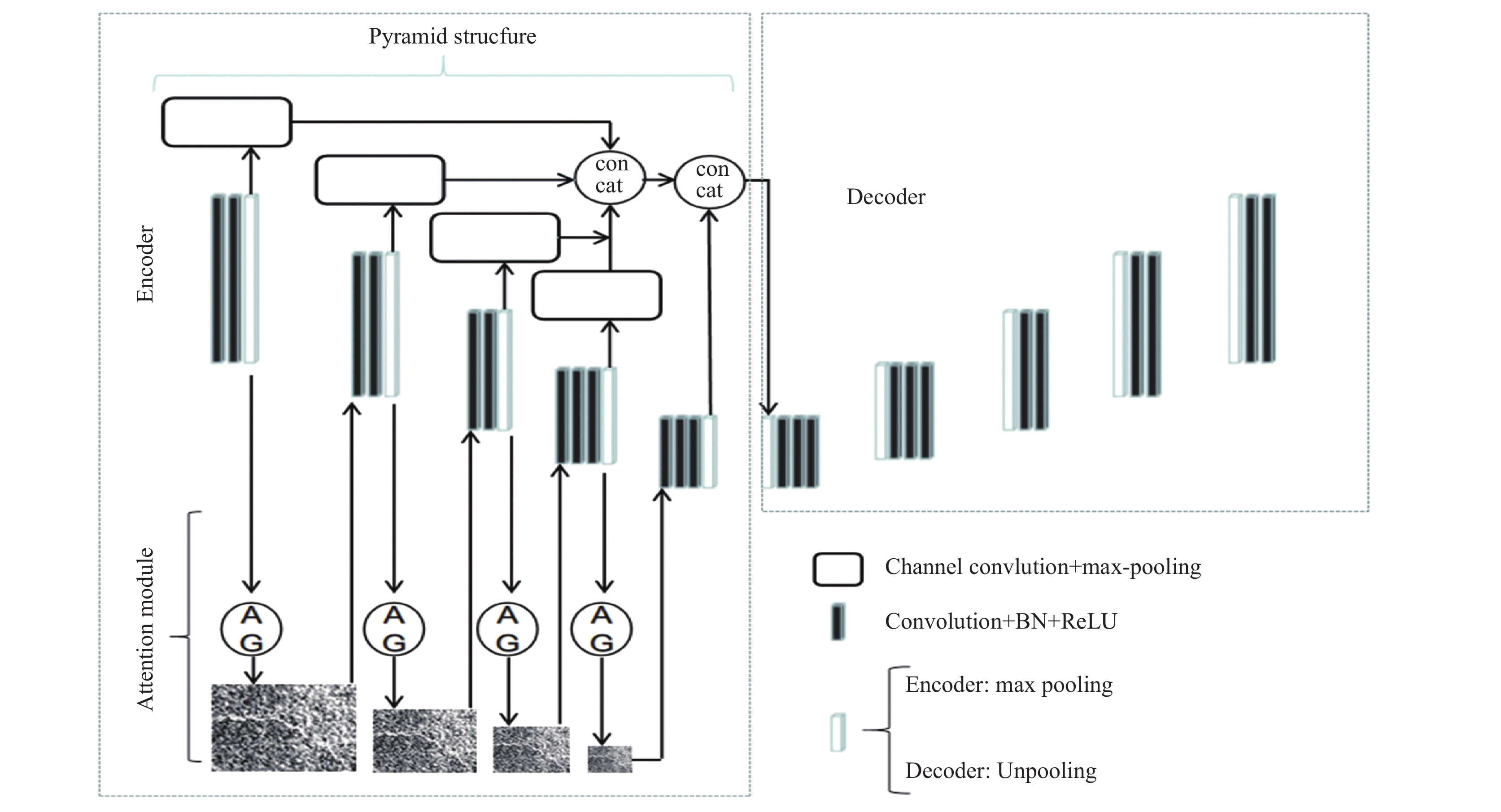
2 本文提出的模型CACPNet的整体设计结构如图2所示, 左边虚线框出的部分为编码器, 右边为解码器, 编码器上半部分结构为多层卷积金字塔结构, 下半部分为连续注意力机制.
2.1 连续注意力机制路面裂缝通常是连续的, 因此裂缝之间通常不会出现断开的现象. 另外, 在检测过程中经常会混淆背景和裂缝, 这就导致了断裂和裂纹信息丢失问题. 受注意力门控[18]的启发, 我们设计了一个连续特征注意机制模块, 以保证路面裂缝的连续性.
连续特征注意机制结构如图3所示. 输入图像或特征经过的上一层为Encoder模块, 下一层为连续注意力机制模块. 连续注意力机制模块中, 输入的原始图片或者上层特征图依次经过1×1×1的卷积, 批量归一化处理和ReLU函数激活, 接着通过Softmax函数激活和最大值池化处理生成注意力参数与上层特征进行加权, 得到本层的特征输出. 通常在Encoder-Decoder框架中添加注意力机制是和Attention UNet[18]类似, 在编码层和解码层的跳跃连接中添加注意力机制, 而本文则是在编码层之间添加注意力机制, 因为我们只是关注裂缝特征在特征提取过程中的细节特征丢失, 所以采用了在编码层之间连续使用符合各个解码层特征的注意力门控机制来对各层特征进行加权.
|
图 2 CACPNet网络结构 |

|
图 3 连续注意力机制结构 |
当前层的输入特征F∈
| ${F'} = \alpha \times F + F$ | (1) |
注意力参数的生成过程为:
| $F_{\rm att}^l = {\sigma _1}\left( {B{N_{\gamma ,\beta }}\left( {W_i^{\rm{T}}x_i^l + b_i^l} \right)} \right)$ | (2) |
| ${F^l} = F_{\rm att}^L\left( {x_i^l;\Theta _i^l} \right)$ | (3) |
| $\alpha = P\left( {{\sigma _2}\left( {{F^l}} \right)} \right)$ | (4) |
在式(2)中,
传统的特征金字塔结构[19,20]主要从不同尺度的图像中提取特征, 但这增加了训练数据量, 降低了效率. 目前用于路面裂缝检测的特征金字塔网络[9,21]大多是利用网络最后一层的特征映射来构造特征金字塔, 从而保证了裂缝特征对路面裂缝的完整性. 但是在一定程度上缺乏解决裂纹边缘信息丢失的能力. 因此, 我们提出了一种多层卷积特征金字塔结构, 利用各编码层的卷积特征进行特征融合. 多层卷积特征金字塔结构可以充分利用各层图像特征, 既能保证裂纹特征的连续性, 同时也减少了裂纹边缘信息的丢失.
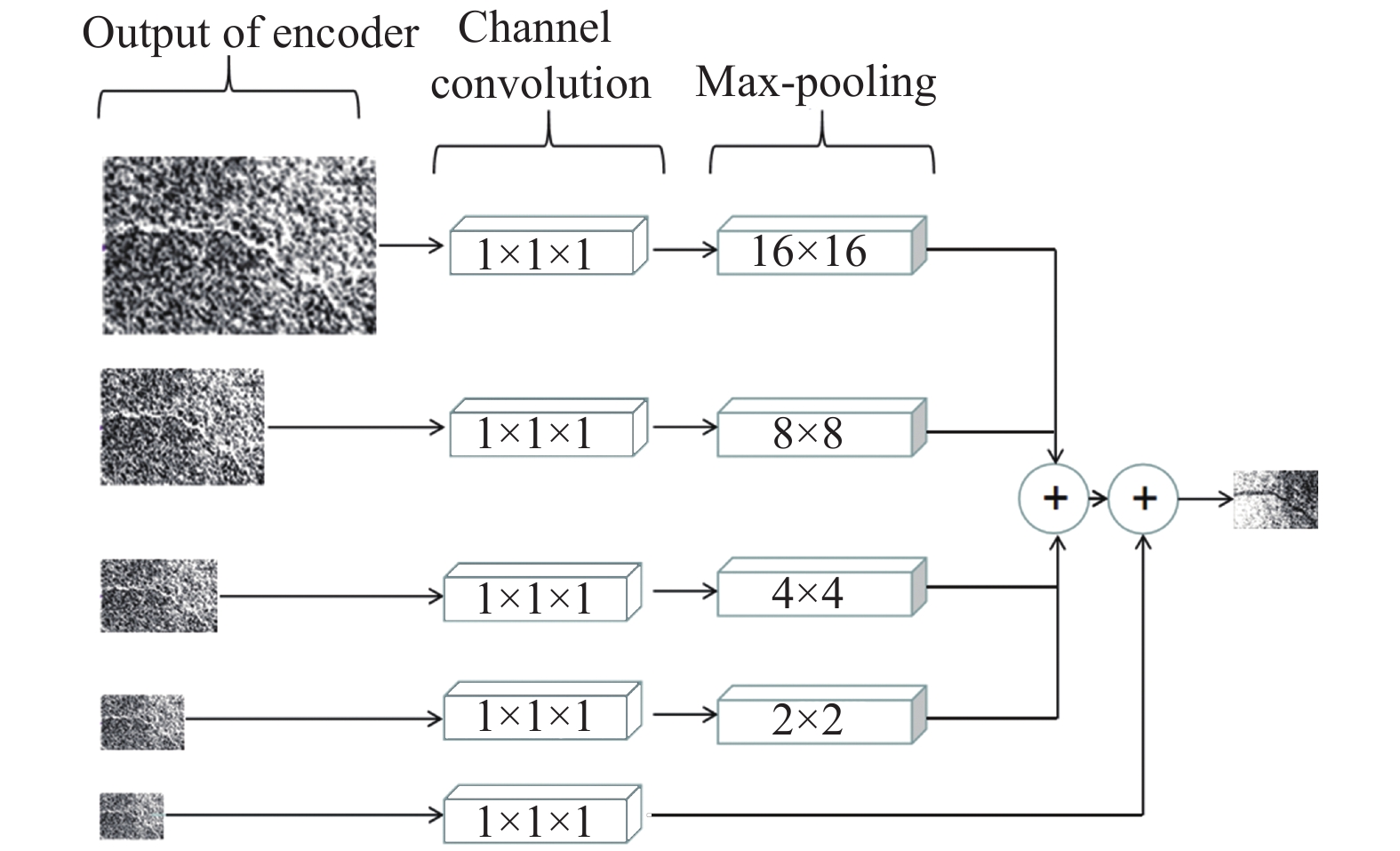
多层卷积特征金字塔如图4所示. 每层的输入为编码器每一层的输出特征. 从上到下每层的特征图尺寸为64×240×160、128×120×80、256×60×40、512×30×20、512×15×10.
|
图 4 多层卷积金字塔结构 |
因为各层的特征通道数和图像尺度不同, 无法直接进行特征融合. 使用1×1×1卷积对通道数进行变换, 然后通过最大池改变图像特征尺寸的大小, 最后, 前四层金字塔结构融合生成512通道特征映射, 再与编码器的最后一个特征层进行特征融合, 最后得到解码层的输入特征图.
3 实验分析 3.1 训练细节整个网络是由PyTorch实现的, 训练环境为3.5 GHz, 8 GB RAM, NVIDIA 2080Ti GPU, 且在Ubuntu环境下运行.
3.2 数据集比较实验采用3个公共数据集, 包括Crack500数据集[9], Crack200数据集[4]以CrackForest数据集(CFD)[22]. 因为3种数据集图片的大小是不同的, 我们有所有的图像和地面真相调整到480×320分辨率. 同时, 由于CFD和crack200数据集中的数据量太小, 我们随机选取翻转输入图像以增强数据以防止过度拟合.
3.3 评价指标为了比较生成的分割图像与真实分割图像的像素级相似度, 分割任务中主要使用4个指标, 分别是Precision、Recall、F1-measure和MIoU.
Precision是指所有样本中真正样本占所有正样本的百分比, Recall是正样本被模型判定为正样本的百分比, F1-measure是衡量二分类精度的一个指标. 它同时考虑了分类器的准确性和召回率.
因此, Precision可以定义为:
| $ {{Precision}} =\frac{{TP}}{{TP + FP}} $ | (6) |
Recall可以被定义为:
| $ {{Recall}} =\frac{{TP}}{{TP + FN}} $ | (7) |
F1-measure可以定义为:
| $ {F1} = \frac{{{\rm{2*}}Precision*Recall}}{{Precision + Recall}} $ | (8) |
MIoU可以被定义为:
| $ {{MIoU}} =\frac{{TP}}{{TP + FN + FP}} $ | (9) |
式(6)–式(9), 要计算这4个指标, 我们需要计算3个指标, TP是正样本预测为正样本的个数, FP是预测为负样本的正样本个数, FN是预测为负样本的负样本个数.
3.4 参数设置进行训练时我们设置了两个停止训练的条件, 一个是训练步数达到了设定值, 第二个是学习率下降到1e–9. 训练的batch设置为6.
由于交叉熵损失不适用分布不均匀的数据集, 因此我们采用Tversky损失[23]和L1正则损失的加权作为此次实验的损失函数. Tversky系数是Dice系数和Jaccard系数加权之后的广义系数. 不平衡分布路面裂缝可能导致某些数据出现异常值, 但L1正则损失可以处理数据中的异常值. 因此, 我们采用L1损失来提高系统的鲁棒性.
因此损失函数可以定义为:
| $loss(t,p) = \alpha *T(t,p) + (1 - \alpha )(L1(t,p))$ | (5) |
式(11)中, t为真实分割图像, p为预测分割图像, T为Tversky损失函数, L1为L1正则损失函数, α为权重系数, 设置为0.7.
3.5 实验结果如表1和表2所示, 为本文定量实验结果. 图5至图7为3种数据集上可视化检测结果. 从图5可以看出, 与图5(a)–图5(e)裂缝检测器的结果相比, CACPNet检测的裂缝边缘信息更丰富, 而不是平滑的. 从图6可以看出, 裂缝在原始图像和真实检测图像中是连续分布的, 没有断开, 但是除CACPNet的检测结果外, 其他的裂缝检测器检测出的裂缝发生了断裂. 图7是CFD数据上的检测结果, 可以看出检测的效果也是要优于其他的检测器. 图8为3种不同数据集训练时的损失和MIoU指标曲线图.
| 表 1 3种数据集上的MIoU指标比较 |
|
表 2 CFD数据集上Precision, Recall, |

|
图 5 Crack500数据集可视化检测结果 |

|
图 6 Crack200数据集可视化检测结果 |

|
图 7 CFD数据集可视化检测结果 |
3.6 消融实验
我们通过消融实验验证了CACPNet各个部分的重要性, 在CFD数据集上设计了与原生SegNet的对比实验, 所有参数设置, 包括学习率和损失函数都保持一致. 消融实验一共为3组, 第1组为原生SegNet, 第2组为原生SegNet加上连续注意力机制, 第3组为第二组的基础上加上多层卷积金字塔结构. 具体结果见表3.
此外, 我们还绘制了P-R曲线来验证添加注意机制和金字塔模型的有效性. 一般来说, 精确度降低, 召回率提高. 从图9中可以看出, 融合了注意机制和金字塔模型的曲线高于其他曲线, 进一步证明了我们提出的方法的必要性.

|
图 8 Crack500, Crack200和CFD数据集上训练的MIoU和loss |
| 表 3 消融实验结果 |
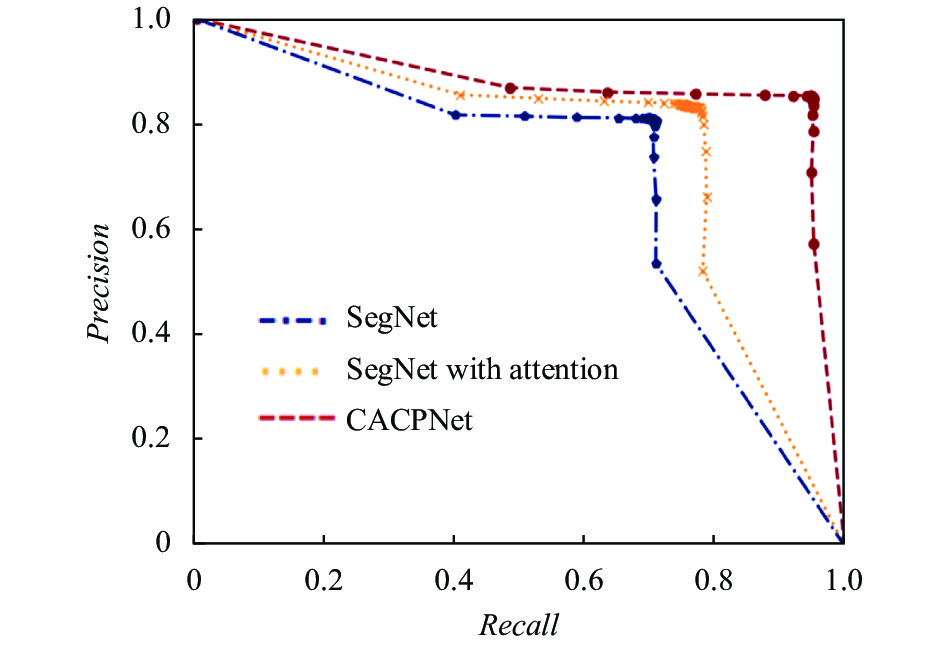
|
图 9 消融实验P-R曲线 |
4 结论与展望
本文提出了一种基于SegNet的路面裂缝检测模型. 我们基于SegNet融合了连续特征注意机制与多层卷积金字塔结构. 连续特征注意力机制可以保证裂纹之间的连续性, 在某种程度上, 减少了检测裂缝的断裂. 多层卷积金字塔结构采用对每层特征输出进行再利用, 保证全局信息的完整性, 包括可以对细微裂缝检测, 同时可以保证裂缝边缘信息的完整性. 此外, CACPNet已经在3个公共数据集上进行了实验验证, 包括Crack500数据集, Crack200数据集和Crack Forest数据集. 与现有的方法相比, 经过实验验证, 我们的网络在各种指标上都得到了一定的提升. 此外, 还进行了消融实验以验证其每个模块的有效性.
| [1] |
Nejad FM, Zakeri H. An optimum feature extraction method based on wavelet-radon transform and dynamic neural network for pavement distress classification. Expert Systems with Applications, 2011, 38(8): 9442-9460. DOI:10.1016/j.eswa.2011.01.089 |
| [2] |
Hu Y, Zhao CX, Wang HN. Automatic pavement crack detection using texture and shape descriptors. IETE Technical Review, 2010, 27(5): 398-405. DOI:10.4103/0256-4602.62225 |
| [3] |
Oliveira H, Correia PL. Automatic crack detection on road imagery using anisotropic diffusion and region linkage. Proceedings of the 18th European Signal Processing Conference. Aalborg, Denmark. 2010. 274–278.
|
| [4] |
Zou Q, Cao Y, Li QQ, et al. Cracktree: Automatic crack detection from pavement images. Pattern Recognition Letters, 2012, 33(3): 227-238. DOI:10.1016/j.patrec.2011.11.004 |
| [5] |
Oliveira H, Correia PL. CrackIT—An image processing toolbox for crack detection and characterization. Proceedings of 2014 IEEE International Conference on Image Processing (ICIP). Paris, France. 2014. 798–802.
|
| [6] |
Peng L, Chao W, Li SM, et al. Research on crack detection method of airport runway based on twice-threshold segmentation. Proceedings of the 5th International Conference on Instrumentation and Measurement, Computer, Communication and Control (IMCCC). Qinhuangdao, China. 2015. 1716–1720.
|
| [7] |
Zhang KG, Cheng HD, Zhang BY. Unified approach to pavement crack and sealed crack detection using preclassification based on transfer learning. Journal of Computing in Civil Engineering, 2018, 32(2): 04018001. DOI:10.1061/(ASCE)CP.1943-5487.0000736 |
| [8] |
Zou Q, Zhang Z, Li QQ, et al. Deepcrack: Learning hierarchical convolutional features for crack detection. IEEE Transactions on Image Processing, 2019, 28(3): 1498-1512. DOI:10.1109/TIP.2018.2878966 |
| [9] |
Yang F, Zhang L, Yu SJ, et al. Feature pyramid and hierarchical boosting network for pavement crack detection. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(4): 1525-1535. DOI:10.1109/TITS.2019.2910595 |
| [10] |
Dorafshan S, Thomas RJ, Maguire M. Comparison of deep convolutional neural networks and edge detectors for 33-8044-based crack detection in concrete. Construction and Building Materials, 2018, 186: 1031-1045. DOI:10.1016/j.conbuildmat.2018.08.011 |
| [11] |
Zhang KG, Zhang YT, Cheng HD. CrackGAN: Pavement crack detection using partially accurate ground truths based on generative adversarial learning. arXiv: 1909.08216, 2019.
|
| [12] |
Li HF, Song DZ, Liu Y, et al. Automatic pavement crack detection by multi-scale image fusion. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(6): 2025-2036. DOI:10.1109/TITS.2018.2856928 |
| [13] |
Yusof NAM, Ibrahim A, Noor MHM, et al. Deep convolution neural network for crack detection on asphalt pavement. Journal of Physics: Conference Series, 2019, 1349(1): 012020. |
| [14] |
Ai DH, Jiang GY, Kei LS, et al. Automatic Pixel-level pavement crack detection using information of multi-scale neighborhoods. IEEE Access, 2018, 6: 24452-24463. DOI:10.1109/ACCESS.2018.2829347 |
| [15] |
Badrinarayanan V, Handa A, Cipolla R. SegNet: A deep convolutional encoder-decoder architecture for robust semantic pixel-wise labelling. arXiv: 1505.07293, 2015.
|
| [16] |
Badrinarayanan V, Kendall A, Cipolla R. SegNet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(12): 2481-2495. DOI:10.1109/TPAMI.2016.2644615 |
| [17] |
Schmugge SJ, Rice L, Lindberg J, et al. Crack segmentation by leveraging multiple frames of varying illumination. Proceedings of 2017 IEEE Winter Conference on Applications of Computer Vision (WACV). Santa Rosa, CA, USA. 2017. 1045–1053.
|
| [18] |
Oktay O, Schlemper J, Le Folgoc L, et al. Attention U-Net: Learning where to look for the pancreas. arXiv: 1804.03999, 2018.
|
| [19] |
Lazebnik S, Schmid C, Ponce J. Beyond bags of features: Spatial pyramid matching for recognizing natural scene categories. Proceedings of 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06). New York, NY, USA. 2006. 2169–2178.
|
| [20] |
Young J. Spatial pyramid match kernels for brain image classification. Proceedings of 2016 International Workshop on Pattern Recognition in Neuroimaging (PRNI). Trento, Italy. 2016. 1–4.
|
| [21] |
Xiang XZ, Zhang YQ, El Saddik A. Pavement crack detection network based on pyramid structure and attention mechanism. IET Image Processing, 2020, 14(8): 1580-1586. DOI:10.1049/iet-ipr.2019.0973 |
| [22] |
Shi Y, Cui LM, Qi ZQ, et al. Automatic road crack detection using random structured forests. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(12): 3434-3445. DOI:10.1109/TITS.2016.2552248 |
| [23] |
Salehi SSM, Erdogmus D, Gholipour A. Tversky loss function for image segmentation using 3D fully convolutional deep networks. Proceedings of the 8th International Workshop on Machine Learning in Medical Imaging. Quebec City, QC, Canada. 2017. 379–387.
|
 2021, Vol. 30
2021, Vol. 30



